2. 天津大学化工协同创新中心, 天津 300072
2. Collaborative Innovation Center of Chemical Science of Engineering, Tianjin 300072, China
二苯甲酮是一种常见的光引发剂,广泛应用于防晒化妆品、香水、医药工业、紫外线吸收剂和光敏剂等多个方面[1-2],其结构式如图 1所示。二苯甲酮主要由苯甲酰氯与苯反应合成,传统工业上往往采用精馏操作来实现二苯甲酮的纯化分离。然而,精馏操作存在能耗高和难以得到高纯度二苯甲酮产品等问题,在使用上存在一定的局限性。目前文献对于二苯甲酮合成方法的研究较多,但是相关的结晶提纯工艺研究比较少。

|
| 图 1 二苯甲酮结构式 Fig.1 The structure of benzophenone |
| |
结晶是化学工业中最重要的分离和纯化方法之一,可以生产高纯度的产品。化工热力学数据可以为结晶过程的开发和设计提供基础数据。然而,虽然已有二苯甲酮在一些纯溶剂中的溶解度数据报道[3],但是缺乏二苯甲酮在混合溶剂中的溶解度及相应的热力学数据。此外,文献报道二苯甲酮在纯溶剂中的溶解度较大,采用冷却结晶方式产品过程收率较低;同时,采用溶析结晶产品在过程中极易产生油析现象,这种液液相分离的现象会阻碍晶体成核和生长过程[4-5]。因此,测定混合溶剂中二苯甲酮溶解度数据和热力学性质对于设计和优化结晶过程至关重要。
本研究测定了不同比例的甲醇-乙腈混合溶剂中二苯甲酮的溶解度数据。分别使用改进的Apelblat方程和λh方程对溶解度数据进行拟合,并基于NRTL模型与溶解度数据,计算溶解过程中混合和溶解热力学性质, 为开发结晶新工艺提供理论依据。
1 实验部分 1.1 实验装置与试剂本实验采用静态法测定二苯甲酮在不同比例甲醇-乙腈混合溶剂中的溶解度。
实验装置:采用如图 2中的装置进行溶解度测定。

|
| 图 2 溶解度测定的实验装置图 Fig.2 Equipment for the solubility determination |
| |
实验试剂:甲醇和乙腈(分析纯,质量分数高于99.5%),天津光复精细化工研究所,没有进行二次提纯;二苯甲酮(分析纯,质量分数高于99%),上海阿拉丁公司。
本实验中所用设备列于表 1中。
| 设备 | 型号 | 生产厂家 |
| 玻璃夹套结晶器 | 70 mL | 天津易普佳玻璃工作室 |
| 精密电子天平 | AL204-N | 梅特勒-托利多仪器(上海) 有限公司 |
| 高精度低温恒温槽 | XOGDH | 南京先欧仪器 |
| 磁力搅拌器 | 07HWS-2 | 杭州仪表电机有限公司 |
| 干燥箱 | DZF-2BC | 天津市泰斯特仪器有限公司 |
| 注射器 | 5 mL | 天津大学鹏翔采购中心 |
| 滤膜 | 0.22 μm | 天津大学鹏翔采购中心 |
| 温度计 | 精度0.1 ℃ | 天津市华兴科学仪器厂 |
按照一定的物质的量比例配制甲醇和乙腈的混合溶剂,将过量的二苯甲酮放入70 mL带夹套的玻璃结晶器中,在预定温度下连续搅拌。使用精度为(±0.1) K的恒温器将系统保持在特定温度。通过磁力搅拌(150 r/mim)将混合物保持搅拌超过10 h,以确保固液两相最终处于平衡状态。之后,将溶液保持在相同的温度下,停止搅拌并静置2 h,以确保不溶解的固体完全沉淀。然后,通过注射器取出上层澄清溶液,并通过膜过滤器进行过滤。将滤液倒入预先称质量的培养皿中,并使用精确度为(±0.000 1) g的电子天平快速称质量。然后将滤液在真空烘箱中(40 ℃下)进行干燥,并定期称质量直至完全干燥(质量变化<0.05%),所有实验重复3次,并且使用平均值来计算在相应条件下的摩尔分率溶解度。相应的溶解度计算公式如式(1)所示[6]。
| $ {x_1} = \frac{{{m_1}/{M_1}}}{{{m_1}/{M_1} + {m_2}/{M_2} + {m_3}/{M_3}}} $ | (1) |
式(1)中,x1表示溶质的摩尔分率溶解度,mol· mol-1;m表示质量,g;M表示摩尔质量,g·mol-1;下标1、2和3分别表示二苯甲酮、乙腈以及甲醇。
此外,为保证测定溶解度前后的晶型一致,对实验前后的二苯甲酮进行了XRD与DSC分析。
1.2.1 XRD测试为了确定溶解度测定前后的晶体形态,将实验前后的产品用粉末X射线衍射(Rigaku D/max-2500 (Rigaku, Japan) Cu_Kα(0.154 06 nm)测定,衍射角(2θ)的范围为2°~50°,扫描速率为0.067 (°)/s,电流为100 mA,电压为40 kV。
1.2.2 DSC测试DSC测试即使用差示扫描量热法表征样品的熔融温度和熔化焓。物质的晶格能与其熔点相关,在一定的压力条件下,可以用熔点来表征晶体晶型是否发生变化。在测试开始之前,通过使用铟和锌进行仪器校准。测试过程中,通过分析天平称质量5~10 mg的二苯甲酮样品并置于铝盘中,在氮气的保护下,通过使用空坩埚作为对照品,将样品以5 K/min的加热速率从298.15 K加热至353.15 K,实验重复3次。
1.3 溶解度模型 1.3.1 modified Apelblat equation方程改进的Apelblat equation方程[6-10]是使用最广泛的经验方程之一,该方程假定溶液的焓变是温度的线性函数,忽略了溶质的活度系数,并且认为溶液的摩尔焓随着温度的变化而变化,由Clausius-Clapeyron方程积分推导而得出,表述简单,方程如式(2)。
| $ \ln x = A + B{T^{ - 1}} + C\ln T $ | (2) |
式(2)中:x为溶解度;A,B,C为模型参数;T为绝对温度,K。此方程形式比较简单、使用方便、拟合效果好,对于各种物系溶解度均具有较好的拟合效果。
1.3.2 λh方程λh方程[11-13]也是溶解度数据拟合常用的经验方程,由Buchowski等于1980年提出。该方程不仅考虑了温度对溶解度的影响,同时考虑了分子间的缔合作用,其溶解度方程如式(3)。
| $ \ln \left[ {1 + \lambda \left( {1 - {x_2}} \right)/{x_2}} \right] = \lambda h/\left( {{T^{ - 1}} - T_{\rm{m}}^{ - 1}} \right) $ | (3) |
式(3)中:T为温度,K;Tm为熔点温度,K;h和λ为模型拟合的参数,通常通过回归实验数据得到。其中,h代表焓因子,λ是反应饱和溶液非理想性的量度,定义式分别为:
| $ \lambda = \frac{{\partial \ln \left( {1 - {\alpha _1}} \right)}}{{\partial \ln {\alpha _2}}} $ | (4) |
| $ hR = \Delta {H_{{\rm{mtl}}}} + {H^{\rm{E}}}/{x_1} $ | (5) |
式(4)中:α1和α2分别为溶剂和溶质的活度;HE为剩余焓;ΔHmt1为溶质的熔化焓;x1是饱和溶液中溶质的摩尔分率。
1.3.3 混合热力学性质混合热力学性质包括混合吉布斯自由能ΔGmix、混合熵ΔSmix和混合焓ΔHmix,混合热力学性质对非理想的二元混合过程的研究是非常必要的。在非理想溶液中,溶质的混合热力学性质是由剩余性质(ME)和理想溶液混合热力学性质(ΔMid)组成,而计算剩余性质必须用到活度系数γ。
| $ \Delta {G_{{\rm mix}}} = {G^{\rm{E}}} + \Delta {G^{{\rm{id}}}} $ | (6) |
| $ \Delta {S_{{\rm mix}}} = {S^{\rm{E}}} + \Delta {S^{{\rm{id}}}} $ | (7) |
| $ \Delta {H_{{\rm mix}}} = {H^{\rm{E}}} + \Delta {H^{{\rm{id}}}} $ | (8) |
式(6)~(8)中,ΔGmixid、ΔSmixid和ΔHmixid表示理想溶液混合性质;GE、SE和HE表示真实溶液的剩余性质。
| $ \Delta {G^{{\rm{id}}}} = RT\sum\nolimits_{j = 1}^n {{x_j}\ln {x_j}} $ | (9) |
| $ \Delta {S^{{\rm{id }}}} = \frac{{\Delta {G^{{\rm{id}}}}}}{T} $ | (10) |
| $ \Delta {H^{{\rm{id}}}} = 0 $ | (11) |
式(9)中,xj表示溶液中各组分的摩尔分数。此外对于二元混合溶剂体系而言,组分数n=3[14-15]。
| $ {G^{\rm{E}}} = RT\sum\nolimits_{j = 1}^n {{x_j}\ln {\gamma _j}} $ | (12) |
| $ {S^{\rm{E}}} = \frac{{{H^{\rm{E}}} - {G^{\rm{E}}}}}{T} $ | (13) |
| $ {H^{\rm{E}}} = - R{T^2}\sum\nolimits_{j = 1}^n {{x_j}{{\left( {\frac{{\partial \ln {\gamma _j}}}{{\partial T}}} \right)}_{{\rm{p,x}}}}} $ | (14) |
式(12)和(14)中γj代表在非理想溶液中的活度系数,可以由NRTL模型得出。
对于非理想溶液,溶质在溶剂中的溶解过程可描述为由加热、熔化、冷却及混合4个阶段组成。故二苯甲酮在溶剂中的溶解性质可通过下列公式计算得到。
| $ \Delta {M_{{\rm{dis}}}} = {x_1}\left( {\Delta {M_{{\rm{heat}}}} + \Delta {M_{{\rm{fus}}}} + \Delta {M_{{\rm{cool}}}}} \right) + \Delta {M_{{\rm{mix}}}} $ | (15) |
式(15)中,M意指吉布斯自由能(G)、焓(H)或熵(S);x1为二苯甲酮的摩尔分率溶解度;ΔMfus指的是二苯甲酮的熔化热力学性质。这里,加热和冷却过程中的热力学性质(即ΔMheat和ΔMcool)可表示为:
| $ \Delta {H_{{\rm{heat}}}} = {C_{p\left( {\rm{s}} \right)}}\left( {{T_{\rm{m}}} - T} \right) $ | (16) |
| $ \Delta {H_{{\rm{cool}}}} = {C_{p\left( {\rm{l}} \right)}}\left( {T - {T_{\rm{m}}}} \right) $ | (17) |
| $ \Delta {S_{{\rm{heat}}}} = {C_{p\left( {\rm{s}} \right)}}\ln \frac{{{T_{\rm{m}}}}}{T} $ | (18) |
| $ \Delta {S_{{\rm{cool}}}} = {C_{p\left( {\rm{l}} \right)}}\ln \frac{T}{{{T_{\rm{m}}}}} $ | (19) |
真实溶液中的溶解性质可由式(20)~(22)计算得到。
| $ \Delta {H_{{\rm{dis}}}} = \Delta {H_{{\rm{fus }}}} + \Delta {H_{{\rm{mix }}}} $ | (20) |
| $ \Delta {S_{{\rm{dis}}}} = {x_1}\Delta {S_{{\rm{fus }}}} + \Delta {S_{{\rm{mix }}}} $ | (21) |
| $ \Delta {G_{{\rm{dis }}}} = {x_1}\Delta {H_{{\rm{dis }}}} - T\Delta {S_{{\rm{mix}}}} $ | (22) |
二苯甲酮的原料和溶解度实验测试后的XRD和DSC曲线保持一致,如图 3和图 4所示。结果表明实验过程中二苯甲酮的晶型未发生改变,没有生成新的晶型。
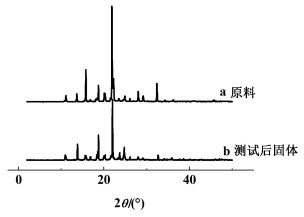
|
| 图 3 溶解度测试前后二苯甲酮的粉末X射线衍射图谱 Fig.3 X-ray power diffraction pattern patterns of benzophenone |
| |

|
| 图 4 测试前后二苯甲酮的热分析图谱 Fig.4 Thermal analysis (DSC) curve of benzophenone |
| |
实验测定了常压下278.15~313.15 K温度范围内,二苯甲酮在甲醇-乙腈混合溶剂中的溶解度,结果列于表 2并通过图 5直观表示。结果表明,当混合溶剂组成一定时,随着温度的升高,二苯甲酮在混合溶剂中的溶解度逐渐增加;此外,温度一定的条件下,随着混合溶剂比例的变化出现了潜溶现象,最大值位于0.2~0.4之间。因此,二苯甲酮的溶解度不仅受温度的影响而且也受溶剂组成的影响。
| x2 | x1exp | |||||||
| 278.15 K | 283.15 K | 288.15 K | 293.15 K | 298.15 K | 303.15 K | 308.15 K | 313.15 K | |
| 0 | 2.72e-2 | 3.62e-2 | 4.84e-2 | 6.48e-2 | 8.92e-2 | 0.125 | 0.179 | 0.302 |
| 0.100 | 0.124 | 0.136 | 0.154 | 0.177 | 0.212 | 0.252 | 0.311 | 0.426 |
| 0.200 | 0.201 | 0.218 | 0.239 | 0.278 | 0.305 | 0.357 | 0.432 | 0.551 |
| 0.300 | 0.251 | 0.274 | 0.306 | 0.338 | 0.383 | 0.442 | 0.539 | 0.643 |
| 0.400 | 0.289 | 0.306 | 0.349 | 0.396 | 0.457 | 0.527 | 0.596 | 0.719 |
| 0.500 | 0.292 | 0.334 | 0.386 | 0.446 | 0.502 | 0.580 | 0.636 | 0.731 |
| 0.600 | 0.310 | 0.355 | 0.435 | 0.493 | 0.536 | 0.620 | 0.673 | 0.750 |
| 0.700 | 0.330 | 0.369 | 0.431 | 0.481 | 0.531 | 0.627 | 0.678 | 0.771 |
| 0.800 | 0.369 | 0.400 | 0.436 | 0.479 | 0.530 | 0.592 | 0.667 | 0.773 |
| 0.900 | 0.353 | 0.387 | 0.420 | 0.456 | 0.519 | 0.566 | 0.646 | 0.752 |
| 1.000 | 0.307 | 0.338 | 0.384 | 0.418 | 0.471 | 0.537 | 0.624 | 0.732 |

|
| 图 5 二苯甲酮在甲醇-乙腈混合溶剂中的溶解度数据3D图(278.15~313.15 K) Fig.5 3D-Diagrams of mole fraction solubility system of benzophenone in methanol-acetonitrile (278.15~313.15 K) |
| |
使用Matlab软件应用Apelblat方程和λh方程对二苯甲酮在甲醇-乙腈混合溶剂中的溶解度进行了进一步的关联。DSC测定得二苯甲酮的熔点为320.92 K。关联得到模型参数A,B,C和参数λ、h以及相对应的ARD和RMSD值。相应结果列于表 3~表 6中。
| x2 | x1 | |||||||
| 278.15 K | 283.15 K | 288.15 K | 293.15 K | 298.15 K | 303.15 K | 308.15 K | 313.15 K | |
| 0 | 2.80e-2 | 3.56e-2 | 4.70e-2 | 6.38e-2 | 8.93e-2 | 0.128 | 0.189 | 0.285 |
| 0.100 | 0.125 | 0.135 | 0.152 | 0.176 | 0.209 | 0.256 | 0.322 | 0.414 |
| 0.200 | 0.203 | 0.217 | 0.238 | 0.268 | 0.309 | 0.365 | 0.439 | 0.538 |
| 0.300 | 0.253 | 0.273 | 0.300 | 0.337 | 0.386 | 0.450 | 0.533 | 0.642 |
| 0.400 | 0.284 | 0.313 | 0.350 | 0.395 | 0.452 | 0.521 | 0.608 | 0.715 |
| 0.500 | 0.290 | 0.336 | 0.387 | 0.443 | 0.505 | 0.572 | 0.646 | 0.726 |
| 0.600 | 0.309 | 0.364 | 0.423 | 0.485 | 0.550 | 0.615 | 0.680 | 0.745 |
| 0.700 | 0.328 | 0.374 | 0.424 | 0.480 | 0.542 | 0.611 | 0.686 | 0.769 |
| 0.800 | 0.370 | 0.399 | 0.434 | 0.477 | 0.530 | 0.595 | 0.673 | 0.767 |
| 0.900 | 0.356 | 0.383 | 0.418 | 0.460 | 0.512 | 0.575 | 0.652 | 0.745 |
| 1.000 | 0.309 | 0.338 | 0.375 | 0.419 | 0.475 | 0.542 | 0.625 | 0.727 |
| x2 | x1 | |||||||
| 278.15 K | 283.15 K | 288.15 K | 293.15 K | 298.15 K | 303.15 K | 308.15 K | 313.15 K | |
| 0 | 2.62e-2 | 3.52e-2 | 4.73e-2 | 6.43e-2 | 8.86e-2 | 0.126 | 0.186 | 0.298 |
| 0.100 | 0.125 | 0.138 | 0.155 | 0.177 | 0.206 | 0.249 | 0.314 | 0.428 |
| 0.200 | 0.202 | 0.220 | 0.242 | 0.270 | 0.307 | 0.358 | 0.432 | 0.552 |
| 0.300 | 0.250 | 0.274 | 0.303 | 0.340 | 0.386 | 0.446 | 0.529 | 0.648 |
| 0.400 | 0.283 | 0.315 | 0.352 | 0.396 | 0.451 | 0.518 | 0.605 | 0.720 |
| 0.500 | 0.306 | 0.342 | 0.383 | 0.432 | 0.490 | 0.560 | 0.647 | 0.757 |
| 0.600 | 0.332 | 0.371 | 0.416 | 0.468 | 0.529 | 0.600 | 0.685 | 0.788 |
| 0.700 | 0.338 | 0.377 | 0.422 | 0.473 | 0.533 | 0.604 | 0.688 | 0.790 |
| 0.800 | 0.369 | 0.400 | 0.436 | 0.478 | 0.529 | 0.592 | 0.670 | 0.771 |
| 0.900 | 0.357 | 0.385 | 0.419 | 0.460 | 0.509 | 0.570 | 0.649 | 0.752 |
| 1.000 | 0.312 | 0.342 | 0.377 | 0.418 | 0.468 | 0.533 | 0.621 | 0.733 |
| x2 | modified Apelblat equation | ||||
| A | 10-3B | C | 102ARD | 103RMSD | |
| 0 | -902.182 | 34.765 | 137.455 | 2.855 | 7.042 |
| 0.100 | -785.213 | 32.027 | 118.687 | 1.564 | 6.118 |
| 0.200 | -640.542 | 26.137 | 96.831 | 1.659 | 7.158 |
| 0.300 | -527.000 | 21.233 | 79.829 | 0.931 | 4.372 |
| 0.400 | -350.370 | 13.462 | 53.430 | 1.159 | 6.062 |
| 0.500 | 15.833 | -2.672 | -1.326 | 0.737 | 4.910 |
| 0.600 | 198.004 | -10.629 | -28.601 | 1.559 | 8.338 |
| 0.700 | -29.901 | -0.514 | 5.443 | 1.182 | 8.207 |
| 0.800 | -300.589 | 11.688 | 45.766 | 0.439 | 3.150 |
| 0.900 | -310.366 | 12.097 | 47.234 | 1.011 | 5.727 |
| 1.000 | -327.690 | 12.611 | 49.959 | 0.775 | 4.498 |
| x2 | λh equation | |||
| 10-3λ | 103h | 102ARD | 103RMSD | |
| 0 | 151.304 | 26.052 | 1.905 | 2.807 |
| 0.100 | -48.727 | 17.889 | 1.101 | 2.776 |
| 0.200 | -117.323 | 11.048 | 0.814 | 3.366 |
| 0.300 | -81.467 | 7.171 | 0.743 | 4.692 |
| 0.400 | 49.523 | 4.976 | 1.302 | 6.322 |
| 0.500 | 156.359 | 4.054 | 2.803 | 15.070 |
| 0.600 | 268.821 | 3.360 | 4.038 | 21.600 |
| 0.700 | 253.441 | 3.322 | 2.058 | 12.730 |
| 0.800 | -98.083 | 3.909 | 0.127 | 1.290 |
| 0.900 | -144.528 | 4.365 | 0.698 | 4.452 |
| 1.000 | -9.896 | 4.717 | 0.559 | 3.002 |
由表 5和表 6知,2种方程均能较好地关联二苯甲酮在甲醇-乙腈中的溶解度。ARD的最大值均小于5%,λ值表示溶液非理想性的量度,从表 6可以看出甲醇-乙腈混合溶剂的λ值均偏离1,说明其为非理想溶液。此外,对比2种模型的偏差结果,Apelblat方程的拟合效果优于λh方程。
2.4 混合热力学性质二苯甲酮的混合和溶解过程的热力学性质计算结果列于表 7。从表 7中可以看出二苯甲酮在甲醇-乙腈溶剂中的混合熵ΔSmix和混合焓ΔHmix均为正值,混合吉布斯自由能ΔGmix为负值,说明二苯甲酮的混合过程是自发、吸热且熵驱动的过程。同时,二苯甲酮的溶解性质也满足类似规律,即ΔSdis>0、ΔHdis>0且ΔGdis < 0,这表明二苯甲酮的溶解过程也是自发的,吸热的且熵驱动的过程。溶解和混合焓均大于0,验证了二苯甲酮的溶解度应随温度上升而上升。
| T/K | x2 | ΔGmix/ (kJ·mol-1) |
ΔSmix/ (kJ·K-1·mol-1) |
103ΔHmix/ (kJ·mol-1) |
ΔGdis/ (kJ·mol-1) |
ΔSdis/ (kJ·K-1·mol-1) |
102ΔHdis/ (kJ·mol-1) |
| 278.15 | 0.100 | -9.777 | 14.928 | 4.143 | -9.511 | 14.934 | 4.145 |
| 0.200 | -10.915 | 13.229 | 3.669 | -10.482 | 13.239 | 3.672 | |
| 0.300 | -11.146 | 11.647 | 3.229 | -10.606 | 11.660 | 3.233 | |
| 0.400 | -11.089 | 10.467 | 2.900 | -10.468 | 10.482 | 2.905 | |
| 0.500 | -11.251 | 9.938 | 2.753 | -10.623 | 9.953 | 2.758 | |
| 0.600 | -11.063 | 9.388 | 2.600 | -10.395 | 9.403 | 2.605 | |
| 0.700 | -10.746 | 8.994 | 2.491 | -10.037 | 9.010 | 2.496 | |
| 0.800 | -10.042 | 8.559 | 2.371 | -9.249 | 8.577 | 2.377 | |
| 0.900 | -9.776 | 9.538 | 2.643 | -9.016 | 9.556 | 2.649 | |
| 283.15 | 0.100 | -9.569 | 14.683 | 4.148 | -9.310 | 14.690 | 4.150 |
| 0.200 | -10.682 | 13.043 | 3.683 | -10.266 | 13.054 | 3.686 | |
| 0.300 | -10.856 | 11.403 | 3.218 | -10.335 | 11.417 | 3.222 | |
| 0.400 | -10.886 | 10.286 | 2.902 | -10.305 | 10.302 | 2.907 | |
| 0.500 | -10.729 | 9.428 | 2.659 | -10.094 | 9.445 | 2.664 | |
| 0.600 | -10.514 | 8.833 | 2.491 | -9.841 | 8.851 | 2.496 | |
| 0.700 | -10.261 | 8.492 | 2.394 | -9.560 | 8.510 | 2.400 | |
| 0.800 | -9.664 | 8.180 | 2.306 | -8.904 | 8.200 | 2.313 | |
| 0.900 | -9.358 | 9.154 | 2.583 | -8.622 | 9.174 | 2.589 | |
| 288.15 | 0.100 | -9.312 | 14.385 | 4.136 | -9.059 | 14.393 | 4.138 |
| 0.200 | -10.413 | 12.822 | 3.684 | -10.019 | 12.834 | 3.688 | |
| 0.300 | -10.459 | 11.063 | 3.177 | -9.955 | 11.079 | 3.182 | |
| 0.400 | -10.328 | 9.780 | 2.808 | -9.752 | 9.797 | 2.813 | |
| 0.500 | -10.044 | 8.784 | 2.521 | -9.407 | 8.803 | 2.527 | |
| 0.600 | -9.452 | 7.817 | 2.243 | -8.736 | 7.839 | 2.250 | |
| 0.700 | -9.461 | 7.701 | 2.210 | -8.751 | 7.723 | 2.217 | |
| 0.800 | -9.206 | 7.733 | 2.219 | -8.487 | 7.755 | 2.226 | |
| 0.900 | -8.953 | 8.801 | 2.527 | -8.261 | 8.822 | 2.534 | |
| 293.15 | 0.100 | -9.011 | 14.040 | 4.107 | -8.764 | 14.049 | 4.110 |
| 0.200 | -9.922 | 12.397 | 3.624 | -9.534 | 12.411 | 3.629 | |
| 0.300 | -10.044 | 10.711 | 3.130 | -9.572 | 10.728 | 3.135 | |
| 0.400 | -9.705 | 9.229 | 2.696 | -9.151 | 9.249 | 2.702 | |
| 0.500 | -9.232 | 8.050 | 2.351 | -8.608 | 8.072 | 2.358 | |
| 0.600 | -8.647 | 7.085 | 2.068 | -7.958 | 7.110 | 2.076 | |
| 0.700 | -8.784 | 7.063 | 2.062 | -8.112 | 7.087 | 2.069 | |
| 0.800 | -8.644 | 7.201 | 2.102 | -7.975 | 7.225 | 2.110 | |
| 0.900 | -8.487 | 8.393 | 2.452 | -7.850 | 8.416 | 2.459 | |
| 298.15 | 0.100 | -8.598 | 13.588 | 4.043 | -8.355 | 13.599 | 4.046 |
| 0.200 | -9.571 | 12.093 | 3.596 | -9.221 | 12.108 | 3.601 | |
| 0.300 | -9.451 | 10.205 | 3.033 | -9.013 | 10.224 | 3.039 | |
| 0.400 | -8.866 | 8.503 | 2.526 | -8.342 | 8.526 | 2.534 | |
| 0.500 | -8.448 | 7.368 | 2.188 | -7.873 | 7.393 | 2.196 | |
| 0.600 | -8.029 | 6.546 | 1.944 | -7.414 | 6.573 | 1.952 | |
| 0.700 | -8.085 | 6.433 | 1.910 | -7.477 | 6.460 | 1.919 | |
| 0.800 | -7.942 | 6.561 | 1.948 | -7.335 | 6.588 | 1.957 | |
| 0.900 | -7.648 | 7.616 | 2.263 | -7.052 | 7.642 | 2.271 | |
| 303.15 | 0.100 | -8.142 | 13.086 | 3.959 | -7.917 | 13.099 | 3.963 |
| 0.200 | -8.920 | 11.519 | 3.483 | -8.601 | 11.537 | 3.489 | |
| 0.300 | -8.648 | 9.519 | 2.877 | -8.253 | 9.541 | 2.884 | |
| 0.400 | -7.871 | 7.664 | 2.315 | -7.400 | 7.690 | 2.324 | |
| 0.500 | -7.301 | 6.407 | 1.935 | -6.783 | 6.436 | 1.944 | |
| 0.600 | -6.766 | 5.496 | 1.659 | -6.212 | 5.527 | 1.669 | |
| 0.700 | -6.646 | 5.214 | 1.574 | -6.085 | 5.246 | 1.584 | |
| 0.800 | -7.043 | 5.783 | 1.746 | -6.514 | 5.813 | 1.756 | |
| 0.900 | -6.996 | 7.070 | 2.136 | -6.490 | 7.099 | 2.146 | |
| 308.15 | 0.100 | -7.492 | 12.385 | 3.809 | -7.292 | 12.401 | 3.814 |
| 0.200 | -7.954 | 10.649 | 3.273 | -7.677 | 10.670 | 3.280 | |
| 0.300 | -7.275 | 8.338 | 2.562 | -6.928 | 8.365 | 2.571 | |
| 0.400 | -6.837 | 6.807 | 2.091 | -6.454 | 6.837 | 2.101 | |
| 0.500 | -6.430 | 5.706 | 1.752 | -6.021 | 5.738 | 1.762 | |
| 0.600 | -5.933 | 4.844 | 1.487 | -5.500 | 4.878 | 1.498 | |
| 0.700 | -5.859 | 4.604 | 1.413 | -5.424 | 4.638 | 1.424 | |
| 0.800 | -5.914 | 4.871 | 1.495 | -5.485 | 4.905 | 1.506 | |
| 0.900 | -5.849 | 6.096 | 1.873 | -5.434 | 6.129 | 1.883 | |
| 313.15 | 0.100 | -6.272 | 11.037 | 3.450 | -6.105 | 11.059 | 3.457 |
| 0.200 | -6.362 | 9.131 | 2.853 | -6.146 | 9.159 | 2.862 | |
| 0.300 | -5.737 | 6.977 | 2.179 | -5.485 | 7.009 | 2.189 | |
| 0.400 | -4.900 | 5.199 | 1.623 | -4.619 | 5.235 | 1.635 | |
| 0.500 | -4.901 | 4.508 | 1.407 | -4.615 | 4.545 | 1.419 | |
| 0.600 | -4.667 | 3.903 | 1.218 | -4.374 | 3.941 | 1.230 | |
| 0.700 | -4.318 | 3.489 | 1.088 | -4.016 | 3.528 | 1.101 | |
| 0.800 | -4.204 | 3.624 | 1.131 | -3.902 | 3.663 | 1.143 | |
| 0.900 | -4.221 | 4.792 | 1.496 | -3.927 | 4.830 | 1.509 |
本研究采用静态法测定了二苯甲酮在甲醇-乙腈中的溶解度。结果表明,在特定溶剂组成下,二苯甲酮溶解度随温度的升高而逐渐增大。在相同温度下,二苯甲酮的溶解度随乙腈的摩尔分数先增大后减小。此外,本研究采用了修正的Apelblat方程和λh方程对二苯甲酮在甲醇-乙腈溶解度进行了关联,模型预测效果较好。最后,本研究基于修正的NRTL方程计算了二苯甲酮在甲醇-乙腈中的混合与溶解过程的焓、熵和吉布斯自由能。结果表明,二苯甲酮的混合和溶解过程均是自发的,吸热的且熵驱动的过程。以上二苯甲酮溶解度的测定与关联结果能够为其结晶工艺的开发提供重要理论依据。
| [1] |
Zhang Z, Ren N, Li Y, et al. Determination of benzotriazole and benzophenone UV filters in sediment and sewage sludge[J]. Environmental Science & Technology, 2011, 45(9): 3909-3916. |
| [2] |
Xue J, Liu W, Kannan K. Bisphenols, benzophenones, and bisphenol-A diglycidyl ethers in textiles and infant clothing[J]. Environmental Science & Technology, 2017, 51(9): 5279-5286. |
| [3] |
Ouyang J B, Na B, Xiong G, et al. Corrigendum to Determination of solubility and thermodynamic properties of benzophenone in different pure solvents[J]. Journal of Chemical & Engineering Data, 2018, 63(5): 1833-1840. |
| [4] |
Yang H, Rasmuson A C. Investigation of batch cooling crystallization in a liquid-liquid separating system by PAT[J]. Organic Process Research & Development, 2012, 16(6): 1212-1224. |
| [5] |
Wang G, Wang Y, Hu X, et al. Determination and correlation of cefoperazone solubility in different pure solvents and binary mixture[J]. Fluid Phase Equilibria, 2014, 361: 223-228. DOI:10.1016/j.fluid.2013.11.005 |
| [6] |
沈致名, 谢闯, 杜威, 等. 布洛芬-烟酰胺共晶制备及其溶解度测定[J]. 化学工业与工程, 2014, 31(1): 38-42. Shen Zhiming, Xie Chuang, Du Wei, et al. Preparation of ibuprofen-nicotinamide cocrystal and its solubility measurement[J]. Chemical Industry and Engineering, 2014, 31(1): 38-42. DOI:10.3969/j.issn.1006-7906.2014.01.009 (in Chinese) |
| [7] |
姜波, 李弥异, 王利生. LiBr在丙酮与水的混合溶剂中溶解度的测定与关联[J]. 化学工业与工程, 2012, 29(5): 23-27, 52. Jiang Bo, Li Miyi, Wang Lisheng. Measurement and correlation of solubility of LiBr in acetone-water mixed solvent[J]. Chemical Industry and Engineering, 2012, 29(5): 23-27, 52. DOI:10.3969/j.issn.1006-7906.2012.05.006 (in Chinese) |
| [8] |
Li J, Hao H, Guo N, et al. Solubility and thermodynamic properties of maltol in different pure solvents[J]. Journal of Molecular Liquids, 2017, 243: 313-323. DOI:10.1016/j.molliq.2017.08.054 |
| [9] |
岳金彩, 朱南南, 刘先红, 等. 对叔丁基苯酚在盐水中溶解度的测定及关联[J]. 化学工业与工程, 2014, 31(1): 33-37. Yue Jincai, Zhu Nannan, Liu Xianhong, et al. Measurement and correlation of the solubility of 4-tert-butylphenol in NaCl solution[J]. Chemical Industry and Engineering, 2014, 31(1): 33-37. (in Chinese) |
| [10] |
Lou Y, Wang Y, Li Y, et al. Thermodynamic equilibrium and cosolvency of florfenicol in binary solvent system[J]. Journal of Molecular Liquids, 2018, 251: 83-91. DOI:10.1016/j.molliq.2017.12.046 |
| [11] |
王海蓉, 张春桃, 梁文懂. 赤藓糖醇在水中的结晶热力学及结晶过程研究[J]. 化学工业与工程, 2018, 35(3): 50-54. Wang Hairong, Zhang Chuntao, Liang Wendong. Crystallization thermodynamics and its crystallization process of meso-erythritol in water[J]. Chemical Industry and Engineering, 2018, 35(3): 50-54. (in Chinese) |
| [12] |
Buchowski H, Ksiazczak A, Pietrzyk S. Solvent activity along a saturation line and solubility of hydrogen-bonding solids[J]. The Journal of Physical Chemistry, 1980, 84(9): 975-979. DOI:10.1021/j100446a008 |
| [13] |
Wang G, Wang Y, Ma Y, et al. Determination and correlation of cefuroxime acid solubility in (acetonitrile+water) mixtures[J]. The Journal of Chemical Thermodynamics, 2014, 77: 144-150. DOI:10.1016/j.jct.2014.05.018 |
| [14] |
马沛生, 常贺英, 夏淑倩, 等. 化工热力学[M]. 北京: 高等教育出版社, 2005.
|
| [15] |
Wang Y, Yin Q, Sun X, et al. Measurement and correlation of solubility of thiourea in two solvent mixtures from T=(283.15 to 313.15)K[J]. The Journal of Chemical Thermodynamics, 2016, 94: 110-118. DOI:10.1016/j.jct.2015.11.004 |
 2019, Vol. 36
2019, Vol. 36





