化学工业与工程  2019, Vol. 36 Issue (5): 70-79
   Abstract               PDF                Figures                Tables
引用本文 0
段明德, 盛青志, 张壮雅, 杨保旭, 刘静波. 胀接压力与初始间隙对换热器胀接质量的影响[J]. 化学工业与工程, 2019, 36(5): 70-79.
Duan Mingde, Sheng Qingzhi, Zhang Zhuangya, Yang Baoxu, Liu Jingbo. Effect of Expansion Pressure and Initial Clearance on Expansion Joint Quality of Heat Exchanger[J]. Chemical Industry and Engineering, 2019, 36(5): 70-79.
胀接压力与初始间隙对换热器胀接质量的影响
段明德 , 盛青志 , 张壮雅 , 杨保旭 , 刘静波     
河南科技大学机电工程学院, 河南 洛阳 471003
收稿日期: 2018-05-03
作者简介: 段明德(1966-), 男, 博士, 教授, 现从事化工结构数值模拟的研究.
通信作者: 盛青志, E-mail:shengqz0826@163.com.
摘要：为研究换热管-管板胀接压力与初始间隙对换热器胀接质量的影响，采用胀接参数化模拟研究方法对液压胀接进行可靠性研究，建立换热管-管板胀接的弹塑性参数化几何模型，对不同的换热管-管板胀接压力和初始间隙进行研究，得到换热管残余等效应力、残余接触应力大小及分布规律。研究表明：胀接压力相同、间隙不同时，卸载后残余等效应力和残余接触应力值差别较小；初始间隙相同，胀接压力不同时，卸载后残余应力和残余接触应力值差别较大；换热管的残余等效应力和残余接触应力随着胀接压力的增大而增大，其变化趋势一致；当材料为Ti31钛合金、胀接压力为183 MPa时换热管与管板的初始间隙消除。研究结果为换热器最佳胀接性能优化及胀接质量的提高提供了依据。
关键词：换热器    胀接压力    初始间隙    残余接触应力    胀接质量    
Effect of Expansion Pressure and Initial Clearance on Expansion Joint Quality of Heat Exchanger
Duan Mingde , Sheng Qingzhi , Zhang Zhuangya , Yang Baoxu , Liu Jingbo     
College of Mechanical and Electrical Engineering, Henan University of Science and Technology, Henan Luoyang 471003, China
Abstract: In order to study the effects of heat transfer tube-tube plate expansion pressure and initial gap on heat exchanger expansion quality, the reliability of the hydraulic expansion joint was studied by the method of expansion parameterized simulation, and the elasto-plastic parameterized geometric model of heat exchange tube-tube plate expansion joint was established, and different expansion joint pressure and initial clearance of heat exchange tube-tube plate were performed. The residual equivalent stress, residual contact stress and distribution law of heat transfer tubes were obtained. The results show that when the expansion joint pressure is the same and the gap is different, the different of residual equivalent stress and residual contact stress value after unloading are smaller; When the initial gap is the same and the expansion pressure is different, residual stress and residual contact stress after unloading are quite different. The residual contact stress on the outer surface of the heat exchange tube increases with the increase of expansion joint pressure, and the residual equivalent stress also increases with the increase of the expansion joint force, and the change trend is consistent. When the material is Ti31 titanium alloy and the expansion pressure is 183 MPa, the initial clearance between heat exchanger tube and tube sheet is eliminated. The results provide the basis for optimizing the optimal expansion joint performance of heat exchangers and improving the quality of expansion joints.
Keywords: heat exchanger    expansion pressure    initial gap    residual contact stress    expansion quality    

换热器是一种将热流体的热能传递给冷流体的装置，在工业、化学、能源及其他很多领域中占有重要地位。换热管和管板的连接方式对换热器的质量有很大影响，常用的有焊接、胀接和胀焊结合，其中胀接又包括机械胀接、液压胀接及爆炸胀接等[1-3]。液压胀接过程对换热管及管板没有机械损伤，施载压力大小和胀接长度能自由调节，胀接步骤简单，得到广泛的应用[4-6]。胀接阶段随着施加载荷的作用换热管开始发生变形，直到换热管和管板孔相互贴合，继续增大胀接压力，管板也会发生弹性或者塑性变形，胀接压力卸载以后，换热管和管板发生不完全弹性回弹，这一阶段换热管和管板孔始终因残余接触应力而贴合，满足胀接结果所需要的密封要求和抗拉要求。因此，换热管的残余接触应力对胀接结果的好坏有较大的影响[7-8]。

针对换热器胀接后，换热管-管板的残余接触应力较小以及胀接压力过大时出现换热管胀裂的问题，目前国内外学者进行了比较深入的研究，Bouzid等[9]建立了一个解析模型来预测液压胀接接头的残余接触压力，并对有限元结果进行比较。Merah等[10-11]用二维有限元的方法研究了换热管伸出长度、初始间隙对胀接的影响。倪鹏等12]通过蒸汽发生器液压胀管的数值模拟研究，得出残余接触应力随施载的增大而增大。这些研究主要是针对普通的换热管和管板，且主要用简化的力学解析法和简单的二维有限元法进行研究。Akisanya等[13]利用弹塑性理论建立胀接模型，得到液压胀接压力、换热管的几何尺寸与胀接后的残余接触应力的关系；Merah等[14]建立了三维有限元模型模拟热交换器管子胀接过程，考察了接头材料和胀接间隙对径向位移和应力分布的影响。闫宗宝等[15]用三维有限元法对不同胀接压力下的胀接及拉脱力学行为进行了数值模拟。王相兵等[16]建立胀接成形过程有限元仿真模型，分析了不同规格胀头下，胀接成形过程中应力变化及分布；倪鹏等[17]针对蒸汽发生器液压胀接进行了胀接试验及拉脱力试验。于洪杰等[18]通过换热管和管板表面残余接触应力的结果，得到残余接触应力的密封。李涛等[19]通过ASME工程材料曲线对胀接进行模拟计算，模拟了换热管贴胀过程。

现有的文献对换热管和管板胀接已经有了比较深入的研究，但胀接压力和初始间隙对换热管-管板胀接质量进行联合仿真研究得较少，有待进一步完善。基于此，本研究采用胀接参数化模拟研究方法对液压胀接进行可靠性研究，建立换热管-管板胀接的弹塑性参数化几何模型，基于ABAQUS软件研究换热管-管板不同的胀接压力和初始间隙对胀接质量的影响。

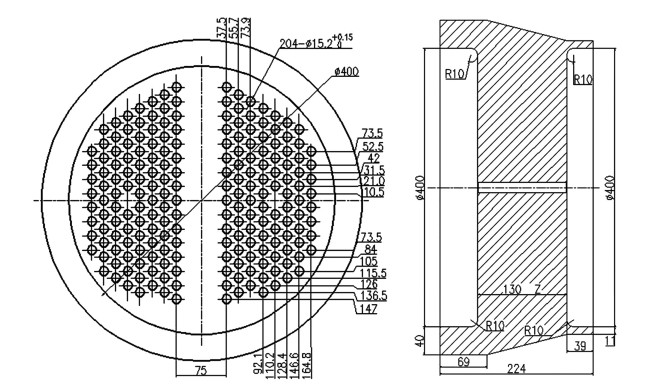
1 换热器管板结构

本研究研究换热器的胀接质量，故只需考虑换热管和管板的几何结构，如图 1所示，换热器管板孔和换热管共有204个，其中换热管的内直径D1为12.5 mm，换热管的外直径D2为15.0 mm，管板的厚度为130 mm，管板孔内的直径D3为15.2 mm，换热管的总长度为1 000 mm。在实际胀接过程中，端部焊接容易出现焊接应力集中等问题，为避免这一问题，施载位置从接近管板封端15 mm处开始，到远离管板封端15 mm处终止，防止出现端部焊接应力集中。

图 1 管板二维模型结构 Fig.1 Tube plate two-dimensional model structure
图选项
2 液压胀接过程的力学分析

假设换热管和管板为标准的塑性变形材料，胀接过程符合VonMises准则。其理论分析分为3个阶段，第1阶段：在换热管的内表面需要胀接的位置施加载荷，随着压力的增大换热管开始发生形变，换热管外表面和管板内孔开始贴合；第2阶段：持续增加胀接压力，换热管受到足够大的压力而促使换热管和管板同时发生形变，管板内壁部分或者完全发生塑性变形；第3阶段：当胀接压力加载到最大胀接压力后，保压一段时间并开始卸载，换热管和管板发生不完全弹性回复。

换热管恰好产生塑性变形时的施载：

$ p_{\mathrm{i}}=\frac{2}{\sqrt{3}} \sigma_{\mathrm{st}} \ln K_{\mathrm{t}} $ (1)

管板开始变形阶段的施载：

$ {p_{\rm{t}}} = \frac{2}{{\sqrt 3 }}{\sigma _{{\rm{st}}}}\ln {K_{\rm{i}}} + \frac{{{\sigma _{{\rm{ss}}}}}}{{\sqrt 3 }}\left( {1 - \frac{{R_{\rm{c}}^2}}{{R_{\rm{o}}^2}} + 2\ln \frac{{{R_{\rm{c}}}}}{{{R_{\rm{i}}}}}} \right) $ (2)

换热管和管板恰好贴合时的施载：

$ {p_{{\rm{imin }}}} = \frac{{\frac{2}{{\sqrt 3 }}{\sigma _{{\rm{st }}}}\ln {K_{\rm{t}}}}}{{(1 - 2c)}} $ (3)

管板孔内表面恰好发生塑性变形时的施载：

$ {p_{{\rm{isy}}}} = \frac{2}{{\sqrt 3 }}{\sigma _{{\rm{st}}}}\ln {K_{\rm{t}}} + \frac{{{\sigma _{{\rm{ss}}}}}}{{\sqrt 3 }}\left( {1 - \frac{1}{{K_{\rm{s}}^2}}} \right) $ (4)

管板孔外表面开始发生塑性变形时的施载：

$ {p_{{\rm{imax }}}} = \frac{2}{{\sqrt 3 }}{\sigma _{{\rm{st }}}}\ln {K_{\rm{t}}} + \frac{2}{{\sqrt 3 }}{\sigma _{{\rm{ss}}}}{K_{\rm{s}}} $ (5)

贴胀的胀接压力范围为：

$ {p_{{\rm{imin }}}} < {p_{\rm{i}}} \le {p_{{\rm{isy }}}} $ (6)

强度胀的胀接压力范围为：

$ {p_{{\rm{isy }}}} \le {p_{\rm{i}}} \le {p_{{\rm{imax }}}} $ (7)

式(6)和式(7)中：pi为胀接压力，MPa；Rc为屈服界面半径，mm；Ri为管板孔内半径；Ro为管板外半径；σss为管板材料的屈服强度，MPa；σst为管子的屈服强度，MPa；Kt和Ks分别为管子和管板的外内半径比。

胀接阶段，施载过小，换热管和管板发生弹性变形或不完全弹性变形，卸载后换热管和管板回弹，残余接触应力较小，达不到换热器的抗拉和密封要求；施载过大，超过材料的屈服极限，换热管和管板发生塑性变形，甚至会出现管材胀裂破坏。

3 液压胀接数值模拟

换热管和管板液压胀接过程为标准的弹塑性形变过程，材料所用的应力-应变曲线是由拉伸试验得到，具有高度非线性特征。基于ABAQUS软件模拟复杂的非线性问题，可以不断调节各项参数来保证在模拟过程中可以得到有效的准确解。

3.1 几何模型的建立

对换热器进行胀接压力和初始间隙进行研究时，换热管和管板的胀接过程近似为换热管内壁受载产生应力和变形过程，根据圣维南原理对模型非重要研究位置进行局部细小改动，减少计算机运算量，加快计算速度，且采用简化几何模型的计算结果与完整几何模型计算结果进行对比，结果没有产生太大变化。故对管板的参数化几何模型进行相应的局部简化进行模拟。

3.2 材料选取

充分考虑几何模型材料力学性能，换热器各部件材料力学性能参数如表 1所示。

表 1 换热器各部件材料力学性能参数 Table 1 Heat exchanger parts material mechanical properties parameters
部件 E/GPa μ ρ/(kg·m-3) Rp/MPa Rm/MPa
管板 108 0.34 4 500 ≥490 ≥590
换热管 108 0.34 4 500 ≥490 ≥635
表选项

材料的应变是由弹性应变和塑性应变构成，设置材料的塑性力学指标时，需将应变中的弹性范围应变去掉，只考虑材料的塑性应变：

$ \varepsilon_{\mathrm{P} 1}=\left|\varepsilon_{\text {true }}\right|-\left|\varepsilon_{\text {el }}\right| $ (8)

式(8)中，εtrue为真实应变；εP1为塑性应变；εe1为弹性应变。

胀接过程中，换热管发生弹塑性变形，Ti31材料的真实应力-应变曲线如图 3所示。

图 3 钛合金Ti31的真实应力-应变曲线 Fig.3 True stress-strain curve of titanium alloy Ti31
图选项
3.3 约束、边界条件及载荷的施加

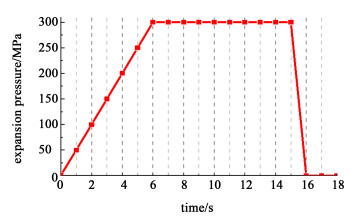
模拟实际工况, 施加载荷，0~6 s为升压阶段，胀接压力从0 MPa上升为最大压力值p，保压阶段为6~15 s，保压后卸载，p值减小到0 MPa。压力施加过程如图 4所示。

图 4 胀接压力施加过程 Fig.4 Expansion pressure application process
图选项

以换热管和管板的实际胀接工况为依据设定边界条件，换热管结构为对称结构，因此采用对称边界条件，在边界轴向位移为0，管板孔内表面、换热管外表面为自由表面，管板外侧表面在实际工况中限制位移约束，故对管板外表面施加轴向位移约束和法向位移约束。

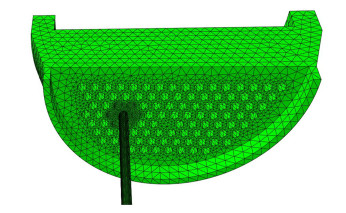
3.4 换热器几何模型网格划分

换热器在胀接过程中，管板与换热管接触部分具有较高的精度要求，而换热器的其他部分则不需要过高的精度要求。基于此，在管板与换热管接触部分采用密度较大的网格，而其他部位采用较为稀疏的网格，这样既可以保证精度，又可以加快计算速度。因管壳式换热器结构如图 2所示，属于上下对称结构，左右结构不对称，故在数值模拟过程中采用1/2对称模型进行计算。胀接模型网格划分如图 5所示。

图 2 换热器管板简化几何模型 Fig.2 Simplified geometric model of heat exchanger tube plate
图选项
图 5 胀接模型网格划分 Fig.5 Expanding model mesh
图选项
3.5 模型验证

运用ABAQUS/Standard分析求解器，使用隐式求解方法，可以精确地模拟多个领域的非线性问题，包括静态、动态以及非线性耦合物理场分析等，适合模拟静力问题，且有较高的精度。

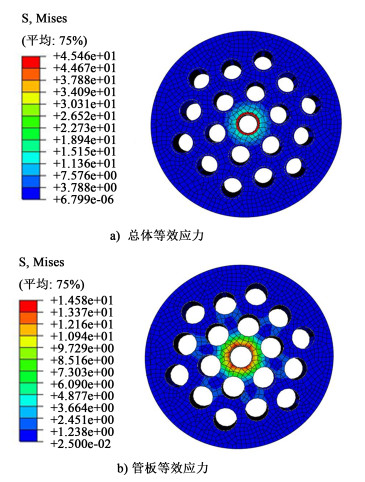
单根换热管胀接，卸载以后残余等效应力对周围区域管板孔的影响如图 6所示。

图 6 单根管胀接等效应力 Fig.6 Single tube expansion joint equivalent stress
图选项
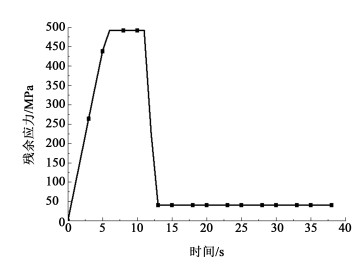
图 7 单根管胀接的换热管残余应力-时间 Fig.7 Variation of residual stress of a heat exchanger tube expanded by a single tubewith time
图选项
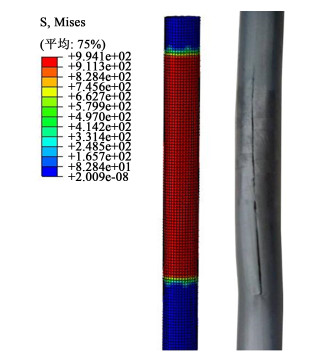
图 8 换热管胀裂实验结果对比 Fig.8 Comparison of explosion test results of heat exchange tubes
图选项

根据单根管模拟情况，不断增大胀接压力，当施载在183 MPa时，卸载后，换热管的法向变形刚好为0.10 mm，继续增加胀接压力，当增量很小的时候，换热管法向变形量会发生激增，因此Ti31钛合金材料在液压胀接过程中，施载为183 MPa时，管板与换热管之间的间隙由初始间隙0.10 mm变为0 mm。

继续增大胀接压力，换热管与管板变形增大，等效应力和等效变形也不断增大，当胀接压力增大到460 MPa时，换热管出现应力畸变，产生损坏，与实验结果相符合。因此本研究采用的管板简化模型是准确的。

4 数值模拟结果对比 4.1 冷却器换热管-管板数值分析

通过改变胀接压力和管板与换热器初始间隙，得到卸载后不同的残余等效应力和残余接触面应力，对模拟结果进行对比，云图及数值大小如图 9~图 23所示。

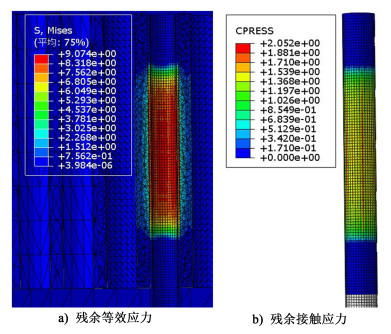
图 9 250 MPa压力、0.10 mm初始间隙模拟结果 Fig.9 Simulation results at 250 MPa pressure and 0.10 mm clearance
图选项
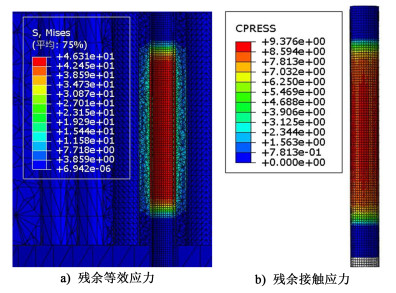
图 10 300 MPa压力、0.10 mm初始间隙模拟结果 Fig.10 Simulation results at 300 MPa pressure and 0.10 mm clearance
图选项
图 11 350 MPa压力、0.10 mm初始间隙模拟结果 Fig.11 Simulation results at 350 MPa pressure and 0.10 mm clearance
图选项
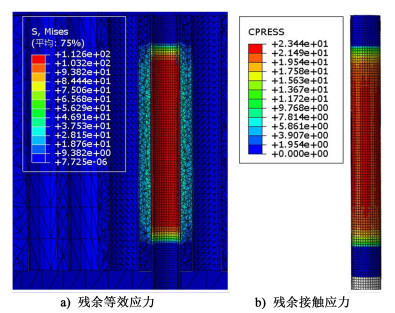
图 12 400 MPa压力、0.10 mm初始间隙模拟结果 Fig.12 Simulation results at 400 MPa pressure and 0.10 mm clearance
图选项
图 13 250 MPa压力、0.15 mm初始间隙模拟结果 Fig.13 Simulation results at 250 MPa pressure and 0.15 mm clearance
图选项
图 14 300 MPa压力、0.15 mm初始间隙模拟结果 Fig.14 Simulation results at 300 MPa pressure and 0.15 mm clearance
图选项
图 15 350 MPa压力、0.15 mm初始间隙模拟结果 Fig.15 Simulation results at 350 MPa pressure and 0.15 mm clearance
图选项
图 16 400 MPa压力、0.15 mm初始间隙模拟结果 Fig.16 Simulation results at 400 MPa pressure and 0.15 mm clearance
图选项
图 17 250 MPa压力、0.20 mm初始间隙模拟结果 Fig.17 Simulation results at 250 MPa pressure and 0.20 mm clearance
图选项
图 18 300 MPa压力、0.20 mm初始间隙模拟结果 Fig.18 Simulation results at 300 MPa pressure and 0.20 mm clearance
图选项
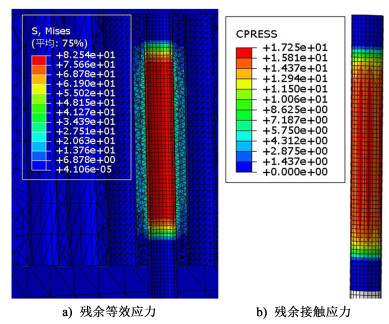
图 19 350 MPa压力、0.20 mm初始间隙模拟结果 Fig.19 Simulation results at 350 MPa pressure and 0. 20 mm clearance
图选项
图 20 400 MPa压力、0.20 mm初始间隙模拟结果 Fig.20 Simulation results at 400 MPa pressure and 0.20 mm clearance
图选项
图 21 0.10 mm初始间隙、不同初始压力时接触面结点的应力-时间曲线 Fig.21 Stress-Time curve of the contact point at the initial gap of 0.10 mm and different initial pressure
图选项
图 22 0.15 mm初始间隙不同初始压力时接触面结点的应力-时间历程 Fig.22 Stress-Time curve of the contact point at the initial gap of 0.15 mm and different initial pressure
图选项
图 23 0.20 mm初始间隙不同初始压力时接触面结点的应力-时间历程 Fig.23 Stress-Time curve of the contact point at the initial gap of 0.20 mm and different initial pressure
图选项

对胀接压力分别为200、250、300、350和400 MPa，初始间隙分别为0.10、0.15和0.20 mm时的胀接模拟结果进行对比分析，换热器卸载后残余等效应力如表 2所示。

表 2 不同胀接压力卸载后残余等效应力(MPa) Table 2 Residual equivalent stress after unloading at different initial pressure (MPa)
间隙/mm 胀接压力/MPa
200 250 300 350 400
0.10 0.294 9.074 46.31 81.15 112.6
0.15 0.298 9.639 46.69 81.80 113.4
0.20 0.297 10.18 47.32 82.54 114.4
表选项

残余等效应力与胀接压力大小有关，胀接压力越大，残余等效应力越大；胀接压力相同，间隙分别为0.10、0.15和0.20 mm时的残余等效应力几乎相同，初始间隙对胀接质量的影响很小，几乎可以忽略不计。

换热器胀接压力卸载后，残余接触应力如表 3所示。

表 3 不同胀接压力卸载后残余接触应力(MPa) Table 3 Residual contact stress after unloading at different initial pressure (MPa)
间隙/mm 胀接压力/MPa
200 250 300 350 400
0.10 0.004 7 2.052 9.376 16.67 23.44
0.15 0.005 2 1.984 9.439 16.94 23.94
0.20 0.004 8 2.104 9.592 17.25 23.93
表选项

当施载为200 MPa的时候，残余接触应力几乎为0，与施载为183 MPa时，换热管和管板刚好接触的实验结果相符合，验证了研究方法的正确性。

4.2 拔出力理论计算

数值模拟完全卸载以后，胀接过程换热管和管板材料力学性能不完全相同，导致管板内孔表面和换热管外表面伸缩量不同，管板内孔表面和换热管外表面并非完全接触，故采用平均残余接触应力进行计算。

当管板为薄壁管时，拉脱力可按式(9)进行计算。

$ F = fP_{\rm{c}}^*{\rm{ \mathsf{ π} }}{d_{\rm{o}}}L $ (9)

其中：F为拉脱力；L为胀接长度；f为摩擦系数；Pc*为残余接触压力；do为外直径。

当管板为厚壁管时，拉脱力可按式(10)进行计算。

$ {F = \alpha {\rm{ \mathsf{ π} }}\left( {R_{\rm{i}}^2 - r_{\rm{i}}^2} \right)P_{\rm{c}}^*\left[ {1 - \frac{{ - 2f{R_{\rm{i}}}L}}{{{e_\alpha }\left( {R_{\rm{i}}^2 - r_{\rm{i}}^2} \right)}}} \right]} $ (10)
$ {\alpha = \frac{1}{{{\mu _{\rm{t}}}}}\left[ {\frac{{{E_{\rm{t}}}}}{{{E_{\rm{s}}}}}\left( {\frac{{R_{\rm{o}}^2 + R_{\rm{i}}^2}}{{R_{\rm{o}}^2 - R_{\rm{i}}^2}} + {\mu _{\rm{s}}}} \right) + \left( {\frac{{r_{\rm{o}}^2 + r_{\rm{i}}^2}}{{r_{\rm{o}}^2 - r_{\rm{i}}^2}} - {\mu _{\rm{s}}}} \right)} \right]} $ (11)

其中：Ri为管板孔内半径；Ro为管板外半径；ri为换热管内半径；ro为换热管外半径；Et和Es分别为换热管和管板的弹性模量；μt和μs分别为换热管和管板的泊松比。

数值模拟研究结果表明：初始间隙对胀接结果影响较小。胀接压力相同，间隙不同时，卸载后残余应力值和残余接触面应力值变化较小。

胀接压力对胀接结果的影响较大。初始间隙相同，胀接压力不同时，卸载后残余应力值和残余接触应力值变化较大。随着胀接压力的增大，卸载后的残余应力值和残余接触应力值明显变大。

表 4 不同胀接压力卸载后换热管面拉脱力(MPa) Table 4 Heat exchange tube surface pull off force after unloading at different initial pressure (MPa)
间隙/mm 胀接压力/MPa
200 250 300 350 400
0.10 0.004 7 2.052 9.376 16.67 23.44
0.15 0.005 2 1.984 9.439 16.94 23.94
0.20 0.004 8 2.104 9.592 17.25 23.93
表选项
5 结论

1) Ti31合金材料在胀接过程中，当施加的胀接压力大小约为183 MPa时，换热管的法向变形量为0.10 mm，此时换热管外壁恰好与管板接触，管板与换热管的间隙由0.10 mm变为0，继续增大胀接压力，换热管的法向变形开始明显变大。

2) 初始间隙不同时，200、250、300、350和400 MPa胀接压力下，卸载后的残余接触应力值变化没有规律，最大变化率分别为9.6%、5.7%、2.3%、3.3%和2.3%。

3) 初始间隙相同，胀接压力不同时，卸载后残余应力和残余接触应力值变化较大。换热管外表面的残余接触应力随着胀接压力的增加而增加，残余等效应力也随着胀接力的增加而增加，其变化趋势一致。

参考文献
[1]
蒋祥荣, 李凯, 李大永, 等. 含支撑板结构的管-翅式换热器胀接工艺仿真[J]. 塑性工程学报, 2015, 22(4): 93-98.
Jiang Xiangrong, Li Kai, Li Dayong, et al. Finite element analysis of expand-joint forming of fin-tube heat exchanger with support planes[J]. Journal of Plasticity Engineering, 2015, 22(4): 93-98. (in Chinese)
[2]
宋京凯, 薛松龄, 姚祺峰, 等. 管板和传热管胀接应力应变的数值模拟及分析[J]. 哈尔滨工程大学学报, 2009, 30(6): 639-643.
Song Jingkai, Xue Songling, Yao Qifeng, et al. Numerical simulation of stress and strain of stube sheetand heat-transfer tubes[J]. Journal of Harbin Engineering University, 2009, 30(6): 639-643. DOI:10.3969/j.issn.1006-7043.2009.06.009 (in Chinese)
[3]
刘宝亮, 闫秀娟, 刘军, 等. 聚丙烯中空纤维换热器的数值模拟[J]. 化学工业与工程, 2017, 34(1): 90-95.
Liu Baoliang, Yan Xiujuan, Liu Jun, et al. Numerical simulation for polypropylene hollow fiber heat exchanger[J]. Chemical Industry and Engineering, 2017, 34(1): 90-95. (in Chinese)
[4]
李伟, 王强, 杨笑瑾, 等. 镍基合金换热管与镍基合金管板液压胀接试验研究[J]. 化工机械, 2017, 44(4): 386-389.
Li Wei, Wang Qiang, Yang Xiaojin, et al. Experimental study on hydraulic expansion of nickel-base alloy tube to nickel-base alloy tubesheet[J]. Chemical Engineering & Machinery, 2017, 44(4): 386-389. DOI:10.3969/j.issn.0254-6094.2017.04.004 (in Chinese)
[5]
王玉刚, 黄翔. 一种新型管式间接蒸发冷却器的性能[J]. 化工学报, 2012, 63(S2): 49-52.
Wang Yugang, Huang Xiang. Performance of a novel tubular indirect evaporative cooler[J]. CIESC Journal, 2012, 63(S2): 49-52. (in Chinese)
[6]
王晓静, 王磊, 郜维栋. 基于Ansys Workbench的换热管断裂行为模拟分析[J]. 化学工业与工程, 2016, 33(1): 90-95.
Wang Xiaojing, Wang Lei, Gao Weidong. Failure analysis of heat exchange tubes based on ansys workbench[J]. Chemical Industry and Engineering, 2016, 33(1): 90-95. (in Chinese)
[7]
杜婷婷, 杜文静, 程林. 新型椭圆管螺旋折流板换热器特性研究[J]. 工程热物理学报, 2018, 39(1): 193-199.
Du Tingting, Du Wenjing, Cheng Lin. Research on characteristics of a novel helical baffled heat exchanger with oval tubes[J]. Journal of Engineering Thermophysics, 2018, 39(1): 193-199. (in Chinese)
[8]
丁宇奇, 董日治, 刘巨保, 等. 换热器管板与换热管胀接密封性能影响因素分析[J]. 化工机械, 2018, 45(1): 90-95.
Ding Yuqi, Dong Rizhi, Liu Jubao, et al. Influencing factors of expansion and sealing performance of heat exchanger tube plate and heat exchanger[J]. Chemical Machinery, 2018, 45(1): 90-95. DOI:10.3969/j.issn.0254-6094.2018.01.023 (in Chinese)
[9]
Bouzid A H, Laghzale N E. Analytical modeling of tube-to-tubesheet joints subjected to plastic deformation and creep[J]. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 2016, 10(4): JAMDSM0055. DOI:10.1299/jamdsm.2016jamdsm0055
[10]
Merah N, Al-Aboodi A, Shuaib A N, et al. Combined effects of tube projection, initial tube-tubesheet clearance, and tube material strain hardening on rolled joint strength[J]. Journal of Pressure Vessel Technology, 2009, 131(5): 051201. DOI:10.1115/1.3142387
[11]
Al-Aboodi A, Merah N, Shuaib A N, et al. Effects of friction on roller expanded tube-tubesheet joint strength[J]. International Journal of Material Forming, 2010, 3(4): 253-257. DOI:10.1007/s12289-010-0686-3
[12]
倪鹏, 惠虎, 王晓东, 等. 蒸汽发生器管板液压胀管数值模拟研究[J]. 核动力工程, 2015, 36(5): 204-207.
Ni Peng, Hui Hu, Wang Xiaodong, et al. Numerical simulation of hydraulically expanded tube-to-tube sheet joints in steam generator[J]. Nuclear Power Engineering, 2015, 36(5): 204-207. (in Chinese)
[13]
Akisanya A R, Khan F U, Deans W F, et al. Cold hydraulic expansion of oil well tubulars[J]. International Journal of Pressure Vessels and Piping, 2011, 88(11/12): 465-472.
[14]
Merah N, Al-Aboodi A, Shuaib A N, et al. 3-D finite element analysis of roller-expanded heat exchanger tubes in over-enlarged tubesheet holes[J]. Applied Petrochemical Research, 2012, 1(1/2/3/4): 45-52.
[15]
闫宗宝, 王国珍, 轩福贞, 等. 核电蒸汽发生器管子与管板胀接力学行为与接头性能研究[J]. 核动力工程, 2011, 32(S1): 173-178.
Yan Zongbao, Wang Guozhen, Xuan Fuzhen, et al. Study on mechanical behavior of expanding tube-to-tubesheet and joint performance for steam generator of nuclear power[J]. Nuclear Power Engineering, 2011, 32(S1): 173-178. (in Chinese)
[16]
王相兵, 张响, 陈辉, 等. 胀接成形工艺对管翅式换热器结构性能的影响[J]. 塑性工程学报, 2016, 23(4): 61-68.
Wang Xiangbing, Zhang Xiang, Chen Hui, et al. Effects of expand-joint forming on structure performance of fin-tube heat exchanger[J]. Journal of Plasticity Engineering, 2016, 23(4): 61-68. (in Chinese)
[17]
倪鹏, 惠虎, 王晓东, 等. 蒸汽发生器液压胀接保压时间及拉脱力的研究[J]. 原子能科学技术, 2015, 49(12): 2234-2238.
Ni Peng, Hui Hu, Wang Xiaodong, et al. Steam generator hydraulic expansion study on the time of holding pressure and pull-off force[J]. Atomic Energy Science and Technology, 2015, 49(12): 2234-2238. DOI:10.7538/yzk.2015.49.12.2234 (in Chinese)
[18]
于洪杰, 钱才富. 液压胀接接头密封性能的力学表征[J]. 化工机械, 2010, 37(6): 758-762.
Yu Hongjie, Qian Caifu. Mechanical description of the tightness of hydraulic expanded tube joints[J]. Chemical Engineering & Machinery, 2010, 37(6): 758-762. DOI:10.3969/j.issn.0254-6094.2010.06.023 (in Chinese)
[19]
李涛, 段成红. 换热管与管板连接接头的液压胀接压力分析[J]. 化工机械, 2016, 43(6): 759-763.
Li Tao, Duan Chenghong. Analysis of hydraulic expansion pressure for tube-to-sheet joints[J]. Chemical Engineering & Machinery, 2016, 43(6): 759-763. DOI:10.3969/j.issn.0254-6094.2016.06.014 (in Chinese)