2. 非常规冶金教育部重点实验室, 昆明 650093;
3. 微波能工程应用及装备技术国家地方联合工程实验室, 昆明 650093
2. Key Laboratory of Unconventional Metallurgy of Ministry of Education, Kunming 650093, China;
3. National Local Joint Laboratory of Engineering Application of Microwave Energy and Equipment Technology, Kunming 650093, China
微波是一种频率范围介于红外线和无线电,对应波长在1 m~1 mm之间的电磁波[1]。与基于热传导、热对流和热辐射的传统加热方式不同,微波加热通过电磁损耗材料直接将电磁能转化为热能,具有选择性加热、体积加热、快速加热、易于控制以及环保节能等优点[2]。微波加热作为一种新型加热方式,目前不仅被广泛应用在化学合成、环境工程等中低温领域[3, 4],而且在陶瓷烧结、矿物预处理、矿物煅烧和火法冶金等高温领域颇受欢迎[5]。
由于微波具有选择性加热的特性,对于某些室温下吸波能力较弱的物质,微波对它们的加热效果不显著,甚至不能加热,从而限制了微波对这些物质的加热处理[6]。虽然可以通过掺杂二次强吸波材料来实现对电磁波的良好吸收,但是当对微波加热的物料有严格工艺要求时,这种提高吸波性能的方法是不被允许的[7],这种方法改变了原材料的化学成分从而限制了其应用[8]。因此,在材料化学成分不改变的情况下,可以考虑将吸波能力强的材料作为外部感受器加入微波反应腔来以提供热能辅助加热[9]。
感受器是指即使在室温下也能被微波快速加热的一类高损耗材料(如石墨、碳化硅、木炭、Fe3O4和MoSi2)。在低温初始阶段,物料介电参数不随温度变化,感受器快速吸收微波升温并将热能通过传统的传热方式传递给物料;但是一旦达到耦合临界温度,物料的介电参数急剧增加,不再需要感受器辅助加热,能够直接与微波互相作用。感受器通过提供双向加热并减少材料表面的热损失,进一步加速微波处理,加热效率优于直接微波加热或常规加热,其双向加热也改善了微波加热的均匀性。Bhattacharya等[8]对感受器在促进微波加热方面的作用进行了探讨,结果表明感受器为这些材料与微波相互作用提供了一个通道,同时感受器的使用还减轻了微波加热对材料介电性能的依赖性。
目前,Ghorbe等[10]将常作为感受器材料的碳化硅样品置于2.45 GHz单模腔,对碳化硅平行六面体进行模拟仿真,结果表明碳化硅样品取向对电场分布和加热效率有很大影响;Fu等[11]通过碳化硅辅助处理铀尾矿土壤,发现原先介电特性较差的介质也可以对微波能有效利用;Bhatt等[12]通过利用石墨和碳化硅板,发现金属块也可以被微波加热到一定的温度;Manière等[13]研究了微波混合加热氧化锆陶瓷,结果表明混合加热配置改善了样品热不均匀性以及致密均质化。但是,很少有研究者在考虑电磁热流全耦合的基础上探究感受器不同配置对腔体内电磁场分布和物料加热效率的影响。
尽管部分微波被感受器吸收后热辐射物料,但仍需微波直接作用于物料,所以应合理地选择感受器的结构形状或数量,使感受器热辐射和微波体积加热物料的能量转化平衡达到最优[9]。本研究基于电磁学、传热学及流体力学理论,以微波冶金常用物料赤铁矿为例,针对不同感受器辅助加热结构,借助COMSOL Multiphysics仿真平台建立了内置物料、感受器和保温层的有限元模型,研究了4种感受器配置对微波加热效果的影响,以在此基础上提高电磁热流耦合中物料的加热特性。本研究可为微波弱吸收物质的辅助性加热提供参考,对拓宽微波加热技术的应用领域具有一定的意义。
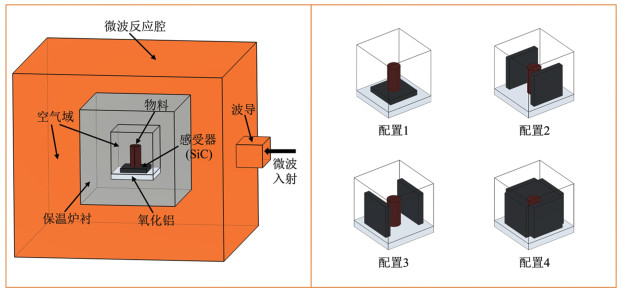
1 理论与模型 1.1 几何模型及假设本研究采用的微波加热三维腔体模型来源于昆明理工大学教育部非常规冶金重点实验室设计的微波加热系统。如图 1所示,谐振腔尺寸为400 mm×380 mm×350 mm,波导尺寸为86.4 mm×43.2 mm的国际标准型BJ-26,加热物料尺寸为ϕ10 mm×40 mm,基座尺寸为80 mm×80 mm×10 mm,感受器(碳化硅)尺寸为50 mm×50 mm×8 mm。
|
| 图 1 微波腔体三维模型 Fig.1 3D model of microwave cavity |
| |
此外,为减少热损失,考虑了厚度为50.3 mm的保温炉衬,其值来源于本课题组先前的研究(在大温度梯度下得到的含锆型硅酸铝纤维板优选透波峰)[14]。物料被放置在基座中心,而基座被放置在保温层内下底面。由于物料在腔体中的位置始终保持不变,因此在配置1中将基座的位置下移8 mm,以满足建模要求(基座位置微弱变化对整体电场分布的影响可以忽略不计)。微波功率为2 000 W,加热时间为500 s。
为提高计算效率,确保计算结果收敛,便于误差控制,在模型构建时做出以下假设:(1)过程中不发生相变,没有化学反应进行;(2)所有材料是均质且各向同性的,初始温度为20 ℃;(3)微波频率固定为2.45 GHz;(4)忽略磁损耗对赤铁矿微波加热的贡献[15]。
1.2 物性参数设置本模型中涉及的仿真参数来源于相关文献或市场厂家提供的资料。表 1列出了物料赤铁矿的相关参数[15-17];铜、空气的材料属性来源于COMSOL内置材料库;基座的材料属性来源于文献[12];感受器的材料属性来源于文献[10, 13]。
| 参数 | 属性 | 单位 |
| ε′r(T) | 5.899×10-16T6-1.828×10-12T5+2.286×10-9T4-1.345×10-6T3+3.671 ×10-4T2-0.03866T+8.182 | 1 |
| ε″r(T) | 5.668×10-18T7-1.979×10-14T6+2.68×10-11T5-1.78×10-8T4+ 6.102×10-6T3-1.031×10-3T2+0.07285T-1.348 | 1 |
| ρ(T) | -1.377×10-14T6+4.743×10-11T5-5.693×10-8T4+3.04×10-5T3-7.356×10-3T2+0.6696T+2773 | kg·m-3 |
| σ | 0 | S·m-1 |
| k | 0.3 | W·(m·K)-1 |
| Cp | 780 | J·(kg·K)-1 |
微波腔内电磁场的分布可以通过求解Maxwell方程组来描述,频域中电场强度的控制方程如式(1)和式(2)[18, 19]:
| $ \begin{gather*} \nabla \times\left(\mu_{\mathrm{r}}^{-1} \nabla \times \boldsymbol{E}_{\mathbf{r}}\right)=k_{0}^{2}\left(\varepsilon_{\mathrm{r}}-\frac{j \sigma}{\omega \varepsilon_{0}}\right) \boldsymbol{E}_{\mathbf{r}} \end{gather*} $ | (1) |
| $ \begin{gather*} k_{0}=\omega \sqrt{\mu_{0} \varepsilon_{0}} \end{gather*} $ | (2) |
式(1)和式(2)中:μr为相对复磁导率;εr相对复介电常数;k0为真空波数;σ为电导率,S·m-1;ω为角频率,rad·s-1;μ0为真空磁导率;ε0为真空中的介电常数;Er由谐振电场表达式
在一般的电磁热耦合计算时,大多研究者普遍假设相对复介电常数εr和相对复磁导率μr为固定值,而实际上微波加热过程中电磁热是一个双向耦合的过程[7]。因此本研究中εr和μr均考虑为温度T的函数,即:
| $ \begin{align*} & \varepsilon_{\mathrm{r}}(T)=\varepsilon_{\mathrm{r}}^{\prime}(T)-j \varepsilon_{\mathrm{r}}^{\prime \prime}(T) \end{align*} $ | (3) |
| $ \begin{align*} \mu_{\mathrm{r}}(T)=\mu_{\mathrm{r}}^{\prime}(T)-j \mu_{\mathrm{r}}^{\prime \prime}(T) \end{align*} $ | (4) |
式(3)和式(4)中:ε′r为相对复介电常数实部,表征材料储存电能的能力;ε″r为相对复介电常数虚部,表征材料将电能转化为热能的能力;μ′r为相对复磁导率实部,表征材料储存磁能的能力;μ″r为相对复磁导率虚部,表征材料将磁能转化为热能的能力。
材料由于吸收微波辐射而升温,其固体的温度分布可由Fourier方程表示:
| $ \begin{equation*} \rho C_{p} \frac{\partial T}{\partial t}+\nabla \cdot(-k \nabla T)=Q \end{equation*} $ | (5) |
式(5)中:ρ为材料密度,kg·m-3;Cp为恒压热容,J·(kg·K)-1;k为导热系数,W·(m·K)-1;Q为热源,W·m-3。
以电磁功率损耗密度Qe表示的热源主要来源于电阻损耗Qrh和磁损耗Qml,即[20]:
| $ \begin{equation*} Q_{\mathrm{e}}=Q_{\mathrm{rh}}+Q_{\mathrm{ml}}=\frac{1}{2} \mathit{Re}\left(\boldsymbol{J} \cdot \boldsymbol{E}^{*}\right)+\frac{1}{2} \mathit{Re}\left(i \omega \boldsymbol{B} \cdot \boldsymbol{H}^{*}\right) \end{equation*} $ | (6) |
式(6)中:E*为电场强度E的共轭复数;H*为磁场强度H的共轭复数;当有耗介质为磁性材料时,电磁能的损耗也要考虑磁场的功率耗散。
在保温层内,由于空气温度变化会引起其密度的变化,从而由密度差产生的浮力流会造成空气自然对流。对流对于加热系统的传热问题是至关重要的,因为在加热物料时,对流通量可能是强冷却或均匀化的来源[21]。Navier-Stones对流问题主要由以下3个控制方程定义:
质量守恒方程:
| $ \begin{equation*} \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho \boldsymbol{u})=0 \end{equation*} $ | (7) |
考虑压力、黏性和体积力的动量方程:
| $ \begin{gather*} \rho\left(\frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u} \cdot \nabla \boldsymbol{u}\right)=-\nabla p+\boldsymbol{F}_{\mathrm{g}}+ \\ \nabla \cdot\left[\mu\left(\nabla \boldsymbol{u}+(\nabla \boldsymbol{u})^{T}\right)-\frac{2}{3} \mu(\nabla \cdot \boldsymbol{u}) \boldsymbol{I}\right] \end{gather*} $ | (8) |
以及能量平衡方程,其等效于流体中的热方程,并考虑对流项、附加压力Qp和黏性耗散Qvd热源项,这些项对于本研究来说通常非常低且被忽略[21]:
| $ \begin{gather*} \rho C_{p}\left[\frac{\partial T}{\partial t}+(\boldsymbol{u} \cdot \nabla) T\right]+\nabla(-k \nabla T)=Q+Q_{\mathrm{p}}+Q_{\mathrm{vd}} \end{gather*} $ | (9) |
式中:u为流体速度,m·s-1;p为流体压力,N·m-2;μ为动力黏度,Pa·s;I为单位矩阵;Fg为体积力源项,N·m-3;Qp为压力热源项,W·m-3;Qvd为黏性耗散热源项,W·m-3。
1.4 边界条件谐振腔及波导侧壁为金属材质,其金属壁的厚度远小于腔体,由于“趋肤效应”,电磁场在金属壁面的穿透深度微乎其微。所以谐振腔及波导侧壁面设置为阻抗边界条件:
| $ \begin{equation*} \sqrt{\frac{\mu_{0} \mu_{\mathrm{r}}}{\varepsilon_{0} \varepsilon_{\mathrm{r}}-j \frac{\sigma}{\omega}}} {\boldsymbol{n}} \cdot \boldsymbol{H}+\boldsymbol{E}-(\boldsymbol{n} \cdot \boldsymbol{E}) \boldsymbol{n}=\left(\boldsymbol{n} \cdot \boldsymbol{E}_{\mathrm{s}}\right) \boldsymbol{n}-\boldsymbol{E}_{\mathrm{s}} \end{equation*} $ | (10) |
式(10)中:n为边界面外法线方向矢量;Es为源电场,用于指定边界上源表面电流。
当微波频率不超过波导横截面尺寸下的截止频率时,电磁波能在矩形波导中传播,根据截止频率表达式[式(11)]:当微波频率为2.45 GHz时,电磁波以横电波TE10模式传播,此时X、Y方向均无电场分布,仅有Z方向存在电场[22]。
| $ \begin{equation*} \left(\nu_{\mathrm{c}}\right)_{m n}=\frac{c_{0}}{2} \sqrt{\left(\frac{m}{a}\right)^{2}+\left(\frac{n}{b}\right)^{2}} \end{equation*} $ | (11) |
式(11)中:νc为截止频率,Hz;c0为光速,取3×108 m·s-1;m和n为电磁波模数;a和b表示矩形波导横截面的尺寸。
在工作频率ν下所需的传播系数β为:
| $ \begin{equation*} \beta=\frac{2 \mathtt{π}}{c_{0}} \sqrt{\nu^{2}-\nu_{c}^{2}} \end{equation*} $ | (12) |
保温层外部边界考虑对流和表面到环境冷却通量的影响,这些通量由以下方程描述[21]:
| $ \begin{gather*} \varphi_{\mathrm{csa}}=h\left(T_{\mathrm{air}}-T\right) \end{gather*} $ | (13) |
| $ \begin{gather*} \varphi_{\mathrm{ras}}=\sigma_{\mathrm{s}} \varepsilon\left(T_{\mathrm{air}}^{4}-T^{4}\right) \end{gather*} $ | (14) |
式(13)和式(14)中:h为对流换热系数,W·(m2·K)-1;ε为表面发射率;Tair为环境温度,K。
感受器、物料、基座表面及保温层内表面,这些暴露在空气中的部分,一方面受到流体动力学的影响,另一方面需要考虑由每种材料发射率引起的表面到表面辐射。对于相互辐射的表面,总出射辐射热通量J(辐射度)定义为外部入射辐射G的反射部分Gref与壁面热辐射εeb(T)之和[18, 19]:
| $ \begin{equation*} J=\varepsilon e_{\mathrm{b}}(T)+G_{\text {ref }}=\varepsilon n^{2} \sigma_{\mathrm{s}} T^{4}+\rho_{\mathrm{r}} G \end{equation*} $ | (15) |
发射率和反射率的关系为:
| $ \begin{equation*} \varepsilon=1-\rho_{\mathrm{r}} \end{equation*} $ | (16) |
净向内热通量φrss为:
| $ \begin{equation*} \varphi_{\mathrm{rss}}=\varepsilon\left[G-e_{\mathrm{b}}(T)\right] \end{equation*} $ | (17) |
式(17)中:σs为Stefsn-Boltzmann常数;n为折射率;eb(T)为产生的表面辐射,W·m-2。
1.5 网格划分及独立性验证为同时兼顾计算精度与效率,在模型所有网格尺寸均满足Nyquist准则[23]基础上,对涉及温度场的保温层、物料、感受器和基座进行加密处理,并对同时涉及温度场和流场的空气域(保温层内空气域)进行单独角细化及边界层网格剖分。其中划分为结构化六面体网格的物料、感受器、基座单元在0.675~4.600 mm之间,划分为自由四面体网格的空气域和保温层最大网格不超过14.7 mm,整体平均网格质量为0.66。
| $ \begin{equation*} S_{\max } \leqslant \frac{\mathit{λ}}{2}=\frac{c}{2 f \sqrt{\varepsilon_{\mathrm{r}}^{\prime} \mu_{\mathrm{r}}^{\prime}}} \end{equation*} $ | (18) |
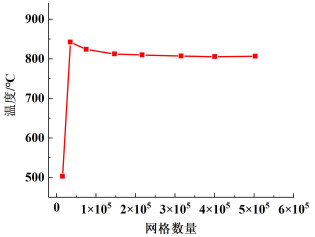
以配置1中物料的平均温度作为评价指标进行网格无关性验证。图 2给出了物料温度与网格数量的变化曲线图。
|
| 图 2 网格无关性分析 Fig.2 Grid independence analysis |
| |
从图 2可以看出,物料温度随着网格数量的增加而逐渐趋于稳定。当网格数量大于315 024时,配置1中物料的温度不再随网格数量而大幅度变化。这也就意味着,该网格数量满足模拟准确性要求。
2 结果与讨论 2.1 反射损耗S11分析减小谐振腔内电磁波的反射,不仅能够提高加热效率,而且还可以延长磁控管的使用寿命[3]。反射损耗系数S11表示反射回馈口的电磁能与进入谐振腔内电磁能的比例,是研究微波加热过程的重要参数。表 2描述了4种碳化硅配置下反射损耗系数S11的变化。由表 2可知,不同的碳化硅配置对应的S11值是不同的,初始时刻下配置1的反射损耗系数为-1.622 3,腔体内馈入的能量最多,而配置3的反射损耗系数为-0.500 3,微波能利用率最低;然而,S11随着时间的更新而不断变化,原先微波能利用率最高的配置1在500 s时微波能利用率反而最低,反射损耗系数仅有-0.925 4,这一现象是由于谐振腔内材料电磁参数变化时,空气和介质间阻抗不匹配引起的。这也说明在微波加热过程中,不止温度场,电磁场也是一个动态变化的过程。
| 结构方式 | 0 s | 100 s | 200 s | 300 s | 400 s | 500 s |
| 配置1 | -1.622 3 | -1.238 9 | -1.259 0 | -0.924 4 | -0.904 1 | -0.925 4 |
| 配置2 | -1.177 7 | -1.553 5 | -1.815 4 | -2.048 6 | -1.579 4 | -1.639 3 |
| 配置3 | -0.500 3 | -0.633 8 | -0.741 0 | -0.823 1 | -0.891 0 | -0.957 8 |
| 配置4 | -1.469 8 | -1.613 2 | -1.777 8 | -1.944 2 | -2.120 5 | -2.286 2 |
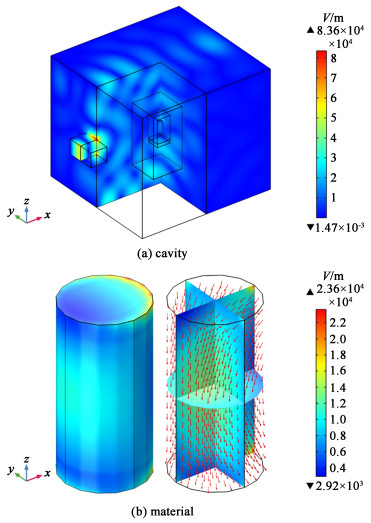
由于S11仅表示进入腔体内微波能量的多少,并不能表征物料对微波的有效利用率最优。为研究碳化硅配置对电场的影响,还需进一步分析谐振腔内电场空间分布及随时间的变化。图 3和图 4描述了不同碳化硅配置下初始阶段谐振腔及物料电场分布云图,矢量箭头表示电场方向及强度。
|
| 图 3 直接加热初始阶段电场分布 Fig.3 Electric field distribution at the initial stage of direct heating |
| |
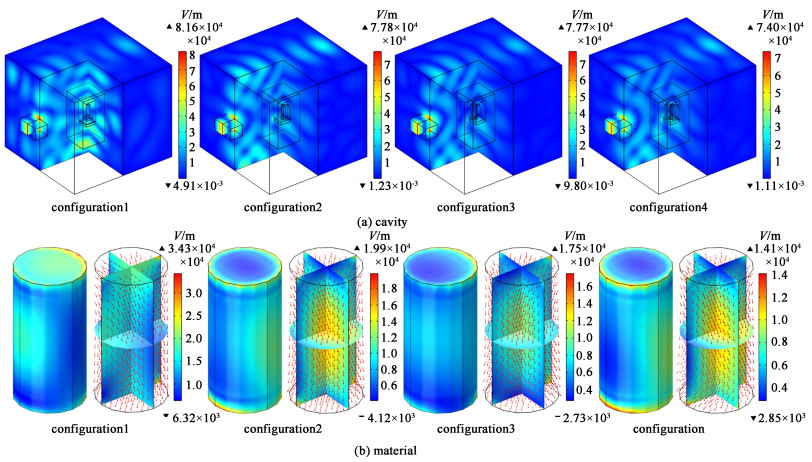
|
| 图 4 混合加热初始阶段电场分布:(a)腔体;(b)物料 Fig.4 Electric field distribution at the initial stage of hybrid heating: (a) cavity; (b) material |
| |
由图 4可以看出电场在空间的分布是不均匀的,冷热点相互交错出现,符合多模腔的场分布规律。在馈口及物料的一些边角处,电场强度显著高于周围,这是由于微波场的尖角效应致使物料的棱角处会承受更强的电场,这种情况必然会导致过热现象[3]。另外馈口处微波能量聚集比较明显,为保护磁控管不被损坏,需要时刻监测其反射系数并对反射回馈口的能量进行处理。
Monzó-Cabrera等[3]在研究介质层包裹被加热样品对其均匀性影响时,发现介质层可以增强物料内电场强度。对比图 3不难发现,加载碳化硅对谐振腔内电场分布影响较小,对其电场强度影响较大;而碳化硅的加载使得物料内电场分布及强度均有较大的改变。与物料直接加热时平均电场模(9 183.1 V·m-1)相比,内置碳化硅后,配置1~4内初始阶段物料平均电场模分别增强了45.7%、16.8%、-23.5%和-14.8%。
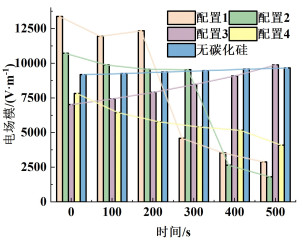
图 5描述了不同配置下物料平均电场模随时间的变化规律。
|
| 图 5 不同配置下物料平均电场模随时间的变化 Fig.5 Variation of the average electric field mode of the materials with time for different configuration |
| |
由图 5可知,无碳化硅时物料电场模随时间变化幅度很小,仅从9 183.1增加至9 672.9 V·m-1;配置1、2、4内物料电场模总体变化趋势相似,皆从13 379、10 729和7 825 V·m-1分别逐步减小至2 881.2、1 814.8和4 099.6 V·m-1,并且配置1和2存在急剧下降现象;配置3内物料电场模随加热时间从7 024.9增加至9 887.4 V·m-1。这是因为物料相对介电常数会随温度变化,在450 ℃后存在跳跃变化,并且变化的电磁参数会导致电磁波在介质中的波长发生变化,从而引起电场谐振模式变化。值得注意的是,由于微波在介质内的穿透深度会随着温度的升高而减小,配置4容易在物料外形成1个屏蔽罩,严重削弱透射到物料的电场强度。
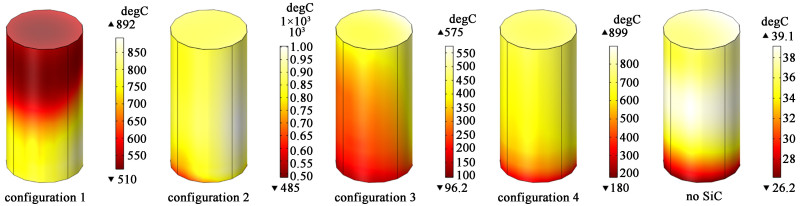
2.3 物料温度场分析图 6描述了不同碳化硅配置下物料在500 s时的温度分布云图。
|
| 图 6 不同配置下物料在500 s时的表面温度分布云图 Fig.6 Cloud picture of surface temperature distribution of materials in different configurations at 500 s |
| |
由图 6可知,在没有碳化硅的情况下,物料温度远远低于微波混合加热,因此后续不再分析。在不同碳化硅配置下,物料的最高温度分别为892、1 000、575和899 ℃,最低温度为510、485、96.2和180 ℃,温差为382、515、478.8和719 ℃。不同模型间物料温度差异现象非常明显,即使同一模型下的物料,也存在明显的高温区和低温区。这除了与物料内电场分布有关外,也与碳化硅相对于物料的位置密切相关。受碳化硅位置影响,配置2~4中物料在垂直方向并不存在明显的大范围的温度梯度,而配置1中物料被微波加热的同时,也受到碳化硅通过物料下底面以热传导方式传递的大量热量,但物料的导热能力较弱,仅为0.3 W·(m·K)-1,不能及时将热量向上传递,并且在随温度升高而显著增大的介电参数的影响下,导致系统在没有向稳态靠近前,物料垂直方向电磁能转化为热的能力相差越来越大,温差也越来越大。
温度变异系数COVT已被证明是测量温度不均匀性的有效方法,其值越大表示温度空间分布越不均匀。因此引入COVT来进一步评价加热过程中物料温度的均匀性,如式(19)所示:
| $ \begin{equation*} \mathrm{COV}_{\mathrm{T}}=\frac{1}{\bar{T}-T_{0}} \sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left(T_{i}-\bar{T}\right)} \end{equation*} $ | (19) |
式(19)中:Ti指取样点的温度;T指样品平均温度;T0为20 ℃;N指取样点的数量。
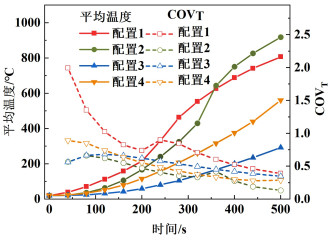
图 7描述了不同配置下物料体平均温度和温度变异系数COVT随时间的变化规律。
|
| 图 7 不同配置下物料平均电场温度和COVT随时间的变化 Fig.7 Variation of the average temperature and COVT of the materials with time for different configuration |
| |
由图 7可知,配置1~4内物料的COVT随加热时间呈整体减小趋势,其中配置1在20~200 s范围内下降幅度最大(72.69%),而配置2、3、4在20~500 s范围内变化较平缓,表明混合加热时物料温度均匀性会随着时间的推移而逐渐改善;在500 s时4种配置下的物料体平均温度分别为806.83、918.86、292.45和560.33 ℃,配置2的加热效率显著优于其他3种配置,结合配置1可以发现,与微波直接加热类似,混合加热时的电场强度与其温度变化在一定程度上仍具有一致性,电场强度大的物料在500 s时对应的物料温度高。此外,配置1~4各物料体平均温度变化曲线并非直线,这是因为其升温速率随时间变化浮动导致。
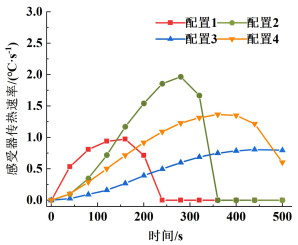
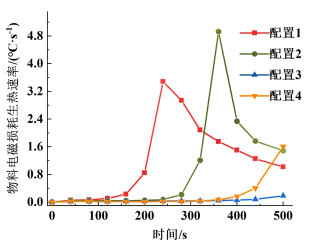
物料整体加热效果是感受器通过传统传热方式和物料自身电磁损耗共同作用的结果,为区分2种方式在物料升温中的贡献程度,图 8和图 9分别描述了配置1~4内物料在2种方式下的传热与生热速率变化规律。
|
| 图 8 感受器传热速率随时间的变化 Fig.8 Variation of the heat transfer rate of the susceptor with time |
| |
|
| 图 9 物料电磁损耗生热随时间的变化 Fig.9 Variation of the heat generation rate from electromagnetic loss of the materials with time |
| |
由图 8可知,配置1和2内感受器传热速率曲线变化明显,均呈倒V形分布,传热速率曲线在前期迅速上升并在后期持续为0;配置3和4内感受器传热速率曲线相对较平缓,在整个加热过程中持续缓慢给物料传热。
由图 9可知,配置1~2内前期物料电磁损耗生热速率几乎为零,微波对物料的贡献程度很小,随着时间的推移其物料生热速率明显大幅度上升,表明感受器在加热前期已起到良好的辅助作用,能够使微波与物料良好耦合;配置3和4内物料生热速率除后期有小范围上升外,其他阶段几乎均无贡献。总体来说,微波混合加热效率不仅要保证感受器高的传热速率,也要确保物料高的生热速率。
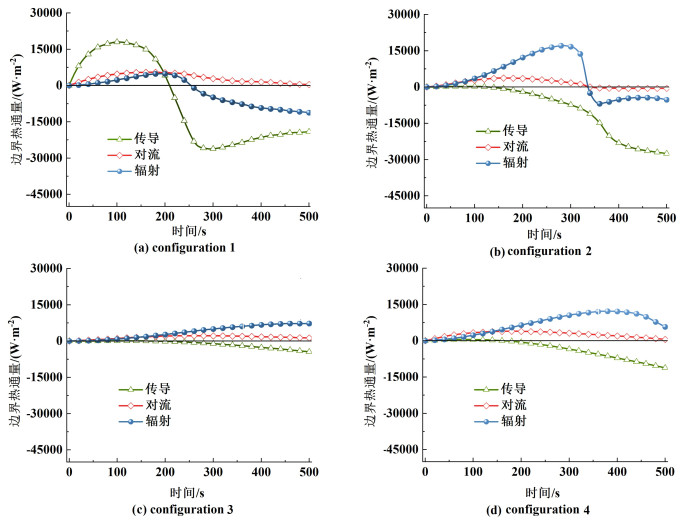
2.4 碳化硅配置对边界热通量的影响分析感受器辅助微波加热时,既有介质内的热量传递,又有不同介质间的相互传热与散热。图 10展示了物料表面与周围环境间热量传递的变化规律,其中热通量为正表示物料吸热,为负表示物料散热。
|
| 图 10 不同配置下物料的边界热通量曲线 Fig.10 Boundary heat flux curves of materials in different configurations |
| |
由图 10可知,图 10(a)和图 10(b)边界热通量变化起伏交错、有负有正,加热前期感受器升温较快,后期相反;而图 10(c)和图 10(d)边界热通量变化相对较平缓,对流和辐射热通量始终为正值,传导热通量几乎全程为负,物料持续吸热或散热,物料温度始终低于感受器,但其温差在后期逐渐减小。具体来看,配置1中,传导热通量在100 s时达到极值17 986 W·m-2,在210 s后从吸热转变为散热;辐射热通量在180 s时达到极值4 863 W·m-2,在260 s后实现了传热状态的转变。在配置2中,辐射热通量在280 s时达到极值17 060 W·m-2,在335 s后由吸热开始散热;而传导热通量在120 s前几乎为0,从120 s开始逐渐减小,并且在340~400 s间急剧变化。此外,配置3和4在加热时间内没有传热状态的转变,不过配置4在加热后期辐射热通量曲线已经开始明显下降。综上所述,微波混合加热过程可分为2个阶段:低温阶段以加热感受器为主导,感受器温度明显高于周围环境,部分热量会被物料所接收,其热量将通过传导、对流和辐射传递至物料;高温阶段,加热模式转变,感受器主导的加热模式转变为物料主导,此时物料介电损耗所产生的热能除了维持其自身温升外,还会有部分以冷却通量的形式散失,这些模型间存在的无效热量损耗差异也解释了为何在加热前期,配置1的平均电场模最高,但在后期温度却低于配置2。因此理想的辅助加热应该是感受器的加热温度跟随物料变化,并且适当提前于物料[21],可以在材料的微结构处理等方向加以利用,开发合成梯度功能材料。此外,在设计外部感受器时,除了考虑感受器对物料电场分布的影响外,降低无效能量损耗也至关重要。
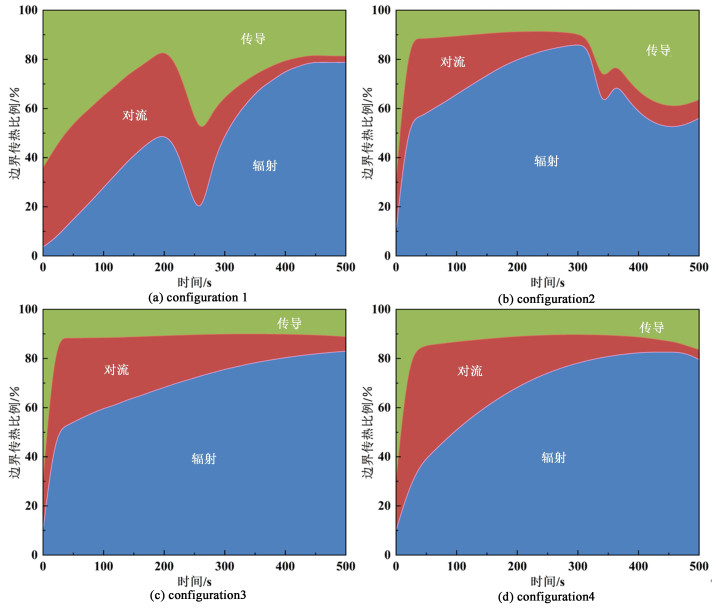
为评估3种边界热通量在物料表面的相对大小,图 11给出了物料表面与周围环境间辐射热通量、对流热通量及传导热通量面积分后的比例图。通过上述数据,可以清楚得观察到每种热通量在物料加热中的相对贡献比例。
|
| 图 11 不同配置下物料的边界热通量面积分占比图 Fig.11 Surface integral ratio of boundary heat flux of materials in different configurations |
| |
从图 11中可以看出,在配置1中,由于感受器与物料直接接触,在加热初期物料周围的热量传递以热传导为主,当加热模式发生转变后,辐射热通量的贡献比例显著增加,直至达到78.8%。而在其它3种结构中,由于物料与感受器结构位置的差异,热量传递以热辐射为主,并且在500 s时,辐射热通量分别占总通量的56.1%、82.9%和79.6%,这表明当介质表面温度较高时,辐射可能会成为主导的热传递方式。总的来说,感受器辅助加热是3种传热方式共同作用的过程,它们的贡献比例取决于介质结构、物性参数与周围环境,合理利用这些机制的相互作用对优化加热过程、提高能量效率和确保加热均匀性至关重要。
3 结论为提高弱吸波介质微波加热效率,在高温微波反应器内引入外部感受器,利用感受器来增强物料有效加热效果,基于电磁热流耦合理论,建立有限元多物理场仿真模型,探讨不同碳化硅配置对微波有效加热效率的影响,发现:(1) 当内置感受器后,因感受器吸收、反射微波能从而改变腔内电场强度及微波传播途径,并且物料和感受器的电磁参数与热物性参数会随着加热过程变化,导致整个过程腔体内电场分布复杂变化,感受器对微波能的吸收效率复杂变化,感受器辅助加热转化效率与物料介电损耗加热吸收效率复杂变化;(2) 借助COMSOL Multiphysics建立的多物理场耦合模型可以实现电磁热流的全耦合分析,研究各变量耦合作用的影响。当感受器布置在物料两侧,并与波导侧面平行时辅助加热效果最优;(3) 在高温微波反应器内,热辐射是主要的热传递方式,并且温度越高传热越剧烈。
| [1] |
张柔佳, 王易芬, 栾东磊. 微波加工过程中食品温度分布规律及其均匀性研究[J]. 食品与发酵工业, 2018, 44(4): 270-278. ZHANG Roujia, WANG Yifen, LUAN Donglei. A review of temperature distribution and heating uniformity of food during microwave thermal processing[J]. Food and Fermentation Industries, 2018, 44(4): 270-278. (in Chinese) |
| [2] |
GAO X, LIU X, YAN P, et al. Numerical analysis and optimization of the microwave inductive heating performance of water film[J]. International Journal of Heat and Mass Transfer, 2019, 139: 17-30. DOI:10.1016/j.ijheatmasstransfer.2019.04.122 |
| [3] |
彭金辉, 梅毅, 巨少华, 等. 微波化工技术[M]. 北京: 化学工业出版社, 2020. PENG Jinhui, MEI Yi, JU Shaohua. Chemical engineering intensification with microwave technology[M]. Beijing: Chemical Industry Press, 2020. (in Chinese) |
| [4] |
马春元, 宋占龙, 赵希强, 等. 微波在能源环境中的应用研究[M]. 北京: 科学出版社, 2019. MA Chunyuan, SONG Zhanlong, ZHAO Xiqiang, et al. Study on the application of microwave in energy environment[M]. Beijing: Science Press, 2019. (in Chinese) |
| [5] |
彭金辉, 夏洪应, 巨少华, 等. 微波冶金[M]. 北京: 科学出版社, 2016. PENG Jinhui, XIA Hongying, JU Shaohua, et al. Microwave metallurgy[M]. Beijing: Science Press, 2016. (in Chinese) |
| [6] |
彭金辉, 刘秉国. 微波煅烧技术及其应用[M]. 北京: 科学出版社, 2013. PENG Jinhui, LIU Bingguo. Microwave calcination technology and application[M]. Beijing: Science Press, 2013. (in Chinese) |
| [7] |
尚小标. 微波冶金炉加热效率的若干问题基础研究[D]. 昆明: 昆明理工大学, 2015 SHANG Xiaobiao. Basic research on some problems of heating efficiency of microwave metallurgical furnace[D]. Kunming: Kunming University of Science and Technology, 2015 (in Chinese) |
| [8] |
BHATTACHARYA M, BASAK T. A review on the susceptor assisted microwave processing of materials[J]. Energy, 2016, 97: 306-338. DOI:10.1016/j.energy.2015.11.034 |
| [9] |
崔凯辉. 微波加热德拜媒质热-电磁耦合特性研究[D]. 昆明: 昆明理工大学, 2020 CUI Kaihui. Study on thermo-electromagnetic coupling characteristics of Debye medium heated by microwave[D]. Kunming: Kunming University of Science and Technology, 2020 (in Chinese) |
| [10] |
GHORBEL I, GANSTER P, MOULIN N, et al. Experimental and numerical thermal analysis for direct microwave heating of silicon carbide[J]. Journal of the American Ceramic Society, 2021, 104(1): 302-312. DOI:10.1111/jace.17451 |
| [11] |
FU M, HUANG P, TAO Z, et al. Mechanism analysis using multi-physical field coupling: Silicon carbide-assisted microwave heating of UMT-coated soil[J]. International Journal of Thermal Sciences, 2023, 194: 108570. DOI:10.1016/j.ijthermalsci.2023.108570 |
| [12] |
BHATT S C, GHETIYA N D. 3D multiphysics simulation of microwave heating of bulk metals with parametric variations[J]. Chemical Engineering and Processing-Process Intensification, 2023, 184: 109271. DOI:10.1016/j.cep.2023.109271 |
| [13] |
MANIÈRE C, ZAHRAH T, OLEVSKY E A. Fully coupled electromagnetic-thermal-mechanical comparative simulation of direct vs hybrid microwave sintering of 3Y-ZrO2[J]. Journal of the American Ceramic Society, 2017, 100(6): 2439-2450. DOI:10.1111/jace.14762 |
| [14] |
尚小标, 李广超, 肖利平, 等. 大温度梯度下含锆型硅酸铝纤维板的透波性能[J]. 化工进展, 2023, 42(3): 1551-1561. SHANG Xiaobiao, LI Guangchao, XIAO Liping, et al. Wave transmission performance of zirconium aluminum silicate fiberboard under large temperature gradient[J]. Chemical Industry and Engineering Progress, 2023, 42(3): 1551-1561. (in Chinese) |
| [15] |
PENG Z. Heat transfer in microwave heating[D]. Michigan: Michigan Technological University, 2012
|
| [16] |
PENG Z, LI Z, LIN X, et al. Microwave power absorption in materials for ferrous metallurgy[J]. JOM, 2017, 69(2): 178-183. DOI:10.1007/s11837-016-2174-9 |
| [17] |
LI Q, WANG Q, ZHANG Y, et al. One dimensional numerical analysis of high temperature microwave heating hematite[C]//2015 International Conference on Computational Intelligence and Communication Networks (CICN). Jabalpur, India. IEEE, 2015: 39-43
|
| [18] |
MANIÈRE C, HARNOIS C, RIQUET G, et al. Rapid microwave sintering of centimetric zirconia: Scalability and electromagnetic-thermal-fluid-dynamic simulation[J]. Journal of the American Ceramic Society, 2023, 106(2): 848-859. DOI:10.1111/jace.18787 |
| [19] |
谢蒙优, 石建军, 陈国平, 等. 微波烧结陶瓷热均匀性的三维模拟研究[J]. 应用力学学报, 2020, 37(4): 1663-1669, 1867-1868. XIE Mengyou, SHI Jianjun, CHEN Guoping, et al. Numerical simulation of thermal uniformity of microwave sintering ceramics[J]. Chinese Journal of Applied Mechanics, 2020, 37(4): 1663-1669, 1867-1868. DOI:10.11776/cjam.37.04.D019 (in Chinese) |
| [20] |
梁少荣, 蔡达健, 陈浩彬, 等. 微波加热金属导体的仿真研究[J]. 建模与仿真, 2021, 10(1): 58-69. LIANG Shaorong, CAI Dajian, CHEN Haobin, et al. Simulation study on microwave heating of metallic conductor[J]. Modeling and Simulation, 2021, 10(1): 58-69. (in Chinese) |
| [21] |
MANIÈRE C, BORIE F, MARINEL S. Impact of convection and radiation on direct/hybrid heating stability of field assisted sintering[J]. Journal of Manufacturing Processes, 2020, 56: 147-157. DOI:10.1016/j.jmapro.2020.04.075 |
| [22] |
王晓娟. 微波辐射下煤储层电磁-热-流-固耦合及数值模拟[D]. 河南焦作: 河南理工大学, 2020 WANG Xiaojuan. Electromagnetic-thermal-hydraulic-mechanica L coupling and numerical simulation of coal reservoir under microwave irradiation[D]. Henan Jiaozuo: Henan Polytechnic University, 2020 (in Chinese) |
| [23] |
TOPCAM H, KARATAS O, EROL B, et al. Effect of rotation on temperature uniformity of microwave processed low-high viscosity liquids: A computational study with experimental validation[J]. Innovative Food Science & Emerging Technologies, 2020, 60: 102306. |
 2025, Vol. 42
2025, Vol. 42





