
水是航天员赖以生存和进行科学研究的物质基础[1],在一般情况下,水由地面上搭载的货运航天器补充,但由于空间站的存储空间非常有限, 由地面货运航天器补充的水成本非常高昂。根据国际空间站资料表明,美国NASA和中国宇航局通过向航天飞机/货运航天器输送的饮用水,人均要花费11 000美元·L-1, 折合成人民币大约7万元[2]。而中国神舟飞船的供水量则是每人平均2.5~3.0 L·d-1,按3.0 L来计算,光是运水,每天就要花费3×7×3=63万元[3]。因此,除了自带外,目前我国空间站采取的办法是废水处理再利用。所以,冷凝水的处理技术对航天事业起了尤为重要的作用,成为各国航天技术研究的热点。
俄罗斯开展冷凝水处理研究较早[4],具体工艺如下:首先冷凝水经过收集储存在罐中,然后被引入装有活性炭的床层,过滤去除非挥发性有机物,然后经过加热后送入催化反应器中,去除无法被吸附的有机物,反应过后流经气体分离器,去除多余的氧气和析出的气体,随后进入一个过滤系统,最后经过接触灭菌和高温灭菌后,作为饮用水进行存储[5]。
活性炭在水处理过程中起了很大的作用,被广泛应用于各种污水处理,如含硝酸盐废水[6]、含铜废水[7]、饮用水的深度处理[8]等。空间站冷凝水处理中,活性炭主要用来吸附冷凝水中的部分大分子有机物。沥青基球形活性炭具有机械强度高、吸附性能好、灰分含量低、微孔发达等优点,与商业颗粒活性炭相比得到了广泛的应用[9-11]。沥青基活性炭所拥有的这些特性十分有利于冷凝水中有机污染物的去除。因此,本研究选用的吸附剂为沥青基球形活性炭。
根据空间站所提供的冷凝水模型,其中包含了苯甲醇、己内酰胺、丙酮、乙酸、N,N-二甲基甲酰胺、乙醇、异丙醇、1.2-丙二醇、乙二醇、甲酸、甲醛和甲醇12种有机物质。由于冷凝水模型中物质种类较多且每种物质含量不同,活性炭对每一种物质的吸附能力也存在很大的差异,所以在实际实验过程中进行每种物质的穿透实验显得费时费力。
本研究通过利用Aspen adsorption V11程序对冷凝水吸附过程进行动态模拟,找出合适的动力学模型,结合吸附等温线,模拟出冷凝水中的12种物质在特定的温度、填充床尺寸和流速下通过特定活性炭的穿透曲线。成功建立穿透模型后,可顺利预测该活性炭对冷凝水的吸附效果。可通过模拟预测不同条件下活性炭对冷凝水的吸附情况,得到吸附效果最为理想的吸附条件,判断活性炭是否符合冷凝水吸附要求,同时也可以预测活性炭在空间站的使用寿命,方便及时更换。
1 实验 1.1 吸附剂和分析方法本研究采用的吸附剂为沥青基球形活性炭(PSAC.太原,中国)。采用Micromeritics ASAP 2020全自动氮气吸附仪测定PSAC在77 K下的氮吸附。比表面积采用Brunauer-Emmett-Teller方法[12]计算。孔隙体积采用密度泛函理论估算,平均孔隙大小采用DFT方法[13]计算。
1.2 冷凝水的制备按表 1所示配制苯甲醇、己内酰胺、丙酮、乙酸、N, N-二甲基甲酰胺、乙醇、异丙醇、1, 2-丙二醇、乙二醇、甲酸、甲醛和甲醇12种有机物质不同浓度的溶液。
| 有机物 | 浓度/(mg·L-1) | 相对分子质量 | 极性 | 溶解度/g |
| 苯甲醇 | 30 | 108.13 | / | 4.29 |
| 己内酰胺 | 5 | 113.16 | / | 456 |
| 丙酮 | 5 | 58.08 | 35.5 | |
| 乙酸 | 60 | 60.05 | 64.8 | |
| N, N-二甲基甲酰胺 | 15 | 73.09 | 40.4 | |
| 异丙醇 | 30 | 60.095 | 54.6 | |
| 乙醇 | 100 | 46.07 | 65.4 | |
| 1, 2-丙二醇 | 25 | 76.09 | 72.2 | |
| 乙二醇 | 30 | 62.068 | 79.0 | |
| 甲醛 | 10 | 30.03 | / | |
| 甲醇 | 10 | 32.04 | 76.2 | |
| 甲酸 | 15 | 46.03 | / |
取25 mL配置完成溶液,加入0.1 g活性炭,放入锥形瓶中,在30 ℃恒温摇床中振荡24 h。(在此之前已对冷凝水中的组分进行了吸附动力学预实验,确定24 h后所有组分都能达到吸附平衡)。随后,取出锥形瓶后静置5 min,用0.45 μm过滤网滤除活性炭,然后用总有机碳分析仪(TOC)测出滤液中总有机碳的含量,最后用公式(1)换算出滤液中剩余有机物的浓度,用公式(2)计算出平衡吸附量qe。按照上述实验依次确定12种物质的吸附等温线,确定等温线模型,为之后的模拟提供依据。
| ce=12nMc | (1) |
| qe=(c0−ce)Vm | (2) |
式(1)和式(2)中:c为滤液中总有机碳的浓度,mg·L-1;c0为溶液初始浓度,mg·L-1;n为每种物质中含碳原子的个数;M为每种有机物所对应的相对分子质量;ce为吸附质平衡浓度,mg·L-1;m为活性炭的质量,g;V是溶液的体积,mL;qe为平衡吸附量,g·L-1。
图 1为固定床流程示意图。吸附柱的内径为10 mm,柱长100 mm。
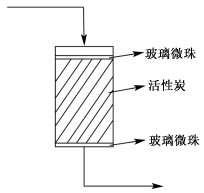
|
| 图 1 固定床流程示意图 Fig.1 Flow diagram of fixed bed |
| |
首先将0.5 g实心玻璃微珠装入吸附柱内,然后装入1.984 9 g活性炭,最后装入等质量的实心玻璃微珠。将吸附柱放入恒温箱内,温度设定为30 ℃,蠕动泵的流量设定为23.63 mL·min-1,在出口处用自动取样器收集样品,并用TOC测定出被处理后的溶液浓度。固定床吸附量q的计算式为式(3):
| q=Vρm[c0L−∫L0c(L)dL] | (3) |
式(3)中:V为进口流速,mL·min-1;ρ为模拟冷凝水的密度,g·mL-1;L为模拟冷凝水的处理量,mL。
2 数学模型 2.1 等温吸附模型Langmuir在1918年从动力学理论推导出单分子层吸附等温线式,Langmuir吸附理论是理想的单层定位吸附理论[14]。Freundlich方程[15]是从经验出发得出的一个经验公式,非常适用于非均匀相表面吸附。Langmuir和Freundlich模型分别见方程(4)和式(5)。
| qe=qmKLce1+KLce | (4) |
式(4)中:KL和qm分别为Langmuir吸附平衡常数(L·g-1)和饱和吸附量(g·L-1)。
| qe=KFc1ne | (5) |
式(5)中:KF吸附平衡常数,量纲随着ce和qe的单位变化;n为吸附平衡常数,无量纲。
IAST模型最早由Radke和Prausnitz针对无限稀释溶液系统提出[16],IAST模型最大的优势在于其有热力学基础,并且在预测多组分的吸附等温线时,只需要实验条件和单组分吸附等温线数据。在活性炭吸附有机物实验中,Edward等[17]通过IAST模型有效描述了多组分吸附的穿透行为。
2.2 固定床传质系数活性炭固定床吸附处理空间站冷凝水的LDF模型基于以下假设:(1)固定床柱在整个运行的过程中是等温的。(2)固定床柱内的流速保持恒定。(3)流体流动被视为平推流,忽略轴向扩散。(4)流体通过固定床柱的压降可忽略不计。
提出这些假设是基于以下几个理由:在固定床动态吸附过程中,有机物浓度远低于1%,属于纯化过程。在纯化过程中,固定床的径向扩散可忽略不计,吸附过程对流体流速和传热的影响也可忽略不计[18]。吸附过程在30 ℃的保温箱内进行并且吸附热可忽略不计,因此该动态吸附可看作等温过程。当Pe大于40时(Pe≈Hb/Rp),固定床的轴向扩散影响可忽略不计[19]。在动态吸附实验中,床层的堆积高度为44.5 mm,吸附剂颗粒半径为0.35 mm,Pe的近似值为127远大于40,因此可忽略轴向扩散的影响。冷凝水模型在固定床内流速恒定,并且轴向扩散和径向扩散均可忽略不计,所以平推流假设是合理的。
在气相吸附中压力的变化会引起吸附质浓度的变化,但是在液相吸附中压力的变化对吸附质浓度的影响可忽略不计,床层压降对液相吸附的影响较小。因此,在动态吸附模拟中没有考虑床层压降的影响。
LDF模型由Glueckaif[20]提出,该方程以线性形式表示内扩散传质速率方程,用1个集成内扩散系数来表示总的内扩散系数,极大简化了内扩散,可表达为式(6)。
| dq dt=ke(qi−q∗i) | (6) |
式(6)中:qi表示吸附剂的平衡浓度;qi*表示吸附剂的平均吸附量;ke为有效传质系数,s-1。
当内扩散系数为表面扩散控制时方程可变为式(7)。
| ke=15DsR2p | (7) |
式(7)中:Ds为表面扩散系数,cm2·s-1;Rp为活性炭颗粒半径,cm。
在该模型中,涉及到2种影响吸附的传质因素,包括了外部传质阻力和内部扩散阻力,这些阻力可以根据Ruthven[21]提出的动量理论来进行计算。
外传质系数kEMTR:
| kEMTR=dp6kf,i | (8) |
内传质系数kIMTR:
| kIMTR=d2p60Dp,iεp | (9) |
同时考虑上述2种因素后可以得出[22]:
| 1ki=dp6kf,i+d2p60Dp,iεp | (10) |
式(8)~式(10)中:i代表吸附质组分,kf,i为外膜传质系数,cm·s-1;dp为活性炭颗粒直径,cm;εp为颗粒孔隙率;Dp,i为有效孔扩散系数,cm2·s-1。
有效孔扩散系数Dp,i可通过Mackie-Meares方程来计算[23, 24]:
| Dp,i=εp(2−εp)2DAB | (11) |
式(11)中:DAB为组分A在溶剂B中的分子扩散系数,cm2·s-1。通常对于非电解质稀溶液,DAB值可通过Wilke-Chang方程进行估算[25]:
| DAB=7.410−8(αMAB)0.5TμV0.6A | (12) |
式(12)中:α为缔合因子,水的缔合因子为2.6;MAB为溶剂B的摩尔质量,g·mol-1;μ为溶液黏度,mPa·s;VA为组分A在常沸点下的摩尔体积,cm3·mol-1;T为绝对温度,K。
估算传质系数kf,i可采用Carberry[26]经验公式:
| kf,iνSc23=1.15(Reεp)−0.5 | (13) |
式(13)中的Schmidt数Sc和Reynolds数Re可由式(14)计算得出。
| Sc=μρDAB,Re=dpνεpρμ | (14) |
式(14)中:ρ为溶液的密度,g·cm-3;ν为流体在床层间隙间的线速度,cm3·g-1。
通过传质Biot数的大小可以判断扩散的控制步骤,如式(15)[27]。
| Bi=kf,iRpεpDp,i | (15) |
根据Hand判断规则[28],当Bi < 0.5时,传质由外膜扩散控制;当0.5<Bi < 30时,传质由内扩散和外扩散共同控制;当Bi>30时,传质由内扩散控制。
2.3 模型验证通常用绝对平均误差(AAD)方程来分析模拟结果与实验值的偏差[22]:
| AAD=1nn∑i=1|cexp−cmodel c0| | (16) |
式(16)中:n为实验数据点的个数;cexp为出口浓度的实验值;cmodel为出口浓度的模拟值。以实验室为规模的前提下,当AAD < 0.05时,模拟结果十分理想;当AAD < 0.1时,模拟结果较为理想;当AAD>0.1时,模拟结果较差。
3 结果与分析 3.1 吸附剂特征空间站冷凝水的吸附实验采用沥青基球形活性炭,为分析样品的孔结构特征,对其进行了表征研究。氮气吸脱附曲线和孔径分布如图 2所示。
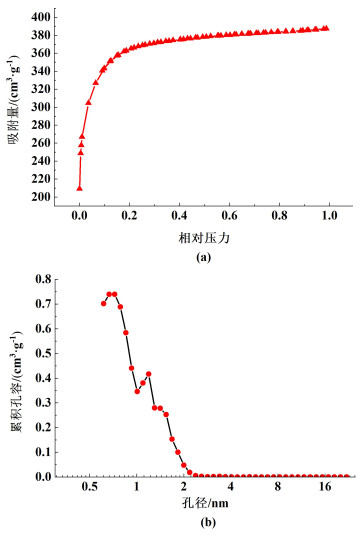
|
| 图 2 (a) 氮气吸脱附曲线;(b)孔径分布图 Fig.2 (a) Nitrogen adsorption desorption curve; (b) pore size distribution |
| |
在图 2(a)中可以看出,p/p0<0.2后,氮气的含量迅速上升,表明活性炭中存在大量微孔,此时出现微孔吸收。随着压力的逐渐上升,吸收量趋于稳定,而且吸附曲线与脱吸附曲线全部吻合,无滞后环,表明活性炭中基本没有中大孔,而以小孔居多。从图 2(b)中,可看出样品的孔普遍集中于2 nm以内,而在1 nm以内的孔则比较发达,是吸附的重点区域。
表 2为活性炭孔结构相关参数。
| 样品 | 比表面积/(cm2·g-1) | 微孔比表面积/(cm2·g-1) | 总孔孔容/(cm3·g-1) | 微孔孔容/(cm3·g-1) |
| 活性炭 | 1 362.321 | 1 274.547 | 0.600 6 | 0.532 |
从表 2中可以看出,样品的总比表面积为1 362.321 cm2·g-1,微孔的总比表面积为1 274.547 cm2·g-1,占总比表面积的93.56%。由DFT法得出,活性炭的总孔孔容为0.600 6 cm3·g-1,微孔孔容为0.532 cm3·g-1,占总孔孔容的88.58%,说明本研究所使用活性炭是微孔型的,进一步说明微孔为吸附的主要部位。
3.2 吸附等温线分别采用Langmuir模型和Freundlich模型对冷凝水中的12种有机物的单组分吸附实验数据进行拟合,点为实验数据,直线为拟合结果。图 3(a)和图 3 (b)分别为Langmuir模型和Freundlich模型的吸附等温线拟合图。
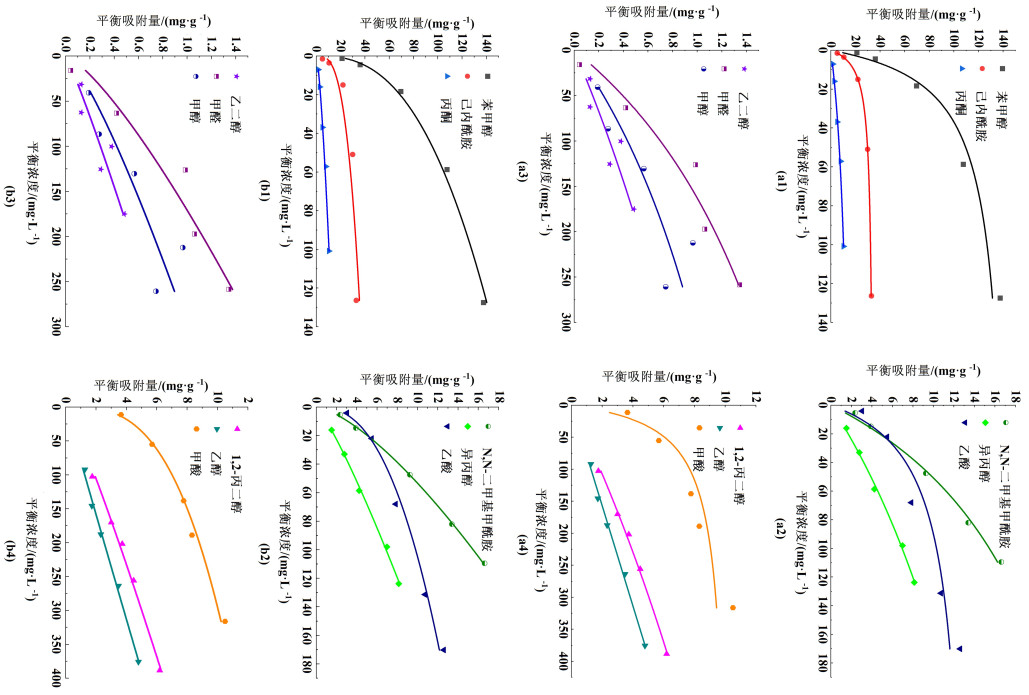
|
| 图 3 (a) Langmuir模型和(b)Freundlich模型的拟合图 Fig.3 Fitting diagram of (a) Langmuir model and (b) Freundlich model fitting diagram |
| |
从拟合结果可以看出,2种模型对于苯甲醇和己内酰胺的拟合效果都较好,但对于乙二醇和甲醇,Langmuir模型的拟合结果偏差较大,远不如Freundlich模型的拟合效果。
为进一步探讨活性炭对冷凝水中有机物的吸附效果,将2种模型的拟合参数列于表 3。由表 3可知,对于乙二醇和甲醇,Langmuir模型的R2分别为0.770 94、0.774 31,偏差较大,说明该模型对这些有机物单组分吸附等温线拟合较差。对于Freundlich模型,从表 3可以看出几乎所有组分的R2都超过0.95,表明Freundlich模型的拟合结果较为理想。KF代表吸附能力,可以通过比较KF的大小来得出样品对于12种有机物的吸附能力顺序为:乙二醇<甲醇<乙醇<丙二醇<甲醛<异丙醇 < N,N-二甲基甲酰胺<丙酮<乙酸<甲酸<己内酰胺<苯甲醇。
| 有机物 | Langmuir | Freundlich | |||||
| qm | KL | R2 | KF | 1/n | R2 | ||
| 苯甲醇 | 150.658 0 | 0.053 44 | 0.998 64 | 23.657 0 | 0.384 45 | 0.985 34 | |
| 己内酰胺 | 35.245 9 | 0.109 30 | 0.994 82 | 5.206 48 | 0.595 44 | 0.984 74 | |
| 丙酮 | 21.132 3 | 0.011 93 | 0.988 18 | 0.645 90 | 0.735 51 | 0.994 07 | |
| 乙酸 | 14.170 6 | 0.026 67 | 0.907 24 | 1.534 76 | 0.402 85 | 0.988 26 | |
| N, N-二甲基甲酰胺 | 35.448 8 | 0.007 73 | 0.991 28 | 0.625 45 | 0.696 89 | 0.998 88 | |
| 异丙醇 | 31.315 8 | 0.002 85 | 0.996 53 | 0.148 12 | 0.833 92 | 0.997 25 | |
| 乙醇 | 23.674 2 | 2.019 1×10-4 | 0.994 53 | 0.016 49 | 0.972 86 | 0.994 72 | |
| 1, 2-丙二醇 | 32.659 3 | 6.082 7×10-4 | 0.993 97 | 0.013 62 | 0.958 21 | 0.986 19 | |
| 乙二醇 | 3.274 7 | 9.639 3×10-4 | 0.770 94 | 0.004 58 | 0.898 08 | 0.829 21 | |
| 甲醛 | 3.126 8 | 0.002 88 | 0.950 12 | 0.036 54 | 0.766 12 | 0.947 95 | |
| 甲醇 | 2.455 5 | 0.002 14 | 0.774 31 | 0.011 09 | 0.789 29 | 0.814 64 | |
| 甲酸 | 10.548 8 | 0.026 91 | 0.833 15 | 1.543 33 | 0.328 53 | 0.994 18 | |
如表 3所显示,除了苯甲醇和己内酰胺之外,其它的化学物质均可与水互溶,说明了苯甲醇和己内酰胺的亲水性都较弱。同时,苯甲醇的水溶解性约为0.042 9 g·g-1,远低于己内酰胺的最大溶解性(4.56 g·g-1),这与吸附能力苯甲醇大于己内酰胺相对应。在本研究体系下,有机物的亲水性大小成为了决定有机物吸附能力强弱的关键因素。
对于甲酸、乙酸、丙酮和N, N-二甲基甲酰胺,它们的吸附能力顺序为甲酸>乙酸>丙酮>N,N-二甲基甲酰胺。从溶解角度看,这些物质都能溶于水,故这些物质与水的亲和度相差不大,因此活性炭与有机物之间的作用力决定了对这些物质的吸附能力。活性炭对非极性物质具有较强的吸附能力[29]。
表 4为活性炭表面官能团含量。
| 基团/(mmol·g-1) | 碱性基团/(mmol·g-1) | 酸性基团/(mmol·g-1) | 内酯基/(mmol·g-1) | 羧基/(mmol·g-1) | 酚羟基/(mmol·g-1) | 酸性基团占比/% |
| 0.86 | 0.22 | 0.64 | 0.27 | 0.36 | 0.01 | 74.42 |
丙酮和N,N-二甲基甲酰胺的极性分别是35.5和40.4,虽然高于乙酸和甲酸,但却与它们的吸附功能完全相反,从表 4可以得知,活性炭中还存在碱式基团,能够与乙酸和甲酸进行相互作用,从而提高了后者在活性炭表面上的吸附。表 5列出了5种烷基醇在平衡浓度为30 mg·L-1时的平衡吸附量以及分子内疏水基团和亲水基团的比值f[30]。
| 有机物 | 吸附量/(mg·g-1) | 疏水-亲水基团比值f |
| 甲醇 | 0.162 50 | 0.882 |
| 乙二醇 | 0.097 15 | 0.824 |
| 1, 2-丙二醇 | 0.354 60 | 1.206 |
| 乙醇 | 0.415 50 | 1.590 |
f值的大小与极性大小相对应,从表 5中可以看出随着f值的增大,吸附量也随之增大。f为疏水基团和亲水基团的比值,f越大表明该物质含有的疏水基团较多,亲水基团较少,亲水性较差,活性炭对其的吸附能力增强[31]。甲醛在平衡浓度小于46 mg·L-1时,平衡吸附量要比乙醇大,但随着浓度的增加其吸附量小于乙醇。这是由于活性炭上存在酚羟基以及其它含氧基团,会与甲醛发生反应[32],促进了其对甲醛的吸附作用,所以当平衡含量很低时,对甲醛的吸收量很大,但同时由于吸收点位的迅速减少,活性炭对甲醛的吸附量也急速减小。
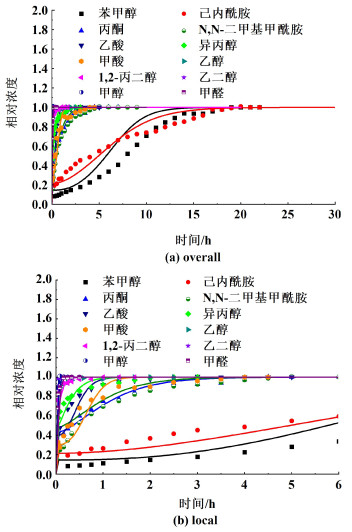
3.3 单组分穿透曲线为了探究固定床对冷凝水中的12种物质的吸附能力,并验证动态吸附模型的合理性,分别做出了每种物质的穿透曲线如图 4和图 5所示,其中实线为模型预测值,点代表实验值。为了使模拟预测值更加准确,分别使用了Langmuir模型和Freundlich模型对吸附值进行了预测。
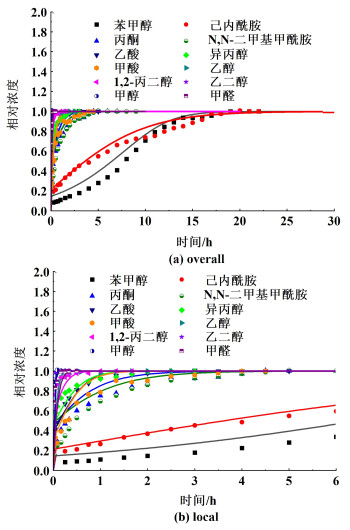
|
| 图 4 基于Langmuir模型的单组分模拟冷凝水穿透曲线模拟结果 Fig.4 Simulation results of one-component condensate penetration curve based on Langmuir model |
| |
|
| 图 5 基于Freundlich模型的单组分模拟冷凝水穿透曲线模拟结果 Fig.5 Simulation results of one-component condensate penetration curve based on Freundlich model |
| |
从图 4和图 5可以看出,无论是哪种模型,除苯甲醇和己内酰胺外,其余物质的出口浓度迅速上升,直至达到饱和,穿透曲线较为陡峭,说明传质速率较快。苯甲醇和己内酰胺的穿透曲线较为平缓,说明其传质速率较慢。
表 6显示了冷凝水中每种吸附质有效传质系数k的估算值,以及所有吸附质的AAD值。
| 有机物 | Dm/(10-5 cm2·s-1) | Dp/(10-6 cm2·s-1) | k | AAD | |
| Langmuir | Freundlich | ||||
| 苯甲醇 | 0.963 7 | 2.972 1 | 0.411 30 | 0.058 336 | 0.087 577 |
| 己内酰胺 | 0.679 6 | 2.095 9 | 0.325 90 | 0.042 242 | 0.055 972 |
| 丙酮 | 1.448 8 | 4.468 1 | 0.177 40 | 0.093 510 | 0.040 346 |
| 乙酸 | 1.583 6 | 4.883 8 | 0.193 91 | 0.020 780 | 0.045 094 |
| N, N-二甲基甲酰胺 | 1.260 7 | 3.888 7 | 0.154 37 | 0.095 363 | 0.088 400 |
| 异丙醇 | 1.316 5 | 4.060 1 | 0.161 20 | 0.049 981 | 0.041 857 |
| 乙醇 | 1.571 8 | 4.847 4 | 0.192 47 | 0.020 242 | 0.018 947 |
| 1, 2-丙二醇 | 1.212 2 | 3.738 4 | 0.148 43 | 0.078 127 | 0.038 287 |
| 乙二醇 | 1.410 2 | 4.349 1 | 0.172 68 | 0.017 357 | 0.002 922 |
| 甲醛 | 2.510 5 | 7.742 3 | 0.307 41 | 0.092 195 | 0.060 334 |
| 甲醇 | 2.046 8 | 6.312 3 | 0.247 78 | 0.007 397 | 0.037 284 |
| 甲酸 | 2.046 8 | 6.312 3 | 0.250 63 | 0.079 141 | 0.067 291 |
可以看出,无论是Langmuir模型或者Freundlich模型,所有物质的AAD值都小于0.1,说明穿透曲线的模拟误差在可接受范围内。虽然每种物质的AAD值均小于0.1,但对于个别物质AAD值依旧偏大(0.05 < AAD < 0.1),同一种物质对于不同的吸附等温线模型的模拟结果也存在较大差别。
从表 6也可以看出,苯甲醇、丙酮和丙二醇对于不同种模型的AAD值存在较大差异。苯甲醇Langmuir模型的AAD值为0.058 336,小于Freundlich的AAD值0.087 577,说明吸附等温线采用Langmuir模型要优于采用Freundlich模型,而这与吸附等温线的拟合的相关性系数R2大小相对应。在吸附等温线的拟合中,Langmuir模型拟合的相关性系数为0.998 64,Freundlich为0.985 34,可以看出,拟合较好的Langmuir模型,其对于动态吸附过程的模拟能够得到更好的模拟结果。这种情况对于丙酮和丙二醇也同样适用。
表 7为N,N-二甲基甲酰胺、甲醛和甲酸模拟的饱和吸附量。
| 有机物 | 实验值 | Langmuir模型拟合结果 | Freundlich模型拟合结果 | ||||||
| 动态 | 静态 | 动态 | AAD | 静态 | 动态 | AAD | |||
| N, N-二甲基甲酰胺 | 1.228 80 | 0.405 90 | 0.943 70 | 0.095 36 | 0.824 60 | 0.955 70 | 0.087 58 | ||
| 甲醛 | 0.027 31 | 0.035 27 | 0.065 32 | 0.092 20 | 0.041 75 | 0.054 62 | 0.060 33 | ||
| 甲酸 | 2.337 20 | 0.433 00 | 1.636 30 | 0.079 14 | 1.798 10 | 1.789 40 | 0.067 29 | ||
对于N, N-二甲基甲酰胺、甲醛和甲酸,它们的AAD值均偏大。可以通过比较静态和动态的吸附饱和量来分析模拟误差来源,其中静态吸附饱和量由吸附等温线来求出。由表 7可知,N, N-二甲基甲酰胺的动态饱和量为1.228 80 mg·g-1,Langmuir模型估算的静态饱和吸附量仅为0.405 90 mg·g-1。因此可以推测Langmuir模型对等温线的预测值偏低是导致N, N-二甲基甲酰胺饱和量预测值偏低的主要原因。而甲醛的动态饱和量低于Langmuir模型估算的静态饱和吸附量,推测出Langmuir模型对等温线的预测值偏高导致甲醛饱和量预测值偏高。基于Freundlich模型,也能得出类似的结论。
对于己内酰胺、乙酸、异丙醇、乙醇、乙二醇和甲醇,它们的Langmuir模型和Freundlich模型拟合结果的AAD值都小于0.5,表明这2种模型对这些组分的预测都很准确,与实际值很接近。
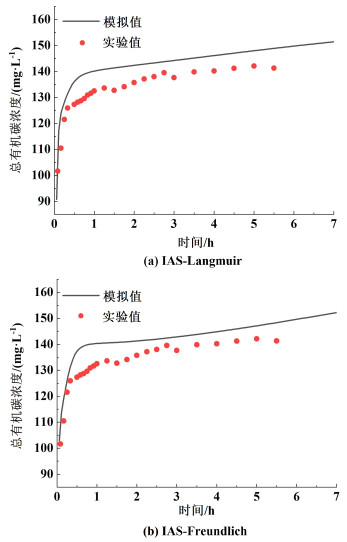
3.4 冷凝水动态吸附穿透曲线在冷凝水动态吸附模拟过程中,多组分吸附等温线分别采用IAS-Freundlich模型和IAS-Langmuir模型,将各组分的模拟值换算成TOC,并在同一时间点进行加和,得到固定床出口TOC值随时间变化情况,结果如图 6所示。
|
| 图 6 基于2种模型冷凝水穿透曲线模拟结果 Fig.6 The simulation results of condensate penetration curve based on two models |
| |
从图 6中可以看出,2种模型所得的模拟值与实验值都比较接近,通过计算它们的AAD值可以发现2种模型的AAD值都小于0.05,表明2种模型均适用于本实验。
3.5 探究不同浓度苯甲醇和己内酰胺对模型的适应性活性炭对苯甲醇和己内酰胺的吸附效果十分显著,但在实际情况中,冷凝水中苯甲醇和己内酰胺的浓度是在不断变化的。因此,需要探究不同浓度的2种物质对模型的适应性是十分重要的。
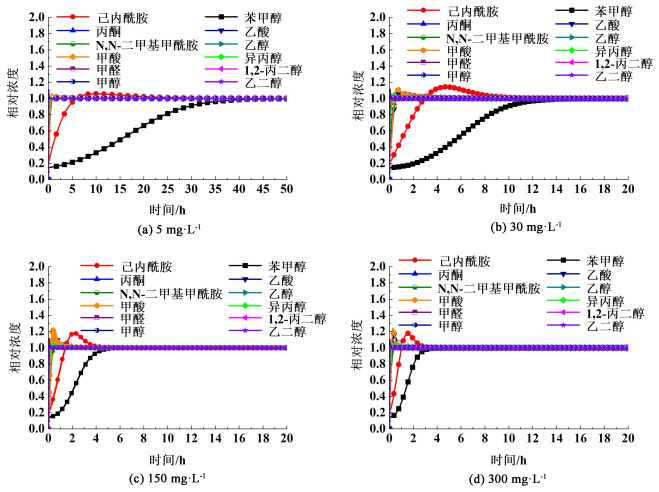
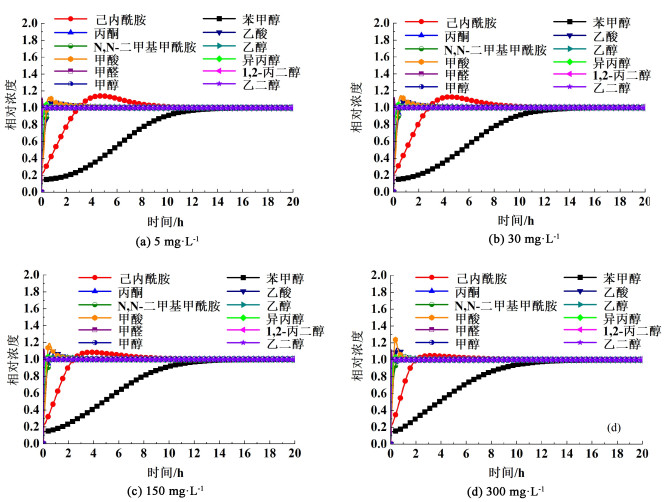
上文已经验证多组分模拟冷凝水动态吸附模型的合理性,通过改变苯甲醇和己内酰胺的初始浓度来探究其对模型的适用性。因此本节采用IAS-Freundlich模型,冷凝水中其余物质的初始浓度保持不变,不同初始浓度下苯甲醇和己内酰胺的模拟结果如图 7和图 8所示。
|
| 图 7 苯甲醇在不同初始浓度下的穿透曲线模拟结果 Fig.7 Simulation results of penetration curves of benzyl alcohol at different initial concentrations |
| |
|
| 图 8 己内酰胺在不同初始浓度下的穿透曲线模拟结果 Fig.8 Simulation results of penetration curves of caprolactam at different initial concentrations |
| |
从图 7可知,随着苯甲醇初始浓度不断增加,其穿透时间发生了很明显的缩短。当苯甲醇浓度为5 mg·L-1时,其穿透时间大概在33.5 h,随着初始浓度的不断增加,其对应的穿透时间也随之出现很大的缩短,当初始浓度为300 mg·L-1时,对应的穿透时间为2.7 h左右,发生了很大的变化。然而这一现象与己内酰胺有很大差异。
如图 8所示,在初始浓度为5 mg·L-1的条件下,己内酰胺达到穿透的时间为2.7 h,随着浓度不断增加,对应的穿透时间却与苯甲醇表现的完全不一样。当初始浓度为30、150和300 mg·L-1时,对应的穿透时间分别为2.5、2.1和1.7 h。在相同的浓度梯度下,己内酰胺的穿透时间变化与苯甲醇相比更为稳定。但这种现象却与前文的结论相反。由3.2中的结论可知,苯甲醇的吸附能力是大于己内酰胺的,因此,在相同浓度梯度的情况下,苯甲醇的穿透时间变化应该要比己内酰胺稳定。模拟结果与实际存在很大差异,可以推断出当冷凝水中苯甲醇含量较高时,IAS-Freundlich模型无法准确预测苯甲醇的实际穿透曲线,IAS-Freundlich模型对含有高浓度苯甲醇的冷凝水的穿透曲线预测情况较差,但是IAS-Freundlich模型对高浓度的己内酰胺穿透曲线仍然具有良好的预测性。
4 结论沥青球基活性炭对冷凝水中的有机物吸附顺序具体表现为:乙二醇<甲醇<乙醇 < 1, 2-丙二醇<甲醛<异丙醇 < N, N-二甲基甲酰胺<丙酮<乙酸<甲酸<己内酰胺<苯甲醇。其中活性炭对苯甲醇和己内酰胺具有出色的吸附能力,对其它有机物的吸附能力较弱,这可能因为苯甲醇和己内酰胺在水中的溶解度较小,与水之间的亲和力较弱。冷凝水的动态吸附模拟结果表明,多组分吸附等温线符合IAS-Langmuir模型和IAS-Freundlich模型,传质模型符合LDF模型。以IAS-Freundlich模型为例,讨论了不同初始浓度梯度的苯甲醇和己内酰胺对模型的适应性。从结果可以看出,当冷凝水中苯甲醇浓度较高时,对IAS-Freundlich模型的适应性比较差,模型无法准确预测冷凝水的穿透情况。对于己内酰胺,不同浓度下,该模型依旧具有良好的预测性。因此,当实际冷凝水中苯甲醇含量大于10%时,该模型无法准确预测冷凝水的实际穿透情况。
| [1] |
卢勋. 空间站冷凝水制备生活用水工艺研究[D]. 哈尔滨: 哈尔滨工业大学, 2017 LU Xun. Study on preparation of domestic water by condensed water from space station[D]. Harbin: Harbin Institute of Technology, 2017 (in Chinese) |
| [2] |
管春磊, 余青霓. 俄罗斯空间站水回收和管理系统及其使用经验[J]. 载人航天信息, 2011(3): 1-14. GUAN Chunlei, Yu Qinxia. Russian space station water recovery and management system and its use experience[J]. Manned Space Information, 2011(3): 1-14. (in Chinese) |
| [3] |
杨松林, 丁平, 赵成坚, 等. 中国空间站水回收系统关键技术分析[J]. 航天医学与医学工程, 2013, 26(3): 221-226. YANG Songlin, Ding Ping, Zhao Chenjian, et al. Key technologies of water recovery system in China space station[J]. Aerospace Medicine and Medical Engineering, 2013, 26(03): 221-226. (in Chinese) |
| [4] |
MITCHELL K L, BAGDIGIAN R M, CARRASQUILLO R L. Technical assessment of MIR-1 life support hardware for the international space station, NASA TM1994-108441[R]. Washington D C: NASA, 1994
|
| [5] |
PARKE R D S, O'CONNOR E W, BAGDIGIAN I R. Water reclamation system design[J]. SAE paper, 1999, 1: 950. |
| [6] |
柴丽娜. 聚吡咯改性废菌渣活性炭对水中硫酸盐和硝酸盐吸附研究[D]. 太原: 太原理工大学, 2022 CHAI Lina. Study on adsorption of sulfate and nitrate in water by polypyrrole modified activated carbon[D]. Taiyuan: Taiyuan University of Technology, 2022 (in Chinese) |
| [7] |
许智华, 张道方, 陈维芳. 纳米铁/活性炭新型材料的制备及其对铜离子的吸附性能研究[J]. 水资源与水工程学报, 2015, 26(2): 7-11. XU Zhihua, ZHANG Daofang, CHEN Weifang. Research on preparation of a new material of nano-iron and activated carbon with its adsorptive properties to copper ion[J]. Journal of Water Resources and Water Engineering, 2015, 26(2): 7-11. (in Chinese) |
| [8] |
朱鹏宇. 饮用水处理吸附用活性炭的多指标耦合选炭方法研究[D]. 济南: 山东建筑大学, 2022 ZHU Pengyu. Study on multi-index coupling carbon selection method of activated carbon for drinking water treatment and adsorption[D]. Jinan: Shandong Jianzhu University, 2022 (in Chinese) |
| [9] |
MA L, HE M, FU P, et al. Adsorption of volatile organic compounds on modified spherical activated carbon in a new cyclonic fluidized bed[J]. Separation and Purification Technology, 2020, 235: 116146. DOI:10.1016/j.seppur.2019.116146 |
| [10] |
KAMEDA T, HORIKOSHI K, KUMAGAI S, et al. Adsorption of urea, creatinine, and uric acid onto spherical activated carbon[J]. Separation and Purification Technology, 2020, 237: 116367. DOI:10.1016/j.seppur.2019.116367 |
| [11] |
HOSHI T, ENDO M, HIRAI A, et al. Encapsulation of activated carbon into a hollow-type spherical bacterial cellulose gel and its indole-adsorption ability aimed at kidney failure treatment[J]. Pharmaceutics, 2020, 12(11): 1076. DOI:10.3390/pharmaceutics12111076 |
| [12] |
BRUNAUER S, EMMETT P H, TELLER E. Adsorption of gases in multimolecular layers[J]. Journal of the American Chemical Society, 1938, 60(2): 309-319. DOI:10.1021/ja01269a023 |
| [13] |
BARRETT E P, JOYNER L G, HALENDA P P. The determination of pore volume and area distributions in porous substances. Ⅰ. Computations from nitrogen isotherms[J]. Journal of the American Chemical Society, 1951, 73(1): 373-380. DOI:10.1021/ja01145a126 |
| [14] |
LANGMUIR I. The adsorption of gases on plane surfaces of glass, mica and platinum[J]. Journal of the American Chemical Society, 1918, 40(9): 1361-1403. DOI:10.1021/ja02242a004 |
| [15] |
FREUNDLICH H. Vber Die adsorption in lösungen[J]. Zeitschrift Für Physikalische Chemie, 1907, 57U(1): 385-470. DOI:10.1515/zpch-1907-5723 |
| [16] |
RADKE C, PRAUSNITZ J. Thermodynamics of multi-solute adsorption from dilute liquid solutions[J]. AIChE Journal, 1972, 18: 761-768. DOI:10.1002/aic.690180417 |
| [17] |
SMITH E H, WEBER W J. Modeling activated carbon adsorption of target organic compounds from leachate-contaminated groundwaters[J]. Environmental Science & Technology, 1988, 22(3): 313-321. |
| [18] |
GUTIÉRREZ O F J, BARRAGÁN R M, YANG R. Modeling of fixed-bed columns for gas physical adsorption[J]. Chemical Engineering Journal, 2019, 378: 121985. DOI:10.1016/j.cej.2019.121985 |
| [19] |
RAGHAVAN N S, RUTHVEN D M. Numerical simulation of a fixed-bed adsorption column by the method of orthogonal collocation[J]. AIChE Journal, 1983, 29(6): 922-925. DOI:10.1002/aic.690290608 |
| [20] |
GLUECKAUF E. Theory of chromatography. Part 10. Formula for diffusion into spheres and their application to chromatography[J]. Trans Faraday Soc, 1955, 51: 1540-1551. DOI:10.1039/TF9555101540 |
| [21] |
RUTHVEN D M. Principles of adsorption and adsorption processes[J]. Journal of Colloid and Interface Science, 1984, 106(2): 567. |
| [22] |
SIAHPOOSH M, FATEMI S, VATANI A. Mathematical modeling of single and multi-component adsorption fixed beds to rigorously predict the mass transfer zone and breakthrough curves[J]. Iranian Journal of Chemistry and Chemical Engineering, 2009, 28(3): 25-44. |
| [23] |
GU T, TSAO G T, TSAI G J, et al. Displacement effect in multicomponent chromatography[J]. AIChE Journal, 1990, 36(8): 1156-1162. DOI:10.1002/aic.690360805 |
| [24] |
GU T, TSAI G J, TSAO G T. New approach to a general nonlinear multicomponent chromatography model[J]. AIChE Journal, 1990, 36(5): 784-788. DOI:10.1002/aic.690360517 |
| [25] |
WILKE C R, CHANG P. Correlation of diffusion coefficients in dilute solutions[J]. AIChE Journal, 1955, 1(2): 264-270. DOI:10.1002/aic.690010222 |
| [26] |
CARBERRY J J. A boundary-layer model of fluid-particle mass transfer in fixed beds[J]. AIChE Journal, 1960, 6(3): 460-463. DOI:10.1002/aic.690060323 |
| [27] |
YAO C, ZHU C. A new method of characterizing mass transfer controlling mechanism in pollutant adsorption from aqueous solutions[J]. Journal of Molecular Liquids, 2020, 301: 112455. |
| [28] |
HAND D W, CRITTENDEN J C, THACKER W E. Simplified models for design of fixed-bed adsorption systems[J]. Journal of Environmental Engineering, 1984, 110(2): 440-456. |
| [29] |
王靖诗, 梁晓怿, 崔广志, 等. 球形活性炭对空间站舱室冷凝水模型中微量有机物吸附的研究[J]. 航天医学与医学工程, 2015, 28(1): 52-57. WANG Jingshi, LIANG Xiaoyi, CUI Guangzhi, et al. Research on adsorption of trace organics in condensated water model of space station cabin by globular activated carbon[J]. Space Medicine & Medical Engineering, 2015, 28(1): 52-57. (in Chinese) |
| [30] |
肖芳, 寇晓康, 王亚宁, 等. 后交联型St-DVB大孔吸附树脂对低级醇类的吸附性能研究[J]. 离子交换与吸附, 2004, 20(2): 152-157. XIAO Fang, KOU Xiaokang, WANG Yaning, et al. Studies on adsorption properties for low carbon alcohols with backcrosslinked St-DVB macroporous resins[J]. Ion Exchange and Adsorption, 2004, 20(2): 152-157. (in Chinese) |
| [31] |
LIU Z, LING L, QIAO W, et al. Effects of various metals and their loading methods on the mesopore formation in pitch-based spherical activated carbon[J]. Carbon, 1999, 37(8): 1333-1335. |
| [32] |
安凯博, 王忠华, 武传燕, 等. 活性炭对甲醛吸附的强化方法及模拟研究[J]. 当代化工, 2021, 50(8): 1952-1955. AN Kaibo, WANG Zhonghua, WU Chuanyan, et al. Enhancement method and simulation study of activated carbon adsorption of formaldehyde[J]. Contemporary Chemical Industry, 2021, 50(8): 1952-1955. (in Chinese) |
 2025, Vol. 42
2025, Vol. 42






