2. 中国科学院山西煤炭化学研究所, 太原 030001
2. Institute of Coal Chemistry, Chinese Academy of Sciences, Taiyuan 030001, China
芳烃作为一种重要的化工材料[1],广泛应用于能源、交通和服饰贸易等方面,在我国拥有巨大的市场需求量[2-4]。由于我国呈现“富煤贫油少气”的能源特征,煤基甲醇制芳烃(MTA)工艺可以有效降低芳烃生产成本,因而极具研究价值[5-7]。芳烃中轻质芳烃(BTX)的收率极大影响了该工艺的经济价值,因此建立高精度模型来准确预测MTA产物BTX的收率就成为了一个重要课题。
施丽丽等[8]和徐亚荣等[9]对甲醇制芳烃的反应动力学进行研究,建立五集总稳态动力学模型,但分别设定了等温条件和消除内外扩散作用对反应影响的前提条件。这些机理建模针对使用场景和使用目的均进行不同程度的假设和简化,使用条件苛刻,得到的模型对实际生产的指导意义有限。许雄飞等[10]提出一种用于两段法甲醇制芳烃产物预测的多元非线性模型,具有预测精度高、计算量小的优势。刘鹏龙等[11]提出一种K-means-PSO-SVR局部建模方法用于甲醇制芳烃产物预测,并通过优化寻找最优工况条件。以上数据建模只针对获得的数据挖掘信息建立黑箱模型,摆脱了对反应机理的依赖,相比于机理模型有更好的适用性。
但传统数据搭建的软测量模型的精度很大程度上取决于样本容量的大小,考虑到MTA工艺过程复杂,副反应多,反应参数的非线性强,反应流程长,数据获取的时间成本高,且MTA工艺过程数据有着化工行业生产数据的共性问题,即稳定运行时数据量大,但样本趋同,多样性差,用于建模的有效数据少,不同工况下数据信息间隔大,这导致MTA工艺过程数据呈现出“大数据,小样本”的特征[12-14]。因此,通过合理方法填补MTA小样本数据的信息间隔,有利于建立产物的精确预测模型。
针对上述分析,目前主要有机器学习、灰色理论以及虚拟样本生成技术等研究方向,机器学习的小样本建模方法比较典型的有支持向量机(SVM)、随机森林(RF)、K最近邻算法(KNN)、决策树(DT)、卷积神经网络(CNN)和生成式对抗网络(GAN)等。该方法多用于图像分类、模式识别等领域;灰色理论主要研究的是“外延明确,内涵不明确”的小样本问题,不适用于数学分布不均匀的数据;而虚拟样本生成技术(Virtual sample generation, VSG)按照生成思想可分为3类[15]:(1)基于信息扩散的虚拟样本生成,这类方法的主要理论基础是信息扩散和模糊理论。朱宝等[16]提出一种整体趋势扩散技术生成虚拟样本并应用于精对苯二甲酸生产过程中的电导率预测;陆荣秀等[17]提出一种基于混合虚拟样本生成的稀土萃取过程组分含量预测方法;Chen等[18]提出一种树趋势扩散模型(TBTD),该模型基于趋势扩散和树形结构建立,是专门面向制造业中小样本数据集问题设计的。(2)基于特征表达的虚拟样本生成,采用在原始样本的特征空间合成虚拟样本的生成策略,典型的方法包括基于核空间的虚拟样本生成方法、神经网络插值方法、基于奇异值分解的虚拟样本生成方法[15]等。Zhu等[19]先利用距离准则识别信息空隙区域再进行Kriging插值;Zhang等[20]先采用流形学习Isomap识别样本稀疏区域再进行插值;Chen等[21]先采用查询策略获取稀疏区域再插值。(3)基于深度学习的虚拟样本生成,深度学习是含有多隐含层的深度人工神经网络模型,基于深度学习的虚拟样本生成技术的典型方法包括变分自编码器(VAE)及生成式对抗网络(GAN)。Wang等[22]提出一种模块化设计的变分自编码器,用于学习并自动生成音乐旋律;陈忠圣等[23]中提出了QRCGAN模型,将回归器作为条件模型加入到GAN的对抗结构中,通过调整分位数回归的置信区间范围来提高虚拟样本生成质量。
本研究基于信息扩散的思想提出利用多分布趋势扩散技术的虚拟样本生成方法,结合遗传算法(GA)优化的极限学习机对该过程进行建模,并通过MTA实验数据对比原始模型和单一优化模型,验证该建模方法的合理性、有效性和泛化性。
1 MTA工艺流程及数据准备MTA反应机理极其复杂,主要有甲醇脱水生成二甲醚反应、烯烃的生成反应、以及烯烃发生聚合氢转移、环化脱氢等二次反应生成芳烃和氢转移生成烷烃等反应类型。本研究基于两段式固定床甲醇制芳烃的小试装置,主要原料包括甲醇及催化剂,其中一段反应器所用催化剂为HZSM-5催化剂,二段反应器所用催化剂为Zn改性的ZSM-5催化剂。
该小试装置的工艺流程如下:甲醇通过平流泵预热气化后分别进入一段反应器和二段反应器,催化剂装填在反应器的中间部分,2个反应器分别设有6个测温点来采集反应的中心温度。经过两段反应器的反应,高温产物经冷却循环系统进行冷凝,通过气液分离罐后液相产物进入储罐,由储罐出口取样分析。气相产物通过湿式流量计计量后收集分析。
甲醇制芳烃一段反应器主要是甲醇制烯烃,二段反应器里是未反应完的甲醇和烯烃在催化剂作用下转化为以芳烃为主的产物。温度、空速和压力作为影响MTA反应的主要因素,会影响到BTX的收率[12]。反映到两段式固定床MTA工艺中,这些工艺条件分别是:压力(p)、甲醇体积空速(τ)、一段中心温度(T1)、二段中心温度(T2)。参考相关文献[7, 24, 25]确定变动范围如表 1。
| 工艺条件 | p/MPa | τ/h-1 | T1/℃ | T2/℃ |
| 上限 | 0.8 | 0.5 | 510 | 510 |
| 下限 | 0 | 0.1 | 390 | 450 |
实验完成后,从装置尾端的产品罐中取出液相产物进行称量记录和成分检测,然后对实验收集到的生产数据进行预处理。通过对反应过程的质量守恒计算,并对数据进行初步筛选,考虑到实验的操作性误差,去除离群点后获得的部分实验数据如表 2所示。
| 序号 | p/MPa | τ/h-1 | T1/℃ | T2/℃ | BTX收率/% |
| 1 | 0.66 | 0.2 | 476 | 465 | 21.23 |
| 2 | 0.86 | 0.2 | 397 | 450 | 28.32 |
| 3 | 0.84 | 0.2 | 399 | 510 | 29.41 |
| 4 | 0.88 | 0.2 | 402 | 480 | 28.76 |
| … | … | … | … | … | … |
| 70 | 0.88 | 0.5 | 462 | 450 | 44.55 |
| 71 | 0.85 | 0.5 | 455 | 510 | 47.40 |
考虑到经济成本及时间成本,本实验数据是依据Design-expert软件设计的4因素5水平的试验方案所得,因此很难反映真实样本空间的全部特征,数据分布离散,只能提供一定的有效信息,用传统数据建模方式得到的产物预测模型的精度较低。
2 MD-MTD虚拟样本生成方法Poggio在图像识别领域首先提出了虚拟样本(VSG)[26]的思想,虚拟样本是指在未知样本概率分布函数的情况下,利用所研究的领域的先验知识,结合已有的训练样本产生待研究问题的样本。Niyogi等[27]从数学上证明了通过领域先验知识构造的虚拟样本能够像真实样本一样提供信息有效扩展训练集。针对本研究来说,虚拟样本即是基于原始MTA数据集,通过多分布趋势扩散技术结合数据模型获得的新样本集。
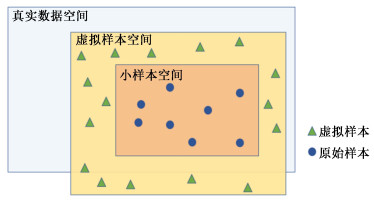
VSG的本质是根据原始小样本尽可能生成符合真实数据分布的虚拟样本。虚拟样本、原始样本、虚拟样本空间、小样本空间和真实数据空间之间的关系如图 1所示。
|
| 图 1 真实样本与虚拟样本的关系 Fig.1 Relationship between real sample and virtual sample |
| |
由图 1可知,小样本集是真实数据集的子集,不能全面表征实际数据空间,且小样本在实际数据空间中分布不均匀,提供的信息是离散且稀疏的。通过添加虚拟样本填补信息空缺,使虚拟样本空间尽可能靠近实际数据空间,同时采用F检验的方法判断虚拟样本的合理性,尽可能排除不符合真实数据空间的“坏”样本的影响,以便更好的描述总体特征。
多分布整体趋势扩散技术(MD-MTD[16])是一种基于分布思想的虚拟样本生成技术。该方法根源于模糊数学和信息扩散,通过三角隶属度函数来估计总体分布并非对称的扩大属性区间,并在不同取值区间采用不同的分布来描述数据属性分布,避免了增加虚拟属性,有着良好的适用性。
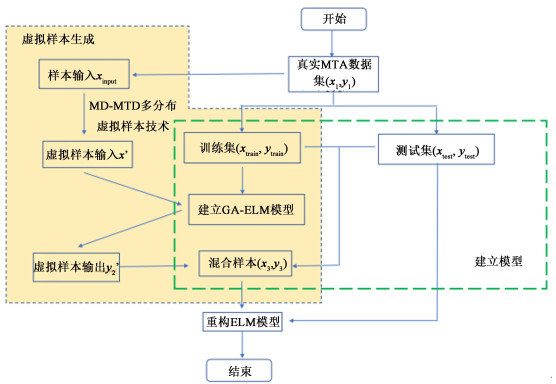
本研究基于MD-MTD技术建立MTA产物预测模型的流程如图 2所示。
|
| 图 2 MD-MTD-GA-ELM工作流程 Fig.2 MD-MTD-GA-ELM workflow |
| |
首先,利用真实MTA数据集结合遗传算法(GA)优化的极限学习机建立合适的BTX预测模型,然后用MD-MTD获得虚拟样本输入属性,通过预测模型得到完整的虚拟样本集,将虚拟样本集与原样本集混合后重构预测模型并测试其性能。
2.1 MD-MTD工作流程针对MTA工艺输入属性压力(p)、甲醇体积空速(τ)、一段中心温度(T1)、二段中心温度(T2),记为X=[x1, x2, x3, x4],利用MD-MTD方法扩展属性区间如下:记小样本属性区间的上下限分别为max、min,拓展后的上下限分别为UB、LB。在X的属性区间[min,max]内已知其分布,利用三角分布产生不均匀虚拟样本,在拓展区域[LB,min]和[max,UB]内未知分布,采用均匀分布产生虚拟样本。
(1) 计算X的数据中心点M,公式为:
| $ M=\operatorname{median}(x)=\left\{\begin{array}{cl} x_{\left[\frac{n+1}{2}\right]} & n \text { 为奇数 } \\ \frac{1}{2}\left(x_{\left[\frac{n}{2}\right]}+x_{\left[\frac{n}{2}+1\right]}\right) & n \text { 为偶数 } \end{array}\right. $ | (1) |
各属性区间中心点如表 3。
(2) 计算中心点的左偏度SKL和右偏度SKU:
| $ S_{\mathrm{KL}}=\frac{N_{\mathrm{L}}}{N_{\mathrm{U}}+N_{\mathrm{L}}+S_{\mathrm{P}}} $ | (2) |
| $ S_{\mathrm{KU}}=\frac{N_{\mathrm{U}}}{N_{\mathrm{U}}+N_{\mathrm{L}}+S_{\mathrm{P}}} $ | (3) |
式(2)和式(3)中:NL表示小于样本中心点的样本数;NU表示大于样本中心点的样本数;SP是修正参数,本研究计算中取SP=1[16]。
计算结果如表 4。
| 输入属性 | x1 | x2 | x3 | x4 |
| SKL | 0.54 | 0.67 | 0.48 | 0.69 |
| SKU | 0.44 | 0.32 | 0.51 | 0.29 |
(3) 确定属性扩展的上下边界UB和LB,计算公式如式(4)和式(5)。
| $ L_{\mathrm{B}}=\left\{\begin{array}{cl} M-S_{\mathrm{KL}} \sqrt{-2 \times \frac{\hat{S_{\mathrm{x}}^2}}{N_{\mathrm{L}}} \times \ln \left(10^{-20}\right)} & L_{\mathrm{B}} \leqslant \min \\ \min & L_{\mathrm{B}}>\min \end{array}\right. $ | (4) |
| $ U_{\mathrm{B}}=\left\{\begin{array}{cl} M+S_{\mathrm{KU}} \sqrt{-2 \times \frac{\hat{S_{\mathrm{x}}^2}}{N_{\mathrm{U}}} \times \ln \left(10^{-20}\right)} & U_{\mathrm{B}} \geqslant \max \\ \max & U_{\mathrm{B}}<\max \end{array}\right. $ | (5) |
式(4)和式(5)中:
| $ \hat{S}_x^2=\frac{\sum\nolimits_{i-1}^n(x-\bar{x})^2}{n-1} $ | (6) |
计算结果如表 5。
| 输入属性 | x1 | x2 | x3 | x4 |
| UB | 1.27 | 0.59 | 575.27 | 523.89 |
| LB | 0 | 0 | 323.48 | 380.59 |
(4) 生成虚拟样本属性,在[LB,min]区域内:
| $ x=L_{\mathrm{B}}+s\left(\min -L_{\mathrm{B}}\right) $ | (7) |
在[min,max]区域内:
| $ x=\left\{\begin{array}{l} L_{\mathrm{B}}+\sqrt{s\left(M-L_{\mathrm{B}}\right)\left(M-L_{\mathrm{B}}\right)} \\ ~~~~~0<s<\frac{U_{\mathrm{B}}-M}{U_{\mathrm{B}-} L_{\mathrm{B}}} \\ U_{\mathrm{B}}-\sqrt{(1-s)\left(M-L_{\mathrm{B}}\right)\left(U_{\mathrm{B}}-M\right)} \\ \\ ~~~~~\frac{U_{\mathrm{B}}-M}{U_{\mathrm{B}}-L_{\mathrm{B}}}<s<1 \end{array}\right. $ | (8) |
在[max,UB]区域内:
| $ x=\max +s\left(U_{\mathrm{B}}-\max \right) $ | (9) |
式(8)和式(9)中:s表示在[0, 1]上服从均匀分布的随机数。
按照上述MD-MTD方法得到虚拟样本输入属性,为了保证虚拟样本输出的可靠性,查阅文献[28]后发现:如果总体超平面H和小样本推估超平面H^分别充分反应了总体和小样本的特征,为了得到更符合小样本特征的虚拟样本,一般H^的平均绝对百分比误差(MAPE)不大于10%,此时可以通过H^产生与虚拟输入X对应的虚拟输出Y。因此必须利用合适的可通过合适的监督式学习方法建立起总体超平面H和小样本集推估超平面H^, 本研究采用的是遗传算法优化的极限学习机模型。
2.2 GA-ELM模型建立极限学习机模型(Extreme learning machine,ELM)[29]是由黄广斌教授等提出的单隐藏层神经网络(Single-hidden layer feedforward neural network, SLFN),该模型采用的是一种全新快速的学习方式。极限学习机随机选取输入层权重和隐藏层偏置,输出层权重通过最小化由训练误差项和输出层权重范数的正则项构成的损失函数,依据Moore-Penrose(MP)广义逆矩阵理论计算解析求出。理论研究表明,即使随机生成隐藏层节点,ELM仍保持SLFN的通用逼近能力;且相比传统BP神经网络,ELM具有训练参数少、学习速度快、占用计算资源少和易取得全局最优的优点。故选择ELM模型作为产物预测模型。
由ELM原理可知,只需设置隐藏层节点数就能构建ELM模型,节点数的多少直接影响模型的学习效果,Michalbpoulos等[30]经研究提出可使用输入层神经元个数和输出层神经元个数来大致计算神经网络隐含层节点数,其计算如式(10)。
| $ H=\sqrt{m+n}+L(1 \leqslant L \leqslant 10) $ | (10) |
式(10)中:m是输入层节点数,n是输出层节点数,L是常数,H是节点数,L取值可调整。利用上述公式可计算出1个节点数的大致范围,随后在这个范围内进行测试,确定最优节点数。
针对MTA小样本数据集,在71组数据集中选60组作为训练集,11组为测试集,建立ELM模型,以模型输出结果和测试集的相对误差为评价标准,计算最优节点数。m=4,n=1,H的大致范围是[3, 13],按照取值范围构建不同隐含层节点数的神经网络,并计算网络输出与测试集的平均绝对误差,根据平均绝对误差的变化趋势确定是否继续往该取值方向构建神经网络。经计算,当节点数为5时模型精度相对最高,确定模型隐藏层节点数为5。
为了保证对应的虚拟样本输出的可靠性,对原始样本建立的ELM模型有一定的精度要求。因此,本研究采用计算效率高、具有优秀全局搜索能力的GA优化算法,对所建立的ELM模型的超参数进行优化,使模型满足预设的误差阈值。GA算法数学描述为:
| $ \begin{aligned} & \min : \quad g(x) \text { ubject to}: \min \leqslant x_t \leqslant \max , \\ & ~~~~~~~~~~~~~~~~~~~\quad t=1, 2, \cdots, n_t \\ & ~~~~~~~~~~~~~G_k(x) \leqslant 0, k=1, 2, \cdots, n_{\mathrm{c}} \end{aligned} $ |
其中:g(x)是优化的适应度函数,本研究中选择为平均绝对百分比误差(MAPE),其阈值条件为MAPE≤10%,xt={x1, x2, …, xn}是n个决策变量。原始小样本集为S1=(X1,Y1),通过MD-MTD-GA-ELM方法得到的虚拟样本数据集为S2=(X2,Y2)。本研究采用的GA算法参数如下:种群数N=100,遗传代数F=200,交叉概率p1=0.9, 变异概率p2=0.01,代沟GGAP为0.9。
综上,可获得完整的虚拟样本集,部分数据如表 6所示。
| 序号 | p/MPa | τ/h-1 | T1/℃ | T2/℃ | BTX收率/% |
| 1 | 0.44 | 0.19 | 370.4 | 456.4 | 32.72 |
| 2 | 0.51 | 0.22 | 385.2 | 468.9 | 33.59 |
| 3 | 0.58 | 0.24 | 440.1 | 477.9 | 31.97 |
| 4 | 0.69 | 0.29 | 490.0 | 491.9 | 28.55 |
| … | … | … | … | … | … |
| 49 | 0.95 | 0.46 | 523.6 | 531.0 | 36.49 |
| 50 | 1.03 | 0.53 | 536.5 | 538.9 | 38.88 |
为了检验生成的VSG混合样本与原始小样本分布的符合程度,验证所生成的虚拟数据的合理性,定义η作为评价数据集a和b的分布相似度指标[31],定义如式(11)。
| $ \eta=\frac{1}{N} \sum\limits_{i=1}^N D_{\mathrm{H}}\left(p_{\mathrm{s} 1}^i \| p_{\mathrm{s} 2}^i\right) $ | (11) |
式(11)中:N表示数据集a和b的属性数量; ps1和ps2分别表示si1∈a和si2∈b的概率分布;DH表示数据集a和b属性的Hellinger距离, 这是F散度的一种, 本研究中用于度量2个概率分布的相似度, 定义如式(12)。
| $ D_{\mathrm{H}}\left(p_{\mathrm{s} 1}^i \| p_{\mathrm{s} 2}^i\right)=\sqrt{\frac{\sum\nolimits_x\left[\sqrt{p_1(x)}-\sqrt{p_2(x)}\right]^2}{2}} $ | (12) |
根据Hellinger距离定义,η取值范围[0, 1]。当η越趋近0时,说明2个分布相似度越高,生成的虚拟样本质量越好。
采用测试集的平均绝对百分比误差(MAPE)和决定系数(R2)表现作为模型性能的评价指标,MAPE用来度量模型预测的精准度,R2用来度量模型预测值的拟合度优劣,定义如下:
| $ \text { MAPE }=\frac{1}{n} \sum\limits_{i=1}^n\left|\frac{y_i-\hat{y}_i}{y_i}\right| $ | (13) |
| $ R^2=\frac{\sum\limits_{i=1}^n\left(\hat{y}_i-\bar{y}_i\right)^2}{\sum\limits_{i=1}^n\left(y_i-\bar{y}_i\right)^2} $ | (14) |
将原始小样本71组数据集中,随机划分60组作为训练集,剩余11组作为测试集,设置对比实验。a组:以原始小样本建立的ELM产物预测模型,b组:以原始小样本建立的GA-ELM产物预测模型,c组:以混合样本S3建立的ELM产物预测模型,均采用原数据集中的预留测试集测试回归效果。每组别均做10次重复试验,取模型评价指标的平均值。
3.2.1 合理性分析向MTA小样本集依次添加虚拟样本,以10组为间隔,按照3.1所提的合理性原则,计算样本分布相似度,表 7为各实验组计算结果。
| 特征数 | 添加虚拟样本数 | η |
| 4 (p、τ、T1、T2) |
10 | 0.55 |
| 20 | 0.50 | |
| 30 | 0.49 | |
| 40 | 0.54 | |
| 50 | 0.68 |
由表 7可知,本研究所用方法建立的虚拟样本分布,与原小样本数据空间的分布拟合度均落在了合理范围内,证明了利用该方法得到的虚拟样本的合理性。同时注意到η先减小后增大,说明添加的虚拟样本数量存在1个最佳取值。
3.2.2 有效性分析利用a、b和c组模型分别对MTA主要产物BTX的收率进行预测,各个模型在预测集上的表现情况如表 8。
| 虚拟样本数量 | a组 MAPE |
b组 MAPE |
c组 MAPE |
性能提升/% |
| 0 | 0.203 | 0.085 | ||
| 10 | 0.079 | 7 | ||
| 20 | 0.077 | 9 | ||
| 30 | 0.065 | 24 | ||
| 40 | 0.068 | 20 | ||
| 50 | 0.067 | 21 |
分析表 8,对比a组和b组可以发现,由于原始MTA数据集的数量少,样本信息缺失,以此建立的原始ELM模型预测平均绝对百分比误差超过了20%,难以做出有效预测,而GA优化后的ELM模型将预测误差降低到10%以内。说明对ELM模型超参数进行优化能较好的改善原模型的预测能力。对于c组,当加入的虚拟样本数量从0增加到50的过程中,模型的MAPE值均比a、b组有着更优秀的表现,当增加30组虚拟样本时,模型性能提高幅度最大,MAPE相比GA-ELM模型提高了24%, 说明采用虚拟样本生成技术的预测模型相比未使用该技术的模型性能更好;同时注意到,随着虚拟样本数量的增加,预测性能表现先提高后下降并趋于稳定,这说明增加虚拟样本的数量会存在一个最优阈值,当虚拟样本的数量增加到该阈值后,模型性能不会再有提升。
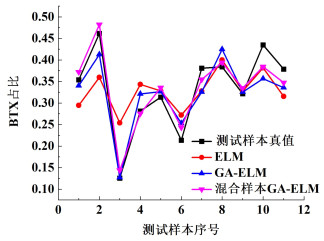
a、b和c组模型对BTX的总收率预测结果如图 3所示,其中c组为添加30组虚拟样本的情况。
|
| 图 3 各收率模型预测结果图 Fig.3 Prediction results of yield models |
| |
综合表 9和图 3,可以看出,相比未使用虚拟样本的b组,使用了虚拟样本的c组模型,R2平均提升了15%左右,说明添加虚拟样本的模型对测试样本有更好的拟合度。
| 虚拟样本数量 | R2 | 性能提升/% | ||
| a组 | b组 | c组 | ||
| 0 | 0.51 | 0.79 | ||
| 10 | 0.90 | 14 | ||
| 20 | 0.88 | 11 | ||
| 30 | 0.93 | 18 | ||
| 40 | 0.91 | 15 | ||
| 50 | 0.92 | 16 | ||
进一步,为了说明上述方法生成的虚拟样本的适用性和泛化性,设计以下实验:在原始样本集中随机选取15、30、45和60个样本做训练集,在剩余样本中选取10个作为测试集,在训练集中分别添加50组虚拟样本,取10次独立实验的平均值(aveMAPE)和方差(δMAPE)作为评价指标,对上述模型效果进行评估。对比结果如下表 10和表 11。
| 样本数 | 添加前 | 添加后 | 性能提升/% |
| 15 | 0.093 | 0.086 | 8 |
| 30 | 0.091 | 0.088 | 3 |
| 45 | 0.088 | 0.079 | 10 |
| 60 | 0.086 | 0.068 | 20 |
| 样本数 | 添加前 | 添加后 |
| 15 | 4.2×10-6 | 7.1×10-6 |
| 30 | 4.1×10-6 | 6.9×10-6 |
| 45 | 6.8×10-6 | 7.3×10-6 |
| 60 | 6.9×10-6 | 8.1×10-6 |
从表 10可以看到,添加50组虚拟样本之后,各模型性能都得到了一定提升。最大可提升20%左右,这说明本研究方法生成的虚拟样本有效填补了原MTA样本间的信息间隙,适用性良好。表 11显示添加虚拟样本后,不同样本集构建的GA-ELM模型在不同测试集的δMAPE值均接近0,表明模型性能稳定,综合以上说明添加虚拟样本可以提高原模型的泛化性能。
4 结论采用一种基于虚拟样本生成的MD-MTD-GA-ELM模型用于MTA工艺过程建模,对产物BTX的总收率进行预测。主要工作如下:(1)利用MD-MTD方法对MTA小样本数据集进行数据扩充;(2)利用GA优化算法对ELM模型参数进行优化,建立MD-MTD-GA-ELM模型进行BTX收率预测;(3)设置对比实验,从生成虚拟样本的合理性、改进模型的有效性和泛化性3个方面进行分析,证明了虚拟样本生成技术能够有效提高两段式甲醇制芳烃过程BTX收率预测模型的性能,MD-MTD-GA-ELM模型能够适用于MTA复杂非线性系统的产物预测。此外,如何确定虚拟样本最佳数量的评价指标将是未来工作的重点开展方向。
| [1] |
陈诗瑶, 申峻, 王玉高, 等. 甲醇制芳烃反应及生产工艺研究进展[J]. 现代化工, 2022, 42(2): 57-60, 67. CHEN Shiyao, SHEN Jun, WANG Yugao, et al. Progress in reaction and production process for methanol to aromatics[J]. Modern Chemical Industry, 2022, 42(2): 57-60, 67. (in Chinese) |
| [2] |
NIZIOLEK A M, ONEL O, GUZMAN Y A, et al. Biomass-based production of benzene, toluene, and xylenes via methanol: Process synthesis and deterministic global optimization[J]. Energy & Fuels, 2016, 30(6): 4970-4998. |
| [3] |
MEYERS R A. Handbook of petroleum refining processes[M]. 3rd ed. New York: McGraw-Hill, 2004.
|
| [4] |
KENT J A. Kent and Riegel's Handbook of industrial chemistry and biotechnology[M]. Boston, MA: Springer US, 2007.
|
| [5] |
WITTCOFF H A, REUBEN B G, PLOTKIN J S. Industrial organic chemicals[M]. New York: John Wiley & Sons Inc, 2004.
|
| [6] |
黄格省, 包力庆, 丁文娟, 等. 我国煤制芳烃技术发展现状及产业前景分析[J]. 煤炭加工与综合利用, 2018(2): 6-10. HUANG Gesheng, BAO Liqing, DING Wenjuan, et al. An analysis on status and prospect of Chinese coal to aromatics technologies[J]. Coal Processing & Comprehensive Utilization, 2018(2): 6-10. (in Chinese) |
| [7] |
代成义, 陈中顺, 杜康, 等. 甲醇制芳烃催化剂及相关工艺研究进展[J]. 化工进展, 2020, 39(12): 5029-5041. DAI Chengyi, CHEN Zhongshun, DU Kang, et al. Research progress of catalysts and related technologies for methanol to aromatics[J]. Chemical Industry and Engineering Progress, 2020, 39(12): 5029-5041. (in Chinese) |
| [8] |
施丽丽, 方栩, 刘殿华, 等. Zn改性ZSM-5催化甲醇制芳烃反应动力学[J]. 天然气化工(C1化学与化工), 2017, 42(2): 40-44, 49. SHI Lili, FANG Xu, LIU Dianhua, et al. Kinetic model for reaction of methanol to aromatics on Zn modified ZSM-5 catalyst[J]. Natural Gas Chemical Industry, 2017, 42(2): 40-44, 49. (in Chinese) |
| [9] |
徐亚荣, 蒋斌波, 冯丽梅, 等. 甲醇制芳烃(MTA)反应动力学的研究[J]. 聚酯工业, 2019, 32(6): 7-12. XU Yarong, JIANG Binbo, FENG Limei, et al. Study on reaction dynamic of methanol to aromatic[J]. Polyester Industry, 2019, 32(6): 7-12. (in Chinese) |
| [10] |
许雄飞, 刘鹏龙, 张玮, 等. 两段法固定床甲醇制芳烃产物预测多元非线性回归模型[J]. 化工学报, 2022, 73(2): 838-846. XU Xiongfei, LIU Penglong, ZHANG Wei, et al. Multivariate nonlinear regression model of methanol to aromatics by two-state fixed bed for product prediction[J]. CIESC Journal, 2022, 73(2): 838-846. (in Chinese) |
| [11] |
刘鹏龙, 许雄飞, 张玮, 等. 甲醇制芳烃K-means-PSO-SVR局部建模及优化[J]. 化工进展, 2022, 41(9): 4691-4700. LIU Penglong, XU Xiongfei, ZHANG Wei, et al. Local modeling and optimization of K-means-PSO-SVR for methanol to aromatics[J]. Chemical Industry and Engineering Progress, 2022, 41(9): 4691-4700. (in Chinese) |
| [12] |
陈良臣, 傅德印. 面向小样本数据的机器学习方法研究综述[J]. 计算机工程, 2022, 48(11): 1-13. CHEN Liangchen, FU Deyin. Survey on machine learning methods for small sample data[J]. Computer Engineering, 2022, 48(11): 1-13. (in Chinese) |
| [13] |
赵凯琳, 靳小龙, 王元卓. 小样本学习研究综述[J]. 软件学报, 2021, 32(2): 349-369. ZHAO Kailin, JIN Xiaolong, WANG Yuanzhuo. Survey on few-shot learning[J]. Journal of Software, 2021, 32(2): 349-369. (in Chinese) |
| [14] |
ROYLE J A, DORAZIO R M, LINK W A. Analysis of multinomial models with unknown index using data augmentation[J]. Journal of Computational and Graphical Statistics, 2007, 16(1): 67-85. |
| [15] |
张晓晗. 基于机器学习的工业过程数据驱动建模及数据扩充方法研究[D]. 北京: 北京化工大学, 2022 ZHANG Xiaohan. Research on data-driven modeling and data augmentation method for industrial processes based on machine learning[D]. Beijing: Beijing University of Chemical Technology, 2022 (in Chinese) |
| [16] |
朱宝, 陈忠圣, 余乐安. 一种新颖的小样本整体趋势扩散技术[J]. 化工学报, 2016, 67(3): 820-826. ZHU Bao, CHEN Zhongsheng, YU Lean. A novel mega-trend-diffusion for small sample[J]. CIESC Journal, 2016, 67(3): 820-826. (in Chinese) |
| [17] |
陆荣秀, 赖路璐, 杨辉, 等. 基于虚拟样本生成的铈镨/钕组分含量预测[J]. 传感器与微系统, 2022, 41(7): 152-156, 160. LU Rongxiu, LAI Lulu, YANG Hui, et al. Prediction of CePr/Nd component content based on virtual sample generation[J]. Transducer and Microsystem Technologies, 2022, 41(7): 152-156, 160. (in Chinese) |
| [18] |
LI D, CHEN C, CHANG C, et al. A tree-based-trend-diffusion prediction procedure for small sample sets in the early stages density estimation and confidence level method[J]. Chinese Journal of Aeronautics, 2012, 25(6): 879-886. |
| [19] |
ZHU Q, CHEN Z, ZHANG X, et al. Dealing with small sample size problems in process industry using virtual sample generation: A Kriging-based approach[J]. Soft Computing, 2020, 24(9): 6889-6902. |
| [20] |
ZHANG X, XU Y, HE Y, et al. Novel manifold learning based virtual sample generation for optimizing soft sensor with small data[J]. ISA Transactions, 2021, 109: 229-241. |
| [21] |
CHEN Z, ZHU Q, XU Y, et al. Integrating virtual sample generation with input-training neural network for solving small sample size problems: Application to purified terephthalic acid solvent system[J]. Soft Computing, 2021, 25(8): 6489-6504. |
| [22] |
WANG Y, HUANG Y, LIN T, et al. Modeling melodic feature dependency with modularized variational auto-encoder[EB/OL]. 2018: arXiv: 1811.00162. http://arxiv.org/abs/1811.00162
|
| [23] |
陈忠圣, 朱梅玉, 贺彦林, 等. 基于分位数回归CGAN的虚拟样本生成方法及其过程建模应用[J]. 化工学报, 2021, 72(3): 1529-1538. CHEN Zhongsheng, ZHU Meiyu, HE Yanlin, et al. Quantile regression CGAN based virtual samples generation and its applications to process modeling[J]. CIESC Journal, 2021, 72(3): 1529-1538. (in Chinese) |
| [24] |
李文怀, 李凯旋, 张庆庚, 等. 一种固定床绝热反应器两步法甲醇转化制取烃类混合物的方法: CN106220462B[P]. 2019-01-25 LI Wenhuai, LI Kaixuan, ZHANG Qinggeng, et al. Method for preparing hydrocarbon mixture by means of two-step method methanol conversion through adiabatic fixed-bed reactor: CN106220462B[P]. 2019-01-25 (in Chinese) |
| [25] |
张宝珠. 甲醇转化制芳烃(MTA)反应的研究[D]. 辽宁大连: 大连理工大学, 2013 ZHANG Baozhu. Study on methanol to aromatics (MTA) reaction[D]. Liaoning Dalian: Dalian University of Technology, 2013 (in Chinese) |
| [26] |
POGGIO T, VETTER T. Recognition and structure from one 2D model view: Observations on prototypes, object classes and symmetries[R]. Technical Report A. I. Memo 1347, MA, USA, Massachusetts Institute of Technology Cambridge, 1992
|
| [27] |
NIYOGI P, GIROSI F, POGGIO T. Incorporating prior information in machine learning by creating virtual examples[J]. Proceedings of the IEEE, 1998, 86(11): 2196-2209. |
| [28] |
LI D, WEN I. A genetic algorithm-based virtual sample generation technique to improve small data set learning[J]. Neurocomputing, 2014, 143: 222-230. |
| [29] |
HUANG G, ZHU Q, SIEW C K. Extreme learning machine: A new learning scheme of feedforward neural networks[C]//2004 IEEE International Joint Conference on Neural Networks. Budapest, Hungary. IEEE, 2004: 985-990
|
| [30] |
MICHALOPOULOS J, PAPADOKONSTADAKIS S, ARAMPATZIS G, et al. Modelling of an industrial fluid catalytic cracking unit using neural networks[J]. Chemical Engineering Research and Design, 2001, 79(2): 137-142. |
| [31] |
王丹丹, 汤健, 夏恒, 等. 基于多目标PSO混合优化的虚拟样本生成[J]. 自动化学报, 2024, 50(4): 790-811. WANG Dandan, TANG Jian, XIA Heng, et al. Virtual sample generation method based on hybrid optimization with multi-objective PSO[J]. Acta Automatica Sinica, 2024, 50(4): 790-811. (in Chinese) |
 2025, Vol. 42
2025, Vol. 42





