旋风/旋流分离器是利用离心力对气固(液固)体系进行相分离的常见设备,应用广泛,对旋风分离器内流场特性的研究,有助于指导旋风分离器结构的优化和分离效率的提高[1-5]。
黄鹏升[6]采用响应曲面法和CFD模拟方法对吸尘旋风分离器排气管结构进行优化,发现排气管插入深度和内扩直径对旋风分离器的性能有显著影响。田晓庆[7]用CFD模拟对入口螺旋下倾旋风分离器的入口结构进行优化,发现入口螺旋下倾旋风分离器的颗粒分级效率随着入口旋转角的增加而减小,随着入口截面角增加出现非单调变化;入口速度越大,压降的增幅越大;但分离效率的增幅却变小。Chuah等[8]采用适用的湍流模型,通过CFD模拟评估锥体尺寸对旋风分离器流体动力学、离心力和性能方面的影响,出口锥径较小的旋风分离器,其收集效率和压降较之较大锥径时有所提高。Demir等[9]建立了10种不同筒锥比高度的Stairmand高效旋风分离器优化模型,发现压降会随着筒锥比的增大而减小。Shastri等[10]采用大涡模型对用于滑石粉颗粒气固分离的旋风分离器内部流场进行数值模拟,考察了不同筒锥比的旋风分离器方案,筒体长度较短的旋风分离器有利于提高分离效率,筒体长度较长的旋风分离器可以改善压降。谭礼斌等[11]采用CFD模拟分析研究旋风分离器排气管直径及插入深度、颗粒口直径、筒体长度、锥体段长度和气体入口截面结构等对颗粒分离率的影响并对其进行优化,得到了较好的分离效率。Brar等[12]采用RSM湍流模型研究旋风分离器锥体尺寸和筒体尺寸对性能参数的影响,发现筒体和锥体的长度是显著影响压力降和收集效率的重要因素。
针对不同的物系和应用场合,许多学者对旋风分离器的适用结构进行大量的研究考察,确定各结构参数合理范围。尽管旋风分离器模拟已有很多报道,但旋风分离器总高度和圆锥段相对高度影响的报道相对缺乏,筒锥比的改变会影响分离效率和压降,这2个指标对旋风分离器分离性能至关重要;因为内部流场的复杂性,若不对其进行适当模拟预测,在实际操作过程中,会给设备的设计和操作带来很多不确定性。本论文针对烟草烘丝尾气气固分离体系,保持旋风分离器圆柱筒和锥体的总高度不变的前提下,采用CFD-DPM模型和RSM湍流模型对9个不同筒体高度与锥体高度比例下旋风分离器的内部流场和颗粒切割直径进行了模拟,以考察分析其流场分布规律及变化,以期对旋风分离器的结构优化提供指导。
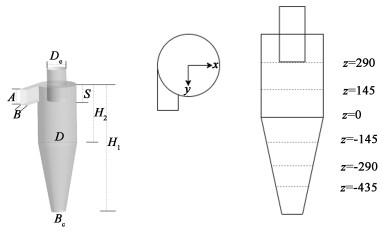
1 计算模型 1.1 旋风分离器模型建立本研究中所考察的旋风分离器以Hoekstra等[13]的模型为原型,其结构形态如图 1所示(图示单位为mm),以此为依据使用Gambit软件建立相应的旋风分离器模型,基于表 1所示的旋风分离器原型,保持总高度不变(4倍的筒体直径),改变圆柱筒体和圆锥体的相对高度,提出了9种不同筒体和锥体比例的旋风分离器结构方案,不同筒体高度与锥体高度的比例见表 2。
|
| 图 1 旋风分离器结构尺寸示意图 Fig.1 Schematic diagram of the structure and size of the cyclone separator |
| |
| 结构参数 | 变量名符号 | 尺寸/mm |
| 入口高度 | A | 58 |
| 入口宽度 | B | 145 |
| 筒体直径 | D | 290 |
| 升气管高度 | S | 145 |
| 筒体高度 | H2 | 435 |
| 总体高度 | H1 | 1 160 |
| 锥底直径 | Bc | 107.3 |
| 构型编号 | 筒高·锥高 |
| a | 0.85(1.84D·2.16D) |
| b | 1.00(2.00D·2.00D) |
| c | 1.25(2.22D·1.78D) |
| d | 1.50(2.40D·1.60D) |
| e | 2.00(2.67D·1.33D) |
| f | 2.50(2.85D·1.15D) |
| g | 3.00(3.00D·1.00D) |
| h | 3.50(3.10D·0.90D) |
| i | 4.00(3.20D·0.80D) |
对于不可压缩流来说,其湍流时均连续性和动量守恒方程如下[14]:
| $ \frac{\partial \rho}{\partial t}+\frac{\partial}{\partial x_i}\left(\rho u_i\right)=0 $ | (1) |
式(1)中:ui是坐标轴xi方向的速度分量(i=1,2,3),x1、x2、x3分别代表直角坐标系中的x轴、y轴和z轴;ρ是密度。
| $ \begin{gathered} \frac{\partial}{\partial t}\left(\rho u_i\right)+\frac{\partial}{\partial x_j}\left(\rho u_i u_j\right)=-\frac{\partial p}{\partial x_i}+\frac{\partial}{\partial x_j}\left[\mu\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)\right]+ \\ \frac{\partial}{\partial x_j}\left(-\rho \overline{u_i^{\prime}} u_j^{\prime}\right) \end{gathered} $ | (2) |
式(2)中:p是静压;ui和uj是坐标轴xi和xj方向的速度分量(i, j=1,2,3);
根据雷诺应力模型(RSM),雷诺应力项的输运方程如式(3)。
| $ \frac{\partial}{\partial t}\left(\rho \overline{u_i^{\prime}} u_j^{\prime}\right)+\frac{\partial}{\partial x_k}\left(\rho u_k \overline{u_i^{\prime}} u_j^{\prime}\right)=D_{\mathrm{T}, i j}+P_{i j}+\phi_{i j}+\varepsilon_{i j} $ | (3) |
式(3)中:uk是坐标轴xk方向的速度分量(k=1,2,3)。
在湍流流动的模拟中,需要确定合适的湍流模型来预测动量方程中雷诺应力等未知项,以封闭微分方程并获得求解。式(3)左边2项分别为应力和对流扩散项对时间等的偏导数,右边4项依次为湍流扩散项(DT,ij)、浮力产生项(Pij)、压力应变项(Φij)和耗散相(εij)。
旋风分离器在操作中会产生强旋湍流流场,雷诺应力模型能够更好地反映强旋内部流场的各向异性,且相较双方程模型准确性得到了很大的提高,更适合对旋风分离器内部流场进行模拟,故本研究对气相流体采用雷诺应力模型进行模拟。
1.2.3 模型离散方法本研究模拟对象为气固非均一体系。通过求解时间平均的Navier-Stokes方程,将流体相作为连续体来求解,而采用拉格朗日轨迹法单独跟踪大量颗粒来求解分散相[15]。根据欧拉-拉格朗日方法(单向耦合),粒子运动的方程如式(4)。
| $ \frac{\mathrm{d} u_{\mathrm{p} i}}{\mathrm{~d} t}=F_{\mathrm{D}}\left(u_i-u_{\mathrm{p} i}\right)+\frac{g_i\left(\rho_{\mathrm{p}}-\rho\right)}{\rho_{\mathrm{p}}} $ | (4) |
| $ \frac{\mathrm{d} x_{\mathrm{p} i}}{\mathrm{~d} t}=u_{\mathrm{p} i} $ | (5) |
式(4)和式(5)中:ρp是颗粒密度;gi是i方向的重力加速度;ui和upi是i方向的气体和颗粒速度分量;FD(ui-upi)是每单位颗粒质量的阻力。
| $ F_{\mathrm{D}}=\frac{18 \mu}{\rho_{\mathrm{p}} d_{\mathrm{p}}^2} \frac{C_{\mathrm{D}} R e_{\mathrm{p}}}{24} $ | (6) |
| $ R e_{\mathrm{p}}=\frac{\rho_{\mathrm{p}} d_{\mathrm{p}}\left|u-u_{\mathrm{p}}\right|}{\mu} $ | (7) |
式(6)和式(7)中:dp是颗粒直径;CD是阻力系数;Rep是相对雷诺数;u和up是气体和颗粒流速。
| $ C_{\mathrm{D}}= \begin{cases}24 / Re_{\mathrm{p}} & 0<R e_{\mathrm{p}} \leqslant 1 \\ 24 / Re_{\mathrm{p}}\left(1+0.15 R e_{\mathrm{p}}^{0.687}\right) & 1<R e_{\mathrm{p}} \leqslant 1000\end{cases} $ | (8) |
旋风分离器入口为速度入口边界条件,在合理入口速度下,选择入口湍流强度I和水力直径Dh作为输入参数,其中I=5%,参照式(9)计算,水力直径参照式(10)计算,Dh=82.86 mm,升气管出口设置为自由流出,除尘口和旋风分离器内壁都设置为壁面边界条件,无滑移速度。
| $ I=0.16 R e_{\mathrm{p}}^{-1 / 8} $ | (9) |
| $ D_{\mathrm{h}}=\frac{4 A}{C} $ | (10) |
式(10)中:A是流体流动截面积,m2;C是湿周,m。
1.3.2 离散相边界条件离散相入口设置为反弹(reflect),颗粒注入速度等同于气相入口速度,升气管出口设置为逃逸(escape),除尘口设置为捕捉(trap),壁面设置为反弹(reflect)。
气相为连续相,采用欧拉法追踪,颗粒为离散相,采用拉格朗日法追踪,压力-速度耦合设置为SIMPLEC算法,压力梯度项离散格式设置为PRESTO,动量离散格式设置为二阶迎风格式,湍动能κ设置为二阶迎风格式,湍流耗散率ε设置为二阶迎风格式,雷诺应力设置为一阶迎风格式。
1.3.3 烟草颗粒粒径分布本研究对旋风分离结构的优化,着眼于细小固形物颗粒的捕集。如烟草加工中,湿烟丝的烘干是重要的工艺步骤,大量致香成分进入气相。为了有效分离和回收烘丝尾中的致香成分,首先需要通过气固分离捕获尾气携带的烟丝颗粒,保证固形物不进入后续过程。烟草颗粒粒径分布可采用Rosin-Rammler[16]分布表示。
| $ F(d)=1-\exp \left[-\left(\frac{d}{d_{\mathrm{m}}}\right)^s\right] $ | (11) |
式(11)中:d是颗粒直径,μm;F(d)代表颗粒粒径的累积质量分率;dm为中位径(Mean diameter),μm;s为传播系数。实测的烟草颗粒粒径分布如表 3。
| 粒径范围/μm | d/μm | F(d) |
| < 2 | 2 | 0.005 70 |
| < 4 | 4 | 0.085 30 |
| < 6 | 6 | 0.445 34 |
| < 8 | 8 | 0.873 93 |
| < 10 | 10 | 1.000 00 |
当取边界条件d=dm时,F(d)=1-e-1≈0.632。
通过线性插值法,得出实测烟草分布中累积质量分率0.632时的粒径,即为中位径,之后代入其他数值即可得出计算公式。
计算得知,烟草颗粒中位径为7.8 μm,其传播系数为4.26,相应的Rosin-Rammler分布为:
| $ F(d)=1-\exp \left[-\left(\frac{d}{7.8}\right)^{4.26}\right] $ | (12) |
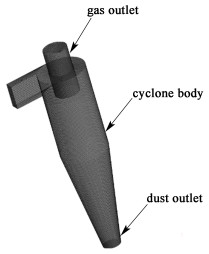
网格是采用Fluent中的ICEM划分而成,为结构性网格,其精度较非结构性网格好。网格划分如图 2。
|
| 图 2 旋风分离器网格划分 Fig.2 Cyclone meshing |
| |
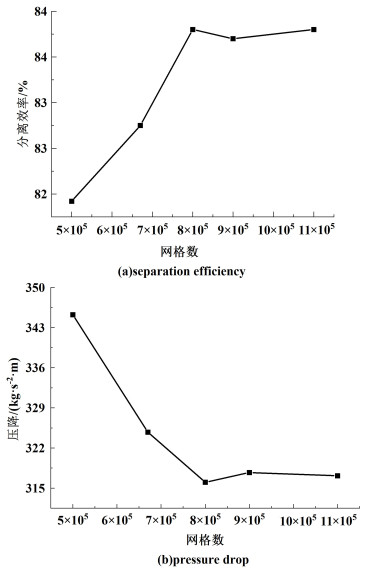
网格数分别取5×105、6.7×105、8×105、9×105和11×105,对图 2所示的旋风分离器进行模拟,考察网格数设置对粒度1~10 μm颗粒的捕捉效率和压力降模拟结果的影响。由图 3所展示的结果来看,网格数在8×105及以上时,其分离效率和压差已经稳定。综合考虑,选定8×105网格作为本模拟研究中使用的计算网格数。
|
| 图 3 网格无关性检查 Fig.3 Grid independence checking |
| |
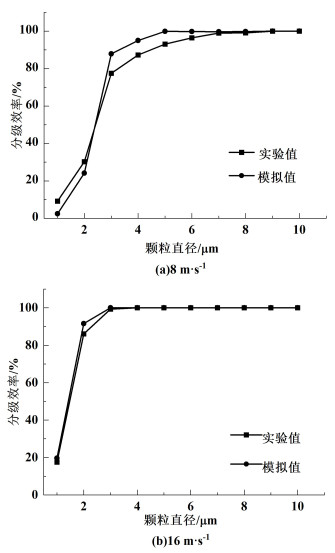
本研究考察的旋风分离器基础模型是以Hoekstra[13]文献中模型为原型,分别以进口速度8 m ·s-1和16 m ·s-1对旋风分离器基础模型进行模拟计算,颗粒质量流率为2.5 g ·m-3,密度为2 700 kg ·m-3。其分级效率对比如图 4所示。
图 4所示,实验值略小于模拟值,考虑到旋流场的复杂性,且误差在可接受范围内,模拟数据与实验数据吻合程度良好,可视为本研究采用的模型方法和有关参数设置可以较好地反映旋风分离器对固体颗粒的收集特性,可以对同样或相似体系进行预测。以下运用已得到验证的模型方法,对用于烟草烘丝尾气中颗粒分离的旋风分离器进行模拟分析。
2 模拟结果与讨论 2.1 气相流场分布 2.1.1 静压分布规律旋风分离器压降是评估旋风分离器分离性能的重要指标之一,同时其静压分布能更好体现出流场分布形态。
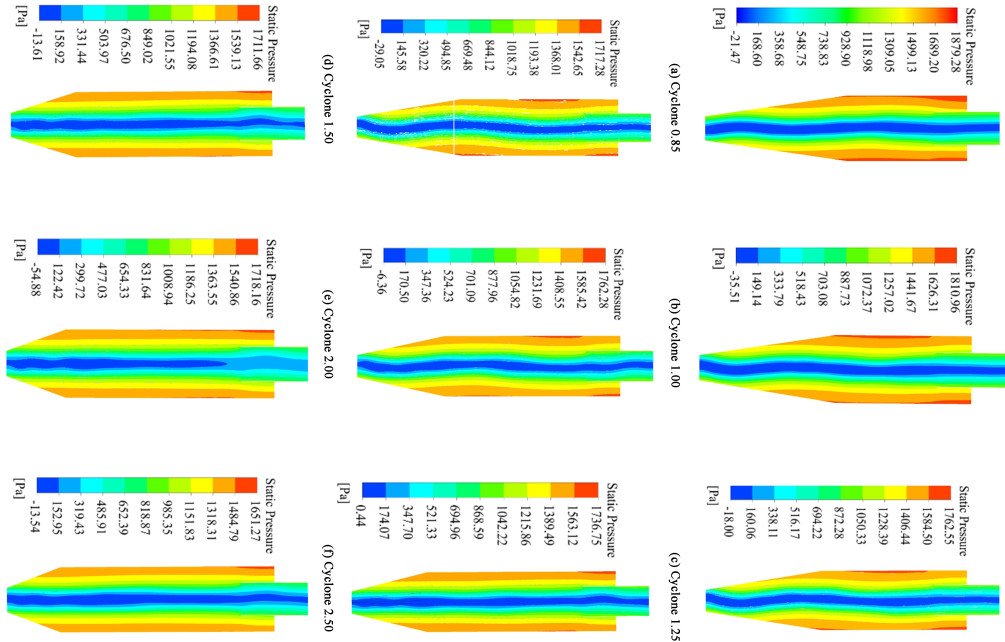
图 5所绘9个不同筒锥比的旋风分离器在X=0截面上的静压分布图。进口流速为16 m ·s-1,静压分布呈现明显的轴对称分布,但在径向位置上急剧变化,中心是负压区,两侧是正压区;在强旋流情况下,外旋流高速旋转形成中心负压,使其静压分布为2个区域,中心区域为向上的旋流,外侧区域为向下的旋流。在一定总高度下,随着筒锥比例增大,全域范围内静压波动不是很大,但依总体趋势来看,轴截面最大静压随着圆筒段相对占比的增加而减小。表 4为9种构型的旋风分离器模型在进出口截面上采用面积加权平均法(Area-weighted Average)进行压降计算所得结果,其中Eu=Δp · ρuin2;进出口压降随着筒锥比的增加,除了e、f和g 3种构型有小幅的回弹外,总的趋势有小幅度的下降,构型i与构型a相比,压力降降低了17.5%。静压的绝对大小与上游的压力有关,并且其与速度的关系也较为紧密,而此时入口速度和体积流率并未改变,所以静压浮动不大。
|
| 图 5 不同筒锥体比下旋风分离器中的静压分布 Fig.5 Static pressure profiles in gas cyclones with different cylinder-to-cone ratios |
| |
| 构型编号 | 静压降Δp/Pa | 欧拉数Eu |
| a | 1 106.16 | 3.35 |
| b | 1 053.12 | 3.19 |
| c | 1 016.29 | 3.08 |
| d | 975.87 | 2.96 |
| e | 1 020.25 | 3.09 |
| f | 994.51 | 3.01 |
| g | 1 231.13 | 3.73 |
| h | 937.36 | 2.84 |
| i | 912.65 | 2.76 |
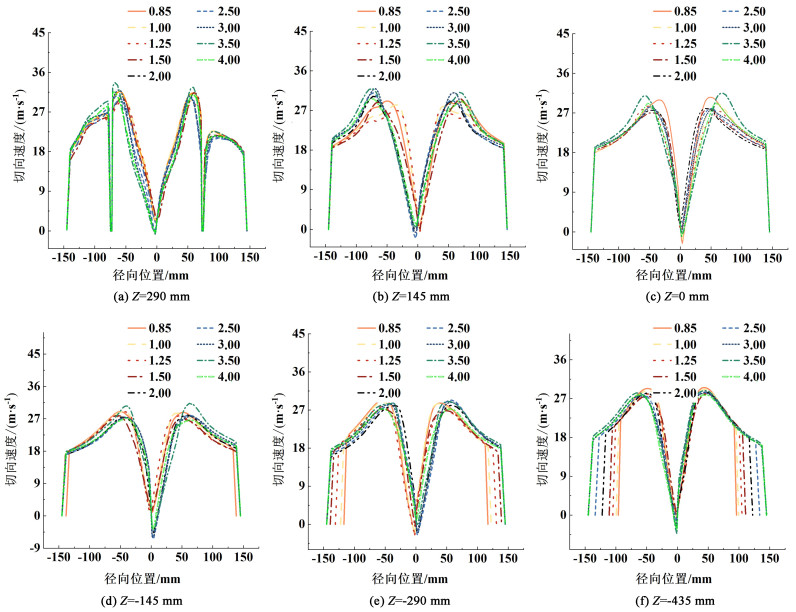
切向速度通过改变颗粒的行动轨迹,进而影响颗粒分离效率。图 6为9种筒锥比下的旋风分离器模型在Y=0截面上6个不同高度位置处的切向速度分布图。切向速度沿径向的分布呈明显的“M”型,在中心位置处,切向速度存在正值,其为中心处的上旋流动,表明该旋风分离器中存在“二次涡流”。由这些等高线图可以看出,其类似于“兰金型涡流”,其内部涡流为强制涡流区,而外部涡流为自由涡流区。以旋风分离器筒锥比为2作为分界点,该比例为0.85、1.00、1.25和1.50时旋风分离器中的切向速度分布较为相似,可以记为“A”组,而筒锥比为2.50、3.00、3.50和4.00时旋风模型的切向速度分布较为相似,可记为“B”组。“A”组中心位置处切向速度大于“B”组中心位置附近切向速度,但由图 6可以看出,“B”组的几何中心线位置会产生一定的“偏移”,“A”组中则几乎不存在这种“偏移”,该结论与周韬[18]所得模拟结论相同,从切向速度图可以观测到,涡核出现了偏心的现象,造成了气流扰动,其切向速度图大部分为正值,在中心附近处存在小部分负值。在图 6中给出的6个截面处(Z=290、145、0、-145、-290和-435 mm),最大切向速度为进气速度的1.7~2.0倍。
|
| 图 6 不同筒锥比及垂直截面处旋风分离器中的切向速度分布 Fig.6 Tangential velocity distribution in cyclone separator with different cylinder-cone ratio and vertical section |
| |
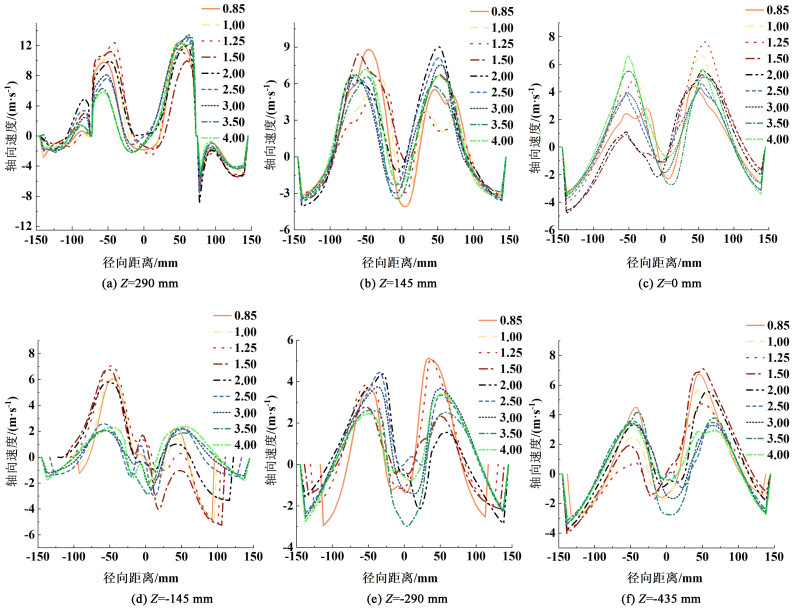
图 7所示为9种筒锥比下的旋风分离器模型在Y=0截面的6个不同高度处的轴向速度分布。图 7中可见,轴向速度分布呈典型的“M”型分布。但其并不是严格的对称分布,可能是因为旋风分离器内流场存在紊流,导致这一现象的产生。轴向速度值从壁面开始沿径向先增大后减小,这一分布规律再次验证了“双涡”存在,且近壁面处轴向速度方向向下,促使颗粒的“排出”。“B”组旋风分离器(筒锥比2.50、3.00、3.50和4.00时)中上行速度的最大值较“A”组(筒锥比0.85、1.00、1.25和1.50)小。Gimbun等[19]认为,轴向速度大小会影响压降,存在中心涡流的轴向修正,较大的轴向速度会导致压降增大;本研究考察的“B”组旋风分离器中,轴向速度相对较小,压降也会随之减小。
|
| 图 7 不同筒锥体比和垂直截面处旋风分离器中的轴向速度分布 Fig.7 Axial velocity distribution in cyclone separator with different cylinder-cone ratio and vertical section |
| |
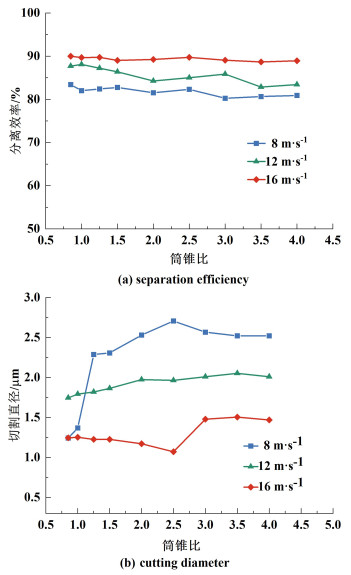
本研究采用DPM模型,模拟分析了不同筒锥体比下旋风分离器对进气携带固体颗粒的收集分离效率。本模拟中烟草固相颗粒的流率为2.5 g ·m-3,其进口速度于输入气相速度相同,密度为1 200 kg ·m-3。对1~10 μm范围颗粒的分离效率如图 8(a),随着筒锥比的增大,分离效率轻微浮动,呈现“增大-减小-增大-减小”的趋势,在筒锥比大于3之后,分离效率基本维持不变,在气相入口速度为16 m ·s-1时,分离效率整体不变,入口速度为8和12 m ·s-1时,分离效率总体呈减小趋势。随着筒锥比的增大,筒体高度增大,锥体高度减小,筒体高度的增大会使涡流强度减小,致使切向速度降低,减小分离效率;但同时轴向速度的减小,会延长固体颗粒在旋风分离器内部分离区的停留时间,增加颗粒分离效率,所以分离效率整体会呈现“增大-减小-增大-减小”的趋势。随着入口速度增大,其分离效率明显升高,进口气速对分离效率也起着重要的影响。Zheng等[4]考察了带有灰斗分流器的旋风分离器的分离效率,筒锥比在0.4~3.2范围,总分离效率保持在较高水平(>80%),当筒锥比为1.63时达到峰值;本研究考察的对象是没有灰斗分流器的旋风分离器,研究发现:分离效率随着筒锥比的变化,并非简单地单调变化,变化幅度不大,这在一定程度上与Zheng等[4]的研究结果相近。
|
| 图 8 不同入口气速下筒锥比对分离效率和颗粒切割直径的影响 Fig.8 Effect of cylinder-cone ratio on separation efficiency and particle cutting diameter at different inlet gas velocities |
| |
切割直径也是评估旋风分离性能的重要指标。保持旋风分离器总高度固定,随着筒锥比的增加,8和16 m ·s-1入口气速时切割直径(d50)整体呈增大趋势,但由图 8(b)明显可以看出在12 m ·s-1入口气速时,其切割直径随筒锥比并无明显变化,且当入口气速为16 m ·s-1,筒锥比为2.50时,切割直径最小;当入口气速为8 m ·s-1,筒锥比为0.85时,切割直径最小。可以得出,当入口气速小于12 m ·s-1时,较小的筒锥比更有利于分离,当入口气速大于12 m ·s-1时,只要筒锥比小于2.50,选用较大的筒锥比更有利于分离。当筒锥比大于3时,切割直径基本不随筒锥比的改变而改变。
综合分析各种筒锥比下优化旋风分离器中的压力降和对进气固体的收集分离效率,可以发现:应根据气固分离工艺具体需要,确定合适的切割直径,选择合适的筒锥比参数和进气速率,在保证气固分离效率的前提下,降低旋风分离器在实际操作中的能耗。
3 结论采用CFD-DPM计算模型,研究了4倍于筒体直径的总高下,筒锥比的变化对旋风分离器中气相流场和切割直径的影响,主要结论如下。
(1) 保持旋风分离器总高度不变,增大筒锥比,对压力分布形态的改变不大,但压力降有一定幅度的减少。
(2) 筒锥比为0.85、1.00、1.25和1.50的“A”组旋风分离器,与筒锥比2.50、3.00、3.50和4.00的“B”组旋风分离器有相似形态的切向速度分布,但“B”组切向速度分布与设备的几何中心线有略微的偏移,且“B”组中心位置切向速度比“A”较小。
(3) 进口气速越大,切割直径越小。筒锥段高度比对颗粒切割直径的影响,在不同的进口气速下有显著的差别。12 m ·s-1入口气速时,其切割直径随筒锥比并无明显变化,且当筒锥比大于3时,切割直径基本不随筒锥比的改变而改变。
(4) 在旋风分离器总高度恒定的前提下,通过筒锥比的优化,使旋风分离器的效率更好适应具体气固分离的需要。对于高进气流量和低进气流量,分别选择筒锥比为2.50和0.85的旋风分离器,有利于改善烟草烘丝尾气中细颗粒分离效率。
| [1] |
VENKATESH S, SAKTHIVEL M, SARANAV H, et al. Performance investigation of the combined series and parallel arrangement cyclone separator using experimental and CFD approach[J]. Powder Technology, 2020, 361: 1070-1080. DOI:10.1016/j.powtec.2019.10.087 |
| [2] |
KOWALCZYK A, KUŚ P, MARIJANOVIĆ Z, et al. Headspace solid-phase micro-extraction versus hydrodistillation of volatile compounds from leaves of cultivated Mentha taxa: Markers of safe chemotypes[J]. Molecules, 2022, 27(19): 6561. DOI:10.3390/molecules27196561 |
| [3] |
HAN S, YANG J, ZHANG R, et al. Forming and breaking the ceiling of inlet gas velocity regarding to separation efficiency of cyclone[J]. Particuology, 2023, 79: 85-94. DOI:10.1016/j.partic.2022.11.004 |
| [4] |
ZHENG Y, NI L. Numerical study on particles separation using a cyclone enhanced by shunt device: Effects of cylinder-to-cone ratio and vortex finder-to-cylinder ratio[J]. Powder Technology, 2022. DOI:10.1016/j.powtec.2022.117767 |
| [5] |
LE D, YOON J Y. A hybrid CFD-Deep learning methodology for improving the accuracy of pressure drop prediction in cyclone separators[J]. Chemical Engineering Research and Design, 2023, 190: 296-311. DOI:10.1016/j.cherd.2022.12.035 |
| [6] |
黄鹏升. 基于响应曲面法的旋风分离器排气管优化研究[J]. 现代矿业, 2021, 37(8): 169-173. HUANG Pengsheng. Optimization of exhaust pipe of cyclone separator based on response surface method[J]. Modern Mining, 2021, 37(8): 169-173. (in Chinese) |
| [7] |
田晓庆. 高效节能旋风分离器的开发—数值模拟与实验研究[D]. 福建厦门: 集美大学, 2013 TIAN Xiaoqing. Developing a new type of energy-saving cyclone separator-numerical simulation and experimental study[D]. Fujian Xiamen: Jimei University, 2013 (in Chinese) |
| [8] |
CHUAH T G, GIMBUN J, CHOONG T S Y. A CFD study of the effect of cone dimensions on sampling aerocyclones performance and hydrodynamics[J]. Powder Technology, 2006, 162(2): 126-132. DOI:10.1016/j.powtec.2005.12.010 |
| [9] |
DEMIR S, KARADENIZ A, AKSEL M. Effects of cylindrical and conical heights on pressure and velocity fields in cyclones[J]. Powder Technology, 2016, 295: 209-217. DOI:10.1016/j.powtec.2016.03.049 |
| [10] |
SHASTRI R, BRAR L S. Numerical investigations of the flow-field inside cyclone separators with different cylinder-to-cone ratios using large-eddy simulation[J]. Separation and Purification Technology, 2020. DOI:10.1016/j.seppur.2020.117149 |
| [11] |
谭礼斌, 袁越锦, 黄灿, 等. 旋风分离器流场分析与结构优化的数值模拟[J]. 陕西科技大学学报, 2018, 36(3): 152-159. TAN Libin, YUAN Yuejin, HUANG Can, et al. Numerical simulation on flow field analysis and structural optimization of cyclone separator[J]. Journal of Shaanxi University of Science & Technology, 2018, 36(3): 152-159. (in Chinese) |
| [12] |
BRAR L S, SHARMA R P, ELSAYED K. The effect of the cyclone length on the performance of Stairmand high-efficiency cyclone[J]. Powder Technology, 2015, 286: 668-677. DOI:10.1016/j.powtec.2015.09.003 |
| [13] |
HOEKSTRA A. Gas flow field and collection efficiency of cyclone separators[D]. Netherlands: Technical University Delft, 2000
|
| [14] |
SONG C, PEI B, JIANG M, et al. Numerical analysis of forces exerted on particles in cyclone separators[J]. Powder Technology, 2016, 294: 437-448. DOI:10.1016/j.powtec.2016.02.052 |
| [15] |
ZHAO B, SU Y, ZHANG J. Simulation of gas flow pattern and separation efficiency in cyclone with conventional single and spiral double inlet configuration[J]. Chemical Engineering Research and Design, 2006, 84(12): 1158-1165. DOI:10.1205/cherd06040 |
| [16] |
熊攀, 鄢曙光. 基于Rosin-Rammler函数的数值模拟对旋风除尘器粒径分布规律的研究[J]. 粉末冶金工业, 2019, 29(2): 29-32. XIONG Pan, YAN Shuguang. Numerical simulation of particle size distribution of cyclone dust collector based on Rosin-Rammler function[J]. Powder Metallurgy Industry, 2019, 29(2): 29-32. (in Chinese) |
| [17] |
GRIFFITHS W D, BOYSAN F. Computational fluid dynamics (CFD) and empirical modelling of the performance of a number of cyclone samplers[J]. Journal of Aerosol Science, 1996, 27(2): 281-304. DOI:10.1016/0021-8502(95)00549-8 |
| [18] |
周韬. 旋风分离器的气固两相特性研究与数值模拟[D]. 上海: 上海交通大学, 2007 ZHOU Tao. Study and numerical simulation on gas-solid two-phase characteristic of cyclone separator[D]. Shanghai: Shanghai Jiao Tong University, 2007 (in Chinese) |
| [19] |
GIMBUN J, CHUAH T G, FAKHRU'L-RAZI A, et al. The influence of temperature and inlet velocity on cyclone pressure drop: A CFD study[J]. Chemical Engineering and Processing: Process Intensification, 2005, 44(1): 7-12. DOI:10.1016/j.cep.2004.03.005 |
 2025, Vol. 42
2025, Vol. 42