蛋氨酸(D, L-Methionine)又称甲硫氨酸,是人体必须的氨基酸之一,参与蛋白质的合成,被广泛应用于饲料、生物医药和化妆品等行业[1]。各种蛋氨酸生产工艺都需将蛋氨酸进行结晶精制[2]。目前已有较多学者对蛋氨酸的结晶动力学、热力学性质进行研究[3, 4],但对蛋氨酸的连续结晶设备研究较少。在蛋氨酸结晶过程中,晶体难以各向均匀生长,容易造成形状不规则,因此在工业中蛋氨酸的生长需要分布均匀的过饱和度;另一方面,蛋氨酸晶体析出速率过快会导致晶体颗粒细小,因此需要避免生产过程中因过饱和度过高而产生大量晶核。DTB(Draft tube baffled)结晶器带有搅拌装置,可以为蛋氨酸的生产提供分布均匀的生长环境,且作为一种典型的晶浆内循环型结晶器,DTB结晶器可以不断地消耗过饱和度,使之维持在较低水平,因此,工业上常选用DTB结晶器作为蛋氨酸的生产设备。
随着数值模拟的高速发展,计算流体力学(CFD)被广泛应用于DTB结晶器的研究,以充分了解流体在DTB结晶器中的流动特性和颗粒悬浮状态,有利于对DTB结晶器进行结构和操作条件的优化[5-7]。除此之外,利用CFD对结晶过程[8-10]和DTB结晶器的放大[11, 12]进行研究,可以大幅度降低时间成本,对结晶器的设计与结晶过程的控制具有重要意义。
内循环是DTB结晶器的重要特征,在蒸发冷却结晶过程中,搅拌桨推动流体沿导流筒到达沸腾液面,是DTB结晶器内循环的动力来源,因此许多学者针对结晶器的搅拌桨进行研究[6, 12-14],希望通过改进搅拌桨的型式提高晶浆密度,降低搅拌速度,减少过剩晶核的形成。除此之外,导流筒是保证结晶器在较低的压头损失(约100~200 mm H2O)下就能实现良好内循环的关键结构[15],尤其在蒸发结晶和真空蒸发冷却结晶过程中,导流筒将大量晶浆送到沸腾液面,逐渐消耗溶液产生的过饱和度,避免了爆发成核,也降低了结晶疤的产生速率,有利于连续结晶的稳定运行;环形挡板将结晶器分为晶体生长区和澄清区,可以有效控制产品的粒度和粒径分布,对工业生产有重要作用。
目前DTB结晶器的研究主要集中在实验室规模,少有学者关注工业级DTB结晶器的结构特性和流场分布情况,因此,本研究通过CFD技术探究增加导叶结构提高内循环的可行性,研究导流筒和挡板长度对工业级DTB结晶器的流场特性和颗粒悬浮状态的影响,为工业结晶器的设计提供参考。
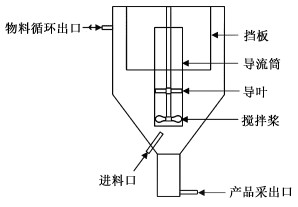
1 DTB结晶器的模型建立与计算方法 1.1 DTB结晶器模型的简化在实际工业生产过程中,为方便操作,DTB结晶器常设有支架、人孔等辅助结构,这些结构对DTB结晶器的内部流场不会造成明显影响,因此本研究在建模过程中将这些辅助结构忽略[16]。模拟的DTB结晶器具体结构如图 1所示,该结晶器总体积为26.05 m3,结晶器直径为3.2 m,高度为5.4 m,进料口、物料循环出口和产品采出口的直径都为0.1 m,搅拌桨和导叶直径为0.76 m,导流筒直径为0.8 m,挡板直径为2.4 m。
|
| 图 1 DTB结晶器的结构 Fig.1 Structure of DTB crystallizer |
| |
标准k-ε模型忽略分子黏性对湍流流动的影响,通过湍动黏度描述湍流动能k和湍流耗散率ε,适用于湍流充分发展的流动,适用范围广,计算结果精确,计算规模相对较小[17-19]。
式(1)和式(2)分别表示湍流动能k方程和湍流耗散率ε方程[20]。
| $ \begin{gathered} \frac{\partial}{\partial t}(\rho k)+\frac{\partial}{\partial x_i}\left(\rho k u_i\right)=\frac{\partial}{\partial x_j}\left[\left(\mu+\frac{\mu_{\mathrm{t}}}{\sigma_k}\right) \frac{\partial k}{\partial x_j}\right]+ \\ G_{\mathrm{k}}+G_{\mathrm{b}}-\rho \varepsilon-Y_{\mathrm{M}}+S_k \end{gathered} $ | (1) |
| $ \begin{gathered} \frac{\partial}{\partial t}(\rho \varepsilon)+\frac{\partial}{\partial x_i}\left(\rho \varepsilon u_i\right)=\frac{\partial}{\partial x_j}\left[\left(\mu+\frac{\mu_{\mathrm{t}}}{\sigma_k}\right) \frac{\partial \varepsilon}{\partial x_j}\right]+ \\ C_{1 \varepsilon} \frac{\varepsilon}{k}\left(G_{\mathrm{k}}+C_{3 \varepsilon} G_{\mathrm{b}}\right)-C_{2 \varepsilon} \rho \frac{\varepsilon^2}{k}+S_{\varepsilon} \end{gathered} $ | (2) |
| $ \mu_{\mathrm{t}}=\rho C_\mu \frac{k^2}{\varepsilon} $ | (3) |
| $ G_{\mathrm{k}}=\mu_{\mathrm{t}} \frac{\partial u_i}{\partial u_j}\left(\frac{\partial u_i}{\partial u_j}+\frac{\partial u_j}{\partial u_i}\right) $ | (4) |
式(1)~式(4)中:t为时间;x为空间位置;ρ为密度;μt为湍动黏度,可以用式(3)表示;Gk是由平均速度梯度产生的湍流动能,如式(4)所示;Gb为浮力产生的湍流动能;YM是可压缩流体湍流中脉动扩张的湍流动能;σk和σε分别为k和ε的湍流Prandtl数;C1ε、C2ε、Cμ为经验常数;Sk和Sε表示用户自定义源项。
在Fluent中,C1ε=1.44,C2ε=1.92,Cμ=0.09,σk=1.0,σε=1.3,当流体不可压缩且无自定义源项时,Gb=0,YM=0,Sk=0,Sε=0。
1.3 欧拉模型的基本理论在研究晶体颗粒在液体中的悬浮状态时无法忽略固、液两相之间的相互作用,因此选择欧拉-欧拉模型对固、液两相进行模拟分析。在欧拉-欧拉模型中,每一相都被看作是连续的,每一相的体积分数都可以由连续性方程求得:
| $ \frac{\partial}{\partial t}\left(\alpha_{\mathrm{q}} \rho_{\mathrm{q}}\right)+\nabla\left(\alpha_{\mathrm{q}} \rho_{\mathrm{q}} \overrightarrow{\boldsymbol{v}}_{\mathrm{q}}\right)=\sum\nolimits_{p=1}^n\left(\dot{m}_{\mathrm{pq}}-\dot{m}_{\mathrm{qp}}\right) $ | (5) |
式(5)中:α为液相或固相的体积分数;
欧拉-欧拉模型中液相和固相的动量方程需要分别定义[21-23]。液相q的动量方程可以写为:
| $ \begin{gathered} \frac{\partial}{\partial t}\left(\alpha_{\mathrm{q}} \rho_{\mathrm{q}} \overrightarrow{\boldsymbol{v}}_{\mathrm{q}}\right)+\nabla \cdot\left(\alpha_{\mathrm{q}} \rho_{\mathrm{q}} \overrightarrow{\boldsymbol{v}}_{\mathrm{q}} \overrightarrow{\boldsymbol{v}}_{\mathrm{q}}\right)=-\alpha_{\mathrm{q}} \nabla \boldsymbol{p}+\nabla \cdot \overline{\overline{\boldsymbol{\tau}}}_{\mathrm{q}}+ \\ \alpha_{\mathrm{q}} \rho_{\mathrm{q}} g+\sum\nolimits_{p=1}^n\left[K_{\mathrm{pq}}\left(\overrightarrow{\boldsymbol{v}}_{\mathrm{p}}-\overrightarrow{\boldsymbol{v}}_{\mathrm{q}}\right)+\dot{m}_{\mathrm{pq}} \overrightarrow{\boldsymbol{v}}_{\mathrm{pq}}-\dot{m}_{\mathrm{qp}} \overrightarrow{\boldsymbol{v}}_{\mathrm{qp}}\right]+ \\ \left(\vec{F}_{\mathrm{q}}+\vec{F}_{\mathrm{lift}, \mathrm{q}}+\vec{F}_{\mathrm{vm}, \mathrm{q}}\right) \end{gathered} $ | (6) |
固相p的动量方程可以写为:
| $ \begin{gathered} \frac{\partial}{\partial t}\left(\alpha_{\mathrm{p}} \rho_{\mathrm{p}} \overrightarrow{\boldsymbol{v}}_{\mathrm{p}}\right)+\nabla \cdot\left(\alpha_{\mathrm{p}} \rho_{\mathrm{p}} \overrightarrow{\boldsymbol{v}}_{\mathrm{p}} \overrightarrow{\boldsymbol{v}}_{\mathrm{p}}\right)=-\alpha_{\mathrm{p}} \nabla \boldsymbol{p}-\nabla \boldsymbol{p}_{\mathrm{p}}+ \\ \nabla \cdot \overline{\overline{\boldsymbol{\tau}}}_{\mathrm{p}}+\alpha_{\mathrm{p}} \rho_{\mathrm{p}} g+\sum\nolimits_{q=1}^n\left[K_{\mathrm{qp}}\left(\overrightarrow{\boldsymbol{v}}_{\mathrm{q}}-\overrightarrow{\boldsymbol{v}}_{\mathrm{p}}\right)+\right. \\ \left.\dot{m}_{\mathrm{qp}} \overrightarrow{\boldsymbol{v}}_{\mathrm{qp}}-\dot{m}_{\mathrm{pq}} \overrightarrow{\boldsymbol{v}}_{\mathrm{pq}}\right]+\left(\vec{F}_{\mathrm{p}}+\vec{F}_{\mathrm{lift}, \mathrm{p}}+\vec{F}_{\mathrm{vm}, \mathrm{p}}\right) \end{gathered} $ | (7) |
其中:
多相流中不同相之间的相互作用力有虚拟质量力、曳力、升力和湍流分散力等,在实际工业结晶过程中,液相与固相之间的曳力占主导作用。因此本研究主要考虑两相之间的曳力作用。
选择精度较高的Syamlal-O′Brien模型[24]计算固体颗粒在连续液相中受到的曳力,其表达式为:
| $ f=\frac{C_{\mathrm{D}} R e_{\mathrm{s}} \alpha_1}{24 v_{\mathrm{r}, \mathrm{~s}}^2} $ | (8) |
式(8)中CD为Dalla Valla推导所得的曳力系数[25]:
| $ C_{\mathrm{D}}=\left(0.63+\frac{4.8}{\sqrt{\operatorname{Re}_{\mathrm{s}} / v_{\mathrm{r}, \mathrm{~s}}^2}}\right)^2 $ | (9) |
vr, s为与分散相相关的最终速度[26]:
| $ \begin{gathered} v_{\mathrm{r}, \mathrm{~s}}=0.5\left(A-0.06 R e_{\mathrm{s}}+\right. \\ \sqrt{\left(0.06 R e_{\mathrm{s}}\right)^2+0.12 R e_{\mathrm{s}}(2 B-A)+A 2} \end{gathered} $ | (10) |
| $ A=\alpha_1^{4.14} $ | (11) |
| $ \left\{\begin{array}{l} \alpha_1 \leqslant 0.85, \quad B=0.8 \alpha_1^{1.28} \\ \alpha_1>0.85, \quad~~ B=\alpha_1^{2.65} \end{array}\right. $ | (12) |
Res为相对雷诺数[27],其速度由液固两相的相对瞬时速度表示:
| $ R e_{\mathrm{s}}=\frac{\rho_1 d_{\mathrm{s}}\left(v_{\mathrm{s}}-v_1\right)}{\mu_1} $ | (13) |
式(13)中:下标l和s分别表示液相和固相;ds为固体颗粒的直径。
1.5 数值模拟方法DTB结晶器壁面与底面设置为wall,顶部假设为静液面,设置为symmetry,进料口设置为velocity-inlet,产品采出管口和物料循环管口设为pressure-outlet,由于DTB结晶器带有搅拌桨,考虑到搅拌桨与结晶器之间的相对运动,本研究采用多重参考系法(MRF)[28]将搅拌区域设置为旋转区域,搅拌桨相对搅拌区的速度为0,其它区域设置为静区域。
模拟过程中以水相为连续相,密度为998.2 kg ·m-3,黏度为0.001 Pa ·s;蛋氨酸颗粒为分散相,密度为1 340 kg ·m-3,黏度为0.004 4 Pa.s,粒径为0.3 mm,假设流体为不可压缩流体。表 1为其它模拟参数设置。本研究模拟时忽略晶体成核生长过程,因此结晶器内部颗粒全部源于进口管,进口物料为3 m ·s-1、蛋氨酸体积分数为12%的固-液混合物,搅拌桨转速设为400 r ·min-1。
| 参数 | 模型/值 |
| granular viscosity/(kg·m-1·s-1) | Syamlal-O′Brien |
| granular bulk viscosity/(kg·m-1·s-1) | Lun et al |
| liquid-particle phase interaction | Syamlal-O′Brien |
| particle-particle phase interaction | Syamlal-O′Brien-symmetry |
| granular temperature/(m-2·s-2) | algebraic |
| particle-particle coefficient of restitution | 0.9 |
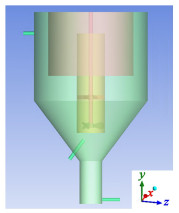
利用ICEM软件对DTB结晶器模型进行四面体非结构网格划分,图 2为结晶器导入ICEM后的结构简图,以结晶器底部中心为坐标原点,在确定结晶器主体网格后,对变化梯度较大的搅拌桨、进料管、产品采出管和物料循环管进行网格加密处理,从而得到最优网格数量。
|
| 图 2 DTB结晶器结构图 Fig.2 Structure diagram of DTB crystallizer |
| |
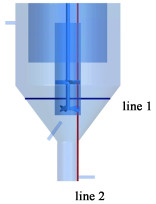
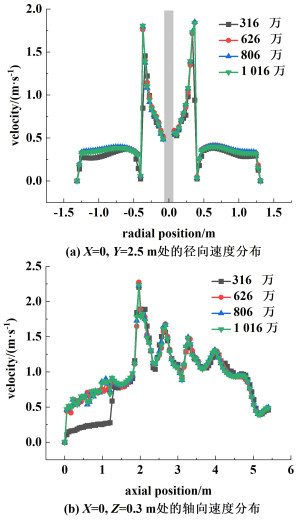
将DTB结晶器的模型按照合适的尺寸划分为4种不同的网格数:316万、626万、806万和1 026万,然后利用Fluent 2022 R1软件计算相同物性参数和操作条件下流体的运动状态,待流场稳定后选择靠近搅拌桨附近流动剧烈的区域进行监控,监测区如图 3所示,读取该处的速度值并绘制成图,结果如图 4所示。由图 4可知,806万网格与1 026万相比,在轴向和径向方向的速度几乎重合,可以保证所需的计算精度,因此本论文选择网格数量为806万的计算模型,最终划分的网格如图 5所示。
|
| 图 3 交线X=0 m, Y=2.5 m和X=0 m, Z=0.3 m位置示意图 Fig.3 Position diagram of lines of X=0 m, Y=2.5 m and X=0 m, Z=0.3 m |
| |
|
| 图 4 速度分布示意图 Fig.4 Schematic diagram of velocity distribution |
| |

|
| 图 5 DTB结晶器网格结构图 Fig.5 Cell structure diagram of DTB crystallizer |
| |
DTB结晶器中导流筒下端搅拌桨以较低转速旋转,可以看作内循环轴流泵装置[29],而导叶作为轴流泵中的一个重要部件,可将搅拌桨叶轮流出的流体由旋转运动转为轴向运动,对轴流泵的高效运行起着重要的作用,因此借鉴轴流泵的结构特点,本研究在导流筒内增加如图 6所示的导叶结构(导叶叶片数为6,倾斜角度为45°),希望提高DTB结晶器的轴流效果,增大内循环。

|
| 图 6 导叶结构示意图 Fig.6 Schematic diagram of the guide vane |
| |
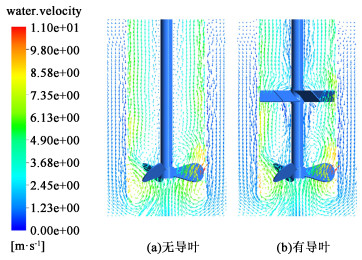
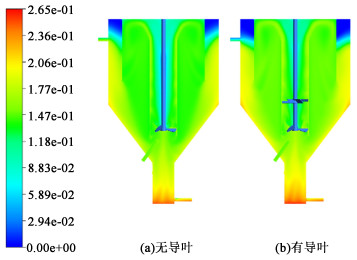
图 7为DTB结晶器纵剖面的局部速度矢量图,图 8为纵剖面的体积分数云图。由图 7和图 8可见,常规DTB结晶器在搅拌轴附近的流场较为混乱且流速很慢,颗粒分布较少,部分流体在重力作用下向下流动,不利于晶浆的内循环;增加导叶结构后,通过导叶的流体在到达导流筒液面之前全部往上运动,不仅提高了结晶器的轴流效果,还增强了流场的稳定性。表 2的计算结果也证明导叶结构确实增加了DTB结晶器的内循环流量,更多的晶浆被送到沸腾液面,表层随时存在大量晶体,可以消耗不断产生的过饱和度进行晶体的生长,从而避免过饱和度过高发生爆发成核而降低产品粒度。
|
| 图 7 DTB结晶器纵剖面X=0 m处的局部速度矢量图 Fig.7 Local velocity vector diagram at plane X=0 m of DTB crystallizer |
| |
|
| 图 8 DTB结晶器纵剖面X=0 m处的固体体积分数分布图 Fig.8 Distribution of solid volume fraction at plane X=0 m of DTB crystallizer |
| |
| 有无导叶 | 循环出口流量/(kg·s-1) | 采出口流量/(kg·s-1) | 内循环流量/(kg·s-1) | 搅拌功率/kW | 循环出口颗粒/进口颗粒 | 采出口颗粒/进口颗粒 |
| 无导叶 | 18.9 | 5.78 | 981.75 | 65.28 | 0.687 9 | 0.312 1 |
| 有导叶 | 17.37 | 6.98 | 1 102.51 | 65.52 | 0.485 0 | 0.515 0 |
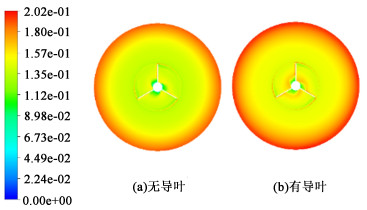
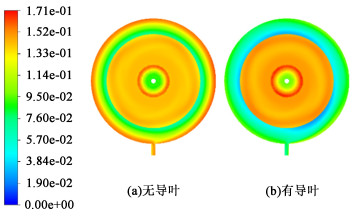
图 9和图 10分别为结晶器横剖面Y=2.2 m和Y=4.8 m处的固体体积分数分布图。
|
| 图 9 DTB结晶器横剖面Y=2.2 m处的固体体积分数分布 Fig.9 Distribution of solid volume fraction at plane Y=2.2 m of DTB crystallizer |
| |
|
| 图 10 DTB结晶器横剖面Y=4.8 m处的固体体积分数分布 Fig.10 Distribution of solid volume fraction at plane Y=4.8 m of DTB crystallizer |
| |
由图 9和图 10可知,导叶明显增强了颗粒的沉降效果、降低了循环出口的颗粒占比,这是由于导叶使内循环速度加快,从而降低了澄清区流体的运动速度,使颗粒未达到循环出口就发生沉降,但更多的晶体从产品出口采出,可能会加宽粒径分布。此外,晶体与导叶的碰撞可能会引发二次成核,影响产品粒径,因此实际工业过程中要根据生产目标,选择是否增加导叶结构。
2.2 导流筒长度对流动特性的影响导流筒形成的内循环通道可以使DTB结晶器的各个流动截面维持较高的流动速度,因此对结晶器的流场分布具有重要的影响,本节以导流筒长度为研究对象(导流筒长度h为1.6、2.0、2.4、2.8和3.2 m),探究DTB结晶器内的流场和颗粒悬浮状态。
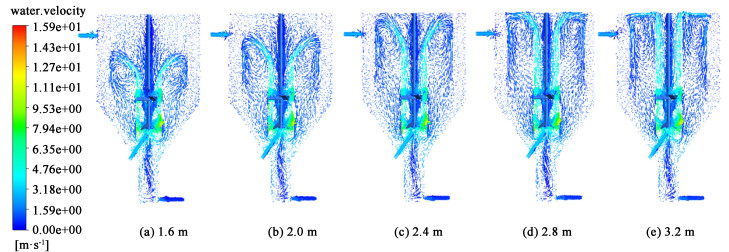
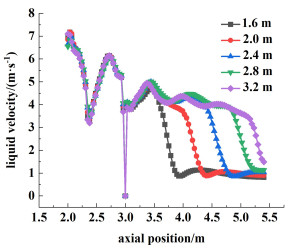
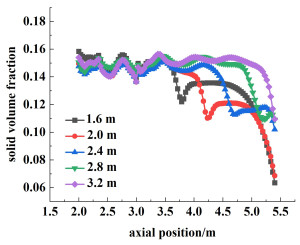
图 11为不同导流筒长度时DTB结晶器的纵剖面矢量图。从图 11中可以看出,当导流筒长度较短时,内循环作用无法充分发挥,大量晶浆难以到达沸腾液面,无法消耗蒸发浓缩所产生的过饱和度;当导流筒长度增加时,循环路程变长,越来越多的流体被送到沸腾液面,为结晶过程提供较大的生长表面,有利于消耗不断产生的过饱和度,使之维持在较低的水平,避免因晶核生成量过多而影响产品粒度。但如果导流筒长度太长,距离沸腾液面过近,到达沸腾区的流体速度过大(如图 12和图 13所示),不仅会增加颗粒与颗粒、颗粒与器壁的碰撞频率,导致晶体容易发生破碎现象,而且容易造成沸腾区流场不稳定,不利于过饱和度的稳定和均匀生成。
|
| 图 11 DTB结晶器纵剖面速度矢量图 Fig.11 Velocity vector diagram at longitudinal profile of DTB crystallizer |
| |
|
| 图 12 X=0 m, Z=0.3 m处的轴向液相速度分布 Fig.12 Distribution of axial solution velocity at X=0 m, Z=0.3 m |
| |
|
| 图 13 X=0, Z=0.3 m处的颗粒体积分数分布 Fig.13 Distribution of particle volume fraction at X=0 m, Z=0.3 m |
| |
表 3列出了不同导流筒长度时结晶器内的流动特性。由表 3可知,导流筒长度在1.6~2.8 m范围内,结晶器的内循环流量随着导流筒长度的增加而增加,功率随之下降;但当导流筒长度超过2.8 m后,从导流筒出去的流体在参与漩涡之前先一步接触液面,动能损失较大,导致内循环流量下降,功率消耗增加。由此可以说明,导流筒长度太长不仅影响结晶过程的稳定运行,而且会降低结晶器的使用效率。
| 导流筒长度/m | 循环出口流量/(kg·s-1) | 采出口流量/(kg·s-1) | 内循环流量/(kg·s-1) | 搅拌功率/kW | 循环出口颗粒/进口颗粒 | 采出口颗粒/进口颗粒 |
| 1.6 | 19.29 | 5.25 | 988.44 | 67.8 | 0.661 2 | 0.338 8 |
| 2.0 | 18.59 | 5.89 | 1 032.98 | 67.23 | 0.616 5 | 0.383 5 |
| 2.4 | 17.96 | 6.51 | 1 082.71 | 65.94 | 0.578 3 | 0.421 7 |
| 2.8 | 17.37 | 6.98 | 1 102.51 | 65.52 | 0.485 0 | 0.515 0 |
| 3.2 | 16.74 | 7.52 | 952.53 | 70.15 | 0.378 4 | 0.621 6 |
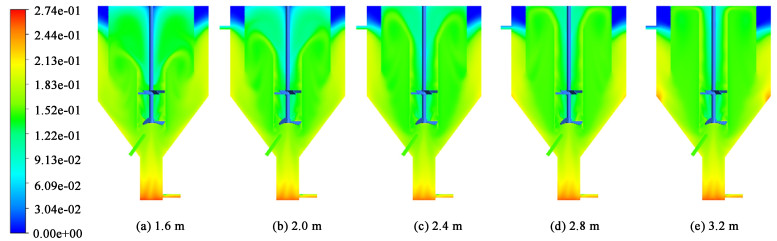
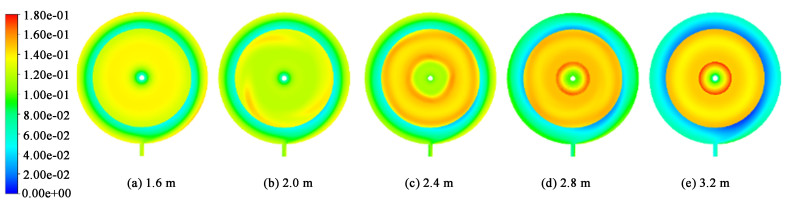
从导流筒出来的流体在参与内循环时容易产生漩涡,造成沸腾液面颗粒分布不均匀,如图 14所示,随着导流筒长度加长,导流筒与挡板之间的漩涡中心逐渐上移,颗粒分布不均现象得到改善。结晶器的横剖面图(图 15)显示,导流筒长度增加,澄清区颗粒的体积分数越来越小,这是由于循环阻力增大,使流体到达澄清区的速度减小,导致循环母液量减少,颗粒不能被带出,不利于细晶消除,这在工业上对生产粒度较大的产品是不利的,因此工业过程中要根据生产需要合理调整导流筒长度。
|
| 图 14 不同导流筒长度时平面X=0 m处的固体体积分数分布云图 Fig.14 Distribution of solid volume fraction at plane X=0 m of DTB crystallizer under different draft tube length |
| |
|
| 图 15 不同导流筒长度时平面Y=4.8 m处的固体体积分数分布云图 Fig.15 Distribution of solid volume fraction at plane Y=4.8 m of DTB crystallizer at different draft tube length |
| |
DTB结晶器中的挡板能控制流体向上的流速,使不同粒度的晶体颗粒实现分级,沉降速度较大的晶体颗粒发生沉降,从母液中分离出来,沉降速度较小的细晶随母液从循环出口排出,从而实现对微晶量的控制。因此本工作探究了挡板长度(挡板长度分别为1.8、2.0、2.2、2.4和2.6 m)对DTB结晶器内颗粒悬浮状态的影响。
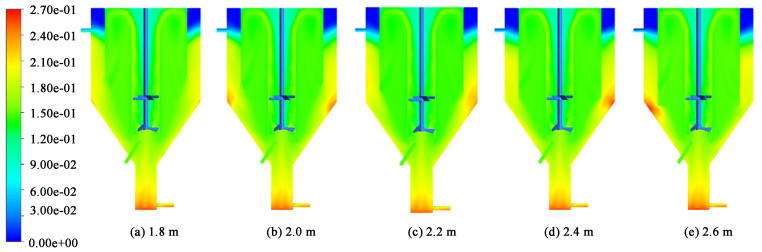
图 16和图 17分别为平面X=0、Y=2.2 m处的固体颗粒体积分数分布云图,由图 16和图 17可知,挡板的长度对澄清区的颗粒分布影响不大,但随着挡板的加长,流体对结晶器锥型壁面的碰撞冲击力增大,颗粒容易在此处分布不均,造成局部沉积,晶体既不能从循环口排出进行微晶消除,也不能从产品出口采出得到晶体产品,这对工业生产非常不利。
|
| 图 16 不同挡板长度平面X=0 m处的固体体积分数分布图 Fig.16 Distribution of solid volume fraction at plane X=0 m of DTB crystallizer at different baffle length |
| |
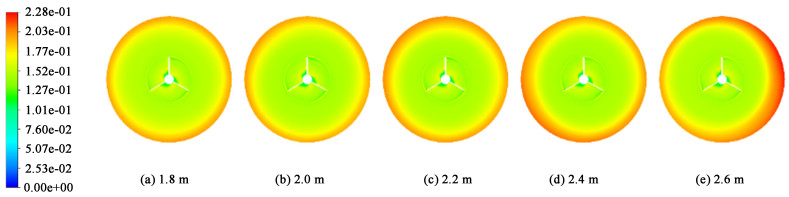
|
| 图 17 不同挡板长度平面Y=2.2 m处固体体积分数分布图 Fig.17 Distribution of solid volume fraction at plane Y=2.2 m of DTB crystallizer at different baffle length |
| |
表 4结果显示,挡板长度对DTB结晶器的功率消耗、内循环流量流量和外循环流量的影响不大,这是因为挡板位于澄清区,搅拌的影响已经消失,无法改变结晶器的内循环情况,因此只对晶体分级有影响。
| 挡板长度/m | 循环出口流量/(kg·s-1) | 采出口流量/(kg·s-1) | 内循环流量/(kg·s-1) | 搅拌功率/kW | 循环出口颗粒/进口颗粒 | 采出口颗粒/进口颗粒 |
| 1.8 | 17.37 | 6.98 | 1 102.51 | 65.52 | 0.485 0 | 0.515 0 |
| 2.0 | 17.33 | 6.81 | 1 100.00 | 65.46 | 0.412 9 | 0.587 1 |
| 2.2 | 17.46 | 6.68 | 1 098.33 | 65.55 | 0.374 6 | 0.625 4 |
| 2.4 | 17.38 | 6.74 | 1 094.46 | 65.40 | 0.353 0 | 0.647 0 |
| 2.6 | 17.50 | 6.60 | 1 095.34 | 65.54 | 0.342 7 | 0.657 3 |
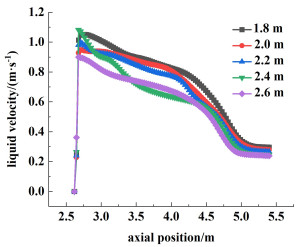
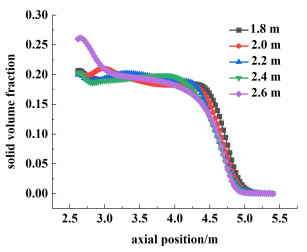
图 18和图 19分别为X=0 m, Z=-1.4 m处的轴向液相速度分布图和颗粒体积分数分布图。由图 19可知,随着挡板长度的增加,澄清区循环出口的颗粒分布越来越少,这是因为沉降区域逐渐增大,母液到达循环出口的路径变长,溶液的主体速度下降,无法携带晶体从循环出口流出,更多的晶体产品发生沉降或从产品出口采出,因此不利于通过细晶消除得到粒径较大的产品。
|
| 图 18 X=0 m, Z=-1.4 m处的轴向液相速度分布 Fig.18 Distribution of axial solution velocity at X=0 m, Z=-1.4 m |
| |
|
| 图 19 X=0 m, Z=-1.4 m处的颗粒体积分数分布 Fig.19 Distribution of particle volume fraction at X=0 m, Z=-1.4 m |
| |
除此之外,挡板长度过长,可能会加剧颗粒与器壁的碰撞,大颗粒在沉降之前可能会发生破碎,导致产品粒度变小。因此,在实际工业生产过程中,如果对产品的粒度要求比较高,不适合安装过长的挡板。
3 结论利用欧拉-欧拉模型模拟获得了不同内部结构时DTB结晶器内流体的流动特性和颗粒的悬浮状况,得到结论如下:(1)在DTB结晶器的导流筒内增加导叶结构可以提高结晶器的轴流效果,增加内循环量,有利于晶体的均匀生长。(2)导流筒控制着DTB结晶器的内循环。增加导流筒长度可以为结晶过程提供更大的生长表面,避免产生过量的晶核。但导流筒过长,内循环产生的漩涡容易影响沸腾液面,造成二次成核,因此工业生产过程中要控制导流筒长度,使之维持在合适的长度范围。(3)挡板长度主要影响DTB结晶器的澄清区。挡板越长,晶体越容易在澄清区的锥形壁面局部沉积,不利于结晶器的稳定运行;而且随着挡板长度的增加,沉降区域逐渐增大,不利于细晶消除,得到较大粒径的产品。
| [1] |
谭圣君, 邵友元, 李卫. 蛋氨酸的研究现状及其应用前景[J]. 湖北工业大学学报, 2006, 21(6): 66-71. TAN Shengjun, SHAO Youyuan, LI Wei. Current research and application prospects of methionine[J]. Journal of Hubei University of Technology, 2006, 21(6): 66-71. DOI:10.3969/j.issn.1003-4684.2006.06.019 (in Chinese) |
| [2] |
周容帆. 蛋氨酸结晶过程研究[D]. 杭州: 浙江大学, 2021 ZHOU Rongfan. Crystallization process of D, L-methionine[D]. Hangzhou: Zhejiang University, 2021 (in Chinese) |
| [3] |
WANTHA L, FLOOD A E. Growth and dissolution kinetics of α and γ polymorphs of DL-methionine[J]. Journal of Crystal Growth, 2013, 362: 66-70. DOI:10.1016/j.jcrysgro.2011.10.064 |
| [4] |
SAWAMURA S, KUNIMASA N. High-pressure solubility of L-methionine in water[J]. Journal of Solution Chemistry, 2014, 43(9): 1810-1815. |
| [5] |
PAN H, LI J, JIN Y, et al. Numerical investigation of the effect of bottom shape on the flow field and particle suspension in a DTB crystallizer[J]. International Journal of Chemical Engineering, 2016. DOI:10.1155/2016/6862152 |
| [6] |
SONG X, ZHANG M, WANG J, et al. Optimization design for DTB industrial crystallizer of potassium chloride[J]. Industrial & Engineering Chemistry Research, 2010, 49(21): 10297-10302. |
| [7] |
SHU C, WANG X, SHA Z. CFD simulation on solid suspension with continuous operation[J]. Advanced Materials Research, 2011, 233/234/235: 1177-1183. |
| [8] |
ASHRAF A B, BÖRNER M, PEGLOW M, et al. Coupled computational fluid dynamics-discrete element method simulations of a pilot-scale batch crystallizer[J]. Cryst Growth Des, 2014, 15(1): 145-155. |
| [9] |
MENON A, KRAMER H, GRIEVINK J, et al. Modelling the cyclic behaviour in a DTB crystallizer—A two-population balance model approach[J]. Journal of Crystal Growth, 2004, 275(1): e1373-e1381. |
| [10] |
HAMAMURA T, NAGATA H, SOTOWA K, et al. Ease of control of imperfectly mixed continuous DTB crystallizers[J]. Kagaku Kogaku Ronbunshu, 2001, 27: 359-366. DOI:10.1252/kakoronbunshu.27.359 |
| [11] |
HOON O D, YOUNG J R, HYUNG K J, et al. Scale-up of a semi-batch draft tube baffled crystallizer for hexanitrohexaazaisowurtzitane based on experiments and computational fluid dynamics simulation[J]. Crystal Growth & Design, 2019, 19(2): 658-671. |
| [12] |
OH D H, JEON R Y, ADAMS D, et al. Software platform for computation fluid dynamics simulation of mixing and crystallization in a stirred vessel[J]. Crystal Growth & Design, 2019, 20(2): 1172-1185. |
| [13] |
徐勇泳. 碳酸锂结晶器CFD数值模拟研究[D]. 上海: 华东理工大学, 2013 XU Yongyong. CFD simulation research on crystallizer of lithium carbonate[D]. Shanghai: East China University of Science and Technology, 2013 (in Chinese) |
| [14] |
汤俊杰, 易争明, 郭璐. 基于CFD对DTB结晶器内搅拌桨构型的优选[J]. 现代化工, 2019, 39(1): 209-212. TANG Junjie, YI Zhengming, GUO Lu. CFD-based optimization of configuration of agitator blade in DTB crystallizer[J]. Modern Chemical Industry, 2019, 39(1): 209-212. (in Chinese) |
| [15] |
丁绪淮, 谈遒. 工业结晶[M]. 北京: 化学工业出版社, 1985. DING Xuhuai, TAN Qiu. Industrial crystallization[M]. Beijing: Chemical Industry Press, 1985. (in Chinese) |
| [16] |
赵思源. 光卤石及氯化钾结晶设备混合与闪蒸的CFD研究[D]. 天津: 天津大学, 2018 ZHAO Siyuan. CFD study on mixing and flash evaporation of carnallite and potassium chloride crystallization equipments[D]. Tianjin: Tianjin University, 2018 (in Chinese) |
| [17] |
JAWORSKI Z. The use of angle resolved LDA data to compare two different turbulence models applied to sliding mesh CFD flow simulations in a stirred tank[J]. Recent Progres en Genie des Procedes, 1997, 11: 187-194. |
| [18] |
SYNOWIEC P M, MAŁYSIAK A, WÓJCIK J. Fluid-dynamics scale-up problems in the DTM crystallizer[J]. Chemical Engineering Science, 2012, 77: 78-84. DOI:10.1016/j.ces.2012.04.018 |
| [19] |
ZHU Z, WEI H. Flow field of stirred tank used in the crystallization process of ammonium sulphate[J]. ScienceAsia, 2008, 34(1): 97-101. DOI:10.2306/scienceasia1513-1874.2008.34.097 |
| [20] |
MALIK R, SHI T, TANG Z, et al. Computational fluid dynamics (CFD) based simulated study of multi-phase fluid flow[J]. Defect and Diffusion Forum, 2010, 307: 1-11. DOI:10.4028/www.scientific.net/DDF.307.1 |
| [21] |
OGAWA S, UMEMURA A, OSHIMA N. On the equations of fully fluidized granular materials[J]. Zeitschrift Für Angewandte Mathematik Und Physik ZAMP, 1980, 31(4): 483-493. DOI:10.1007/BF01590859 |
| [22] |
DING J, GIDASPOW D. A bubbling fluidization model using kinetic theory of granular flow[J]. AIChE Journal, 1990, 36(4): 523-538. DOI:10.1002/aic.690360404 |
| [23] |
LUN C K K, SAVAGE S B, JEFFREY D J, et al. Kinetic theories for granular flow: Inelastic particles in Couette flow and slightly inelastic particles in a general flow field[J]. Journal of Fluid Mechanics, 1984, 140: 223-256. DOI:10.1017/S0022112084000586 |
| [24] |
SYAMLAL M, O'BRIEN T J. Computer simulation of bubbles in a fluidized bed[J]. AIChE Symposium Series, 1989, 85(270): 22-31. |
| [25] |
DALLAVALLE J M. Coagulation and sedimentation[J]. Proceedings of the American Society of Civil Engineers, 1956, 82(4): 1051-1052. |
| [26] |
GARSLDE J, AL-DIBOUNI M R. Velocity-voidage relationships for fluidization and sedimentation in solid-liquid systems[J]. Industrial and Engineering Chemistry Process Design and Development, 1977, 16(2): 206-214. DOI:10.1021/i260062a008 |
| [27] |
RICHARDSON J F, ZAKI W N. Sedimentation and fluidisation: Part Ⅰ[J]. Chemical Engineering Research and Design, 1997, 75(1 SUPPL): 82-100. |
| [28] |
LUO J, ISSA R I, GOSMAN A D. Prediction of impeller induced flows in mixing vessels using multiple frames of reference[J]. Institution of Chemical Engineers Symposium Series, 1994, 136: 549-556. |
| [29] |
SHENG J, MENG H, FOX R. Validation of CFD simulations of a stirred tank using particle image velocimetry data[J]. Canadian Journal of Chemical Engineering, 1998, 76: 611-625. DOI:10.1002/cjce.5450760333 |
 2025, Vol. 42
2025, Vol. 42





