活性炭是一种炭质吸附材料,具有丰富的孔隙结构和巨大的比表面积[1],在环保、医疗和化工领域应用甚广。从外形上可分为粉状、粒状、球状和纤维状,其中关于粉状、粒状和纤维状活性炭方面的报道已经很多,而对于沥青基球状活性炭方面的研究报道较少。沥青基球状活性炭不仅具有常规炭的吸附性能,而且有助于提高填充密度和减小床层压降,目前工业上常用做吸附剂,其利用率不仅与孔隙率有关,还与颗粒流化质量有关,反应器主要有固定床和流化床。
流化床反应器具有结构简单和传热传质性能良好的特点,广泛应用于石油化工、能源环保和生物制药等行业[2-7]。随着流化床技术的广泛应用,对流体动力学的理论研究也逐渐增多。如Behjat等[8]在气固流化床中研究床层内2种不同固相的流体力学和传热现象,发现其颗粒直径越小,分布在床层底部的含量越少,顶部的越多。Lu等[9]用多流体模型研究混合物在鼓泡流化床中颗粒的流动特性,在鼓泡流化床中取得了颗粒流体特性与相间作用力有关的结果。Xing等[10]采用双流体法研究入口气体分布器对鼓泡流化床内气泡分布的影响,研究发现鼓泡流化床中的气泡分布可以通过改变分配器角度和位置实现。大量研究表明两相流动的均匀性有助于提高流化质量,从而提高物系的利用率。由于两相流动的复杂性,实验难以精准测量流化床床层内流动特性,因此可以借助模拟手段进行研究。
目前ANSYS Fluent是世界上应用最广泛的计算流体动力学[11, 12](Computational fluid dynamics, CFD)软件,可以完成各种复杂装置及反应的数值模拟。不仅能节省人力、物力和时间,而且对实验规律的发现能够起到指引预判的作用。CFD中应用广泛的模型是欧拉-拉格朗日和欧拉-欧拉[13-18]。其中,欧拉-拉格朗日方法适用于稀疏气固流体体系;而欧拉-欧拉方法因其计算量小,能满足一定精度要求,广泛应用于流化床的研究。气固流化取决于相间作用力,而气固相间作用力主要通过气固曳力来耦合[19, 20]。因此,曳力模型的正确选择是决定流体对固体颗粒夹带和输送能力的关键。
本工作借助计算流体力学的手段,从实验和数值模拟两方面分析沥青基球状活性炭在气固流化床中的流动特性。基于欧拉-欧拉模型,利用ANSYS Fluent软件全面对比了Syamlal-O’Brien、Gidaspow、Wen-yu、Huilin-gidaspow和Gibilaro 5种曳力模型的模拟云图,从中选出最佳曳力模型。在数值计算方面,进一步验证数值计算参数对模拟结果的影响。然后从颗粒体积分布、床层压降和膨胀高度分析进气速度对气固混合的影响,确定是否存在最佳进气速度使床层颗粒均匀流化,同时验证模型选择的准确性。
1 实验部分 1.1 实验材料沥青基球状活性炭的成分主要由C、H、N和S等元素组成。球状的外形具有良好的滚动性,一方面使颗粒均匀填充,相互之间的磨损减少,另一方面使颗粒对气体的流动阻力较小。沥青基球状活性炭的性能参数测试结果如表 1所示。
| 形状 | 强度/% | 比表面/(m2·g-1) | 粒径/mm | 堆密度/(g·mL-1) | 真密度/(kg·m-3) |
| 球形 | 95 | 1 231 | 0.64~0.73 | 0.60 | 1 000 |
在流化床中,流速范围在最小流化速度和带出速度之间。当入口流体速度增加到一定值时,堆积颗粒床层开始膨胀,颗粒开始进入流化状态,此时的流体速度就是最小流化速度。而带出速度是床层内固体颗粒被流体夹带而悬浮的最小速度,是操作流速的上限。本实验所采用的炭颗粒粒径较小,最小流化速度和带出速度计算公式如式(1)和式(2)。
| $ v_{\mathrm{mf}}=\frac{d_{\mathrm{s}}^2\left(\rho_{\mathrm{s}}-\rho_{\mathrm{g}}\right) \mathrm{g}}{1650 \mu_{\mathrm{g}}} $ | (1) |
| $ v_{\mathrm{t}}=\left\{\begin{array}{lc} \frac{d_{\mathrm{s}}^2\left(\rho_{\mathrm{s}}-\rho_{\mathrm{g}}\right) g}{18 \mu_{\mathrm{g}}}, & R e_{\mathrm{t}}<0.4 \\ {\left[\frac{2 d_{\mathrm{s}}\left(\rho_{\mathrm{s}}-\rho_{\mathrm{g}}\right) g R e_{\mathrm{t}}^{0.5}}{15 \rho_{\mathrm{g}}}\right]^{1 / 2}, } & 0.4<R e_{\mathrm{t}}<500 \\ {\left[\frac{4}{3} \frac{d_{\mathrm{s}}\left(\rho_{\mathrm{s}}-\rho_{\mathrm{g}}\right) g}{0.43 \rho_{\mathrm{g}}}\right]^{1 / 2}, } & R e_{\mathrm{t}}>500 \end{array}\right. $ | (2) |
式(1)和式(2)中:v为速度;d为直径;ρ为密度;g为重力加速度;μ为剪切黏度;Re为雷诺数;下标g和s分别代表气相和固相;下标mf和t分别代表最小流化和带出。带出速度下的雷诺数按式(3)计算。
| $ R e_{\mathrm{t}}=\frac{d_{\mathrm{s}} v_{\mathrm{t}} \rho_{\mathrm{g}}}{\mu_{\mathrm{g}}} $ | (3) |
由式(3)计算得最小流化速度为0.153 m·s-1,带出速度为2.920 m·s-1。即流速范围在0.153~2.920 m·s-1之间。但研究所选用的炭颗粒粒径较小,在流化时容易产生大气泡和腾涌现象,使气固两相接触不均匀。为了使颗粒流化均匀,实际最大入口流速要小于带出速度。综合考虑,确定实验的流速范围为0.16~0.45 m·s-1。
1.3 实验流程及装置实验采用了定制直径0.05 m的圆筒型有机玻璃流化床,高度为0.20 m。在不同入口进气速度下(0.16~0.45 m·s-1),在流化床中对沥青基球状活性炭进行实验。其中颗粒的堆积高度为0.04 m。实验装置及流程图如图 1所示。
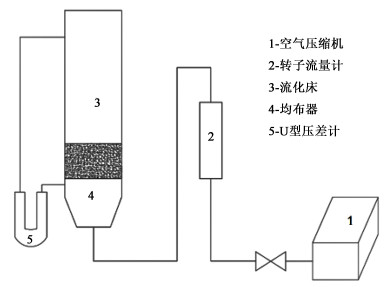
|
| 图 1 实验装置及流程图 Fig.1 Experimental apparatus and flowchart |
| |
表 2为实验仪器信息。该实验气体由空气压缩机供给,在均布器中形成均匀气体。通过调整转子流量计,使气体在流化床中形成稳定流场,使沥青基球状炭颗粒在床层内均匀流化。床层压降由U型压差计测得,其中需要测量的床层压降为Δp实际=Δp总-Δp空床。实验针对每一个变量均进行了从小到大和从大到小各3组重复实验,由于从小到大的数据结果缓慢,为确保实验结果能够代表长期稳定运行的效果,结果均采用变量由大到小的数据。
| 序号 | 仪器/设备 | 参数 | 公司 |
| 1 | 空气压缩机 | 体积40 L | 上海曲晨机电技术有限公司 |
| 2 | 转子流量计 | 流速100 L·min-1 | 余姚伟创流量仪表有限公司 |
| 3 | 有机玻璃组成的流化床 | 直径0.05 m,高度0.20 m | 徐州雷佳科学仪器有限公司 |
| 4 | U型压差计 | 压力1 000 Pa | 河北省武强县胜启仪表厂 |
数值计算的控制方程包含质量、动量和能量守恒方程。冷模试验研究的是气固流化床的流动特性,没有热量和化学反应,主要控制方程是质量和动量守恒方程。
质量守恒方程的气相和固相计算公式分别为公式(4)和(5)。
| $ \frac{\partial\left(\rho_{\mathrm{g}} \varepsilon_{\mathrm{g}}\right)}{\partial t}+\nabla \cdot\left(\rho_{\mathrm{g}} \varepsilon_{\mathrm{g}} \nu_{\mathrm{g}}\right)=0 $ | (4) |
| $ \frac{\partial\left(\rho_{\mathrm{s}} \varepsilon_{\mathrm{s}}\right)}{\partial t}+\nabla \cdot\left(\rho_{\mathrm{s}} \varepsilon_{\mathrm{s}} \nu_{\mathrm{s}}\right)=0 $ | (5) |
式(4)和式(5)中:ε是体积分数,εg+εs=1。
动量守恒方程的气相和固相计算分别为公式(6)和(7)。
| $ \begin{gathered} \frac{\partial\left(\rho_{\mathrm{g}} \varepsilon_{\mathrm{g}} \nu_{\mathrm{g}}\right)}{\partial t}+\nabla \cdot\left(\rho_{\mathrm{g}} \varepsilon_{\mathrm{g}} \nu_{\mathrm{g}}{ }^2\right)=\nabla \cdot \tau_{\mathrm{g}}+\rho_{\mathrm{g}} \varepsilon_{\mathrm{g}} g- \\ \varepsilon_{\mathrm{g}} \nabla p-\beta\left(\nu_{\mathrm{g}}-\nu_{\mathrm{s}}\right) \end{gathered} $ | (6) |
| $ \begin{gathered} \frac{\partial\left(\rho_{\mathrm{s}} \varepsilon_{\mathrm{s}} \nu_{\mathrm{s}}\right)}{\partial t}+\nabla \cdot\left(\rho_{\mathrm{s}} \varepsilon_{\mathrm{s}} \nu_{\mathrm{s}}^2\right)=\nabla \cdot \tau_{\mathrm{s}}+\rho_{\mathrm{s}} \varepsilon_{\mathrm{s}} g- \\ \nabla p_{\mathrm{s}}-\varepsilon_{\mathrm{s}} \nabla p-\beta\left(\nu_{\mathrm{s}}-\nu_{\mathrm{g}}\right) \end{gathered} $ | (7) |
式(6)和式(7)中:p是压力;β是气固相间曳力系数;τ是应力张量。气相和固相的应力张量的计算分别为公式(8)和(9)。
| $ \tau_{\mathrm{g}}=\varepsilon_{\mathrm{g}} \mu_{\mathrm{g}}\left(\nabla \nu_{\mathrm{g}}+\left(\nabla \nu_{\mathrm{g}}\right)^T\right)-\frac{2}{3} \varepsilon_{\mathrm{g}} \mu_{\mathrm{g}}\left(\nabla \cdot \nu_{\mathrm{g}}\right) \cdot I $ | (8) |
| $ \begin{gathered} \tau_{\mathrm{s}}=\varepsilon_{\mathrm{s}} \mu_{\mathrm{s}}\left(\nabla \nu_{\mathrm{s}}+\left(\nabla \nu_{\mathrm{s}}\right)^T\right)+ \\ \varepsilon_{\mathrm{s}}\left(\lambda_{\mathrm{s}}-\frac{2}{3} \mu_{\mathrm{s}}\right)\left(\nabla \cdot \nu_{\mathrm{s}}\right) \cdot I \end{gathered} $ | (9) |
式(8)和式(9)中:I为单位张量。
气固相间曳力系数和颗粒弛豫时间的定义分别为公式(10)和(11)。
| $ \beta=\frac{\varepsilon_{\mathrm{s}} \rho_{\mathrm{s}} f}{\tau_p} $ | (10) |
| $ \tau_p=\frac{\rho_{\mathrm{s}} d_{\mathrm{s}}{ }^2}{18 \mu_{\mathrm{g}}} $ | (11) |
式(10)和式(11)中:f为曳力函数。
2.2 曳力模型在欧拉-欧拉模型下,气固相间作用需要建立封闭关系,而气固相间的封闭关系主要通过气固曳力来耦合。不同的曳力模型函数具有不同的表达式,气固两相动量交换系数的主要数学模型是Syamlal-O’Brien、Gidaspow、Wen-yu、Huilin-gidaspow和Gibilaro。
(1) Syamlal-O’Brien模型[21]表达式为式(12)~式(15)。
| $ f=\frac{C_{\mathrm{D}} R e_{\mathrm{s}} \varepsilon_{\mathrm{g}}}{24 \nu_{\mathrm{r}, \mathrm{~s}}^2} $ | (12) |
| $ \beta=\frac{3 \varepsilon_{\mathrm{g}} \varepsilon_{\mathrm{s}} \rho_{\mathrm{g}}}{4 \nu_{\mathrm{r}, \mathrm{~s}}{ }^2 d_{\mathrm{s}}} C_{\mathrm{D}} \frac{R e_{\mathrm{s}}}{\nu_{\mathrm{r}, \mathrm{~s}}}\left|\nu_{\mathrm{g}}-\nu_{\mathrm{s}}\right| $ | (13) |
| $ C_{\mathrm{D}}=\left(0.63+\frac{4.8}{\sqrt{R e_{\mathrm{s}} \sqrt{\nu_{\mathrm{r}, \mathrm{~s}}}}}\right)^2 $ | (14) |
| $ \begin{gathered} \nu_{\mathrm{r}, \mathrm{~s}}=0.5\left[\varepsilon_{\mathrm{g}}^{4.14}-0.06 R e+\right. \\ \left.\sqrt{(0.06 R e)^2+0.12 {Re}\left(2 A-\varepsilon_{\mathrm{g}}^{4.14}\right)+\left(\varepsilon_{\mathrm{g}}^{4.14}\right)^2}\right] \end{gathered} $ | (15) |
式(12)~式(15)中:CD为曳力系数;νr, s为颗粒终端速度;且当εg≤0.85时,A=0.8εg1.28; 当εg>0.85时,A=εg2.65。
(2) Gidaspow模型[22]表达式为公式(16)。
| $ \beta= \begin{cases}\frac{3}{4} C_{\mathrm{D}} \frac{\rho_{\mathrm{g}} \varepsilon_{\mathrm{g}} \varepsilon_{\mathrm{s}}\left|\nu_{\mathrm{g}}-\nu_{\mathrm{s}}\right|}{d_{\mathrm{s}}} \varepsilon_{\mathrm{g}}^{-265}, & \varepsilon_{\mathrm{g}}>0.8 \\ 150 \frac{\varepsilon_{\mathrm{g}}\left(1-\varepsilon_{\mathrm{g}}\right) \mu_{\mathrm{g}}}{\varepsilon_{\mathrm{g}} d_{\mathrm{s}}^2}+1.75 \frac{\rho_{\mathrm{g}} \varepsilon_{\mathrm{g}}\left|\nu_{\mathrm{g}}-\nu_{\mathrm{s}}\right|}{d_{\mathrm{s}}}, & \varepsilon_{\mathrm{g}} \leqslant 0.8\end{cases} $ | (16) |
(3) Wen-yu模型[23]表达式为公式(17)和(18)。
| $ \beta=\frac{3}{4} C_D \frac{\rho_{\mathrm{g}} \varepsilon_{\mathrm{g}} \varepsilon_{\mathrm{s}}\left|\nu_{\mathrm{g}}-\nu_{\mathrm{s}}\right|}{d_{\mathrm{s}}} \varepsilon_{\mathrm{g}}^{-2.65} $ | (17) |
| $ C_{\mathrm{D}}=\frac{24}{\varepsilon_{\mathrm{g}} R e_{\mathrm{s}}}\left[1+0.15\left(\varepsilon_{\mathrm{g}} R e_{\mathrm{s}}\right)^{0.687}\right] $ | (18) |
(4) Huilin-gidaspow模型[24]表达式为式(19)。
| $ \begin{gathered} \beta=\psi\left[150 \frac{\varepsilon_{\mathrm{s}}\left(1-\varepsilon_{\mathrm{g}}\right) \mu_{\mathrm{g}}}{\varepsilon_{\mathrm{g}} d_{\mathrm{s}}^2}+1.75 \frac{\varepsilon_{\mathrm{s}} \rho_{\mathrm{g}}\left|\nu_{\mathrm{s}}-\nu_{\mathrm{g}}\right|}{d_{\mathrm{s}}}\right]+ \\ (1-\psi)\left(\frac{3 C_{\mathrm{D}} \varepsilon_{\mathrm{g}}^{-1.65} \varepsilon_{\mathrm{s}} \rho_{\mathrm{g}}\left|\nu_{\mathrm{s}}-\nu_{\mathrm{g}}\right|}{4 d_{\mathrm{s}}}\right) \end{gathered} $ | (19) |
式(19)中:ψ为平滑过渡函数,ψ=0.5+arctant[262.5(εs-0.2)]/π。
(5) Gibilaro模型[25]表达式为式(20)。
| $ \beta=\left(\frac{18}{\varepsilon_{\mathrm{g}} R e}+0.33\right)\left(\frac{\rho_{\mathrm{g}}\left|\nu_{\mathrm{s}}-\nu_{\mathrm{g}}\right|}{d_{\mathrm{s}}} \varepsilon_{\mathrm{s}} \varepsilon_{\mathrm{g}}^{-1.8}\right) $ | (20) |
利用Geometry程序,绘制二维流化床几何模型,如图 2所示。由于计算区域是规则几何,采用四边形单元结构为主划分网格,四边形网格具有简捷、数量少和质量高的特点。

|
| 图 2 流化床几何模型 Fig.2 Geometry model of fluidized bed |
| |
在模拟早期进行了网格无关性分析,比较了尺寸为颗粒直径的2倍、7倍和10倍的网格,网格数量分别为400、10 000和40 000。图 3显示了不同网格尺寸下,压降随时间的变化。结果表明,当网格数量为400时,床层压降的预测值与网格数量为10 000和40 000时相比有较大的差别,而网格数为10 000和40 000的计算结果较为接近,误差在可接受的范围内。从计算精度考虑,研究采用40 000的网格尺寸。
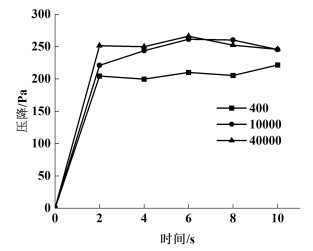
|
| 图 3 不同网格尺寸下的压降数据比较 Fig.3 Comparison of pressure drop data with different grid sizes |
| |
在欧拉-欧拉模型下,空气作为连续相,沥青基球状活性炭作为弥散相,在柱内相互渗透和相互作用。实验中的炭颗粒具有较好的球形且强度高,动力研究中忽略颗粒与壁面的摩擦力,故假设壁面边界无滑移。实验过程中所采用的均布器已经降低了速度的不均匀性,对气固两相流动的不稳定性可忽略不计,因此假设流化床底部入口速度均匀。其中,边界条件采用速度进口和压力出口。相关模拟参数见表 3。
| 名称 | 设置 |
| 颗粒黏度 | Syamlal-O’Brien |
| 曳力模型 | Syamlal-O’Brien, Gidaspow, Wen-Yu, Huilin-Gidaspow, Gibilaro |
| 颗粒密度/(kg·m-3) | 1 000 |
| 空气密度/(kg·m-3) | 1.225 |
| 平均颗粒直径/m | 0.000 7 |
| 初始固体高度/m | 0.04 |
| 进气速度/(m·s-1) | 0.20~0.45 |
| 床层宽度/m | 0.05 |
| 床层高度/m | 0.20 |
| 出口边界条件 | 压力出口 |
| 壁面边界条件 | 无滑移 |
| 时间步长/s | 0.000 1, 0.000 5 |
| 最大迭代次数 | 20 |
| 收敛范围 | 10-3和10-4 |
| 离散格式 | 一阶和二阶 |
通过对Syamlal-O’Brien等5种曳力模型进行比较,选出与实验结果拟合最好的曳力模型。研究考虑了时间步长、离散格式和收敛准则对炭颗粒体积分布的影响,并讨论了进气速度、床层压降和膨胀高度对气固流化床中炭颗粒运动特性的影响。
3.1 不同曳力模型的对比在建立的气固二维流化床的模型网格上,将沥青基球状炭对照实验参数设置模拟参数。在多相流模型下,对比Syamlal-O’Brien、Gidaspow、Wen-yu、Huilin-gidaspow和Gibilaro 5种不同曳力模型与实验结果的颗粒体积分布情况,从中选出最佳曳力模型。图 4为0.16 m·s-1速度下不同曳力模型球状炭颗粒体积分布云图。由该图可知曳力模型的不同导致模拟出来的膨胀高度和气泡大小以及形状区别明显。其中Wen-yu和Gibilaro模型气泡较大,Gidaspow和Gibilaro模型的气泡较小,Syamlal-O’Brien模型没有较明显的气泡,但对照实验的流动情况后发现Syamlal-O’Brien模型更为符合条件。故后续模拟计算中均选择Syamlal-O’Brien曳力模型。
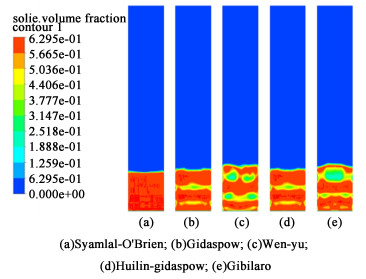
|
| 图 4 0.16 m·s-1速度下不同曳力模型球状炭颗粒体积分布云图 Fig.4 Cloud plot of volume fraction of spherical carbon particles at 0.16 m·s-1 for different traction models |
| |
在速度v=0.40 m·s-1的Syamlal-O’Brien模型下,对时间步长、离散格式和收敛准则的模拟结果进行比较,结果如图 5所示。在模拟云图中,整体流动形状没有显著差异,说明了所选的数值模拟足以测量颗粒在流化床中的流动特性。本研究对比了时间步长0.000 1和0.000 5 s条件下的颗粒流动情况,计算10 s的时间分别为42和20 h。从计算精度考虑,研究选用时间步长0.000 1 s的二阶离散格式进行计算,用于监测质量流残差的收敛范围为10-3。
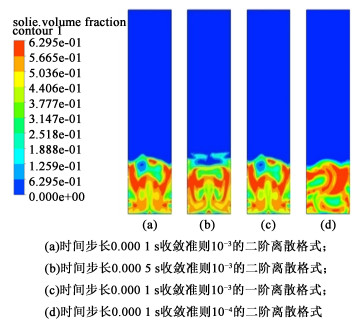
|
| 图 5 不同时间步长、离散格式和收敛准则下固体体积分布云图 Fig.5 Cloud plot of volume fraction of solid for different time steps, discrete formats, and convergence criteria |
| |
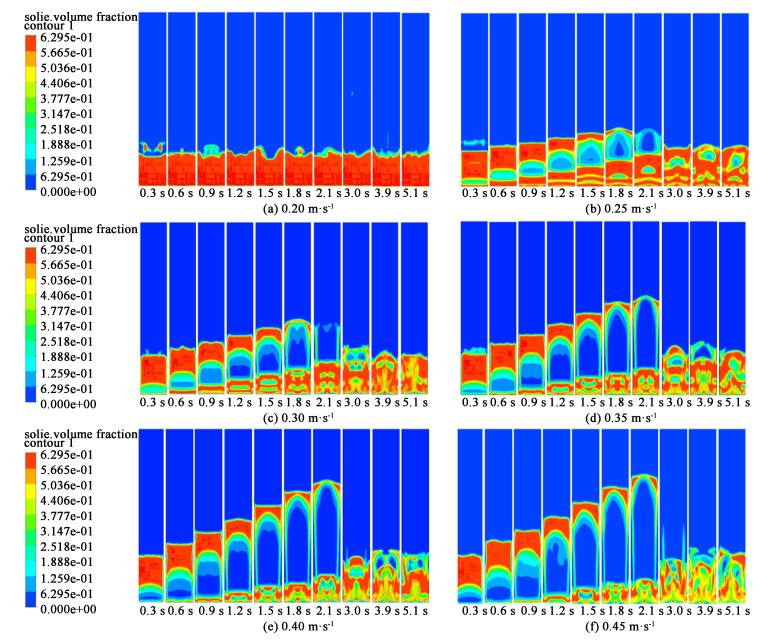
为研究实验中流化床的流化现象以及最优流化速度,在Syamlal-O’Brien曳力模型下,对入口进气速度0.20~0.45 m·s-1范围内,所选取时刻分别为0.3、0.6、0.9、1.2、1.5、1.8、2.1、3.0、3.9和5.1 s的球状活性炭体积分布进行模拟。不同入口进气速度、不同时刻的云图如图 6所示。
|
| 图 6 不同进气速度下炭体积分布云图 Fig.6 Volume distribution clouds of carbon at different inlet velocities |
| |
由图 6可以发现,随着进气速度的增大,床层高度和气泡尺寸逐渐增大,气泡的数量也愈来愈多。出现这种现象的原因是,当气相速度略高于初始流化速度时,气体进入床层使颗粒群均匀膨胀而后以气泡的形式流化。随着进气速度的增大,进气量增大,气泡的大小也逐渐增大。在相同进气速度下,小气泡逐渐积累成大气泡,而后破裂[26]。以上分析结果和Gera等[27]采用离散元模型研究大颗粒流化床的流体力学、Rao等[28]对圆柱鼓泡流化床中气泡运动进行计算流体力学模拟的分析结果相对应。
图 6(a)~图 6(f)清晰地显示了气泡聚并及形状变化的过程。其中,图 6(a)流化床床层高度基本不变,表面波动且有部分小气泡。这是因为入口进气速度较小造成的,此时颗粒的表观重力与曳力相平衡,流化类似于最小流化速度下的运动情况,与实验中炭颗粒流动分布情况相似。从图 6(b)和6(c)中可得炭颗粒均有着缓慢的流化行为。分析图 6(d)~图 6(f)可得,大于0.30 m·s-1速度的云图中可以观察到入口进气速度越大冲击流化现象越明显。当床层在较高的流速下,床层内的颗粒会向床层顶部移动,发生湍流和腾涌。当流速超过0.45 m·s-1时,可能会发生淘洗。因此床层流化的理想速度是在0.35~0.45 m·s-1之间,此时床内有明显气泡,颗粒流化均匀。
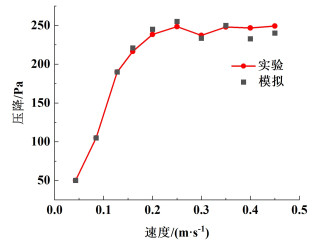
3.4 进气速度对实验与模拟床层压降的影响对比随着流化床流化状态的变化,床内球状炭颗粒的分布出现不同的变化,从而直接影响床层压降的变化。因此在模拟及实验中,床层压降参数十分重要。图 7为不同进气速度下模拟与实验压降对比图。
|
| 图 7 不同进气速度下模拟与实验压降对比图 Fig.7 Comparison of simulated and experimental pressure drop at different inlet velocities |
| |
在数值模拟计算中,每0.03 s保存一次计算结果。因此图 7中模拟计算得到的床层压降为该进气速度下稳定流化的床层压降的平均值,速度的改变对气固两相流动的不稳定性已经减弱。由图 7可以发现模拟计算得到的床层压降与实验值吻合的较好。压降均随着进气速度的增加而增加,当增加到一定速度时,床层压降变化缓慢,直至基本稳定。在进气速度较大的情况下,模拟计算值与实验值之间误差明显。其主要原因是在数值模拟计算中,气固流化床被简化为二维模型,对气泡的考虑存在误差,而且床层的膨胀受气泡的影响较大,因此这种误差在速度较大时尤其明显。
3.5 进气速度对实验与模拟膨胀高度的影响对比随着进气速度的增加,流化床内球状炭颗粒的膨胀高度也发生变化,但受床体高度的影响,速度、膨胀高度受到限制。因此,可通过膨胀高度来验证最佳速度范围。表 4为不同进气速度下气固流化床的膨胀参数。
| 进气速度/ (m·s-1) | 实验膨胀高度/m | 模拟膨胀高度/m | 实验膨胀高度/模拟膨胀高度 |
| 0.16 | 0.045 | 0.041 | 1.098 |
| 0.20 | 0.048 | 0.044 | 1.091 |
| 0.25 | 0.050 | 0.048 | 1.042 |
| 0.30 | 0.055 | 0.050 | 1.100 |
| 0.35 | 0.060 | 0.055 | 1.091 |
| 0.40 | 0.070 | 0.056 | 1.250 |
| 0.45 | 0.080 | 0.059 | 1.360 |
由表 4可以发现,床层的膨胀高度均随着进气速度的增加而增加。在一定速度内,实验值与模拟值的比值约等于1,但速度越大,模拟值与实验值之间的误差就越大。误差原因一方面是模拟计算时存在的误差。在数值模拟计算中,气固流化床被简化为二维模型,对气泡行为的计算有一定的误差,从而导致床层的膨胀高度受到影响,这种误差在速度较大时尤为突出;另一方面是实验测量时存在的误差。实验所选用的颗粒材料是沥青基球状活性炭,具有物理吸附作用,在流化的过程中容易吸附在壁面上影响读数。为了减小误差,在稳定流化的实验中,利用静电消除器消除吸附影响,并采用多次求平均值的方法进行测量。
4 结论基于双流体欧拉模型下,在气固流化床中对沥青基球状活性炭流动特性进行模拟及实验。研究表明:(1)模拟云图结果表明Syamlal-O’Brien模型比其它模型更能准确的预测床层膨胀高度和颗粒体积分布,并且模拟的床层压降和膨胀高度与实验结果具有一致性,更加证实了Syamlal-O’Brien曳力模型的正确性。(2)模拟结果发现流化床的床层压降、膨胀高度和气泡尺寸与进气速度有直接的关系,进气速度越大,膨胀高度和气泡尺寸就越大,进气速度太大会引起腾涌和淘洗,影响气固两相混合。最佳流化速度为0.35~0.45 m·s-1,在此范围内气固均匀混合,颗粒流化质量好。(3)模拟可以合理地预测炭颗粒在流化床反应器内的流体力学行为,将有助于进一步预测颗粒在工业规模流化床上均匀流化的操作条件,从而提高炭颗粒的利用率,节省实验成本。
符号说明:
CD—曳力系数;
ds—颗粒直径,m;
f—曳力函数;
g—重力加速度,m·s-2;
I—单位张量;
p—压力,Pa;
Reg—气相雷诺数;
Res—固相雷诺数;
Ret—带出速度下的雷诺数;
t—时间,s;
vg—气相速度,m·s-1;
vmf—最小流化速度,m·s-1;
vr, s—固相终端速度,m·s-1;
vs—固相速度,m·s-1;
vt—带出速度,m·s-1;
β—气固两相间曳力系数;
εg—气相体积分数;
εs—固相体积分数;
λs—固相体积黏度,Pa·s;
μg—气相剪切黏度,Pa·s;
μs—固相剪切黏度,Pa·s;
τg—气相应力张量;
τp—颗粒弛豫时间;
τs—固相应力张量;
ρg—气相密度,kg·m-3;
ρs—固相密度,kg·m-3;
ψ—平滑过渡函数。
| [1] |
WILLIAMS P, REED A. Development of activated carbon pore structure via physical and chemical activation of biomass fibre waste[J]. Biomass and Bioenergy, 2006, 30(2): 144-152. DOI:10.1016/j.biombioe.2005.11.006 |
| [2] |
RIDHA H, AL-AZAWY M G. Effect of wall heat transfer on the fluidization process[J]. International Journal of Heat and Technology, 2021, 39(2): 615-620. DOI:10.18280/ijht.390232 |
| [3] |
MA S, ZHENG J, ZHAO J, et al. Experimental analysis on thermodynamic stability and methane leakage during solid fluidization process of methane hydrate[J]. Fuel, 2021, 284: 119020. DOI:10.1016/j.fuel.2020.119020 |
| [4] |
NATH H, SAHOO P, SAHOO A. Characterization of Red Mud treated under high temperature fluidization[J]. Powder Technology, 2015, 269: 233-239. DOI:10.1016/j.powtec.2014.09.011 |
| [5] |
VICENTE J, MONTERO C, EREÑA J, et al. Coke deactivation of Ni and Co catalysts in ethanol steam reforming at mild temperatures in a fluidized bed reactor[J]. International Journal of Hydrogen Energy, 2014, 39(24): 12586-12596. DOI:10.1016/j.ijhydene.2014.06.093 |
| [6] |
XUE Y, ZHOU S, BROWN R C, et al. Fast pyrolysis of biomass and waste plastic in a fluidized bed reactor[J]. Fuel, 2015, 156: 40-46. DOI:10.1016/j.fuel.2015.04.033 |
| [7] |
WANG C, ZHU C, HUANG J, et al. Enhancement of depolymerization slag gasification in supercritical water and its gasification performance in fluidized bed reactor[J]. Renewable Energy, 2021, 168: 829-837. DOI:10.1016/j.renene.2020.12.104 |
| [8] |
BEHJAT Y, SHAHHOSSEINI S, HASHEMABADI S H. CFD modeling of hydrodynamic and heat transfer in fluidized bed reactors[J]. International Communications in Heat and Mass Transfer, 2008, 35(3): 357-368. DOI:10.1016/j.icheatmasstransfer.2007.09.011 |
| [9] |
LU H, HE Y, GIDASPOW D. Hydrodynamic modelling of binary mixture in a gas bubbling fluidized bed using the kinetic theory of granular flow[J]. Chemical Engineering Science, 2003, 58(7): 1197-1205. DOI:10.1016/S0009-2509(02)00635-8 |
| [10] |
XING X, ZHANG C, JIANG B, et al. Numerical study of the effect of the inlet gas distributor on the bubble distribution in a bubbling fluidized bed[J]. Chemical Engineering Research and Design, 2022, 177: 70-82. DOI:10.1016/j.cherd.2021.10.021 |
| [11] |
GRACE J R, TAGHIPOUR F. Verification and validation of CFD models and dynamic similarity for fluidized beds[J]. Powder Technology, 2004, 139(2): 99-110. DOI:10.1016/j.powtec.2003.10.006 |
| [12] |
武恒, 金亚丹, 康守国, 等. 气固流化床CFD模拟曳力模型的选用及验证[C]//Ansys中国技术大会. 安世亚太科技股份有限公司, 2014
|
| [13] |
BI H T, ELLIS N, ABBA I A, et al. A state-of-the-art review of gas-solid turbulent fluidization[J]. Chemical Engineering Science, 2000, 55(21): 4789-4825. DOI:10.1016/S0009-2509(00)00107-X |
| [14] |
曹玉春, 吴金星, 李言钦, 等. 基于欧拉-欧拉模型的气固鼓泡床数值模拟研究[J]. 热力发电, 2008, 37(11): 35-38. CAO Yuchun, WU Jinxing, LI Yanqin, et al. Study on numerical simulation of gas-solid flowin bubbling bed based on Eulerian-Eulerian model[J]. Thermal Power Generation, 2008, 37(11): 35-38. (in Chinese) |
| [15] |
TSUJI Y, TANAKA T, YONEMURA S. Cluster patterns in circulating fluidized beds predicted by numerical simulation (discrete particle model versus two-fluid model)[J]. Powder Technology, 1998, 95(3): 254-264. DOI:10.1016/S0032-5910(97)03349-4 |
| [16] |
SAHOO P, SAHOO A. A comparative study on effect of different parameters of CFD modeling for gas-solid fluidized bed[J]. Particulate Science and Technology, 2015, 33(3): 273-289. DOI:10.1080/02726351.2014.952393 |
| [17] |
SCHMIDT A, RENZ U. Numerical prediction of heat transfer in fluidized beds by a kinetic theory of granular flows[J]. International Journal of Thermal Sciences, 2000, 39(9/10/11): 871-885. |
| [18] |
SINGH R I, BRINK A, HUPA M. CFD modeling to study fluidized bed combustion and gasification[J]. Applied Thermal Engineering, 2013, 52(2): 585-614. DOI:10.1016/j.applthermaleng.2012.12.017 |
| [19] |
WANG T, WANG S, SHEN Y. Particle-scale study of gas-solid flows in a bubbling fluidised bed: Effect of drag force and collision models[J]. Powder Technology, 2021, 384: 353-367. DOI:10.1016/j.powtec.2021.02.034 |
| [20] |
ADNAN M, SUN J, AHMAD N, et al. Validation and sensitivity analysis of an Eulerian-Eulerian two-fluid model (TFM) for 3D simulations of a tapered fluidized bed[J]. Powder Technology, 2022, 396: 490-518. DOI:10.1016/j.powtec.2021.08.057 |
| [21] |
SYAMLAL M, O'BRIEN T J. Simulation of granular layer inversion in liquid fluidized beds[J]. International Journal of Multiphase Flow, 1988, 14(4): 473-481. DOI:10.1016/0301-9322(88)90023-7 |
| [22] |
DIMITRI G, RUKMINI B J D. Hydrodynamics of circulating fluidized beds: Kinetic theory approach[R]. Illinois Institute of Technology, Department of Chemical Engineering, Chicago, IL, USA, 1991
|
| [23] |
WEN C, YU Y. Mechanics of fluidization[J]. Chem Eng Prog Symp Ser, 1966. |
| [24] |
LU H, GIDASPOW D. Hydrodynamics of binary fluidization in a riser: CFD simulation using two granular temperatures[J]. Chemical Engineering Science, 2003, 58(16): 3777-3792. DOI:10.1016/S0009-2509(03)00238-0 |
| [25] |
GIBILARO L G, DI FELICE R, WALDRAM S P, et al. Generalized friction factor and drag coefficient correlations for fluid-particle interactions[J]. Chemical Engineering Science, 1985, 40(10): 1817-1823. DOI:10.1016/0009-2509(85)80116-0 |
| [26] |
ADAM A M M M, BORRÀS N, PÉREZ E, et al. Electrochemical corrosion of an Al-Mg-Cr-Mn alloy containing Fe and Si in inhibited alkaline solutions[J]. Journal of Power Sources, 1996, 58(2): 197-203. DOI:10.1016/S0378-7753(96)02399-3 |
| [27] |
GERA D, GAUTAM M, TSUJI Y, et al. Computer simulation of bubbles in large-particle fluidized beds[J]. Powder Technology, 1998, 98(1): 38-47. DOI:10.1016/S0032-5910(98)00017-5 |
| [28] |
RAO B M, RAO K S, RANGA JANARDHANA G. CFD analysis of hydrodynamic studies of a bubbling fluidized bed[J]. IOP Conference Series: Materials Science and Engineering, 2018, 330: 012090. DOI:10.1088/1757-899X/330/1/012090 |
 2025, Vol. 42
2025, Vol. 42





