分离是化工生产过程中的重要环节,其能耗约占化工生产总能耗的60%[1]。近年来,国家对环境保护的高度重视,对化工分离设备的节能降耗提出了更高要求。
填料塔是一种应用广泛的气液两相接触分离设备[2-4]。交叉波纹规整填料具有单位理论板压降低、放大效应小和易于生产安装等优点,在实际工业中应用最为广泛。自20世纪60年代Sulzer公司发明以来,仅在20世纪末有一次重大的革新,即新一代高通量波纹规整填料(Mellapak Plus),其相邻填料盘界面处的波纹通道被调整为直角,从而消除通量的瓶颈。
填料压降的大小决定填料塔的能耗和通量,对于真空操作以及压降受限的填料塔,单位效率压降为填料选型的关键参数。为了减小填料塔的压降,研究人员不断地努力开发新型规整填料。Wen等[5]设计开发出一种新型的垂直片状结构填料,通过减小气体流动的倾角来减小压降。Luo等[6]通过优化梯形波纹几何结构,减小了填料内交叉流动气体接触面积,从而减小了气相压降。Olenberg等[7]在板波纹填料流道中加入螺旋纽带,与同比表面积的传统填料相比,新型填料压降较小。Sun等[8]甚至采用3D打印的方法开发出高比表面积、低压降填料。但到目前为止,获得广泛应用的规整填料还只是波纹规整填料一种。
对于高理论板数的难分离物系和塔径受到运输限制的场合,填料塔不得不拆分成多塔并联和(或)串联,因此开发高效低阻的新型填料具有重要的应用价值,然而超过半个世纪的努力表明,这很困难。
新型填料开发之所以困难,主要有2个方面原因,首先,填料层内流道曲折,两相流动复杂,通常又是湍流,机理并不完全清晰;其次,填料形状多变,其几何参数比较多,而一般采用的检测方法又是传统的“黑箱”实验,即热模实验。在流动机理不完全清楚的情况下,采用完全依赖实验的方法来开发填料不仅周期长,成本高,而且难以优化。
规整填料的性能主要包括压降、通量等流体力学性能和传质性能。随着计算机科学的发展,越来越多的研究人员使用CFD数值模拟方法研究规整填料层内的流动与传质。CFD数值模拟方法具有经济、高效和易于观察流动细节等一系列优点,合理的CFD模型可以有效地应用于填料开发,尤其是结构规则的波纹规整填料,其物理模型的建立也相对容易。
规整填料气相单相流的压降大小可以充分反映其两相流的压降和通量,Petre等[9]利用CFD方法研究规整填料内气相单相流的压降机制。由于流道交叉,气体在规整填料内的流动为湍流,压降主要消耗于主体流动,形体阻力占比很小,Nikou等[10]和Saleh等[11]通过CFD模拟发现利用各种湍流模型对填料压降计算的准确性均比较高。
规整填料的传质CFD模型可以精确计算填料表面每个点的效率分布,但合理的模型需要建立在实验之上。由于填料流道狭窄、曲折,只能采用非介入的检测方法,以免干扰流体流动。到目前为止,还无法检测填料表面液相的点传质效率,因此,有关液相传质的CFD模型都是建立在填料段整体性能的“黑箱”实验之上,比如Haroun等[12]和Sebastia-Saez等[13]的工作。Zhang等[14]进行气相单相流模拟,通过建立表面快反应模型得到了填料表面气相的点传质效率分布,以非介入的显色化学反应[15, 16]检测方法验证了数值模型的准确性。
规整填料内气相为连续相,与塔板、散堆填料相比具有更好的气相传质性能,因而多用于气相传质控制的物系,比如常压、减压精馏,因此,气相传质系数是规整填料重要的传质性能。目前,规整填料多相流的传质模拟还不成熟,CFD只能较好地模拟气相单相流的传质。对于气相传质控制的操作而言,传质效率只需对填料表面润湿率进行修正,因此,模拟填料表面气相单相传质系数可用于新型填料的开发。
在规整填料中,液相对填料性能的影响同样表现在流体力学和传质效率2个方面。在载点之前,液体对阻力影响比较小,载点之后逐渐增强,取决于两相相对速度。除了液体喷淋密度特别低或表面张力特别高的情况,规整填料的润湿并不是影响效率的关键因素,影响填料效率最显著因素在于液体的不良分布[17]。液体在规整填料表面的流动主要有2种形式,一种是沿三角形通道中朝上表面向两侧流动,表征填料液体自分布能力,一定程度上消除液体不良分布;另一种流动形式是在毛细作用下液体在相邻填料片的波峰接触点处聚集、混合,再流向朝下的表面。液体在波峰接触点处的聚集、混合可以消除液体不良分布导致的浓度差,对填料效率影响显著。
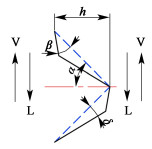
针对交叉波纹规整填料内部气液两相流动的特性,本研究把原有的三角形通道(图 1中蓝色虚线所示)修正为四边形(图 1中粗实线所示)。对于位于同一片填料两侧的气液两相流动而言,其迎背方向的几何结构均保持一致。
|
| 图 1 新型填料流道形状 Fig.1 Channel shape of new packing |
| |
气体在交叉流道的规整填料片之间流动,其主体流动可以分解为2个:沿通道方向的直线流动和在流道截面上的旋转流动,通道由三角形改为四边形后,流道的水力半径增大,无论直线流动和旋转流动都更加流畅,阻力均会降低,同时,由于更流畅的旋转流动,传质系数分布更均匀,以弥补湍动下降造成传质系数的下降,避免了阻力与效率间的“跷跷板”效应。对于液相而言,一方面朝上表面倾角减小了δ角,更为平坦,液体更好地向两侧流动,提高液体再分布能力,且几乎与通道中的气相成逆向流动;靠近波峰朝下的表面增大了β角,毛细作用增强,又加上有气相托举的作用,波峰接触点处的持液量增加,同时靠近波峰的下表面倾角更大,有利于聚集于接触点附近的液体流向朝下表面。
本研究建立规整填料的流体力学和传质CFD模型,经传质可视化实验验证后,使用该模型和正交试验探究新型填料的传质和压降特性,以优化新型填料的结构。
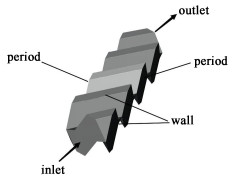
1 CFD数值模型 1.1 物理模型图 2是新型填料物理模型。
|
| 图 2 新型填料物理模型 Fig.2 Geometry model of new packing |
| |
在压力变化不大和流速低的工况下,气体的压缩性可以忽略。本研究视气体为不可压缩流体,并设过程等温,则满足以下守恒方程。
连续性方程:
| $ \nabla \cdot \boldsymbol{u}=0 $ | (1) |
动量守恒方程:
| $ \frac{\partial}{\partial t}(\rho \boldsymbol{u})+\nabla \cdot(\rho \boldsymbol{u} \boldsymbol{u})=-\nabla p+\nabla \cdot(\overline{\overline{\tau}})+\rho g $ | (2) |
式(1)和式(2)中:ρ为气体密度;u为气体流速;t为时间;
湍流模型选择Olenberg等[7]在规整填料研究中曾使用的Realizable k-ε模型。Realizable k-ε模型是针对具有强逆压梯度、分离和回流流动而开发的,这些改进更加适合模拟气体在规整填料内的流动[18]。
Realizable k-ε湍流模型方程如式(3)和式(4)。
k方程:
| $ \begin{gathered} \frac{\partial}{\partial t}(\rho k)+\frac{\partial}{\partial x_j}\left(\rho k u_j\right)= \\ \frac{\partial}{\partial x_j}\left[\left(\mu+\frac{\mu_{\mathrm{t}}}{\sigma_k}\right) \frac{\partial k}{\partial x_j}\right]+G_k-\rho \varepsilon \end{gathered} $ | (3) |
ε方程:
| $ \begin{gathered} \frac{\partial}{\partial t}(\rho \varepsilon)+\frac{\partial}{\partial x_j}\left(\rho \varepsilon u_j\right)=\frac{\partial}{\partial x_j}\left[\left(\mu+\frac{\mu_{\mathrm{t}}}{\sigma_{\varepsilon}}\right) \frac{\partial \varepsilon}{\partial x_j}\right]+ \\ \rho C_1 S \varepsilon-\rho C_2 \frac{\varepsilon^2}{k+\sqrt{\nu \varepsilon}} \end{gathered} $ | (4) |
式(3)和式(4)中:k为湍流动能;ε为湍流动能耗散率;μ为气体黏度;μt为湍流黏度;Gk为由速度梯度所产生的湍流动能;S是平均应变率张量的模;ν为运动黏度;C1、C2、σk、σε是模型常数,其中C2、σk、σε取值分别为1.9、1.0、1.2,C1由下式决定:
| $ C_1=\max \left(0.43, \frac{\eta}{\eta+5}\right), \eta=S \frac{k}{\varepsilon} $ | (5) |
通过求解对流扩散方程得到每个组分的局部质量分数,该方程形式如式(6):
| $ \frac{\partial}{\partial t}\left(\rho Y_i\right)+\nabla \cdot\left(\rho \boldsymbol{u} Y_i\right)=-\nabla \cdot \boldsymbol{J}_i+R_i $ | (6) |
式(6)中:Yi为组分i的质量分数;Ji为组分i的扩散通量;Ri为组分i的反应产生速率。
1.2.4 表面化学反应模型利用表面快反应模型[7, 14]模拟气相在填料表面的传质过程,所定义的化学反应如下:
| $ 2 \mathrm{NH}_3+\mathrm{H}_2 \mathrm{O}_2+\mathrm{MnCl}_2 \xrightarrow{k_{\mathrm{f}, \mathrm{r}}} 2 \mathrm{NH}_4 \mathrm{Cl}+\mathrm{MnO}_2 $ | (7) |
将过氧化氢(H2O2)、氯化锰(MnCl2)、氯化铵(NH4Cl)和二氧化锰(MnO2)均设为壁面物质,氨气(NH3)流经填料壁面时发生反应,反应速率由速率常数kf, r决定。
| $ k_{\mathrm{f}, \mathrm{r}}=A_{\mathrm{r}} T^\beta e^{-\frac{E_{\mathrm{r}}}{R T}} $ | (8) |
式(8)中:Ar为指前因子,将其设为1×1015以确保反应瞬时完成;β为温度指数;Er为反应活化能;R为摩尔气体常数;T为反应温度。
根据双膜理论,NH3在填料内流动时,由气相主体经气膜扩散到相界面发生化学反应,由于化学反应速率足够快,故可忽略化学反应阻力,所以,整个传质过程由气膜传质控制。
为了评价传质过程,根据文献[7],NH3气相传质系数κ由式(9)给出:
| $ \kappa=\frac{V}{h_{\mathrm{p}} A a_{\mathrm{p}}} \ln \left[\frac{c\left(\mathrm{NH}_3\right)_{\text {inlet }}}{c\left(\mathrm{NH}_3\right)_{\text {outlet }}}\right] $ | (9) |
式(9)中:V为气相体积流率;hp为填料高度;A为塔横截面积;ap为填料比表面积;c(NH3)inlet和c(NH3)outlet分别为填料进口和出口NH3浓度。
1.2.5 边界条件及计算参数设置Macfarlan等[19]的工作表明合理设置边界条件,模拟多个具有代表性结构单元(Representative Elementary Unit,REU)的流体力学和传质性能即可预测规整填料的整体性能。本研究借鉴这种方法,计算域为多个REU组成,将模型前、后面分别设为气体入口和出口,左、右面分别设为周期边界,上、下面则为填料壁面。入口、出口和填料壁面的边界条件为:入口:采用速度入口边界条件,物料为含有组分NH3的空气,NH3质量分数为0.01。出口:采用压力出口边界条件。填料壁面:采用恒定壁温、无滑脱边界条件,设置表面快反应。
计算参数设置取双精度。为使填料表面传质计算更加准确,壁面函数选择增强壁面处理。压力-速度耦合算法选择Coupled。选择二阶格式离散压力项,选择二阶迎风格式离散动量、组分输运控制方程,选择一阶迎风格式离散湍动能方程和湍动能耗散率方程。当迭代残差低于设定值且监测面的传质量稳定时停止计算。
1.2.6 网格特征本研究使用Fluent Meshing软件进行网格划分。由于规整填料结构错综复杂且多面体网格的生成技术已经成熟,故采用多面体非结构化网格对填料进行网格划分。同时,为了确保对边界层内流动计算的准确性,在填料壁面附近采用棱柱层网格加密边界层。经网格无关化验证后,全局网格大小取0.8 mm。图 3是网格划分示意图。

|
| 图 3 网格划分示意图 Fig.3 Schematic diagram of mesh division |
| |
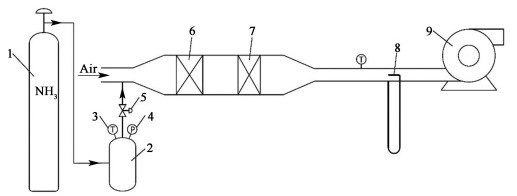
本研究以工业中应用广泛的JKB-250Y填料作为参照对象,对其进行显色化学反应传质可视化实验[15, 16],以测定气相传质系数,图 4为实验装置示意图。实验采用真空泵引风,空气由左侧进入装置,定量罐中的氨气由电磁阀控制注入,两者经静态混合器混合均匀后流入风洞内的填料层,进行传质与反应。
|
| 1 氨气钢瓶; 2 定量罐; 3 温度计; 4 压力表; 5 电磁阀; 6 静态混合器; 7 填料; 8 皮托管; 9 真空泵 图 4 实验装置示意图 Fig.4 Schematic diagram of the experimental setup |
| |
实验方法如下:将均匀润湿、浸有MnCl2和H2O2混合液的滤纸紧贴在填料表面,与其余不贴滤纸的同型号填料组成填料盘放入风洞中的测定点处,随后通入NH3和空气的混合气体,NH3流经滤纸表面时会被迅速吸收,然后发生快速反应。
| $ \begin{gathered} \mathrm{NH}_3+\mathrm{H}_2 \mathrm{O} \leftrightarrow \mathrm{NH}_3 \cdot \mathrm{H}_2 \mathrm{O} \\ 2 \mathrm{NH}_3 \cdot \mathrm{H}_2 \mathrm{O}+\mathrm{MnCl}_2 \rightarrow 2 \mathrm{NH}_4 \mathrm{Cl}+\mathrm{Mn}(\mathrm{OH})_2 \\ \mathrm{Mn}(\mathrm{OH})_2+\mathrm{H}_2 \mathrm{O}_2 \rightarrow \mathrm{MnO}_2 \downarrow+2 \mathrm{H}_2 \mathrm{O} \end{gathered} $ | (10) |
反应产物MnO2呈深棕色,在滤纸表面产生颜色分布,如图 5所示,颜色的差异反映出传质系数的大小。使用Epson Perfection V600 Photo扫描仪将反应完成后的滤纸进行图像采集。因为图像上每个像素均可分解成红、绿、蓝三原色且任意一种颜色均可反映颜色强度,所以本研究利用Adobe Photoshop软件读取图像的红色数值(r value),将颜色与数值关联起来。

|
| 图 5 滤纸上的颜色分布 Fig.5 Color distribution on filter paper |
| |
在传质可视化实验中,NH3由气相主体传递到相界面发生化学反应,由于NH3易溶于水且反应足够快,所以,整个对流传质过程由气膜阻力控制:
| $ \int_{t=0}^{t_1} N_{\mathrm{i}} \mathrm{~d} t=\int_{t=0}^{t_1} \kappa\left(c_{\mathrm{i}}-c_{\mathrm{w}}\right) \mathrm{d} t $ | (11) |
NH3在填料表面反应迅速,则壁面NH3浓度cw=0,而且:
| $ \int_{t=0}^{t_1} N_{\mathrm{i}} \mathrm{~d} t=N $ | (12) |
| $ \int_{t=0}^{t_1} c_{\mathrm{i}} \mathrm{~d} t=\int_{t=0}^{t_1} \frac{m_{\mathrm{i}}}{V} \mathrm{~d} t=\frac{m}{V} $ | (13) |
结合式(11)~式(13)可得:
| $ \kappa=\frac{N V}{m} $ | (14) |
式(11)~式(14)中:Ni为传质速率;N为单位面积传质的总量;ci为NH3主体浓度;m为NH3的质量。
2.2 标定曲线的建立规整填料表面气相传质系数需要借助标定曲线求得。在温度、压力一定的条件下,传质系数与流速存在关联式如式(15)和式(16)[20]:
| $ j_{\mathrm{D}} \sqrt{\frac{G D_{\mathrm{p}}}{\mu}}=1.08 $ | (15) |
| $ j_{\mathrm{D}}=\frac{\kappa}{u} S c^{2 / 3} $ | (16) |
式(15)、式(16)中:jD为传质j因子;G为气体单位时间、单位面积的质量流率;Dp为标定薄片的水力学直径;Sc为施密特数。
结合式(14)~式(16)可得:
| $ N=\frac{1.08}{\left(\frac{D_{\mathrm{p}} u \rho}{\mu}\right)^{0.5}} \cdot \frac{u m}{S c^{2 / 3} V} $ | (17) |
由式(17)可知:保持流速不变,通入不同质量的NH3,就可获得不同的传质量,进而得到传质量N与红色数值r的关系式。
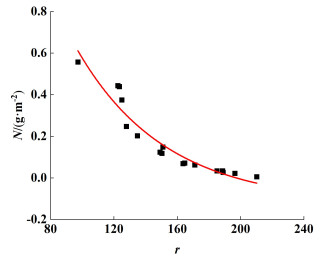
在温度293 K,压力101 325 Pa,气相动能因子F =1.5 Pa0.5的条件下,得到图 6所示的标定曲线。经过数据回归拟合,得到曲线方程如式(18)。
| $ N=4.17 \mathrm{e}^{-\frac{r}{55.98}}-0.12 $ | (18) |
|
| 图 6 标定曲线 Fig.6 Calibration curve |
| |
拟合曲线与实验数据吻合良好,其拟合优度R2=0.91。
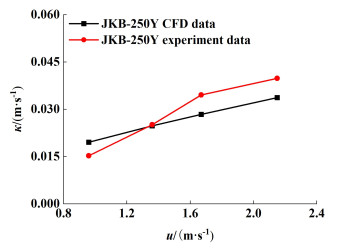
3 结果与讨论 3.1 模型验证如图 7所示,是JKB-250Y填料在温度293 K,压力101 325 Pa的条件下,经传质实验、图像采集和数据处理后得到的气相传质系数。
|
| 图 7 JKB-250Y气相传质系数实验数据与模拟数据对比 Fig.7 Comparison of experiment data and simulation data of JKB-250Y gas phase mass transfer coefficient |
| |
CFD模拟数据与传质实验数据的平均相对误差约为15%,表明本研究传质CFD模型可信;由文献[10, 11, 18]可知各种湍流模型均能比较准确的计算填料压降。由此可知,本研究所建立的流体力学及传质CFD模型可用于预测规整填料的压降和传质特性。
3.2 新型填料结构参数优化选择 3.2.1 正交试验设计以JKB-250Y填料作为参照对象,则在探究新型填料最佳结构时,应保证比表面积与JKB-250Y相同。新型填料比表面积ap计算如式(19):
| $ a_{\mathrm{p}}=4 \frac{S_1+S_2}{h \cdot 2 h \tan \alpha} $ | (19) |
S1、S2由式(20)计算得到:
| $ \frac{h / \cos \alpha}{\sin [180-(\beta+\delta)]}=\frac{S_1}{\sin \beta}=\frac{S_2}{\sin \delta} $ | (20) |
结合式(19)和式(20)可得:
| $ a_{\mathrm{p}}=\frac{2(\sin \beta+\sin \delta)}{h \cdot \sin \alpha \cdot \sin (\beta+\delta)} $ | (21) |
可见,新型填料在比表面积为250 m2·m-3的约束条件下,当h、α、β、δ中任意3个值确定后,剩下的第4个值也随之确定。本研究选择3个角度α、β和δ作为自由变量,采用正交试验的方法对其进行设计,以得到传质性能和压降性能均较好的流道结构参数。
正交试验的3个因素是填料流道的3个角度α、β、δ,每个因素取4个水平,其中角α分别为20°、30°、40°和50°;角β分别为5°、15°、25°和35°;角δ分别为1°、5°、9°和13°。根据正交试验设计原则要求,设计了如表 1所示的正交试验表,表 1中1(20)指水平1的值为20,表中其余各项类似。
| 试验编号 | 因素 | ||||
| A | B | C | |||
| α/(°) | β/(°) | δ/(°) | |||
| 1 | 1(20) | 1(5) | 1(1) | ||
| 2 | 1(20) | 2(15) | 2(5) | ||
| 3 | 1(20) | 3(25) | 3(9) | ||
| 4 | 1(20) | 4(35) | 4(13) | ||
| 5 | 2(30) | 1(5) | 2(5) | ||
| 6 | 2(30) | 2(15) | 1(1) | ||
| 7 | 2(30) | 3(25) | 4(13) | ||
| 8 | 2(30) | 4(35) | 3(9) | ||
| 9 | 3(40) | 1(5) | 3(9) | ||
| 10 | 3(40) | 2(15) | 4(13) | ||
| 11 | 3(40) | 3(25) | 1(1) | ||
| 12 | 3(40) | 4(35) | 2(5) | ||
| 13 | 4(50) | 1(5) | 4(13) | ||
| 14 | 4(50) | 2(15) | 3(9) | ||
| 15 | 4(50) | 3(25) | 2(5) | ||
| 16 | 4(50) | 4(35) | 1(1) | ||
模拟采用的填料入口气速为1.70 m·s-1,此时气相动能因子F =1.9 Pa0.5,与一般情况下填料塔在操作条件下的气相动能因子水平相当。
3.2.2 正交试验结果分析针对新型填料流道结构参数的优化,从传质性能、压降性能和单位效率的压降3方面考虑,分别使用气相传质系数κ、压降Δp和单位效率的压降Δp·κ-1作为量化指标进行考察。
根据正交试验表,共有16个试验组,对各组正交试验结果使用极差分析法进行分析,其中:Kij为量化指标在同一因素、不同水平下的均值,通过Kij的大小可以确定某因素的最优水平,得到最优组合;Ri是量化指标均值在同一因素、不同水平下的最大、最小值之差,其值反映了某因素水平发生变化时,量化指标的变化幅度,Ri越大,说明该因素对量化指标的影响越大。
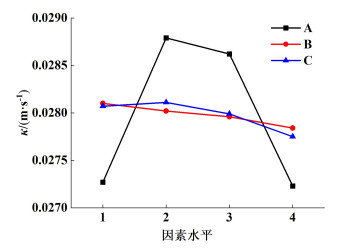
如图 8所示,是气相传质系数κ在不同因素、不同水平下的均值。由图 8可知:(1)A、B、C 3个因素中,对应的最佳水平分别为A2、B1、C2,即当角α为30°、角β为5°、角δ为5°时,气相传质系数最大;(2)RA>RC>RB,表明角α对气相传质系数的影响最大,角δ次之,角β的影响最小。
|
| 图 8 气相传质系数的均值 Fig.8 Mean value of gas mass transfer coefficient |
| |
根据以上分析,气相传质系数最适宜的结构参数组合为A2B1C2,该组合在已计算样本内,其气相传质系数为0.028 6 m·s-1,是计算样本中的最大值,说明极差分析法的预测准确。因此,当角α为30°、角β为5°、角δ为5°时,新型填料具有最大的气相传质系数。
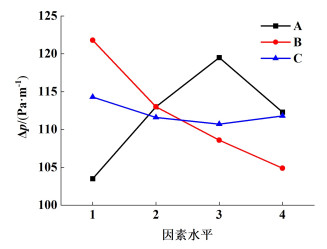
如图 9所示,是压降Δp在不同因素、不同水平下的均值。由图 9可知:(1)A、B、C 3个因素中,对应的最佳水平分别为A1、B4、C3,即当角α为20°、角β为35°、角δ为9°时,压降最小;(2)RB>RA>RC,表明角β对压降的影响最大,角α次之,角δ的影响最小。
|
| 图 9 压降的均值 Fig.9 Mean value of pressure drop |
| |
根据以上分析,压降最小的结构参数组合为A1B4C3,该组合不在已计算样本内。补充计算了A1B4C3组合,得到其压降值为96.73 Pa·m-1,较样本中压降的最低值96.36 Pa·m-1大,说明极差分析法的预测出现一定偏差。因为角α和角β对压降的影响远大于角δ,在预测角δ的最优水平时会受到角α和角β的影响,造成预测出现偏差。在已计算样本中压降最小的结构参数组合A1B4C4和预测结果A1B4C3附近继续取点计算,最终得到压降最小的结构参数组合为A1B4C4,即角α为20°、角β为35°、角δ为13°。
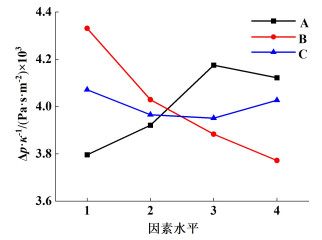
如图 10所示,是单位效率压降Δp·κ-1在不同因素、不同水平下的均值。由图 10可知:(1)A、B和C 3个因素中,对应的最佳水平分别为A1、B4、C3,即当角α为20°、角β为35°、角δ为9°时,单位效率压降最小;(2)RB>RA>RC,表明角β对单位效率压降的影响最大,角α次之,角δ的影响最小。
|
| 图 10 单位效率压降的均值 Fig.10 Mean value of pressure drop per unit of efficiency |
| |
根据以上分析,单位效率压降最佳的结构参数组合为A1B4C3,该组合不在已计算样本内。补充计算了A1B4C3组合,得到其单位效率压降3 544.40 Pa·s·m-2,较样本中单位效率压降的最小值3 524.96 Pa·s·m-2大,表明极差分析法的预测结果出现一定偏差。因为角β对单位效率压降的影响大于角α,在预测角α的最优水平时会受到角β的影响,造成预测出现偏差。在已计算样本中单位效率压降最小的结构参数组合A2B4C3和预测结果A1B4C3附近继续取点计算,最终得到单位效率压降最小的结构参数组合为:角α为30°、角β为35°、角δ为9°。
由不同的量化指标可优选出不同结构的最适宜填料,本研究旨在开发高效低阻的新型填料,这就要求在相同的气相传质系数下,能够获得尽可能低的压降,所以应使用单位效率压降Δp·κ-1作为新型填料流道结构优化的量化指标。
3.3 最优新型填料与传统填料比较由正交试验结果分析可知,当角α为30°、角β为35°、角δ为9°时,新型填料单位效率压降最小,为评价该新型填料,将其与JKB-250Y进行比较,JKB-250Y与优化后的新型填料的结构参数如表 2所示。
| 名称 | α/(°) | β/(°) | δ/(°) | h/mm |
| JKB-250Y | 41 | 0 | 0 | 12.0 |
| 新型填料 | 30 | 35 | 9 | 16.8 |
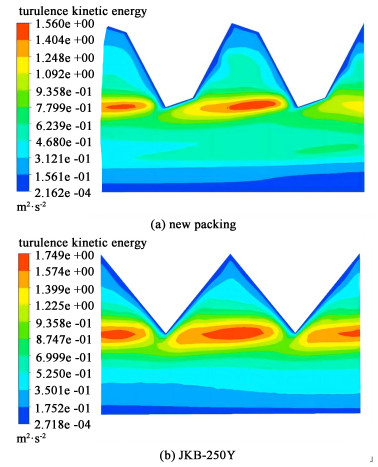
如图 11所示,分别为新型填料、JKB-250Y在填料进口流速为1.89 m·s-1时,填料流道的湍动能分布云图。
|
| 图 11 湍动能分布云图 Fig.11 Cloud map of distribution of turbulence kinetic energy |
| |
湍流动能反映了流场中流体的湍流程度。湍流动能数值越大,流体湍动程度越大。由图 11可知,新型填料和JKB-250Y填料的湍流动能分布整体上呈现出相同特点,即在2片填料交叉连接区域处湍流动能最大,而在连接区域上部和下部的湍流动能较小。这是因为上、下2股气体在连接区域处相遇,湍动加剧,因而湍流动能增大。
但是,可以明显看出新型填料交叉连接区域处的湍流动能小于JKB-250Y填料,表明新型填料在连接区域处流体质点的湍动程度弱于JKB-250Y填料。所以,新型填料因流体质点相互碰撞所引起的能量损失低于JKB-250Y填料,这是新型填料压降减小的本质原因。
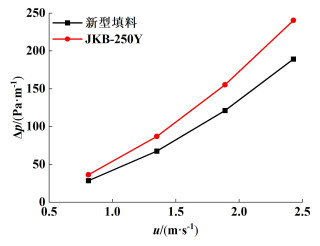
3.3.2 压降如图 12所示为新型填料、JKB-250Y填料的压降Δp与气体流速的关系,压降随入口流速的增大而呈幂函数型增长。
|
| 图 12 压降与气体流速的关系 Fig.12 Relationship between pressure drop and gas velocity |
| |
新型填料通过改变流道形状减少了2股交叉气流相互作用所引起的能量损失,因此压降减小。在u=0.81~2.43 m·s-1范围内,新型填料压降比JKB-250Y填料减少22.22%~23.03%,这表明新型填料具有良好的压降性能。
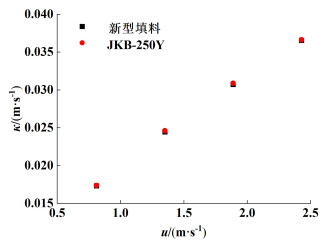
3.3.3 传质效率如图 13所示,是新型填料、JKB-250Y填料的气相传质系数κ与气体流速的关系,气相传质系数随流速的增加而增大。2种填料在不同气速下,效率几乎没有差异。
|
| 图 13 气相传质系数与气体流速的关系 Fig.13 Relationship between gas mass transfer coefficient and gas velocity |
| |
规整填料由于气-气摩擦作用和流动方向变化导致的压降占总压降的80%以上,但这部分压降对传质无显著贡献[21]。新型填料通过改变流道形状减弱气-气摩擦相互作用,所以,在压降明显减小的条件下仍能保持良好的传质性能。
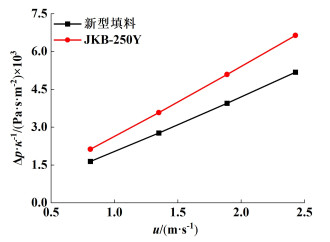
3.3.4 单位效率压降如图 14所示,是新型填料和JKB-250Y填料的单位效率压降Δp·κ-1与气体流速的关系。随着气体流速的增加,压降的增加程度远大于气相传质系数的增加程度,因此单位效率压降Δp·κ-1随入口气速增加而增大。
|
| 图 14 Δp·κ-1与气体流速的关系 Fig.14 Relationship between Δp·κ-1 and gas velocity |
| |
单位效率压降Δp·κ-1越小,表明在相同传质效率下的压降越小。在u=0.81~2.43 m·s-1范围内,新型填料的Δp·κ-1值比JKB-250Y填料减小22.05%~22.73%,表明新型填料是一种高效低阻填料。
4 结语采用数值模拟和正交试验的方法开发了一种水力半径更大的新型规整填料,分析了新型填料流道几何结构对填料性能的影响。其中,角β对单位效率压降的影响最大,角α次之,角δ的影响最小,优选出单位效率压降最小的新型填料流道几何参数:角α为30°、角β为35°、角δ为9°。
当气速为0.81、1.35、1.89和2.43 m·s-1时,经过优化的新型填料传质效率与传统规整填料几乎相同,压降分别比传统规整填料减少23.03%、22.71%、22.58%和22.22%。
| [1] |
李群生, 毛明华. 化工分离工程中的节能降耗的研究及其应用[C]//全国化工合成氨设计技术中心站: 2003年技术交流会论文集, 2003 LI Qunsheng, MAO Minghua. Research and application of energy saving and consumption reduction in chemical separation engineering[C]//Proceedings of the 2003 Technical Exchange Conference of the National Chemical Ammonia Design Technology Center Station, 2003 (in Chinese) |
| [2] |
DE HAAN A B, DE GRAAUW J. Mass transfer in supercritical extraction columns with structured packings for hydrocarbon processing[J]. Industrial & Engineering Chemistry Research, 1991, 30(11): 2463-2470. |
| [3] |
SIMOES P C, MATOS H A, CARMELO P J, et al. Mass transfer in countercurrent packed columns: Application to supercritical CO2 extraction of terpenes[J]. Industrial & Engineering Chemistry Research, 1995, 34(2): 613-618. |
| [4] |
WROŃSKI S, MOLGA E. Mass transfer model for the film countercurrent flow of two liquid phases in a packed bed column[J]. Chemical Engineering and Processing: Process Intensification, 1998, 37(1): 47-54. DOI:10.1016/S0255-2701(97)00035-4 |
| [5] |
WEN X, AFACAN A, NANDAKUMAR K, et al. Development of a novel vertical-sheet structured packing[J]. Chemical Engineering Research and Design, 2005, 83(5): 515-526. DOI:10.1205/cherd.03003 |
| [6] |
LUO S, FEI W, SONG X, et al. Effect of channel opening angle on the performance of structured packings[J]. Chemical Engineering Journal, 2008, 144(2): 227-234. DOI:10.1016/j.cej.2008.01.026 |
| [7] |
OLENBERG A, RESCHETNIK W, KULLMER G, et al. Optimization of structured packings using twisted tape inserts[J]. Chemical Engineering Research and Design, 2018, 132: 1-8. DOI:10.1016/j.cherd.2017.12.036 |
| [8] |
SUN B, BHATELIA T, UTIKAR R P, et al. Hydrodynamics of a novel 3D printed structured packing-SpiroPak[J]. Chemical Engineering and Processing-Process Intensification, 2021, 167: 108533. DOI:10.1016/j.cep.2021.108533 |
| [9] |
PETRE C F, LARACHI F, ILIUTA I, et al. Pressure drop through structured packings: Breakdown into the contributing mechanisms by CFD modeling[J]. Chemical Engineering Science, 2003, 58(1): 163-177. DOI:10.1016/S0009-2509(02)00473-6 |
| [10] |
KHOSRAVI NIKOU M R, EHSANI M R. Turbulence models application on CFD simulation of hydrodynamics, heat and mass transfer in a structured packing[J]. International Communications in Heat and Mass Transfer, 2008, 35(9): 1211-1219. DOI:10.1016/j.icheatmasstransfer.2008.05.017 |
| [11] |
RAFATI SALEH A, HOSSEINI S H, SHOJAEE S, et al. CFD studies of pressure drop and increasing capacity in MellapakPlus 752.Y structured packing[J]. Chemical Engineering & Technology, 2011, 34(9): 1402-1412. |
| [12] |
HAROUN Y, RAYNAL L, LEGENDRE D. Mass transfer and liquid hold-up determination in structured packing by CFD[J]. Chemical Engineering Science, 2012, 75: 342-348. DOI:10.1016/j.ces.2012.03.011 |
| [13] |
SEBASTIA-SAEZ D, GU S, RANGANATHAN P, et al. Meso-scale CFD study of the pressure drop, liquid hold-up, interfacial area and mass transfer in structured packing materials[J]. International Journal of Greenhouse Gas Control, 2015, 42: 388-399. DOI:10.1016/j.ijggc.2015.08.016 |
| [14] |
ZHANG Y, ZHU H, YIN Q. CFD study on the local mass transfer efficiency in the gas phase of structured packing[J]. Chemical Engineering & Technology, 2013, 36(7): 1138-1146. |
| [15] |
KOTTKE V, KVHNEL W, BECKER S. A new technique for visualization and determination of local mass transfer at solid walls in liquid flow[M]//Flow Visualization VI. Berlin, Heidelberg: Springer Berlin Heidelberg, 1992: 535-539
|
| [16] |
GAISER G, KOTTKE V. Flow phenomena and local heat and mass transfer in corrugated passages[J]. Chemical Engineering & Technology, 1989, 12(1): 400-405. |
| [17] |
MULLIN J W. The effect of maldistribution on the performance of packed columns[J]. Industrial Chemist, 1957, 33: 408-417. |
| [18] |
RAYNAL L, BOYER C, BALLAGUET J P. Liquid holdup and pressure drop determination in structured packing with CFD simulations[J]. The Canadian Journal of Chemical Engineering, 2004, 82(5): 871-879. DOI:10.1002/cjce.5450820502 |
| [19] |
MACFARLAN L H, SEIBERT A F, PHAN M T, et al. CFD-based study on structured packing geometry[J]. Chemical Engineering Science, 2021, 243: 116767. DOI:10.1016/j.ces.2021.116767 |
| [20] |
SOGIN H H. Sublimation from disks to air streams flowing normal to their surfaces[J]. Journal of Fluids Engineering, 1958, 80(1): 61-67. |
| [21] |
OLUJIC Z, JANSEN H, KAIBEL B, et al. Stretching the capacity of structured packings[J]. Industrial & Engineering Chemistry Research, 2001, 40(26): 6172-6180. |
 2025, Vol. 42
2025, Vol. 42





