气升式反应器是通过反应器底部的气体输入,使混合液在提升管与降液管之间产生密度差进而使液体产生循环动力的一种自循环反应器[1]。气升式反应器被广泛应用于微生物培养、苯酚降解以及含COD的石油污水处理等领域[2]。气升式反应器分为内循环气升式反应器(IALR)和外循环气升式反应器(EALR)2大类。IALR与EALR除结构不同外,最明显的区别在于EALR的下降管中不存在气体,而IALR在循环液速超过气泡滑移速度时下降管内将出现气体。
气升式反应器一般由4个区域组成,分别为提升管、降液管、反应器顶部气液固分离区和反应器底部进气区,4个区域相互影响,各区域物理量相互关联。20世纪以来,很多科学家对气升式反应器的结构进行了不断的研究和优化[3],但对其数学模型的研究报导较少。
目前,气升式工业反应器设计中应用较多的数学模型有4个,分别由Heijnen、Garcla-Calvo、Carla Freitas和Livingston提出[4-7]。研究发现,降液管和提升管中气含率之比(α)的大小对反应器模拟结果有很大的影响,但上述模型均将α设为Bello[8]文章中出现的定值0.89,这会对模拟结果带来很大的误差。并且上述模型仅限于反应器的全局稳态模拟,而未体现出局部特征以及各物理量随时间的变化结果。在实际操作中,局部物理量对反应器的结构优化有重要的影响[9, 10]。目前,虽然已有一些文献[11, 12]提出了局部气含率的经验关系式,但适用性并不好,因此构建一个更具有普适性的反应器轴向局部模型显得尤为必要。
本研究将针对三相内循环气升式反应器的传质反应过程建立动态模型,并使用计算机语言Fortran来对所建立模型进行动态求解。通过模型计算可以得到气含率、循环液速等物理量在反应器轴向上的分布情况以及随时间的变化结果,并得到不同操作条件下反应器的α值和反应器顶部气体回流比(β)。最后,使用微生物一级反应动力学模拟计算了三相IALR中微生物降解苯酚的过程,将模拟结果中微生物浓度和苯酚浓度与文献中实验数据进行对比,验证了所建立传质反应模型的准确性。
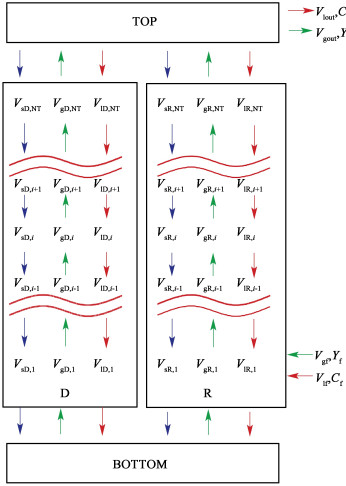
1 模型建立 1.1 假设内循环气升式反应器结构示意如图 1所示。针对三相反应器中传质反应模型的建立,提出以下假设:(1)反应器由提升管、降液管、反应器顶部和反应器底部4个部分组成;(2)液相可以被认为是“拟均相混合物”,且液体密度均匀、不可压缩;(3)气体为理想气体;(4)气泡的破裂和聚集是有限的。
|
| 图 1 内循环气升式反应器轴向图 Fig.1 Partial axial diagram of the internal airlift reactor |
| |
在三相气升式反应器操作过程中,提升管与降液管各相含率、线速度等物理量作为主要操作参数被用到,因此在建立模型时,首先要对上述参数进行求解。如图 1所示,上升管和下降管被划分为NT个单元进行物料衡算。
1.2.1 提升管与降液管表观速度的计算表观速度通过质量守恒和能量守恒计算。在三相内循环气升式反应器中连续相是液相,分散相是气相和固相,在Weinstein的文章[13]中,体积流量可以由式(1)表示。
| $ Q_{j, i}=A v_{j, i} e_{j, i} $ | (1) |
式(1)中: Q为体积流量,v为表观气速,e为某相在单元体积中所占的比率,A为横截面积,j为气相、液相或固相, i为轴向位置。
由于提升管与降液管的轴向横截面积不变,因此引入流量U。
| $ U_{j, i}=\frac{Q_{j, i}}{A} $ | (2) |
则式(1)可以写为式(3)。
| $ Q_{j, i}=A U_{j, i}=A v_{j, i} e_{j, i} $ | (3) |
液相体积衡算为:
| $ Q_{1, \text { in }}-Q_{1, \text { out }}=-\sum\limits_1^i\left[\left(e_{\mathrm{g}, i}^{t+1}+e_{\mathrm{s}, i}^{t+1}-e_{\mathrm{g}, i}^t-e_{\mathrm{s}, i}^t\right) A \Delta Z\right] $ | (4) |
式(4)中:Ql, in为液体流入流量,Ql, out为液体流出流量,i为轴向位置,ΔZ为单元高度。
根据Heijnen的文献[4],利用能量守恒计算vlD, 1。
| $ v_{\mathrm{ID}, 1}=\sqrt{\frac{2}{\rho_1 K_{\mathrm{f}}}\left(P_{\mathrm{D}, 1}-P_{\mathrm{R}, 1}\right)} $ | (5) |
式(5)中:Kf为摩擦系数,ρl为液相密度,PD, 1为降液管底部压力,PR, 1为提升管底部压力。
1.2.2 提升管与降液管气含率的计算由式(3)可以得到基于提升管与降液管横截面积上的气相体积流量,如式(6)所示。
| $ \frac{Q_{\mathrm{g}, i}}{A}=U_{\mathrm{g}, i}=e_{\mathrm{g}, i} v_{\mathrm{g}, i} $ | (6) |
将式(6)进行微分,并将密度相代入,可得到式(7)。
| $ \frac{\partial\left(e_{\mathrm{g}} \rho\right)}{\partial t}=-\frac{\partial\left(U_{\mathrm{g}} \rho\right)}{\partial z}-N_{0, i}=-\frac{\partial\left(e_{\mathrm{g}} v_{\mathrm{g}} \rho\right)}{\partial z}-N_{0, i} $ | (7) |
式(7)中,NO, i为传质通量。利用理想气体状态,式(7)可写为式(8)。
| $ \begin{gathered} \frac{1}{R_{\mathrm{g}} T} \frac{\partial\left(e_{\mathrm{g}} P\right)}{\partial t}=-\frac{1}{R_{\mathrm{g}} T} \frac{\partial\left(U_{\mathrm{g}} P\right)}{\partial z}-N_{0, i}= \\ -\frac{1}{R_{\mathrm{g}} T} \frac{\partial\left(e_{\mathrm{g}} v_{\mathrm{g}} P\right)}{\partial z}-N_{0, i} \end{gathered} $ | (8) |
式(8)中压力P的计算方程如式(9)所示。
| $ P_i^t=P_{\mathrm{top}}+\rho_1 g_0 \Delta Z \sum\limits_i^{N_{\mathrm{T}}} e_{1, i}^t+\rho_{\mathrm{s}} g_0 \Delta Z \sum\limits_i^{N_{\mathrm{T}}} e_{\mathrm{s}, i}^t $ | (9) |
式(9)中:Ptop为反应器顶部的压力。
将式(8)离散化后求解气含率。提升管的边界条件为i=1,边界项计算如式(10)所示。
| $ \frac{1}{R_{\mathrm{g}} T} P_{\mathrm{R}, 1}^t e_{\mathrm{gR}, 1}^t v_{\mathrm{gR}, 1}=\frac{v_{\mathrm{gf}}}{m} \frac{P_{\mathrm{f}}}{R_{\mathrm{g}} T_{\mathrm{f}}}+\frac{P_{\mathrm{D}, 1}^t e_{\mathrm{gD}, 1}^t v_{\mathrm{gD}, 1}}{R_{\mathrm{g}} T} \frac{1-m}{m} $ | (10) |
式(10)中:vgf为反应器进气速度,Pf为进气压力,Tf为进气的温度,m为提升管与反应器横截面积之比。
降液管求解的边界条件为i=NT,边界项计算如式(11)所示。
| $ \frac{1}{R_{\mathrm{g}} T} P_{\mathrm{D}, N_{\mathrm{T}}}^t e_{\mathrm{gD}, N_{\mathrm{T}}}^t v_{\mathrm{gD}, N_{\mathrm{T}}}=\frac{m}{1-m} \frac{1}{R_{\mathrm{g}} T} \beta P_{\mathrm{R}, N_{\mathrm{T}}}^t e_{\mathrm{gR}, N_{\mathrm{T}}}^t v_{\mathrm{gR}, N_{\mathrm{T}}} $ | (11) |
式(11)中:β是反应器顶部气体回流比。
降液管与提升管总气含率通过式(12)计算。
| $ e_{\mathrm{g}}=\frac{\Delta Z \sum\limits_{i=1}^{N_{\mathrm{T}}} e_{\mathrm{g}, i}}{N_{\mathrm{T}}} $ | (12) |
固含率与气含率的计算方法基本相同,即:
| $ \frac{\partial e_{\mathrm{s}}}{\partial t}=-\frac{\partial\left(e_{\mathrm{s}} v_{\mathrm{s}}\right)}{\partial z} $ | (13) |
降液管与提升管总固含率计算式为:
| $ e_{\mathrm{s}}=\frac{\Delta Z \sum\limits_{i=1}^{N_{\mathrm{T}}} e_{\mathrm{s}, i}}{N_{\mathrm{T}}} $ | (14) |
提升管和降液管的进料分别来自于反应器底部和顶部。反应器底部和顶部是三相混合区,混合状态是全混流状态,通过物料衡算计算,不同相间计算方法相同,以气相为例,在某一时刻t,反应器底部气相物料衡算为:
| $ V_{\mathrm{g}, \text { bot }}^t=A_{\mathrm{T}} L_{\mathrm{bot}} \mathrm{e}_{\mathrm{g}, \text { bot }}^{t-1}+v_{\mathrm{gD}, 1} e_{\mathrm{gD}, 1}^t A_{\mathrm{D}} \Delta t $ | (15) |
式(15)中,V为反应器底部或顶部中物料的总体积。
反应器顶部气相物料衡算为:
| $ V_{\mathrm{g}, \text { top }}^t=A_{\mathrm{T}} L_{\mathrm{top}} e_{\mathrm{g}, \text { top }}^{t-1}+v_{\mathrm{gR}, \mathrm{~N}_{\mathrm{T}}} e_{\mathrm{gR}, \mathrm{~N}_{\mathrm{T}}}^t A_{\mathrm{R}} \Delta t $ | (16) |
式(16)中:Lbot和Ltop分别为反应器底部和顶部的高度,Vg, bot和Vg, top分别为反应器底部和顶部气体的体积。
1.3 传质模型 1.3.1 气相传质模型通过反应器内质量守恒得到质量衡算式,如式(17)所示。
| $ \frac{\partial\left(Y e_{\mathrm{g}}\right)}{\partial t}=-\frac{\partial\left(v_{\mathrm{g}} Y e_{\mathrm{g}}\right)}{\partial z}-N_{0, i} $ | (17) |
式(17)的等量代换如式(18)所示。
| $ \frac{1}{R_{\mathrm{g}} T} \frac{\partial\left(P F_{\mathrm{g}}\right)}{\partial t}=-\frac{1}{R_{\mathrm{g}} T} \frac{\partial\left(v_{\mathrm{g}} P F_{\mathrm{g}}\right)}{\partial z}-N_{0, i} $ | (18) |
式(18)中,单元传质通量NO由式(19)计算。
| $ N_{0, i}=A \Delta Z K_{\mathrm{y}} a\left(Y_i^*-Y_i\right) $ | (19) |
式(19)中:Y*为氧气相平衡浓度,Ky为反应器中的传质系数,a为气泡的比表面积,Yi为氧气浓度,A为提升管或降液管横截面积。
氧气相平衡浓度Y*通过式(20)得到。
| $ Y^*=\frac{P_0}{H} $ | (20) |
式(20)中:H为亨利系数,PO为氧气分压。
Ky和a的求解方法分别在Tobajas[14]和Wilke[15]的文章中给出,如式(21)和式(22)所示。
传质系数:
| $ K_{\mathrm{y}}=\frac{2}{\sqrt{\pi}} \sqrt{D e}\left(\frac{v_{\mathrm{g} s} \rho_1 g_0 e_{\mathrm{g}}}{\mu}\right)^{0.25} $ | (21) |
比表面积:
| $ a=\frac{6 e_{\mathrm{g}}}{d_{\mathrm{b}}} $ | (22) |
联立式(19)、(20)、(21)和(22),可得:
| $ \begin{aligned} N_{0, i}=\frac{12}{d_{\mathrm{b}}} & \sqrt{\frac{D e}{\pi}}\left(\frac{v_{\mathrm{gs}} \rho_1 g_0}{\mu}\right)^{0.25}\left(\frac{e_{\mathrm{g}, i}^{0.25} P_i F_{\mathrm{g}, i}}{H}-\right. \\ & \left.\frac{e_{\mathrm{g}, i}^{1.25}}{1-e_{\mathrm{s}, i}-e_{\mathrm{g}, i}} F_{1, i}\right) \end{aligned} $ | (23) |
式(23)中:db为气泡直径,De为氧气的扩散系数,Fg和Fl分别为Yeg和Cel。
以提升管为例,对气相传质系数进行求解。当i=1时,方程(18)离散化后的边界项为:
| $ \begin{gathered} v_{\mathrm{gR}, i-1} P_{\mathrm{R}, i-1}^t F_{\mathrm{gR}, i-1}^t=\frac{v_{\mathrm{f}}}{m} \frac{P_{\mathrm{f}} T}{T_{\mathrm{f}}} Y_{\mathrm{O}, \mathrm{f}}+ \\ v_{\mathrm{g}, \text { bot }, \text { out }} P_{\mathrm{bot}, \text { out }}^t F_{\mathrm{g}, \text { bot }, \text { out }}^t \end{gathered} $ | (24) |
式(24)中:vg, bot, out、Pbot, outt和Fg, bot, outt是反应器底部出口的物理量。降液管的计算方法与提升管相同。
1.3.2 液相传质模型在加入一级反应的同时求解液相传质,将氧气的消耗速度和扩散速度加到传质中,得到式(25)。
| $ \frac{\partial F_1}{\partial t}=\frac{\partial\left(v_1 F_1\right)}{\partial z}+N_{0, i}+D e \frac{\partial^2 F_1}{\partial z^2}-R_0 $ | (25) |
式(25)中,RO为氧气消耗的量。
将式(23)代入式(25)中即可求出液相传质系数的普遍化方程,如式(26)所示。
| $ \begin{gathered} \frac{\partial F_1}{\partial t}=\frac{\partial\left(v_1 F_1\right)}{\partial z}+\frac{12}{d_{\mathrm{b}}} \sqrt{\frac{D e}{\pi}}\left(\frac{v_{\mathrm{gs}, } \rho_1 g_0}{\mu}\right)^{0.25}\left(\frac{e_{\mathrm{g}, i}^{0.25} P_i F_{\mathrm{g}, i}}{H}-\right. \\ \left.\frac{e_{\mathrm{g}, i}^{1.25}}{1-e_{\mathrm{g}, i}-e_{\mathrm{s}, i}} F_{1, i}\right)+D e \frac{\partial^2 F_1}{\partial z^2}-R_0 \end{gathered} $ | (26) |
将式(26)离散化后再使用追赶法求解,即可求出液相中氧气的分布情况。
2 结果与讨论对处于不同操作条件下的三相内循环气升式反应器进行了动态模拟,研究了α、eg、vl等物理量轴向上的分布情况和随时间的变化结果;并在 2.1节中加入了微生物反应,将模拟结果与文献对比,验证本论文模型的普遍适用性。
2.1 动态模拟结果分析本次模拟的三相物系为水-空气-与水密度相近的固体。气泡的滑移速度为0.2 m ·s-1,固体的滑移速度为0.01 m ·s-1。模拟结果如图 2所示。

|
| 图 2 (a) 循环液速的动态模拟结果;(b)反应器顶部固含率的动态模拟结果 Fig.2 Dynamic simulation results of (a) circulating liquid velocity; (b) solids content at the top of the reactor |
| |
由图 2可以看出,顶部固含率和循环液速稳定前在随时间不断震荡。循环液速的震荡因为随着循环液速的增大,越来越多的气泡被夹带进降液管,造成提升管和降液管气含率差值变小,循环动力减小,进而造成循环液速开始下降,而随着循环液速的减小,被夹带进入降液管中的气泡开始减少,提升管和降液管中气含率差值开始变大,由此造成循环液速变大,当降液管和提升管中气含率达到平衡时反应器运行稳定。为验证本文模型的普适性,在Dhaouadi[16]实验的循环液速数据中找到了相同的运行趋势。
2.2 稳定操作状态下模拟结果分析利用所建立的模型计算气含率之比α和β,结果见图 3和图 4。

|
| 图 3 (a) 横截面积比对气体回流比影响积;(b) 进气速度对气体回流比影响 Fig.3 (a) Influence of cross-sectional area on gas return ratio; (b) influence of gas feed velocity on gas return ratio |
| |
|
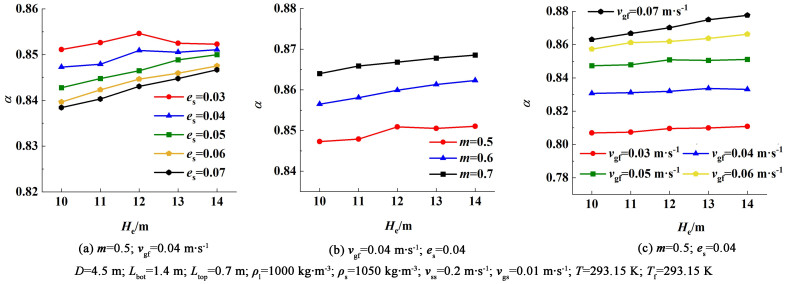
| 图 4 (a) 固含对气含率之比影响率;(b) 横截面积对气含率之比影响;(c) 进气速度对气含率之比影响 Fig.4 (a) Solids effect on the ratio of gas content; (b) cross-sectional area effect on the ratio of gas content; (c) gas feed velocity effect on the ratio of gas content |
| |
由图 4可知,不同的操作条件对α值影响很大,由于α的大小对其他物理量的求解影响很大,并且从图 4中可以看到,α的大小随着操作条件在0.80~0.89的范围内变化,因此不同操作条件下反应器的流体力学计算应选用适当的α[17, 18]。同时通过对比图 3和图 5中循环液速的变化,可以看到β的变化和循环液速的变化趋势相似,可以说β的大小主要和循环液速的大小有关,同时从图 3可以看出,随着操作条件的不同,β的大小在0.44~0.56的范围内变化。
|
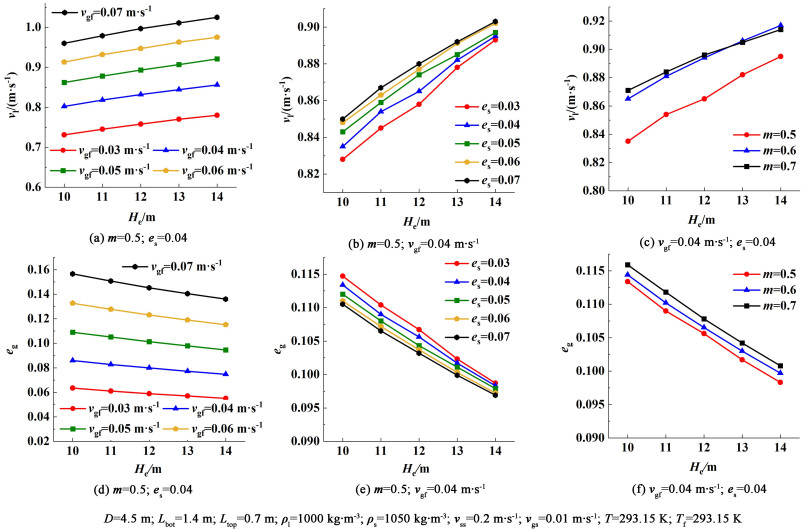
| 图 5 反应器高度、进气速度、固体加入量及横截面积之比对循环液速和气含率的影响 Fig.5 The effects of reactor height, gas feed, solid input, and ratio of cross-sectional area on the liquid circulation velocity and reactor gas hold-up |
| |
通过式(4)和式(7)求出的eg和vl在不同操作条件下的变化如图 4所示。由图 5(b)和图 5(e)可知,随着es的增加,eg减少,vl增加,这是因为固体的加入使液体扰动变大,更多的气泡从反应器中逸出,导致反应器内eg变小[19]。在模拟计算中,使用的固体密度与液体密度接近,因此固体的加入仅仅增加了液体的扰动和气泡的聚集,这会使得提升管中逸出更多的气泡,提升管与降液管气含率差值变大,液体循环动力变大,因此液体循环速度会随着固含率的增加而增加,这与Freitas等[20]文章中的结论相同。气含率和循环液速随m的变化则与Pelivanoski等[21]的报告一致。
2.3 传质系数模拟结果分析通过式(21)和式(22),计算得到了不同操作条件下的传质系数,结果如图 6所示。
|
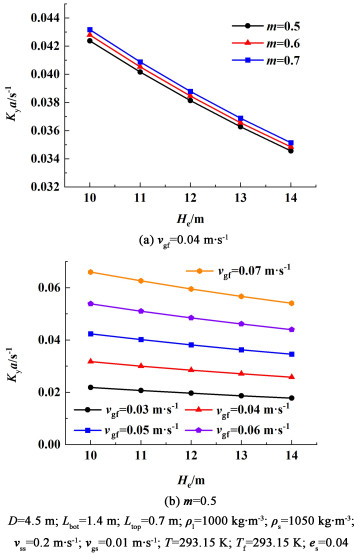
| 图 6 (a) 固含率对传质系数影响;(b) 进气速度对传质系数影响 Fig.6 (a) Solids rate effect on mass transfer coefficients; (b) gas feed velocity effect on mass transfer coefficients |
| |
对于传质系数,Kilonzo和Garcia-Ochoa分别对其求解方程做了较为全面的综论[22, 23],几乎涵盖了所有求解方法。在图 6(a)可以看出,当横坐标He相同的情况下,m从0.5变化到0.7的过程中,纵坐标Kya增大了4%左右,从图 6(b)中可以看出,当横坐标He相同的情况下,vgf从0.3 m ·s-1变化到0.7 m ·s-1的过程中,纵坐标Kya增大了近3倍,而图 6(a)和图 6(b)中纵坐标随横坐标的变化趋势均显示出Kya随He的变化较大。朱慧红等[24]对造成传质系数增大或减小的原因进行了分析,认为传质系数的增大是因为循环液速的增大使液膜的阻力下降;传质系数变小是因为固体的存在,使气泡的聚集更多,大气泡所占比例变大,气泡在反应器内停留时间变小,这不利于传质。如图 5(a)和图 6(a)所示,循环液速随反应器高度变化较小,因此气泡在反应器内存在时间更多,聚集更多,随着反应器高度的增加,大气泡比例更多,传质系数下降。而根据图 5(a)和图 5(c)所示,相同高度下循环液速会随着m和vgf的增大而增大,由于相同反应器高度下循环液速越快,气泡的聚集性越差,相反较大的循环液速使液膜的阻力下降,因此传质系数会随着m和vgf的增大而增大。
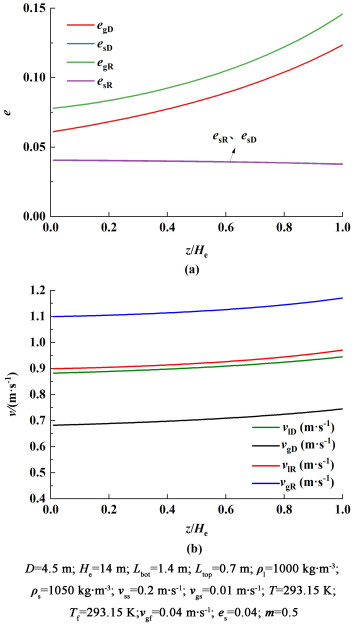
2.4 相含率和表观气速轴向模拟结果分析通过流体力学模型计算得到了气固相含率和各相速度在轴向上的变化规律,结果如图 7所示。由于固体的加入,且反应器内液体循环速度较大,增加了反应器内的混合效果,因此在轴向上固体的分布较为均匀。同时由图 7可以看出,随着高度增加,气含率曲线的斜率增大,说明各单元间气含率的差值在轴向上逐渐增大,造成液体循环速度的动力变大,从而使得轴向上各相物料的速度变大。
|
| 图 7 (a) 气、固含率轴向分布;(b)各相速度轴向分布 Fig.7 (a) Gas and solid holdup axial distribution; (b) each phase velocity axial distribution |
| |
在传质模型中加入微生物的反应。利用Alberty的速率方程[25]以及Ryder的生成消耗方程[26]模拟微生物降解苯酚过程。
苯酚、微生物含量方程如式(27)和式(28)所示。
| $ \frac{\partial\left(B \cdot e_1\right)}{\partial t}=\frac{\partial\left(B \cdot e_1 v_1\right)}{\partial z}-\frac{\mu_{\mathrm{x}} X}{Y_{\mathrm{B}}} $ | (27) |
| $ \frac{\partial\left(X \cdot e_1\right)}{\partial t}=\mu_{\mathrm{x}} X-b_1 X-b_2 S+\frac{\partial\left(X \cdot e_1 v_1\right)}{\partial z} $ | (28) |
微生物生长速率方程如式(29)所示。
| $ \mu_{\mathrm{x}}=\frac{\mu_{\mathrm{x}, \max } B \cdot O}{K_{\mathrm{B}} O+K_0 B+B \cdot O+K_0 K_{\mathrm{B}}} $ | (29) |
式(29)中:B为反应器中苯酚的质量浓度,X为反应器中微生物的质量浓度,O为反应器中氧气的质量浓度,μX是微生物的生长速率,μX, max是微生物在底物充足时的最大生长速率,YB为微生物在苯酚是限制性底物时的细胞产量,KB和KO分别为Monod的苯酚与氧气的反应速率常数,b1为微生物衰减系数,b2为底物抑制系数。
利用以上参数即可求出氧气消耗速率。
| $ R_{\mathrm{o}}=\frac{\mu_{\mathrm{x}} X}{Y_{\mathrm{o}}} $ | (30) |
式(30)中:YO为微生物在氧气是限制性底物时的细胞产量。
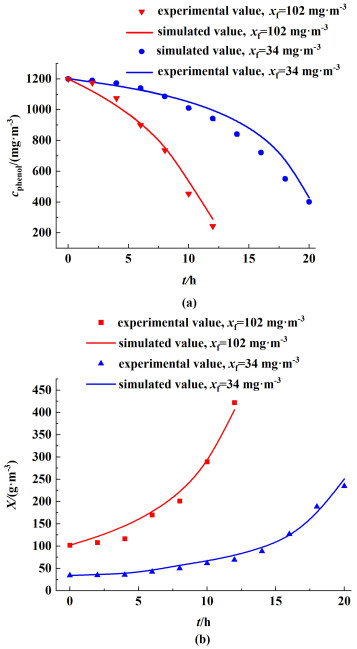
为了验证本文模型准确度,利用WeiFeng等[27]报道的循环气升式反应器中的苯酚降解实验条件进行模拟计算。实验条件如下:He=2 m,D=0.2 m, m=0.49,vf=0.02 m ·s-1,Bf=1200 g ·m-3,xf=34和102 mg ·m-3。
将实验数据与模拟结果对比,如图 8所示。由图 8可以看出,在微生物初始浓度为102 mg ·m-3时,模型模拟结果和实验数据的总平均相对误差为8.81%。微生物初始浓度为34 mg ·m-3时相较于102 mg ·m-3时吻合更好,总平均相对误差为6.8%。
|
| 图 8 (a) 微生物降解苯酚过程苯酚质量浓度模拟结果;(b) 微生物降解苯酚过程微生物质量浓度模拟结果 Fig.8 (a) Microbial degradation of phenol phenol simulation results; (b) Microbial degradation of phenol microbial simulation results |
| |
通过建立三相内循环气升式反应器的传质反应动态模型,计算得到了液体循环速度、气含率等物理量随轴向位置分布和时间的变化结果,以及在稳态条件下各个物理量随操作条件的变化结果。计算结果表明,下降管与提升管气含率之比并非常数,而是随着操作条件在0.80~0.89的范围内变化,而顶部气体回流比则在0.44~0.56的范围内变化,充分说明在三相内循环气升式反应器的计算时不能简单地将该参数看作定值。最后,通过利用微生物一级反应动力学方程,模拟了不同微生物初始浓度下降解苯酚的过程,对比不同条件下的模拟计算结果和文献中实验数据,结果显示仅有8.81%和6.86%的相对误差,模型拟合很好,验证了模型的准确性。本论文模型具有很好的普适性和适用性,为未来三相内循环气升式反应器的设计计算提供了新的理论指导和方法。
符号说明:
A—反应器,降液管,提升管横截面积, m2;
a—比表面积, m2;
b1—微生物衰减系数;
b2—底物抑制系数;
B—苯酚的质量浓度, g ·m-3;
C—液体中氧气的浓度, mol ·L-1;
D—反应器,降液管,提升管直径, m;
De—氧气在水中的扩散系数;
db—气泡直径, m;
e—提升管和降液管中的气体、液体和固体的比率;
Fl—液相传质参数,mg ·L-1;
Fg—气相传质参数,mg ·L-1;
g0—重力常数, m ·s-2;
H—亨利系数, Pa ·m-3 ·mol-1;
He—提升管的有效高度, m;
k—化学反应速率常数,s-1;
Kf—摩擦系数;
Ky—传质系数,s-2;
KB/O—Monod反应速率常数,g ·m-3;
L—反应器顶部或底部高度;
m—提升管和反应器横截面积之比;
No—氧气传递损失,mg ·L-1;
NT—分层数;
O—氧气的质量浓度, g ·m-3;
P—压力, Pa;
Patm—大气压力, Pa;
Q—气体或液体的体积流量, m3 ·s-1;
RO—反应所消耗氧气量,mg ·L-1;
Rg—摩尔气体常数, J · (mol ·K)-1;
t—时间,s;
T—温度, ℃;
U—气体、液体和固体的表观速度,基于立管和导流管的横截面积的表观速度, m ·s-1;
vgs—气体滑移速度, m ·s-1;
vss—颗粒的最终沉降速度, m ·s-1;
v—提升管和降液管中的气体、液体或固体的绝对速度, m ·s-1;
V—反应器某区域内物料总体积, m3;
X—微生物的质量浓度, g ·m-3;
Y—气体中氧气的百分比;
Y*—氧平衡浓度,mg ·L-1;
Yo/s—基底为限制基质时微生物产量;
ΔZ—单元高度,m;
希腊字母:
α—提升管气体的体积分数与降液管的体积分数之比;
β—反应器顶部气体回流比;
ρ—液体或固体的密度, kg ·m-3;
μ—黏度, Pa ·s;
μX—微生物生长速率;
μX, max—微生物的最大生长速度;
σ—表面张力, mN·m-1;
下标:
B—苯酚;
D—下降管;
f—外部进料;
g—气体;
i—某一区域;
in—某区域的进料;
j—气相、液相或固相;
l—液体;
O—氧气;
out—某处域的出料;
R—提升管;
Return—回流量;
s—固体;
bot—反应器底部;
top—反应器顶部;
T—反应器;
X—微生物。
| [1] |
ZHANG T, WE C, REN Y, et al. Advances in airlift reactors: Modified design and optimization of operation conditions[J]. Reviews in Chemical Engineering, 2017, 33(2): 163-182. DOI:10.1515/revce-2016-0005 |
| [2] |
冯加和, 王一平, 黄群武, 等. 硅油光-热老化气升式反应器数值模拟[J]. 化学工业与工程, 2016, 33(3): 82-88. FENG Jiahe, WANG Yiping, HUANG Qunwu, et al. Numerical simulation of an airlift reactor for silicone oil light and heat aging[J]. Chemical Industry and Engineering, 2016, 33(3): 82-88. DOI:10.13353/j.issn.1004.9533.20141052 (in Chinese) |
| [3] |
ZHANG T, WEI C, FENG C, et al. Advances in characteristics analysis, measurement methods and modelling of flow dynamics in airlift reactors[J]. Chemical Engineering and Processing-Process Intensification, 2019, 144: 107633. DOI:10.1016/j.cep.2019.107633 |
| [4] |
HEIJNEN J J, HOLS J, VAN DER LANS R G J M, et al. A simple hydrodynamic model for the liquid circulation velocity in a full-scale two- and three-phase internal airlift reactor operating in the gas recirculation regime[J]. Chemical Engineering Science, 1997, 52(15): 2527-2540. DOI:10.1016/S0009-2509(97)00070-5 |
| [5] |
GARCÍA-CALVO E, RODRÍGUEZ A, PRADOS A, et al. A fluid dynamic model for three-phase airlift reactors[J]. Chemical Engineering Science, 1999, 54(13/14): 2359-2370. |
| [6] |
FREITAS C, FIALOVÁ M, ZAHRADNIK J, et al. Hydrodynamic model for three-phase internal- and external-loop airlift reactors[J]. Chemical Engineering Science, 1999, 54(21): 5253-5258. DOI:10.1016/S0009-2509(99)00256-0 |
| [7] |
LIVINGSTON A G, ZHANG S F. Hydrodynamic behaviour of three-phase (gas-Liquid-Solid) airlift reactors[J]. Chemical Engineering Science, 1993, 48(9): 1641-1654. DOI:10.1016/0009-2509(93)80124-9 |
| [8] |
BELLO R A, ROBINSON C W, MOO-YOUNG M. Gas holdup and overall volumetric oxygen transfer coefficient in airlift contactors[J]. Biotechnology and Bioengineering, 1985, 27(3): 369-381. DOI:10.1002/bit.260270323 |
| [9] |
卢哲, 史嘉帧, 郭凯, 等. 二级环流反应器中收缩-膨胀隔板的性能优化[J]. 化学工业与工程, 2024, 41(1): 125-135. LU Zhe, SHI Jiazhen, GUO Kai, et al. Optimization of contraction-expansion partition in a two-stage internal airlift loop reactor[J]. Chemical Industry and Engineering, 2024, 41(1): 125-135. DOI:10.13353/j.issn.1004.9533.20220115 (in Chinese) |
| [10] |
翟瑞国, 党晓峰, 夏勇, 等. 双反应器选择性氧化硫回收工艺改进与优化[J]. 化学工业与工程, 2019, 36(5): 17-24. ZHAI Ruiguo, DANG Xiaofeng, XIA Yong, et al. Improvement and optimization of two reactor H2 S selective oxidative in sulfur recovery process[J]. Chemical Industry and Engineering, 2019, 36(5): 17-24. DOI:10.13353/j.issn.1004.9533.20181060 (in Chinese) |
| [11] |
LO C, HWANG S J. Local hydrodynamic properties of gas phase in an internal-loop airlift reactor[J]. Chemical Engineering Journal, 2003, 91(1): 3-22. DOI:10.1016/S1385-8947(02)00042-6 |
| [12] |
WANG J, XU X, WANG W, et al. Hydrodynamics of an airlift column for aeration in molten sulfur[J]. Applied Sciences, 2021, 12(1): 117. DOI:10.3390/app12010117 |
| [13] |
WEINSTEIN O, SEMIAT R, LEWIN D R. Modeling, simulation and control of liquid-liquid extraction columns[J]. Chemical Engineering Science, 1998, 53(2): 325-339. DOI:10.1016/S0009-2509(97)00310-2 |
| [14] |
TOBAJAS M, GARCÍA-CALVO E, SIEGEL M H, et al. Hydrodynamics and mass transfer prediction in a three-phase airlift reactor for marine sediment biotreatment[J]. Chemical Engineering Science, 1999, 54(21): 5347-5354. DOI:10.1016/S0009-2509(99)00262-6 |
| [15] |
WILKE C R, CHANG P. Correlation of diffusion coefficients in dilute solutions[J]. AIChE Journal, 1955, 1(2): 264-270. DOI:10.1002/aic.690010222 |
| [16] |
DHAOUADI H, PONCIN S, HORNUT J M, et al. Hydrodynamics of an airlift reactor: Experiments and modeling[J]. Chemical Engineering Science, 1996, 51(11): 2625-2630. DOI:10.1016/0009-2509(96)00127-3 |
| [17] |
BLAŽEJ M, KIŠA M, MARKOŠ J. Scale influence on the hydrodynamics of an internal loop airlift reactor[J]. Chemical Engineering and Processing: Process Intensification, 2004, 43(12): 1519-1527. DOI:10.1016/j.cep.2004.02.003 |
| [18] |
LU W, HWANG S, CHANG C. Liquid velocity and gas holdup in three-phase internal loop airlift reactors with low-density particles[J]. Chemical Engineering Science, 1995, 50(8): 1301-1310. DOI:10.1016/0009-2509(95)98842-3 |
| [19] |
GOURICH B, AZHER N E, SOULAMI BELLHAJ M, et al. Contribution to the study of hydrodynamics and gas-liquid mass transfer in a two- and three-phase split-rectangular airlift reactor[J]. Chemical Engineering and Processing: Process Intensification, 2005, 44(10): 1047-1053. DOI:10.1016/j.cep.2004.12.002 |
| [20] |
FREITAS C, TEIXEIRA J A. Hydrodynamic studies in an airlift reactor with an enlarged degassing zone[J]. Bioprocess Engineering, 1998, 18(4): 267-279. DOI:10.1007/s004490050441 |
| [21] |
PELIVANOSKI B, DETMANN B, OOMS K, et al. Design of a 1000 L pilot-scale airlift bioreactor for nitrification with application of a three-phase hydrodynamic mathematical model and prediction of a low liquid circulation velocity[J]. Chemical Engineering Research and Design, 2020, 153: 257-262. DOI:10.1016/j.cherd.2019.10.018 |
| [22] |
KILONZO P M, MARGARITIS A. The effects of non-Newtonian fermentation broth viscosity and small bubble segregation on oxygen mass transfer in gas-lift bioreactors: A critical review[J]. Biochemical Engineering Journal, 2004, 17(1): 27-40. DOI:10.1016/S1369-703X(03)00121-9 |
| [23] |
GARCIA-OCHOA F, GOMEZ E. Bioreactor scale-up and oxygen transfer rate in microbial processes: An overview[J]. Biotechnology Advances, 2009, 27(2): 153-176. DOI:10.1016/j.biotechadv.2008.10.006 |
| [24] |
朱慧红, 刘永民, 于大秋. 气液固三相环流反应器的研究进展[J]. 化工科技, 2003, 11(4): 48-52. ZHU Huihong, LIU Yongmin, YU Daqiu. Study and progress on loop reactor for the system of gas-liquid-solid three phases[J]. Science & Technology in Chemical Industry, 2003, 11(4): 48-52. (in Chinese) |
| [25] |
BADER F G. Analysis of double-substrate limited growth[J]. Biotechnology and Bioengineering, 1978, 20(2): 183-202. DOI:10.1002/bit.260200203 |
| [26] |
RYDER D N, SINCLAIR C G. Model for the growth of aerobic microorganisms under oxygen limiting conditions[J]. Biotechnology and Bioengineering, 1972, 14(5): 787-798. DOI:10.1002/bit.260140508 |
| [27] |
FENG W, WEN J, LIU C, et al. Modeling of local dynamic behavior of phenol degradation in an internal loop airlift bioreactor by yeast Candida tropicalis[J]. Biotechnology and Bioengineering, 2007, 97(2): 251-264. DOI:10.1002/bit.21215 |
 2025, Vol. 42
2025, Vol. 42





