2. 化学工程联合国家重点实验室, 天津 300354
2. State Key Laboratory of Chemical Engineering, Tianjin 300354, China
规整填料塔具有分离效率高,能量耗散小,处理量大的特点,在工业生产中具有广泛的应用[1, 2]。加强填料塔高效节能技术的开发应用,能够有效地降低能量损耗,减少二氧化碳排放,是实现碳中和、全面建立清洁低碳能源体系的重要手段。
为了进一步的优化填料塔的设计,解决局部气相返混、局部液泛、壁效应、沟流和放大效应等问题,需要全面系统地了解流体在塔内流经填料的行为,以及压降[3-5]、持液量[6, 7]等重要性能参数的变化。传统的实验方法已经无法实现,另外由于计算机性能的限制,无法直接采用数值模拟模拟整个设备内部流体的所有细节行为。因此,有学者提出应用多尺度计算的分析方法对规整填料塔内的流体流动行为进行探讨。
徐崇嗣[8]最早建立了结点网络模型研究规整填料内液相流动分布,后续被很多学者引用和改进,提出了各自的模型[9-11]。但其模型参数需要通过实验数据回归,限制了该模型的应用。Petre[12]和Larachi[13]根据规整填料片的结构特征,总结归纳出5种具有代表性的最小特征单元,由这5种特征单元组合计算了气相单相通过规整填料层的压力损失。Raynal[14]提出一个计算大型规整填料塔气液两相流动的多尺度CFD模拟方法,这2种方法都比较有效地估算了全塔的压降,但是仍不能得到填料塔内的流体分布信息。
本研究采用多尺度计算技术,把计算分解为微观和宏观尺度,在保证计算精度的前提下,大大减少了计算量。首先,对填料特征单元重新进行了划分,弥补了在研究塔壁单元和层间转换单元产生压降方面的缺陷,根据特征单元的实际尺寸建立小尺度CFD模型;其次,根据模拟得到的特征单元内的流体分布,提出新的流体分布方法和单元网络模型,并且根据CFD计算结果拟合单元网络模型参数;再次,利用得到的模型参数以及结点网络模型计算获得全塔的流体分布;最后,利用CFD计算收集到的数据集训练BP人工神经网络模型,计算干塔压降和持液量等重要的性能参数。同时将预测结果与其他学者的实验结果进行对比,证明了模型的有效性。
BP人工神经网络模型可以扩展到所有的填料类型和工况,在需要计算其它填料类型塔上流体分布、压降和持液量时,仅需要对该填料最小特征单元做CFD模拟计算,拟合结点网络模型参数、更换数据集训练BP神经网络模型即可。
1 CFD模拟 1.1 物理模型波纹规整填料[15]是由一些垂直排列的波纹板片组装而成,填料片波纹宽度为2B,板片上倾斜的波纹棱与填料塔轴线形成的角度,即波纹倾角为α。填料中两相邻板片上波纹棱的倾斜方向相反,形成了一系列相互交错的通道,把2通道所包围的空间定义为结点。规整填料与随机填料不同,虽然结构复杂,但是其规整的空间结构可以允许在其大量的重复结构中总结归纳出具有代表性的特征单元,如图 1。

|
| 图 1 单气相模拟计算物理模型 Fig.1 Physical model for single-gas phase simulation |
| |
以Mellapak 250Y型号的板波纹规整填料为例,根据填料的实际尺寸建立规整填料片气相CFD模拟物理模型,几何尺寸见表 1。
| 型号 | 比表面积/ (m2·m-3) | 波纹倾角/ (°) | 峰高/ m | 波距/ m | 空隙率/ % |
| 250Y | 250 | 45 | 11.7(±0.05) | 24(±0.05) | 97 |
为加快计算机的处理速度,在不改变影响流体流动的填料主要特征的前提下对模型稍作调整,假设填料表面没有开孔,没有印纹。
图 1展示了根据填料的结构特征构想的4种特征单元。
气相在通道内部流动,在2填料板围成的通道交叉处发生混合;液相沿着填料板板面流动,来自同一特征单元不同填料板的液体在2板接触点发生混合。根据液相流动规律,对于每一个内部特征单元,其流体来源于其左上侧单元、右上侧单元和上部单元;而塔壁单元上的流体受其左(右)上侧和上部单元影响。气液相流动方式不同,需要建立与气相不同的液相分布模型,并且在做气液两相小尺度研究时,重新建立CFD的物理模型,如图 2所示,通过研究这2个代表性单元上的两相流动,把握全塔的流体分布。
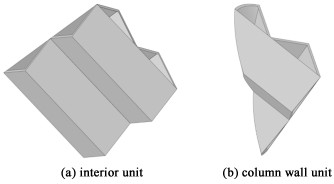
|
| 图 2 气液两相模拟计算物理模型 Fig.2 Physical model for gas-liquid two-phase simulation |
| |
在模拟计算中,使用空气作流体进行三维CFD模拟计算,假设是等温不可压缩流体,ρ=1.225 kg ·m-3,μ=17.894 μPa ·s。描述特征单元内流体流动的一般守恒方程包括连续性方程和用于描述层流的N-S方程或用于描述湍流的RANS方程。
气相连续性方程:
| $ \frac{\partial}{\partial x_i}\left(\rho u_i\right)=0 $ | (1) |
动量方程:
| $ \frac{\partial}{\partial x_j}\left(\rho u_i u_j\right)=-\frac{\partial}{\partial x_i} p+\frac{\partial}{\partial x_j} \tau_{i j}+\frac{\partial}{\partial x_j}\left(-\rho u_i^{\prime} u_j^{\prime}\right)+\rho g_i $ | (2) |
式(2)中:p表示静压;τij表示层流剪切应力张量;-ρu′ iu′ j表示湍流雷诺应力张量(在层流流动模拟中取0);ρgi表示重力。
在Choudhury[16]和Raynal等[17]的研究中认为RNG k-ε模型最适合模拟规整填料塔压降,所以本研究用RNG k-ε模型代替Standard k-ε模型。
湍动能运输方程,k:
| $ \frac{\mathrm{D}}{\mathrm{D} t} \rho k=\frac{\partial}{\partial x_i}\left(\mu_{\mathrm{e}} \frac{\partial}{\partial x_i} k\right)+G_k-\rho \varepsilon $ | (3) |
Gk是由于平均速度梯度而产生的湍动能。
耗散速率的运输方程,ε:
| $ \frac{\mathrm{D}}{\mathrm{D} t} \rho \varepsilon=\frac{\partial}{\partial x_i}\left(\mu_{\mathrm{e}} \frac{\partial}{\partial x_i} \varepsilon\right)+C_{1 \varepsilon} \frac{\varepsilon}{k} \times G_k-C_{2 \varepsilon} \rho \frac{\varepsilon^2}{k}-R $ | (4) |
另外在方程式(4)中涉及到的一些常量,在FLUENT中默认为:C1ε=1.44,C2ε=1.92。
1.2.2 两相计算CFD模型采用Hirt等[18]提出的适用于追踪两非混相界面的VOF模型模拟气液两相流动过程。采用Brackbill等[19]提出的连续表面力(Continuum surface force,CSF)模型,把由表面张力产生的壁面黏附力以动量源项的形式加入到VOF的计算中,如式(5)。
| $ F_{\mathrm{Vol}}=\sigma_{i j} \frac{\rho \kappa_i \nabla \alpha_i}{\frac{1}{2}\left(\rho_i+\rho_j\right)} $ | (5) |
式(5)中:σ为表面张力;κ为界面曲率。
| $ \kappa=\nabla \cdot \hat{n}=\frac{1}{|n|}\left[\left(\frac{n}{|n|} \cdot \nabla\right)|n|-(\nabla \cdot n)\right] $ | (6) |
式(6)中:
由于模型结构复杂,采用非结构化四面体网格划分。图 1中(a)入口单元、(b)交叉单元、(c)层间交换和(d)塔壁单元4种特征单元划分的网格数量分别为67 739、182 532、133 817和232 561。图 2中(a)内部单元和(b)边壁单元划分的网格单元总数为362 224和232 561。
单气相模拟在稳态下进行,采用有限体积法对控制方程进行离散,压力-速度耦合方程求解选用SIMPLEC算法。气液两相模拟过程中,压力-速度耦合方程选用PISO算法,模型计算推进时间步长取1×10-5 s。
1.3 模拟结果单气相模拟结果通过描绘流体流线展示在图 3中。
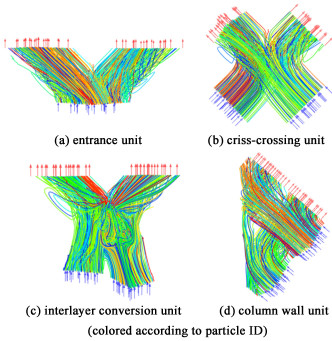
|
| 图 3 3D气相流线图 Fig.3 3D air flow path lines |
| |
(a) 入口单元的气体流型与根据物理模型的推测相符,气体进入该特征单元后分别各一半通过左右2个流道流出;(b)交叉单元的气体进入该特征单元后,一部分在结点处混合,一部分沿该流道流动,2部分的比例受入口流量大小影响;(c)层间转换单元的气体进入该单元后一部分与另一流道的流体混合,一部分直接沿波纹板面方向流入下一盘填料中与其相近的流道;(d)塔壁单元的流体撞击壁面后一部分返回到填料内部,剩余气体沿塔壁流入下一塔壁单元。
图 4是0°接触角气液逆向流动条件下液相在填料表面流动的相分布图。
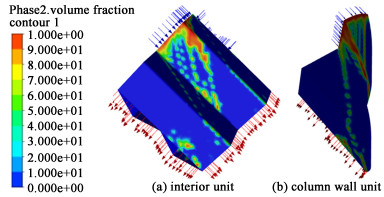
|
| 图 4 液膜在填料相分布图 Fig.4 Phase distribution of liquid film flowing on the surface of packing |
| |
从图 4可以看出,液体在填料(a)内部单元表面主要呈3个流动方向:液相沿着填料板通道方向流动;仅有小部分液体通过结点混合的形式流到下部填料单元;一部分液体发生横向流动,流入左下侧单元。液体在填料(b)边壁单元表面主要呈2个流动方向,一部分沿塔壁流动,一部分横向流动到左下侧单元。沿塔壁流动的部分又分成2股, 1股继续沿塔壁流下,1股沿着下部单元的左斜流道流道。
2 结点网络模型 2.1 结点编号将填料盘简化为1个三维空间,建立直角坐标系。如图 5结点编号示意图所示。
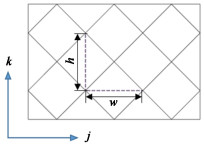
|
| 图 5 结点编号示意图 Fig.5 Schematic diagram of node numbers |
| |
i表示两两填料片之间围成的计算域;j表示相邻2填料片围成的计算域上结点的横向,每向右移动半个结点单元距离(w/2),j值增加1,J代表最右侧结点横向位置;k表示计算域上结点的纵向,每向上移动半个结点单元高度(h/2),k值增加1,K代表最顶端结点纵向位置;塔截面ioj平面被划分为有序排列的结点。
结点单元宽w为:
| $ w=\frac{2 B}{\cos \alpha} $ | (7) |
结点单元高h为:
| $ h=\frac{2 B}{\sin \alpha} $ | (8) |
式(1)和式(2)中:2B为填料片波纹宽度;α为波纹倾角。
2.2 气相模型假设为了建立气相结点网络模型,根据对CFD模拟结果的观察分析,对该模型做以下假设:(1)气体以充满整个流道的方式在填料形成的流道内流动;(2)气体一经进入结点,只在围成该流道的2片填料所夹区域内流动,不与相邻计算域的流体混合;(3)进入填料内部结点的气体,分为沿原流道流动和结点混合2个方向;结点混合部分的气体均分为2部分,分别沿左右2斜流道流动;(4)上下2盘填料旋转90°叠放,进入层间转换结点的气体,一部分沿原流道方向流动,进入下一盘填料通道,另一部分在结点与另一通道的气体混合;结点混合部分的气体均分为2部分,分别沿左右2斜流道流动;(5)气体在塔壁处的流动还受到塔内件的影响,部分返回到填料内部,部分沿塔壁流动。
2.3 气相模型参数根据模型假设(3),引入模型参数f表示结点混合部分,1-f表示沿原流道流动部分;引入模型参数PL和PR表征结点混合部分的液体的流动分配情况,并且PL=PR=0.5。根据模型假设(4),引入模型参数fi表示层间交换的结点混合部分,1-fi表示暂时沿原流道流动部分。根据模型假设(5),引入模型参数fw和r,r表示气体在填料壁面处的反射系数,其余气体沿塔壁流动。设塔壁单元处气体混合系数是fw。综上所述,本模型引入f、fw、r和fi 4个独立未知参数。
2.4 气相模型计算过程具体的气相结点网络模型方程如下。
2.4.1 初始气相分配(k=1)| $ L(i, j, k)=0.5 Q_0 $ | (9) |
| $ R(i, j, k)=0.5 Q_0 $ | (10) |
式(9)~式(10)中:L为左斜流道流量;R为右斜流道流量;Q0为填料盘最上端结点的气相初始流量。
2.4.2 填料内部结点以及塔壁结点上的气相分配(2≤k < K)塔壁单元(左):
(1) 当k=2时:
| $ Q_{\text {mix }}(i, 1, 2)=L(i, j+1, k-1) f_{\mathrm{w}}+0.5 Q_0 $ | (11) |
| $ W(i, 1, 2)=Q_{\operatorname{mix}}(i, j, k)(1-r) $ | (12) |
| $ R(i, 1, 2)=Q_{\operatorname{mix}}(i, j, k) r+L(i, j+1, k-1)\left(1-f_{\mathrm{w}}\right) $ | (13) |
(2) 当k>2时:
| $ Q_{\text {mix }}(i, 1, 2)=L(i, j+1, k-1) f_{\mathrm{w}}+W(i, j, k-2) $ | (14) |
| $ W(i, 1, 2)=Q_{\text {mix }}(i, j, k)(1-r) $ | (15) |
| $ R(i, 1, 2)=Q_{\text {mix }}(i, j, k) r+L(i, j+1, k-1)\left(1-f_{\mathrm{w}}\right) $ | (16) |
右侧塔壁单元同理。
内部单元(1 < j < J):
| $ \begin{gathered} Q_{\text {mix }}(i, j, k)=L(i, j+1, k-1) f_{\mathrm{L}}+ \\ R(i, j-1, k-1) f_{\mathrm{R}} \end{gathered} $ | (17) |
| $ \begin{gathered} L(i, j, k)=Q_{\text {mix }}(i, j, k) 0.5+ \\ L(i, j+1, k-1)\left(1-f_{\mathrm{L}}\right) \end{gathered} $ | (18) |
| $ \begin{gathered} R(i, j, k)=Q_{\text {mix }}(i, j, k) 0.5+ \\ R(i, j-1, k-1)\left(1-f_{\mathrm{R}}\right) \end{gathered} $ | (19) |
式(17)~式(19)中:Qmix为在特征单元内参与混合的流体流量;W为该节点壁流流量。
2.4.3 填料片最底端气相分配(k=K)塔壁单元(左):
| $ Q_{\mathrm{t}}(i, 1, K)=W(i, 1, k-2)+L(i, j+1, k-1) $ | (20) |
右侧塔壁单元同理。
内部单元(1<j < J):
| $ Q_1(i, j, K)=L(i, j+1, k-1)+R(i, j-1, k-1) $ | (21) |
式(20)~式(21)中:Qt为从填料片最底端结点流出流量。
实际填料塔内上下2相邻填料盘旋转90°叠放,所以在1盘填料计算结束后,其下游填料盘的依旧按照上述方法进行结点编号。
2.5 液相模型简介根据对CFD模拟结果的观察分析建立液相分布模型:(1)对于内部结点,(i, j, k)结点的液体分3部分流出,一部分分别沿原流道流入左下侧(i, j-1, k-1)和右下侧单元(i, j+1, k-1),另一部分在填料板接触点混合后流入下部单元(i, j, k-2)的左右两侧通道。(2)对于边壁结点(以左侧为例,右侧同理),(i, j, k)结点的液体分2部分流出,沿边壁垂直向下流入(i, j, k-2)和返回填料内部单元(i, j+1, k-1)。
以此液相分布模型可建立液相结点网络模型,实现宏观意义上的流体分布计算。
建立式(9)所示的目标函数,采用非线性最小二乘优化法,拟合上述气液相结点网络模型中的模型参数:
| $ F\left(\mathrm{f}_L, f_{\mathrm{R}}, f_{\mathrm{W}} \cdots\right)=\sum\limits_{i=1}^n\left[Q_{\mathrm{cal}}(i)-Q_{\mathrm{sim}}(i)\right]^2 $ | (22) |
式(22)中:Qsim代表对特征单元做CFD计算得到的无因次流量;Qcal表示结点网络模型计算得到的无因次流量。
通过之前对特征单元上CFD模拟结果的观察,可以确定模型参数受流量的影响显著,因此把其拟合为雷诺数(Re)的函数。编制相应Matlab程序计算得到各个填料特征单元的模型参数,见表 2。
| 参数类别 | 表达式 |
| f | -8.2450Re0.0020+9.1826 |
| fw | 3.5237Re0.0393-4.1338 |
| r | 33.6435Re0.0013-33.7350 |
| fi | 6.7671Re0.0196-7.2498 |
BP神经网络[20]包括输入层、隐含层和输出层,输出结果向后传播,误差向前传播,采用梯度下降法根据误差不断调整权重和阈值,直到得到的输出和检测样本集之间的误差在允许的范围内时,停止训练。
标准BP算法只在当前位置上沿着负梯度方向更新,忽略了之前位置的梯度方向,从而使学习过程常常发生振荡,收敛缓慢。这里采用Momentum算法[21]改进优化BP算法,通过引入1个新的变量
规整填料的流体力学性能计算复杂,不管是采用实验或者经验公式计算,都需要设计实验以及为了方便计算而对流动机理进行简化。本研究建立BP预测模型,无需事先确定输入输出之间的映射关系,仅通过自身的训练,在给定输入值后得到最接近期望输出值的结果,通过人工神经网络训练的方式避免了方程过度简化对计算结果的影响。
3.2 模型建立以干塔压降预测为例,具体建模过程如下:
将结点入口流量和出口流量4个参量设为输入层变量,压降ΔP设为输出层变量,隐含层神经元个数l根据Kolmogorov定理进行计算:
| $ l=\sqrt{m+n}+a $ | (23) |
式(23)中:m为输入层神经元个数;n为输出层神经元个数;a为1~10之间的常数,本研究m为4,n为1,所以l的取值范围是[3, 13]。经过多次实验,发现当l为10时,预测精确度最高,因此选取10作为隐含层神经元数目。学习率取0.001,momentum参数取0.9。为了减少偶然性,采用随机的方式,从CFD计算所得的424组数据中选取80%作为训练集,20%作为检验集。预测结果与其他学者的实验结果进行对比,证明本研究方法的有效性。
压降预测中其它特征单元以及持液量预测中各个特征单元的模型建立过程与上述过程类似。
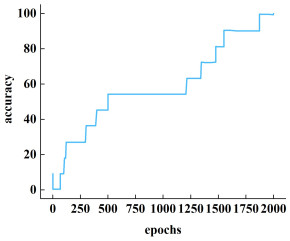
4 结果与讨论图 6显示的是BP神经网络训练过程中的准确率变化。
|
| 图 6 神经网络训练过程中准确率变化 Fig.6 The trend of accuracy in neural network training process |
| |
从图 6可以看出,在初始阶段准确率低并且存在波动,表明当前训练的神经网络模型实际值与预测值之间存在很大的偏差。随着训练不断进行,准确率阶梯型上升,最后在1 870步附近达到允许的误差范围,至2 000步训练结束。
|
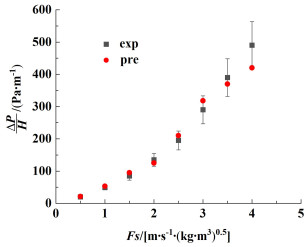
| 图 7 Mellapak 250Y填料塔干压降实验值与模拟值比较 Fig.7 The comparison of dry pressure drops between the prediction and experimental results for Mellapak 250Y packing column |
| |
从图 7可以看出在气相动能因子较小的条件下,本研究所建BP神经网络预测模型的模拟结果与实验值基本一致。随气相动能因子增大,预测精度开始波动。所有预测结果的平均相对偏差约为8.63%,最大相对偏差为14.02%。当要求相对偏差为10% 以内时,命中率约为75%。比较结果说明基于BP神经网络和CFD所建立的压降预测模型具有较高的命中率,该训练好的人工神经网络模型预测能力突出。
分析偏差存在的原因除了预测模型的精度外,用于做验证的实验数据中的填料塔干压降还受其他塔内件的影响。
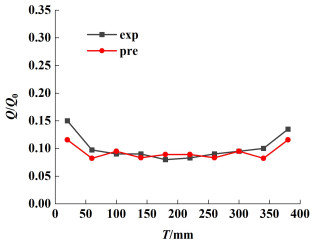
图 8是在60 m3 ·m-2 ·h-1喷淋密度条件下250Y填料的液相结点网络模型计算结果和实验[23]中的液相分布结果比较,Q/Q0是填料片底端每个结点单元流出的无因次流量。
|
| 图 8 Mellapak 250Y填料片液相分布实验值与模拟值比较 Fig.8 The comparison of liquid distribution between the simulation and experimental results for Mellapak 250Y packing |
| |
本研究建立的结点网络模型计算结果与实验值差别不大,最大无因次流量出现在塔壁处,填料中部液相分布均匀。尤其在远离壁面的填料处,两者数据吻合很好,从填料片尺度证明液相结点网络模型在预测流体分布上具有很大的准确度。
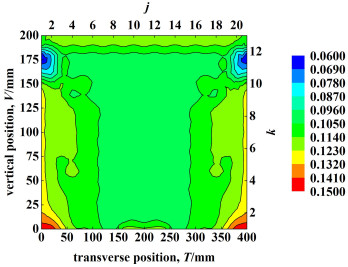
图 9是BP神经网络模型预测的80 m3 ·m-2 ·h-1喷淋密度条件下250Y填料片局部持液量等势图,采用双坐标系,上轴和右轴表示节点编号,下轴和左轴表示填料片具体位置,填料板横向T为400 mm,纵向V为200 mm。
|
| 图 9 Mellapak 250Y填料片局部持液量等势图 Fig.9 Contours of local liquid holdup for Mellapak 250Y packing |
| |
图 9显示填料片顶端几行结点的持液量分布均匀,基本呈现1个色阶。随着向下流动,液体开始向壁面聚集,边壁处持液量逐渐大于填料内部。当达到一定填料高度,边壁处持液量也趋于稳定。预测结果与其他文献[23, 24]中描述流体在填料内部流动的分配方式相符。
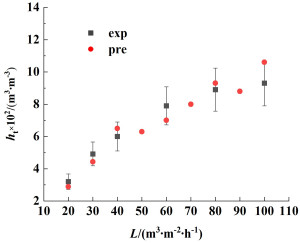
|
| 图 10 Mellapak 250Y填料持液量实验值与模拟值比较 Fig.10 The comparison of liquid holdup between the prediction and experimental results for Mellapak 250Y packing column |
| |
整个预测结果与实验值的平均相对偏差约为9.63%,最大相对偏差为13.97%。当要求相对偏差为10%以内时,命中率约为66.67%。这个结果说明所建立的持液量预测模型具有较高的命中率,该训练好的人工神经网络模型具有较好的预测能力,结果较为可信。
5 结论从Mellapak 250Y规整填料大量重复结构中总结归纳出具有代表性的特征单元,建立三维立体CFD模型,通过该模型研究了填料塔单气相和气液两相流体流动分布方式。以此为根据建立结点网络模型,计算全塔的流体分布等宏观信息。另外训练了2个神经网络模型,以结点流量为输入分别预测压降和持液量,根据预测结果给出了填料片局部持液量等势图。通过与相关实验数据比较,验证了模型的准确性,当要求相对偏差为10%以内时,干塔压降预测模型的命中率约为75%;持液量预测模型的命中率约为66.67%,预测结果较为可信。
本研究为规整填料塔的结构优化提供了较好的分析方法,但对于填料塔持液量的预测精度还需要做进一步的研究。
| [1] |
SPIEGEL L, MEIER W. Distillation columns with structured packings in the next decade[J]. Chemical Engineering Research and Design, 2003, 81(1): 39-47. DOI:10.1205/026387603321158177 |
| [2] |
OLUJIĆ, KAIBEL B, JANSEN H, et al. Fractionation research Inc. test data and modeling of a high-performance structured packing[J]. Industrial & Engineering Chemistry Research, 2013, 52(13): 4888-4894. |
| [3] |
AMINI Y, KARIMI-SABET J, ESFAHANY M N. Experimental and numerical simulation of dry pressure drop in high-capacity structured packings[J]. Chemical Engineering & Technology, 2016, 39(6): 1161-1170. |
| [4] |
WEN X, AKHTER S, AFACAN A, et al. CFD modeling of columns equipped with structured packings: I. Approach based on detailed packing geometry[J]. Asia-Pacific Journal of Chemical Engineering, 2007, 2(4): 336-344. DOI:10.1002/apj.90 |
| [5] |
SAID W, NEMER M, CLODIC D. Modeling of dry pressure drop for fully developed gas flow in structured packing using CFD simulations[J]. Chemical Engineering Science, 2011, 66(10): 2107-2117. DOI:10.1016/j.ces.2011.02.011 |
| [6] |
SINGH R K, GALVIN J E, SUN X. Multiphase flow studies for microscale hydrodynamics in the structured packed column[J]. Chemical Engineering Journal, 2018, 353: 949-963. DOI:10.1016/j.cej.2018.07.067 |
| [7] |
LU X, XIE P, INGHAM D B, et al. A porous media model for CFD simulations of gas-liquid two-phase flow in rotating packed beds[J]. Chemical Engineering Science, 2018, 189: 123-134. DOI:10.1016/j.ces.2018.04.074 |
| [8] |
徐崇嗣, 楼建中, 姜庆泉. 金属板波纹填料液流分布的研究[J]. 化工学报, 1986, 37(4): 402-411. XU Congsi, LOU Jianzhong, JIANG Qingquan. Liquid distribution for metallic corrugated plate packings[J]. Journal of Chemical Industry and Engineering, 1986, 37(4): 402-411. (in Chinese) |
| [9] |
裘俊红, 陈国标, 计建炳. 波纹板规整填料塔液体分布[J]. 化工学报, 2003, 54(5): 646-652. QIU Junhong, CHEN Guobiao, JI Jianbing. Liquid distribution in corrugated sheet structured packed column[J]. CIESC Journal, 2003, 54(5): 646-652. DOI:10.3321/j.issn:0438-1157.2003.05.015 (in Chinese) |
| [10] |
AROONWILAS A, CHAKMA A, TONTIWACHWUTHIKUL P, et al. Mathematical modelling of mass-transfer and hydrodynamics in CO2 absorbers packed with structured packings[J]. Chemical Engineering Science, 2003, 58(17): 4037-4053. DOI:10.1016/S0009-2509(03)00315-4 |
| [11] |
AROONWILAS A, TONTIWACHWUTHIKUL P. Mechanistic model for prediction of structured packing mass transfer performance in CO2 absorption with chemical reactions[J]. Chemical Engineering Science, 2000, 55(18): 3651-3663. DOI:10.1016/S0009-2509(00)00035-X |
| [12] |
PETRE C F, LARACHI F, ILIUTA I, et al. Pressure drop through structured packings: Breakdown into the contributing mechanisms by CFD modeling[J]. Chemical Engineering Science, 2003, 58(1): 163-177. DOI:10.1016/S0009-2509(02)00473-6 |
| [13] |
LARACHI F, PETRE C F, ILIUTA I, et al. Tailoring the pressure drop of structured packings through CFD simulations[J]. Chemical Engineering and Processing: Process Intensification, 2003, 42(7): 535-541. DOI:10.1016/S0255-2701(02)00073-9 |
| [14] |
RAYNAL L, ROYON-LEBEAUD A. A multi-scale approach for CFD calculations of gas-liquid flow within large size column equipped with structured packing[J]. Chemical Engineering Science, 2007, 62(24): 7196-7204. DOI:10.1016/j.ces.2007.08.010 |
| [15] |
AMINI Y, NASR ESFAHANY M. CFD simulation of the structured packings: A review[J]. Separation Science and Technology, 2019, 54(15): 2536-2554. DOI:10.1080/01496395.2018.1549078 |
| [16] |
CHOUDHURY D. Introduction to the renormalization group method and turbulence modeling[M]. Fluent Incorporated, 1973
|
| [17] |
RAYNAL L, BOYER C, BALLAGUET J P. Liquid holdup and pressure drop determination in structured packing with CFD simulations[J]. The Canadian Journal of Chemical Engineering, 2004, 82(5): 871-879. DOI:10.1002/cjce.5450820502 |
| [18] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5 |
| [19] |
BRACKBILL J U, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335-354. DOI:10.1016/0021-9991(92)90240-Y |
| [20] |
SHARMA R, SINGH K, SINGHAL D, et al. Neural network applications for detecting process faults in packed towers[J]. Chemical Engineering and Processing: Process Intensification, 2004, 43(7): 841-847. DOI:10.1016/S0255-2701(03)00103-X |
| [21] |
RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323: 533-536. DOI:10.1038/323533a0 |
| [22] |
KHOSRAVI NIKOU M R, EHSANI M R. Turbulence models application on CFD simulation of hydrodynamics, heat and mass transfer in a structured packing[J]. International Communications in Heat and Mass Transfer, 2008, 35(9): 1211-1219. DOI:10.1016/j.icheatmasstransfer.2008.05.017 |
| [23] |
谷芳, 刘春江, 袁希钢, 等. 板波纹规整填料液相分布模型[J]. 天津大学学报, 2005, 38(7): 586-591. GU Fang, LIU Chunjiang, YUAN Xigang, et al. Liquid distribution model for sheet corrugated structured packing[J]. Journal of Tianjin University, 2005, 38(7): 586-591. DOI:10.3969/j.issn.0493-2137.2005.07.005 (in Chinese) |
| [24] |
SUN B, HE L, LIU B, et al. A new multi-scale model based on CFD and macroscopic calculation for corrugated structured packing column[J]. AIChE Journal, 2013, 59(8): 3119-3130. DOI:10.1002/aic.14082 |
 2025, Vol. 42
2025, Vol. 42





