2. 天津海关动植物与食品检测中心, 天津 300402
2. The Animal, Plant & Foodstuff Inspection Center of Tianjin Customs, Tianjin 300402, China
结晶是一种重要的分离和纯化单元操作,已广泛地应用于化工、医药和精细化工等行业[1]。特别是在制药行业中,大部分的产品以固体的形式进行生产和销售,对这类产品质量的一致性要求也越来越高[2]。在药物晶体产品的流程开发上,生产者面临着来自监管和经济的双重挑战[3]。从监管的角度看,晶体产品的开发应基于对系统的过程理解和控制上,也确保晶体产品的质量符合“质量源于设计(QbD)”的理念,因此,必须获得与过程相关的充分信息,以确保质量和设计之间的相关性;从经济的角度看,结晶仍是一门“半科学与半艺术”的学科,结晶过程缺乏相应的成本效益控制和可靠的数学建模工具,可能需要消耗大量的时间和资源。因此,有必要建立结晶过程的模型,使其应用到结晶的设计与过程控制中,并据此制定一个更加高效而稳健的流程。
结晶过程主要包括2个基本步骤,即晶体成核过程和晶体生长过程。溶质从过饱和溶液析出到晶体的进一步生长,显著影响晶体的纯度、形态和粒度分布(CSD)等性质。而结晶系统的混合性能、质量和热量传递效果会直接影响结晶动力学过程(成核与生长)。因此,流体力学研究对于结晶过程以及晶体产品的精准控制至关重要。近些年来,随着计算机计算能力的提高,计算流体力学(CFD)依靠其独特优势,被广泛应用于结晶领域。此外,基于描述颗粒数量密度函数的粒数衡算方程(又称群体平衡方程PBE),结合结晶动力学模型能够预测晶体的尺寸分布。同时,为了解决非理想混合问题,可以将PBE与质量、动量和能量输运方程相结合,共同模拟晶体的尺寸与形态的演化过程,建立CFD-PBE耦合模型,为深入理解结晶过程提供新的思路和方法[4]。
1 粒数衡算方程及数值解法粒数衡算方程是一个用来描述颗粒数量密度函数的偏微分方程,在结晶过程中通常引入数密度函数(Number density function, NDF)的概念来表示颗粒群。NDF表示颗粒在任何时间和空间上所关注的属性上的数量分布n(t, x, ξ),这些属性可以是颗粒的尺寸与组成,也以是温度T、质量m等,这些属性称为颗粒的内坐标ξ。值得一提的是,如果内坐标为颗粒的速度v时,则粒数衡算方程(PBE)转变为普适性粒数衡算方程(GPBE)[5]。颗粒在t时刻的状态由其外部坐标x和内部坐标ξ共同确定,合称为颗粒的状态向量(x,ξ)。当内坐标不包含颗粒速度v时,在非均相体系中PBE写为以下形式[6]:
| $ \begin{gathered} \frac{\partial n(t, x, \boldsymbol{\xi})}{\partial t}+\frac{\partial\left[\boldsymbol{U}_{\mathrm{d}} n(t, x, \boldsymbol{\xi})\right]}{\partial x}+ \\ \frac{\partial[\boldsymbol{G} n(t, x, \boldsymbol{\xi})]}{\partial \boldsymbol{\xi}}=B+S \end{gathered} $ | (1) |
式(1)中:Ud表示颗粒的速度;G表示颗粒的生长或溶解速率;B表示成核速率。S是方程源项,表示由于颗粒聚集或破碎引起的颗粒净生成率,一般分为零阶、一阶和二阶过程。其中,零阶表示不存在聚集或破碎,一阶表示只存在聚集的情况或只存在破碎,二阶表示聚集和破碎同时存在。对于一维PBE(即只考虑一个内坐标的情况),且内坐标为颗粒质量或体积时,源项S写为:
| $ \begin{gathered} S(\boldsymbol{\xi})=B^{\mathrm{a}}-D^{\mathrm{a}}+B^{\mathrm{b}}-D^{\mathrm{b}}= \\ \frac{1}{2} \int_0^{\boldsymbol{\xi}} a\left(\boldsymbol{\xi}-\boldsymbol{\xi}^{\prime}, \boldsymbol{\xi}\right) n\left(\boldsymbol{\xi}-\boldsymbol{\xi}^{\prime}\right) n(\boldsymbol{\xi}) \mathrm{d} \boldsymbol{\xi}^{\prime}- \\ n(\boldsymbol{\xi}) \int_0^{\infty} a\left(\boldsymbol{\xi}, \boldsymbol{\xi}^{\prime}\right) n\left(\boldsymbol{\xi}^{\prime}\right) \mathrm{d} \boldsymbol{\xi}^{\prime}+ \\ \int_{\boldsymbol{\xi}}^{\infty} b\left(\boldsymbol{\xi}^{\prime}\right) \beta\left(\boldsymbol{\xi} \mid \boldsymbol{\xi}^{\prime}\right) n\left(\boldsymbol{\xi}^{\prime}\right) \mathrm{d} \boldsymbol{\xi}^{\prime}-b(\boldsymbol{\xi}) n(\boldsymbol{\xi}) \end{gathered} $ | (2) |
式(2)中:a(ξ, ξ′)表示内坐标为ξ和ξ′的颗粒聚集率(核);b(ξ)表示内坐标为ξ的颗粒破碎率(核);β(ξ|ξ′)为内坐标为ξ′的颗粒破碎为ξ后的NDF子分布。Ba、Da分别表示由于聚集而造成的颗粒生成率和损失率;Bb、Db分别表示由于破碎而造成的颗粒生成率和损失率,依次对应等号最右侧的4项。颗粒的聚集与破碎受流体力学环境的影响很大,如在搅拌釜中结晶时,在叶轮附近的高剪切力区域,晶体颗粒会经历更强的破碎过程,而在其他低剪切力的区域,晶体颗粒可能经历更多的聚集过程。所以聚集核和破碎核函数高度依赖于外坐标,此时破碎和聚集可能对方程(1)起到主要的控制作用。
一般而言,PBE足以完成结晶过程的模拟,但结合方程(1)和方程(2)来看,PBE是一个典型的双曲型积分-偏微分方程,只有在非常严格的假定下,PBE具有解析解[7, 8]。所以通常情况下,需要采用数值解法对PBE进行求解。目前开发的方法包括矩量法(MOM)、分组法(CM)、加权残差法(WRM)和一些随机方法等[9-11]。下面重点综述了矩量法和分组法在求解粒数衡算方程中的应用。
1.1 矩量法MOM矩量法最开始由Randolph[12]及Hulburt等[13]提出。该方法并不直接跟踪NDF,而是通过在内坐标上积分的矩量来跟踪,将PBE转换为一系列的NDF矩量输运方程。利用这些矩量,可以计算得到颗粒分布的整体属性,如颗粒数量、表面积、体积、平均尺寸和变异系数等信息。例如,k阶矩量定义为:
| $ \begin{gathered} m_{k_1, k_2, \cdots, k_d}(t, \boldsymbol{x})= \\ \int_{\Omega_{{\boldsymbol{\xi}}}} \xi_1^{k_1} \xi_2^{k_2} \cdots \xi_d^{k_d} u_1^{k_{d+1}} u_2^{k_{d+2}} u_3^{k_{d+3}} n(t, \boldsymbol{x}, \boldsymbol{\xi}) \mathrm{d} \boldsymbol{\xi} \end{gathered} $ | (3) |
式(3)中:Ωξ为内坐标的域,k=k1, k2, …, kd表示相应内坐标下的矩量的阶数。可以看出,矩量是时间和空间的函数,矩量法与CFD中现有的求解方法完全兼容。并且,低阶矩量与颗粒的一些宏观性质相关,例如当内坐标仅为粒径时,m0表示颗粒的总数目,m1表示颗粒的粒径,m2表示颗粒的总面积,m3表示颗粒的总体积。此时,矩量输运方程可表示为:
| $ \begin{gathered} \frac{\partial m_k}{\partial t}+\frac{\partial\left(\boldsymbol{U}_{\mathrm{d}, k} m_k\right)}{\partial x}=(0)^k B(t, x)+ \\ \int_0^{\infty} k L^{k-1} G(L) n(L) \mathrm{d} L+\overline{B_k^a}-\overline{D_k^a}+\overline{B_k^b}-\overline{D_k^b} \end{gathered} $ | (4) |
式(4)中:B(t, x)为成核速率,
McGraw[16]提出,可以通过N个节点的高斯求积公式来近似矩量输运方程的未封闭项,即正交矩量法QMOM。假设以下形式来逼近NDF:
| $ n(t, {\boldsymbol{x}}, {\boldsymbol{\xi}}) \approx \sum\limits_{p=1}^N \omega_p(t, {\boldsymbol{x}}) \delta\left[\xi-\xi_p(t, {\boldsymbol{x}})\right] $ | (5) |
式(5)中:ωp(t, x)和ξp(t, x)是正交节点p的权重和坐标。δ表示Dirac delta函数,此时NDF的k阶矩可以近似表示为:
| $ m_k=\int_{\mathbb{R}^{+}} \xi^k n(\xi) \mathrm{d} \xi \approx \sum\limits_{p=1}^N \omega_p \xi_p^k $ | (6) |
式(6)中:
| $ \begin{gathered} \frac{\partial m_k}{\partial t}+\frac{\partial\left(\boldsymbol{U}_{\mathrm{d}, k} m_k\right)}{\partial x}=\delta_{k, 0} G(0) n(0)+ \\ k \int_{\mathbb{R}^{+}} \xi^{k-1} G n \mathrm{~d} \xi+\int_{\mathbb{R}^{+}} \xi^k \operatorname{Sd} \xi \end{gathered} $ | (7) |
式(7)中:δk, 0为Kronecker delta符号,Ud, k表示k阶矩的传输速度,定义为:
| $ \boldsymbol{U}_{\mathrm{d}, k}=\frac{1}{m_k} \int_{\mathbb{R}^{+}} \xi^k \boldsymbol{U}_{\mathrm{d}}(\xi) n \mathrm{~d} \xi $ | (8) |
虽然QMOM方法多数情况下是为气溶胶的研究而开发[19, 20],但可以扩展到结晶过程的研究中,并在耦合CFD与PBE方面显示出了显著优势[21-23]。如Marchisio等使用QMOM对晶体破碎进行建模,得到了不同聚集破碎核函数、子分布和初始条件下的计算结果,并与Vanni等[24]利用CM方法得到的结果进行了比较。结果表明,QMOM能够以较小的误差预测多个矩量。在上述研究基础上,Jin等[25]对QMOM算法进行改进,该算法提高了QMOM求解的鲁棒性,并且在高阶矩量的求解上表现优异。
然而,QMOM存在2个比较严重的问题,一是对于内坐标和颗粒速度存在强耦合的多相分散体系,仅仅通过求解矩量方程难以得到准确的数值解;二是对于多维PBE,使用QMOM方法来求解十分复杂和低效。因此,在这个基础上,又发展出了许多新的方法,如直接正交矩量法(DQMOM)和拓展正交矩量法(EQMOM)[14, 26, 27]。Selma等[28]在OpenFOAM中植入了CM和DQMOM,对鼓泡塔和搅拌釜中的多相流动进行建模。结果表明,在平均轴向速度、气含率和气泡直径方面,数值计算与实验结果均吻合较好,且DQMOM的计算成本明显低于CM[29, 30]。Askari等[31]在OpenFOAM中采用EQMOM对径向和轴向2种搅拌釜的气液两相流动进行了数值模拟,数值结果在轴向和径向液体速度分布和溶解氧的浓度变化方面与实验结果相吻合[32]。此外,条件正交矩量法[33, 34](CQMOM)也是一种基于条件密度函数(CDF)的数值解法,适用于多维PBE的算法,并可以处理具有多个内部坐标的复杂体系。
综上,目前已经开发了大量的矩量法来解决一维或多维PBE,证明其是一种有效地求解PBE的方法,特别是在与CFD相结合的方面,矩量法可以在计算精度和计算资源之间取得了很好的平衡[35]。但由于矩量法不能直接预测NDF,其自身的局限性与面临的数值挑战依然存在,未来仍需进一步地研究更加健壮而高效的算法。
1.2 分组法CM分组法也称为离散法,其基本思想是将颗粒的内坐标划分为若干个相邻的子区间,每个小区间的颗粒群用一个代表节点表示,在每个子区间内分别进行积分,从而将PBE转化为一系列离散的方程组。假设将内坐标ξ使用M+1个网格点划分为M个区间(ξ1, ξ2, …, ξM+1),将第i个区间定义为Ii=[ξi, ξi+1],则区间内的NDF为:
| $ N_i(t, \boldsymbol{x})=\int_{\xi_i}^{\xi_{i+1}} n(t, \boldsymbol{x}, \boldsymbol{\xi}) \mathrm{d} \xi $ | (9) |
离散化的PBE为:
| $ \frac{\partial N_i}{\partial t}+\frac{\partial\left(\boldsymbol{U}_i N_i\right)}{\partial x}+\int_{\xi_i}^{\xi_{i+1}} \frac{\partial(G n)}{\partial \xi} \mathrm{d} \xi=\int_{\xi_i}^{\xi_{i+1}} S \mathrm{~d} \xi $ | (10) |
为了封闭方程(10),Kumar和Ramkrishna提出了式(11)[36, 37]。
| $ n(t, {\boldsymbol{x}}, \xi)=\sum\limits_{i=1}^M N_i \delta\left(\xi-\zeta_i\right) $ | (11) |
然而,上述公式在聚集破碎存在时通常难以保证积分性质守恒。为此,Kumar等[36]提出了固定节点法(Fixed pivot method),通过将聚集或破碎产生的新颗粒按一定的比例将其分别分配到邻近的节点处,从而保证颗粒的总个数和总质量守恒,并且可以用于任意的网格类型,是目前使用最广泛的方法。另外,Alopaeus等[30]提出,将新颗粒分配到2个以上的节点处时,可以进一步提高守恒特性。然而,固定节点法虽然对低阶矩的数值计算结果比较精确,但是对大颗粒数密度和高阶矩的预测经常偏高,特别是在存在聚集的情况下。因此,Kumar等[38, 39]随后提出了移动节点法(Moving pivot)和单元平均法(Cell average method)来解决这一问题,该方法在很大程度上缓解了固定节点法预测偏高的问题。
在数值求解PBE时,需要考虑这些尖锐的界面和不连续性对数值解的影响,以确保数值解的准确性和稳定性[40]。所以,必须谨慎处理方程(10)的对流生长项,以避免引入人工黏性[41, 42]。一方面可以使用限制器,如MUSCL限制器和WENO限制器,这些限制器可以在界面处自适应地调整数值解,以避免数值振荡和人工黏性的出现,从而保持解的高精度。Jiang等[43]提出了一种与五阶Runge-Kutta方案结合的WENO格式,它允许以非常小的时间步长进行高效率求解,并在结晶过程中得到了一些应用[44, 45]。另一方面可以使用高分辨率数值方法,如高分辨率有限体积法和高分辨率有限差分法,这些方法可以有效地处理尖锐的界面或不连续性,同时保持解的高精度。Kurganov等[40]提出了一种高分辨率有限体积格式(K-T格式),由于该方法满足minmod重构的全标量递减特性,因此不会产生非物理振荡。在此基础上,Cheng等[46]将其扩展到通用化的形式,如通用K-T高精度有限体积中心差分格式,以便用于均匀或几何离散的内网格中。相对于迎风差分格式,特别是在颗粒比较大时,K-T高精度有限体积中心差分法计算精度的提升较为显著。
综上,相比于矩量法,分组法的优势在于可以直接预测连续的NDF,缺点在于为了捕捉完整的NDF分布,可能需要将内坐标离散成大量的组,计算成本高。但随着计算机技术的飞速发展,在可预见的未来内算力将得到快速提升,分组法也将获得更好的应用前景。
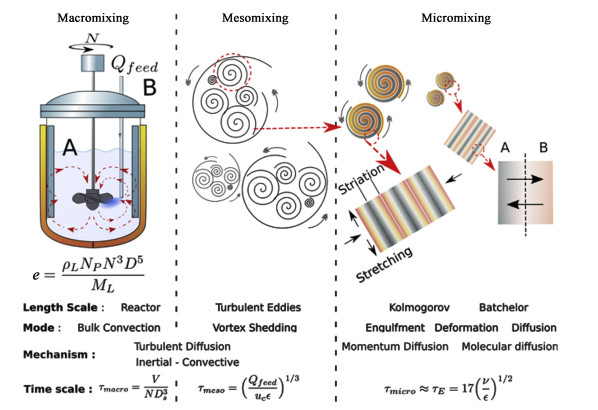
2 CFD-PBE在结晶过程数值模拟中应用对结晶过程的CFD模拟主要集中在溶析结晶和反应结晶过程中,CFD模型包括不同尺度的混合,即微观混合、介观混合和宏观混合。以搅拌釜为例,图 1展示了湍流状态下不同尺度的混合效应[47]。由于微观混合能够在分子水平上影响着溶质与溶剂分子的扩散程度和体系的过饱和度,因此其直接影响晶体的成核和生长过程,并决定产品的纯度、粒度晶体形貌等质量指标。
CFD中的宏观混合模型主要由湍流输运方程组成,对微观混合有重要的间接影响,即微观混合和宏观混合是相互依赖。此外,在CFD框架中介观混合通常被归入宏观混合,而微观混合模型成为宏观混合的子网格建模组件。因此,当采用CFD方法来描述宏观输送时,必须包括相互兼容的微观混合建模。在反应和溶析结晶过程研究中,常用的微混合模型包括涡流卷吸模型(E模型)和基于联合组成概率密度函数模型(PDF)模型[48-53]。
2.1 溶析结晶溶析结晶由于不产生较大的温度变化而有利于热敏性药物的结晶,尤其广泛应用于制药行业中以生产粒径小而分布窄的晶体[54]。由于此方法需要将溶析剂与溶液快速而充分地混合,因此基于CFD可以获得对结晶过程中混合效应的深入理解。目前,科研人员已经对混合在溶析结晶过程中的影响进行了细致的研究工作,主要集中在结晶器基础设计和模拟方法优化改进2个方面。
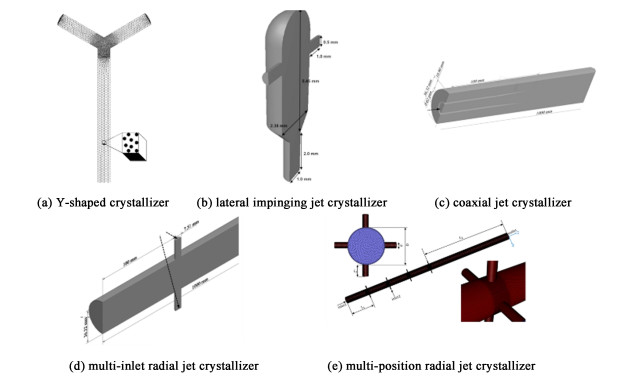
结晶器设计方面,近年来先后开发了Y型结晶器、同轴射流结晶器以及多种横向、径向撞击射流结晶器等,如图 2所示。Choi等[55]采用CFD-PBE的方法,利用矩量法求解了PBE并模拟了环四亚甲基四硝胺在小型的Y型结晶器[图 2(a)]中的稳态溶析结晶。在不考虑微混合的条件下研究了速度比、过饱和度、平均晶体尺寸和变异系数的空间分布,发现即使在小型的结晶器中,混合效应依旧显著。Woo等[56]采用CFD-PBE-PDF方法,研究了洛伐他汀在横向撞击射流结晶器[图 2(b)]的溶析结晶。结果表明,微混合对CSD的影响取决于微混合特征时间和结晶诱导时间的相对大小。Pirkle等[49]在Woo的基础上,同样采用CFD-PBE-PDF的方法考虑了混合热与结晶热的影响,模拟了洛伐他汀在同轴射流结晶器[图 2(c)]中的溶析结晶过程。结果表明,较高的流量带来较短的停留时间和高雷诺数,从而得到较窄的CSD分布和较小的颗粒平均尺寸。Rosa等[48]提出了一种多入口径向结晶器的新设计[图 2(d)],与只有1个入口的径向结晶器相比,多个入口的设计提供了更好的混合。Chen等[57]在此基础上进行改进,将多入口径向结晶器扩展到多位置入口的径向结晶器的设计[图 2(e)],结果表明,多位置进料点的设计有助于在保持良好混合的同时,降低局部过饱和度从而获得更窄的CSD和更大的平均晶体尺寸。上述研究表明,采用CFD-PBE耦合方法是溶析结晶器开发的有力工具,为获得粒度均匀的晶体,径向撞击射流结晶器是撞击流结晶器发展的新方向。
上述工作虽然采用了CFD-PBE耦合方法对溶析结晶过程进行了数值模拟,然而模拟过程均是在拟均相假设下进行的。为了进一步提升模拟准确性,Cheng等[46, 58]采用CFD-PBE-PDF方法基础上,进一步考虑了颗粒和溶液间的相互作用,采用Mixture-欧拉多相流模型的模拟了洛伐他汀在横向射流结晶器中的溶析结晶过程。结果表明,随颗粒尺寸增大,颗粒与溶液间的相互作用不可忽视,拟均相假设的偏离逐渐增大。在此基础上,Farias等[59]提出了耦合PBE的欧拉-欧拉模型来模拟同轴结晶器中的冷却-溶析结晶过程。结果表明,溶剂与溶析剂的质量分数、成核生长速率的分布可能是不对称的,且入口处的进料速度对最终粒度分布产生显著影响。总之,在工业规模的计算中,拟均相假设因其计算量小而被大规模使用,但这是以牺牲计算精度为前提的。随着计算机能力的提升,在计算中需充分考虑颗粒间相互作用,无论是采用基于欧拉框架的CFD-PBE-PDF方法还是基于拉格朗日框架下的MP-PIC-PE方法,都将是未来溶析结晶建模的主流方法。
2.2 反应结晶早在1958年,Danckwerts[60]便讨论了混合对反应结晶的影响。当特征反应时间小于特征混合时间或两者处在相同数量级时,混合效应对反应结晶中悬浮液的性质、颗粒产品的产率、纯度等许多方面产生显著影响。如Wei等[61]采用CFD-PBE模型模拟了半间歇搅拌釜中BaSO4的反应结晶过程,得到的晶体平均尺寸随转速变化与实验结果相差接近4倍。Jaworski等[62]采用CFD-PBE方法对双进料连续搅拌釜中BaSO4反应结晶过程进行了建模,但与实验结果存在较大偏差。以上模拟结果的偏差主要是因为未考虑微混合效应且采用SMOM方法求解PBE,忽略了结晶过程中的聚集和破碎过程。
针对这一问题,Cheng等[63]对同样双进料搅拌釜中的BaSO4反应结晶进行CFD-PBE建模,利用QMOM方法对PBE求解,考虑了聚集和破碎的过程。结果表明,在较高进料浓度下,模拟值与实验值偏差较大。随后Cheng等[64]利用离散法求解PBE,得到了完整的CSD,但与实验结果的CSD相比峰值略大,且分布略宽。以上研究工作中模拟结果与实验结果的偏差,主要是由于双进料口距离较远和预混合进料的原因,并未考虑微混合效应对实验的影响[63, 64]。在此基础上,Marchisio等[65, 66]采用CFD-PBE-PDF方法对BaSO4反应结晶进行建模。结果表明,在不考虑颗粒聚集时,高浓度反应物下的模拟结果较差,而考虑颗粒间的聚集效应后,得到了更好的结果。这也证明BaSO4反应结晶中,聚集破碎现象明显,在高浓度体系下甚至主导了产品质量。为了更好地描述聚集破碎问题对结晶过程的影响,Bal等[67]开发了一个包含混合、反应成核、生长、聚集和Ostwald熟化的耦合CFD-PBE模型,能够在广泛的操作条件下预测二氧化硅纳米颗粒的大小。
从上述研究工作结果中可以看出,相比于溶析结晶,反应结晶过程中的聚集和破碎现象更加常见,因此除了要关注微混合效应,对晶体聚集和破碎的建模也更加重要。因此,对CFD-PBE耦合模型的完善和计算方法的改进仍需加以深入探讨和研究。
3 CFD-PBE耦合模拟在结晶器放大设计中的应用在实验室规模的结晶器中,通常能够达到良好的混合进而有利于质量和热量的传递,且整个溶液中的过饱和度几乎保持一致。然而,随着结晶器从实验室规模增大到工业规模,流动、混合、传质和传热的一致性放大成为一个巨大的挑战。为了实现这一目标,这就需要对结晶器的工业放大实现模型化和数字化。
结晶过程的准确放大需要充分了解混合及其对结晶过程中关键性能的影响。对于冷却结晶过程,其主要受传热影响,微观和宏观混合影响通常较小。但与之相比,溶析结晶和反应结晶受微观混合的影响最大,结晶器中的流体力学决定了流动、传质、传热以及晶体的分散特性。同时,在溶析和反应结晶过程中涉及众多影响过饱和度分布和产品质量的关键工艺参数,如溶析剂添加方式、反应物混合方式、混合速度和结晶器型式等。因此,在溶析结晶和反应结晶放大过程需重点对流体力学性质进行系统研究。此外,结晶器的设计参数和操作参数决定了流体力学特性,因此,在相应结晶设备开发过程中同样需要重点关注设备特点对流体力学的影响,包括(1)结晶器几何形状(尺寸、纵横比等);(2)结晶器内部配置(叶轮和挡板类型、尺寸、位置、数量等);(3)溶液和晶体的物理化学属性;(4)操作参数(转速,填充率,进料速率、位置,流速等)。前文主要综述了CFD-PBE耦合技术应用于辅助实验研究和实验过程设计,而CFD在辅助结晶器放大过程中同样发挥了十分重要的作用,有助于加深对结晶过程理解、缩短开发周期、降低开发成本、优化结晶器设计等。
Kramer等[68]对工业结晶器进行了系统研究,提出了工业结晶器的设计和放大策略:对于溶析结晶,溶析剂的添加速率起主要控制作用,并且需要注意由于溶析剂与溶液的混合产生的热效应。对于反应结晶过程,反应物的添加速率和反应热是影响放大的关键参数。以结晶中最常见的DTB结晶器为例,Zaunr等[69]开发了一种半间歇和连续操作下,双进料反应结晶DTB结晶器的CFD-PBE模型,在实验室规模下测定了结晶动力学,并将模拟结果与不同规模的结晶器中获得的实验数据进行对比。结果表明,当结晶由微观或介观尺度的混合控制时,恒定搅拌速率、恒定叶尖速度和恒定的比功率等常规的放大策略不可行。针对这一问题,Oh等[70]通过实验和CFD模拟研究了500和300 L的DTB溶析结晶器的放大,证明叶尖速度、Froude数和比功率是主要放大标准。并指出双引流管的DTB比单引流管DTB轴向流动可获得充分发展,因而可以获得更均匀的混合效果,表现出更好的性能(如图 3所示)。
但从上述2个案例中看出,恒定叶尖速度、恒定比功率输入,在结晶器放大过程中也并不是都适用的,不同的操作条件,不同的结晶方式都对结晶器放大产生着影响。这是因为目前对于结晶器放大设计过程中,大多是基于实验-整体放大-CFD建模的策略,其中一个重要的因素是保持结晶器的几何相似性。理想情况下,混合、悬浮、流体剪切、传热等指标在放大时都应该保持恒定。但实际情况是,保持一项指标恒定的同时总会使其他指标发生变化。因此,这些指标往往是相互制衡的,很难实现所有指标的恒定。针对几何相似放大的问题,需要明确并非要对所有指标进行复现,许多结晶过程并不是对这些指标都很敏感,这可以大大简化放大工作。因此,未来的研究工作中,可以在放大之前通过中等规模的实验与CFD模拟,明确敏感变量,进而为放大工作提供理论基础。此外,还可以考虑放弃几何相似的制约,便于使不同结构、不同尺寸的结晶器中有更多的参数保持一致。
4 总结与展望综述了用于结晶过程的数值模拟的PBE与CFD耦合求解的几种数值方法,重点介绍了矩量法与分组法。在此基础上,综述了CFD-PBE方法在溶析结晶与反应结晶过程模拟以及结晶器设备放大领域的研究进展。整体来看,虽然直接数值模拟可以获得不同结晶方式条件下全尺度上的混合信息,但在目前的计算能力下,仍然需要附加额外的微混合模型来建模。此外,尽管我们可以通过几何相似性来复制一些参数,但在不同规模下,流体力学特性、传质特性、混合过程等因素给设备放大开发带来诸多挑战。同时,晶体的形成过程也受到初始溶液浓度、温度、pH值、添加剂等因素的影响,这使得从实验室到工业规模的放大更加困难。
因此,虽然CFD在辅助结晶过程开发和结晶器设计上是一个强有力的工具,然而目前研究仍存在一定不足,未来的研究中可重点关注以下几方面:首先,在利用矩量法求解PBE时,仍然需要建立更加稳健高效的算法来解决从低阶矩量重构CSD的问题;而在分组法上,虽然计算能力的提升促进了分组法的发展,但求解聚集破碎和生长的数值方法的提升依然是一个挑战。其次,将一维PBE扩展到多维PBE也是一项重要的工作,利用计算流体力学技术模拟晶体的尺寸和晶习是未来结晶过程模拟的一个重要研究方向。最后,在结晶器放大设计中,进行多尺度的CFD-微混合-PBE建模可以更深入地揭示结晶过程中流体动力学和结晶动力学之间的相互作用机理,帮助我们建立更准确的放大策略。
| [1] |
WANG T, LU H, WANG J, et al. Recent progress of continuous crystallization[J]. Journal of Industrial and Engineering Chemistry, 2017, 54: 14-29. DOI:10.1016/j.jiec.2017.06.009 |
| [2] |
陈奎, 王静康, 冯瑶光, 等. 连续管式结晶器研究进展[J]. 化学工业与工程, 2022, 39(6): 36-53. CHEN Kui, WANG Jingkang, FENG Yaoguang, et al. Development of continuous tubular crystallizer[J]. Chemical Industry and Engineering, 2022, 39(6): 36-53. DOI:10.13353/j.issn.1004.9533.20220125 (in Chinese) |
| [3] |
陈铭宇. 扑热息痛结晶过程研究[D]. 天津: 天津大学, 2021 CHEN Mingyu. Study on the crystallization process of paracetamol[D]. Tianjin: Tianjin University, 2021(in Chinese) |
| [4] |
傅笑言. 基于CFD耦合的扑热息痛结晶过程模拟与优化研究[D]. 天津: 天津大学, 2018 FU Xiaoyan. CFD-coupled modeling and optimization of crystallization for production of paracetamol[D]. Tianjin: Tianjin University, 2018(in Chinese) |
| [5] |
LI D, LI Z, GAO Z. Quadrature-based moment methods for the population balance equation: An algorithm review[J]. Chinese Journal of Chemical Engineering, 2019, 27(3): 483-500. DOI:10.1016/j.cjche.2018.11.028 |
| [6] |
JAIN S S, ALI M N. A computational model for transport of immiscible scalars in two-phase flows[J]. Journal of Computational Physics, 2023, 476: 111843. DOI:10.1016/j.jcp.2022.111843 |
| [7] |
WU S, YANG S, TAY K L, et al. A hybrid sectional moment projection method for discrete population balance dynamics involving inception, growth, coagulation and fragmentation[J]. Chemical Engineering Science, 2022, 249: 117333. DOI:10.1016/j.ces.2021.117333 |
| [8] |
LEHNIGK R, BAINBRIDGE W, LIAO Y, et al. An open-source population balance modeling framework for the simulation of polydisperse multiphase flows[J]. AIChE Journal, 2022, 68(3): e17539. DOI:10.1002/aic.17539 |
| [9] |
SINGH M, WALKER G. New discrete formulation for reduced population balance equation: An illustration to crystallization[J]. Pharmaceutical Research, 2022, 39(9): 2049-2063. DOI:10.1007/s11095-022-03349-0 |
| [10] |
屈雪婧, 安敏, 管小平, 等. 气液鼓泡塔的CFD-PBM耦合模拟: 离散法与QMOM方法的对比[J]. 过程工程学报, 2020, 20(7): 788-797. QU Xuejing, AN Min, GUAN Xiaoping, et al. Comparison of discrete method and QMOM in CFD-PBM simulation of gas-liquid bubble column[J]. The Chinese Journal of Process Engineering, 2020, 20(7): 788-797. (in Chinese) |
| [11] |
SHIEA M, BUFFO A, VANNI M, et al. Numerical methods for the solution of population balance equations coupled with computational fluid dynamics[J]. Annual Review of Chemical and Biomolecular Engineering, 2020, 11: 339-366. |
| [12] |
RAMKRISHNA D. Population balances theory and applications to particulate systems in engineering[M]. San Diego: Academic Press, 2000.
|
| [13] |
HULBURT H M, KATZ S. Some problems in particle technology[J]. Chemical Engineering Science, 1964, 19(8): 555-574. |
| [14] |
KUMAR S D, BRITO-PARADA PABLO R, GAURAV B. An open-source computational framework for the solution of the bivariate population balance equation[J]. Computers and Chemical Engineering, 2022, 161: 107780. DOI:10.1016/j.compchemeng.2022.107780 |
| [15] |
SUN F, LIU T, NAGY Z K, et al. Extended sectional quadrature method of moments for crystal growth and nucleation with application to seeded cooling crystallization[J]. Chemical Engineering Science, 2022, 254: 117625. DOI:10.1016/j.ces.2022.117625 |
| [16] |
SCHÄFER J, HLAWITSCHKA M W, ATTARAKIH M M, et al. Experimental investigation of local bubble properties: Comparison to the sectional quadrature method of moments[J]. AIChE Journal, 2019, 65(10): e16694. DOI:10.1002/aic.16694 |
| [17] |
GORDON R G. Error bounds in equilibrium statistical mechanics[J]. Journal of Mathematical Physics, 1968, 9(5): 655-663. DOI:10.1063/1.1664624 |
| [18] |
WHEELER J C. Modified moments and Gaussian quadratures[J]. Rocky Mountain Journal of Mathematics, 1974, 4(2): 287-296. |
| [19] |
MOSBACH S, KRAFT M, ZHANG H R, et al. Towards a detailed soot model for internal combustion engines[J]. MTZ Worldwide, 2009, 70(5): 44-48. DOI:10.1007/BF03226953 |
| [20] |
RAJ A, CELNIK M, SHIRLEY R, et al. A statistical approach to develop a detailed soot growth model using PAH characteristics[J]. Combustion and Flame, 2009, 156(4): 896-913. DOI:10.1016/j.combustflame.2009.01.005 |
| [21] |
JAMAL D, ALI J, SHAHRIAR T. A hybrid compartmental-CFD model to investigate forced circulation crystallizer performance[J]. Desalination, 2022, 533: 115743. DOI:10.1016/j.desal.2022.115743 |
| [22] |
ZHANG H, SAYYAR A, WANG Y, et al. Generality of the CFD-PBM coupled model for bubble column simulation[J]. Chemical Engineering Science, 2020, 219: 115514. DOI:10.1016/j.ces.2020.115514 |
| [23] |
GKOGKOS G, BESENHARD M O, STOROZHUK L, et al. Fouling-proof triple stream 3D flow focusing based reactor: Design and demonstration for iron oxide nanoparticle co-precipitation synthesis[J]. Chemical Engineering Science, 2022, 251: 117481. DOI:10.1016/j.ces.2022.117481 |
| [24] |
VANNI M. Approximate population balance equations for aggregation-breakage processes[J]. Journal of Colloid and Interface Science, 2000, 221(2): 143-160. DOI:10.1006/jcis.1999.6571 |
| [25] |
JIN C, WANG Y, SUN F, et al. Augmented quadrature method of moments for solving population balance equations of industrial crystallization processes[C]//2019 Chinese Automation Congress (CAC). Hangzhou, China. IEEE, 2019: 5724-5729
|
| [26] |
YUAN C, LAURENT F, FOX R O. An extended quadrature method of moments for population balance equations[J]. Journal of Aerosol Science, 2012, 51: 1-23. DOI:10.1016/j.jaerosci.2012.04.003 |
| [27] |
FOX R O, LAURENT F, PASSALACQUA A. The generalized quadrature method of moments[J]. Journal of Aerosol Science, 2023, 167: 106096. DOI:10.1016/j.jaerosci.2022.106096 |
| [28] |
SELMA B, BANNARI R, PROULX P. Simulation of bubbly flows: Comparison between direct quadrature method of moments (DQMOM) and method of classes (CM)[J]. Chemical Engineering Science, 2010, 65(6): 1925-1941. DOI:10.1016/j.ces.2009.11.018 |
| [29] |
LIANG H, LI W, FENG Z, et al. Numerical simulation of gas-liquid flow in the bubble column using Wray-Agarwal turbulence model coupled with population balance model[J]. Chinese Journal of Chemical Engineering, 2023, 58: 205-223. DOI:10.1016/j.cjche.2022.11.001 |
| [30] |
ALOPAEUS V, LAAKKONEN M, AITTAMAA J. Solution of population balances with breakage and agglomeration by high-order moment-conserving method of classes[J]. Chemical Engineering Science, 2006, 61(20): 6732-6752. DOI:10.1016/j.ces.2006.07.010 |
| [31] |
ASKARI E, ST-PIERRE LEMIEUX G, PROULX P. Application of extended quadrature method of moments for simulation of bubbly flow and mass transfer in gas-liquid stirred tanks[J]. The Canadian Journal of Chemical Engineering, 2019, 97(9): 2548-2564. DOI:10.1002/cjce.23470 |
| [32] |
DEEN N G, SOLBERG T, HJERTAGER B H. Flow generated by an aerated rushton impeller: Two-phase PIV experiments and numerical simulations[J]. The Canadian Journal of Chemical Engineering, 2002, 80(4): 1-15. |
| [33] |
LAVINO A D, FERRARI M, BARRESI A A, et al. Effect of different good solvents in flash nano-precipitation via multi-scale population balance modeling-CFD coupling approach[J]. Chemical Engineering Science, 2021, 245: 116833. DOI:10.1016/j.ces.2021.116833 |
| [34] |
VAN CAPPELLEN M, VETRANO M R, LABOUREUR D. Higher order hyperbolic quadrature method of moments for solving kinetic equations[J]. Journal of Computational Physics, 2021, 436: 110280. DOI:10.1016/j.jcp.2021.110280 |
| [35] |
SINGH M, RANADE V, SHARDT O, et al. Challenges and opportunities concerning numerical solutions for population balances: A critical review[J]. Journal of Physics A: Mathematical and Theoretical, 2022, 55(38): 383002. DOI:10.1088/1751-8121/ac8a42 |
| [36] |
KUMAR S, RAMKRISHNA D. On the solution of population balance equations by discretization—Ⅰ. A fixed pivot technique[J]. Chemical Engineering Science, 1996, 51(8): 1311-1332. DOI:10.1016/0009-2509(96)88489-2 |
| [37] |
BURNS M, SHEEHAN M, SCHNEIDER P A. Nucleation and crystal growth kinetic parameter optimization of a continuous Poiseuille flow struvite crystallizer using a discretized population balance and dynamic fluid model[J]. Chemical Engineering Journal, 2021, 405: 126607. DOI:10.1016/j.cej.2020.126607 |
| [38] |
KUMAR J, PEGLOW M, WARNECKE G, et al. Improved accuracy and convergence of discretized population balance for aggregation: The cell average technique[J]. Chemical Engineering Science, 2006, 61(10): 3327-3342. DOI:10.1016/j.ces.2005.12.014 |
| [39] |
KUMAR J, PEGLOW M, WARNECKE G, et al. An efficient numerical technique for solving population balance equation involving aggregation, breakage, growth and nucleation[J]. Powder Technology, 2008, 182(1): 81-104. DOI:10.1016/j.powtec.2007.05.028 |
| [40] |
KURGANOV A, TADMOR E. New high-resolution central schemes for nonlinear conservation laws and convection—Diffusion equations[J]. Journal of Computational Physics, 2000, 160(1): 241-282. DOI:10.1006/jcph.2000.6459 |
| [41] |
ALZYOD S, CHARTON S. A meshless Radial Basis Method (RBM) for solving the detailed population balance equation[J]. Chemical Engineering Science, 2020, 228: 115973. DOI:10.1016/j.ces.2020.115973 |
| [42] |
BRAATZ R D. Advanced control of crystallization processes[J]. Annual Reviews in Control, 2002, 26: 87-99. DOI:10.1016/S1367-5788(02)80016-5 |
| [43] |
JIANG G, SHU C. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 |
| [44] |
HERMANTO M W, BRAATZ R D, CHIU M S. High-order simulation of polymorphic crystallization using weighted essentially nonoscillatory methods[J]. AIChE Journal, 2009, 55(1): 122-131. DOI:10.1002/aic.11644 |
| [45] |
RUAN C L, LIANG K, CHANG X, et al. Weighted essentially nonoscillatory method for two-dimensional population balance equations in crystallization[J]. Mathematical Problems in Engineering, 2013, 2013: 125128. |
| [46] |
CHENG J, YANG C, JIANG M, et al. Simulation of antisolvent crystallization in impinging jets with coupled multiphase flow-micromixing-PBE[J]. Chemical Engineering Science, 2017, 171: 500-512. DOI:10.1016/j.ces.2017.06.011 |
| [47] |
TEYCHENÉ S, RODRÍGUEZ-RUIZ I, RAMAMOORTHY R K. Reactive crystallization: From mixing to control of kinetics by additives[J]. Current Opinion in Colloid & Interface Science, 2020, 46: 1-19. |
| [48] |
DA ROSA C A, BRAATZ R D. Multiscale modeling and simulation of macromixing, micromixing, and crystal size distribution in radial mixers/crystallizers[J]. Industrial & Engineering Chemistry Research, 2018, 57(15): 5433-5441. |
| [49] |
OREHEK J, TESLIĆ D, LIKOZAR B. Mechanistic modeling of a continuous multi-segment multi-addition antisolvent crystallization of benzoic acid in a coiled flow inverter (CFI) crystallizer[J]. Separation and Purification Technology, 2022, 298: 121571. DOI:10.1016/j.seppur.2022.121571 |
| [50] |
PIRKLE C J, FOGUTH L C, BRENEK S J, et al. Computational fluid dynamics modeling of mixing effects for crystallization in coaxial nozzles[J]. Chemical Engineering and Processing: Process Intensification, 2015, 97: 213-232. DOI:10.1016/j.cep.2015.07.006 |
| [51] |
EMAMI M S, HAGHSHENASFARD M, ZARGHAMI R, et al. CFD simulation and experimental study of antisolvent precipitation through impinging jets for synthesis of nanodrug particles[J]. Journal of Molecular Liquids, 2022, 367: 120348. DOI:10.1016/j.molliq.2022.120348 |
| [52] |
DUAN Z, LIU T, LI W, et al. Numerical simulation and experimental study of an efficient multi-orifice-impinging transverse (MOIT) jet mixer[J]. International Journal of Chemical Reactor Engineering, 2022, 20(8): 791-803. DOI:10.1515/ijcre-2021-0298 |
| [53] |
WU B, LI J, LI C, et al. Antisolvent crystallization intensified by a jet crystallizer and a method for investigating crystallization kinetics[J]. Chemical Engineering Science, 2020, 211: 115259. DOI:10.1016/j.ces.2019.115259 |
| [54] |
THAKUR A K, KUMAR R, VIPIN KUMAR V K, et al. A critical review on thermodynamic and hydrodynamic modeling and simulation of liquid antisolvent crystallization of pharmaceutical compounds[J]. Journal of Molecular Liquids, 2022, 362: 119663. DOI:10.1016/j.molliq.2022.119663 |
| [55] |
CHOI Y J, CHUNG S T, OH M, et al. Investigation of crystallization in a jet Y-mixer by a hybrid computational fluid dynamics and process simulation approach[J]. Crystal Growth & Design, 2005, 5(3): 959-968. |
| [56] |
WOO X Y, TAN R B H, CHOW P S, et al. Simulation of mixing effects in antisolvent crystallization using a coupled CFD-PDF-PBE approach[J]. Crystal Growth & Design, 2006, 6(6): 1291-1303. |
| [57] |
CHEN M, WANG J, LI S, et al. CFD-PBE model and simulation of continuous antisolvent crystallization in an impinging jet crystallizer with a multiorifice at different positions[J]. Industrial & Engineering Chemistry Research, 2021, 60(31): 11802-11811. |
| [58] |
YANG L, ZHANG Y, LIU P, et al. Kinetics and population balance modeling of antisolvent crystallization of polymorphic indomethacin[J]. Chemical Engineering Journal, 2022, 428: 132591. DOI:10.1016/j.cej.2021.132591 |
| [59] |
FARIAS L F, DE SOUZA J A, BRAATZ R D, et al. Coupling of the population balance equation into a two-phase model for the simulation of combined cooling and antisolvent crystallization using OpenFOAM[J]. Computers and Chemical Engineering, 2019, 123: 246-256. DOI:10.1016/j.compchemeng.2019.01.009 |
| [60] |
DANCKWERTS P V. The effect of incomplete mixing on homogeneous reactions[J]. Chemical Engineering Science, 1958, 8(1/2): 93-102. |
| [61] |
WEI H, ZHOU W, GARSIDE J. Computational fluid dynamics modeling of the precipitation process in a semibatch crystallizer[J]. Industrial & Engineering Chemistry Research, 2001, 40(23): 5255-5261. |
| [62] |
JAWORSKI Z, NIENOW A W. CFD modelling of continuous precipitation of Barium sulphate in a stirred tank[J]. Chemical Engineering Journal, 2003, 91(2/3): 167-174. |
| [63] |
CHENG J, YANG C, MAO Z, et al. CFD modeling of nucleation, growth, aggregation, and breakage in continuous precipitation of barium sulfate in a stirred tank[J]. Industrial & Engineering Chemistry Research, 2009, 48(15): 6992-7003. |
| [64] |
CHENG J, YANG C, MAO Z. CFD-PBE simulation of premixed continuous precipitation incorporating nucleation, growth and aggregation in a stirred tank with multi-class method[J]. Chemical Engineering Science, 2012, 68(1): 469-480. DOI:10.1016/j.ces.2011.10.032 |
| [65] |
MARCFFLSIO D L, FOX R O, BARRESI A A, et al. On the simulation of turbulent precipitation in a tubular reactor via computational fluid dynamics (CFD)[J]. Chemical Engineering Research and Design, 2001, 79(8): 998-1004. DOI:10.1205/02638760152721550 |
| [66] |
MARCHISIO D L, BARRESI A A, GARBERO M. Nucleation, growth, and agglomeration in Barium sulfate turbulent precipitation[J]. AIChE Journal, 2002, 48(9): 2039-2050. DOI:10.1002/aic.690480917 |
| [67] |
BAL V, BANDYOPADHYAYA R. Generalized model for nano- and submicron particle formation in liquid phase, incorporating reaction kinetics and hydrodynamic interaction: Experiment, modeling, and simulation[J]. The Journal of Physical Chemistry C, 2018, 122(35): 20489-20499. DOI:10.1021/acs.jpcc.8b03521 |
| [68] |
KRAMER H J M, JANSENS P J. Tools for design and control of industrial crystallizers-state of art and future needs[J]. Chemical Engineering & Technology, 2003, 26(3): 247-255. |
| [69] |
ZAUNER R, JONES A G. Scale-up of continuous and semibatch precipitation processes[J]. Industrial & Engineering Chemistry Research, 2000, 39(7): 2392-2403. |
| [70] |
OH D H, JEON R Y, KIM J H, et al. Scale-up of a semi-batch draft tube baffled crystallizer for hexanitrohexaazaisowurtzitane based on experiments and computational fluid dynamics simulation[J]. Crystal Growth & Design, 2019, 19(2): 658-671. |
 2024, Vol. 41
2024, Vol. 41