结晶技术广泛应用于现代化工、制药、食品等行业,是有关生产行业提取产物和去除杂质的主要手段[1]。
与传统的批次间歇结晶工艺相比,连续结晶工艺能够节省9%~40%的生产成本[2, 3],同时,管式连续结晶器能够更好地控制停留时间分布和局部混合,更高的表面积比可带来更有效地传热,从而改善对温度分布的调控[4-6]。在管式连续结晶器中,温度控制尤为重要,直接关系到连续结晶过程能否顺利进行。例如,已有文献报导因管式连续结晶器冷却过快而造成结晶器内壁结垢现象[7, 8]。然而现有文献大多数没有阐明管式连续结晶器中的温度分布情况。因此,如何确定管式连续结晶器中的温度分布已成为目前有待于解决的一个研究课题。
为确定管式连续结晶器温度分布,有文献通过管壳式换热器换热原理与双流体模型等手段分析了管式连续结晶器中的传热性能并提出了结晶器中温度分布的解析解[9-11]。该方法能够从传热原理角度解析换热器中温度分布,对于不同的物料和工艺条件有较好的适应性,但该方法也存在着壳层热量逸散难以计量、考虑参数过多导致模型计算困难等缺点。为了克服以上缺点,一些学者采用实际温度检测数据进行管式连续结晶器的温度分布建模,基于混合神经网络与物理信息神经网络等构建结晶器整体温度分布的模型[12-14]。这样的建模方法虽然有拟合程度高、不依赖参数的优点,但有依赖于大量数据集做训练的缺点。
本研究通过测量DN15管式连续结晶器4个直管段的温度,基于高斯过程回归(Gaussian Process Regression, GPR)拟合得到结晶器各管段温度分布模型。而且,针对不同夹套流速操作条件下构建连续结晶管段温度分布预测模型,提出一种智能优化算法以确定模型参数,能有效提高模型预测的准确性。最后,通过β-LGA连续结晶过程在不同夹套流速下的各管段温度测量实验与模型预测,验证了所提出方法的有效性与优点。
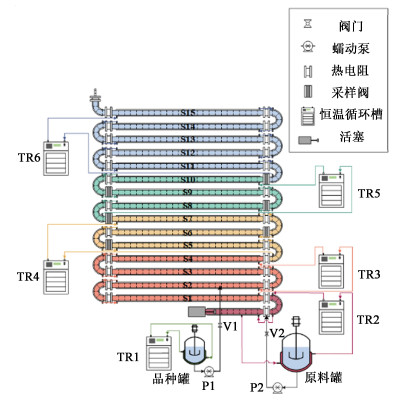
1 连续振荡挡板式结晶器 1.1 连续振荡挡板结晶器及温度传感器以NiTech公司生产的内管径为15 mm的连续振荡挡板结晶器(Continuous Oscillating Baffled Crystallizer, COBC)为例进行研究,该COBC由一系列挡板玻璃直管和弯管组成,如图 1所示,管段总长1 400 cm。
|
| 图 1 COBC实验平台示意图 Fig.1 Illustration of COBC for experiments |
| |
从S1管段开始的降温过程分为4段,分别由4台JULABO恒温循环浴槽控制。在COBC中每条直管两端分别安装1个温度传感器用于测试管段温度,总共在COBC中安装了29个温度传感器,以监测整个COBC管段中的温度变化过程,DN15结晶器实验平台与温度传感器安装位置如图 2所示。

|
| 图 2 DN15连续振荡挡板式结晶器实验装置示意图 Fig.2 Scenary of DN15 COBC |
| |
对照传统批次结晶罐中的降温曲线,这里对管式连续结晶器4个直管段区提出一种温度分布建模方法,从而定量地描述温度随着管段位置变化情况。在如图 1所示的COBC中,温度控制分别由4台恒温循环浴槽控制,因此COBC中的温度分布也分为4段,每2段温度分布之间有一段弯管过渡,因弯管部分长度较小,停留时间短暂,不会对晶体生长产生明显作用,因此这里从各管段过渡点将DN15连续结晶器分为4个管段,进行温度分布建模,以排除弯管部分的影响。
为克服现有文献利用COBC传热机理或利用神经网络进行连续管式结晶器温度分布建模的缺点,提高连续管式结晶器中的温度分布建模效果,本研究提出了一种基于高斯过程回归的COBC中温度分布模型的建模方法。
2 高斯过程回归与智能优化算法 2.1 高斯过程回归高斯过程回归是一种非参数的回归方法,它利用高斯过程对数据进行建模和预测,通常适用于低维和小规模的数据[15, 16],具有灵活、预测准确性高、易于实行的特点,因此适用于连续结晶器的温度分布建模。在GPR的计算过程中,假设回归问题中的未知函数遵循某个高斯过程,然后使用观察到的数据来估计这个高斯过程的参数。GPR的求解通常基于贝叶斯推断,即根据观察到的数据来更新对未知函数的先验分布。
在使用高斯过程回归拟合得到COBC温度分布模型时,温度测量数据为(X, T),其中X为温度测量点沿管段的位置,而T为该测量点对应的温度,此时基于GPR,可以对一个新测量点X*对应的温度T*进行估计预测。由于测量温度和预测温度服从一个高斯过程,因此T和T*服从一个多元高斯分布,即:
| $ \left[\begin{array}{l} T \\ T^* \end{array}\right] \sim \mathscr{N}\left(\left[\begin{array}{l} \boldsymbol{\mu}_T \\ \boldsymbol{\mu}_{T ^*} \end{array}\right], \left[\begin{array}{cc} K(X, X) & K\left(X, X^*\right) \\ K\left(X^*, X\right) & K\left(X^*, X^*\right) \end{array}\right]\right) $ | (1) |
式(1)中:μ为温度分布的均值,而K为高斯过程的协方差函数。根据多元高斯分布的条件分布性质,T*|T服从一个高斯分布,即:
| $ \begin{aligned} & T^* \mid T \sim \mathscr{N}\left[K\left(X^*, X\right) K(X, X)^{-1} T\right., \\ & \left.K\left(X^*, X^*\right)-K\left(X^*, X\right) K(X, X)^{-1} K\left(X, X^*\right)\right] \end{aligned} $ | (2) |
根据高斯分布的性质,当:
| $ T^*=K\left(X^*, X\right) K(X, X)^{-1} T $ | (3) |
此时p(T*|T)最大,也就是说,T*预测值的期望与方差为:
| $ \left\{\begin{array}{l} T_{\text {mean }}^*=K\left(X^*, X\right) K(X, X)^{-1} T \\ T_\sigma^*=K\left(X^*, X^*\right)-K\left(X^*, X\right) K(X, X)^{-1} K\left(X, X^*\right) \end{array}\right. $ | (4) |
式(4)中,K为高斯过程的协方差函数,也被称作核函数(Kernel Function),最简单的核函数为线性核(Linear Kernal),该核函数由式(5)表示。
| $ K\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right)=\sigma_0^2+\sigma_{\text {Linear }}^2 \boldsymbol{x}_1^{\mathrm{T}} \boldsymbol{x}_2 $ | (5) |
式(5)中:σ0为常数,用于保证核函数的正定性;σLinear为控制线性核函数幅度的参数。因线性核函数不足以描述复杂非线性问题而不被应用于高斯过程回归建模非线性对象,因此平方指数核(Squared Exponential Kernel,SE核)由于具有较好的平滑效果而成为高斯过程回归常用的核函数[17],即:
| $ K\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right)=\sigma_{\mathrm{f}}^2 \exp \left[-\frac{1}{2} \frac{\left(\boldsymbol{x}_1-\boldsymbol{x}_2\right)^{\mathrm{T}}\left(\boldsymbol{x}_1-\boldsymbol{x}_2\right)}{\sigma_1^2}\right] $ | (6) |
式(6)中:x1, x2分别为高斯过程回归的2组输入向量;σf, σl分别为核函数的标准差参数以及长度参数。此外,在平方指数核的基础上,文献[18]通过引入一个额外的参数构建一个有理二次型核(Rational Quardratic Kernel, RQ核),即:
| $ K\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right)=\sigma_{\mathrm{f}}^2\left[1+\frac{\left(\boldsymbol{x}_1-\boldsymbol{x}_2\right)^T\left(\boldsymbol{x}_1-\boldsymbol{x}_2\right)}{2 \alpha \sigma_1^2}\right]^{-\alpha} $ | (7) |
该核函数可以看作不同特征尺度下平方指数核的混合,其中α为混合参数,它直接影响核函数在不同尺度下的行为,该核函数相比于传统的平方指数核具有更好的灵活性。
而在不同夹套流速下COBC温度分布的预测建模当中,温度测量数据为(X, Q, T),其中Q为夹套流速,此时预测模型输入为预测点沿管段位置与夹套流速(X*, Q*),输出为预测温度T*,此时利用式(1)~式(4),可以得出不同夹套流速下的温度分布预测模型为:
| $ T^*=K\left[\left(X^*, Q^*\right), (X, Q)\right] K[(X, Q), (X, Q)]^{-1} T $ | (8) |
由于不同夹套流速下COBC中的温度分布模型为多变量输入模型,此时在高斯过程回归中选用的核函数为自动相关性判定平方指数核(ARD Squared Exponential Kernel)即:
| $ K\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right)=\sigma_{\mathrm{f}}^2 \exp \left[-\frac{1}{2} \sum\limits_{m=1}^2 \frac{\left(\boldsymbol{x}_{1, m}-\boldsymbol{x}_{2, m}\right)^2}{\sigma_m^2}\right] $ | (9) |
在该核函数中σf仍然为核函数的标准差参数而σm(m=1, 2)则代表着每一输入变量对应的单独的长度尺度参数,这使得核函数能够更加灵活的适应数据的不同特征。
在如式(5)、式(6)、式(7)和式(9)的核函数当中,每一核函数都包含了对应的参数,这些参数的集合被称为超参数,为了提高GPR建模预测的准确性,在实际建模过程当中需要对超参数进行优化求解,在传统GPR当中,通常利用取偏导数后的负对数边际似然最小化来求解超参数。但也有文献报导利用智能优化算法例如粒子群优化算法(Particle Swarm Optimization, PSO)[19]求解超参数以提高GPR的预测精度。
2.2 基于北方苍鹰算法的高斯过程回归(NGO-GPR)现有PSO算法对GPR可以在核函数超参数优化中发挥一定效果,但该方法存在着依赖初值,容易陷入局部最优的问题。为了克服这一问题,可以这里考虑采用北方苍鹰算法(Northern Goshawk Optimization, NGO)。它是一种启发式优化算法,其灵感来源于北方苍鹰的捕猎行为[20]。该算法过程主要分为猎物识别以及追逐与逃生2个部分,利用该算法可以对高斯过程回归中式(9)所示核函数中参数进行优化求解,计算过程如下。
2.2.1 群体位置初始化核函数中超参数为(σf, σ1, σ2),设置每一参数的上下界分别为10与0.01。群体中每一苍鹰位置代表着搜索空间中1组可行解,首先随机初始化苍鹰位置:
| $ \boldsymbol{\sigma}=l_{\mathrm{b}}+\operatorname{rand} \cdot\left(u_{\mathrm{b}}-l_{\mathrm{b}}\right) $ | (10) |
式(10)中,σ代表苍鹰位置,即σ =(σf, σ1, σ2);lb, ub分别代表搜索空间下界与上界;rand为一个[0, 1)范围内的随机数。
2.2.2 计算种群适应度将苍鹰位置作为核函数参数的解带入式(6)所示的GPR温度预测模型当中,此时可计算出每个温度测量点通过预测模型预测得到的温度Ti*(i=1, 2, …., n),n为测量点个数,将其与实际测量的温度Ti(i=1, 2, …, n)进行比较,利用均方根误差(RMSE)作为种群适应度。
| $ F=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(T_i^*-T_i\right)^2} $ | (11) |
在此阶段,苍鹰随机选择一个“猎物”p,即解空间内的1组可能解进行攻击。
| $ \boldsymbol{p}=\left(\sigma_{\mathrm{fp}}, \sigma_{1 \mathrm{p}}, \sigma_{2 \mathrm{p}}\right) $ | (12) |
对于该“猎物”而言,同样利用式(9)作为核函数带入GPR预测模型进行建模,利用式(11)计算“猎物”对应的适应度Fp并与F进行比较并更新苍鹰位置,位置更新公式如式(13):
| $ \boldsymbol{\sigma}_j^{\mathrm{new}, {\boldsymbol{p}}}= \begin{cases}\boldsymbol{\sigma}_j+r_1\left(\boldsymbol{p}_j-I \boldsymbol{\sigma}_j\right), & F_{{\boldsymbol{p}}_j}<F_j \\ \boldsymbol{\sigma}_j+r_1\left(\boldsymbol{\sigma}_j-\boldsymbol{p}_j\right), & F_{{\boldsymbol{p}}_j} \geqslant F_j\end{cases} $ | (13) |
式(13)中:j为迭代次数;σj为更新前的苍鹰位置;σjnew, p为更新后的苍鹰位置;pj为本次选中的猎物位置;r1为一个[0, 1)范围内的随机数;I随机取1或2以增强搜索的多样性;Fpj, Fj分别表示猎物位置以及当前位置的适应度。
2.2.4 追逐与逃生(开发阶段)在此阶段,算法主要模拟苍鹰追逐猎物以及猎物试图逃生的行为,计算公式如式(14):
| $ \boldsymbol{\sigma}_j^{\text {new }}=\boldsymbol{\sigma}_j^{\text {new }, \boldsymbol{p}}+R\left(2 r_2-1\right) \boldsymbol{\sigma}_j^{\text {new }, \boldsymbol{p}} $ | (14) |
式(14)中:σjnew为通过开发阶段更新后的位置;r2为一个[0, 1)范围内的随机数;R为苍鹰在追逐逃生阶段的搜索半径,由式(15)计算:
| $ R=0.02 \times\left(1-\frac{j}{T}\right) $ | (15) |
这里T为预先设定的迭代总次数。利用式(11)计算追逐阶段更新位置对应的适应度Fjnew并与Fjnew, p进行比较并更新苍鹰位置,从而得到本次迭代得到的苍鹰位置σj。
| $ \boldsymbol{\sigma}_j= \begin{cases}\boldsymbol{\sigma}_j^{\mathrm{new}}, & F_j^{\mathrm{new}}<F_j^{\mathrm{new}, {\boldsymbol{p}}} \\ \boldsymbol{\sigma}_j^{\mathrm{new}, \mathrm{p}}, & F_j^{\mathrm{new}} \geqslant F_j^{\mathrm{new}, {\boldsymbol{p}}}\end{cases} $ | (16) |
重复2.2.2~2.2.4,直到达到预定迭代次数,最终得到的苍鹰位置σT即为通过NGO得到的GPR核函数参数。
在NGO算法当中,勘探阶段可以提高算法的全局搜索能力,开发阶段则可以增强算法的局部搜索能力,将2个步骤相结合,NGO可以兼顾全局搜索和局部搜索,更有效地找到空间的最优解,避免陷入局部最优。
3 实验结果与分析 3.1 实验过程与结果 3.1.1 实验设备与实验步骤采用DN15 COBC实验装置,该结晶器使用内径为15 mm、管段总长1 400 cm的COBC,其示意图如图 1所示。
溶质是β-LGA(C5H9NO4, 质量分数99%, Sigma公司生产),溶剂是蒸馏水。在实验中,首先将β-LGA溶解于蒸馏水中,将其加入原料罐中并加热至稍高于50 ℃,打开控制4段冷却过程的制冷循环浴槽,分别设置为45、40、35与30 ℃,通过冷却油阀门,调节COBC夹套流速。待温度达到设定值并稳定后,打开原料罐阀门,将β-LGA高温溶液注入COBC。通过温度传感器读取COBC管段温度,待温度稳定后,记录29个测试点温度。
同时,通过实验测定了夹套流速对COBC中温度分布模型的影响。在该实验中,因β-LGA浓度不是影响温度分布模型的主要因素,使用蒸馏水代替β-LGA溶液进行实验。在原料罐中加入蒸馏水并加热至稍高于50 ℃后,恒温循环浴分别设置为45、40、35与30 ℃,通过调节循环浴槽阀门,分别调节控制第4段COBC的冷却浴槽冷却油流速为500、750、1 000、1 250和1 500 mL·min-1,待COBC中温度稳定时,记录温度传感器示数。
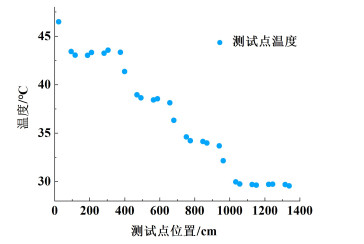
3.1.2 实验结果在夹套流速为500 mL·min-1时,β-LGA溶液在COBC中从50降温至30 ℃,管段中温度分布测量值如图 3所示。
|
| 图 3 夹套流速500 mL·min-1下的管段温度分布测量值 Fig.3 Distribution of temperature measured in pipe segment at a jacket flow rate of 500 mL·min-1 |
| |
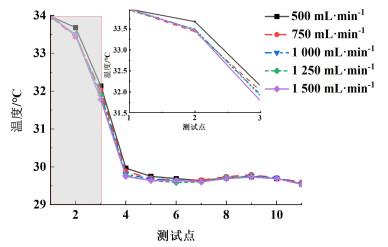
从图 3中可以看出,每个冷却区段中,管段中温度先下降,待与夹套中循环冷却油设定温度基本一致后保持温度稳定。而对于不同夹套流速对COBC温度分布影响实验而言,以第4管段为例,该管段中,COBC管段温度由35降至30 ℃,对于夹套流速分别为500、750、1 000、1 250、1 500 mL·min-1,第4管段温度分布如图 4所示。
|
| 图 4 不同夹套流速下结晶器第4管段温度分布测量结果与测量点1~3放大说明 Fig.4 Measurement results on the temperature distribution in the fourth pipe segment under different jacket flow rates and zoom-out illustration on measurement points 1—3 |
| |
从图 4中可以看出,随着夹套流速的改变,管段温度分布也发生改变,夹套流速越大,对应图 4中温度分布模型的斜率越大,这与管壳式换热器的换热原理相符。
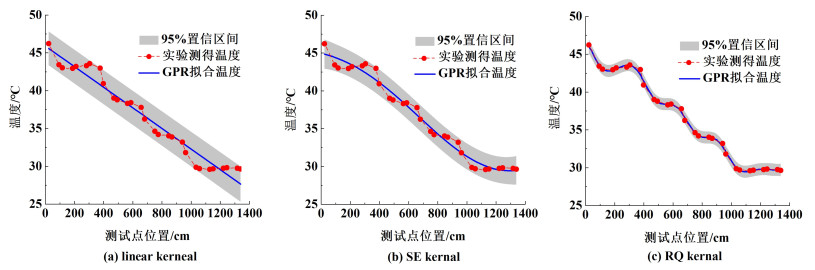
3.2 基于GPR的COBC管段温度分布建模对于如图 4所示的COBC温度分布测量值而言,通过GPR分别使用式(5)、式(6)和式(7)对应的3种核函数利用29个温度测量值对COBC管段中的温度分布进行建模拟合,结果如5所示。
从图 5可以看出,使用3种核函数进行GPR拟合得到的温度分布模型拟合程度不同,定义如式(17)指标评估拟合效果:
| $ R^2=1-\frac{\sum\limits_{i=1}^n\left(T_i-T_i^*\right)^2}{\sum\limits_{i=1}^n\left(T_i-\bar{T}_i\right)^2} $ | (17) |
|
| 图 5 使用不同核函数得到的全管段温度分布的GPR拟合结果 Fig.5 Fitting results of GPR for temperature distribution in the entire pipe segments using different kernal functions |
| |
式(17)中:Ti为实验测得温度的均值;n为GPR预测点总数;R2越接近1说明拟合效果越好。对于以上3种核函数,分别算得RLinear2=0.980,RSE2=0.990,RRQ2=0.999。因此,使用RQ核进行高斯过程回归平滑效果最好,此时GPR对COBC中温度分布建模具有较好的拟合效果。
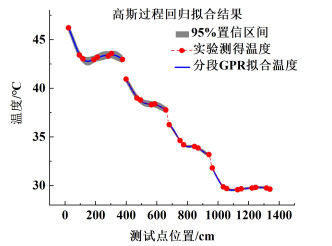
将该模型中29个温度测量点的测量温度与拟合模型中对应位置的预测温度进行比较,最大温度差为0.7 ℃,误差较大,模型精确程度有待提升。可以看出误差主要存在于弯管部分,因此从过渡点将COBC分为4个管段温度区间分布进行建模,以排除弯管部分的影响。4管段温度分布的高斯过程回归的拟合结果如图 6所示。
|
| 图 6 4管段温度分布的GPR拟合结果 Fig.6 Fitting results of GPR for temperature distribution in the 4 pipe segments |
| |
值得指出,将COBC中的温度分布分为4段管段,分别利用GPR进行建模拟合后,29个温度测量点与预测值最大误差降低为0.132 ℃,相比于全管段温度拟合有明显改善,由此说明分4个管段对温度分布预测能显著提高准确性。
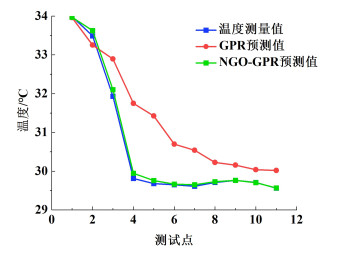
此外,通过夹套流速为500、750、1 250和1 500 mL·min-1时第4管段的温度分布检测数据,建立GPR模型预测夹套流速为1 000 mL·min-1时的第4管段温度分布,并与实际测得该流速下的温度分布对比以验证预测模型的准确性。同时,使用NGO智能优化算法进行GPR核函数参数优化,对比验证智能优化算法的有效性,预测模型结果如图 7所示。
|
| 图 7 DN15第4管段温度分布预测 Fig.7 Prediction of temperature distribution of the fourth pipe segment of DN15 |
| |
从图 7中可以看出,使用GPR建立的预测模型平均相对误差为2.60%,而使用NGO-GPR的预测模型平均相对误差仅为0.18%。这说明使用NGO优化求解核函数中参数,可以显著提高GPR建模的准确性,而且NGO-GPR建模方法可以应用于COBC在不同操作条件下的管段温度分布预测。
4 总结提出了一种连续结晶器温度分布的高斯过程回归建模方法,通过对DN15型COBC冷却结晶过程的温度建模实验,有效验证了该方法的可行性。值得说明的是,从过渡弯管位置将COBC温度分布模型分为4段分别进行GPR建模,提高了温度分布模型的准确性。为了分析不同夹套流速对COBC温度分布的影响,利用GPR建立了不同夹套流速下COBC温度分布预测模型,并引入智能优化算法NGO对GPR中核函数中的超参数进行优化,通过实验与仿真对比,验证了该优化算法能够提高高斯过程回归模型的准确性。需要指出,COBC中的温度分布还受到其他因素的影响,在后续研究中将考虑更多其他因素如晶体悬浮液流速、降温区间等引入温度分布建模,从而进一步提高管式连续结晶器温度分布预测的可靠性和准确性。
| [1] |
龚俊波, 孙杰, 王静康. 面向智能制造的工业结晶研究进展[J]. 化工学报, 2018, 69(11): 4505-4517. GONG Junbo, SUN Jie, WANG Jingkang. Research progress of industrial crystallization towards intelligent manufacturing[J]. CIESC Journal, 2018, 69(11): 4505-4517. (in Chinese) |
| [2] |
SCHABER S D, GEROGIORGIS D I, RAMACHANDRAN R, et al. Economic analysis of integrated continuous and batch pharmaceutical manufacturing: A case study[J]. Industrial & Engineering Chemistry Research, 2011, 50(17): 10083-10092. |
| [3] |
赵洺延, 杨思维, 刘涛. 基于实验设计的L-谷氨酸连续结晶过程优化[J]. 化学工业与工程, 2023, 40(1): 53-59. ZHAO Mingyan, YANG Siwei, LIU Tao. Process optimization based on the design of experiments for continuous crystallization of L-glutamic acid[J]. Chemical industry and Engineering, 2023, 40(1): 53-59. DOI:10.13353/j.issn.1004.9533.20223010 (in Chinese) |
| [4] |
ANDERSON N G. Practical use of continuous processing in developing and scaling up laboratory processes[J]. Organic Process Research & Development, 2001, 5(6): 613-621. |
| [5] |
CALABRESE G S, PISSAVINI S. From batch to continuous flow processing in chemicals manufacturing[J]. AIChE Journal, 2011, 57(4): 828-834. DOI:10.1002/aic.12598 |
| [6] |
PLUMB K. Continuous processing in the pharmaceutical industry[J]. Chemical Engineering Research and Design, 2005, 83(6): 730-738. DOI:10.1205/cherd.04359 |
| [7] |
BRIGGS N E B, SCHACHT U, RAVAL V, et al. Seeded crystallization of β-L-glutamic acid in a continuous oscillatory baffled crystallizer[J]. Organic Process Research & Development, 2015, 19(12): 1903-1911. |
| [8] |
MCGLONE T, BRIGGS N E B, CLARK C A, et al. Oscillatory flow reactors (OFRs) for continuous manufacturing and crystallization[J]. Organic Process Research & Development, 2015, 19(9): 1186-1202. |
| [9] |
BRIGGS N E B, MCGINTY J, MCCABE C, et al. Heat transfer and residence time distribution in plug flow continuous oscillatory baffled crystallizers[J]. ACS Omega, 2021, 6(28): 18352-18363. DOI:10.1021/acsomega.1c02215 |
| [10] |
HUANG W, ZHANG C, LI Z, et al. Assessments of the heat transfer performance of a novel continuous oscillatory baffled crystallizer via two-fluid model[J]. Chemical Engineering Science, 2023, 275: 118701. DOI:10.1016/j.ces.2023.118701 |
| [11] |
ONYEMELUKWE I I, BENYAHIA B, REIS N M, et al. The heat transfer characteristics of a mesoscale continuous oscillatory flow crystalliser with smooth periodic constrictions[J]. International Journal of Heat and Mass Transfer, 2018, 123: 1109-1119. DOI:10.1016/j.ijheatmasstransfer.2018.03.015 |
| [12] |
WANG J, CAO L, WU H, et al. Dynamic modeling and generalized PI control for temperature distribution of the tubular polymerization[J]. Control Theory, 2012, 29(8): 1043-1050. |
| [13] |
CAO L, LI D, ZHANG C, et al. Control and modeling of temperature distribution in a tubular polymerization process[J]. Computers & Chemical Engineering, 2007, 31(11): 1516-1524. |
| [14] |
PATEL R, BHARTIYA S, GUDI R. Optimal temperature trajectory for tubular reactor using physics informed neural networks[J]. Journal of Process Control, 2023, 128: 103003. DOI:10.1016/j.jprocont.2023.103003 |
| [15] |
SCHULZ E, SPEEKENBRINK M, KRAUSE A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions[J]. Journal of Mathematical Psychology, 2018, 85: 1-16. DOI:10.1016/j.jmp.2018.03.001 |
| [16] |
WANG J. An intuitive tutorial to Gaussian process regression[J]. Computing in Science & Engineering, 2023, 25(4): 4-11. |
| [17] |
OLIVIER B, ULRIKE L, GUNNAR R. Advanced Lectures on Machine Learning[M]. Berlin, Heidelberg: Springer, 2004.
|
| [18] |
RASMUSSEN C E, WILLIAMS C K I. Gaussian processes for machine learning[M]. Cambridge, Mass.: MIT Press, 2006.
|
| [19] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of ICNN'95-International Conference on Neural Networks. Perth, WA, Australia. IEEE, 2002: 1942-1948
|
| [20] |
DEHGHANI M, HUBÁLOVSKY Š, TROJOVSKY P. Northern goshawk optimization: A new swarm-based algorithm for solving optimization problems[J]. IEEE Access, 2021, 9: 162059-162080. DOI:10.1109/ACCESS.2021.3133286 |
 2024, Vol. 41
2024, Vol. 41





