2. 天津市化工安全与装备技术重点实验室, 天津 300350
2. Tianjin Key Laboratory of Chemical Process Safety and Equipment Technology, Tianjin 300350, China
气相换热广泛存在于众多生产过程,如工业加热与冷却、能源的利用与回收等。然而,由于气相的热导率、密度和比热容等较小,其对流传热热阻较大,一般约占换热过程总热阻的80%以上;同时,在气相换热过程中也广泛存在着结垢问题,严重制约了设备的传热效率,增加能耗,影响生产[1, 2]。因此,采取一定的措施来解决气相的强化传热和防、除垢问题,是非常必要和重要的。
在现有的气相换热强化技术中,螺纹管是一种高效的被动强化传热元件;因其具有传热面积大、换热效率高、结构简单且成本低廉等优点,被国内外的研究者予以了较多的关注[3-9]。
流化床换热防垢节能技术开发于20世纪80年代。该技术将流化床技术与换热过程相结合,通过流化惰性固体颗粒对换热壁面的剪切和碰撞,破坏流动和传热边界层,尤其是层流底层,并延长结垢的诱导期,进而实现换热设备的在线强化传热和防、除垢[10-13]。该技术因为适用范围广、操作稳定、运行成本低等特点而具有广阔的应用前景,但目前其在气相换热过程中的应用,主要集中于气-固流化床,而在循环流化床中的报道则相对较少[14-16]。
由流化床换热防垢节能技术的机理可知,流化颗粒对换热壁面的剪切和碰撞对强化传热和防、除垢效果具有重要的影响。因此,一些研究者围绕此方面开展了相应的研究[17-23]。
Pronk等[17]利用压电传感器考察了换热器中颗粒对壁面的碰撞及相应的防垢性能。结果表明,颗粒与壁面以及颗粒之间碰撞强度和频率能影响流化床的去污垢能力。Abbasi等[18, 19]利用加速度计测量了气-固流化床的振动信号,并利用小波和快速傅里叶变换进行了频域分析。结果发现,气泡产生的振动频率在1 000~3 000 Hz之间,且不同的流体力学现象可以根据不同频率分量的振动信号来区分。Ma等[20]和Xu等[21]利用振动信号分析方法考察了汽-液-固沸腾流中固体颗粒对石墨管壁的碰撞。他们通过分析信号的时间序列和功率谱密度,发现颗粒的加入增加了系统振动加速度信号的振幅和能量。Jiang等[22, 23]实验分析了循环流化床蒸发器中的颗粒碰撞行为和硫酸钠溶液的蒸发传热性能,并考察了颗粒特性的影响。结果表明,颗粒的碰撞频率为6 000~16 000 Hz,且其对多相流的碰撞起主导作用;传热性能和颗粒碰撞行为与颗粒的表面润湿性能、沉降速度和密度等明显相关。
上述对于颗粒碰撞行为的研究主要集中在液-固两相和气-液-固三相,而对气-固两相,特别是气-固循环流化床的研究则鲜见报道。同时,目前流化床换热防垢节能技术主要应用于光管,而对于其与螺纹管换热器的结合尚缺乏探索。因此,本研究拟设计并构建内螺纹管气-固循环流化床换热装置,利用非侵入式碰撞加速度测量技术,通过频域分析,考察操作参数对颗粒碰撞行为、传热性能和压降的影响。研究结果有助于进一步促进气相传热过程的强化和拓展流化床换热防垢节能技术的应用。
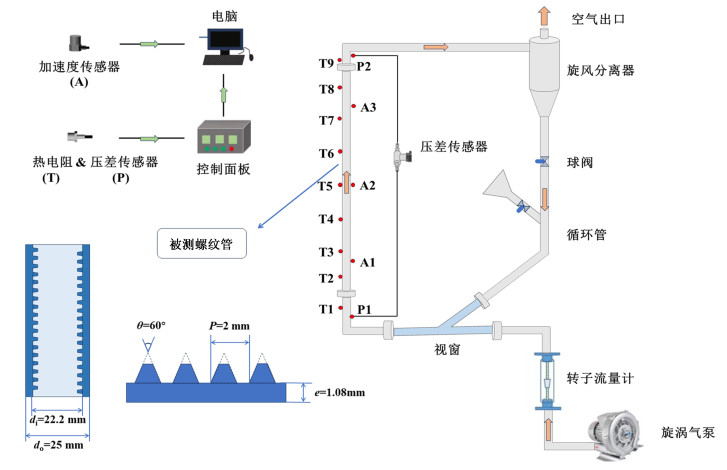
1 实验部分 1.1 实验装置及流程图 1所示为内螺纹气-固循环流化床换热装置,主要包括旋风分离器、螺纹加热管、转子流量计、旋涡气泵以及数据采集系统等。为了便于观察颗粒在装置内的循环状态,视窗采用有机玻璃制成,而其他部分均由304不锈钢制成。
|
| 图 1 气-固循环流化床螺纹管换热装置以及螺纹尺寸 Fig.1 Heat exchange apparatus of gas-solid circulating fluidized bed with threaded tube and the size of the threads |
| |
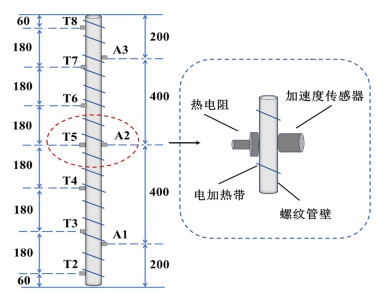
装置的核心为内螺纹管,其长度为1 200 mm,螺纹的具体形状和尺寸如图 1所示。螺纹管采用额定功率为600 W的镍铬合金丝制成的电加热带加热。在装置外包裹保温棉,以减少热损失。沿加热管轴向一侧安装有7个热电阻(RTD)以测量外壁温,流体的进、出口温度也采用热电阻进行测量。在加热管另一侧沿轴向设置3个加速度传感器,用以采集气-固两相流与壁面碰撞的加速度信号,其测量点分别为A1、A2和A3,如图 2所示。采用差压传感器测量加热管进、出口的压差。温度和压差数据由“King-View”软件自动采集。加速度信号通过“Weekend Dynamic”软件进行记录和分析,采样频率为64 kHz,采集时间为120 s。实验所用相关仪表的规格如表 1所示。
|
| 图 2 热电阻和传感器在螺纹加热管上的相对位置 Fig.2 Relative position of the RTDs and sensors on the thread heating tube |
| |
| 仪表 | 型号 | 量程 | 精度 | 最大测量误差 |
| 热电阻温度传感器 | Pt100 | -100~300 ℃ | A | ±(0.15+0.002|t|*) |
| 差压传感器 | SM84320GP | 0~10 kPa | 0.25%(FS) | (±25) Pa |
| 加速度传感器 | KZ020 | (±50) g | 0.50%(FS) | (±0.5)% |
| 转子流量计 | LZB-25-0.6 MPa | 2.5~25 m3·h-1 | 1.5 | (±0.2)% |
| *:|t|为温度的绝对值,℃。 | ||||
首先,将循环管阀门关闭,再将一定量的惰性固体颗粒加入系统。然后,调整频率使旋涡气泵的流量达到指定值,打开循环管阀门至指定开度,空气带动固体颗粒流化进入加热管,形成气-固两相流,开启加热系统。实验中,当5 min内所有热电阻的温度变化小于0.1 ℃,认为系统达到稳态,采集加速度信号、温度和压降数据。改变操作参数,重复上述步骤。每次实验运行3次,以检查数据的重复性。
1.2 实验工质及参数实验中以空气作为气相工质,选择聚甲醛和3种粒径的玻璃珠颗粒为惰性固体颗粒。聚甲醛和玻璃珠理化性质稳定,来源方便,适合工业化推广应用。所用颗粒的相关物性参数如表 2所示。
| 颗粒种类 | 形状 | 颗粒粒径/ mm | 密度/ (kg·m-3) | 热导率/ (W·m-1·K-1) | 比热容/ (kJ·kg-1·K-1) | 沉降速度*/ (m·s-1) |
| 聚甲醛(POM) | 椭球形 | 2.5 | 1 390 | 0.23 | 1.46 | 9.25 |
| 玻璃珠1(GB1) | 球形 | 0.6~0.8 | 2 500 | 1.10 | 0.78 | 5.52 |
| 玻璃珠2(GB2) | 球形 | 0.8~1.0 | 2 500 | 1.10 | 0.78 | 7.10 |
| 玻璃珠3(GB3) | 球形 | 1.0~1.5 | 2 500 | 1.10 | 0.78 | 8.77 |
| *:空气中的计算值(20 ℃,常压)。 | ||||||
研究中主要考察空气流量V(12、14、16、18和20 m3 ·h-1)、热通量q(1、2和3 kW ·m-2)和颗粒类型等对颗粒碰撞行为和传热性能的影响。
1.3 数据处理和误差分析 1.3.1 碰撞加速度信号处理功率谱密度(Power Spectral Density,PSD)在信号处理领域中可用来分析信号中的频率组成及能量占比。计算功率谱密度需先对信号进行加窗操作预处理,再进行快速傅里叶变换,其计算如式(1)所示。
| $ P(f)=\frac{1}{\sum\limits_{n=1}^N w^2(n)}\left[\sum\limits_{n=1}^N x(n) w(n) \mathrm{e}^{-2 j {\rm{ \mathsf{ π}}} n f}\right]^2 $ | (1) |
式(1)中:f为频率;N为总采样点数;w(n)为窗函数;x(n)为时间序列。选用Welch法对PSD进行校正[24],如式(2)所示。
| $ [P(f), f]=\text { pwelch }\left[x(n), \text { window, overlap }, \mathrm{nfft}, f_{\mathrm{s}}\right] $ | (2) |
式(2)中:window为窗函数;overlap为重叠率;nfft为采样长度;fs为采样频率。
选择汉明窗作为窗函数[25],重叠率设置为75%。根据实验条件和精度要求,nfft设置为32 768[25],其相应的频率分辨率为1.953 1 Hz。
信号功率Ps用来描述信号的强度或能量分布,是指信号在单位时间内传输或消耗的能量,是信号的基本特征之一,在一定程度上可以反映气-固两相流碰撞信号的强度。信号功率可将PSD按指定范围进行积分计算得到,如式(3)所示。
| $ P_{\mathrm{s}}=\int_{f_1}^{f_2} P(f) \mathrm{d} f $ | (3) |
式(3)中:f1和f2分别为频率范围的下限和上限。
1.3.2 传热和压降数据处理研究中,气-固循环流化床螺纹管换热器的传热性能采用对流传热系数α和传热增强因子E进行评价。α可由式(4)进行计算。
| $ \alpha=\frac{Q}{S_{\mathrm{i}}\left(t_{\mathrm{wi}}-t_{\mathrm{f}}\right)} $ | (4) |
| $ Q=Q_{\mathrm{in}}-Q_{\text {loss }} $ | (5) |
| $ t_{\mathrm{wi}}=t_{\mathrm{wo}}-\frac{Q \ln \left(\frac{d_{\mathrm{o}}}{d_{\mathrm{i}}}\right)}{2 {\rm{ \mathsf{ π}}} L \lambda} $ | (6) |
| $ t_{\mathrm{f}}=\frac{t_{\mathrm{fi}}+t_{\mathrm{fo}}}{2} $ | (7) |
式(4)~式(7)中:Q为扣除热损失后的加热功率;Qm和Qloss分别为输入功率和热损失;Si为螺纹管内表面积;twi和two分别为内螺纹管的内、外壁面平均温度;tf为空气的平均温度;tfi和tfo分别为空气的进、出口温度;di和do分别为螺纹管的中径和外径;L和λ分别为管长和管壁热导率。
实验中的热损失采用式(8)进行计算。
| $ \left.Q_{\text {loss }}=\left[9.4+0.052\left(t_{\mathrm{c}}-t_{\mathrm{a}}\right)\right] {\rm{ \mathsf{ π}}} d_{\mathrm{c}} L\left(t_{\mathrm{c}}-t_{\mathrm{a}}\right)\right] $ | (8) |
式(8)中:dc为保温棉的外径;ta和tc分别为实验环境和保温棉的外壁面温度。
可由式(9)计算传热增强因子E。
| $ E=\frac{\alpha_{\mathrm{gs}}-\alpha_{\mathrm{g}}}{\alpha_{\mathrm{g}}} \times 100 \% $ | (9) |
式(9)中:αg和αgs分别为空气和气-固两相流在螺纹管内的对流传热系数。
实验中,添加颗粒后系统压降的变化采用压降比率S进行评估,可由式(10)计算。
| $ S=\frac{\Delta p_{\mathrm{gs}}-\Delta p_{\mathrm{g}}}{\Delta p_{\mathrm{g}}} \times 100 \% $ | (10) |
式(10)中:Δpg和Δpgs分别为空气和气-固两相流在螺纹管内的压降。
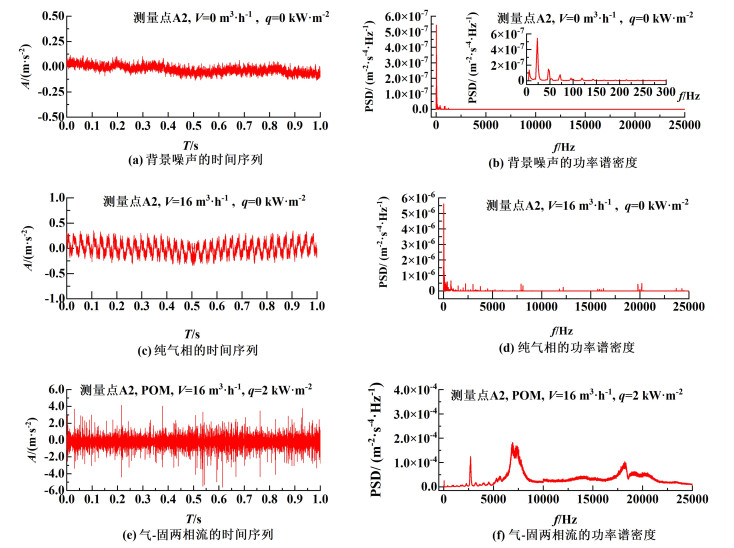
2 结果与讨论 2.1 气-固两相流碰撞加速度信号的特征频率范围 2.1.1 设备背景噪声信号的特征频率范围图 3(a)和图 3 (b)所示为设备背景噪声信号的时间序列和PSD。此时,将一定量的颗粒加入循环管中,关闭下降管的阀门,离心泵和电加热系统未开启,进行背景噪声信号的采集。由图 3(b)可知,PSD图中出现了唯一的峰值,此即背景噪声的特征峰,其频率分布范围为0~100 Hz。图 3表明,背景噪声信号很弱,因此在本研究中,其与气-固两相流的碰撞信号相比可以忽略不计。
|
| 图 3 碰撞加速度信号的时间序列和PSD Fig.3 Time series and PSD of the collision acceleration signals |
| |
图 3中(c)和(d)所示为气相碰撞信号的加速度时间序列和PSD。此时,开启离心泵和电加热系统,空气在螺纹管内被加热后由旋风分离器排出。由图 3(c)和(d)可知,PSD中大致在0~1 000 Hz范围内出现特征峰,且其值在不同测量点相差很小。因此,气相碰撞信号的特征频率范围为0~1 000 Hz。
2.1.3 固相的特征频率范围图 3中(e)和图 3(f)所示为气-固两相流碰撞加速度信号的时间序列和PSD。此时,打开下降管阀门,同时启动离心泵,空气携带着流化的颗粒混合进入螺纹管。打开电加热带电源,气-固两相流在管内进行对流传热。对比图 3(c)和图 3(d)可知,加入颗粒后,加速度信号明显增强;气相特征峰的频率范围几乎无变化,但强度略有增加;在5 000~25 000 Hz范围出现了新的特征峰,且对于不同类型的颗粒,特征峰的频率范围一致。因此,可以得知固相碰撞信号的特征频率范围为5 000~25 000 Hz。
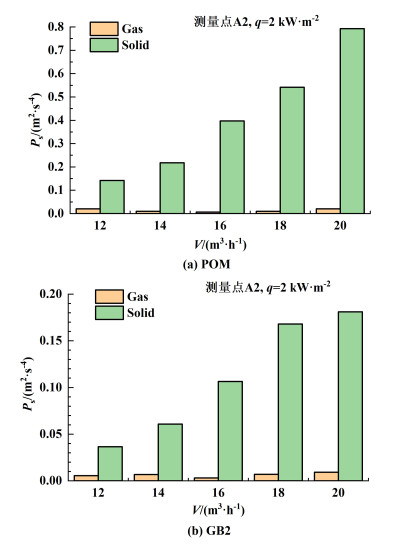
图 4所示为气-固两相流碰撞的信号功率。
|
| 图 4 气-固两相流碰撞的信号功率 Fig.4 Signal power of the gas-solid two-phase flow collision |
| |
由图 4可知,固相的信号功率远高于气相,说明颗粒在气-固两相流的碰撞中起主导作用。故在本研究后续分析中,将主要考虑颗粒碰撞行为和传热性能之间的关系。
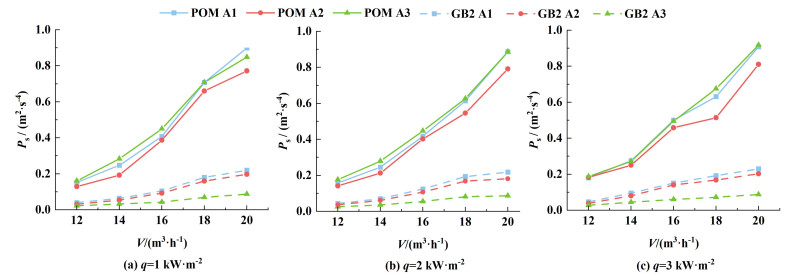
2.2 颗粒碰撞行为的轴向分布图 5为气-固两相流中颗粒碰撞的信号功率随螺纹管轴向位置的变化规律。
|
| 图 5 轴向位置对颗粒碰撞信号功率的影响 Fig.5 Effect of axial position on particle collision signals |
| |
由图 5可知,POM颗粒的信号功率沿轴向先减小、后增大,管子两端(A3和A1)的信号功率较为接近,且高于中部。GB2颗粒的信号功率则沿轴向逐渐减小。
螺纹管进、出口流向的改变增加了气-固两相流,尤其是颗粒径向运动的无序性,因此加剧了颗粒对加热壁面的碰撞。GB颗粒的直径较小,与螺纹齿高接近,螺纹对颗粒的轴向运动阻力较大,消耗了颗粒的动能,导致信号功率则沿轴向逐渐减小。而POM颗粒的直径是齿高的近3倍,齿高对其阻力和碰撞动能的影响较小,故在螺纹管出口处颗粒对加热壁面的作用仍较强。
图 5还表明,信号功率随操作参数的变化在不同的轴向位置呈现出相同的趋势,故在后续讨论中,信号功率取3个测量点的平均值。
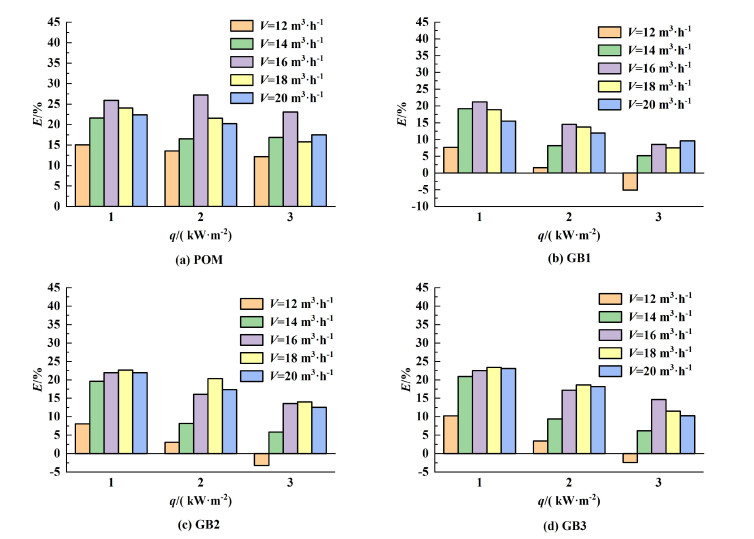
2.3 操作参数对颗粒碰撞行为和传热性能的影响 2.3.1 空气流量和热通量的影响图 6所示为不同操作条件下的传热增强因子。
|
| 图 6 不同操作条件下的传热增强因子 Fig.6 Heat transfer enhancing factor under different operating conditions |
| |
由图 6可知,添加惰性颗粒可以明显地强化螺纹管的传热。传热增强因子在实验范围内最大可达27.2%,此时,V=16 m3 ·h-1,q=2 kW ·m-2,相应的颗粒为POM颗粒。传热增强因子均基本上随空气流量的增加先增大、后减小,随热通量的增加而减小。
如前所述,加入惰性颗粒并充分流化,可以破坏和减薄流动和传热边界层,特别是层流底层,进而减小对流传热热阻,增强传热。同时,POM和GB颗粒的热导率明显高于空气,可增强颗粒与加热壁面接触时的瞬时热传导。因此,颗粒的加入增强了传热。
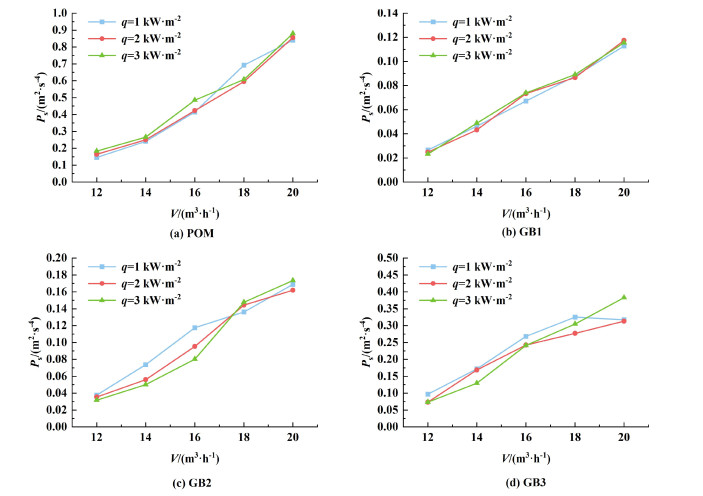
空气流量增加,一方面,螺纹加热管内气速增大,湍流程度加剧,有利于单位时间携带更多的颗粒进入加热管,增加颗粒对换热壁面的碰撞频率;同时,颗粒运动速度增加,单颗粒的碰撞动能增大,这有利于强化传热。信号功率综合反映了颗粒对壁面的碰撞频率和单颗粒的碰撞动能。因此,信号功率随空气流量增加而增大,如图 7所示。另一方面,空气流速的增加,增大了颗粒的轴向速度,减小了其在加热管中的停留时间,不利于增加对加热壁面的碰撞频率;同时,颗粒的径向分布变得更加均匀,进一步抑制了流体的湍流[26, 27],不利于对流传热;此外,空气流量增加也增加了纯气相的对流传热系数,因此一定程度上削弱了颗粒对传热的强化作用。所以,综上所述,随着空气流量的增加,传热增强因子基本上先增大、后减小。
|
| 图 7 空气流量对气-固两相流信号功率的影响 Fig.7 Effect of air flow rate on the signal power of gas-solid two-phase flow |
| |
热通量增加,加热管内空气的平均温度上升,黏度增大而密度减小,不利于颗粒的流化和径向运动,因此削弱了颗粒对加热壁面的作用,传热增强因子减小。但同空气流量相比,热通量对信号功率的影响较小。
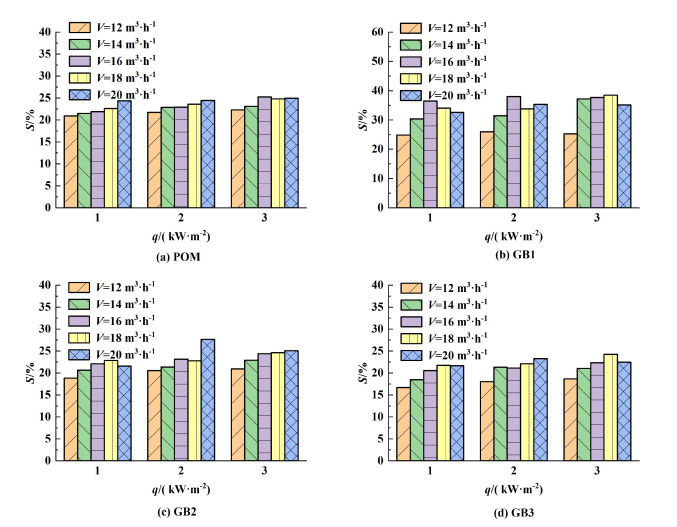
图 8反映了操作参数对压降比率的影响。在实验范围内,颗粒的加入明显增加了系统的压降。压降比率最大为38.5%,此时V=18 m3 ·h-1,q=3 kW ·m-2,加入的颗粒为GB1。
|
| 图 8 不同操作条件下的压降比率 Fig.8 Pressure drop ratio under different operating conditions |
| |
压降比率随着空气流量或热通量的增加主要呈现出增大的趋势。空气流量增加,流化颗粒的数量增加,流体的表观密度随之增大,同时颗粒之间以及颗粒与加热壁面之间的碰撞频率也有所增加,加剧了能量损失。热通量增加,空气的平均温度升高,黏度增大,增加了气-固两相流的流动阻力。
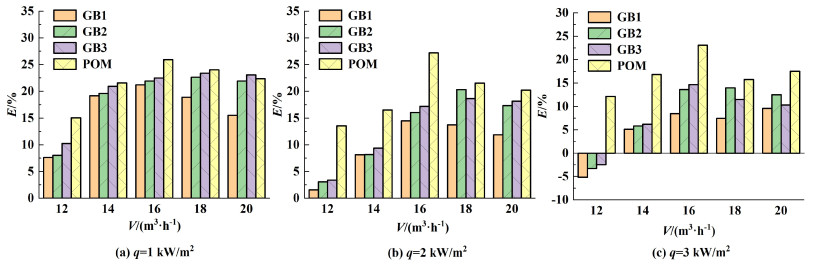
2.3.2 颗粒类型的影响图 9对比了不同类型颗粒的传热增强因子。空气流量较小时,POM颗粒的传热增强因子明显高于GB颗粒,但随着空气流量的增加,这种差异逐渐减小。在大多数实验条件下,传热增强因子随着GB颗粒直径的增加而增大。
|
| 图 9 不同类型颗粒的传热增强因子 Fig.9 Heat transfer enhancing factors for different types of particles |
| |
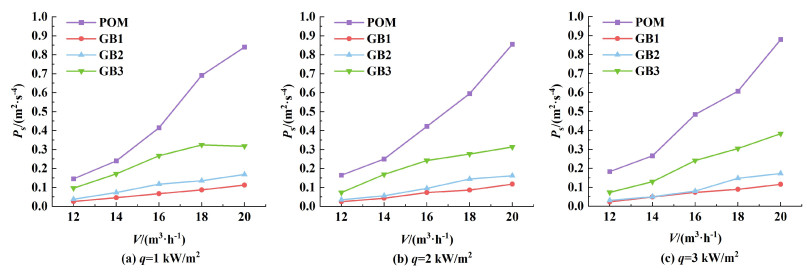
图 10比较了不同类型颗粒的信号功率。POM颗粒的信号功率高于GB颗粒,且信号功率的差异随着空气流速的增加而逐渐增大。
|
| 图 10 颗粒类型对碰撞信号功率的影响 Fig.10 Effect of particle type on collision signal power |
| |
如上所述,信号功率反映了碰撞频率和单颗粒的碰撞动能的共同作用效果。实验范围内,POM颗粒的密度仅为GB颗粒密度的一半左右,但其体积至少为GB颗粒体积的5倍。与颗粒密度相比,颗粒尺寸对颗粒碰撞动能的影响更为显著。因此,POM颗粒可能比GB颗粒具有更大的碰撞动能,这有利于加强对热边界层和流动边界层的破坏,提高传热增强效果。GB颗粒与POM颗粒相比尺寸较小,在加热管中的固含率较高;同时,由于其密度较大,流化效果较差,更多的颗粒集中在加热壁面附近[28, 29],这有利于增加颗粒对壁面的碰撞频率。在低空气流量下,流体的湍流程度较弱,加热壁面附近GB颗粒的运动速度和碰撞强度明显小于POM颗粒。此时,单颗粒的碰撞动能对信号功率起主导作用,因此,GB颗粒的强化传热增强效果明显小于POM颗粒。随着空气流量的增加,GB颗粒可以被更好地流化,运动速度和碰撞强度增大。此时,碰撞频率对强化传热的贡献增大。因此,POM和GB颗粒传热增强效果之间的差异减小。
与POM颗粒相比,3种GB颗粒由于尺寸小,在加热管中均具有较高的固含率。影响其与加热壁面碰撞的主要因素不是碰撞频率,而是单颗粒的碰撞动能和碰撞强度。GB3尺寸较大,具有较高的碰撞动能和碰撞强度。因此,信号功率和传热增强因子基本上随GB颗粒粒径的增加而增大。
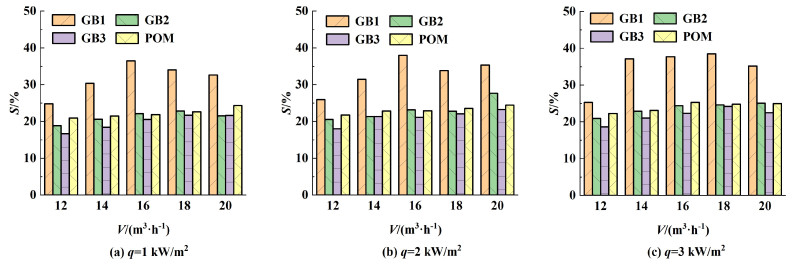
图 11比较了4种类型颗粒的压降比率。
|
| 图 11 不同颗粒类型的压降比率 Fig.11 Pressure drop ratio for different types of particles |
| |
由图 11可知,对于密度相同的GB颗粒,压降比率随颗粒粒径的增大而减小;而对于沉降速度相近的GB3和POM颗粒,粒径较大的POM颗粒压降比率略大。
GB1颗粒粒径较小,在相同流量下流化数量更多,加热管内固含率较高,颗粒与壁面之间和颗粒之间的碰撞频率更大,因此,压降比率较大。如前所述,由于尺寸较大,POM颗粒比沉降速度相近的GB3具有更大的碰撞动能,因此压降比率略大。
3 结论设计并构建了内螺纹气-固循环流化床换热装置,利用非侵入式碰撞加速度测量技术,考察了热通量、空气流量和颗粒类型等操作参数对传热性能、颗粒碰撞行为和压降的影响。主要结论如下:
(1) 惰性固体颗粒的加入可以强化螺纹管的传热,同时也增加了系统的压降。实验范围内,传热增强因子最大可达27.2%,此时V=16 m3 ·h-1,q=2 kW ·m-2,加入的颗粒为POM颗粒。压降比率最大不超过38.5%。
(2) 气-固循环流化床螺纹管换热器中,气相和固相的碰撞加速度信号的特征频率范围分别为0~1 000 Hz和5 000~25 000 Hz。颗粒碰撞在两相流碰撞中起主导作用。
(3) 随着空气流量的增加,信号功率增大,而传热增强因子先增大、后减小。总体来说,传热增强因子随着热通量的增加而减小;热通量同空气流量相比对信号功率的影响较小。GB颗粒的传热增强因子和信号功率均小于POM颗粒,且基本上随着GB颗粒粒径的增加而增大。
(4) 压降比率主要随空气流量或热通量的增加而增大,随GB颗粒粒径增加而减小。对于沉降速度相近的GB3和POM颗粒,粒径更大的POM颗粒的压降比率更大。
| [1] |
JI W, JACOBI A M, HE Y, et al. Summary and evaluation on the heat transfer enhancement techniques of gas laminar and turbulent pipe flow[J]. International Journal of Heat and Mass Transfer, 2017, 111: 467-483. DOI:10.1016/j.ijheatmasstransfer.2017.03.080 |
| [2] |
AWAIS M, BHUIYAN A A. Recent advancements in impedance of fouling resistance and particulate depositions in heat exchangers[J]. International Journal of Heat and Mass Transfer, 2019, 141: 580-603. DOI:10.1016/j.ijheatmasstransfer.2019.07.011 |
| [3] |
YANG J, XIAO Y, HE Q, et al. Study on flow boiling heat transfer in segmented internally-threaded tube[J]. Journal of Applied Fluid Mechanics, 2022, 15(5): 1417-1426. |
| [4] |
CHIOU C B, LU D, CHEN C, et al. Heat transfer correlations of forced convective boiling for pure refrigerants in micro-fin tubes[J]. Applied Thermal Engineering, 2011, 31(5): 820-826. DOI:10.1016/j.applthermaleng.2010.10.031 |
| [5] |
NIKOLAENKO Y E, ALEKSEIK Y S, KOZAK D V, et al. Research on two-phase heat removal devices for power electronics[J]. Thermal Science and Engineering Progress, 2018, 8: 418-425. DOI:10.1016/j.tsep.2018.09.012 |
| [6] |
申道明, 桂超, 刘亚萍, 等. 内螺纹管换热器的综合性能分析[J]. 低温工程, 2019(5): 14-20, 74. SHEN Daoming, GUI Chao, LIU Yaping, et al. Comprehensive performance analysis of the heat exchanger with rifled tube[J]. Cryogenics, 2019(5): 14-20, 74. DOI:10.3969/j.issn.1000-6516.2019.05.003 (in Chinese) |
| [7] |
MURALIKRISHNA Y, MOHAN JAGADEESH KUMAR M, ARAVIND B, et al. Comparative studies on performance of plain, perforated, threaded, and threaded-perforated pin fin: A numerical approach[J]. Heat Transfer, 2023, 52(4): 3333-3352. DOI:10.1002/htj.22830 |
| [8] |
LEI X, GUO Z, PENG R, et al. Numerical analysis on the heat transfer characteristics of supercritical water in vertically upward internally ribbed tubes[J]. Water, 2021, 13(5): 621. DOI:10.3390/w13050621 |
| [9] |
LI X, LIU S, MO X, et al. Investigation on convection heat transfer augment in spirally corrugated pipe[J]. Energies, 2023, 16(3): 1063. DOI:10.3390/en16031063 |
| [10] |
ZHANG L, LI X. A study on boiling heat transfer in three-phase circulating fluidized bed[J]. Chemical Engineering Journal, 2000, 78(2/3): 217-223. |
| [11] |
WEN J, ZHOU H, LI X. Performance of a new vapor-liquid-solid three-phase circulating fluidized bed evaporator[J]. Chemical Engineering and Processing: Process Intensification, 2004, 43(1): 49-56. DOI:10.1016/S0255-2701(02)00189-7 |
| [12] |
HASAN B O, JWAIR E A, CRAIG R A. The effect of heat transfer enhancement on the crystallization fouling in a double pipe heat exchanger[J]. Experimental Thermal and Fluid Science, 2017, 86: 272-280. DOI:10.1016/j.expthermflusci.2017.04.015 |
| [13] |
JIANG F, YANG M, QI G, et al. Heat transfer and antiscaling performance of a Na2SO4 circulating fluidized bed evaporator[J]. Applied Thermal Engineering, 2019, 155: 123-134. DOI:10.1016/j.applthermaleng.2019.03.129 |
| [14] |
JIANG F, DONG X, QI G, et al. Heat-transfer performance and pressure drop in a gas-solid circulating fluidized bed spiral-plate heat exchanger[J]. Applied Thermal Engineering, 2020, 171: 115091. DOI:10.1016/j.applthermaleng.2020.115091 |
| [15] |
谭雪梅, 刘世杰, 赵冰, 等. 循环流化床锅炉气-固两相流换热研究进展[J]. 华电技术, 2021, 10(43): 61-67. |
| [16] |
MURATA H, OKA H, ADACHI M, et al. Effects of the ship motion on gas-solid flow and heat transfer in a circulating fluidized bed[J]. Powder Technology, 2012, 231: 7-17. DOI:10.1016/j.powtec.2012.06.060 |
| [17] |
PRONK P, INFANTE FERREIRA C A, WITKAMP G J. Prevention of fouling and scaling in stationary and circulating liquid-solid fluidized bed heat exchangers: Particle impact measurements and analysis[J]. International Journal of Heat and Mass Transfer, 2009, 52(15/16): 3857-3868. |
| [18] |
ABBASI M, SOTUDEH-GHAREBAGH R, MOSTOUFI N, et al. Non-intrusive monitoring of bubbles in a gas-solid fluidized bed using vibration signature analysis[J]. Powder Technology, 2009, 196(3): 278-285. DOI:10.1016/j.powtec.2009.08.012 |
| [19] |
ABBASI M, SOTUDEH-GHAREBAGH R, MOSTOUFI N, et al. Nonintrusive characterization of fluidized bed hydrodynamics using vibration signature analysis[J]. AIChE Journal, 2010, 56(3): 597-603. DOI:10.1002/aic.12046 |
| [20] |
MA Y, LIU M, AN M, et al. Experimental investigation of collision behavior of fluidized solid particles on the tube wall of a graphite evaporator by vibration signal analysis[J]. Powder Technology, 2017, 316: 303-314. DOI:10.1016/j.powtec.2016.12.067 |
| [21] |
XU X, LIU M, MA Y, et al. Effects of fluidized solid particles on vibration behaviors of a graphite tube evaporator with an internal vapor-liquid flow[J]. Applied Thermal Engineering, 2016, 100: 1229-1244. DOI:10.1016/j.applthermaleng.2015.12.126 |
| [22] |
姜峰, 刘艺, 齐国鹏, 等. 液-固下行循环流化床中的颗粒碰撞行为[J]. 化学工业与工程, 2022, 39(3): 49-59. JIANG Feng, LIU Yi, QI Guopeng, et al. Study on particle collision behavior in a liquid-solid down-flow circulating fluidized bed[J]. Chemical Industry and Engineering, 2022, 39(3): 49-59. DOI:10.13353/j.issn.1004.9533.20210311 (in Chinese) |
| [23] |
姜峰, 徐迪, 齐国鹏, 等. Na2SO4循环流化床蒸发器中的颗粒碰撞行为和传热性能[J]. 化学工业与工程, 2023, 40(4): 37-49. JIANG Feng, XU Di, QI Guopeng, et al. Particle collision behavior and heat transfer performance in a Na2SO4 circulating fluidized bed evaporator[J]. Chemical Industry and Engineering, 2023, 40(4): 37-49. DOI:10.13353/j.issn.1004.9533.20210370 (in Chinese) |
| [24] |
ZHAO L, HE Y. Power spectrum estimation of the welch method based on imagery EEG[J]. Applied Mechanics and Materials, 2013, 278/279/280: 1260-1264. |
| [25] |
沈再阳. MATLAB信号处理[M]. 北京: 清华大学出版社, 2017: 240-241. SHEN Zaiyang. MATLAB signal processing[M]. Beijing: Tsinghua University Press, 2017: 240-241. (in Chinese) |
| [26] |
MONJI H, MATSUI G, SAITO T. Pressure drop reduction of liquid-particles two-phase flow with nearly equal density[M]. Amsterdam: Elsevier, 1995: 355-365.
|
| [27] |
JIANG F, ZHAO P, QI G, et al. Flow characteristics in a horizontal liquid-solid circulating fluidized bed[J]. Powder Technology, 2019, 342: 24-35. DOI:10.1016/j.powtec.2018.09.057 |
| [28] |
ESCUDERO D, HEINDEL T J. Bed height and material density effects on fluidized bed hydrodynamics[J]. Chemical Engineering Science, 2011, 66(16): 3648-3655. DOI:10.1016/j.ces.2011.04.036 |
| [29] |
LIU H, LI J, WANG Q. Simulation of gas-solid flow characteristics in a circulating fluidized bed based on a computational particle fluid dynamics model[J]. Powder Technology, 2017, 321: 132-142. DOI:10.1016/j.powtec.2017.07.040 |
 2024, Vol. 41
2024, Vol. 41





