2. 石油化工催化材料与反应工程国家重点实验室, 北京 102200
2. State Key Laboratory of Catalytic Materials and Reaction Engineering, RIPP, SINOPEC, Beijing 102200, China
晶型纯度和稳健的生产工艺是制药过程的要求和目标[1]。由于不同的构效关系,多晶型会对活性药物成分(API)的溶解度、稳定性和生物利用度等理化性质产生影响[2, 3]。多种晶型在某些条件下发生转化甚至伴随结晶会造成晶型混乱[4, 5],在实际生产中这是需要避免的。对于了解多晶型的聚集状态和成核路径,多晶型系统,特别是伴随多晶型可以提供更多相关信息[6, 7]。
伴随多晶型被定义为在同一条件下一种化合物同时出现2种或2种以上的晶型,两相伴随结晶的机理探索并不罕见,自首例伴随多晶型案例苯甲酰胺发现后[8],L-组氨酸[9]、邻氨基苯甲酸[10]、普拉格雷盐酸盐[11]、孕二烯酮[12]和托芬那酸[13]等都被报道存在包括多晶型及其溶剂化物[14, 15]的伴随结晶现象。伴随多晶型现象让人们对Ostwald规则[16]进行重新审视。Cardew等[17]提出了基于两相结晶的Ostwald比值的概念,利用动力学因素提供了一种预测多晶型结晶顺序和组成的手段。
磺胺噻唑(ST)是一种抗菌抗感染的药物(图 1),已被发现5种多晶型,并且在水中出现三相伴随结晶[18]。由于该体系多晶型形成的高灵敏度和复杂性,其已成为研究多晶型选择性制备的成熟模型[19-21]。值得注意的是,磺胺噻唑不同晶型的动力学数据未见报道,三相伴随结晶的机理也未见阐明。
|
| 图 1 磺胺噻唑的分子结构式 Fig.1 Molecular structure of sulfathiazole |
| |
本研究的动机是对磺胺噻唑的三相伴随结晶行为进行完整调研,包括测定纯水中3种晶型的热力学溶解度,探究不同初始过饱和度对磺胺噻唑多晶型产生及其生长速率的影响,分析伴随结晶过程中热力学和动力学的相互作用。本研究的另一目的是尝试将现有理论从两相推广到三相,这有助于实现更多复杂结晶过程的有效预测,对各种工业应用具有重要意义。
1 实验和方法 1.1 实验材料磺胺噻唑(天津希恩斯生化科技有限公司,质量分数98%);蒸馏水(电阻率为18.2 MΩ ·cm),实验室制备。
1.2 纯晶型的制备采用文献方法[22]制备了磺胺噻唑在本研究中的Form Ⅱ/Ⅲ/Ⅳ晶型。纯晶型均通过冷却不同溶剂的磺胺噻唑饱和溶液,结晶后过滤而得到。具体的操作参数见表 1。
| 晶型 | 溶剂 | 冷却速率/(℃·min-1) | 温度范围/℃ |
| Form Ⅱ | 乙腈 | 1.4 | 80→20 |
| Form Ⅲ | 水 | 0.1 | 80→20 |
| Form Ⅳ | 水 | ≈20.0 | 80→4 |
使用D/max2500(日本理学)粉末X射线衍射仪对多晶型进行表征。测试条件:Cu_Kα辐射(λ=1.5417 Å),操作电压40 kV,电流100 mA,扫描范围2θ=2°~40°,扫描步长为0.02°,扫描速度为8(°) ·min-1。使用Mercury4.0.0获得模拟粉末衍射图。
1.3.2 显微拉曼光谱激光显微拉曼光谱仪(英国雷尼绍,RENISHAW)的激光波长532 nm,激光光斑直径是1 μm,激光强度为5%,扫描模式为静态,曝光时间为1 s,扫描次数为10次。样品在室温下置于载玻片上避光测试,光谱范围为100~2 700 cm-1。
拉曼光谱仪为ReactRaman785(Mettler-Toledo, Greifensee, Switzerland)。光谱仪探头为蓝宝石材质,激光波长为785 nm,光谱信号通过光纤探针(MARQMETRI X)进行传输。实验中,在获得磺胺噻唑固相拉曼光谱时,曝光时长为1 s,扫描次数为10次,取样间隔为15 s。在100~2 700 cm-1的光谱范围内达到了70%的饱和度。
1.4 溶解度测定采用动态法测量磺胺噻唑Form Ⅱ/Ⅲ/Ⅳ在15~60 ℃内的溶解度,将低温程序控温仪调至设定温度,在结晶器内插入精密温度计(精度为0.01 ℃);向100 mL结晶器中加入质量为mw的水;多次向溶剂中加入已知质量的晶体,直至结晶器中晶体刚好溶清,再加入少量溶质,不会溶解。溶解完全时加入溶液中的所有磺胺噻唑的量为m。为了使得实验结果准确,每个实验重复测定3次。溶解度可以根据式(1)计算求得。
| $ x=\frac{m / M}{m / M+m_{\mathrm{w}} / M_{\mathrm{w}}} $ | (1) |
式(1)中:m和M分别是磺胺噻唑的质量和相对分子质量;mw和Mw分别是水的质量和相对分子质量。
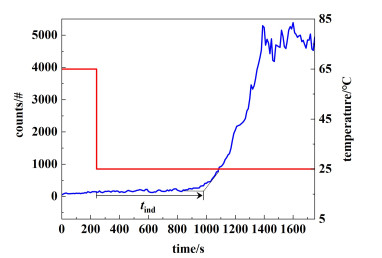
1.5 诱导期的测定采用配备快速冷却系统和聚焦光束反射率测量(FBRM)探头的结晶器来确定磺胺噻唑在不同过饱和度时的诱导期tind。根据Form Ⅱ的溶解度数据,定义过饱和度S=(c-ce)/ce。将一定量的磺胺噻唑转移到700 mL水溶液中,加热到65 ℃并平衡1 h以确保溶质完全溶解。随后,将溶液以约20 ℃ ·min-1的速率快速冷却至25 ℃。然后将结晶器保持恒温和300 r ·min-1恒速搅拌,直到发生成核。诱导期定义为从降温开始到溶液粒子数增大停止的时间,认为曲线的切线交点为成核点(图 2)。诱导期测量完毕后立即取出部分晶体,用显微镜观测晶习。经过过滤,干燥后采用PXRD确定所得晶体的晶型。
|
| 图 2 25 ℃下FBRM对成核诱导期的测定 Fig.2 Determination of nucleation induction period by FBRM at 25 ℃ |
| |
本工作中使用的聚焦光束反射率测量(FBRM)探头(G400型,Mettler Toledo,Swizerland)提供成核的原位监测。FBRM探头配合iC FBRM软件使用,用于记录和分析实验数据。对于所有测量实验,监测范围为1~1 000 m,采样间隔为10 s。
1.6 生长速率的测定采用生长池法测量不同晶型的生长速率。将预热至25 ℃的特制敞口结晶器中放置于体视显微镜下。配制初始过饱和度比为5的磺胺噻唑水溶液,升温至晶体完全溶解后,使用滤膜(0.2 μm)将溶液转移至结晶器中并开始计时。在晶体生长至观察时可以迅速找到目标晶型的晶体,以固定的时间间隔拍摄图像来原位记录其生长。使用ImageJ测量在不同时刻晶体的表面积,之后转化为具有等效表面积的正方形。晶体尺寸(L)定义为等效正方体的边长。
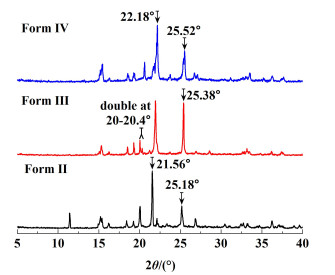
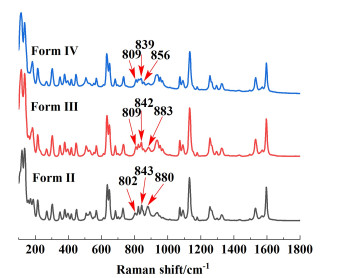
2 结果与讨论 2.1 磺胺噻唑纯晶型的表征依据文献[22]中的方法制备了磺胺噻唑Form Ⅱ/Ⅲ/Ⅳ 3种晶型,3种晶型的PXRD谱图与单晶数据和文献值[23]有较好的一致性。图 3中标注了3种晶型的较为明显的特征峰,其中Form Ⅱ的特征峰为21.56°和25.18°,Form Ⅲ的特征峰为25.38°和20.00°~20.40°的双峰,Form Ⅳ的特征峰为22.18°和25.52°。磺胺噻唑不同晶型具有比较集中的PXRD特征峰区域,样品为混合晶型时会出现特征峰的兼并,为了后续晶型鉴定的准确性,采集了3种晶型的拉曼光谱[24, 25],图 4显示了3种晶型在800~900 cm-1区域内具有较为明显的特征峰,其中Form Ⅱ的特征峰为802、843和880 cm-1,Form Ⅲ的特征峰为809、842和883 cm-1,Form Ⅳ的特征峰为809、839和856 cm-1。
|
| 图 3 磺胺噻唑纯晶型的PXRD图 Fig.3 PXRD pattern of pure crystal form of ST |
| |
|
| 图 4 磺胺噻唑纯晶型的拉曼光谱 Fig.4 Raman spectra of pure crystal form of ST |
| |
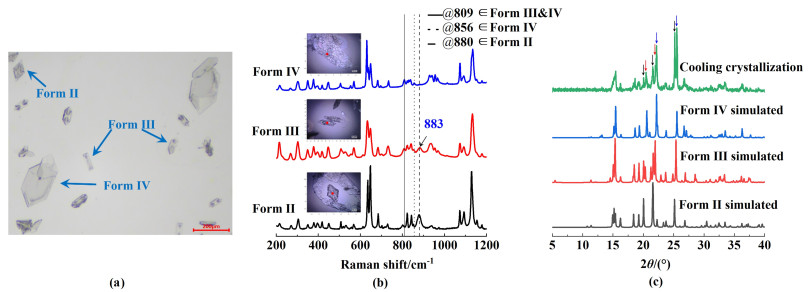
磺胺噻唑Form Ⅱ/Ⅲ/Ⅳ的伴随结晶根据文献条件[18]在水溶液中进行。3种伴随多晶型如图 5(a)所示。这3种多晶型可以从晶习大致区分为六边形板状的Form Ⅳ、棱柱状的Form Ⅲ和菱形板状的Form Ⅱ。晶型由显微拉曼光谱仪进行确认[图 5(b)]。和纯晶型拉曼光谱对比,光谱表明六边形板状晶体具有Form Ⅳ的809和856 cm-1特征峰,六边形棱柱状的晶体具有Form Ⅲ的809和883 cm-1特征峰,菱形板状晶体具有802和880 cm-1特征峰。该条件下的晶体也通过PXRD谱图鉴定,其中含有Form Ⅱ/Ⅲ/Ⅳ3种晶型的特征峰[图 5(c)]。
|
| 图 5 磺胺噻唑在水溶液中的伴随多晶型(a)显微镜图像; (b)显微拉曼光谱; (c)PXRD谱图 Fig.5 The phenomenon of ST concomitant polymorphism in aqueous solution (a) microscope image; (b) Raman microspectroscopies; (c) the XRD patterns |
| |
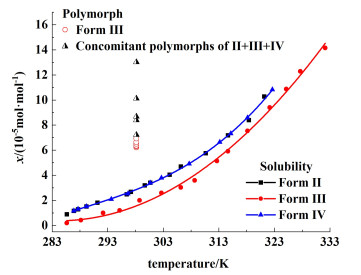
磺胺噻唑3种晶型的溶解度与温度之间的关系如图 6所示,在15~60 ℃的温度范围内,Form Ⅱ & Ⅳ的溶解度总是高于Form Ⅲ。值得注意的是,Form Ⅱ和Form Ⅳ在所测范围内具有高度类似的溶解度,这与文献[26]中报道的规律一致。溶解度曲线表明,在15~60 ℃的温度范围内,Form Ⅲ为热力学稳定晶型,Form Ⅱ和Form Ⅳ为亚稳晶型。同时图中显示了在25 ℃下过饱和度对不同晶型成核的影响,该温度下,溶液浓度低于6.94×10-5 mol ·mol-1时,只有Form Ⅲ成核;高于这个值会观察到3种晶型同时成核和生长的现象。从结晶热力学的角度,低过饱和度时结晶过程趋近稳定热力学,只析出稳定晶型。而在高过饱和度区域,溶质浓度达到了亚稳晶型的超溶解度,开始自发结晶,但2种亚稳晶型伴随Form Ⅲ同时结晶是违背Ostwald规则的。
|
| 图 6 磺胺噻唑多晶型成核区域和溶解度曲线 Fig.6 Nucleation regions and solubility curves of ST polymorphs |
| |
为了进一步了解磺胺噻唑伴随多晶型的机理,对其成核和生长过程进行了详细研究。经典成核理论被广泛应用于有机晶体的动力学研究中,它基于蒸汽冷凝成液体,被扩展到其他的液固平衡体系中[27, 28]。对于非球形晶体,成核过程中相变带来的自由能变化可以用式(2)表示。
| $ \Delta G=4 f_{\mathrm{s}} \gamma r^2+8 f_{\mathrm{v}} r^3 \Delta G_{\mathrm{v}} $ | (2) |
式(2)中:γ为界面能;fs和fv是粒子的表面形状因子和体积形状因子;ΔGv是相变过程中单位体积的自由能变化;r是晶体半径。
假设在溶液中通过添加机制形成分子团簇,这种机制一直持续到达临界粒径。小于该尺寸的分子团簇将溶解,高于临界粒径时,分子团簇将转变为原子核。可以通过d(ΔG)/dr=0得到临界半径
| $ r_{\mathrm{c}}=-\frac{f_{\mathrm{s}} \gamma}{3 f_{\mathrm{v}} \Delta G_{\mathrm{v}}} $ | (3) |
根据Gibbis-Thomson理论,对非电解质
| $ \Delta G_v=-\frac{2 \gamma}{r}=-\frac{k T \ln (S+1)}{v} $ | (4) |
式(4)中:k是玻尔兹曼常数;T是热力学温度;S是过饱和度;υ是分子体积。
给定固相的初级成核速率可表示为:
| $ J=A \exp \left[\frac{-4 f_{\mathrm{s}} \gamma^3 v^2}{27 f_{\mathrm{v}} k^3 T^3 \ln ^2(S+1)}\right] $ | (5) |
式(5)中:A是指前因子,也称动力学参数,在不同的动力学过程中有不同的表达式[29-31]。对于溶液体系,可以表示为:
| $ A=\frac{3}{2} D_{\mathrm{sl}} d_{\mathrm{m}^2}\left(C N_{\mathrm{A}}\right)^{\frac{7}{3}}\left(\frac{\gamma_{\mathrm{sl}} d_{\mathrm{m}}^2}{k T}\right)^{1 / 2} $ | (6) |
式(6)中:Dsl为溶质在溶剂中的扩散系数;dm为分子直径;C是溶液浓度。
成核诱导期(tind)包括分子团簇达到临界粒径的所需时间、成核时间和临界粒子生长到可监测尺寸所需时间,通常认为最后一项可以忽略[32]。此时诱导时间与初级成核速率呈反比,由式(6)可以得到:
| $ \ln t_{\mathrm{ind}}=-\ln B+\frac{4 f_{\mathrm{s}} \gamma^3 v^2}{27 f_{\mathrm{v}} k^3 T^3 \ln ^2(S+1)} $ | (7) |
式(7)中:B为经验常数,一般认为B与A成比例。那么lntind与1/ln2(S+1)成线性关系,直线的斜率为:
| $ \alpha=\frac{4 f_{\rm{s}}^3 \gamma^3 v^2}{27 f_{\rm{v}}^2 k^3 T^3} $ | (8) |
于是,可以使用斜率获得界面张力为:
| $ \gamma_i=\left(\frac{27 \alpha_i f_{\mathrm{v}, i}^2 k^3 T^3}{4 f_{\mathrm{s}, i}^3 v^2}\right)^{1 / 3} $ | (9) |
式(9)中:i为不同的多晶型。
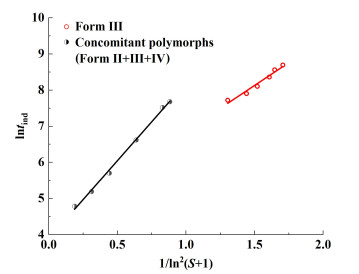
2.4.1 初级成核特征参数的计算为了分析tind的实验数据,图 7显示了lntind与1/ln2(S+1)的关系,由式(9)和该关系可确定磺胺噻唑多晶型的晶体-溶液界面张力(表 2)中。界面张力反映了溶质从溶液中自发成核的能力,其值越高,溶质越难成核。25 ℃下3种晶型的界面张力介于1.77~8.21 mJ ·m-2,与一般难溶于水的有机物相近[33]。稳定晶型Form Ⅲ具有较高的γ,而亚稳晶型中Form Ⅱ,Form Ⅳ具有更低的界面张力。此外,图 7中还显示了成核的多晶型取决于初始过饱和度,图 7中不同的直线代表了纯Form Ⅲ和伴随多晶型的初级成核。
|
| 图 7 25 ℃下不同晶型诱导期与过饱和度的关系 Fig.7 The relationship between supersaturation and the induction periods of different crystal forms at 25 ℃ |
| |
| 晶型 | fs | fv | α | γ/(mJ·m-2) |
| Form Ⅱ | 2.48 | 0.15 | 13.39 | 3.36 |
| Form Ⅲ | 6.49 | 1.33 | 4.31 | 8.21 |
| Form Ⅳ | 2.03 | 0.04 | 4.31 | 1.77 |
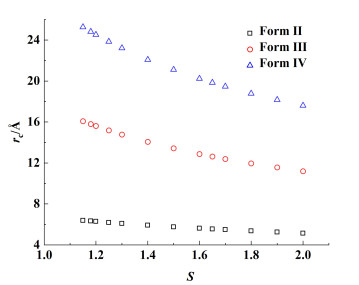
通过计算得到的界面张力,结合式(3)和式(4),可以推导出3种晶型临界核的半径。临界半径越小,成核的活化能垒越低。图 8给出了临界半径与过饱和度之间的关系。在高S区域(1.4~2.0)时,Form Ⅱ表现出最小的临界半径(~6 Å),Form Ⅳ需要最大的临界半径(22 Å),与继承临界核并生长成熟后晶体尺寸相比,这一结果是合理的。尽管Form Ⅳ的界面能小于Form Ⅱ,临界半径顺序的反转可以解释这2种热力学性质相近的亚稳晶型伴随结晶的原因。在热力学和动力学共同作用于结晶过程中时,3种晶型伴随结晶是可能的。
|
| 图 8 25 ℃下临界半径与过饱和度之间的关系 Fig.8 Relationship between critical radius and supersaturation at 25 ℃ |
| |
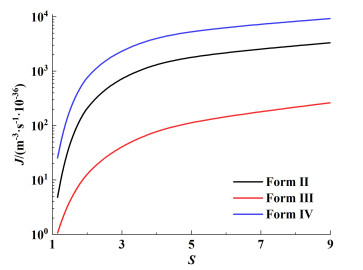
根据经典成核理论,通过成核参数计算了3种晶型的成核速率。在25 ℃下3种晶型的成核速率的演变如图 9所示。
|
| 图 9 不同晶型25 ℃时成核速率与过饱和度的关系 Fig.9 The relationship between nucleation rate and supersaturation of different crystal forms at 25 ℃ |
| |
在整个竞争过饱和度区间内,亚稳晶型Form Ⅱ和Ⅳ具有更高的成核速率。在较低的过饱和度(S<2)下,3种晶型的成核速率还在同一数量级,Form Ⅱ和Ⅳ的成核速率相近;随着S的增加,Form Ⅳ成为动力学优势晶型,成核速率较稳定晶型Form Ⅲ高2个数量级。这解释了在水中通过改变动力学参数制备磺胺噻唑Form Ⅲ和Form Ⅳ纯晶型。在降温结晶中,温度变化提供了过饱和度,当持续给予非常低的过饱和度时,热力学主导结晶过程,由于溶解度的差异,体系会先达到Form Ⅲ的超溶解度曲线而自发结晶释放过饱和度。当降温速率很大时,例如本工作中制备纯Form Ⅳ的骤冷,体系中的初始过饱和度几乎瞬间提升。在大过饱和度下,动力学主导结晶过程,较低的界面能和较大的成核速率使得Form Ⅳ成为该体系下的动力学最优晶型而优先结晶。在这种高结晶驱动力下,成核机制也会改变,螺旋位错[34]和二次成核机制会快速释放过饱和度以至于不会出现其他晶型。
2.4.2 生长动力学生长速率在一些伴随多晶型的动力学研究中是被忽略的。本工作中使用生长池法来测量晶体的线性生长速率。晶体生长是一个两步过程,包括溶质分子从溶液中扩散至晶体表面和晶体表面的添加[6, 12]。生长速率G可以表示为:
| $ G=k_{\mathrm{G}} \ln ^n(S+1) $ | (10) |
式(10)中:kG为生长速率常数;S为过饱和度;n为幂率指数,其值取决于生长机制。
图 10显示了通过显微镜原位观察的不同晶型的生长图像。图 11显示了生长速率[G(t)=dL/dt]与时间的关系。在25 ℃下,体系的过饱和度随着时间逐渐减小,发现Form Ⅱ和Form Ⅲ的整个过程的生长速率基本相同,Form Ⅳ的生长速率在420 s内高于Form Ⅱ和Form Ⅲ,之后3种晶型的以几乎相同的速率生长。可以得出结论,Form Ⅳ在生长过程中具有更强的消耗过饱和度的能力,是生长动力学偏好晶型。

|
| 图 10 不同晶型生长的图像(S=5,T=25 ℃) Fig.10 Images of different crystal forms growing (S=5, T=25 ℃) |
| |

|
| 图 11 不同晶型的生长速率随时间的变化 Fig.11 Growth rates of different crystal forms as a function of time |
| |
结合热力学溶解度和结晶动力学的实验结果,可以解释磺胺噻唑的伴随多晶型现象。磺胺噻唑水溶液中热力学和动力学之间相互作用的结果总结于表 3中。在25 ℃的结晶温度和低过饱和度(1.15<S<1.40)下,溶液浓度处于稳定晶型Form Ⅲ超溶解度和亚稳晶型Form Ⅱ和Form Ⅳ超溶解度之间,在均相成核条件下,不存在热力学竞争和动力学偏好。此时热力学主导结晶过程,体系仅结晶出纯的稳定晶型Form Ⅲ,这也是纯水中可以制备Form Ⅲ的原因。在高过饱和度(1.90<S<9.00), JⅣ>JⅡ>JⅢ且GⅣ>GⅢ≈GⅡ说明动力学最优晶型是Form Ⅳ,而热力学因素更倾向于稳定晶型Form Ⅲ。同时,Form Ⅱ显示出在临界半径rc上的有利地位,这使得溶质分子在以Form Ⅱ结构堆积时,更容易越过自由能壁垒从而成核。3种晶型的热稳定性已被报道,说明在水中3种晶型一旦成核,不会互相转化[23]。在本工作中,Form Ⅱ的成核并不能快速消耗过饱和度,动力学和热力学的竞争使得Form Ⅱ/Ⅲ/Ⅳ伴随结晶。可以预想到3种多晶型之间的比例不会是相等的。
| S | 动力学偏好 | 热力学偏好 | 结果 |
| 1.15~1.40 | 无注 | FⅢ | FⅢ |
| 1.90~9.00 | JⅣ>JⅡ>JⅢ, GⅣ>GⅢ≈GⅡ | FⅢ>FII≈FIV | 三相伴随结晶 |
| 注:没有达到亚稳晶型自发成核的超溶解度前,不存在动力学偏好。 | |||
伴随多晶型现象作为Ostwald定律的反例被广泛研究,Cardew等[17]提出了针对两相结晶过程的Ostwald比值:
| $ \varPhi_{\mathrm{os}}=\left(\frac{1}{\beta} \frac{J_{2, i} \rho_2 \phi_2 R_{2, i}^3}{J_{1, i} \rho_1 \phi_1 R_{1, i}^3}\right)^{1 / 3} $ | (11) |
式(11)中:下标j代表相,j=1, 2,Jj是成核速率,在非晶种系统中被认为与多晶型相对核数呈正比;ρj是晶体密度;φj是形状因子(假设生长过程中形状是相似的,等于本工作的体积形状因子fv);Rj是生长速率;下标i表示不同的过饱和度;β是热力学归一化常数,表示为:
| $ \beta=\frac{S_{2, i} c_{2, \mathrm{e}}}{S_{1, i} c_{1, \mathrm{e}}} $ | (12) |
该比率表明两相伴随结晶的条件是Φos=1。值得注意的是,以本研究中的参数求解每一对晶型的Φos都接近于1,这说明该理论在三相伴随结晶中也具备一定的适用性。同时,式(12)给出了一种量化结晶能力的指标,可以预测某个给定溶液状态的多晶型组成。亚稳晶型Form Ⅱ和Form Ⅳ的溶解度几乎一致,在每个过饱和度下的β相等,而稳定晶型的β为1。于是定义每个相的结晶能力正比于其Ostwald因子:
| $ \varPhi_{j, i}=\left(\beta J_{j, i} \rho_j \phi_j R_{j, i}^3\right)^{1 / 3} $ | (13) |
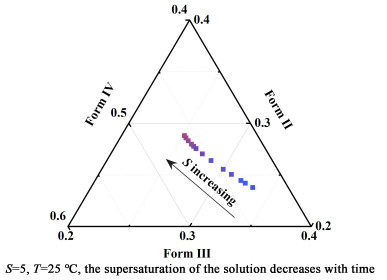
通过计算每个多晶型在某一过饱和度下的质量分数(=Φj, i/∑Φj, i),可以得到不同过饱和度下的三相多晶型相图。该理论假设晶型的竞争期开始于亚稳相的溶解度,而对于均相成核,实际的竞争期应起始于亚稳相的超溶解度,但这并不影响相图中的规律。如图 12所示,若以组成变化最快的阶段(S=1.3)为三相伴随结晶的起始点,在1.3<S<2.0的范围内,随着过饱和度的增加,Form Ⅲ的质量分数由30.02%下降至25.20%,Form Ⅱ和Form Ⅳ的质量分数分别从25.53%,44.45%上升至28.79%,46.02%。该相图预测的Form Ⅱ/Ⅲ/Ⅳ 3种晶型的比例约为1 ∶1 ∶2的多晶型组成与实际均相成核观察的晶型比例吻合。
|
| 图 12 25 ℃下水中降温结晶的多晶型相图,不同的点体现过饱和度的变化(1.15<S<2.00) Fig.12 The polymorphic phase diagram of cooling crystallization in aqueous solution at 25 ℃, different points reflect the change of supersaturation (1.15 < S < 2.00) |
| |
本工作详细研究了磺胺噻唑在水溶液中的伴随结晶行为并解释了其三相伴随结晶的机制。
结合晶习、PXRD和拉曼光谱中显示出显著差异,可联用以准确鉴定磺胺噻唑Form Ⅱ/Ⅲ/Ⅳ晶型。测定了磺胺噻唑Form Ⅱ/Ⅲ/Ⅳ在水中的溶解度,初步解释了降温结晶过程中,在低过饱和度下只形成稳定晶型Form Ⅲ,在高过饱和度下溶解度相同的亚稳晶型Form Ⅱ/Ⅳ与Form Ⅲ伴随结晶。该伴随多晶行为不符合经典Ostwald定律,但可通过热力学和动力学的相互作用来解释。
通过降温结晶成核诱导期测定,计算了不同多晶型的界面能、临界半径和成核速率。通过生长池法测量3种晶型的生长速率。结果表明,低过饱和度下不存在动力学偏好,热力学主导结晶过程,所以只出现稳定晶型Form Ⅲ;高过饱和度下,JⅣ>JⅡ>JⅢ且GⅣ>GⅢ≈GⅡ说明动力学最优的晶型是Form Ⅳ,具有最小临界半径的Form Ⅱ更易于越过自由能壁垒成核。因此,热力学和动力学的相互作用是三相伴随结晶的原因。
通过引入Ostwald比值预测了在水中磺胺噻唑降温结晶伴随多晶型的组成,量化了初始过饱和度的演变对磺胺噻唑多晶型三元相图的影响。预测结果与实际情况相近。这证明了热力学和动力学数据在整个结晶过程中的重要意义。
| [1] |
BERNSTEIN J. Polymorphism in molecular crystals[M]. Oxford: Oxford University Press, 2007.
|
| [2] |
RAZA K. Polymorphism: The phenomenon affecting the performance of drugs[J]. SOJ Pharmacy & Pharmaceutical Sciences, 2014. |
| [3] |
NOGUEIRA B A, CASTIGLIONI C, FAUSTO R. Color polymorphism in organic crystals[J]. Communications Chemistry, 2020, 3: 34. DOI:10.1038/s42004-020-0279-0 |
| [4] |
FOSTER J A, DAMODARAN K K, MAURIN A, et al. Pharmaceutical polymorph control in a drug-mimetic supramolecular gel[J]. Chemical Science, 2017, 8(1): 78-84. DOI:10.1039/C6SC04126D |
| [5] |
SAIKIA B, MULVEE M T, TORRES-MOYA I, et al. Drug mimetic organogelators for the control of concomitant crystallization of barbital and thalidomide[J]. Crystal Growth & Design, 2020, 20(12): 7989-7996. |
| [6] |
BLACK J F B, CARDEW P T, CRUZ-CABEZA A J, et al. Crystal nucleation and growth in a polymorphic system: Ostwald's rule, p-aminobenzoic acid and nucleation transition states[J]. CrystEngComm, 2018, 20(6): 768-776. DOI:10.1039/C7CE01960B |
| [7] |
TEYCHENÉ S, BISCANS B. Nucleation kinetics of polymorphs: Induction period and interfacial energy measurements[J]. Crystal Growth & Design, 2008, 8(4): 1133-1139. |
| [8] |
BERNSTEIN J, DAVEY R J, HENCK J O. Concomitant polymorphs[J]. Angewandte Chemie (International Ed in English), 1999, 38(23): 3440-3461. |
| [9] |
MARK ROELANDS C P, JIANG S F, KITAMURA M, et al. Antisolvent crystallization of the polymorphs of l-histidine as a function of supersaturation ratio and of solvent composition[J]. Crystal Growth & Design, 2006, 6(4): 955-963. |
| [10] |
JIANG S, TER H J H, JANSENS P J. Concomitant polymorphism of o-aminobenzoic acid in antisolvent crystallization[J]. Crystal Growth & Design, 2008, 8(1): 37-43. |
| [11] |
DU W, YIN Q, BAO Y, et al. Concomitant polymorphism of prasugrel hydrochloride in reactive crystallization[J]. Industrial & Engineering Chemistry Research, 2013, 52(46): 16182-16189. |
| [12] |
ZHU L, WANG L, SHA Z, et al. Interplay between thermodynamics and kinetics on polymorphic appearance in the solution crystallization of an enantiotropic system, gestodene[J]. Crystal Growth & Design, 2017, 17(9): 4582-4595. |
| [13] |
TANG W, SIMA A D, GONG J, et al. Kinetic difference between concomitant polymorphism and solvent-mediated phase transformation: A case of tolfenamic acid[J]. Crystal Growth & Design, 2020, 20(3): 1779-1788. |
| [14] |
WANG G, WANG Y, MA Y, et al. Concomitant crystallization of cefuroxime acid and its acetonitrile solvate in acetonitrile and water solution[J]. Industrial & Engineering Chemistry Research, 2014, 53(36): 14028-14035. |
| [15] |
JIA L, YIN Q, ZHOU L, et al. Insights into the mechanism of concomitant nucleation of form Ⅱ and ethanol solvate of spironolactone in cooling crystallization[J]. RSC Advances, 2018, 8(18): 9697-9706. DOI:10.1039/C7RA13094E |
| [16] |
OSTWALD W. Studien über die Bildung und Umwandlung fester Körper[J]. Zeitschrift Für Physikalische Chemie, 1897, 22U(1): 289-330. DOI:10.1515/zpch-1897-2233 |
| [17] |
CARDEW P, DAVEY R J. The Ostwald ratio, kinetic phase diagrams, and polymorph maps[J]. Crystal Growth & Design, 2019, 19(10): 5798-5810. |
| [18] |
SONG S, WANG L, YAO C, et al. Crystallization of sulfathiazole in gel: Polymorph selectivity and cross-nucleation[J]. Crystal Growth & Design, 2020, 20(1): 9-16. |
| [19] |
YU J, YAN J, JIANG L. Crystallization of polymorphic sulfathiazole controlled by femtosecond laser-induced cavitation bubbles[J]. Crystal Growth & Design, 2021, 21(6): 3202-3210. |
| [20] |
BORA P, SAIKIA B, SARMA B. Oriented crystallization on organic monolayers to control concomitant polymorphism[J]. Chemistry, 2020, 26(3): 699-710. DOI:10.1002/chem.201903938 |
| [21] |
LI W, IKNI A, SCOUFLAIRE P, et al. Non-photochemical laser-induced nucleation of sulfathiazole in a water/ethanol mixture[J]. Crystal Growth & Design, 2016, 16(5): 2514-2526. |
| [22] |
ABU BAKAR M R, NAGY Z K, RIELLY C D, et al. Investigation of the riddle of sulfathiazole polymorphism[J]. International Journal of Pharmaceutics, 2011, 414(1/2): 86-103. |
| [23] |
MUNROE Á, RASMUSON Å C, HODNETT B K, et al. Relative stabilities of the five polymorphs of sulfathiazole[J]. Crystal Growth & Design, 2012, 12(6): 2825-2835. |
| [24] |
MUNROE A, CROKER D, RASMUSON Å C, et al. Analysis of FⅡ crystals of sulfathiazole: Epitaxial growth of FⅡ on FIV[J]. CrystEngComm, 2011, 13(3): 831-834. DOI:10.1039/C0CE00221F |
| [25] |
LEE I S, LEE A Y, MYERSON A S. Concomitant polymorphism in confined environment[J]. Pharmaceutical Research, 2008, 25(4): 960-968. DOI:10.1007/s11095-007-9424-z |
| [26] |
TAKEBAYASHI Y, SUE K, FURUYA T, et al. Polymorphic solubility ratio of famotidine and sulfathiazole in various solvents[J]. Crystal Growth & Design, 2021, 21(5): 2868-2875. |
| [27] |
KARTHIKA S, RADHAKRISHNAN T K, KALAICHELVI P. A review of classical and nonclassical nucleation theories[J]. Crystal Growth & Design, 2016, 16(11): 6663-6681. |
| [28] |
FRENKEL J. A general theory of heterophase fluctuations and pretransition phenomena[J]. The Journal of Chemical Physics, 1939, 7(7): 538-547. DOI:10.1063/1.1750484 |
| [29] |
KASHCHIEV D, VAN ROSMALEN G M. Review: Nucleation in solutions revisited[J]. Crystal Research and Technology, 2003, 38(7/8): 555-574. |
| [30] |
VEKILOV P G. Nucleation[J]. Crystal Growth & Design, 2010, 10(12): 5007-5019. |
| [31] |
LIU J, SVÄRD M, RASMUSON Å C. Influence of Agitation and Fluid Shear on Nucleation of m-Hydroxybenzoic Acid Polymorphs[J]. Crystal Growth & Design, 2014, 14(11): 5521-5531. |
| [32] |
LENKA M, SARKAR D. Determination of metastable zone width, induction period and primary nucleation kinetics for cooling crystallization of l-asparaginenohydrate[J]. Journal of Crystal Growth, 2014, 408: 85-90. DOI:10.1016/j.jcrysgro.2014.09.027 |
| [33] |
DAVEY R J, SCHROEDER S L M, TER HORST J H. Nucleation of organic crystals: A molecular perspective[J]. Angewandte Chemie (International Ed in English), 2013, 52(8): 2166-2179. DOI:10.1002/anie.201204824 |
| [34] |
SHTUKENBERG A G, HU L, SAHOTA A, et al. Disrupting crystal growth through molecular recognition: Designer therapies for kidney stone prevention[J]. Accounts of Chemical Research, 2022, 55(4): 516-525. DOI:10.1021/acs.accounts.1c00631 |
 2024, Vol. 41
2024, Vol. 41





