2. 天津大陆制氢设备有限公司,天津 301600
2. Tianjin Mainland Hydrogen Equipment Co., Ltd., Tianjin 301609, China
全球气候变化加剧是目前威胁人类生存发展的巨大挑战,而化石能源使用导致的温室气体的大量排放是影响气候变化的主要因素之一[1]。风能和太阳能等可再生能源由于其不稳定和不连续的特点难以被直接并网利用[2]。因此将这些可再生能源产生的电能利用水电解技术转化为氢气储存起来,有利于可再生能源的有效利用,同时也是未来绿色制氢的重要途径之一[3]。
无膜水电解是指在常规水电解的基本结构中除去隔膜这一组件,从而移除隔膜的成本、使用寿命等因素对水电解系统的影响。为保证产物的纯度通过增大电解液流速将阴阳极产物从多孔电极中带出,从而降低气泡在电极上的覆盖率以降低欧姆过电位和活性表面积变化引起的活化过电位同时促进产物分离。无膜电解水技术相较于传统碱性水电解技术而言,可以有效降低氢气产生的能耗同时在较高电流密度(>800 mA·cm-2)下工作[4]。文献报道的无膜水电解器有平板电极和穿流电极两种类型。基于平板电极的无膜水电解装置是由Hashemi等[5]开发的。电解液平行于电极层流流动将产物从下游出口带出,电极间隙可以缩小到几百微米,但是这种装置只能在较小的流速和电流密度的范围内应用,难以大规模使用,同时产物纯度波动较大。而穿流电极式的无膜水电解装置则是由Gillespie等[6]开发的。相较于平板电极的装置而言,穿流多孔电极增大了活性面积的同时,电解液流动穿过电极也可以及时带走气体产物,使得电极间隙中的气泡产物忽略不计,从而降低电阻。但是其工况的确定需要考虑电极间隙、流体流速以及电流密度大小的配合程度。
本论文首次建立了穿流电极无膜水电解的二维数值模型,考虑了系统内部质量、动量、电荷传递以及电化学反应之间的相互耦合; 分析讨论了其系统压力、流速、通量以及浓度的分布情况。着重考察了电解液流速、电极间距以及电流密度大小的适配情况,分析了有关反应活化、气泡和欧姆阻抗等影响的过电位在总电压中的占比情况,探究了系统的合适运行工况范围,从而为后续设计和过程优化提供参考。
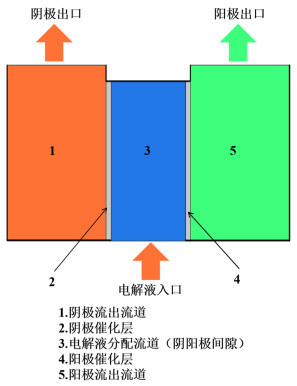
1 模型与求解 1.1 基本模型概述在模型中计算区域可以分成5个主要部分:阴极流出流道、阴极催化层、电解液分配流道(阴阳极间隙)、阳极催化层和阳极流出流道,如图 1所示。在装置运行过程中,电解液从分配流道流入装置,在水压作用下从两侧穿过阴阳极催化层,最后带着反应产物从流出流道顶部流出装置。图 1中粗线部分为不可透过壁面。阴阳极催化层为多孔介质。阴阳极电极反应如式(1)和式(2)。
|
| 图 1 穿流电极无膜水电解过程与计算区域示意图 Fig.1 Schematic diagram of electrode-flow-through membrane-less water electrolysis process and calculation area |
| |
Cathode:
| $ \mathrm{H}_2 \mathrm{O}+\mathrm{e}^{-} \rightarrow \frac{1}{2} \mathrm{H}_2 \uparrow+\mathrm{OH}^{-} $ | (1) |
Anode:
| $ \mathrm{OH}^{-} \rightarrow \frac{1}{2} \mathrm{H}_2 \mathrm{O}+\frac{1}{4} \mathrm{O}_2 \uparrow+\mathrm{e}^{-} $ | (2) |
为简化计算,模型的基本假设如下:(1) 产物H2和O2为理想气体;(2) 忽略重力影响;(3)电解液流速较快,气体产物以气泡形式被均匀分散于电解液中,气体产物与液相无相对运动;(4) 阴极和阳极催化层部分为均匀的多孔介质;(5) 由于电解液在系统中流速较快比热容较高热量易被带出系统,因此忽略电化学反应产生的热量影响,整个系统处于恒温状态;(6)由于气体产物溶解在水中的质量远低于气相质量,因此溶解在水中的气体可以忽略不计。
1.2 基本方程及边界条件 1.2.1 质量传递与动量传递在系统中,由于电解液流速较快,流动相为电解液,产物气体为分散相以气泡形式均匀分散在电解液中。气液两相混合物可以用均质流的混合物模型进行计算,那么对于气液混合物而言,总质量守恒方程可以表示为:
| $ \nabla \cdot N=\nabla \cdot(\rho v)=Q $ | (3) |
式(3)中:N为总质量通量;ρ为气液混合物平均密度;v为体积平均流速;Q为质量源。
气液混合物在系统内的速度与压力关系可以通过Brinkman方程[7]表示:
| $ \begin{gathered} \frac{\rho}{\varepsilon}(\nabla \cdot v) \frac{v}{\varepsilon}=-\nabla p+\nabla \cdot \\ \left\{\frac{1}{\varepsilon}\left[\mu\left(\nabla v+(\nabla v)^{\mathrm{T}}\right)-\frac{2}{3} \mu(\nabla \cdot v) I\right]\right\}- \\ \left(\frac{\mu}{\kappa}+\frac{Q}{\varepsilon^2}\right) v \end{gathered} $ | (4) |
式(4)中:ε为流动区域的孔隙率(在空流道内孔隙率为1);p为混合物压力;μ为流体的黏度;κ为渗透率(空流道时μ/κ不存在);I为单位张量。气液混合物的平均密度、黏度参数可以用以式(5)和式(6)计算:
| $ \rho=\sum x_\alpha \rho_\alpha, \mu=\sum x_\alpha \mu_\alpha $ | (5) |
| $ x_1+x_{\mathrm{q}}=1 $ | (6) |
式(5)和式(6)中:xα表示相α在气液混合物中的体积分数;l为液相;q为气相。
由于在催化层中会产生气体,导致催化层附近的流体的平均密度会低于于电极间隙内流体的平均密度,会发生由密度导致的微小湍流,此时在模型中的相体积分数的传递可以通过式(7)[8]获得:
| $ \nabla \cdot N_\alpha=\nabla\left(x_\alpha \rho_\alpha v_\alpha-\rho_\alpha D_{\mathrm{m}} \nabla x_\alpha\right)=Q_\alpha $ | (7) |
式(7)中:Nα表示相α的质量通量;α表示气相或液相;Dm表示湍流分散相扩散系数(计算时取5×10-6 m2·s-1);vα表示气液相的流速。由于采用均质流的混合物模型,气液相流速相等。
对于系统中的电解液而言,电解液中的阴阳离子不仅受到电解液流动影响,同时还受电势以及扩散影响。由于使用的电解液的浓度较高,为了计算电解液中的离子浓度分布,溶液中阴阳离子传递的通量可以通过Newman等[9]提出的浓电解质理论,此时溶液中阴阳离子的总通量守恒及通量可表示为:
| $ \nabla \cdot N_i^{\prime}=R_i $ | (8) |
| $ N_i^{\prime}=-D_{\mathrm{c}, \text { eff }} \frac{c_0}{c_{\mathrm{T}}} \nabla c_i+\frac{i_{\mathrm{\jmath}} t_i}{z_i F}+c_i v $ | (9) |
式(8)和式(9)中:N′i为组分i的摩尔通量;i为电解质溶液中的阴阳离子(OH-和K+);ci为组分i的浓度;Ri为反应源项;Dc,eff为KOH的有效扩散系数;c0为溶剂的浓度,即H2O的浓度;cT为溶剂及溶质总浓度;il为离子电流密度;zi为电荷数;F为法拉第常数;ti为组分i相对于电解液的离子迁移数。ti由式(10)计算:
| $ t_i=\frac{t_i^0 c_0+c_k}{c_{\mathrm{T}}}, k \neq i $ | (10) |
式(10)中:ti0为组分i的迁移数。同时考虑电中性:
| $ \sum z_i c_i=0 $ | (11) |
KOH的有效整体扩散系数Dc, eff是由整体扩散系数Dc根据Bruggeman修正计算:
| $ D_{\mathrm{c}, \mathrm{eff}}=\frac{\varepsilon_1}{\tau} D_{\mathrm{c}}, \tau=\varepsilon_1^{-\beta} $ | (12) |
式(12)中:εl为液相占计算区域的体积分数;τ为曲折因子;β为关联系数。液相的体积分数与多孔介质的孔隙率ε(空流道为1)以及产物气体的体积分数有关,由式(13)计算。
| $ \varepsilon_1=\varepsilon\left(1-x_{\mathrm{g}}\right) $ | (13) |
本模型中催化层由于发生水电解的电化学反应,因此催化层中存在H2以及O2源项,其大小由法拉第定律计算可得:
| $ Q_{\mathrm{H}_2}=\frac{i_{\text {loc }, \mathrm{c}} M_{\mathrm{H}_2}}{2 F} $ | (14) |
| $ Q_{\mathrm{o}_2}=\frac{i_{\mathrm{loc, a}} M_{\mathrm{O}_2}}{4 F} $ | (15) |
式(14)和式(15)中:iloc, a、iloc, c分为单位体积内的阳极局部电流密度和阴极局部电流密度,M为摩尔质量。同时,在阴阳两极催化层中还包括了反应物水的消耗以及生成过程,水的消耗和生成源项也可以用法拉第定律计算。
| $ Q_{\mathrm{H}_2 \mathrm{O}, \mathrm{c}}=-\frac{i_{\text {loc }, \mathrm{e}} M_{\mathrm{H}_2 \mathrm{O}}}{F} $ | (16) |
| $ Q_{\mathrm{H}_2 \mathrm{O}, \mathrm{a}}=\frac{i_{\mathrm{loc}, \mathrm{a}} M_{\mathrm{H}_2 \mathrm{O}}}{2 F} $ | (17) |
除了电极催化层处存在质量源,空流道处(图 1中1、3、5区域)质量源为0,阴极和阳极流出流道出口处压力设定为常压,即101.325 kPa。电解液入口处为初始输入流量Qin, 0。
对于系统中的电解质溶液而言,在阴极催化层和阳极催化层处由于电化学反应会分别产生和消耗OH-,生成和消耗的源项也通过法拉第定律计算。
| $ R_{\mathrm{OH}^{-}, \mathrm{c}}=\frac{i_{\mathrm{loc}, \mathrm{c}}}{F} $ | (18) |
| $ R_{\mathrm{OH}^{-}, \mathrm{a}}=-\frac{i_{\mathrm{loc}, \mathrm{a}}}{F} $ | (19) |
同时,电解液入口浓度为初始电解液浓度ce,系统的各个壁面均设为无滑移。
1.2.2 电荷传递由于多孔电极催化层的电导率很高,固体部分电势梯度可以忽略不计,催化层各处电势均为φs。
中间电解液分配流道内KOH溶液的电荷守恒方程为:
| $ \nabla \cdot i_1=0 $ | (20) |
式(20)中离子电流密度il表示为[10]:
| $ i_1=-\sigma_1 \nabla \phi_1-\frac{\sigma_1}{F}\left(\frac{t_{+}^0}{z_{+} v_{+}}+\frac{c_{\mathrm{e}}}{2 c_0}\right) \nabla \mu_{\mathrm{e}} $ | (21) |
式(20)和式(21)中:σl为KOH溶液电导率;φl为KOH溶液的电势;ce为KOH的总浓度;μe为KOH的化学势。KOH的化学势梯度和KOH的浓度梯度存在如式(22)关系[9]:
| $ \nabla \mu_{\mathrm{e}}=\frac{\left(v_{+}+v_{-}\right) R T}{c_{\mathrm{e}}}\left[1+\frac{\mathrm{d}\left(\ln \gamma_{ \pm}\right)}{\mathrm{d}(\ln m)}\right]\left[1-\frac{\mathrm{d}\left(\ln c_0\right)}{\mathrm{d}\left(\ln c_{\mathrm{e}}\right)}\right] \nabla c_{\mathrm{e}} $ | (22) |
式(22)中:v+、v-分别为K+和OH-解离度;γ±为KOH的平均活度系数,m为KOH的质量浓度。
将式(22)带入式(21)得到离子电流与电势梯度和浓度梯度的关系:
| $ \begin{gathered} i_1=-\sigma_1 \nabla \phi_1-\frac{\sigma_1}{F} \frac{\left(\nu_{+}+\nu_{-}\right) R T}{c_0} \\ \left(\frac{t_{+}^0}{z_{+} \nu_{+}}+\frac{c_{\mathrm{e}}}{2 c_0}\right)\left[1+\frac{\mathrm{d}\left(\ln \gamma_{ \pm}\right)}{\mathrm{d}(\ln m)}\right]\left[1-\frac{\mathrm{d}\left(\ln c_0\right)}{\mathrm{d}\left(\ln c_{\mathrm{e}}\right)}\right] \nabla c_{\mathrm{e}} \end{gathered} $ | (23) |
由于电极部分为多孔介质区域,此时溶液有效电导率需要用Bruggeman修正计算:
| $ \sigma_{1, \mathrm{eff}}=\frac{\varepsilon_1}{\tau} \sigma_1, \tau=\varepsilon_1^{-\beta} $ | (24) |
考虑到气泡影响,将式(13)带入式(24)以得到溶液有效电导率σl, eff为:
| $ \sigma_{1, \mathrm{eff}}=\varepsilon_1{ }^{1+\beta} \sigma=\left[\varepsilon\left(1-x_{\mathrm{q}}\right)\right]^{1+\beta} \sigma_1 $ | (25) |
考虑到在系统中阴极的电位最低,将阴极电位ϕs, c设定为0 V,因此,阳极电位φs, a等于系统的总电压Ucell。两电极间由于电解液电阻以及气泡空隙产生的欧姆过电位ηohm可以用阴阳极的液相电势差计算。
| $ \eta_{\text {ohm }}=\varphi_{1, \mathrm{a}}-\varphi_{1, \mathrm{c}} $ | (26) |
电极的过电位是指由于浓差、活化等因素导致的实际电极电位偏离平衡电极电位的程度。本模型选用参考浓度cref和实际温度T作为计算过电位的基准,此时电极的平衡电极电位Eeq, T可表示为:
| $ E_{\text {eq }, \mathrm{T}}=E_{\text {eq }, \text { ref }}+\frac{\mathrm{d} E_{\text {eq }}}{\mathrm{d} T}\left(T-T_{\text {ref }}\right) $ | (27) |
式(27)中,Eeq, ref为参考状态(参考温度Tref、参考浓度cref)时的平衡电极电位;dEeq/dT为平衡电极电位的温度系数。
电极的过电位是偏离平衡电位的大小,这里可以用式(28)计算。
| $ \eta=\phi_{\mathrm{s}}-\phi_1-E_{\mathrm{eq}, \mathrm{T}} $ | (28) |
在电解液穿过催化层的过程中,流体流动会带走反应产生的气体,有效减少多孔电极内部的气泡覆盖面积。根据Ojong和Smolinka[11]研究,多孔电极的气泡覆盖率与多孔电极区域的供水-产气速率比(ς)以及多孔电极的空隙气泡比(pore-to-bubble-ratio, RPB)相关,气泡覆盖率的计算经验公式可表示为:
| $ \theta=\frac{R_{\mathrm{PB}}}{\varsigma} $ | (29) |
| $ R_{\mathrm{PB}}=\frac{4 d_{\text {bubble }}^2}{d_{\text {pore }}^2}, \varsigma=\frac{v_1 n F}{V_{\mathrm{m}} i_{\text {loc }}} $ | (30) |
式(30)中:dbubble为气泡直径大小;dpore为多孔介质孔径大小;vl为液体流速;n为转移电荷数;Vm为理想气体的气体摩尔体积。因此实际工作活性面积Aact为:
| $ A_{\mathrm{act}}=A(1-\theta) $ | (31) |
式(31)中:A为本征活性面积。由于实际活性面积的降低,实际电流密度iact高于本征电流密度iact, 0。
| $ i_{\text {act }, 0}=\frac{i_{\text {all }}}{A}, i_{\text {act }}=\frac{i_{\text {all }}}{A_{\text {act }}}=\frac{i_{\text {all }}}{A(1-\theta)} $ | (32) |
式(32)中,iall为总电流大小。
阴极和阳极的过电位ηact与局部电流密度iloc的可以通过Butler-Volmer方程关联:
| $ i_{\text {loc }}=i_0\left\{\exp \left(\frac{\alpha_{\mathrm{f}} F \eta_{\text {act }}}{R T}\right)-\exp \left[\frac{-\left(1-\alpha_{\mathrm{f}}\right) F \eta_{\text {act }}}{R T}\right]\right\} $ | (33) |
| $ i_0=i_{0, T}\left(\frac{c_{\mathrm{R}}}{c_{\text {ref }}}\right)^{\left(1-\alpha_{\mathrm{f}}\right)}\left(\frac{c_{\mathrm{o}}}{c_{\text {ref }}}\right)^{\alpha_{\mathrm{f}}} $ | (34) |
| $ i_{0, \mathrm{~T}}=i_{0, \mathrm{ref}} \exp \left[-\frac{E_{\mathrm{act}}}{R}\left(\frac{1}{T}-\frac{1}{T_{\mathrm{ref}}}\right)\right] $ | (35) |
式(33)~式(35)中:i0为实际温度和浓度下的本征交换电流密度;i0, T为基准状态(T)下的本征交换电流密度;i0, ref为参考状态(Tref,cref)下本征交换电流密度;Eact为电极反应活化能;αf为电极反应的正向传递系数;cR和cO为阴阳极中还原态和氧化态组分浓度。
在电化学过程中,阴阳极的过电位η可以分解为活化过电位ηact以及浓差过电位ηconc 2个部分,由Nernst方程:
| $ E_{\mathrm{eq}}=E_{\mathrm{eq}, \mathrm{T}}-\frac{R T}{F} \ln \frac{c_{\mathrm{R}}}{c_0} $ | (36) |
这里的Eeq表示的是电极表面附件实际浓度ce和实际温度T时候对应的电极平衡电位,那么此时电极的实际活化过电位ηact可以表示为:
| $ \eta_{\mathrm{act}}=\phi_{\mathrm{s}}-\phi_1-E_{\mathrm{eq}} $ | (37) |
由式(28)和(37)可以得到浓差过电位ηconc为:
| $ \eta_{\text {conc }}=\eta-\eta_{\text {act }}=-\frac{R T}{F} \ln \frac{c_{\mathrm{R}}}{c_0} $ | (38) |
通过Butler-Volmer方程可以分别计算实际电流密度iact以及本征电流密度iact, 0下的实际活化过电位ηact以及本征活化过电位ηact, 0从而得到气泡覆盖影响活化过电位。
| $ \Delta \eta_{\text {act }}=\eta_{\text {act }}-\eta_{\text {act }, 0} $ | (39) |
综上,阴极和阳极的过电位可以表示为:
| $ \eta=\eta_{\mathrm{conc}}+\eta_{\mathrm{act}}=\eta_{\mathrm{conc}}+\eta_{\mathrm{act}, 0}+\Delta \eta_{\mathrm{act}} $ | (40) |
所以总压Ucell可以表示为式(41)。
| $ U_{\text {cell }}=E_{\text {eq }, \mathrm{T}}+\eta_{\text {conc }}+\eta_{\mathrm{act}, 0}+\Delta \eta_{\text {act }}+\eta_{\text {ohm }} $ | (41) |
利用COMSOL Multiphysics软件对模型进行有限元求解计算。为了确保精度要求选用细化的自由三角形网格对整个系统进行剖分,求解器相对误差设定为10-5。求解过程分成4个步骤进行,首先对系统内的电流分布进行初始化,随后求解流体流动的质量与动量传递的耦合,再对气液两相之间的相传递过程和流体流动进行耦合计算,将计算结果作为初值,对所有传递过程进行全耦合计算求解得到最终结果。
系统各区域的材料及几何参数如表 1所示。
| 计算区域 | 参数 | 材料 | |||
| 厚度/ mm | 高度/ mm | 孔隙率ε | 孔径dpore/μm | ||
| 阴极流出流道 | 8.0 | 22 | |||
| 阴极催化层 | 0.4 | 20 | 0.85 | 50 | 不锈钢毡 |
| 电解液分配流道 | 6.0 | 20 | |||
| 阳极催化层 | 0.4 | 20 | 0.85 | 50 | 不锈钢毡 |
| 阳极流出流道 | 8.0 | 22 | |||
多孔催化层的绝对渗透率K可按式(42)计算[12]:
| $ K=0.005 \varepsilon^3 d_{\text {pore }}^2 $ | (42) |
则其在非饱和状态下渗透率可表示为[13]:
| $ \kappa=K x_1^{\mathrm{q}} $ | (43) |
模型的其他相关物性参数如下所示:对于气相产物而言,密度ρg按照理想气体进行计算。黏度μg等气体的其他参数可通过COMSOL内置的热力学系统模块获取。
KOH溶液的密度ρl以及电导率σl可以用Gilliam等[14]的经验关联式计算,黏度μl可以用Zhou等[15]的经验关联式计算。KOH的平均活度系数γ±可以采用Akerlof等[16]的关联式计算。
电解液中阴阳离子的离子迁移数t+0和t-0通过离子极限摩尔电导率计算:
| $ t_{+}^0=\frac{\lambda_{+}^0}{\lambda_{+}^0+\lambda_{-}^0}, t_{-}^0=\frac{\lambda_{-}^0}{\lambda_{+}^0+\lambda_{-}^0} $ | (44) |
式(44)中:K+、OH-的离子极限摩尔电导率λ+0、λ-0通过Robinson等[17]的关联式进行计算。KOH的扩散系数Dc可以通过Newman等[9]关联式以及Akerlof和Otakar等关联式[16, 18]计算。
电极反应动力学参数如表 2所示。
| 参数 | 参数值 | 出处 | |
| 阴极 | 阳极 | ||
| 参考浓度ci, ref/(mol·L-1) | 1 | ||
| 参考压力pi, ref/kPa | 100 | ||
| 参考温度Tref/℃ | 25 | ||
| 参考平衡电极电位Eeq, ref/V | 0.828[19] | 0.401[19] | 式(27) |
| 平衡电极电位的温度系数(dEeq/dT)/(mV·K-1) | -0.836[19] | -1.682[19] | 式(27) |
| 参考状态下本征交换电流密度i0, ref/(mA·cm-2) | 7 000[20] | 0.001 029 2 | 式(35) |
| 活化能Eact/(kJ·mol-1) | 29.5[20] | 0.548 | 式(35) |
| 正向传递系数αf | 0.5[20] | 0.896 | 式(34) |
模型进行计算求解的基准条件如表 3所示。
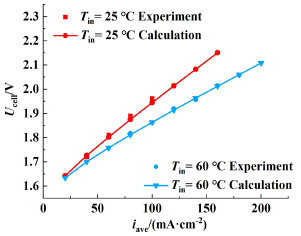
模拟结果与实验数据的对比如图 2所示[22],电解液入口流量为1 000 mL·min-1,电解液浓度为1 mol·L-1时,其他条件同表 1~表 3所示。通过对比可看出模拟结果与实验数据较吻合,模型具有一定的准确性。
|
| 图 2 电解液入口流量为1 000 mL·min-1,电解液浓度为1 mol·L-1时,模拟与实验测定极化曲线的对比情况 Fig.2 Comparison of simulated and experimental polarization curves, when electrolyte inlet flow rate is 1 000 mL·min-1 and concentration of electrolyte is 1 mol·L-1 |
| |
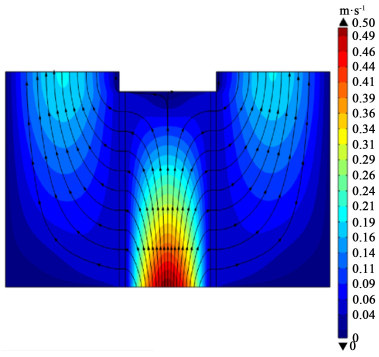
在电解液流动区域的气液混合物流速分布以及总通量的流线分布如图 3所示。由于入口管道直径和间隙厚度一致,电解液从入口进入系统时流动方式未发生变化,因此入口处流速分布满足充分发展的层流流动特点,即中间流速最快,靠近两侧的层流边界层流速逐渐降低。在电解液分配流道中,电解液进入装置后就会在压力作用下在间隙内边流动边穿过催化层,所以整体流速呈现沿垂直方向逐渐降低的趋势。在两侧出口流道内,由于电极两极产气量不同,阴极较多,阳极较少,因此阴极出口混合物流速高于阳极出口混合物流速。
|
| 图 3 入口流量为20 mL·s-1(平均流速为0.33 m·s-1),平均电流密度为400 mA·cm-2时,系统电解液速度分布及总通量流线分布 Fig.3 20 mL·s-1 inlet flow rate (average velocity is 0.33 m·s-1), 100 mA·cm-2 average current density, distribution of electrolyte velocity and distribution of total flux streamline |
| |
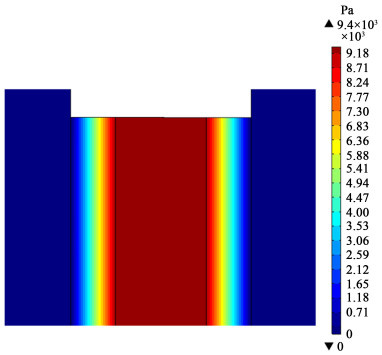
为了将产物从催化层中带走,我们需要让系统内电解液的压降维持在催化层两侧,利用压力差将产物气体带出。选用阻力较大的多孔介质作为电极催化层的基底,会使得整个系统流动阻力主要存在于催化层部分。为了更好的展示催化层处的压力分布,这里将催化层厚度和其他流道部分归一化。此时系统的电解液流动压力分布如图 4所示,其中催化层部分可以明显看到电解液的压力梯度主要集中在催化层部分。
|
| 图 4 入口流量为20 mL·s-1(平均流速为0.33 m·s-1),平均电流密度为100 mA·cm-2时,系统内部电解液压力分布情况 Fig.4 20 mL·s-1 inlet flow rate (average velocity is 0.33 m·s-1), 100 mA·cm-2 average current density, distribution of electrolyte pressure in the system |
| |
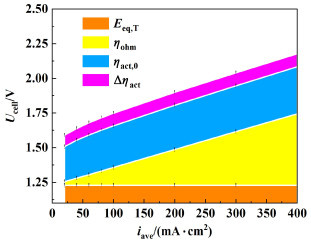
系统中各个部分的过电位在总电压中的占比如图 5所示。在系统中电解液会流动穿过电极,从式(38)以及电极反应式(1)和(2)可知在反应中OH-为还原态组分,电极两侧的浓度极化影响相互抵消,因此在总电压的组成中浓差过电位ηconc近乎于0,可以忽略。由于中间电解液分配流道的初始尺寸为6 mm,电解液部分电阻较大,因此在整个系统中欧姆过电位ηohm占据了总电压的很大一部分。同时在总压中气泡覆盖引起的活化过电位Δηact也在其中占据比较大的部分且随电流密度增大而增大。在入口流量为20 mL·s-1时,由于流体流动速度较快,低电流密度下增大幅度较低。
|
| 图 5 入口流量20 mL·s-1(平均流速为0.33 m·s-1)下,各部分过电位在总电压中的占比 Fig.5 Proportion of each part of overpotential in total voltage at 20 mL·s-1 inlet flow rate (average velocity is 0.33 m·s-1) |
| |
对于无膜水电解系统而言,电解液流动穿过电极,不仅可以带走反应产生的气体降低气泡对过电位的影响、降低阴阳两极的浓差极化引起的浓差过电位,还可以帮助产物气体分离从而提高产物纯度。
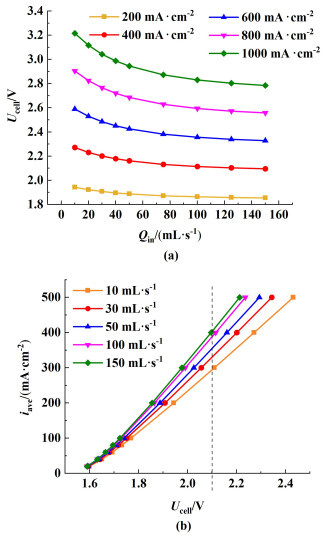
从图 6中可以看出,随着电解液流速的增加系统的总电压会逐渐下降,但是下降的幅度会逐渐降低,高电流密度时流速影响比较明显,低电流密度时流速的影响较低。在相同电位条件下[图 6(b)中虚线处]可看到流量的增大会有效提高电流密度,但是电流密度的提高的比例逐渐下降。从图 6中可以看出流速对水电解的总电压影响存在一定的局限性。在高流速下总电压有小幅度降低,但是这会导致在泵以及装置续流程中产生不必要的能量损耗。
|
| 图 6 (a) 不同电流密度下,入口流量对电压的影响;(b)不同入口流量下,电压和电流密度的关系 Fig.6 (a) Influence of inlet flow rate on voltage at different current densities; (b) the relationship between voltage and current density at different inlet flow rates |
| |
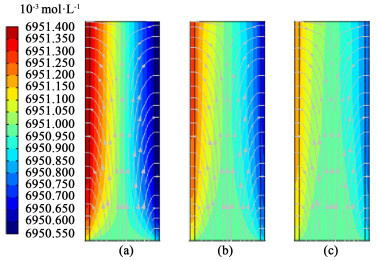
入口流量大小还会影响电解液分配流道及多孔电极区域中的电解液浓度分布,由于阴极反应产生OH-、阳极反应消耗OH-,同时电解液中的K+和OH-会在电场作用下发生迁移现象,所以在阴极附近KOH浓度较高,阳极附近浓度较低。如图 7所示,随着流量的增加阴阳两极附近的浓差降低,整个流道内浓度趋向于均匀化(和输入电解质浓度一致),均匀化的浓度使得阴阳两极的浓度极化程度抵消,从而降低系统的总压降。
|
| 图 7 电流密度为400 mA·cm-2时,不同入口流量下的电解液分配流道及多孔电极内部KOH浓度分布及总通量分布:(a)入口流量为10 mL·s-1(流速为0.16 m·s-1); (b)入口流量为30 mL·s-1(流速为0.5 m·s-1); (c)入口流量为50 mL·s-1 (流速为0.83 m·s-1) Fig.7 Concentration distribution and total flux distribution of KOH in electrolyte distribution channel and porous electrodes under different inlet flow rate at 400 mA·cm-2 current density: (a) 10 mL·s-1 inlet flow rate (0.16 m·s-1 flow velocity); (b) 30 mL·s-1 inlet flow rate (0.5 m·s-1 flow velocity); (c) 50 mL·s-1 inlet flow rate (0.83 m·s-1 flow velocity) |
| |
在电解液中的离子电流主要由2部分组成:离子的扩散通量(Ndiff)导致的扩散电流(Idiff)和离子的电迁移通量(Nelec)导致的扩散电流(Ielect)。
| $ \begin{aligned} & I_{\text {total }}=I_{\text {diff }}+I_{\text {elec }}, \\ & I_{\text {diff }}=\sum F \cdot z_i \cdot N_{\text {diff }, i}, \\ & I_{\text {elec }}=\sum F \cdot z_i \cdot N_{\text {elec }, i} \end{aligned} $ | (45) |
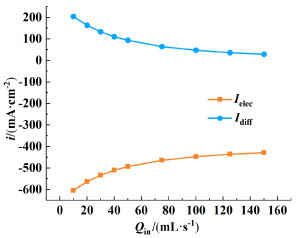
其中扩散通量与两侧浓差大小相关,而电迁移通量则与电解液的两侧溶液电势相关。由于浓度差会受流速的影响,在恒定电流密度条件下总电流大小不变,电迁移通量以及对应的电迁移电流大小也会受流速影响,其变化情况如图 8所示,2种电流方向相反,图中的纵坐标的正负表示的是电流方向。扩散电流密度会随流量增大而降低如图 8中蓝线部分所示,电迁移电流密度(图 8橘线部分)也随流量增大降低,而电迁移电流密度的降低会导致两极的溶液电位降低,阴极和阳极的溶液电位差在系统中就是表观的欧姆过电位,因此入口流量大小也会对系统的欧姆电位产生影响。
|
| 图 8 电流密度为400 mA·cm-2时,电迁移电流和扩散电流与入口流量的关系 Fig.8 The relation of electromigration current and diffusion current to inlet flow rate at 400 mA·cm-2 current density |
| |
电解液分配流道位于系统阴极和阳极之间,是电解过程中欧姆过电位的主要来源,其厚度大小对应的就是系统阴极和阳极之间的间距大小。间距大小会对电解效率产生很大的影响。较大的间距可以让电解液的压力在分配流道内的分布更加均匀,减小电极和分配流道界面的压力梯度,但是这会带来较大的欧姆过电位,从而增大系统的总电压;较小的间距可以有效降低系统的欧姆过电位从而降低系统的总电压,但是这会导致电极催化层和分配流道的界面处压力梯度较大,电极内部流速分布不均匀。
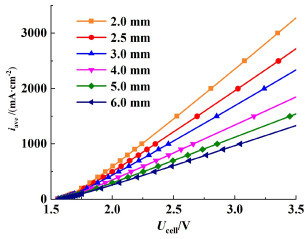
从图 9中可以看到,随着阴极和阳极间距的增加,系统的电压电流曲线也逐渐趋近于1条直线且斜率增大,这是由于在大电极间距时,整个系统的电压降大部分都来自于电极间的欧姆过电位,间距增大也导致欧姆过电位的增大。电流密度越高,厚度的影响也越明显。电极间距越小,系统的欧姆过电位也越小,总电压也就越低。
|
| 图 9 入口流量为40 mL·s-1(催化层平均流速uel为0.10 m·s-1)时, 不同电解液分配流道厚度下的电压电流关系 Fig.9 The Voltage current relationship under different electrolyte distribution channel thickness at 40 mL·s-1 inlet flow rate (0.10 m·s-1 average flow velocity of catalytic layer) |
| |
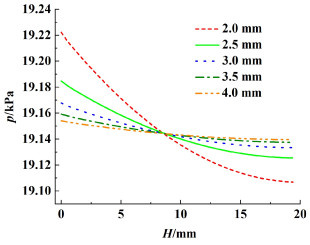
电解液分配流道的厚度会影响电极间隙层内的电解液压力分布情况。电解液的压力分布也会影响到气体产物的排出情况。由于在间隙处高度方向上的压力变化较为显著,因此我们用间隙在某一高度时的平均压力来表示在这一高度下的压力大小。在相同电流密度、相同流量情况下,电极间隙的压力随高度变化情况如图 10所示。
|
| 图 10 入口流量为40 mL·s-1(催化层平均流速uel为0.10 m·s-1),电流密度为500 mA·cm-2时,不同电极间距下平均压力随高度变化情况 Fig.10 The change of average pressure with height at different electrode spacing at 40 mL·s-1 inlet flow rate (0.10 m·s-1 average flow velocity of catalytic layer) and 500 mA·cm-2 current density |
| |
从图 10可看出随着电极间距(电解液分配流道厚度)的增大,分配流道内部电解液的压力分布逐渐趋于均匀化。间隙内压力分布的均匀化可以使得催化层内部的流速分布更加均匀。
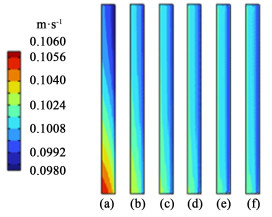
系统的阴极催化层内部气液两相的流速分布情况如图 11所示。
|
| 图 11 入口流量为40 mL·s-1,电流密度为500 mA·cm-2时,电极间距分别为(a) 1.0 mm、(b) 1.5 mm、(c) 2.0 mm、(d)2.5 mm、(e) 3.0 mm、(f) 3.5 mm时,阴极侧催化层内部气液混合流体流速大小分布情况 Fig.11 40 mL·s-1 inlet flow rate, 500 mA·cm-2 current density, velocity distribution of gas-liquid mixed fluid in catalytic layer at cathode side, when electrode gap is (a) 1.0 mm; (b) 1.5 mm; (c) 2.0 mm; (d)2.5 mm; (e) 3.0 mm; (f) 3.5 mm |
| |
从图 11中可以看到催化层内部的流速分布会随间隙厚度的增大而均匀化。由于催化层与流出流道的界面侧压力差极小,因此间隙内的压力差是影响电解液穿过催化层的速度分布的主要因素。可以看到电极间隙小于1.5 mm时,催化层内流速分布呈现明显的上小下大的不均匀情况,随间隙厚度增加,流速分布逐渐均匀。
为了让电极间距带来的欧姆过电位足够小,同时保证催化层内部压力分布均匀,阴阳极间距大小在2.0~3.5 mm之间比较符合系统的要求。
2.4 工况判断对于无膜电解水系统而言,合适工况的确定就是要协调系统中流速、间隙厚度以及电流密度的大小以达到系统的最佳运行状态。由于电解液在系统中流动穿过催化层带走反应产生的气体,从而降低气泡对总电压的影响。因此理论上流速越快系统总电压越低,如图 6(a),但是流速提高对于降低整个系统总电压的影响具有一定的局限性,而且过大的流速会使得装置整体的能量损耗增加,所以我们在考察流速时需要考察系统的电解效率。
对于无膜水电解系统而言,用于水电解产氢产氧的电功耗以及泵的功率可以表示为:
| $ P_{\mathrm{cell}}=I U_{\mathrm{cell}} $ | (46) |
| $ P_{\text {pump }}=\rho_{\text {КоН }} g H_{\text {pump }} Q_{\text {in }} $ | (47) |
式(46)和式(47)中:Hpump为泵的扬程(此处为该系统所需的最小扬程);Qin为入口流量。则系统的效率为:
| $ \phi=\frac{I E_{\mathrm{eq}}}{P_{\mathrm{cell}}+P_{\mathrm{pump}}} $ | (48) |
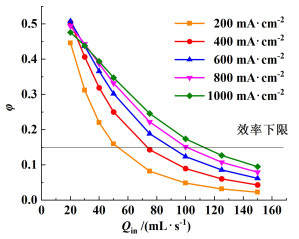
因此效率与流量关系如图 12所示。为了确保系统的所消耗的能量大部分都用于水的电解,这里我们设定为0.15为效率的下限。当效率低于该值时系统在其他方面的损耗远大于水电解的消耗,得不偿失。
|
| 图 12 电极间隙为2.5 mm时,不同电流密度下效率与入口流量的关系 Fig.12 The relationship between efficiency and inlet flow rate in different current densities at 2.5 mm electrode gap |
| |
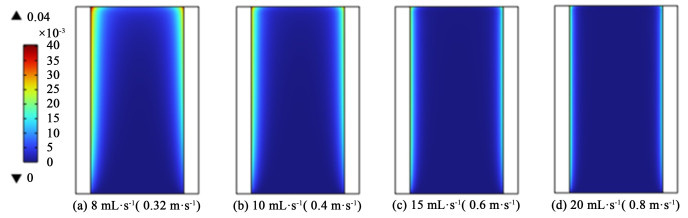
为了将在电极上的产物气体带出电极,确保电解液分配流道中无氢气和氧气的混合,需要确定电解液的最小流速。不同入口流速下,电解液分配流道内气泡体积分数分布情况如图 13所示。
|
| 图 13 电极间隙为2.5 mm,电流密度为3 000 mA·cm-2时,不同入口流量时,间隙内气体体积分数分布情况 Fig.13 Distribution of gas volume fraction in gap at different inlet flow rate at 2.5 mm electrode gap and 3 000 mA·cm-2 current density |
| |
电流密度一定时,入口流速越快,两极间隙中的气体体积分数越低。在电流密度为3 000 mA·cm-2,入口量为8 mL·s-1时,间隙内存在较为明显的气体体积分数分布,并且主要集中在间隙靠近电极位置,且以电极上端区域居多,这是因为在间隙中流体的流动会将气泡带到间隙顶部。而在更高的流速下,气泡则主要集中在催化层附近的薄层中,间隙内的气泡体积分数接近0可以忽略不计。
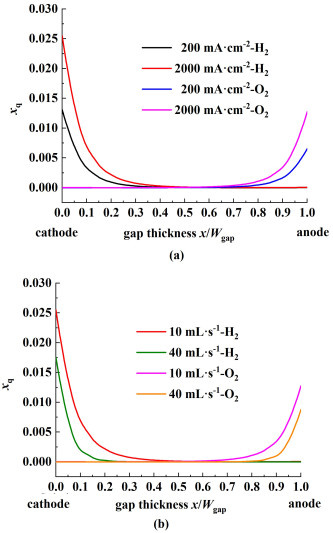
不同电流密度、入口流量下反应产物H2和O2在电极间隙中不同位置的气体的体积分数分布如图 14所示。电极间隙为2.5 mm时,如图 14(a)所示相同入口流量时电流密度越高相同位置的产物气体体积分数越高。整体上阴极附近氢气体积分数最大,阳极附近氧气体积分数最大,受流动以及扩散影响越远离电极,体积分数越低,流速越快体积分数下降越快如图 14(b)所示。
|
| 图 14 电极间隙为2.5 mm时,不同电流密度、入口流量下反应产物H2和O2在电极间隙中不同位置的气体的体积分数分布:(a)入口流量为10 mL·s-1;(b)电流密度为2 000 mA·cm-2 Fig.14 The distribution of the gas volume fraction of reaction products H2 and O2 with the position of the electrode gap under different current density and inlet flow rate at 2.5 mm of electrode gap: (a) 10 mL·s-1 of inlet flow rate; (b) 2 000 mA·cm-2 of current density |
| |
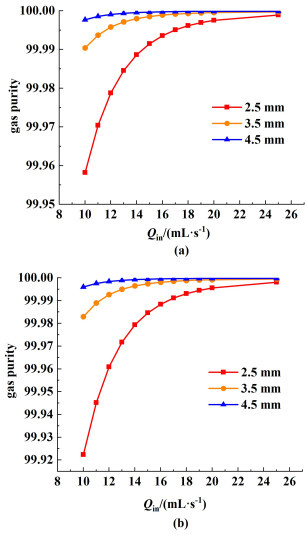
电解槽的产物气体纯度受电解液流速以及间隙厚度的影响。图 15为电流密度为3 000 mA·cm-2时不同间隙厚度下,阴极出口H2纯度以及阳极出口O2纯度随电解液流量的变化情况。气体纯度通过从阴极和阳极出口流出的2种气体的体积通量来计算。从图 15中可以看到随着流量增大,气体纯度在不断趋近于100%,这是由于流量越大,两侧气体越难以穿过分配流道。在相同流量下电极间隙越小,气体纯度越低,这是由于间隙越小,两侧产生的气体越容易穿过电解液分配流道到达另一侧。
|
| 图 15 电流密度为3 000 mA·cm-2时不同间隙厚度下,(a)阴极出口H2纯度以及(b)阳极出口O2纯度随电解液流量变化情况 Fig.15 3 000 mA·cm-2 current density, the change of gas purity with electrolyte flow rate at different electrode gap, (a) H2 at cathode outlet; (b) O2 at anode outlet |
| |
首次建立了一个穿流电极无膜水电解系统的二维数值模型。利用COMSOL软件通过耦合质量、动量、电荷传递以及电化学反应过程,对整个系统内电解液流动、气液混合物流动以及电化学反应过程进行模拟计算,并结合实验数据验证了模型的准确性。在总电压中气泡覆盖活性面积以及欧姆阻抗导致的过电位占据主要地位,这两者可以通过增加电解液流速和减小电极间隙厚度来降低。流速的增加有利于降低总电压,但影响程度有限,考察不同电流密度下流速与效率关系,以0.15为效率下限对应的流速为流量上限。降低阴阳极间距可以有效降低整个系统的总电压降,但是为了保证电极表面的压差处于较低水平从而保证催化层内部流速均匀,阴阳极间距可控制在2.0~3.5 mm之间。在保证气体产物纯度的前提下,电极间隙厚度越小,所需的最小电解液流量越高;而间隙厚度越大,所需的最小电解液流量越小。为了降低电解槽的总电压的同时,保证两侧气体产物的纯度,应尽可能使无膜水电解的流量、电极间隙厚度以及电流密度互相配合,以使得系统始终处于适宜工况下运行。
| [1] |
TURNER J A. A realizable renewable energy future[J]. Science, 1999, 285(5428): 687-689. DOI:10.1126/science.285.5428.687 |
| [2] |
MARBÁN G, VALDÉS-SOLÍS T. Towards the hydrogen economy?[J]. International Journal of Hydrogen Energy, 2007, 32(12): 1625-1637. DOI:10.1016/j.ijhydene.2006.12.017 |
| [3] |
GLENK G, REICHELSTEIN S. Economics of converting renewable power to hydrogen[J]. Nature Energy, 2019, 4: 216-222. DOI:10.1038/s41560-019-0326-1 |
| [4] |
MILLET P, GRIGORIEV S. Water electrolysis technologies[M]//Amsterdam: Elsevier, 2013
|
| [5] |
HASHEMI S M, MODESTINO M A, PSALTIS D. A membrane-less electrolyzer for hydrogen production across the pH scale[J]. Energy & Environmental Science, 2015, 8(7): 2003-2009. |
| [6] |
GILLESPIE M I, VAN DER MERWE F, KRIEK R J. Performance evaluation of a membraneless divergent electrode-flow-through (DEFT) alkaline electrolyser based on optimisation of electrolytic flow and electrode gap[J]. Journal of Power Sources, 2015, 293: 228-235. DOI:10.1016/j.jpowsour.2015.05.077 |
| [7] |
NIELD D A, BEJAN A. Convection in Porous Media[M]. New York: Springer New York, 2013.
|
| [8] |
MANNINEN M, TAIVASSALO V, ENERGY V, et al. On the mixture model for multiphase flow[R]: Technical Research Centre of Finland, Espoo (Finland), 1996
|
| [9] |
NEWMAN J S, THOMAS-ALYEA K E. Electrochemical systems[M]. 3rd ed. Hoboken, NJ: Wiley, 2004
|
| [10] |
KUNZ F. Modeling and simulation of an alkaline fuel cell[D]. Germany: Universität Duisburg-Essen, 2019
|
| [11] |
OJONG E T, KWAN J T H, NOURI-KHORASANI A, et al. Development of an experimentally validated semi-empirical fully-coupled performance model of a PEM electrolysis cell with a 3-D structured porous transport layer[J]. International Journal of Hydrogen Energy, 2017, 42(41): 25831-25847. DOI:10.1016/j.ijhydene.2017.08.183 |
| [12] |
RAJAEI H, RAJORA A, HAVERKORT J W. Design of membraneless gas-evolving flow-through porous electrodes[J]. Journal of Power Sources, 2021, 491: 229364. DOI:10.1016/j.jpowsour.2020.229364 |
| [13] |
RAJORA A, HAVERKORT J W. An analytical model for liquid and gas diffusion layers in electrolyzers and fuel cells[J]. Journal of the Electrochemical Society, 2021, 168(3): 034506. DOI:10.1149/1945-7111/abe087 |
| [14] |
GILLIAM R, GRAYDON J, KIRK D, et al. A review of specific conductivities of potassium hydroxide solutions for various concentrations and temperatures[J]. International Journal of Hydrogen Energy, 2007, 32(3): 359-364. DOI:10.1016/j.ijhydene.2006.10.062 |
| [15] |
ZHOU G. Modeling and simulation of electrolyte transport in alkaline fuel cells[M]. Iowa City: University of Iowa, 2007.
|
| [16] |
AKERLOF G C, BENDER P. Thermodynamics of aqueous solutions of potassium Hydroxide[J]. Journal of the American Chemical Society, 1948, 70(7): 2366-2369. DOI:10.1021/ja01187a016 |
| [17] |
ROBINSON R A, S R H. Electrolyte solutions[M]. New York: Dover Publications, 2002.
|
| [18] |
SÖHNEL O. Densities of aqueous solutions of inorganic substances[G]. Amsterdam: Elsevier. 1985
|
| [19] |
BRATSCH S G. Standard electrode potentials and temperature coefficients in water at 298.15 K[J]. Journal of Physical and Chemical Reference Data, 1989, 18(1): 1-21. DOI:10.1063/1.555839 |
| [20] |
SHENG W C, GASTEIGER H A, SHAO-HORN Y. Hydrogen oxidation and evolution reaction kinetics on platinum: Acid vs alkaline electrolytes[J]. Journal of the Electrochemical Society, 2010, 157(11): B1529. DOI:10.1149/1.3483106 |
| [21] |
IWATA R, ZHANG L, WILKE K L, et al. Bubble growth and departure modes on wettable/non-wettable porous foams in alkaline water splitting[J]. Joule, 2021, 5(4): 887-900. DOI:10.1016/j.joule.2021.02.015 |
| [22] |
沈岑. 穿流电极无膜水电解的数值模拟与装置优化设计[D]. 天津: 天津大学, 2022 SHEN Cen. Numerical simulation and device optimization design of membrane-free water electrolysis with through-flow electrode[D]. Tianjin: Tianjin University, 2022(in Chinese) |
 2024, Vol. 41
2024, Vol. 41





