2. 西南交通大学机械工程学院,成都 610031
2. School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China
在能源转型背景下,发展氢能已成为发达经济体的共识[1]。加氢站是氢能产业的核心基础设施之一,对于氢燃料电池汽车和氢能技术推广来说,加氢站的建设是不可或缺的。另外,在保障加氢速度的同时降低加氢能耗,对实现加氢站商业化推广至关重要。
将氢气压缩到足够的压力以便快速加注到燃料电池车辆中,需要消耗大量能量。另外,加氢过程中通常需要消耗一定能量对氢气进行预冷,以保证氢气在安全的温度范围。因此,近年来众多学者对如何降低加氢站能耗进行了广泛地研究。例如,Kuroki等[2]针对70 MPa的Ⅲ型和Ⅳ型车载储氢瓶,提出了一种与实际加氢站相同的最适宜化加氢动态仿真模型,准确预测加注过程中加氢站任意时间和位置氢气的瞬态温度、压力和质量流量,进而实现最适宜加注且保证能耗最低。Talpacci等[3]通过热力学分析加氢站拓扑结构对冷却装置能耗的影响,结果表明加氢站储氢罐的总容积增大,伴随着冷却能耗增加。Melideo等[4]通过CFD模型研究了不同的加注策略对车载储氢瓶的氢气压力和温度的影响,结果表明对储罐氢气进行预冷,可以在短时间内实现节能。Khamforoush等[5]利用粒子群优化算法确定梯级加注系统中的压缩机和冷却器的能耗最小以及气瓶内剩余容量(State of charge, SOC)最大的最适宜运行条件。Li等[6]针对82 MPa的高压储氢罐加注系统,分析了高压氢气进入储氢罐的初始真空状态和高压加注状态下最终温度和SOC。Xiao等[7]研究了环境温度、初始压力和质量流量这3个单一参数对不同体积的车载储氢瓶加注过程中氢气的影响,得出结论为在能耗最小的前提下降低环境温度、质量流量或增加初始压力可以有效降低最终氢气温度,SOC最大化。Zheng等[8]提出自适应切换机制的优化算法用于控制加注过程,实现了快速加注、高氢利用率,且缩短了时间和降低了成本。Bai等[9]对加注过程的因素如初始氢气压力、初始氢气温度、环境温度、预冷温度和PSC等进行理论和仿真分析。
目前对于梯级储氢加氢站的各储氢罐压力配置没有快速有效的优化方法,基于模型的数据分析方法只能得出压力和容积限定范围,却不能根据加氢站标准需求给出确切的压力级。为此,本研究针对三级储氢加氢站,建立完整的加氢站对车载储氢瓶的快速加注过程热力学模型,采用最小二乘法(LSM)获得整体加氢站的最适宜压力配置,降低了加氢站的能耗。
1 梯级加氢站储供氢系统理论模型 1.1 梯级加氢站梯级加氢站系统运行流程如图 1所示。
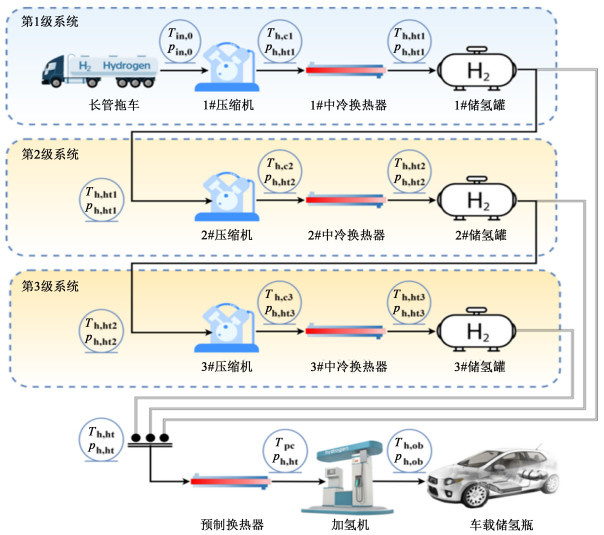
|
| 图 1 梯级加氢站系统工作原理图 Fig.1 Diagram of working principle of cascade hydrogen refueling station |
| |
在加氢站给车载储氢罐加氢结束后,加氢站需要通过1#压缩机和1#中冷换热器将长管拖车中的氢气压缩至1#低压储氢罐。再通过2#压缩机和2#中冷换热器,将1#低压储氢罐中氢气压缩至2#中压储氢罐。最后,通过3#压缩机和3#中冷换热器,将2#中压储氢罐中氢气压缩至3#高压储氢罐,直至3个储氢罐全部达到设定压力。
为了建立加氢系统数学模型,我们做了如下假设:(1)氢气被认为是一种真正的气体,但焓和温度之间的关系使用了简化形式[10];(2)假设储氢罐内部没有余隙而且密封良好,气阀开关及时;(3)基于集总参数热力学模型,假设进入储氢罐的氢气温度恒定,温度和压力分布均匀[11];(4)在高压加氢过程中,速度快,停留时间短,热对流强,热损失很小。假设氢气在管道内流动是绝热过程,忽略与外界的热交换;(5)储氢罐的体积是恒定的。假设在快速加氢过程中不产生机械能,则忽略动能和势能;(6)假设I级、II级和III级储氢罐的压缩过程中多变指数相同且为常数[12];(7)假设加氢机的加氢喷嘴为规则小孔。
1.2 车载储氢瓶数学模型设mh, ob为车载储氢瓶中氢气质量,kg;ṁin, ob为氢气加注质量流量,kg·s-1;Ain, w, ob为内壁表面积,m2;Cv, h, ob和Cp, h, ht分别为车载和站内气罐中氢气的等容和等压比热容,J·kg-1·K-1;Th, ob和Tw, ob分别为氢气和瓶壁的温度,K。Kh, w是氢气与车载储氢瓶内壁之间的热交换系数,W·m-2·K-1。根据能量守恒定律和热传递方程[13],可得:
| $ \begin{gathered} \frac{\mathrm{d}\left[m_{\mathrm{h}, \mathrm{ob}} C_{\mathrm{v}, \mathrm{h}, \mathrm{ob}} T_{\mathrm{h}, \mathrm{ob}}\right]}{\mathrm{d} t}=\dot{m}_{\mathrm{in}, \mathrm{ob}} C_{\mathrm{p}, \mathrm{h}, \mathrm{ht}} T_{\mathrm{pc}}+ \\ K_{\mathrm{h}, \mathrm{w}} A_{\mathrm{in}, \mathrm{w}, \mathrm{ob}}\left(T_{\mathrm{w}, \mathrm{ob}}-T_{\mathrm{h}, \mathrm{ob}}\right) \end{gathered} $ | (1) |
式(1)中:Tpc(K)是加注预冷温度。因此,氢气温度Th, ob(K)为:
| $ T_{\mathrm{h}, \mathrm{ob}}=\frac{\int\left[\dot{m}_{\mathrm{in}, \mathrm{ob}} C_{\mathrm{p}, \mathrm{h}, \mathrm{ht}} T_{\mathrm{pc}}+K_{\mathrm{h}, \mathrm{w}} A_{\mathrm{in}, \mathrm{w}, \mathrm{ob}}\left(T_{\mathrm{w}, \mathrm{ob}}-T_{\mathrm{h}, \mathrm{ob}}\right)\right] \mathrm{d} t}{m_{\mathrm{h}, \mathrm{ob}} C_{\mathrm{v}, \mathrm{h}, \mathrm{ob}}} $ | (2) |
相似地,瓶壁温度Tw, ob(K)的表达式为:
| $ T_{\mathrm{w}, \mathrm{ob}}=\frac{\int\left[\begin{array}{l} K_{\mathrm{h}, \mathrm{w}} A_{\mathrm{in}, \mathrm{w}, \mathrm{ob}}\left(T_{\mathrm{h}, \mathrm{ob}}-T_{\mathrm{w}, \mathrm{ob}}\right)+ \\ K_{\mathrm{w}, \mathrm{a}} A_{\mathrm{out}, \mathrm{w}, \mathrm{ob}}\left(T_{\mathrm{a}}-T_{\mathrm{w}, \mathrm{ob}}\right) \end{array}\right] \mathrm{d} t}{m_{\mathrm{w}, \mathrm{ob}} C_{\mathrm{p}, \mathrm{w}, \mathrm{ob}}} $ | (3) |
式(3)中:Kw, a(W·m-2·K-1)为气缸壁与环境之间的传热系数,mw, ob(kg)为车载储氢瓶壁质量常数,Aout, w, ob(m2)和Ta(K)分别表示缸外壁表面积和环境温度的常数。因此,根据氢气的状态方程[12],氢气压力ph, ob(Pa)为:
| $ p_{\mathrm{h}, \mathrm{ob}}=\frac{m_{\mathrm{h}, \mathrm{ob}} R_{\mathrm{H}_2} T_{\mathrm{h}, \mathrm{ob}}}{V_{\mathrm{ob}}-\alpha m_{\mathrm{h}, \mathrm{ob}} R_{\mathrm{H}_2}} $ | (4) |
式(4)中:α=1.9155×10-6K·Pa-1是修正系数;Th, ob(K)、mh, ob(kg)分别为车载储氢瓶中的氢气温度和质量;Vob(m3)、RH2(J·kg-1·K-1)分别表示车载储氢瓶的体积、氢气气体常数。
1.3 加氢机数学模型加氢机入口质量流量ṁin, ob(kg·s-1)的表达式为[12]:
| $ \dot{m}_{\mathrm{in}, \mathrm{ob}}=\left\{\begin{array}{l} & C_{\mathrm{d}} A_{\mathrm{or}}\left(\frac{2}{\kappa+1}\right)^{\frac{\kappa+1}{2(\kappa-1)}} \sqrt{\kappa p_{\mathrm{h}, \mathrm{h}} \rho_{\mathrm{h}, \mathrm{ht}} Z_{\mathrm{ht}} \gamma} , \\ & \quad \text { if } \frac{p_{\mathrm{h}, \mathrm{ob}}}{p_{\mathrm{h}, \mathrm{ht}}} \leqslant\left(\frac{2}{\kappa+1}\right)^{\frac{\kappa}{\kappa-1}} \\ & C_{\mathrm{d}} A_{\text {or }} \rho_{\mathrm{h}, \mathrm{ht}}\left(\frac{p_{\mathrm{h}, \mathrm{ob}}}{p_{\mathrm{h}, \mathrm{ht}}}\right)^{\frac{1}{\kappa}}\left\{\begin{array}{l} \gamma\left(\frac{2 \kappa}{\kappa-1}\right)\left(\frac{p_{\mathrm{h}, \mathrm{ht}} Z_{\mathrm{ht}}}{\rho_{\mathrm{h}, \mathrm{ht}}}\right) \\ {\left[1-\left(\frac{p_{\mathrm{h}, \mathrm{ob}}}{p_{\mathrm{h}, \mathrm{ht}}}\right)^{\frac{\kappa-1}{\kappa}}\right]} \end{array}\right\}^{\frac{1}{2}} \\ & \text { if } \frac{p_{\mathrm{h}, \mathrm{ob}}}{p_{\mathrm{h}, \mathrm{ht}}}>\left(\frac{2}{\kappa+1}\right)^{\frac{\kappa}{\kappa-1}} \end{array}\right. $ | (5) |
式(5)中:Cd为孔口流量系数;Aor为孔口面积,m2;γ=1;ph, ob和ph, ht分别表示车载储氢瓶和储氢罐中的氢气压力,Pa;Zht为储氢罐中氢气的压缩系数;ρh, ht为储氢罐的氢气密度,kg·m-3。此外,κ=Cp, h, ht/Cv, h, ht为比热比。
1.4 压缩机数学模型当压缩机为储氢罐压缩补氢时,经过压缩后氢气质量流量ṁc, out(kg·s-1)可表达为[12]:
| $ \dot{m}_{\mathrm{c}, \text { out }}=\left\{\begin{array}{l} \kappa \frac{p_{\mathrm{h}, \mathrm{c}, \text { out }}}{a} F\left(\frac{2}{\kappa+1}\right)^{\frac{\kappa+1}{2(\kappa-1)}}, \\ \text { if } \quad \frac{p_{\mathrm{h}, \mathrm{c}, \text { in }}}{p_{\mathrm{h}, \mathrm{c}, \text { out }}} \leqslant\left(\frac{2}{\kappa+1}\right)^{\frac{\kappa}{\kappa-1}}\\ \kappa \frac{p_{\mathrm{h}, \mathrm{c}, \text { out }}}{a}\left(\frac{p_{\mathrm{h}, \mathrm{c}, \text { in }}}{p_{\mathrm{h}, c, \text { out }}}\right)^{\frac{\kappa+1}{2 \kappa}} F\\ \sqrt{\frac{2}{\kappa-1}\left(\left(\frac{p_{\mathrm{h}, \mathrm{c}, \text { out }}}{p_{\mathrm{h}, c, \text { in }}}\right)^{\frac{\kappa-1}{\kappa}}-1\right)}\\ \text { if } \quad \frac{p_{\mathrm{h}, c, \text { in }}}{p_{\mathrm{h}, \mathrm{c}, \text { out }}}>\left(\frac{2}{\kappa+1}\right)^{\frac{\kappa}{\kappa-1}} \end{array}\right. $ | (6) |
式(6)中:F为阀口流通面积,m2;
| $ T_{\mathrm{h}, \mathrm{c}, \text { out }}=T_{\mathrm{h}, \mathrm{cg}}\left(\frac{p_{\mathrm{h}, \mathrm{c}, \text { out }}}{p_{\mathrm{h}, \mathrm{c}, \text { in }}}\right)^{\frac{\kappa-1}{\kappa}} $ | (7) |
式(7)中:Th, cg为外供式加氢站的长管拖车中氢气的温度,K。
1.5 模型验证本研究对70 MPa梯级加氢站进行模型验证,具体参数列于表 1。
| 名称 | 符号 | 单位 | 数值 |
| 70 MPa高压储氢瓶体积 | L | m3 | 174 |
| 氢气等容比热容 | Cv, h, ob | J·kg-1·K | 10.18 |
| 氢气等压比热容 | Cp, h, ht | J·kg-1·K-1 | 14.3 |
| 氢气与储氢瓶内壁之间的热交换系数 | Kh, w | W·m-2·K-1 | 150 |
| 加注预冷温度 | Tpc | K | 298 |
| 气缸壁与环境间的传热系数 | Kw, a | W·m-2·K-1 | 4.5 |
| 车载储氢瓶壁质量常数 | mw, ob | kg | 24 |
| 缸外壁表面积 | Aout, w, ob | m2 | 1.208 5 |
| 环境温度常数 | Ta | K | 298 |
| 车载储氢瓶的体积 | Vob | m3 | 0.140 |
| 氢气气体常数 | RH2 | J·kg-1·K-1 | 8.314 |
| 孔口流量系数 | Cd | 0.62 | |
| 孔口面积 | Aor | m2 | 3.756 |
| 储氢罐内氢气压缩系数 | Zht | 0.85 | |
| 储氢罐氢气密度 | ρh, ht | kg·m-3 | 40 |
| 阀口流通面积 | F | m2 | 3.922 |
| 压缩机内氢气密度 | ρh, c | kg·m-3 | 67.03 |
| 流入压缩机的氢气压 | ph, c, in | MPa | 0.1 |
| 流出压缩机的氢气压 | ph, c, out | MPa | 40 |
| 长管拖车中氢气温度 | Th, cg | K | 298 |
采用文献[15]的实验数据对氢气压力和温度变化进行了验证。设初始压力为5.5 MPa,环境温度为298 K,可得车载储氢瓶内压力梯度分布和温度变化结果如图 2所示。
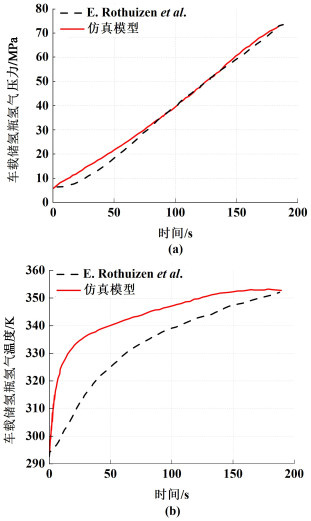
|
| 图 2 (70 MPa)氢气压力和温度验证结果 Fig.2 Verification results of hydrogen pressure (70 MPa) and temperature |
| |
由图 2可以看出,压力模拟结果与实验数据十分吻合,而温度结果与实验数据趋势基本吻合。另外,温度误差由车载储氢瓶模型简化换热不充分引起,但加注完成后最终温度误差也在3 K以内,整体相对准确。
2 基于LSM的压力比优化方法W为3个压缩机单位质量氢气所做的功[12]:
| $ \begin{aligned} & W_{\mathrm{c}, 1}=\frac{\sigma}{\sigma-1} R T_{\mathrm{in}, 0}\left(\varepsilon_1^{\frac{\sigma-1}{\sigma}}-1\right) \\ & W_{\mathrm{c}, 2}=\frac{\sigma}{\sigma-1} R T_{\mathrm{h}, \mathrm{ht} 1}\left(\varepsilon_2^{\frac{\sigma-1}{\sigma}}-1\right) \\ & W_{\mathrm{c}, 3}=\frac{\sigma}{\sigma-1} R T_{\mathrm{h}, \mathrm{ht} 2}\left(\varepsilon_3^{\frac{\sigma-1}{\sigma}}-1\right) \end{aligned} $ | (8) |
式(8)中:σ为压缩多变指数;Tin, 0、Th, ht1、Th, ht2分别为三级压缩机的入口氢气温度,K;
设氢能源汽车加注后每个储气罐所流出的氢气质量为δm, ht1、δm, ht2和δm, ht3,kg。因此,为了给各储氢罐补充这些质量的氢气,压缩机通过压缩补氢过程所消耗的能量计算公式为:
| $ \begin{gathered} E_{\mathrm{c}, \mathrm{all}}=W_{\mathrm{c}, 1} \delta_{\mathrm{m}, \mathrm{ht} 1}+W_{\mathrm{c}, 2} \delta_{\mathrm{m}, \mathrm{h} 12}+W_{\mathrm{c}, 3} \delta_{\mathrm{m}, \mathrm{ht} 1}= \\ \frac{\sigma}{\sigma-1} R\left[\delta_{\mathrm{m}, \mathrm{ht} 1} T_{\mathrm{in}, 0}\left(\varepsilon_1^{\frac{\sigma-1}{\sigma}}-1\right)+\right. \\ \left.\delta_{\mathrm{m}, \mathrm{ht} 2} T_{\mathrm{ht} 1}\left(\varepsilon_2^{\frac{\sigma-1}{\sigma}}-1\right)+\delta_{\mathrm{m}, \mathrm{ht} 3} T_{\mathrm{ht} 2}\left(\varepsilon_3^{\frac{\sigma-1}{\sigma}}-1\right)\right] \end{gathered} $ | (9) |
为了使用LSM方法求解满足系统总能耗最小要求下的最适宜压比,将公式改写为:
| $ \begin{gathered} E_{\mathrm{c}, \mathrm{all}}=\frac{\sigma}{\sigma-1} R\left[\delta_{\mathrm{m}, \mathrm{ht} 1} T_{\mathrm{in}, 0}(x-1)+\right. \\ \left.\delta_{\mathrm{m}, \mathrm{ht} 2} T_{\mathrm{h}, \mathrm{ht} 1}(y-1)+\delta_{\mathrm{m}, \mathrm{ht} 3} T_{\mathrm{h}, \mathrm{ht} 2}\left(\frac{\tau_{\varepsilon}}{x y}-1\right)\right] \end{gathered} $ | (10) |
式(10)中:x=ε1σ-1/σ,y=ε2σ-1/σ,τε=ε/(τϕ1τϕ2),τϕ1=ϕ1σ-1/σ,τϕ2=ϕ2σ-1/σ,其中ϕ1是第一级和第二级压缩机间的压力损失,ϕ2是第二级和第三级压缩机间的压力损失。另外,令ε=ε1ε2ε3ϕ1ϕ2为三级压缩系统的总压比。
为了使三级压缩机的综合能耗降到最低,必须确定三级压缩机的最适宜压力比[16]。根据LSM方法,式(10)中压缩机总能耗对变量x的偏导数为0,则:
| $ \frac{\partial E_{\mathrm{c}, \mathrm{all}}}{\partial x}=0, x^2 y=\left(\frac{\delta_{\mathrm{m}, \mathrm{ht} 3} T_{\ell, \mathrm{in}}}{\delta_{\mathrm{m}, \mathrm{ht} 1} T_{\mathrm{in}, 0}}\right)^{\frac{\sigma}{\sigma-1}} \tau_{\varepsilon} $ | (11) |
同理,有:
| $ \frac{\partial E_{\mathrm{c}, \mathrm{all}}}{\partial y}=0, x y^2=\left(\frac{\delta_{\mathrm{m}, \mathrm{ht} 3} T_{\ell, \mathrm{in}}}{\delta_{\mathrm{m}, \mathrm{ht} 2} T_{\mathrm{h}, \mathrm{ht} 1}}\right)^{\frac{\sigma}{\sigma-1}} \tau_{\varepsilon} $ | (12) |
将x、y和τε代入式(11)和(12)中可以得出:
| $ \varepsilon_1=\left(\frac{\delta_{\mathrm{m}, \mathrm{ht} 2} \delta_{\mathrm{m}, \mathrm{ht} 3}}{\delta_{\mathrm{m}, \mathrm{ht} 1}^2}\right)^{\frac{\sigma}{3(\sigma-1)}}\left(\frac{T_{\mathrm{h}, \mathrm{ht1}} T_{\ell, \text { in }}}{T_{\mathrm{in}, 0}^2}\right)^{\frac{\sigma}{3(\sigma-1)}}\left(\frac{\varepsilon}{\phi_1 \phi_2}\right)^{\frac{1}{3}} $ |
| $ \varepsilon_2=\left(\frac{\delta_{\mathrm{m}, \mathrm{ht} 1} \delta_{\mathrm{m}, \mathrm{h} 13}}{\delta_{\mathrm{m}, \mathrm{ht} 2}^2}\right)^{\frac{\sigma}{3(\sigma-1)}}\left(\frac{T_{\mathrm{in}, 0} T_{\ell, \mathrm{in}}}{T_{\mathrm{h}, \mathrm{h} 11}^2}\right)^{\frac{\sigma}{3(\sigma-1)}}\left(\frac{\varepsilon}{\phi_1 \phi_2}\right)^{\frac{1}{3}} $ |
| $ \varepsilon_3=\left(\frac{\delta_{\mathrm{m}, \mathrm{ht} 1} \delta_{\mathrm{m}, \mathrm{ht} 2}}{\delta_{\mathrm{m}, \mathrm{ht} 3}^2}\right)^{\frac{\sigma}{3(\sigma-1)}}\left(\frac{T_{\mathrm{in}, 0} T_{\mathrm{h}, \mathrm{ht} 1}}{T_{\ell, \mathrm{in}}^2}\right)^{\frac{\sigma}{3(\sigma-1)}}\left(\frac{\varepsilon}{\phi_1 \phi_2}\right)^{\frac{1}{3}} $ |
采用LSM数值计算优化方法,氢源为20 MPa长管拖车的70 MPa级加氢站梯级储氢系统的压比如表 2所示。表 3中第1和第2行展示了LSM与传统序列搜索算法的对比结果,表明LSM可以有效提高能效约2.4%。另外,与传统单级加氢站(表 3第3行数据)相比,显示能效更是提高了36%。
| 加氢站级别 | 第一级压比ε1 | 第二级压比ε2 | 第三级压比ε3 |
| 70 MPa | 1.510 | 1.895 | 1.538 |
| 优化方式 | 低压级/MPa | 中压级/MPa | 高压级/MPa | 加氢时间/s | 总能耗/ (kW·h·kg-1) |
| LSM | 30 | 57 | 88 | 176 | 0.736 |
| 序列搜索 | 30 | 55 | 90 | 174 | 0.754 |
| 90 | 97.1 | 1.150 |
为了验证上述结果合理性,设置Ⅲ型车载储氢瓶入口预冷温度为-15 ℃,加注氢气最终温度不大于85 ℃,低、中、高压比范围分别在1.2~2.5,1.2~2.5,1.3~2.5,获得不同压比下能耗和加氢时间的变化规律,如图 3和图 4所示。
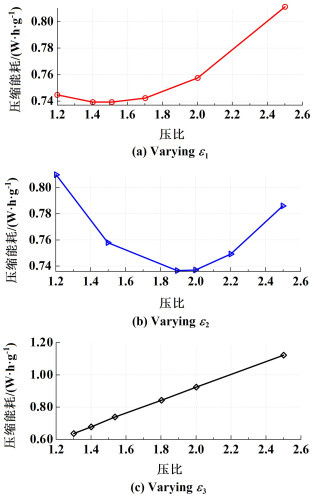
|
| 图 3 70 MPa级压比变化对能耗的影响 Fig.3 Effect of pressure ratio at 70 MPa level on energy consumption |
| |
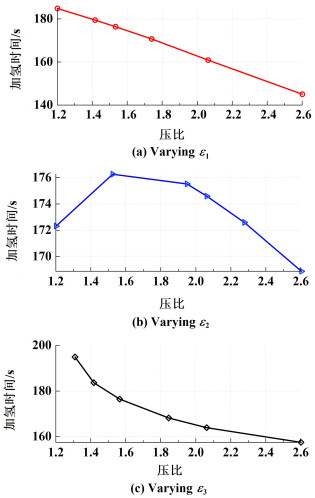
|
| 图 4 70 MPa级压比变化对加氢时间的影响 Fig.4 Effect of pressure ratio at 70 MPa level on hydrogen refueling time |
| |
从图 3中可以看出,取ε2=1.895,ε3=1.538且ε1在1.2~2.5范围内变化,发现ε1=1.510时,此时的加注能耗最低为0.736 kW·h·kg-1;当压比高于或低于该值时,加注能耗都会上升。类似的,取ε1=1.510,ε3=1.538,且ε2在1.2~2.5范围内变化,发现ε2=1.895时,此时的加注能耗也为最低值,而且在该压比两侧的值,能耗都有所上升。取ε1=1.510,ε2=1.895,且ε3=1.3~2.5范围内变化,发现加注能耗随着ε3的增加呈线性上升,当ε3=1.300时,此时的加注能耗最低为0.641 kW·h·kg-1。另外,对于加氢时间方面,从图 4可以得到,当ε3小于1.500时,加氢时间并不满足小于3 min,该压比和本研究中的LSM数值计算优化结果十分接近,因此ε3应该大于1.500才能满足加注时间限制的要求。
从图 4中可以看到,当ε1=1.510和ε2=1.895时,此时能满足加氢时间小于3 min的限制要求,而压比大于这2个值时,加氢时间随之变小,但是伴随着加注能耗也上升。可以说明通过LSM数值计算优化方法所得到的计算结果满足加注能耗最低,具有重要的工程价值。
4 结论梯级加氢站因其能效优势得到了业界的广泛关注。但是,对于如何配置梯级储氢罐的压力,还没有得到深入研究。为此,本研究采用LSM优化方法对低、中、高储罐的压比进行精确求解,得到了70 MPa梯级加氢站储氢系统的压力比,进而可求得压力的最适宜配置,可有效降低加氢站的能耗(参见表 2和表 3)。并在此基础上,分析了不同压比下的能耗和加氢时间。仿真结果表明:采用LSM数值计算优化方法得到的梯级加氢站中储氢系统的最适宜压比,相较传统序列搜索算法优化压力级可以有效提高能效约2.4%。通过不同压比下的能耗对比,最适宜压比下压缩能耗最低。而且,ε1和ε2的增大都会导致能耗呈增加速度逐渐变快的趋势,ε3的增加导致能耗线性增加。另外,与传统单级加氢站相比,梯级加氢的能效提高了36%。
| [1] |
GONG J. Join us to step up to the next generation of sustainable energy[J]. Transactions of Tianjin University, 2020, 26: 1-2. DOI:10.1007/s12209-020-00233-z |
| [2] |
KUROKI T, SAKODA N, SHINZATO K, et al. Dynamic simulation for optimal hydrogen refueling method to fuel cell vehicle tanks[J]. International Journal of Hydrogen Energy, 2018, 43(11): 5714-5721. DOI:10.1016/j.ijhydene.2018.01.111 |
| [3] |
TALPACCI E, REUΒ M, GRUBE T, et al. Effect of cascade storage system topology on the cooling energy consumption in fueling stations for hydrogen vehicles[J]. International Journal of Hydrogen Energy, 2018, 43(12): 6256-6265. DOI:10.1016/j.ijhydene.2018.02.030 |
| [4] |
MELIDEO D, BARALDI D. CFD analysis of fast filling strategies for hydrogen tanks and their effects on key-parameters[J]. International Journal of Hydrogen Energy, 2015, 40(1): 735-745. DOI:10.1016/j.ijhydene.2014.10.138 |
| [5] |
KHAMFOROUSH M, MOOSAVI R, HATAMI T. Compressed natural gas behavior in a natural gas vehicle fuel tank during fast filling process: Mathematical modeling, thermodynamic analysis, and optimization[J]. Journal of Natural Gas Science and Engineering, 2014, 20: 121-131. DOI:10.1016/j.jngse.2014.06.009 |
| [6] |
LI J, LI J, PARK K, et al. An analysis on the compressed hydrogen storage system for the fast-filling process of hydrogen gas at the pressure of 82 MPa[J]. Energies, 2021, 14(9): 2635. DOI:10.3390/en14092635 |
| [7] |
XIAO J, CHENG J, WANG X, et al. Final hydrogen temperature and mass estimated from refueling parameters[J]. International Journal of Hydrogen Energy, 2018, 43(49): 22409-22418. DOI:10.1016/j.ijhydene.2018.10.131 |
| [8] |
ZHENG J, YE J, YANG J, et al. An optimized control method for a high utilization ratio and fast filling speed in hydrogen refueling stations[J]. International Journal of Hydrogen Energy, 2010, 35(7): 3011-3017. DOI:10.1016/j.ijhydene.2009.07.001 |
| [9] |
BAI Y, ZHANG C, DUAN H, et al. Modeling and optimal control of fast filling process of hydrogen to fuel cell vehicle[J]. Journal of Energy Storage, 2021, 35: 102306. DOI:10.1016/j.est.2021.102306 |
| [10] |
ZHANG J, LI Y, ZHAO Y. Hydrogen generation, storage, and utilization[M]. New Jersey: John Wiley & Sons, 2014.
|
| [11] |
MONDE M, WOODFIELD P, TAKANO T, et al. Estimation of temperature change in practical hydrogen pressure tanks being filled at high pressures of 35 and 70 MPa[J]. International Journal of Hydrogen Energy, 2012, 37(7): 5723-5734. DOI:10.1016/j.ijhydene.2011.12.136 |
| [12] |
HANLON P. Compressor handbook[M]. New York: McGraw-Hill Professional, 2001.
|
| [13] |
毛宗强, 毛志明. 氢气生产及热化学利用[M]. 北京: 化学工业出版社, 2015. MAO Zongqiang, MAO Zhiming. Hydrogen production and thermal chemical use[M]. Beijing: Chemical Industry Press, 2015. (in Chinese) |
| [14] |
LIU Y, ZHAO Y, ZHAO L, et al. Experimental studies on temperature rise within a hydrogen cylinder during refueling[J]. International Journal of Hydrogen Energy, 2010, 35(7): 2627-2632. DOI:10.1016/j.ijhydene.2009.04.042 |
| [15] |
ROTHUIZEN E, MÉRIDA W, ROKNI M, et al. Optimization of hydrogen vehicle refueling via dynamic simulation[J]. International Journal of Hydrogen Energy, 2013, 38(11): 4221-4231. DOI:10.1016/j.ijhydene.2013.01.161 |
| [16] |
LÓPEZ-PANIAGUA I, RODRÍGUEZ-MARTÍN J, SÁNCHEZ-ORGAZ S, et al. Step by step derivation of the optimum multistage compression ratio and an application case[J]. Entropy, 2020, 22(6): 678. DOI:10.3390/e22060678 |
 2024, Vol. 41
2024, Vol. 41





