2. 西安交通大学人居环境与建筑工程学院, 西安 710049
2. School of Human Settlements and Civil Engineering, Xi'an Jiaotong University, Xi'an 710049, China
多相流搅拌混合过程在化工[1]、冶金[2]、食品加工[3]和矿物浮选[4, 5]等领域得到广泛应用。在搅拌过程中, 旋转叶轮对搅拌筒内多相混合物进行混合。为了兼顾流体传质混合效果和搅拌能耗, 研究搅拌筒内工质流动特性显得尤为重要[6]。
多年来学者们利用激光多普勒测速和粒子图像测速等测量手段[7-9]对搅拌过程中的液体流动进行了实验研究, 而受限于筒体和浆体可视条件、实验设备尺度及被测量获得程度等, 限制了实验研究的开展应用。最优搅拌叶轮、搅拌筒结构等取决于应用场景的搅拌目的, 因此实验方法针对不同搅拌结构的性能结果也具有m定特异性[10]。相比而言, 数值模拟方法便于取得, 可用于分析搅拌过程的基本规律, 得到的优化筒体结构可作为实验的必要准备。早期数值模拟方法虽然能够对搅拌筒内叶轮搅拌流场取得预测结果, 如黑箱法[11], 但仍需要湍流实验数据, 只能应用在少量取得了实验数据的搅拌结构[12]。Luo等[13]提出了滑移网格法(SG), 将筒内流体可分为包含筒壁、挡板和流体的外域, 以及包含了叶轮和周围流体的内域。Bakker等[14]同样利用SG方法取得的模拟结果与LDV方法下的实验数据呈现出良好的一致性, 但是此方法计算成本高, 需要较长计算时间获得结果。
Luo等[13]提出了与SG方法类似的多重参考系法(MRF), 此方法基于稳态假设, 需将搅拌部件分为2个参考系: 动参考系包括叶轮及其周围流体, 也称为内域, 模拟时设定为与叶轮同步旋转; 固定参考系包括筒壁、挡板以及动参考系外的流体, 也称为外域。有学者利用MRF方法进行模拟, 取得的平均流速与LDV法的实验数据吻合较好[15]。也有学者指出, 当叶轮与挡板的相对作用较弱, 可以使用MRF方法[16, 17]。作为稳态计算方法, 其计算量远小于滑移网格法, 也无需依赖实验数据。此外, 还可用MRF方法的模拟结果作为滑移网格法计算的初始条件, 从而替代滑移网格法, 可应用于数值模拟的启动阶段[18, 19]。
搅拌内域高度和直径决定了MRF方法模拟的准确性。流体的流动特征随着搅拌过程瞬态发展变化, 在叶轮周围一定区域内, 流体流动变量随叶轮运动而剧烈变化, 在挡板附近的流体区域也由于湍流的产生而存在剧烈流动。Tamburini等[16]认为, 若内外域分界面位置选择合适, MRF取得结果可以达到SG的准确度[20]。然而调研发现, 对如何确定旋转内域尺寸尚缺乏明确指导原则, Luo等[13]提出MRF方法时假设内域半径应遵循R=0.62(T/2), 认为内域与外域的流体流动并不完全是瞬态, 可以假定在特定径向位置的流动状态是稳定的且不随时间变化。当内外域界面位置足够接近该位置时, 可以通过稳态模拟预测流场变化, 从而节省计算时间。学者们对典型结构搅拌筒的研究大多以此假设为基础进行研究。Shi等[21]总结了前人应用的内域尺寸, 并分析了内域大小对平均轴向速度分布的影响, 认为交界面应该位于叶轮和挡板中间。Patil等[12]对典型结构搅拌筒划分了不同高度和直径的内域进行MRF模拟, 通过与实验数据比较取得了最适宜内域直径。在实际搅拌过程中, 搅拌筒尺寸因不同搅拌目的存在差异, 无法适用前人研究得到的内域尺寸; 而对内域的确定缺乏通用性的原则, R=0.62(T/2)的定义方式也仅表征其与筒体直径的关系, 缺乏与叶轮或挡板之间相对位置关系的约束, 较大直径的叶轮或较高的挡板可能与R=0.62(T/2)定义下的内外域交界面重叠, 从而导致模拟结果出现较大偏差[22]。
本研究选取了传统Rushton叶轮结构的搅拌筒, 利用MRF方法对搅拌筒内的流体流动进行数值模拟。通过对不同内域划分以及模拟结果与实验数据比较, 研究了旋转内域尺寸对流场特性及转矩的影响; 并提出针对不同搅拌筒结构的内域直径定义法, 用于确定交界面在叶轮和挡板之间的具体位置。成果可为不同结构搅拌筒的数值模拟过程提供理论参考。
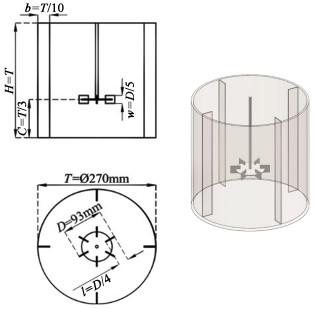
1 几何结构以平底无顶盖搅拌筒为研究对象, 筒内均匀分布4个挡板, 如图 1所示。搅拌筒内径T=0.27 m, 挡板宽度b=T/10, 搅拌筒尺寸与Wu等[9]的实验装置结构相同。筒内工质为水, 液面高度为H。叶轮为标准六直叶Rushton叶轮, 叶轮直径D=0.093 m, 叶片长度l=D/4, 高度w=D/5, 叶轮离底净距为T/3, 搅拌转速N=200 r ·min-1。
|
| 图 1 搅拌筒结构示意图 Fig.1 Front view, top view and 3D view of stirred tank |
| |
搅拌混合过程遵循质量守恒、动量守恒方程。质量守恒方程可表示为:
| $ \frac{\partial \rho}{\partial t}+\operatorname{div}(\rho \vec{u})=0 $ | (1) |
式(1)中: ρ为流体密度;
基于MRF方法, 内域和外域动量守恒方程为:
| $ \frac{\partial(\rho \vec{u})}{\partial t}+\operatorname{div}(\rho \vec{u} \vec{u})=-\operatorname{div}(P)+\operatorname{div}(\tau)+\rho \vec{g} $ | (2) |
| $ \frac{\partial(\rho \vec{u})}{\partial t}+\operatorname{div}(\rho \vec{u} \vec{u})=-\operatorname{div}(P)+\operatorname{div}(\tau)+\rho \vec{g}+F $ | (3) |
式(2)和式(3)中: P为压力; τ为雷诺应力张量;
| $ \frac{\partial(\rho k)}{\partial t}+\operatorname{div}(\rho \vec{u} k)=\operatorname{div}\left[\frac{\mu_T}{\sigma_k} \operatorname{div}(k)\right]+G_k-\rho \varepsilon $ | (4) |
| $ \begin{gathered} \frac{\partial(\rho \varepsilon)}{\partial t}+\operatorname{div}(\rho \vec{u} \varepsilon)=\operatorname{div}\left[\frac{\mu_T}{\sigma_{\varepsilon}} \operatorname{div}(\varepsilon)\right]+ \\ \frac{\varepsilon}{k}\left(C_{1 \varepsilon} G_k-C_{2 \varepsilon} \rho \varepsilon\right) \end{gathered} $ | (5) |
式(4)和式(5)中: Gk为平均速度梯度产生的湍动能; μT为湍流黏性(kg ·m-1 ·s-1); σε为湍流耗散率普朗特数; σk为湍动能普朗特数; C1ε、C1k为模型常数。采用Realizable k-ε湍流模型, 常数分别取定为C1ε=1.44, C1k=1.9, σk=1.0, σε=1.2。
2.2 边界条件数值模拟基于ANSYS FLUENT 2022R1平台, 叶轮旋转运动通过MRF方法实现。筒体壁面及外流体域静止, 绝对速度为0 m ·s-1, 内域和叶轮、旋转轴保持等速旋转, 旋转沿Z轴正向(即在顶面处观察为逆时针)。搅拌筒内固体壁面为无滑移边界条件, 如侧筒壁和筒底、叶轮表面和旋转轴等表面; 筒体顶面设定为压力出口, 表压为0 Pa, 以模拟搅拌筒顶为自由表面的条件。重力加速度设置为Z轴负方向, 大小为9.81 m ·s-2。模拟中采用SIMPLEC算法进行压力与速度耦合, 计算中各方程的收敛残差设定为1×10-5。
2.3 旋转内域与网格划分MRF内外域交界面的位置对数值模拟计算精度具有较大影响, 因此, 为了全面分析内外域交界面的位置对数值模拟计算精度的影响, 需要考虑交界面在靠近挡板和叶轮边缘处的情况, 即搅拌流动过程中非稳态特性明显的区域。
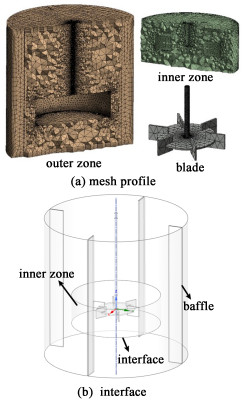
根据Luo等[13]对于MRF方法假设, 内域直径大小占筒体直径din/T=0.62时能够取得接近实验数据的模拟结果; Patil等[12]在Wu等[9]进行实验的搅拌筒结构下对内域划分进行数值模拟, 得出与实验数据吻合最好的内域直径, 其直径关系din/T=0.68。基于上述讨论, 划分4个不同直径大小的内旋转域, 分别为MRF1、MRF3、MRF4和MRF6, 另外分别在中间插值取得MRF2、MRF5, 最终划分6个不同大小的内域, 见图 2和表 1。内域高度统一为3w(w为叶片高度)。
|
| 图 2 网格划分及内外域交界面示意图 Fig.2 Meshing and interface of inner and outer zone |
| |
对流体域划分内域后, 分别对每个模型进行网格划分, 见表 1。搅拌筒壁面附近创建边界层网格, 对内外域交界面位置的网格进行加密, 同时保证网格总数量相近, 以降低网格数量引起的计算偏差。
另外, 还研究了旋转内域划分高度对模拟结果的影响。在确定内域直径后, 以叶片高度的整数倍为划分依据, 划分不同高度的内域。从h=w(即内域与叶片等高)到h=5w, 共划分5个, 见表 2。同样对每个模型分别划分网格, 控制总网格数相近。
| 内域 | 内域高度/mm | 位置特征 | 网格数 |
| w | 18.6 | 与叶轮等高 | 511 999 |
| 2w | 37.2 | h=2w | 654 350 |
| 3w | 55.8 | h=3w | 601 419 |
| 4w | 74.4 | h=4w | 692 206 |
| 5w | 93.0 | h=5w | 698 925 |
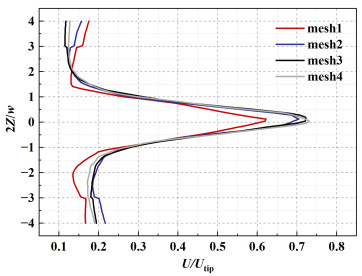
数值模拟计算精度很大程度取决于网格数。本研究选择上述MRF2内域的几何模型进行网格无关性验证。对该模型划分不同数量的网格如表 3。4种网格数下分别得到模拟结果, 并在距离搅拌轴5 cm处提取流体速度随轴向位置变化曲线, 如图 3。
| 序号 | 网格数 |
| mesh1 | 334 852 |
| mesh2 | 433 867 |
| mesh3 | 507 559 |
| mesh4 | 808 590 |
|
| 图 3 不同网格数沿轴向速度曲线 Fig.3 Variation of fluid velocity along axial direction under different mesh numbers |
| |
图 3给出了4种网格数下流体速度沿轴向的变化。结果表明, 从mesh1到mesh2的网格数增加对模拟结果的影响较大, 而mesh2到mesh3的曲线变化较小。当网格数量从mesh3增加到mesh4时, 2条曲线之间的偏差最小。因此, 可以认为网格数在500 000~800 000范围内可以满足模拟精度和计算成本的要求。
2.4 数据处理 2.4.1 搅拌转矩转矩是计算搅拌过程中评价耗功的重要参数[23]。搅拌过程中总力矩是叶轮和搅拌轴上各点对旋转轴的力矩之和, 可用式(6)表示。
| $ \vec{M}_{\mathrm{A}}=\vec{r}_{\mathrm{AB}} \times \vec{F}_{\mathrm{P}}+\vec{r}_{\mathrm{AB}} \times \vec{F}_{\mathrm{V}} $ | (6) |
式(6)中: M为总力矩; A是力矩中心点; B为作用点;
用测量值替换平均值得到均方根误差(RMSE), 可表示模拟结果与实验值之间的偏差[9]。
| $ \text { RMSE }=\sqrt{\frac{\left(Y_i-X_i\right)^2}{n}} $ | (7) |
式(7)中: n为数据点; Yi为该点变量的预测值; Xi为该点变量的实验值。
为了与实验值取点保持一致, 在与实验值相同的位置, 每条曲线分别取得53个数据点计算均方根误差。
2.4.3 归一化处理为了保证搅拌筒内流动特征规律的通用性, 分别对速度和轴向位置无量纲化。流体速度分布以叶轮尖端速度Utip无量纲化。速度曲线的x轴建立在叶轮中心, 测量点到叶轮中心的垂直高度以w/2无量纲化, 即y轴坐标为1时, 测量点与叶轮上边缘处于同一高度, 如图 4所示。
|
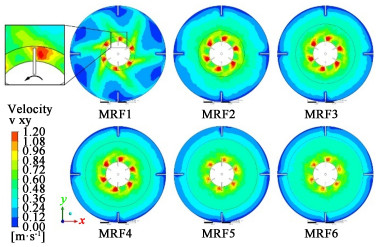
| 图 4 不同内域直径的水平面速度分布 Fig.4 Simulation results of horizontal (XY) plane velocity distribution under different inner zone diameter divisions |
| |
通过对流体域划分旋转内外域, 建立旋转参考系, 旋转叶轮可看作相对于旋转参考系静止。对旋转内域划分直径和高度2个维度, 分别分析对流场的速度分布、模拟值偏差程度和计算转矩的影响。
3.1 内域直径的影响分别研究6种内域直径对搅拌流场的影响, 并比较模拟结果和实验数据确定最适宜直径。
3.1.1 内域直径对速度分布的影响水平速度和垂直速度均在叶轮中心面上取得, 如图 4所示。
由图 4可见, MRF1的高速流体区域未充分发展, 局限在内域未向外发展。MRF2、MRF3、MRF4靠近叶轮流体充分发展, 并且速度向叶片后方逐渐减小。此3种情况下内部区域的速度分布几乎相同, 仅在壁面附近的等速度线略有差异。与MRF2、MRF3、MRF4结果相比, MRF5和MRF6的结果相似, 且叶轮附近转速相对较小。
垂直面上速度分布见图 5。
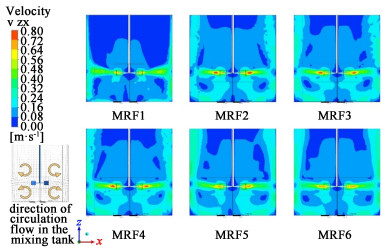
|
| 图 5 不同内域直径的垂直面速度分布 Fig.5 Vertical plane velocity contour maps of simulation results under different divisions of inner zone diameter |
| |
MRF1中叶轮下方未形成速度等值线的环形区域。此环形区域是由叶轮径向排出流被筒壁阻挡并向下流动, 从而形成对称分布在叶轮两侧的循环流。在全封闭搅拌筒中, 叶轮上方也存在循环流, 最终呈现四涡环流。此外, MRF1的结果中叶轮附近的高速区域较小。与MRF2、MRF3和MRF4相比, MRF5和MRF6中叶轮附近的高速区域也相对较小。
3.1.2 内域直径影响的定量分析为了与实验点位置保持一致[9, 12], 在流体域中取平行于搅拌轴的直线, 在直线上取点获得速度曲线。图 6中x轴是以Utip为基准无量纲化的速度, y轴是以w/2为基准无量纲化的轴向位置。

|
| 图 6 不同内域直径的速度曲线: (a)总速度; (b)径向速度Ur; (c)切向速度Uc; (d)轴向速度Uz Fig.6 Total velocity profiles of six inner-zone models: (a) total velocity; (b) radial component ur; (c) tangential component Uc; (d) axial component Uz |
| |
图 6(a)显示了6个内域大小下取得的总速度曲线。MRF1的曲线在叶轮尖端区域出现2个峰值, 与Rushton叶轮实际搅拌过程不符。图 6(b)所示为径向速度曲线, MRF1存在2个峰值, MRF2曲线峰值与实验结果最接近。由此表明MRF2相比Patil等[12]的最佳内域下模拟结果更接近实验值。切向速度曲线如图 6(c)所示。Patil等[12]得到的切向速度偏高。除MRF1外的5个模型的模拟结果比较接近, 峰值速度差别不大。而且, 模拟结果均比实验值偏低, 推测可能是由于k-ε湍流模型对湍流强度预测偏差所致[20], 另外MRF方法基于稳态假设, 从而对瞬态过程计算准确性相比滑移网格法(SG)较低。
由于壁面对径向叶轮排出流的阻碍, 搅拌装置内存在4个涡流, 如图 5所示。在采样线位置, 叶轮下方的轴向速度为正, 而叶轮上方受流动循环的影响, 轴向速度为负。如图 6(d)所示, 所有轴向速度剖面均符合此趋势。模拟结果与实验结果偏差较大。预测的峰值速度大于实验值, 并且轴向速度峰值出现的位置更靠近叶轮, 文献[12]中也存在此偏差。
计算分析速度分量与实验值的均方根误差, 如表 4所示。MRF2径向速度和切向速度的标准偏差最小, 误差均小于Patil的模拟结果[12], 表明MRF2的模拟结果准确性最佳, 而MRF2的轴向速度存在较大偏差。
| 内域 | 均方根误差(RMSE) | ||
| Ur | Uc | Uz | |
| MRF1 | 0.090 2 | 0.113 9 | 0.061 6 |
| MRF2 | 0.072 8 | 0.079 7 | 0.101 2 |
| MRF3 | 0.097 3 | 0.095 9 | 0.096 2 |
| MRF4 | 0.091 5 | 0.095 4 | 0.100 4 |
| MRF5 | 0.103 8 | 0.096 4 | 0.071 1 |
| MRF6 | 0.114 9 | 0.095 5 | 0.069 1 |
| Patil[12] | 0.083 0 | 0.084 1 | 0.053 8 |
转矩是计算搅拌耗功的重要参数, 也是搅拌数值模拟过程中的常用指标。因此对比分析了不同内部区域划分对叶轮计算转矩的影响。图 7所示为各内域的转矩曲线, 横坐标为计算步数, 绿色区域为5%误差带的范围。MRF1的转矩值最小, 而MRF2、MRF3和MRF4的结果几乎相同, 偏差小于0.2%。MRF5和MRF6的计算结果偏低。
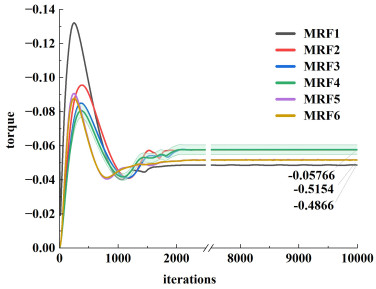
|
| 图 7 不同内域直径下的计算转矩 Fig.7 Calculated torque under six diameters of inner zones |
| |
水平面的速度分布如图 8所示, w高度下的高速区域小于其他高度, 在叶轮附近较明显, 高度2w~5w的模拟结果较接近; 高度为w的模拟结果在叶轮到筒壁的区域流体速度发展不充分, 筒壁附近流体速度较低。
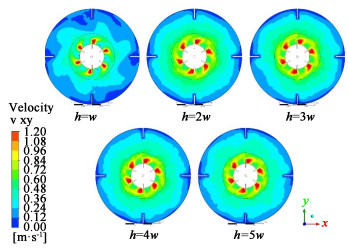
|
| 图 8 不同高度内域水平面的速度分布 Fig.8 Velocity contour on the horizontal plane for different heights of inner zone division |
| |
垂直面上的流速分布如图 9所示。内域高度为w时, 叶轮下方无环形区域。内域高度分别为2w、3w和4w时, 叶轮下方的循环区域和叶轮附近的高速区域基本一致。
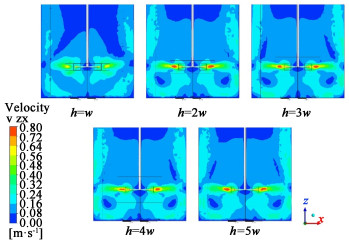
|
| 图 9 不同内域高度垂直面的速度分布 Fig.9 Velocity distribution contours in the vertical plane for different inner zone heights |
| |
每个内域高度的总速度曲线如图 10(a)所示。内域高度为w时, 速度曲线呈现3个峰值, 同样与Rushton叶轮实际搅拌过程不符; 其他模拟结果的趋势相似, 仅在峰值大小上存在细微差别。3w和5w高度下的结果峰值大小一致, 相比2w和4w更大。

|
| 图 10 不同内域高度的速度曲线: (a)总速度; (b)径向速度Ur; (c)切向速度Uc; (d)轴向速度Uz Fig.10 Velocity profiles of five inner zones: (a) total velocity; (b) radial velocity component ur; (c) tangential velocity component Uc; (d) axial velocity component Uz |
| |
图 10(b)显示了不同内域高度下的径向速度曲线。2w到4w的结果几乎相同, 并且峰值比文献[12]中的模拟结果更接近实验数据。图 10(c)为各内域下的切向速度曲线, 内域高度为w的结果依然存在明显偏差, 其他高度下结果相近。图 10(d)显示了不同内域高度下获得的轴向速度曲线。内域高度为w的模拟结果与其他结果和实验曲线存在较大偏差。
表 5为速度分量和实验值间的均方根误差。2w~4w高度的径向速度和切向速度, 偏差均比较接近。5w高度内域的径向速度相对更准确, 而3w高度内域的切向速度更准确。此外, 与前人模拟相比, 模拟结果和实验数据之间的偏离程度更低。对于轴向速度, 各区域得到的速度曲线偏差均大于之前的模拟结果, 3w高度的结果精度相对较高。总体而言, 3w高度下的模拟结果误差最小。
| 内域高度 | 均方根误差(RMSE) | ||
| Ur | Uc | Uz | |
| w | 0.196 5 | 0.197 4 | 0.134 1 |
| 2w | 0.069 3 | 0.088 4 | 0.103 7 |
| 3w | 0.072 8 | 0.079 7 | 0.101 2 |
| 4w | 0.071 3 | 0.082 5 | 0.111 1 |
| 5w | 0.062 8 | 0.080 5 | 0.117 9 |
| Patil[12] | 0.083 0 | 0.084 1 | 0.053 8 |
图 11所示为不同内域高度下计算转矩的对比。与其他高度结果相比, 在w高度处转矩相对较低。其他4个内域的计算转矩值偏差均小于5%。与图 7不同内域直径的结果相比, 内域高度对计算转矩的影响较小。
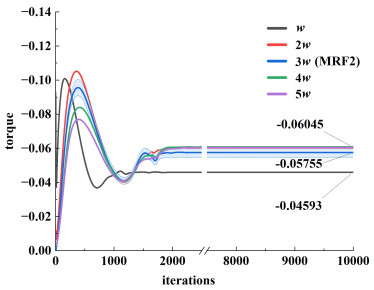
|
| 图 11 不同内域高度下的计算转矩 Fig.11 Calculated torque under five heights of inner zones |
| |
利用MRF方法对旋转搅拌器模拟时广泛采用内域直径与筒体直径之比, 即din=0.62T的方式进行划分, 然而此假设仅体现了交界面和外壁间的相对位置。内外域交界面上的非稳态流动会影响整体稳态流动假设, 因此, 交界面应考虑其与非稳态流动特征较明显区域的相对关系, 如邻近叶轮和挡板的区域。不同功能的搅拌筒存在叶轮直径、挡板高度等结构差异, 例如din=0.62T定义内旋转域直径, 交界面位置随筒直径T固定不变, 若采用更大直径的叶轮, 则会导致交界面与叶轮交叉, 或者交界面与叶轮边缘接近, 导致模拟结果准确性降低。
本研究提出了一种内域直径划分定义方式:
| $ Z=\frac{d_{\text {in }}-D}{T-2 b-D} $ | (8) |
式(8)中: din为内域直径; D为叶轮直径; T为筒体直径; b为挡板宽度; Z值在0~1之间。
如图 12所示, 该定义可直观表征为图中l1/l2, 可将内外域交界面控制在叶轮边缘与挡板之间的指定位置, 对任意挡板和叶轮尺寸的搅拌筒进行划分后的交界面均不会与叶轮或挡板重叠。而当研究模拟结果Z=0.29时, 得出的数值模拟准确性最高。
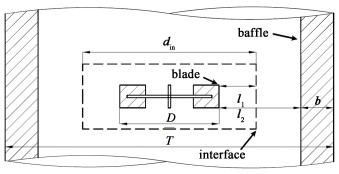
|
| 图 12 内域划分示意图 Fig.12 Schematic diagram of inner zone partitioning |
| |
表 6归纳了研究中搅拌器结构特点及采用内域划分位置[12, 22, 24]: 叶轮与搅拌筒直径之比din/D; 挡板和叶轮的相对位置
| 文献来源 | 参数 | 旋转内域 | 搅拌筒 |
| MRF2 (本研究) | 尺寸 | din=129.6 mm, h=55.8 mm | D=93 mm, b=27 mm, T=270 mm |
| 相对位置 | din/D=1.4, din/T=0.48 | |
|
| Hosseini[24] | 尺寸 | din=240 mm, h=90 mm | D=178 mm, b=42 mm, T=400 mm |
| 相对位置 | din/D=1.34, din/T=0.6 | |
|
| Tamburini[16] | 尺寸 | din=117.8 mm, h=T | D=95 mm, b=19 mm, T=190 mm |
| 相对位置 | din/D=1.24, din/T=0.62 | |
|
| Patil[12] | 尺寸 | din=186 mm, h=57.8 mm | D=93 mm, b=27 mm, T=270 mm |
| 相对位置 | din/D=2, din/T=0.69 | |
需要注意的是, 内域高度对模拟结果准确性的影响比内域直径的影响小。这可能是由叶轮类型所致, 当前研究中针对传统径向流叶轮, 叶轮导致流体的流速变化主要集中在径向, 叶轮附近的轴向速度大小及其变化的剧烈程度相对更低。如图 2(b)所示, 内域直径决定交界面的径向位置, 内域高度决定上下交界面的轴向位置, 因此对径向流叶轮, 内外域交界面所在的径向位置应重点关注。从而可推广至利用MRF方法确定内域大小时, 应在流速变化剧烈方向着重考虑。由此可推测, 对轴向流叶轮应主要考虑内域高度的影响, 后续将对此工作进行开展研究。
4 结论以Rushton叶轮搅拌筒为研究对象, 采用MRF方法, 划分不同直径和高度的旋转内域, 研究了旋转内域尺寸对搅拌流场特性及转矩的影响。得到以下主要结论:
(1) 旋转内域的直径显著影响径流叶轮搅拌槽模拟准确性。搅拌筒最适宜内域尺寸din=129.6 mm、h=55.8 mm。对于与Rushton叶轮类似结构的搅拌过程, 按照
(2) 相较于旋转内域直径的选择, 旋转内域高度位置对径向流叶轮搅拌筒的模拟结果影响较小。这是由于径向流叶轮的排出流在径向的变化更剧烈, 而轴向变化相对较小。
(3) 与对流体速度场的影响相比, 内域尺寸对计算转矩的影响相对较小。内域直径din/T处于0.48~0.68时转矩偏差小于0.2%。大于叶轮高度的不同内域高度之间转矩偏差小于5%。
| [1] |
XIE L, ZHU L, LUO Z, et al. Multiscale modeling of mixing behavior in a 3D atom transfer radical copolymerization stirred-tank reactor[J]. Macromolecular Reaction Engineering, 2017, 11(2): 1600022. DOI:10.1002/mren.201600022 |
| [2] |
ZHANG R, SCHIPPERS A. Stirred-tank bioleaching of copper and cobalt from mine tailings in Chile[J]. Minerals Engineering, 2022, 180: 107514. DOI:10.1016/j.mineng.2022.107514 |
| [3] |
YATMAZ E, GERMEC M, KARAHALIL E, et al. Enhancing β-mannanase production by controlling fungal morphology in the bioreactor with microparticle addition[J]. Food and Bioproducts Processing, 2020, 121: 123-130. DOI:10.1016/j.fbp.2020.02.003 |
| [4] |
YANG L, ZHU Z, QI X, et al. The process of the intensification of coal fly ash flotation using a stirred tank[J]. Minerals, 2018, 8(12): 597. DOI:10.3390/min8120597 |
| [5] |
LIU Y, WACHEMO A C, YUAN H, et al. Anaerobic digestion performance and microbial community structure of corn stover in three-stage continuously stirred tank reactors[J]. Bioresource Technology, 2019, 287: 121339. DOI:10.1016/j.biortech.2019.121339 |
| [6] |
LAI F, WANG Y, EI-SHAHAT S A, et al. Numerical study of solid particle erosion in a centrifugal pump for liquid-solid flow[J]. Journal of Fluids Engineering, 2019, 141(12): 121302. DOI:10.1115/1.4043580 |
| [7] |
DUCCI A, YIANNESKIS M. Direct determination of energy dissipation in stirred vessels with two-point LDA[J]. AIChE Journal, 2005, 51(8): 2133-2149. DOI:10.1002/aic.10468 |
| [8] |
MURTHY B N, JOSHI J B. Assessment of standard k-ε, RSM and LES turbulence models in a baffled stirred vessel agitated by various impeller designs[J]. Chemical Engineering Science, 2008, 63(22): 5468-5495. DOI:10.1016/j.ces.2008.06.019 |
| [9] |
WU H, PATTERSON G K. Laser-Doppler measurements of turbulent-flow parameters in a stirred mixer[J]. Chemical Engineering Science, 1989, 44(10): 2207-2221. DOI:10.1016/0009-2509(89)85155-3 |
| [10] |
YAPICI K, KARASOZEN B, SCHÄFER M, et al. Numerical investigation of the effect of the Rushton type turbine design factors on agitated tank flow characteristics[J]. Chemical Engineering and Processing: Process Intensification, 2008, 47(8): 1340-1349. DOI:10.1016/j.cep.2007.05.002 |
| [11] |
周国忠, 施力田, 王英琛. 搅拌反应器内计算流体力学模拟技术进展[J]. 化学工程, 2004, 32(3): 28-32. ZHOU Guozhong, SHI Litian, WANG Yingchen. Computational Fluid Dynamics progress in stirred tank reactors[J]. Chemical Engineering (China), 2004, 32(3): 28-32. (in Chinese) |
| [12] |
PATIL H, PATEL A K, PANT H J, et al. CFD simulation model for mixing tank using multiple reference frame (MRF) impeller rotation[J]. ISH Journal of Hydraulic Engineering, 2021, 27(2): 200-209. DOI:10.1080/09715010.2018.1535921 |
| [13] |
LUO J, GOSMAN A D, ISSA R I, et al. Full flow field computation of mixing in baffled stirred vessels[J]. Chemical Engineering Research and Design, 1993, 71(A3): 342-344. |
| [14] |
BAKKER A, LAROCHE R D, WANG M H, et al. Sliding mesh simulation of laminar flow in stirred reactors[J]. Chemical Engineering Research and Design, 1997, 75(1): 42-44. DOI:10.1205/026387697523372 |
| [15] |
NAUDE I, XUEREB C, BERTRAND J. Direct prediction of the flows induced by a propeller in an agitated vessel using an unstructured mesh[J]. The Canadian Journal of Chemical Engineering, 1998, 76(3): 631-640. DOI:10.1002/cjce.5450760335 |
| [16] |
TAMBURINI A, BRUCATO A, CIOFALO M, et al. CFD simulations of early-to fully-turbulent conditions in unbaffled and baffled vessels stirred by a Rushton turbine[J]. Chemical Engineering Research and Design, 2021, 171: 36-47. DOI:10.1016/j.cherd.2021.04.021 |
| [17] |
DI S, XU J, CHANG Q, et al. Numerical simulation of stirred tanks using a hybrid immersed-boundary method[J]. Chinese Journal of Chemical Engineering, 2016, 24(9): 1122-1134. DOI:10.1016/j.cjche.2016.05.031 |
| [18] |
OSHINOWO L, JAWORSKI Z, DYSTER K N, et al. Predicting the tangential velocity field in stirred tanks using the Multiple Reference Frames (MRF) model with validation by LDA measurements[M]//10th European Conference on Mixing. Amsterdam: Elsevier, 2000
|
| [19] |
YANG F, ZHOU S, WANG G. Detached eddy simulation of the liquid mixing in stirred tanks[J]. Computers & Fluids, 2012, 64: 74-82. |
| [20] |
李波, 张庆文, 洪厚胜, 等. 搅拌反应器中计算流体力学数值模拟的影响因素研究进展[J]. 化工进展, 2009, 28(1): 7-12. LI Bo, ZHANG Qingwen, HONG Housheng, et al. Several factors of CFD numerical simulation in stirred tank[J]. Chemical Industry and Engineering Progress, 2009, 28(1): 7-12. (in Chinese) |
| [21] |
SHI P, RZEHAK R. Bubbly flow in stirred tanks: Euler-Euler/RANS modeling[J]. Chemical Engineering Science, 2018, 190: 419-435. DOI:10.1016/j.ces.2018.06.001 |
| [22] |
TAMBURINI A, CIPOLLINA A, MICALE G, et al. Influence of drag and turbulence modelling on CFD predictions of solid liquid suspensions in stirred vessels[J]. Chemical Engineering Research and Design, 2014, 92(6): 1045-1063. DOI:10.1016/j.cherd.2013.10.020 |
| [23] |
DE LAMOTTE A, DELAFOSSE A, CALVO S, et al. Identifying dominant spatial and time characteristics of flow dynamics within free-surface baffled stirred-tanks from CFD simulations[J]. Chemical Engineering Science, 2018, 192: 128-142. DOI:10.1016/j.ces.2018.07.024 |
| [24] |
HOSSEINI S, PATEL D, EIN-MOZAFFARI F, et al. Study of solid-liquid mixing in agitated tanks through computational fluid dynamics modeling[J]. Industrial & Engineering Chemistry Research, 2010, 49(9): 4426-4435. |
 2024, Vol. 41
2024, Vol. 41





