气升式反应器由鼓泡塔发展而来,是通过提升管底部气体的加入使反应器内部产生密度差进而拥有循环动力的自循环反应器[1]。气升式反应器分为内循环和外循环2大类,与传统的鼓泡塔相比具有能量输入低、剪切应力低、传质速率快和结构简单等优点,被广泛应用在生物、化工和环境等领域[2, 3]。
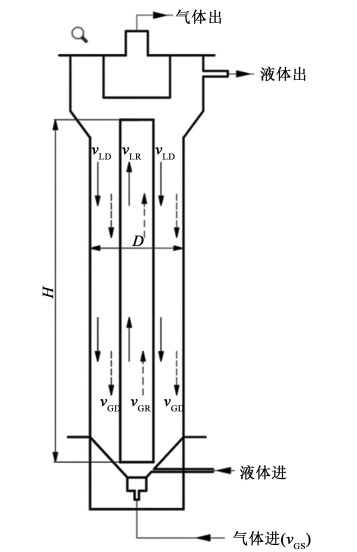
气升式反应器通常包含提升管、下降管、顶部气液固分离区和底部进气区4个部分。20世纪以来人们对气升式反应器的结构做了很多优化,用于提高液体的循环速度、增大气含率、增强反应器内的气液传质[4]。内循环气升式反应器结构及气液流动方向如图 1,图中实线表示液相循环,虚线表示气相循环。依据反应器下降管内气含率的不同,反应器内流动可分为3个阶段, 工业气升式循环反应器常操作于第3阶段,此阶段下降管内存在较高的气含率。
|
| 图 1 内循环气升式反应器内气液流动示意图 Fig.1 Diagram of the direction of gas-liquid flow in internal circulation air-lift reactor |
| |
针对气升式反应器内的流体力学参数的计算提出了多种模型:计算循环液速的Heijnen模型[5]、基于能量与动量守恒的Garcala-Calvo模型[6]和通过迭代求解提升管液速的Livingston数学模型[7]。上述模型已被应用于工业反应器的设计中,如Livingston的模型已成功的应用于1 000 L气升式反应器的设计[8]。然而,上述众多模型计算中,下降管与提升管内气含率的比值(α)常采用Bello和Wang等推荐的0.86~0.92的定值[9, 10],这可能与实际不符。
为减小采用恒定α值计算平均循环液速vL与平均气含率εG带来的误差,本研究引入气相循环比(β)对Heijnen模型进行了修正,建立了vL与εG的计算方法。通过实验结果对β关联方程中的参数c0进行了回归,并与文献模型进行了对比与分析。
1 反应器模型 1.1 文献模型与不足在内循环气升式反应器中,反应器内平均循环液速定义为
| $ \begin{equation*} v_{\mathrm{L}}=m v_{\mathrm{LR}}+(1-m) v_{\mathrm{LD}} \end{equation*} $ | (1) |
式(1)中:m为提升管截面积与反应器截面积比。
Heijnen针对内循环气升式反应器推导了循环液速的计算方程
| $ \begin{equation*} v_{\mathrm{L}}=\left(\frac{4 g H}{k_{\mathrm{f}}}\right)^{\frac{1}{3}}\left[v_{\mathrm{GS}}-\varepsilon_{\mathrm{G}} v_{\mathrm{sb}}-\varepsilon_{\mathrm{S}} v_{\mathrm{sp}}\left(\frac{\rho_{\mathrm{S}}}{\rho_{\mathrm{L}}}-1\right)\right]^{\frac{1}{3}} \end{equation*} $ | (2) |
式(2)中:vGS为表观气速,vsb和vsp分别为气泡和固体的滑移速度,H为提升管高度,kf为反应器内流体流动的阻力系数,平均气含率εG和平均固含率εs定义为
| $ \begin{gather*} \varepsilon_{\mathrm{G}}=m \varepsilon_{\mathrm{GR}}+(1-m) \varepsilon_{\mathrm{GD}} \end{gather*} $ | (3) |
| $ \varepsilon_{\mathrm{s}}=m \varepsilon_{\mathrm{SR}}+(1-m) \varepsilon_{\mathrm{SD}} $ | (4) |
方程(2)中εG可采用式(5)计算
| $ \begin{equation*} \frac{v_{\mathrm{GS}}}{\varepsilon_{\mathrm{G}}}=v_{\mathrm{sb}}+\frac{1-\alpha}{2(m+(1-m) a)} v_{\mathrm{L}} \end{equation*} $ | (5) |
式(5)中:α为下降管与提升管气含率比(εGD/εGR),是Heijnen模型的模型参数,给定α值即可联立方程(2)和(5)计算不同表观气速vGS时的平均循环液速vL和平均气含率εG。
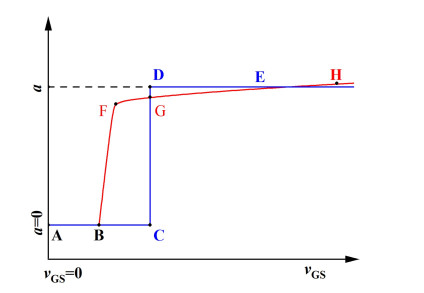
对于上述Heijnen模型,模型参数α的取值直接关系到模型预测的准确性,图 2中线段ABCDE给出了不同运行阶段的取值。线段AB、BC和DE分别对应反应器运行的第1、2和3阶段。反应器运行于第1和2阶段时,Heijnen认为气含率比α=0,当表观气速vGS大于某临界值时,气含率比α发生突跃后进入第3阶段并保持不变。
|
| 图 2 Heijnen模型与改进模型示意图 Fig.2 Schematic diagram of Heijnen model and the improved model |
| |
然而,考虑到反应器运行进入第2阶段后,提升管中气体开始被下降管液体夹带进入下降管,在第2阶段运行期间,气含率比α应逐步增加,直至进入第3阶段后,气含率比α增加速度变缓,最终可能接近文献给定的α=0.86~0.92值范围,即反应器操作应该遵循图 2中ABFGH线段。实际上,文献推荐的α取值正是基于工业反应器操作工况下测得的数据,因此,对于表观气速不高的中试和工业反应器,Heijnen模型的预测可能与实际操作情况存在偏差。
1.2 模型改进为避免采用恒定的气含率比值计算平均循环液速和平均气含率模型存在的不足,本研究针对图 2中ABFGH的反应器操作线建立模型。引入气相循环比β,其物理意义为下降管入口气体与提升管出口气体流量之比。显然,随着下降管液速vLD增大,被夹带进入下降管的气体量增加,因此,β应为下降管液速vLD的函数,且随着vLD增大而增加,筛选得到如下方程:
| $ \begin{equation*} \beta=\max \left(\frac{v_{\mathrm{L}}-v_{c}}{v_{\mathrm{L}}-v_{\mathrm{c}}+c_{0}}, 0.0\right) \end{equation*} $ | (6) |
式(6)中:c0为模型参数,vc为下降管液速等于气泡滑移速度vsb时的vL值,可计算为
| $ \begin{equation*} v_{\mathrm{c}}=2(1-m) v_{\mathrm{sb}} \end{equation*} $ | (7) |
由方程(6)和(7)可知,当vLD < vsb时,下降管内气含率εGD=0,此时反应器运行于第1阶段。随着表观气速vGS增加,vLD增大,当vLD>vsb时,反应器进入第2阶段,此时下降管内气含率升高,模型参数c0反映了循环液体夹带气体进入下降管的能力,其值将通过实验确定。
对于气液两相流,方程(2)可改写为:
| $ \begin{equation*} v_{\mathrm{L}}=\left(\frac{4 g H}{k_{\mathrm{f}}}\right)^{\frac{1}{3}}\left[v_{\mathrm{GS}}-\varepsilon_{\mathrm{G}} v_{\mathrm{sb}}\right]^{\frac{1}{3}} \end{equation*} $ | (8) |
提升管中的气体体积流量衡算为:
| $ \begin{equation*} \left(v_{\mathrm{LR}}+v_{\mathrm{sb}}\right) \varepsilon_{\mathrm{GR}} m=\left(v_{\mathrm{LD}}-v_{\mathrm{sb}}\right) \varepsilon_{\mathrm{GD}}(1-m)+v_{\mathrm{GS}} \end{equation*} $ | (9) |
根据β定义,有:
| $ \begin{equation*} \left(v_{\mathrm{LD}}-v_{\mathrm{sb}}\right) \varepsilon_{\mathrm{GD}}(1-m)=\beta\left(v_{\mathrm{LR}}+v_{\mathrm{sb}}\right) \varepsilon_{\mathrm{GR}} m \end{equation*} $ | (10) |
将方程(3)、(9)和(10)联立,可得:
| $ \begin{equation*} \varepsilon_{\mathrm{G}}=\frac{v_{\mathrm{GS}}}{\left(v_{\mathrm{LR}}+v_{\mathrm{sb}}\right)(1-\beta)}\left[1+\frac{\beta\left(v_{\mathrm{LR}}+v_{\mathrm{sb}}\right)}{v_{\mathrm{LD}}-v_{\mathrm{sb}}}\right] \end{equation*} $ | (11) |
假设气升式反应器内无液体流入和流出,则液相衡算为:
| $ \begin{equation*} v_{\mathrm{LR}} m\left(1-\varepsilon_{\mathrm{CR}}\right)=v_{\mathrm{LD}}(1-m)\left(1-\varepsilon_{\mathrm{CD}}\right) \end{equation*} $ | (12) |
气体滞留量较小时,可以假设:
| $ \begin{equation*} 1-\varepsilon_{\mathrm{GR}}=1-\varepsilon_{\mathrm{GD}} \end{equation*} $ | (13) |
联立方程(3)、(11)、(12) 和(13)可得:
| $ \begin{equation*} \varepsilon_{\mathrm{G}}=\frac{v_{\mathrm{GS}}}{\left(\frac{v_{\mathrm{L}}}{2 m}+v_{\mathrm{sb}}\right)(1-\beta)}\left[1+\frac{\beta\left(\frac{v_{\mathrm{L}}}{2 m}+v_{\mathrm{sb}}\right)}{\frac{v_{\mathrm{L}}}{2(1-m)}-v_{\mathrm{sb}}}\right] \end{equation*} $ | (14) |
将方程(14)代入循环液速计算方程(5)中,即可计算vL和εG。
2 实验部分为对比模型计算结果与实际反应器的偏差,实验测定了气升式循环反应器内流体力学参数。反应器由有机玻璃制成,提升管内径为0.12 m,外筒内径为0.2 m,结构如图 1所示。反应器底部设有气体分布器以及进水口,反应器顶部设有气液分离器,在分离器的液体出口处放置电导率测量探头记录电导率用于求解反应器内循环液体流速。反应器壁上设置多个测压孔用于反应器内局部气含率计算[11]。实验在常温常压下进行,考察表观气速对平均循环液速和平均气含率等参数的影响;其中气含率的测定使用体积膨胀法[12],循环液速的测定使用脉冲法[13]。为对比反应器结构参数的影响,分别在提升管高度为2和6 m的反应器中进行了测定。
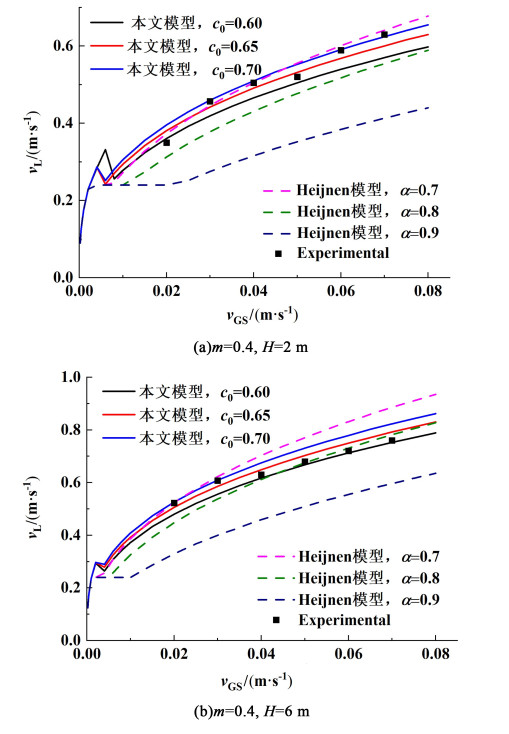
3 结果与讨论 3.1 模型验证循环液速vL和气含率εG是气升式循环反应器的2个最为重要的流体力学参数。图 3和图 4分别给出了不同表观气速vGS下两者的实验与模拟结果。其中模型计算中气泡滑移速度vsb取为0.2 m ·s-1[14]。可以看出,vGS较小时,循环液速vL随vGS增加会出现短暂下降,这是由于反应器运行从第1阶段刚进入第2阶段时,下降管中液体下降速度大于气泡的滑移速度,少量气泡从提升管被循环夹带至下降管,气含率差εGR-εGD减小,反应器循环推动力降低,从而导致循环液速vL变小。继续升高表观气速vGS,气含率差εGR-εGD开始增大,推动力增加,循环液速vL随之升高。
|
| 图 3 表观气速对平均循环液速的影响 Fig.3 Influence of feed gas velocity on fluid cycling velocity |
| |
|
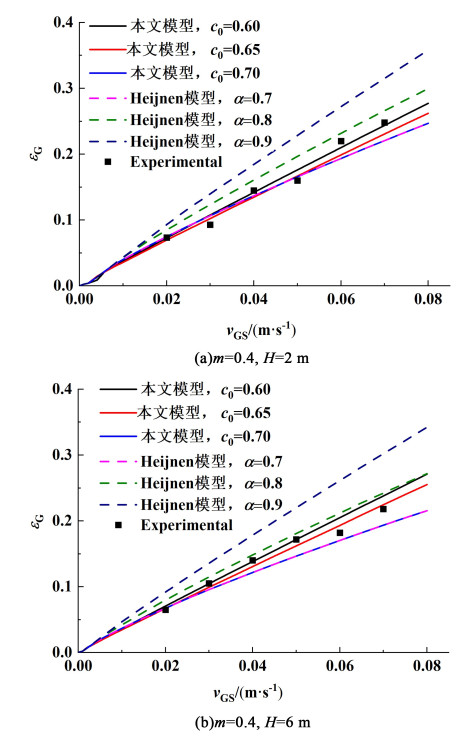
| 图 4 表观气速对平均气含率的影响 Fig.4 Influence of feed gas velocity on gas holdup |
| |
由图 3和图 4还可以看出,2种模型下,循环液速vL随着表观气速vGS的升高均呈现增大的趋势。2种模型相比,Heijnen模型参数α取值对vL和εG的影响尤为明显,α值的较小变化即可引起较大的预测结果变化,当α由0.7升高至0.9时,对应的vL降低接近38%,εG升高42%,这表明不同操作条件下选择准确的α值十分重要,采用固定值进行计算可能会出现较大的误差。
采用实验数据对模型参数c0进行估值,c0=0.65时,平均相对误差最小,对于2种结构参数的反应器(H=2和6 m),vL和εG的模拟结果与实验结果吻合良好,平均相对误差分别为3.9%和6.2%,表明提升管高度在较大的范围内变化时,模型参数c0取值仍可保持恒定,气相循环比β仅决定于vL值,说明改进后的模型对反应器结构参数的变化具有较强的适应性。而对于Heijnen模型,α取值为0.7,0.8和0.9时,预测结果与实验结果存在较大的误差,采用相同的α值无法同时准确预测vL和εG。
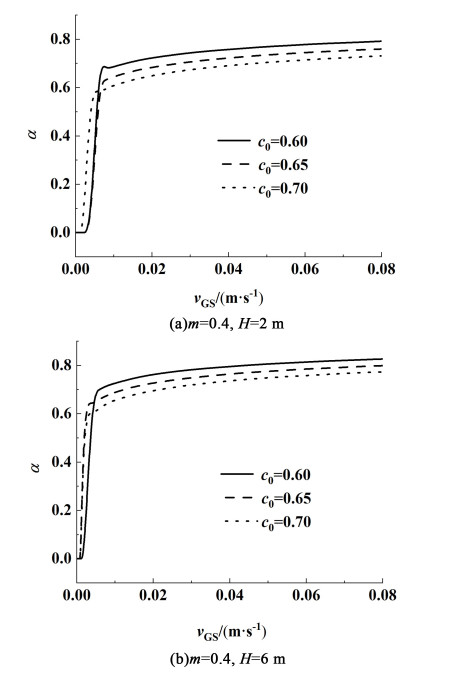
3.2 不同操作条件的模拟计算 3.2.1 表观气速对气含率比的影响表观气速vGS对气含率比α的影响如图 5所示。可以看出,2种提升管高度下,α随vGS的变化均可分为3个阶段:当vGS较低时,下降管内无气泡,α=0,此时为第1阶段;随着vGS增加,下降管内液速vLD大于气泡滑移速度vsb, 进入第2阶段,此时下降管内开始出现气泡,α随着vGS的增加快速升高;随着vGS的继续升高,α进入缓慢增加阶段,与循环液速的变化趋势相同[15],此时为第3阶段,此阶段气含率比α介于0.70~0.82之间,这表明不考虑表观气速及反应器参数影响,采用固定值α计算流体力学参数会带来较大误差。
|
| 图 5 表观气速对下降管与提升管气含率之比的影响 Fig.5 Influence of feed gas velocity on ratio of holdup in the riser and downcomer |
| |
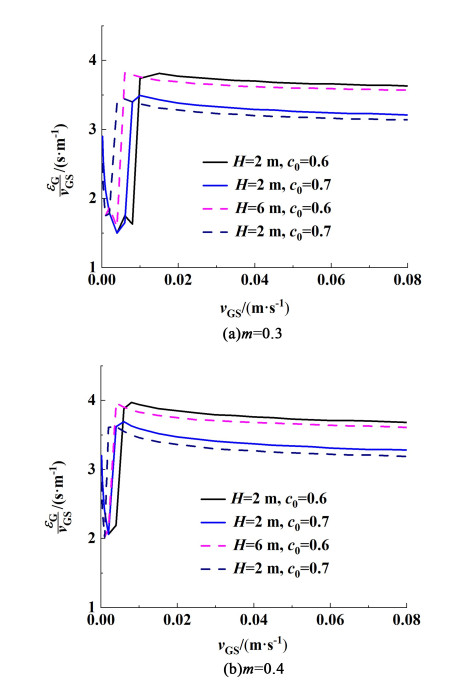
针对2种提升管高度(H=2和6 m),采用本文模型计算了εG/vGS与vGS的定量关系,结果如图 6所示。结果表明,εG/vGS随vGS的变化趋势依然可以分为3个阶段。vGS较小时,εG/vGS随vGS的增加而下降(第1阶段);进入第2阶段后,随着进入下降管内气泡的不断增加,εG/vGS随vGS的增加而快速升高;第3阶段,εG/vGS随vGS的增加有所下降,并稳定于3.5和4.0之间。对比图 6(a)和图 6 (b)可以发现,不同提升管高度时,上述变化趋势基本相同。
|
| 图 6 表观气速对平均气含率的影响 Fig.6 Influence of feed gas velocity on gas holdup |
| |
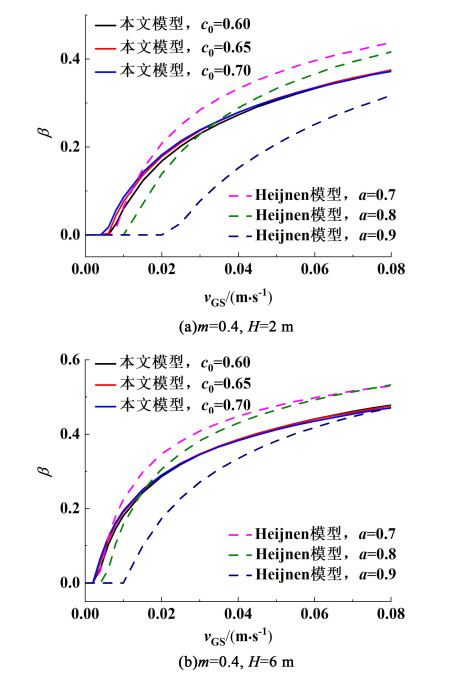
气相循环比β是表征循环反应器循环性能的重要参数,采用本研究模型,模型参数c0分别取值0.60, 0.65和0.70时,β与vGS的关系如图 7所示。第1阶段时,表观气速vGS较低,气泡不能进入下降管内,β=0;进入第2阶段后,进入下降管内的气体量逐渐增加,β迅速升高;随着vGS进一步升高,反应器运行进入第3阶段,β值缓慢增加。从图 7中可以看出,模型参数c0取值对循环比β影响较小。与本文模型不同,Heijnen模型参数α的取值对β影响很大,这表明该模型存在局限性,对于不同反应器尺寸和不同操作条件,α不应取恒定值,但不同条件下α的取值方法属于尚未解决的难题。
|
| 图 7 表观气速对气相循环比的影响 Fig.7 Influence of feed gas velocity on the gas recycling ratio |
| |
对比图 7(a)和图 7(b)可以看出,不同的提升管高度时,β值由0开始上升所对应的表观气速vGS拐点值不同。
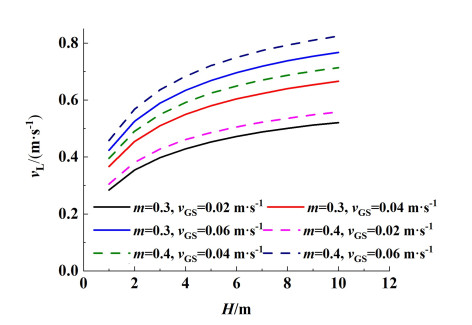
3.2.4 反应器结构参数对循环液速和气含率的影响为进一步分析循环气升式反应器的操作特性,改变提升管与下降管截面积比m和表观气速vGS,模拟计算了循环液速vL和气含率εG随提升管高度H的变化规律,结果如图 8和图 9所示。
|
| 图 8 提升管高度对循环液速的影响 Fig.8 Influence of riser height on liquid recycling velocity |
| |
|
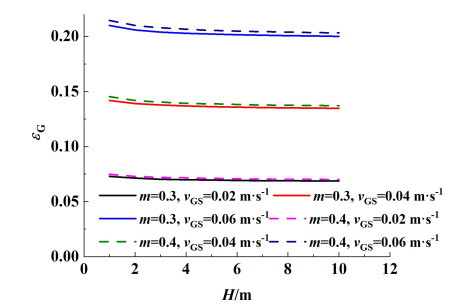
| 图 9 提升管高度对平均气含率的影响 Fig.9 Influence of riser height on gas holdup |
| |
从图 8和图 9中可以看出,随着提升管高度H由1升高至10 m,循环推动力增加,循环液速vL上升;同时,增加提升管高度H,平均气含率εG略有下降,相同的趋势被Blažej[16]报道。另一方面,提升管截面积占比m由0.3升高至0.4时循环液速vL升高,但平均气含率εG变化很小。表观气速vGS由0.2升高至0.6 m ·s-1时,循环液速vL和平均气含率εG都呈增大的趋势。
4 结论针对气液两相体系,建立了内循环气升式反应器内流体流动模型,模型中首次引入气相循环比β,求解计算了不同操作条件下的反应器特性与参数影响规律,并与提升管高度分别为2和6 m的内循环气升式反应器内实测数据进行了对比验证,主要结论如下。
(1) 模型参数c0取值0.65时,计算结果与实验数据吻合良好,相对平均误差小于6.2%,表明模型参数c0取值与反应器高度无关,改进模型对反应器结构的改变具有较强的适应性。
(2) 下降管与提升管内气含率比α在反应器的不同操作阶段呈现出不同的规律,低vGS值时,反应器运行于第1阶段,α=0;随着vGS增加,反应器进入第2阶段,气泡进入下降管,α随着vGS的增加快速升高;更高vGS时,反应器运行进入第3阶段,此时α介于0.70~0.82之间,这表明文献模型中不考虑操作条件采用恒定α值计算vL和εG会带来较大误差。
(3) 所建模型可用于模拟循环气升式反应器的3个运行阶段的主要流体力学参数,包括循环液速vL、气相循环比β、气含率εG和气含率比α,可为此类反应器的设计和放大提供参考。
符号说明:
D—反应器、提升管或下降管的直径, m;
g—引力常数,m ·s-2;
H—提升管高度,m;
kf—摩擦系数;
m—提升管截面积占反应器截面积分数;
vGS—表观速度,m ·s-1;
vsb—气泡滑移速度,m ·s-1;
vsp—固体滑移速度,m ·s-1;
vL—平均液体循环速度,m ·s-1;
vc—临界vL值,m ·s-1。
希腊字母:
α—下降管与提升管内气含率比;
β—气相循环比;
ε—相含率;
ρ—密度,kg ·m-3。
下标:
D—下降管;
G—气体;
L—液体;
R—提升管;
S—固体;
T—反应器。
| [1] |
ZHANG T, WE C, REN Y, et al. Advances in airlift reactors: Modified design and optimization of operation conditions[J]. Reviews in Chemical Engineering, 2017, 33(2): 163-182. DOI:10.1515/revce-2016-0005 |
| [2] |
JIN B, LANT P. Flow regime, hydrodynamics, floc size distribution and sludge properties in activated sludge bubble column, air-lift and aerated stirred reactors[J]. Chemical Engineering Science, 2004, 59(12): 2379-2388. DOI:10.1016/j.ces.2004.01.061 |
| [3] |
XU L, LIU R, WANG F, et al. Development of a draft-tube airlift bioreactor for Botryococcus braunii with an optimized inner structure using computational fluid dynamics[J]. Bioresource Technology, 2012, 119: 300-305. DOI:10.1016/j.biortech.2012.05.123 |
| [4] |
ZHANG T, WEI C, FENG C, et al. Advances in characteristics analysis, measurement methods and modelling of flow dynamics in airlift reactors[J]. Chemical Engineering and Processing-Process Intensification, 2019, 144: 107633. DOI:10.1016/j.cep.2019.107633 |
| [5] |
HEIJNEN J J, HOLS J, VAN DER LANS R G J M, et al. A simple hydrodynamic model for the liquid circulation velocity in a full-scale two- and three-phase internal airlift reactor operating in the gas recirculation regime[J]. Chemical Engineering Science, 1997, 52(15): 2527-2540. DOI:10.1016/S0009-2509(97)00070-5 |
| [6] |
GARCÍA-CALVO E, RODRÍGUEZ A, PRADOS A, et al. A fluid dynamic model for three-phase airlift reactors[J]. Chemical Engineering Science, 1999, 54(13/14): 2359-2370. |
| [7] |
LIVINGSTON A G, ZHANG S. Hydrodynamic behaviour of three-phase (gas-liquid-solid) airlift reactors[J]. Chemical Engineering Science, 1993, 48(9): 1641-1654. DOI:10.1016/0009-2509(93)80124-9 |
| [8] |
PELIVANOSKI B, DETMANN B, OOMS K, et al. Design of a 1000 L pilot-scale airlift bioreactor for nitrification with application of a three-phase hydrodynamic mathematical model and prediction of a low liquid circulation velocity[J]. Chemical Engineering Research and Design, 2020, 153: 257-262. DOI:10.1016/j.cherd.2019.10.018 |
| [9] |
BELLO R A, ROBINSON C W, MOO-YOUNG M. Gas holdup and overall volumetric oxygen transfer coefficient in airlift contactors[J]. Biotechnology and Bioengineering, 1985, 27(3): 369-381. DOI:10.1002/bit.260270323 |
| [10] |
WANG J, XU X, WANG W, et al. Hydrodynamics of an airlift column for aeration in molten sulfur[J]. Applied Sciences, 2021, 12(1): 117. DOI:10.3390/app12010117 |
| [11] |
WANG Y, LIU Y, SHUAI L. Three-phase internal-loop airlift reactor; Gas holdup; Solid holdup; Prediction model[J]. Science & Technology in Chemical Industry, 2013, 21(01): 20-23. |
| [12] |
JIN R, WANG X, XIE J, et al. Study on the characteristics of hydrodynamics and oxygen transfer in new-type structure inner-loop three-phase fluidized bed[J]. Techniques and equipment for environmental pollution control, 2003, 4(5): 30-33. |
| [13] |
BLAŽEJ M, KIŠA M, MARKOŠ J. Scale influence on the hydrodynamics of an internal loop airlift reactor[J]. Chemical Engineering and Processing: Process Intensification, 2004, 43(12): 1519-1527. DOI:10.1016/j.cep.2004.02.003 |
| [14] |
MENDELSON H D. The prediction of bubble terminal velocities from wave theory[J]. AIChE Journal, 1967, 13(2): 250-253. DOI:10.1002/aic.690130213 |
| [15] |
VAN BENTHUM W A J, VAN DER LANS R G J M, VAN LOOSDRECHT M C M, et al. Bubble recirculation regimes in an internal-loop airlift reactor[J]. Chemical Engineering Science, 1999, 54(18): 3995-4006. DOI:10.1016/S0009-2509(99)00097-4 |
| [16] |
BLAŽEJ M, KIŠA M, MARKOŠ J. Scale influence on the hydrodynamics of an internal loop airlift reactor[J]. Chemical Engineering and Processing: Process Intensification, 2004, 43(12): 1519-1527. DOI:10.1016/j.cep.2004.02.003 |
 2024, Vol. 41
2024, Vol. 41





