2. 江南大学机械工程学院, 江苏 无锡 214122;
3. 无锡钡镭新材料技术咨询有限公司, 江苏 无锡 214072
2. School of Mechanical Engineering, Jiangnan University, Jiangsu, Wuxi 214122, China;
3. Wuxi Beilei New Material Technology Consulting Co., Ltd., Jiangsu, Wuxi 214072, China
在诸多工业工程中,化工原料的制备均需通过搅拌混合实现;而大多化工原料为高黏性非牛顿流体,其流动特性较复杂。与低黏性流体相比,高黏性流体所需的功耗更大,且对转速有着苛刻的要求;过高的转速会使搅拌器桨叶受力过高而被损坏,进而甚至引发事故,但过低的转速易造成搅拌混合均匀性的降低[1];与普通的牛顿流体相比,用于特定化工原料的非牛顿流体的动力黏度随剪切速率的变化而变化,转速过高会破坏对剪切敏感的物质分子结构(如润滑脂),影响其成品质量,转速过低则会出现搅拌范围仅局限于桨叶扫掠区域的现象,达不到预期的混合效果。而目前工业生产所用的常规搅拌器缺乏强大的循环能力和显著的剪切作用,还存在搅拌耗时过长、时间成本过高等问题。在控制搅拌功耗的前提下,实现更好的混合效果已成为该行业中较为棘手的问题[2-4]。结构优化可能是提升搅拌效率的重要途径[5]。
随着数值模拟的快速发展,计算流体力学(Computational fluid dynamics,CFD)方法已被广泛应用于搅拌器结构参数的优化研究。这在填补了试验研究局限性的同时,还大幅降低了研发成本。通过数值模拟,发现搅拌强度与介质密度显著影响介质的流动行为[6]。除工况参数和物料性质,搅拌器结构是影响釜内介质搅拌过程的关键因素,如调整挡板位置可实现双层斜叶桨在不增加功耗的条件下改善搅拌效果[7],搅拌桨离底高度对釜体底部的颗粒运动有较大影响[8],叶片的错位布置[9]与不对称分布[10]比常规布置所用的混合时间更短且单位体积混合能大幅提升。近年来,组合式桨也受到行业领域的广泛关注,如Paravisc-锚式组合桨能够在较短的时间内完成均匀混合,混合性能优越[1];3层下压式4折叶涡轮桨和锚框式桨叶的优化组合也能够满足搅拌介质循环流动、均匀悬浮的要求[11]。
然而,在现有的结构改良搅拌器中,涉及到内外层组合式搅拌器应用于非牛顿流体混合搅拌的研究较少,对有效搅拌体积进行量化处理的研究也鲜有关注。本研究提出了一种适用于非牛顿流体混合的搅拌器结构的参数优化方法,即开展了搅拌器的结构设计,验证了搅拌介质剪切稀化的流变特性;采用Laminar模型对该搅拌器的搅拌过程进行流体仿真,深入研究内桨叶片数量、离底高度、叶片倾斜角对单位体积搅拌功率、混合时间和有效搅拌体积分数的影响,并依此进行搅拌器的结构参数优化,研究结果将为非牛顿流体的搅拌器结构设计提供较好的技术参考。
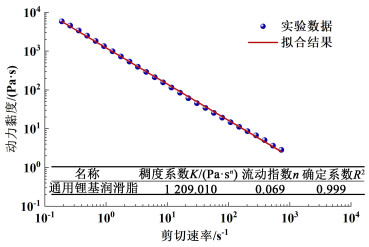
1 材料与方法 1.1 试验材料与搅拌器模型选取通用锂基润滑脂(辽宁海华科技有限公司)作为搅拌介质,通过MCR旋转流变仪(奥地利安东帕公司)测试随剪切速率变化的润滑脂动力黏度。采用0.5 mm的平行板夹具,测试温度为25 ℃,剪切速率为0.1~1 000 s-1,其润滑脂剪切流变特性如图 1所示。发现随着剪切速率的增加,该润滑脂动力黏度呈非线性降低,表现为剪切化稀现象,属于典型非牛顿流体。通过试验数据拟合,该润滑脂的动力黏度μ与剪切速率γ的关系满足式(1)。
|
| 图 1 润滑脂动力黏度随剪切速率的变化 Fig.1 Variation of dynamic viscosity of grease with shear rate |
| |
| $ \mu=K \gamma^{n-1} $ | (1) |
式(1)中:稠化系数K=1 209.01 Pa ·sn,流动指数n=0.069 < 1,这也证实了该润滑脂为假塑性流体。
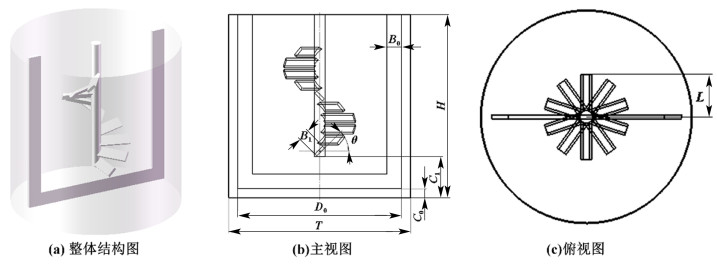
由于通用锂基润滑脂为非牛顿流体且在低速搅拌过程中对应的动力黏度较高,故选取适用于高黏度流体搅拌的锚式桨与具有轴流特性及较强剪切特性的类螺带式桨分别作为新型组合式搅拌器的外层桨和内层桨。拟设计的搅拌器整体结构如 图 2(a)所示,图 2(b)和图 2(c)分别为其主视图与俯视图。搅拌器采用内径T为200 mm的圆柱平底搅拌釜,液位高度H为200 mm,外层锚式桨桨叶直径D0为180 mm,宽度B0为16 mm,内层类螺带式桨桨叶长度L为40 mm,宽度B1为12 mm。
|
| 图 2 搅拌器结构示意图 Fig.2 Schematic diagram of agitator structure |
| |
根据Metzner-Otto[12]公式,平均剪切速率γ·avg与转速N的关系为:
| $ \gamma_{\text {avg }}^{\cdot}=k_{\mathrm{s}} N $ | (2) |
式(2)中:ks为搅拌器Metzner-Otto数;该搅拌器中,内桨ks=13,外桨ks=25.6[13]。搅拌器内流体流动雷诺数计算公式为:
| $ R e=\frac{\rho N D^2}{60 \mu} $ | (3) |
式(3)中:ρ为润滑脂密度,经调定为886.125 kg ·m-3;μ为动力黏度,Pa ·s;D为桨叶直径,mm;N为桨叶转速,r ·min-1。
根据式(1)~式(3)计算,该搅拌器作用下的雷诺数如表 1所示,内、外桨作用下的雷诺数均小于10,属于典型层流。
| 名称 | 直径/mm | 转速/(r·min-1) | 雷诺数 |
| 外桨 | 180 | 30 | 5.8 |
| 内桨 | 80 | 60 | 2.3 |
本研究采用多重参考系法(Multiple Reference Frame,MRF)模拟搅拌器内的相对运动,即将计算域分为内、外桨所在的动区域和内、外静区域,区域之间设置interface用以数据传输;内壁设置为静止无滑移壁面,转轴与桨叶均设置为相对于所在动区域静止的移动壁面,自由液面设置为对称边界,忽略其对搅拌混合过程的影响[10]。流体流动受物理守恒定律的支配,任何流动问题都要满足连续性方程和动量方程。此外,由于本研究使用了示踪剂浓度法,还应满足组分方程[14]。
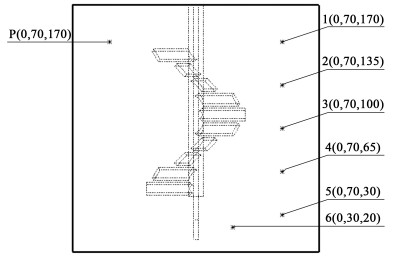
开展其稳态计算时应选用Laminar模型,压力-速度耦合方法选用Coupled算法,差分格式采用二阶迎风,所有变量的收敛残差小于10-7。在计算瞬态浓度场时,应以上述稳态计算的结果为初始条件。需注意的是,启用组分传递模型并激活组分传输项时,不需激活反应项,确保搅拌器内多组分之间仅进行单纯混合。关闭动能方程,仅求解浓度方程,浓度收敛残差设置为10-6,时间步长为0.05 s。本研究选取点P(0, -70, 170)作为示踪剂加料点,同时设置6个监测点,具体位置如图 3所示。
|
| 图 3 加料点和监测点位置 Fig.3 Feeding point and monitoring point location |
| |
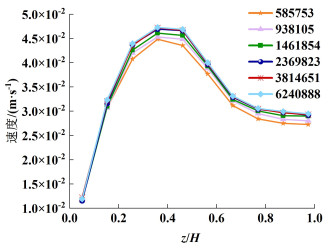
采用Workbench Mesh对计算域进行网格划分,由于内桨结构复杂,故采用非结构四面体网格进行划分。为提高其计算精度,对交界面和桨叶面进行网格加密。网格越密,网格数量越多,计算结果越精确;但过大的网格规模将消耗庞大的计算资源,故有必要进行网格无关性验证。此处,内桨叶片数量为10个,内、外桨转速分别为50和30 r ·min-1,均逆时针转动。表 2为不同划分标准的网格数,图 4为不同网格尺寸下直线Y=-0.05 m上不同高度处的速度。从表 2中发现方案4、5、6中点(0, 0.05, 0.10)处速度相同,且总扭矩差别小于1%;由图 4可知,当网格数量达到2 369 823个时,直线各高度处速度均趋于平稳,继续增加网格数量不会对结果产生影响。因此,本研究采用该划分标准进行网格划分,计算网格如图 5所示。
| 方案 | 网格最小尺寸/mm | 网格数量/个 | v(0, 0.05, 0.1)/(m·s-1) | 总力矩差别比 |
| 1 | 2.4 | 585 753 | 0.041 | 1.849 |
| 2 | 2.0 | 938 105 | 0.043 | 1.297 |
| 3 | 1.7 | 1 461 854 | 0.044 | 1.018 |
| 4 | 1.4 | 2 369 823 | 0.045 | 0.733 |
| 5 | 1.2 | 3 814 651 | 0.045 | 0.476 |
| 6 | 1.0 | 6 240 888 | 0.045 | 0 |
|
| 图 4 X=0 m面内直线Y=-0.05 m上不同高度处的速度 Fig.4 Resultant velocity at different heights on the straight line Y=-0.05 m in the X=0 m plane |
| |

|
| 图 5 计算网格示意图 Fig.5 Schematic diagram of computing grid |
| |
功率消耗是评价搅拌器性能优劣的重要参数之一。在相同转速下,将单位体积搅拌功率Pv作为衡量搅拌特性的关键指标,其计算公式为:
| $ P_{\mathrm{v}}=\frac{2 \pi M N}{V} $ | (4) |
式(4)中:M为搅拌桨所受力矩,N ·m;N为搅拌转速,r ·min-1;V为介质的体积,m3。
1.4.2 混合时间(θM)混合时间(θM)是判断搅拌器搅拌效果最重要的性能指标。θM是指将多种可互溶,但物性有所差异的流体通过搅拌使其达到规定混匀标准时所需的时间。在数值模拟中,通常以示踪剂浓度达到最终稳定浓度(±5)%作为混合完成的标志。
1.4.3 有效搅拌体积分数“搅拌死区”是指搅拌器内基本不参与主体混合的区域,是影响高黏度流体混合时间的关键指标。通常将流速低于0.01Utip的区域定义为“搅拌死区”[15],其余搅拌区域称为有效搅拌区域。本论文将有效搅拌区域占整体搅拌区域的比例称作有效搅拌体积分数,即:
| $ \text { 有效搅拌体积分数 }=\left(1-\frac{V_{U<0.01 U_{\text {tip }}}}{V}\right) \times 100 \% $ | (5) |
式(5)中:VU<0.01Utip为流速低于0.01Utip的体积,m3;Utip为桨叶尖端速度,m ·s-1;V为整体搅拌体积,m3。
2 结果与讨论 2.1 搅拌器内流体流动特性分析通常情况下,流体流动特性分析主要从速度场分布、示踪剂扩散过程、混合时间等方面展开,故本论文以铅锤面速度场、示踪剂扩散过程、浓度响应曲线为例进行分析。搅拌器初始结构参数设置如下:内桨叶片数量为6个,离底高度为45 mm,叶片倾斜角为45°,内/外桨转速分别为60/30 r ·min-1,均逆时针转动。
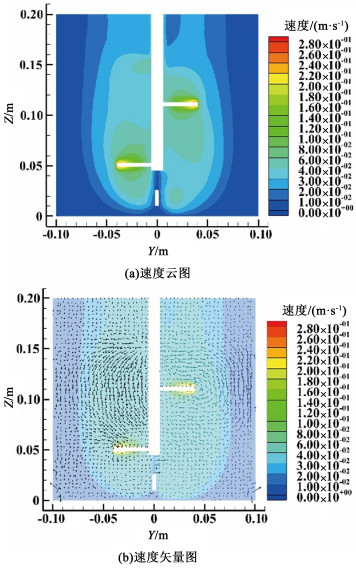
2.1.1 铅锤面速度场的特性图 6为X=0 m处铅锤面的速度场。从图 6(a)可看出,在内桨叶附近的速度最大;沿径向方向速度逐渐减小,搅拌器壁面附近流速较低,易形成死区;由图 6(b)可知,搅拌器左右两侧形成了不对称的轴向循环流,实现搅拌器内上下层流体混合;上方流体下压过程中一部分沿轴向被挤入底部,一部分沿径向被推向内壁;同时,流体在外桨作用下沿切向流动。由此得出该新型搅拌器能够应用于高黏性非牛顿流体的混合搅拌。
|
| 图 6 X=0铅锤面速度场 Fig.6 X=0 plumb surface velocity field |
| |
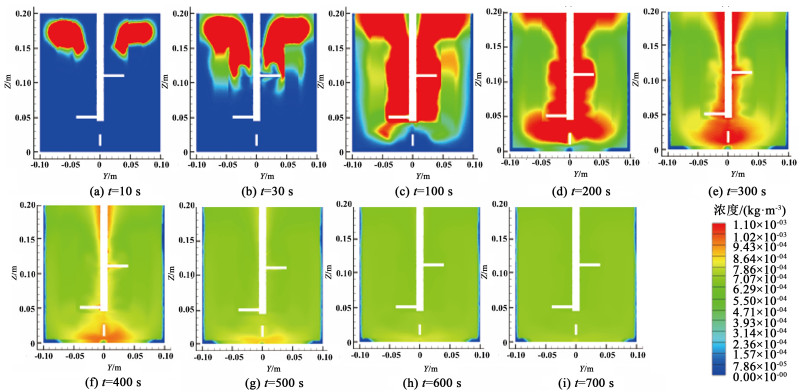
为更加直观地观察搅拌器内流体流动过程,本论文采用示踪剂浓度法。图 7为X=0 m处铅锤面示踪剂浓度随时间变化的分布图,选取100 s为时间间隔,还加入10和30 s 2个时间点,以更好展示搅拌器内初期示踪剂的扩散情况。发现从10 s开始示踪剂依附于内桨转轴向下扩散;直至200 s时基本扩散至底部,遇底撞击后产生径向扩散的分支,进而随循环流沿壁面向上扩散,这与2.1.1所述搅拌器内流型分析相符;当搅拌时间达到600 s时,示踪剂在搅拌器中的浓度分布已近乎均匀,继续搅拌对全局浓度分布基本没有影响,这表明已完成流体的均匀混合。
|
| 图 7 示踪剂扩散图 Fig.7 Diagram of tracer diffusion |
| |
此外,从图 7(h)可直观看出,当监测点1~6处的示踪剂浓度一致时,整个搅拌器中的示踪剂浓度分布亦趋于均匀。因此,本研究所设置的监测点能够较准确地衡量流体的混合进度。
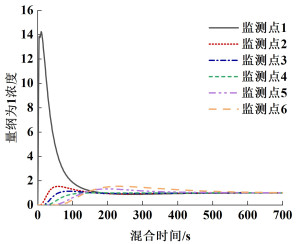
图 8为示踪剂浓度响应曲线,其中各监测点示踪剂浓度响应曲线形态与峰值的差别代表搅拌过程中浓度分布的均匀程度。形态与峰值差别越大,搅拌过程中浓度越不均匀。发现监测点1处的浓度响应曲线曲率最大,示踪剂浓度急剧上升,10 s时达到峰值14.253,说明该处示踪剂浓度发生了剧烈波动,随后急剧下降并于200 s趋于稳定,这可能是投料点在该高度处的缘故。而监测点2、3、4、5和6依次远离投料点,其浓度响应曲线曲率逐渐较小。监测点2、3、5和6处示踪剂浓度均随时间的增加表现为先上升后减小的变化,分别在58、88、199和232 s时达到峰值1.535、1.139、1.322和1.536。由于底部流速低,示踪剂扩散缓慢,监测点6处示踪剂浓度达到稳定值所消耗的时间长达607 s。监测点4处的示踪剂浓度缓慢上升直至平稳,无峰值。观察以上各监测点示踪剂浓度响应曲线能够得到该搅拌器在初始设置条件下的混合时间为607 s。
|
| 图 8 示踪剂浓度响应曲线 Fig.8 Response curve of tracer concentration |
| |
为探究内桨叶片数量、离底高度、叶片倾斜角等结构参数对搅拌特性的影响,研究在初始设置基础上按照内桨叶片数量、离底高度、叶片倾斜角的顺序,依次以前者最佳值为基础展开相关的影响特性研究。
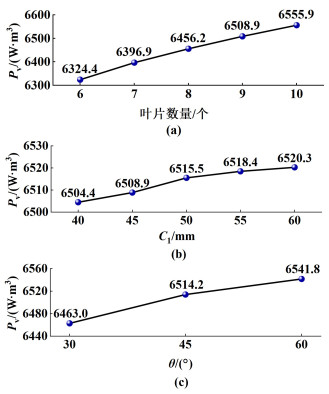
2.2 结构参数对单位体积搅拌功率(Pv)的影响图 9为不同结构参数条件下单位体积搅拌功率。发现Pv随内桨叶片数量增加而增大,这主要是由于内桨所受力矩随叶片数量的增加而增大,进而导致Pv增大。同时,还发现Pv与离底高度C1呈正相关。此外,当倾斜角θ增大时,Pv也明显增加,这可能是由于θ的增大导致内桨桨叶的剪切总面积增大,桨叶受到的阻力矩增大,进而增大了Pv。
|
| 图 9 不同结构参数条件下的单位体积搅拌功率 Fig.9 Stirring power per unit volume under different structural parameters |
| |
不同结构参数条件下混合时间能够通过选取各监测点处示踪剂浓度达到稳定值所需时间的最大值作为最终混合结束的时间,而示踪剂浓度的扩散与搅拌器内轴向速度、径向速度有着密不可分的联系[16],以叶片数量对θM的影响为例,具体阐述如下。
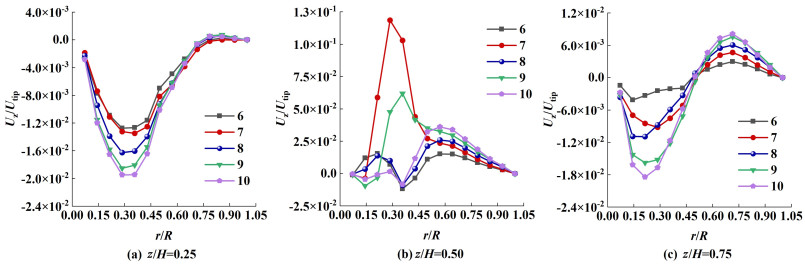
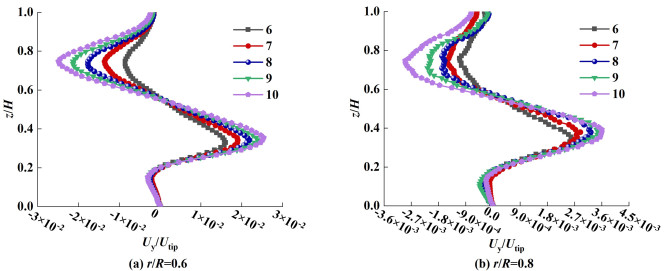
图 10为不同叶片数量条件下X=0 m面内沿径向不同高度处轴向速度的分布曲线,以Z轴正方向为轴向速度正方向,反之为负。图 11为不同叶片数量条件下X=0 m面内沿轴向不同直径处径向速度的分布,以Y轴正方向为径向速度正方向,反之为负。可以发现搅拌器内顶部与底部流场的轴向速度与叶片数量具有一定的正相关性;当叶片数量为9个时,继续增加叶片数量轴向速度整体不会出现较大增幅。但当z/H=0.50时,由于叶片的非对称性分布,叶片数量为7和9个时的轴向速度明显优于其余情况。显而易见的是桨叶附近和搅拌器内轴向中段区域流场径向速度与叶片数量呈正相关;但顶部流场径向速度与叶片数量并无正相关趋势,考虑到示踪剂在顶部扩散较快,故可忽略顶部流场的微小差别。由于示踪剂在底部中心不易扩散,故搅拌器底部流场径向速度尤为关键,由图 11(b)可见叶片数量为9个时,底部流场径向速度最优。
|
| 图 10 不同高度处轴向速度分布曲线 Fig.10 Distribution curves of axial velocity at different heights |
| |
|
| 图 11 不同径向处径向速度分布曲线 Fig.11 Distribution curves of radial velocity at different radial positions |
| |
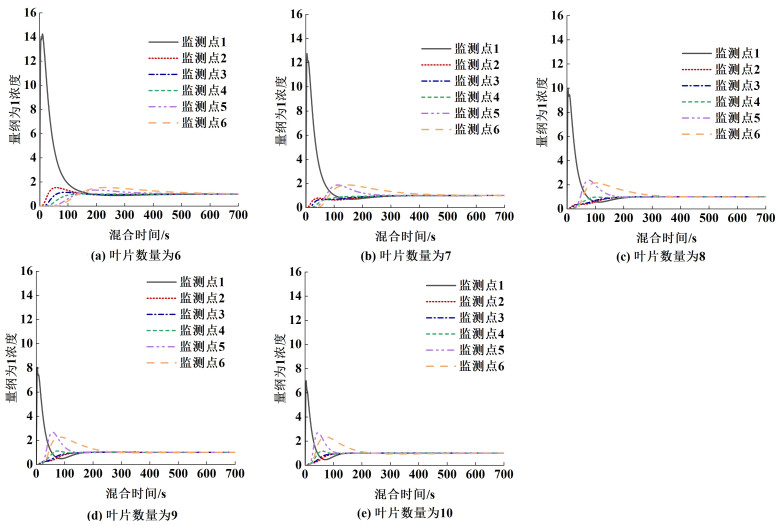
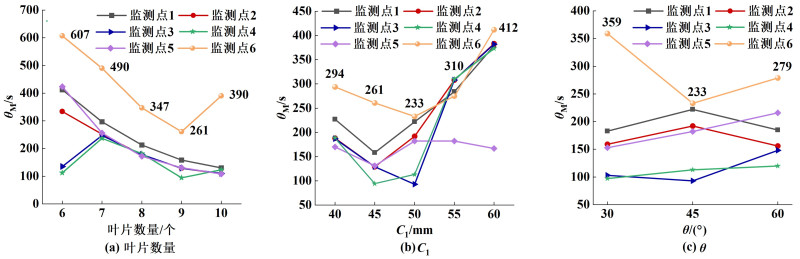
图 12为不同叶片数量条件下各监测点处示踪剂浓度的响应曲线。由于示踪剂投料点与监测点1处于同一高度,故该处示踪剂浓度急剧上升,且峰值始终远高于其余监测点。随着叶片数量的增加,监测点1附近的轴向速度与径向速度均有提升,故该处示踪剂浓度峰值不断降低,且达到峰值后在更短时间内急剧下降。其余监测点也表现出类似的规律。此外,由于监测点6处于搅拌器底部,轴向速度与径向速度均较小,故该点示踪剂扩散较慢,达到稳定值所需的时间最长。当叶片数量为9时,监测点6处示踪剂浓度最先达到稳定,表明此时搅拌器底部径向速度相对最优,与图 11(b)结果一致。离底高度与叶片倾斜角对θM的影响亦可同理分析,3者对搅拌器θM的影响如图 13所示。由图 13(a)可知,内桨叶片数量为9个时θM最短,为261 s,且其各监测点θM差距最小,说明内桨叶片数量为9个时,搅拌器的轴向混合能力最强。另外,由图 13(b)发现,当内桨离底高度为50 mm时所用θM最短,为233 s,比初始设置时所用的θM缩短了61.6%。同时内桨叶片倾斜角为45°时搅拌器所用θM最短,如图 13(c)所示。
|
| 图 12 不同叶片数量条件下浓度响应曲线 Fig.12 Concentration response curve under different number of blades |
| |
|
| 图 13 不同结构参数下各监测点处的混合时间 Fig.13 Mixing time at each monitoring point under different structural parameters |
| |
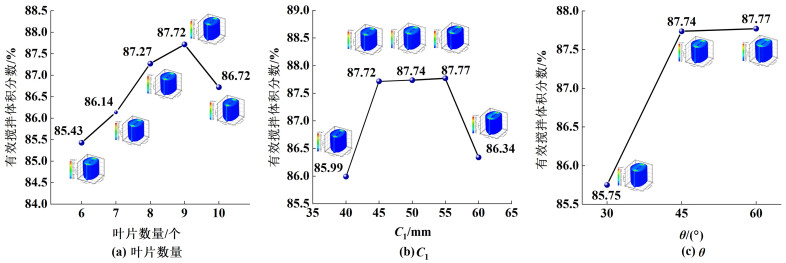
图 14为不同结构参数的有效搅拌体积分数。由图 14(a)发现,有效搅拌体积分数随叶片数量的增加而增大,在叶片数量为9个时达到最大值87.715%,而叶片数量增加到10个时有效搅拌体积分数下降。此外,从图 14(b)可清晰看出,离底高度为45 mm时,有效搅拌体积分数达到87.715%,继续增大离底高度其增加甚微,离底高度为60 mm时,有效搅拌体积分数下降。且由图 14(c)可知,叶片倾斜角为45°时有效搅拌体积分数达到87.737%,继续增大倾斜角其变化不明显。
|
| 图 14 不同结构参数的有效搅拌体积分数 Fig.14 Effective stirring volume fraction of different structural parameters |
| |
综上所述,结构参数的改变对Pv、θM和有效搅拌体积分数均有影响。其中,Pv与有效搅拌体积分数受结构参数影响产生的变化幅度均在4%以下,而θM受结构参数影响产生的变化幅度远超二者,可达其值23倍及以上。此外,通过PIV粒子图像测速技术[17]与酸碱指示剂变色法[18]验证了混合时间能够作为衡量搅拌器搅拌效率的指标,故后续参数优化将以混合时间作为正交试验评价指标。
2.5 正交实验为研究叶片数量、C1、θ结构参数交互作用对搅拌特性的影响,依据上述单因素分析的结果,选用叶片数量、C1、θ为本正交实验的3个因素,并以θM为其分析指标,进行三因素三水平正交实验:叶片数量考虑8、9、10,C1考虑45、50和60 mm,θ考虑30°、45°和60°。实验结果如表 3所示。
| 编号 | 叶片数量 | C1 | θ | θM/s |
| 1 | 8 | 45 | 30 | 388 |
| 2 | 8 | 50 | 45 | 298 |
| 3 | 8 | 55 | 60 | 491 |
| 4 | 9 | 45 | 45 | 261 |
| 5 | 9 | 50 | 60 | 279 |
| 6 | 9 | 55 | 30 | 264 |
| 7 | 10 | 45 | 60 | 323 |
| 8 | 10 | 50 | 30 | 312 |
| 9 | 10 | 55 | 45 | 253 |
| K1 | 1 177 | 972 | 964 | |
| K2 | 804 | 889 | 812 | |
| K3 | 888 | 1 008 | 1093 | |
| k1 | 392.3 | 324 | 321.3 | |
| k2 | 268 | 296.3 | 270.7 | |
| k3 | 296 | 336 | 364.3 | |
| R | 124.3 | 39.7 | 93.6 | |
| 影响主次 | 叶片数量>C1>θ | |||
| 优水平 | 9 | 50 | 45 | |
| 优组合 | 9-50-45 | |||
表 3中K1~K3与k1~k3分别表示各因素在水平1~3的3次混合时间之和与平均混合时间,R为k值分布的极差。根据极差R分析,较高的R值意味着该因素对指标的影响较显著。实验结果表明,各因素对θM的影响从主到次顺序为叶片数量>θ>C1。且根据表 3中计算的k值得到的最优适宜组合为:叶片数量为9个、C1为50 mm、θ为45°,这与前文单因素分析得到的最适宜参数相一致。
3 结论通过对新型搅拌器的结构参数和流场的分析,主要结论如下。
(1) 在组合桨作用下,搅拌器内形成了不对称的轴向流,能够实现高黏性非牛顿流体的混合搅拌。
(2) 单位体积搅拌功率与各结构参数均呈正相关;混合时间随叶片数量、离底高度、叶片倾斜角的增加表现为先减小后增大的趋势,而有效搅拌体积分数随叶片数量、离底高度的增加呈先增大后减小的变化。其中结构参数对混合时间的影响最为显著。
(3) 根据单因素与正交实验分析得到最优结构参数,即叶片数量为9个、离底高度为50 mm、叶片倾斜角为45°,其对应的混合时间为233 s,较初始设置缩短了61.6%;且各结构参数对混合时间影响的主次顺序为:叶片数量>叶片倾斜角>离底高度。
| [1] |
李薇, 高瑾, 张津津, 等. 组合桨搅拌槽内高黏流体混合特性的数值模拟[J]. 化学工程, 2015, 43(11): 66-71, 78. LI Wei, GAO Jin, ZHANG Jinjin, et al. Numerical simulation on mixing performance of high viscosity fluid in stirred tank with combined impeller[J]. Chemical Engineering, 2015, 43(11): 66-71, 78. (in Chinese) |
| [2] |
ZHANG Y, PAN X, WANG Y, et al. Numerical and experimental investigation on surface air entrainment mechanisms of a novel long-short blades agitator[J]. AIChE Journal, 2018, 64(1): 316-325. DOI:10.1002/aic.15865 |
| [3] |
BABU S, PAPADAKIS G, VASSILICOS J C. Reduced power consumption in stirred vessels by means of fractal impellers[J]. AIChE Journal, 2018, 64(4): 1485-1499. DOI:10.1002/aic.16096 |
| [4] |
孙宁, 高鹏飞, 杨潮, 等. 同心双轴搅拌器气液分散性能的实验研究[J]. 高校化学工程学报, 2020, 34(3): 619-625. SUN Ning, GAO Pengfei, YANG Chao, et al. Experimental investigation on gas-liquid dispersion performance in coaxial mixer[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(3): 619-625. DOI:10.3969/j.issn.1003-9015.2020.03.008 (in Chinese) |
| [5] |
廖启江, 秦宏云, 周鸣亮, 等. 高剪切混合器研究与应用进展[J]. 化工进展, 2019, 38(3): 1160-1175. LIAO Qijiang, QIN Hongyun, ZHOU Mingliang, et al. Progress of researches and applications for high shear mixers[J]. Chemical Industry and Engineering Progress, 2019, 38(3): 1160-1175. (in Chinese) |
| [6] |
RASOULI M, MOUSAVI S M, AZARGOSHASB H, et al. CFD simulation of fluid flow in a novel prototype radial mixed plug-flow reactor[J]. Journal of Industrial and Engineering Chemistry, 2018, 64: 124-133. DOI:10.1016/j.jiec.2018.03.008 |
| [7] |
PUKKELLA A K, VYSYARAJU R, TAMMISHETTI V, et al. Improved mixing of solid suspensions in stirred tanks with interface baffles: CFD simulation and experimental validation[J]. Chemical Engineering Journal, 2019, 358: 621-633. DOI:10.1016/j.cej.2018.10.020 |
| [8] |
张昆, 王瀚彬, 刘新卫, 等. 过渡流搅拌槽内单颗粒悬浮特性的实验研究[J]. 北京化工大学学报(自然科学版), 2019, 46(4): 31-37. ZHANG Kun, WANG Hanbin, LIU Xinwei, et al. Experimental study of single particle suspension in transitional flow in a stirred tank[J]. Journal of Beijing University of Chemical Technology (Natural Science Edition), 2019, 46(4): 31-37. (in Chinese) |
| [9] |
朱桂华, 张丽欣, 马凯, 等. 错位桨搅拌槽内污泥与固体颗粒混合过程的数值模拟[J]. 过程工程学报, 2016, 16(3): 402-406. ZHU Guihua, ZHANG Lixin, MA Kai, et al. Numerical simulation on mixing process of sludge and solid particles in a stirred tank equipped with shifted propeller[J]. The Chinese Journal of Process Engineering, 2016, 16(3): 402-406. (in Chinese) |
| [10] |
梁瑛娜, 高殿荣, 拜亮. 偏心组合桨搅拌槽内层流混合过程的数值模拟[J]. 化工进展, 2014, 33(12): 3203-3209. LIANG Yingna, GAO Dianrong, BAI Liang. Numerical simulation of laminar flow and mixing process in eccentrically stirred tank with combined impeller[J]. Chemical Industry and Engineering Progress, 2014, 33(12): 3203-3209. (in Chinese) |
| [11] |
许雯婧, 王璐, 甄卫军, 等. 聚苯硫醚聚合搅拌釜结构优化及流场分析[J]. 化学反应工程与工艺, 2020, 36(3): 203-212, 275. XU Wenjing, WANG Lu, ZHEN Weijun, et al. Structure optimization and flow field analysis of polyphenylene sulfide polymerization stirring reactor[J]. Chemical Reaction Engineering and Technology, 2020, 36(3): 203-212, 275. (in Chinese) |
| [12] |
METZNER A B. Agitation of non-Newtonian fluids[J]. AIChE Journal, 1963, 9(4): 555. |
| [13] |
王嘉骏, 冯连芳, 顾雪萍, 等. 锚式搅拌器功率消耗与Metzner常数研究[J]. 化学工程, 1999, 27(6): 20-23, 30. WANG Jiajun, FENG Lianfang, GU Xueping, et al. A new investigation of power consumption and metzner constant for anchor impellers[J]. Chemical Engineering, 1999, 27(6): 20-23, 30. (in Chinese) |
| [14] |
韩太柏, 金光远, 邹鹏程, 等. 一种连续流反应器内射流耦合搅拌流的混合特性[J]. 化学工业与工程, 2023, 40(2): 133-142. HAN Taibai, JIN Guangyuan, ZOU Pengcheng, et al. Mixing characteristics of continuous flow reactor coupled with jet and mechanical stirring[J]. Chemical Industry and Engineering, 2023, 40(2): 133-142. DOI:10.13353/j.issn.1004.9533.20210808 (in Chinese) |
| [15] |
许言, 王健, 武永军, 等. 多叶片组合式搅拌桨釜内流动特性和混合性能研究[J]. 化工学报, 2020, 71(11): 4964-4970. XU Yan, WANG Jian, WU Yongjun, et al. Study on the flow characteristics and mixing performance of multi-blade combined agitator[J]. CIESC Journal, 2020, 71(11): 4964-4970. (in Chinese) |
| [16] |
丁杨, 宗原, 奚桢浩, 等. 固液两相体系中双层搅拌桨叶的结构优化数值模拟[J]. 华东理工大学学报(自然科学版), 2015, 41(6): 750-757. DING Yang, ZONG Yuan, XI Zhenhao, et al. Structure optimization of dual impellers in solid-liquid system by numerical simulation[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2015, 41(6): 750-757. (in Chinese) |
| [17] |
方玉建, 张敏, 孙先朋, 等. 机械搅拌槽内非牛顿流体内流特性研究[J]. 机械工程学报, 2021, 57(20): 244-253. FANG Yujian, ZHANG Min, SUN Xianpeng, et al. Study on internal flow characteristics of non-Newtonian fluids in mechanical stirred tank[J]. Journal of Mechanical Engineering, 2021, 57(20): 244-253. (in Chinese) |
| [18] |
梁瑛娜, 高殿荣, 拜亮. 双层桨搅拌槽内层流流场与混合时间的数值模拟[J]. 机械工程学报, 2015, 51(16): 185-195. LIANG Yingna, GAO Dianrong, BAI Liang. Numerical simulation of the laminar flow field and mixing time in stirred tank with double layer impeller[J]. Journal of Mechanical Engineering, 2015, 51(16): 185-195. (in Chinese) |
 2024, Vol. 41
2024, Vol. 41





