气升式环流反应器是在鼓泡塔的基础上发展起来的,具有结构简单,传质/传热性能好,操作简便等优点,广泛应用于化工、废气废水处理,生物发酵等气-液或气-液-固多相反应过程,深入研究气升式环流反应器内多相流体力学行为对提高其传质性能具有重要意义[1-4]。
气升式环流反应器性能的评价参数主要有气含率、气泡尺寸及其分布、液相速度、传质速率等。通过提高气含率,减小气泡尺寸,改善气液分布效果,进而实现气-液相间传质速率的提高一直是气升式环流反应器的研究重点和热点[5, 6]。气升式环流反应器内,曝气驱动流体流动和混合,在整个过程中没有其他额外推动力,导流筒作为关键内构件,显著影响气液分布效果和传质性能。为此,国内外众多学者对导流筒结构进行了大量的实验和计算流体力学(CFD)模拟研究。基于测量的实验数据,提出了许多气含率和液相速度经验关联式[7-10]。近年来,随着计算机硬件和数值模拟方法得到极大的发展,CFD模拟可以准确预测反应器内局部的流场分布,特别是对于反应器的结构设计和优化,CFD模拟具有成本低、试验周期短等优点。Farhadian等通过CFD模拟评价了方形气升式反应器内液相的停留时间分布[11]。Teli和Mathpati分析了不同传质模型的影响,同时采用CFD模拟研究了气升式反应器的放大[12]。目前,CFD模拟在研究导流筒结构对气升式环流反应器流体力学性能的影响方面已取得一定的进展,但是定量研究导流筒结构对反应器传质性能的影响还鲜有报道[13-17]。
为此,本研究分别建立欧拉-欧拉气-液两相流模型和气泡粒群衡算模型并实现二者的耦合求解,考察了单个方形导流筒、单个圆形导流筒和6个圆形导流筒结构对气-液两相流体流动特性、气泡尺寸及其分布的影响,研究了反应器的气-液相间传质性能。相关模型和数值模拟结果对气升式环流反应器结构优化和放大具有指导意义。
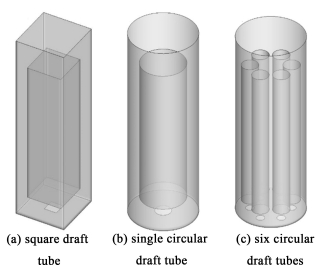
1 模型建立 1.1 物理模型图 1为本研究中采用的3种不同结构的气升式环流反应器,对于方形筒反应器,长和宽均为0.2 m,高为1.0 m。导流筒长和宽均为0.14 m,高为0.45 m,安装在距离反应器底部0.05 m高度处。反应器底部中心处的布气板尺寸为0.05 m×0.05 m,布气孔孔径为0.001 m。对于圆形筒反应器,外筒的直径为0.24 m, 大导流筒的直径为0.16 m,6个小导流筒直径为0.05 m,高度均为0.45 m。6个圆形气体分布器位于环流器的底部,直径为0.03 m。
|
| 图 1 3种气升式环流反应器结构 Fig.1 Three structures of airlift loop reactor |
| |
采用欧拉-欧拉模型来模拟反应器中气-液两相流动,空气是气相,水是液相。主要包括连续性方程、动量方程、RNG k-ε湍流模型和相间作用力模型。
连续性方程:
| $\frac{\partial\left(\alpha_k \rho_k\right)}{\partial t}+\nabla \cdot\left(\alpha_k \rho_k \boldsymbol{u}_k\right)=m_i$ | (1) |
式(1)中:下标k表示气相或液相;α为对应相的体积分数;ρ为密度,kg·m-3;u为速度,m·s-1;mi为质量源项,在本研究中,mi=0。
动量方程:
| $\begin{gathered}\frac{\partial}{\partial t}\left(\alpha_k \rho_k \boldsymbol{u}_k\right)+\nabla \cdot\left(\alpha_k \rho_k \boldsymbol{u}_k \boldsymbol{u}_k\right)=-\alpha_k \nabla p+\alpha_k \rho_k \boldsymbol{g}+ \\ \nabla \cdot\left[\alpha_k \mu_{k, \mathrm{eff}}\left(\nabla \boldsymbol{u}_k+\left(\nabla \boldsymbol{u}_k\right)^T-\frac{2}{3} I \nabla \boldsymbol{u}_k\right)\right]+M_k\end{gathered}$ | (2) |
式(2)中:g为重力加速度,m·s-2;I为单位张量;μeff为有效黏度,kg·m-1·s-1;Mk为包含曳力、升力等相间作用力的动量源项。
RNGk-ε湍流模型:
| $\begin{gathered}\frac{\partial}{\partial t}(\alpha \rho k)+\nabla \cdot(\alpha \rho \boldsymbol{u} k)=\nabla \cdot\left[\alpha\left(\mu_{\mathrm{lam}}+\frac{\mu_{\mathrm{t}}}{\sigma}\right) \nabla k\right]+ \\ G_k-\alpha \rho \varepsilon\end{gathered}$ | (3) |
| $\begin{gathered}\frac{\partial}{\partial t}(\alpha \rho \varepsilon)+\nabla \cdot(\alpha \rho \boldsymbol{u} \varepsilon)=\nabla \cdot\left[\alpha\left(\mu_{\mathrm{lam}}+\frac{\mu_{\mathrm{t}}}{\sigma_{\varepsilon}}\right) \nabla \varepsilon\right]+ \\ \frac{\varepsilon}{k}\left(C_{\varepsilon \mathrm{m}} G_{\mathrm{k}}-C_{\varepsilon 1} \rho \varepsilon\right)\end{gathered}$ | (4) |
| $G_{\mathrm{k}}=\mu_{\mathrm{t}} \nabla \boldsymbol{u}\left(\nabla \boldsymbol{u}+(\nabla \boldsymbol{u})^T\right)-\frac{2}{3} \nabla \boldsymbol{u}\left(3 \mu_{\mathrm{t}} \nabla \boldsymbol{u}+\rho k\right)$ | (5) |
式(3)~式(5)中:k为湍动能,m2·s-2;ε为湍流耗散率,m2·s-3;μlam、μt分别表示分子黏度和湍流黏度,kg·m-1·s-1;Gk为湍动能产生项,m2·s-2;Cεm、Cεl为常数。
Jakobsen等[18]对气升式反应器中的曳力模型和升力模型深入探究,得到曳力模型:
| $\begin{gathered}M_{\mathrm{L}}^{\mathrm{D}}=\frac{3}{4} \frac{C_{\mathrm{D}}}{d_{32}} \alpha_{\mathrm{G}} \rho_{\mathrm{L}}\left|\boldsymbol{u}_{\mathrm{G}}-\boldsymbol{u}_{\mathrm{L}}\right|\left(\boldsymbol{u}_{\mathrm{G}}-\boldsymbol{u}_{\mathrm{L}}\right) \\ C_{\mathrm{D}}=\max \left[\frac{24}{R e}\left(1+0.15 R e^{0.687}\right), \right.\end{gathered}$ | (6) |
| $\left.\min \left(\frac{2}{3} E{\rm{o}}^{0.5} E\left(\alpha_{\rm{G}}\right), \frac{8}{3}\left(1-\alpha_{\rm{G}}\right)^2\right)\right]$ | (7) |
式(6)和(7)中:CD为曳力系数;d32为Sauter气泡直径,m;Eo为奥托斯数。
升力模型:
| $M_{\mathrm{L}}^{\mathrm{L}}=\alpha_{\mathrm{G}} \rho_{\mathrm{L}} C_{\mathrm{L}}\left(\boldsymbol{u}_{\mathrm{G}}-\boldsymbol{u}_{\mathrm{L}}\right) \times\left(\nabla \times \boldsymbol{u}_{\mathrm{L}}\right)$ | (8) |
式(8)中:CL是升力系数,本研究中为常数0.76。
1.2.2 PBM模型本研究采用气泡粒群衡算模型(PBM)计算气泡聚并和破碎效应对气泡平均尺寸及其分布的影响,将直径在0.001 2~0.012 5 m范围内的气泡分为十组,每组气泡的守恒方程如下:
| $\frac{\partial}{\partial t}\left(\alpha_{\mathrm{G}} \rho_{\mathrm{G}} f_j\right)+\nabla \cdot\left(\alpha_{\mathrm{G}} \rho_{\mathrm{G}} \boldsymbol{u}_{\mathrm{G}} f_j\right)=S_j$ | (9) |
式(9)中:fj为第j组气泡的体积分率,Sj为由于气泡的聚并和破碎而产生的源项,其表达式为:
| $\begin{array}{c} {S_j} = \sum\limits_{\begin{array}{*{20}{c}} {m, n}\\ {{v_{j - 1}} \le \left( {{v_m} + {v_n}} \right) \le {v_{j + 1}}} \end{array}}^{m \ge n} {\left( {1 - \frac{1}{2}{\delta _{m, n}}} \right)} \eta c\left( {{v_m}, {v_n}} \right)\frac{{{\alpha _{\rm{G}}}{f_m}}}{{{v_m}}}\frac{{{\alpha _G}{f_n}}}{{{v_n}}}{v_j} - \\ {\alpha _{\rm{G}}}{f_j}\sum\limits_{m = 1}^M c \left( {{v_j}, {v_m}} \right)\frac{{{\alpha _G}{f_m}}}{{{v_m}}} + \sum\limits_{m = j}^M {{\gamma _{j, m}}} b\left( {{v_m}} \right)\frac{{{\alpha _{\rm{G}}}{f_m}}}{{{v_m}}}{v_j} - b\left( {{v_j}} \right){\alpha _{\rm{G}}}{f_j} \end{array}$ | (10) |
式(10)中:
| $\eta= \begin{cases}\frac{v_{j+1}-v}{v_{j+1}-v_j} & v_j \leqslant v \leqslant v_{j+1} \\ \frac{v-v_{j-1}}{v_j-v_{j-1}} & v_{j-1} \leqslant v \leqslant v_j\end{cases}$ | (11) |
| $\gamma_{j, m}=\int_{v_j}^{v_{j+1}} \frac{v_{j+1}-v}{v_{j+1}-v_j} \beta\left(v, v_m\right) \mathrm{d} v+\int_{v_{j-1}}^{v_j} \frac{v-v_{j-1}}{v_j-v_{j-1}} \beta\left(v, v_m\right) \mathrm{d} v$ | (12) |
式(10)~式(12)中:vj是第j组气泡的气泡体积,c(vm, vn)和b(vj)分别代表气泡的聚并和破碎速率,β(v, vm)为子气泡的分布函数。本研究分别采用Luo模型[19]和Lehr模型[20]计算气泡聚并速度和破碎速率。Sauter气泡尺寸d32可由式(13)计算得到:
| $\frac{1}{d_{32}}=\sum\limits_{j=1}^{10}\left(\frac{f_j}{d_j}\right)$ | (13) |
式(13)中dj是第j组气泡的气泡尺寸。
2 网格划分和数值模拟本研究使用商业软件Ansys ICEM对建立的3个气升式环流反应器进行网格划分。对于方形导流筒反应器,采用结构网格进行划分;对于圆形导流筒反应器,采用了O型分割方法来解决圆弧处网格变形问题以便更好地生成理想边界层网格。最大网格尺寸设置为0.002 m,确保模拟结果对网格精度的独立无关性。使用商业软件Ansys Fluent,通过求解CFD-PBM耦合模型得到ALR中的三维流场和气泡粒径分布。入口边界定义为速度入口,出口边界定义为压力出口,反应器壁面采用无滑移边界条件。采用二阶离散方法对方程进行离散化,使用SIMPLE算法实现速度和压力耦合求解,时间步长为0.005 s,收敛精度为1×10-3。
3 结果与讨论 3.1 气-液两相流体流动特性对于气-液两相流体系,气含率、液相速度和气泡尺寸是表征气-液相间传质通量的关键指标。本小节通过考察不同导流筒结构对上述3个指标的影响,为后续研究气升式环流反应器的传质性能奠定理论基础。
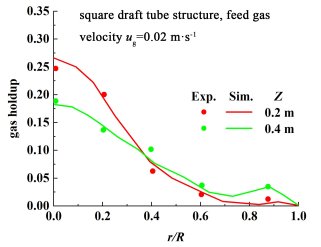
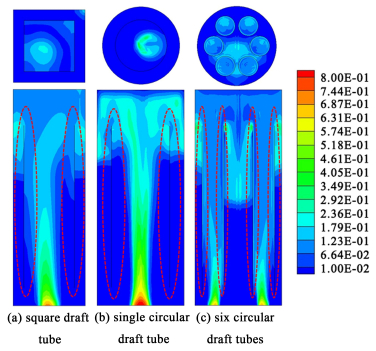
3.1.1 气含率图 2展示了表观气速为0.02 m·s-1时,方形导流筒结构气升式环流反应器不同轴向高度处气含率的径向分布曲线。可以看到,气含率在导流筒的中心取到最大值,随着高度的增加,导流筒中心处的气含率降低,反应器壁面附近的气含率增大,但是气相仍旧没有在提升管和降液管中产生循环。此外,CFD模拟结果和实验结果吻合较好,验证了模型的准确性。图 3为表观气速为0.02 m·s-1时,3种气升式环流反应器中气相含率的轴向分布和径向分布云图。对比可知,增大气升式环流反应器内导流筒的数目,一方面改善进气口气体的分布,进而使得气含率在整个反应器内的分布变得均匀。此外,由于每个导流筒仅可以实现筒内流体和筒外流体的一个循环,因此,多导流筒结构反应器内的流体循环数会明显多于单导流筒结构反应器,这可以促进流体在反应器轴向和径向的混合。通过CFD模拟可计算得到反应器内的体积平均气含率,对于单导流筒结构的反应器a和b,平均气含率分别为0.053和0.059,而反应器c内的平均气含率为0.073,而较高的气含率是提高气-液相间传质通量的基础条件之一。
|
| 图 2 气升式环流反应器内气含率径向分布曲线 Fig.2 The radial distribution curve of gas holdup in airlift loop reactor |
| |
|
| 图 3 3种气升式环流反应器气含率分布云图 Fig.3 The contour of gas holdup distribution in three airlift loop reactors |
| |
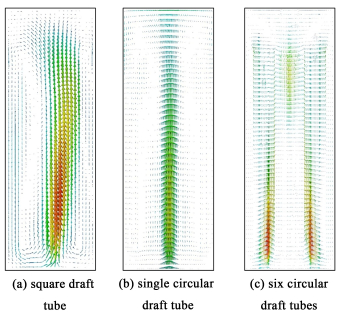
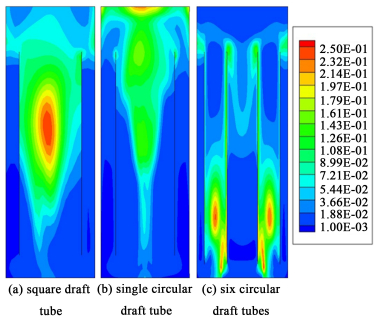
气升式环流反应器内,液相流动是通过曝气驱动的。由于反应大多是在液相中进行,液相循环速度本质上反映了反应器的混合性能,进而可以解释反应发生的强度和产物分布。图 4比较了3种气升式环流反应器内的液相速度分布。由图 4可知,表观气速为0.02 m·s-1时,在考察的3个气升式环流反应器内液相都产生的循环,但是循环通量很小,仍不足以使气相在提升管和降液管中发生循环。从轴向的液相速度分布来看,反应器b和反应器c内部液相流场结构比较规整,反应器a中方形导流筒内液体向上流动过程中存在较宽的速度分布,这使得液相在循环过程中在不同的反应器位置具有完全不同的液相剪应力,当反应器内存在生物降解反应时,较大的液相剪切力可能对微生物产生不可逆的损伤。对于反应器b,流体在导流筒内部的混合较快,但是在导流筒外部的混合速率很慢,流体混合在气升式反应器的径向存在分布;而对于由多个圆形导流筒构成的反应器c,不论是在反应器的径向还是轴向,液相循环速度分布都较为均匀。此外液相混合速率的均匀性还可以体现在湍流耗散速率的分布上(如图 5和表 1所示)。总的来说,含有多个圆形导流筒结构的气升式环流反应器内湍流耗散速率的分布也更为均匀。对于反应器a,湍流耗散速率最大的区域集中在导流筒中部,在反应器b内湍流耗散速率最大的区域集中在反应器顶部,在反应器c内湍流耗散速率最大的区域集中在导流筒下部。3种气升式环流反应器内液相湍流耗散速率平均值比较如表 1所示,通过对比可以看出,反应器b和反应器c中液相湍流耗散速率数值相当,反应器a中液相湍流耗散速率大约是两者的2倍。
|
| 图 4 3种气升式环流反应器液相速度分布 Fig.4 The velocity distribution of liquid phase in three airlift loop reactors |
| |
|
| 图 5 3种气升式环流反应器液相湍动能耗散率分布 Fig.5 The turbulent dissipation rate distribution of liquid phase in three airlift loop reactors |
| |
| 反应器类型 | 湍动能耗散率范围/(m2·s-3) | 体积平均湍动能耗散率/(m2·s-3) | 体积平均气泡尺寸/m |
| 反应器a | 0.000 50~0.505 60 | 0.061 3 | 0.009 21 |
| 反应器b | 0.000 12~0.939 00 | 0.038 1 | 0.009 47 |
| 反应器c | 0.000 25~2.286 00 | 0.033 4 | 0.007 92 |
气升式环流反应器内,通过曝气的方式引入气泡,气泡在反应器内会发生破碎和聚并。由Luo模型和Lehr模型可知,湍流耗散速率显著影响气泡的破碎速率和聚并速率,并最终决定气泡的尺寸,而气泡的尺寸通过影响气-液传质面积决定传质通量,较小的气泡通常意味着较大的气-液传质比表面积。将气升式环流反应器内的气泡群按尺寸分为十组,气泡的Sauter尺寸d32按方程(13)计算。3种反应器中气泡尺寸的分布如表 1所示。由湍流耗散速率分布可知,相比于反应器a和反应器b,反应器c中气泡尺寸分布更加均匀。此外,反应器c中气泡尺寸最小。这和气泡的入口条件有关,本研究假设气泡在入口处尺寸均一,Chen等[21]认为入口气泡直径和分布器的孔径有关:
| $d_{\mathrm{b}}=2.9\left(\frac{\sigma d_{\mathrm{o}}}{g \rho_{\mathrm{L}}}\right)^{1 / 3}$ | (14) |
由于反应器c的气体分布器孔径最小,因而入口处气泡的尺寸也最小。由表 1可知,反应器b和反应器c的平均湍流耗散速率数值相当,由于反应器b中气泡的入口尺寸较大,最终使得反应器b中的平均气泡尺寸明显大于反应器c。
通过对3种反应器流体流动特性和气泡尺寸分布进行对比,可以看出反应器c具有最高的气相含率和最小的气泡尺寸,气含率分布均匀,液相速度规整,并且液相湍流耗散速率与反应器b相差不大,远小于反应器a。因此,反应器c综合性能最优。
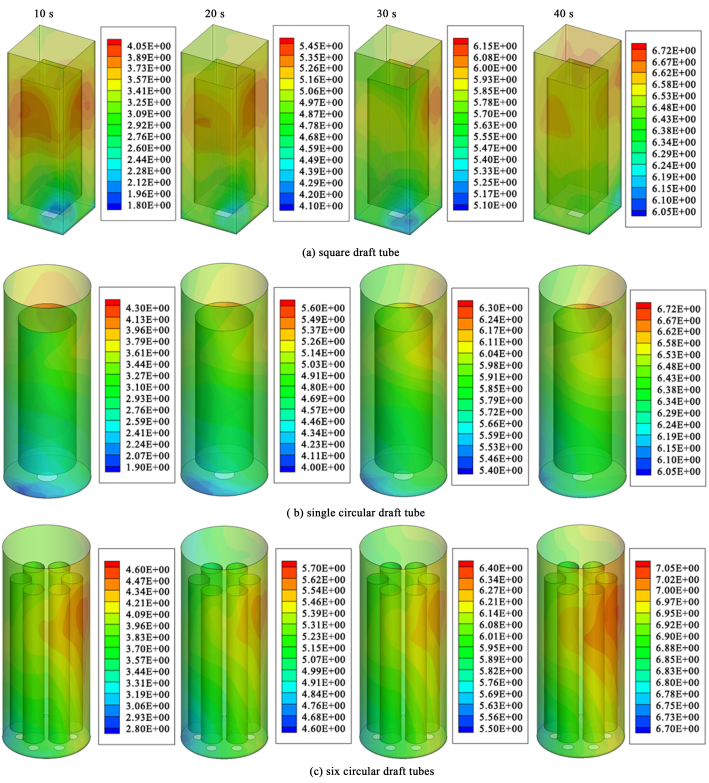
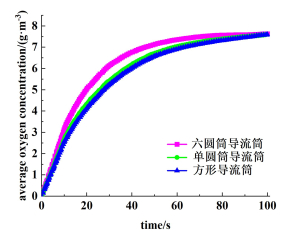
3.2 传质性能在气升式环流反应器中,生物降解反应通常是好氧反应。微生物的代谢水平对液相中氧气的浓度十分敏感。为了定量分析气升式环流反应器的传质性能,本研究通过模拟氧气在气-液相间传质来比较3种气升式环流反应器传质性能。图 6展示了3种气升式环流反应器中氧气浓度随时间变化的云图。图 7展示了3种气升式环流反应器中体积平均氧气浓度随时间的变化,可以看出,具有6个圆形导流筒的反应器c中氧气浓度上升最快,具有最优的传质性能,这是由于反应器c在3种反应器中具有最高的气相含率,且气泡尺寸最小,因此具有最大的气液相界面积,传质速率最快。
|
| 图 6 3种气升式环流反应器中氧气浓度随时间的变化 Fig.6 Oxygen concentration over time in three airlift loop reactors |
| |
|
| 图 7 3种气升式环流反应器内平均氧气浓度随时间的变化 Fig.7 Average oxygen concentration over time in three airlift loop reactors |
| |
由图 7可知,在不考虑生物降解反应好氧的前提下,经过约100 s的时间后,液相中氧气浓度基本达到饱和。实际情况中,微生物会消耗大量的氧气,这会使得氧气浓度达到饱和的时间进一步延长。为了保证液相中氧气浓度处于合适的水平,需要同时优化操作条件参数(例如进气量)和反应器结构参数(例如导流筒结构)。研究表明在相同的气体停留时间条件下,采用多个圆形导流筒的气升式环流反应器可以显著改善传质效率,但是过多的导流筒又同时会增大反应器结构的复杂性,导致生产成本的增加。因此,导流筒的结构和数目往往需要结合实际情况进行优化。
4 结论通过建立CFD-PBM耦合模型,考察了单个方形导流筒、单个圆形导流筒和6个圆形导流筒结构对气-液两相流体流动特性、气泡尺寸分布和气-液相间传质的影响。
(1) 采用多导流筒结构可以改善进气口气体的分布,提高应器内流体的循环数,进而使得气含率在整个反应器内的分布变得均匀,反应器内的平均气含率也更高。
(2) 含多导流筒结构的气升式环流反应器,不论是在反应器的径向还是轴向,液相循环速度和湍流耗散分布都较为均匀,在考察的3个反应器中,其平均湍流耗散速率最小。
(3) 在相同的表观气速条件下,反应器a,b,c内气泡的平均尺寸分别为0.009 21、0.009 47和0.007 92 m。含多导流筒结构的气升式环流反应器内气泡尺寸更小,传质速率更大,液相中氧气浓度上升最快,该反应器的综合性能最优。
| [1] |
JAFARIAN M, CHISTI Y, NATHAN G J. Gas-lift circulation of a liquid between two inter-connected bubble columns[J]. Chemical Engineering Science, 2020, 218: 115574. DOI:10.1016/j.ces.2020.115574 |
| [2] |
SIEGEL M H, ROBINSON C W. Application of airlift gas-liquid-solid reactors in biotechnology[J]. Chemical Engineering Science, 1992, 47(13/14): 3215-3229. |
| [3] |
LIU Z, SHI S, LI Y. Coal liquefaction technologies—Development in China and challenges in chemical reaction engineering[J]. Chemical Engineering Science, 2010, 65(1): 12-17. |
| [4] |
FENG W, WEN J, JIA X, et al. Modeling for local dynamic behaviors of phenol biodegradation in bubble columns[J]. AIChE Journal, 2006, 52(8): 2864-2875. DOI:10.1002/aic.10899 |
| [5] |
ŠIJAČKI I M, TOKIĆ M S, KOJIĆ P S, et al. Sparger type influence on the hydrodynamics of the draft tube airlift reactor with diluted alcohol solutions[J]. Industrial & Engineering Chemistry Research, 2011, 50(6): 3580-3591. |
| [6] |
DENG Z, WANG T, ZHANG N, et al. Gas holdup, bubble behavior and mass transfer in a 5m high internal-loop airlift reactor with non-Newtonian fluid[J]. Chemical Engineering Journal, 2010, 160(2): 729-737. DOI:10.1016/j.cej.2010.03.078 |
| [7] |
刘永民, 袁乃驹. 在多室环流反应器中用FCC干气制备乙醛[J]. 石油学报(石油加工), 2005, 21(2): 92-94. LIU Yongmin, YUAN Naiju. Production of acetaldehyde from fcc off-gasin a multi-component airlift loop reactor[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2005, 21(2): 92-94. (in Chinese) |
| [8] |
孙守华, 刘永民, 路蒙蒙. GLS-MALR中的气含率和循环液速[J]. 石油学报(石油加工), 2011, 27(3): 405-410. SUN Shouhua, LIU Yongmin, LU Mengmeng. Gas holdup and liquid circulation velocity in GLS-MALR[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2011, 27(3): 405-410. (in Chinese) |
| [9] |
李红星. 三相连续环流反应器流动特性研究[D]. 北京: 北京化工大学, 2007 LI Hongxing. Study on flow characteristics of three-phase continuous loop reactor[D]. Beijing: Beijing University of Chemical Technology, 2007(in Chinese) |
| [10] |
刘梦溪, 卢春喜, 储凌, 等. 中心气升式三相强化环流反应器内局部气含率分布的实验研究[J]. 高校化学工程学报, 2005, 19(1): 36-41. LIU Mengxi, LU Chunxi, CHU Ling, et al. Experimental study on local gas holdup in a novel three-phase air loop reactor[J]. Journal of Chemical Engineering of Chinese Universities, 2005, 19(1): 36-41. (in Chinese) |
| [11] |
FARHADIAN N, BEHIN J, PARVAREH A. Residence time distribution in an internal loop airlift reactor: CFD simulation versus digital image processing measurement[J]. Computers & Fluids, 2018, 167: 221-228. |
| [12] |
TELI S M, MATHPATI C S. Experimental and numerical study of gas-liquid flow in a sectionalized external-loop airlift reactor[J]. Chinese Journal of Chemical Engineering, 2021, 32: 39-60. DOI:10.1016/j.cjche.2020.10.023 |
| [13] |
张庆文, 洪厚胜, 欧阳平凯. CFD用于气升式内环流反应器流体力学性质的研究[C]//第一届全国化学工程与生物化工年会论文摘要集(下), 2004
|
| [14] |
沈荣春. 气升式环流反应器内气液两相流动CFD数值模拟的研究[D]. 上海: 华东理工大学, 2005
|
| [15] |
李干禄, 韦策, 吴昊, 等. 气升式反应器气液混合及传质特性的CFD模拟[J]. 南京工业大学学报(自然科学版), 2018, 40(4): 118-124. LI Ganlu, WEI Ce, WU Hao, et al. Simulation of gas-liquid mixing and mass transfer characteristics in the airlift reactor[J]. Journal of Nanjing University of Technology (Natural Science Edition), 2018, 40(4): 118-124. (in Chinese) |
| [16] |
HUANG Q, YANG C, YU G, et al. 3-D simulations of an internal airlift loop reactor using a steady two-fluid model[J]. Chemical Engineering & Technology, 2007, 30(7): 870-879. |
| [17] |
HUANG Q, ZHANG W, YANG C. Modeling transport phenomena and reactions in a pilot slurry airlift loop reactor for direct coal liquefaction[J]. Chemical Engineering Science, 2015, 135: 441-451. |
| [18] |
JAKOBSEN H A, GREVSKOTT S, SVENDSEN H F, et al. Modeling of vertical bubble-driven flows[J]. Industrial & Engineering Chemistry Research, 1997, 36(10): 4052-4074. |
| [19] |
LUO H, SVENDSEN H F. Theoretical model for drop and bubble breakup in turbulent dispersions[J]. AIChE Journal, 1996, 42(5): 1225-1233. DOI:10.1002/aic.690420505 |
| [20] |
LEHR F, MILLIES M, MEWES D. Bubble-size distributions and flow fields in bubble columns[J]. AIChE Journal, 2002, 48(11): 2426-2443. |
| [21] |
CHEN P, DUDUKOVI M P, SANYAL J. Three-dimensional simulation of bubble column flows with bubble coalescence and breakup[J]. AIChE Journal, 2005, 51(3): 696-712. |
 2024, Vol. 41
2024, Vol. 41





