化学工业与工程  2024, Vol. 41 Issue (1): 125-135
   Abstract               PDF                Figures                Tables
引用本文 0
卢哲, 史嘉帧, 郭凯, 刘春江, 郑龙云. 二级环流反应器中收缩-膨胀隔板的性能优化[J]. 化学工业与工程, 2024, 41(1): 125-135.
LU Zhe, SHI Jiazhen, GUO Kai, LIU Chunjiang, ZHENG Longyun. Optimization of contraction-expansion partition in a two-stage internal airlift loop reactor[J]. Chemical Industry and Engineering, 2024, 41(1): 125-135.
二级环流反应器中收缩-膨胀隔板的性能优化
卢哲1 , 史嘉帧1 , 郭凯1 , 刘春江1,2 , 郑龙云1     
1. 天津大学化工学院, 天津 300072;
2. 化学工程联合国家重点实验室(天津大学), 天津 300072
收稿日期: 2022-02-05; 修改日期: 2022-03-21
基金项目: 国家自然科学基金项目(21706182;21706187)
作者简介: 卢哲(1994-), 男, 硕士研究生, 现从事化学工程方面的研究.
通信作者: 郭凯, 讲师, E-mail: guokaitianjin@163.com.
摘要：通过在二级环流反应器两级之间安装具有收缩-膨胀形状的隔板, 可以有效减小两级之间的液相回流流量, 但同时会增加流体流动阻力。为了在减小液相回流流量的前提下减小流动阻力, 本研究对隔板进行优化设计。首先通过模拟计算获得不同隔板下的压降和液相回流流量, 随后对数据进行拟合, 得到压降、液相回流流量与结构参数的关联式。计算结果表明当表观气速较小时, 隔板宽度对压降影响较大, 高度的影响较小。表观气速增大时, 隔板高度对压降的影响变大。在所有气速下, 隔板宽度是影响液相回流流量的决定因素。最后通过多目标优化, 获得了在不同表观气速下最优隔板的Pareto前沿。
关键词：收缩-膨胀隔板    优化    二级气升式环流反应器    气液两相流    计算流体力学    
Optimization of contraction-expansion partition in a two-stage internal airlift loop reactor
LU Zhe1 , SHI Jiazhen1 , GUO Kai1 , LIU Chunjiang1,2 , ZHENG Longyun1     
1. School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China;
2. State Key Laboratory of Chemical Engineering(Tianjin University), Tianjin 300072, China
Abstract: Loop reactors are widely applied in industries because of good characteristics of gas-liquid interaction, and a series of internals are developed and equipped with the reactor to further reinforce the interaction. The installation of a contraction-expansion partition between two stages in a two-stage airlift loop reactor can effectively reduce the reversed liquid flow between the stages, while it increases the flow resistance. To pinpoint the effect of width and height of the partition on flow dynamics and obtain the partition which can reduce the flow resistance while decrease the reversed liquid flow, this study conducts an optimization of the partition utilizing CFD-PBM and multi-objective optimization methods. Firstly, a series of numerical simulation-based experiments with various partitions at three different superficial gas velocities are conducted to obtain the pressure drop and the reversed liquid flow in the two-stage loop reactor. It is found that the width and height of the partition as well as superficial gas velocities lead to different performance of flow dynamics. The width has a greater effect on pressure drop than the height at a low superficial gas velocity, while the effect of height on the pressure drop becomes larger as the superficial gas velocity increases and width is the determinant factor for the reversed liquid flow at all superficial gas velocities in the study. The correlations for pressure drop and the reversed liquid flow with the width and height of the partition are obtained by data fitting. The Pareto fronts for the structure of partition at various superficial gas velocities are obtained using multi-objective optimization with the pressure drop and the reversed liquid flow as the optimization objectives and the width and height of the partition as optimization parameters.
Keywords: contraction-expansion partition    optimization    two-stage airlift loop reactor    gas-liquid flow    computational fluid dynamics    

环流反应器具有结构简单，能耗较低[1, 2]，以及良好的传质特性[2-4]等优点，在工业生产中广泛应用于气液、气液固等多相化学反应与生物发酵过程[1-3, 5-12]。在过去的几十年间，研究人员通过实验测量以及数值模拟技术对环流反应器内的气泡尺寸分布、气含率、循环液速、混合时间、停留时间分布、传热传质速率、反应速率等进行了详细的研究[13-19]，并对不同操作条件、物性参数、设备结构中的关键参数变化进行了讨论[17, 20-26]。研究结果表明反应器内的流体力学行为对相间的传热传质以及反应具有重要的影响，特别是当反应器内形成特定的流动形式时，传热传质以及反应转化率出现明显的提高。

随着对反应器内流体力学行为研究的逐渐深入，研究人员尝试在反应器中安装内构件以改变流动形式，构建特定的流场从而达到强化传递与反应的效果。根据内构件的形式，大致可以分为动构件和静构件两类。Nataša等[27]在单级环流反应器内安装了无动力搅拌桨来强化混合效率，进而提高传质速率。结果表明，在低气速下，无动力搅拌桨可以将传质速率提升82%，而在高气速下也可提升20%~30%。Sérgio等[4]比较了搅拌式环流反应器和其他3种传统反应器的流体力学和传质性能，结果表明搅拌式环流反应器具有更高的气含率和传质速率，但其能耗也较高。Yusuf等[28]发现安装机械搅拌能显著强化反应器的混合性能和传质速率，但会增加额外的能耗。相比于动构件，静构件具有更稳定的操作性能和更低的能耗，并且易于安装。Zhang等[29]在环流反应器的下降段安装筛网，研究了筛网对气泡尺寸分布的影响，发现筛网可以有效的破碎气泡，使反应器内气泡尺寸更为均一。Markus等[30]通过改变曝气式螺旋管在反应器内的位置，发现体积氧传质系数可提高3倍。Zheng等[31]通过在环流反应器内安装螺旋筛板，发现螺旋筛板可以使反应器的气含率和体积氧传质系数分别提高38%~53%和76%~144%。Luo等[32]在环流反应器的下降段安装多孔筛板，发现筛板可以明显提高反应器内的气含率和体积氧传质系数。

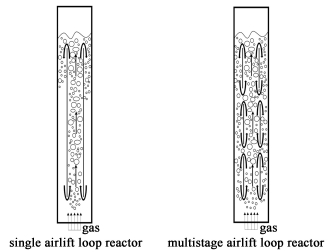
以往对于环流反应器的研究大多集中在单级环流反应器的传递与反应过程。在实际生产中，多级环流反应器也是一种常见的反应器形式。多级环流反应器的结构如图 1所示，与单级环流反应器不同，多级环流反应器在内部安装多段内套筒形成多级环流结构。相比于单级环流反应器，多级环流反应器具有气含率更高，混合效率更高以及气相分布更均匀的优点[25]。在连续化生产中，多级环流反应器内易形成液相返混，反应物返回至第1级中会造成过度反应，而未反应的原料出现短路，从原料进口直接达到反应器出口离开反应器，造成原料在反应器内的停留时间并不一致，产品转化率降低。因此，在连续操作式的反应器中，液相返混一直是工程技术人员重点关注的问题，也是研究热点问题。研究人员尝试在多级环流反应器内安装内构件抑制级间返混。Yu等[33]研究了多孔板和带导管的多孔板这2种内构件对多级环流反应器液相返混的影响。结果表明这2种内构件都可以有效抑制级间液相返混，并且导管多孔板的效果要强于多孔板，最高可达70%左右。Dreher等[34]提出在反应器内安装隔板抑制返混的方案，并研究了隔板开孔面积和液相返混之间的关系，发现18.6%的开孔面积的隔板能够减小90%的液相返混。Zhang等[35]考察了多级反应器中搅拌桨转速和液相返混的关系，发现搅拌桨转速越高，级间返混越小。

图 1 环流反应器示意图 Fig.1 Schematics of airlift loop reactors
图选项

在之前的工作中，本课题组针对二级环流反应器内级间液相交换的问题，提出了一种如图 2所示的收缩-膨胀形状的环形隔板[36]，并通过数值模拟方法考察了其对反应器流体力学的影响。计算结果表明隔板可以有效提升每一级的气含率，并且由于隔板的导流作用，可以在保证循环动力基本不变的情况下，使得流动更为稳定。同时隔板的存在会抑制二级环流反应器内的整体循环，促进级内局部循环，减少液相回流流量，但相应的流动阻力也会增加。为此本论文对隔板进行优化，在减小液相回流流量的同时减小流动阻力，最终以较小的流动阻力为代价，在多级环流反应器内实现了每一级全混流，级间平推流的流动形式，为多级环流反应器的设计提供参考。

图 2 收缩-膨胀隔板形状示意图 Fig.2 Schematic of contraction-expansion partition
图选项
1 数值模拟方法简介

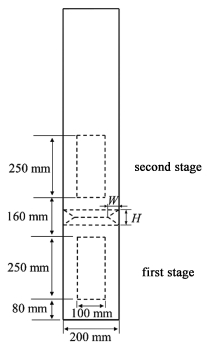
本研究的二级环流反应器的结构参数为：反应器的直径D为200 mm，高度为1 200 mm。两级的内套筒结构完全相同，直径为100 mm，高度为250 mm。在如图 3所示的反应器中，在内套筒之间安装如图 2所示的环形隔板。隔板上下紧邻壁面，安装于距反应器底部410 mm处，W表示环形隔板宽度(50、62.5和75 mm)，H表示环形隔板高度(50、100和150 mm)。下部导流筒(第1级)安装于距反应器底部80 mm处，上部导流筒(第2级)与下部导流筒的顶部之间的距离L为160 mm。初始的静液层高度为1 000 mm。

图 3 安装环形隔板的二级环流反应器结构示意图 Fig.3 Geometric structures of two-stage airlift loop reactor with the partition
图选项

二级环流反应器内气液两相流动过程的三维计算模型基于欧拉欧拉多相流模型，采用群平衡模型(Population balance model, PBM)模拟气泡的聚并与破碎过程，聚并与破碎模型为Luo模型，参照Shi等[36]的实验结果，将气泡尺寸范围定为0.04~1.61 cm，分为了9组不同大小的气泡。采用RNG k-ε模型计算湍流流动特性，壁面函数采用标准壁面函数，具体的控制方程见表 1。反应器进口为速度进口，采用多孔板进气，孔径0.5 mm，孔数为17，气孔分布在反应器底部中心直径为100 mm的圆形区域，出口为压力出口，壁面为无滑移壁面。网格为六面体网格，总数为84 700个，网格尺寸范围为1.52×10-9~1.22×10-6 m3，时间步长为1×10-3 s，控制方程的收敛标准为1×10-4，采用Phase coupled SIMPLE格式求解压力-速度耦合。详细的边界条件、网格划分、网格独立性验证和求解设置见文献[36]，本研究不再赘述。在之前的工作中已经证实，当计算时间在40 s之后，流动达到基本稳定的状态，因此将40~80 s之间的平均值作为最终的计算结果。通过与实验数据对比，数值计算与实验得到的气含率的最大相对误差为8%，平均气泡尺寸的最大相对误差为6%，表明建立的三维模型可以较为准确的预测反应器内的流动状态。

表 1 控制方程 Table 1 CFD governing equations
Computation model Equation
Continuity $\frac{\partial\left(\alpha_{\mathrm{i}} \rho_{\mathrm{i}}\right)}{\partial t}+\nabla \cdot\left(\alpha_{\mathrm{i}} \rho_{\mathrm{i}} \vec{u}_{\mathrm{i}}\right)=0$
Momentum conservation $\frac{\partial\left(\alpha_i \rho_i \vec{u}_{\mathrm{i}}\right)}{\partial t}+\nabla \cdot\left(\alpha_{\mathrm{i}} \rho_{\mathrm{i}} \vec{u}_{\mathrm{i}} \vec{u}_{\mathrm{i}}\right)=-\alpha_{\mathrm{i}} \nabla p+\alpha_{\mathrm{i}} \nabla \cdot \bar{\bar{\tau}}_{\mathrm{i}}+\alpha_{\mathrm{i}} \rho_{\mathrm{i}} \vec{g}+\vec{F}_{\mathrm{i}}$
$\mu_{\mathrm{i}}^1=\rho_{\mathrm{i}} C_\mu \frac{k_{\mathrm{i}}^2}{\varepsilon_{\mathrm{i}}}$
Turbulence $\frac{\partial\left(\alpha_i \rho_i k_{\mathrm{i}}\right)}{\partial t}+\nabla \cdot\left(\alpha_{\mathrm{i}} \rho_{\mathrm{i}} \vec{u}_{\mathrm{i}} k_{\mathrm{i}}\right)=\nabla \cdot\left(\alpha_{\mathrm{i}} \frac{\mu_{\mathrm{i}}^{\mathrm{t}}}{\sigma_{\mathrm{i}}} \nabla k_{\mathrm{i}}\right)+\alpha_{\mathrm{i}}\left(G_{k, \mathrm{i}}-\rho_{\mathrm{i}} k_{\mathrm{i}}\right)+\Pi_{k, \mathrm{i}}$
$\frac{\partial\left(\alpha_i \rho_i \varepsilon_{\mathrm{i}}\right)}{\partial t}+\nabla \cdot\left(\alpha_{\mathrm{i}} \rho_{\mathrm{i}} \vec{u}_{\mathrm{i}} \varepsilon_{\mathrm{i}}\right)=\nabla \cdot\left(\alpha_{\mathrm{i}} \frac{\mu_{\mathrm{i}}^{\mathrm{t}}}{\sigma_{\varepsilon, \mathrm{i}}} \nabla \varepsilon_{\mathrm{i}}\right)+\alpha_{\mathrm{i}} \frac{\varepsilon_{\mathrm{i}}}{k_{\mathrm{i}}}\left(G_{1, \varepsilon} G_{k, \mathrm{i}}-C_{2 \varepsilon} \rho_{\mathrm{i}} k_{\mathrm{i}}\right)-\alpha_{\mathrm{i}} R_{\varepsilon, \mathrm{i}}+C_{3 \varepsilon} \frac{\varepsilon_{\mathrm{i}}}{k_{\mathrm{i}}} \Pi_{\varepsilon, \mathrm{i}}$
Population balance model $\begin{aligned} & \frac{\partial n}{\partial t}+\nabla \cdot\left(n \vec{u}_i\right)=\frac{1}{2} \int\limits_0^v \Omega_{\mathrm{c}}\left(v-v^{\prime}\right) f\left(X, v-v^{\prime}, t\right) f\left(X, v^{\prime}, t\right) \mathrm{d} v^{\prime}- \\ & f(X, v, t) \int\limits_0^{\infty} \Omega_{\mathrm{c}}\left(v, v^{\prime}\right) f\left(X, v^{\prime}, t\right) \mathrm{d} v^{\prime}+\int\limits_0^{\infty} \Omega_{\mathrm{b}}\left(v^{\prime}\right) f\left(X, v^{\prime}, t\right) \mathrm{d} v^{\prime}-\Omega_{\mathrm{b}}(v) f(X, v, t)\end{aligned}$
注：i表示第i相，$\vec{F}_{\mathrm{i}}$包括了虚拟质量力和曳力[37] (N), Ωc为Luo聚并核函数(m-3·s-1)，Ωb为Luo破碎核函数。
表选项

本研究采用和之前工作完全相同的计算模型，气相为空气，密度为1.225 kg·m-3，黏度为1.798 4×10-5 Pa·s，液相为水，密度为998.2 kg·m-3，黏度为1×10-3 Pa·s。在之前的工作中[36]，已经确定了表观气速为0.06 m·s-1时，反应器内流型由均匀气泡流转变为非均匀气泡流，在ug=0.01 m·s-1和ug=0.04 m·s-1(对应均匀气泡流)以及ug=0.08 m·s-1(对应非均匀气泡流)3个不同气速下，对3个不同隔板宽度(50.0、62.5和75.0 mm)和3个不同隔板高度(50、100和150 mm)总共27组反应器内的流动过程进行了CFD模拟。

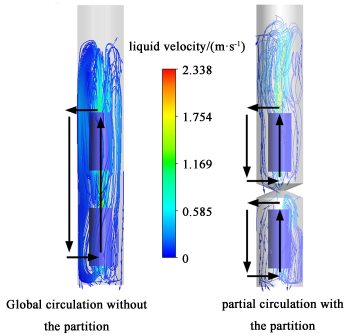
2 隔板优化

如图 4所示，无隔板的二级内环流反应器中第1级上升段中部分具有垂直向上速度的液体会随气体上升直接进入第2级的上升段，而后依次进入第2级的下降段和第1级的下降段，形成一个贯通第1级和第2级的整体循环。当反应器连续操作时，整体循环会导致强烈的液相返混，对气液相间传质和反应造成不利的影响。通过安装环形隔板将第1级上升段的流体引入到第1级的下降段，同时使第2级下降段的流体进入第2级的上升段，形成了第1级和第2级的级内局部循环，抑制了整体循环，减少了2级之间的液相返混。在第1级中处于近似全混流状态的反应物在达到一定的停留时间后，随着液相进料而向上进入到第2级中，而第2级中的反应物通过出料口离开反应器，实现了级间平推流。

图 4 ug=0.08 m·s-1时无隔板和有隔板(W=75 mm，H=50 mm)的二级环流反应器内流型 Fig.4 Flow patterns in two-stage airlift loop reactors with the partition (W=75 mm, H=50 mm) and without the partition at ug=0.08 m·s-1
图选项
2.1 优化参数和目标

首先对隔板宽度和高度进行无量纲化处理。

$W^*=\frac{W}{D}$ (1)
$H^*=\frac{H}{L}$ (2)

式(1)和式(2)中：W*和H*分别为无量纲宽度和高度。D=200 mm为反应器直径，L=160 mm为第1级和第2级导流筒之间的距离。本研究中对隔板的宽度和高度进行优化，对于宽度和高度分别选择了3个不同的水平。无量纲宽度W*分别为0.25、0.312 5和0.375；H*分别为0.312 5、0.625和0.937 5。

由于本研究的隔板结构通过收缩流道达到减小液相回流流量的目的，势必会造成反应器压降的增大，为了在尽量减少压降增加的基础上，达到减小液相回流流量的效果，因此选择压降作为流动阻力指标，反应器的整体压降Δp由式(3)计算。

$\Delta p=p_{\text {in }}-p_{\text {out }}$ (3)

式(3)中：pin和pout分别是环流反应器气相入口和出口处的静压。

如图 5所示，选择隔板中心截面的液相回流流量F作为描述级间液相交换程度以及表征导流板导流作用的指标，由式(4)计算。

$F=\int_{A_1} v_{1, \mathrm{~b}} \mathrm{~d} A_1=\int_A v_{1, \mathrm{~b}} \alpha_1 \mathrm{~d} A$ (4)
图 5 第一和第二级间的液相交换示意图 Fig.5 Liquid exchange between the first and second stages
图选项

式(4)中：A是隔板中心处横截面的面积；Al是隔板中心处横截面的液相面积；vl, b是向下运动的液体速度；αl是中心截面处的液含率。未通气前，液相在反应器中保持静止。通入气体后，第1级中的液体随着气体上升被带入到第2级中，同时第2级中的部分液相会向下运动进入第1级，造成级间液相交换。因此，如果在间歇操作下液相回流流量减少，也就意味着隔板的导流作用有效的抑制了级间的液相交换，促使液体在第1级和第2级形成级内局部循环。在液相连续进料时，隔板的导流作用在一定程度上能起到抑制液相返混的效果，近似实现第1级和第2级级内为全混流，而两级之间为平推流的流动形式。

2.2 隔板参数对压降和液相回流流量的影响

表 2为ug=0.01 m·s-1不同隔板下的压降和液相回流流量的结果。方差分析(Analysis of variance，ANOVA)可以通过分析研究不同自变量对因变量的贡献大小，从而确定不同自变量对因变量影响力的大小。为了明确隔板参数对反应器压降和液相回流流量的影响，对表 2中的无量纲宽度和高度2个自变量进行方差分析，分析结果见表 3。其中，参数F-value表示隔板宽度和高度对压降和液相回流流量的显著性差异的水平，F-value越大，表明对应的自变量对结果的影响更为显著，p-value为F-value对应的检验水平，一般F-value越大，p-value越小，p-value <0.05表明自变量对对应的因变量有显著的影响。由表 3可知，隔板的宽度对压降和液相回流流量的影响都更大。

表 2 ug=0.01 m·s-1时安装不同隔板的反应器压降与液相回流流量的计算值 Table 2 The simulated values of Δp and F in the reactors with different partitions at ug=0.01 m·s-1
Guide vanes W* H* Δp/Pa F/(m3·s-1)
W1H1 0.250 0 0.312 5 2 021.28 5.80×10-4
W1H2 0.250 0 0.625 0 2 023.52 5.89×10-4
W1H3 0.250 0 0.937 5 2 024.22 5.86×10-4
W2H1 0.312 5 0.312 5 2 064.90 2.73×10-4
W2H2 0.312 5 0.625 0 2 063.20 2.96×10-4
W2H3 0.312 5 0.937 5 2 066.54 3.03×10-4
W3H1 0.375 0 0.312 5 2 107.08 8.95×10-5
W3H2 0.375 0 0.625 0 2 123.71 8.55×10-5
W3H3 0.375 0 0.937 5 2 108.20 9.34×10-5
表选项
表 3 ug=0.01 m·s-1时压降和液相回流流量的方差分析结果 Table 3 Analysis of variance for Δp and F at ug=0.01 m·s-1
Source Δp/Pa F/(m3·s-1)
F-value p-value F-value p-value
Model 152.70 <0.000 1 170.99 <0.000 1
W* 458.02 <0.000 1 512.60 <0.000 1
H* 0.086 3 0.775 6 0.369 3 0.558 4
W*H* 0.000 3 0.986 7 0.001 5 0.969 6
表选项

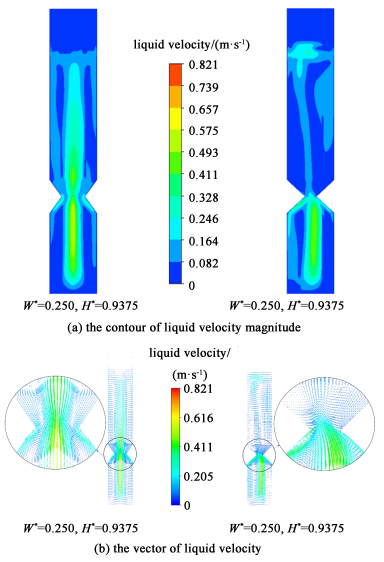
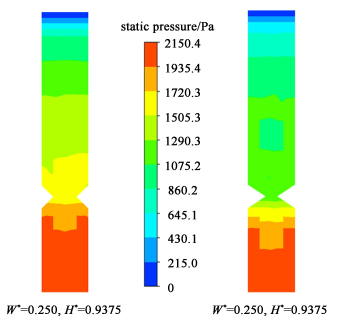
由图 6(该图取自三维计算结果中z=0的截面，在之前的工作[37]中已证实了不同截面上速度分布基本一致，故下文中的图 7以及图 11均为z=0截面的结果)可知，在反应器内安装了隔板(W*=0.25, H*=0.9375)之后，流体沿轴向方向从第1级流入第2级时流道经历了先收缩随后扩张的变化过程，液相和隔板之间的碰撞导致了流体动能的损失，部分液体被导流至第一级的下降段[图 6(b)]。随后在流道扩张处，流体会产生边界层分离的现象，因此隔板处流道截面积的变化会导致反应器压降变化。图 7为对应的压力分布图，从图 6中可以看出压力梯度在2级之间较大，说明经过隔板之后出现了较大的压降。隔板的宽度越大，截面积越小，其对于向上运动的流体的阻挡越明显，流体阻力越大。而在低表观气速下，同宽度增加导致的压降变化相比，隔板高度变化引起的压降变化基本可以忽略。另一方面，随着隔板宽度的增加，流道最窄处的流通面积减小，整体循环得到了明显抑制，使得液相回流流量减小。而相比于隔板宽度，隔板高度对于液相回流流量的影响并不明显。

图 6 安装隔板的反应器中液相速度大小分布云图和液相速度矢量图(t=80 s) Fig.6 The liquid velocity contour and liquid velocity vector in the reactor with the partition at t=80 s
图选项
图 7 安装隔板的反应器中静压分布云图(t=80 s) Fig.7 The contour of static pressure in the reactor with the partition at t=80 s
图选项
2.3 隔板的多目标优化

为了同时兼顾流动阻力和减小液相回流流量的效果，对隔板进行多目标优化，本文以隔板的无量纲宽度和高度为自变量，以压降和液相回流流量为目标函数，进行多目标优化。对表 2中的数据拟合得到液相回流流量和压降的关联式。

$\begin{gathered}\Delta p=1.840 \times 10^3+7.185 \times 10^3 W^*+ \\ 1.272 \times 10^3 H^*+2.252 W^* H^* \\ \left(R^2=0.9743\right)\end{gathered}$ (5)
$\begin{gathered}F=1.534 \times 10^3-3.947 \times 10^3 W^*+ \\ 3.000 \times 10^{-5} H^*-2.700 \times 10^{-5} W^* H^* \\ \left(R^2=0.9770\right)\end{gathered}$ (6)

利用MATLAB优化工具中的多目标优化算法gamultiobj函数求解优化问题，变量为隔板的无量纲宽度和高度，隔板宽度和高度搜索区域的上下边界分别为0.375、0.250和0.937 5、0.312 5，式(5)和式(6)为目标函数，经过对优化算法的参数进行调优，最终确定当最优个体系数为0.2，种群大小为500，最大进化代数为4 000，求解结果基本保持一致，不再发生改变。多目标优化问题存在多个解，每个解都对应1组隔板的宽度和高度，Pareto前沿(Pareto front)[37]上的1组最优解的集合是多目标优化问题的求解结果。从图 8可以看出，Pareto前沿曲线上随着液相回流流量的增加，压降逐渐下降，说明2者之间存在着竞争关系。若要进一步降低液相回流流量，只能通过增加流动阻力实现。反之，若要降低流动阻力，只能降低抑制液相回流的效果。

图 8 ug=0.01 m·s-1时的Pareto前沿曲线 Fig.8 Pareto fronts at ug=0.01 m·s-1
图选项
2.4 不同流型对隔板优化的影响

当ug=0.04 m·s-1和ug=0.08 m·s-1时对隔板进行多目标优化。表 4和表 5为ug=0.04 m·s-1时的反应器压降与液相回流流量的计算值以及对应的方差分析结果，表 6和表 7为ug=0.08 m·s-1时的反应器压降与液相回流流量的计算值以及对应的方差分析结果。

表 4 ug=0.04 m·s-1时不同隔板的反应器压降与液相回流流量的计算值 Table 4 The simulated values of Δp and F in the reactors with different partitions at ug=0.04 m·s-1
Guide vanes W* H* Δp/Pa F/(m3·s-1)
W1H1 0.250 0 0.312 5 2 092.41 7.40×10-4
W1H2 0.250 0 0.625 0 2 119.99 7.91×10-4
W1H3 0.250 0 0.937 5 2 123.93 8.23×10-4
W2H1 0.312 5 0.312 5 2 115.58 3.19×10-4
W2H2 0.312 5 0.625 0 2 202.16 3.61×10-4
W2H3 0.312 5 0.937 5 2 241.29 3.96×10-4
W3H1 0.375 0 0.312 5 2 143.47 5.80×10-5
W3H2 0.375 0 0.625 0 2 247.52 7.43×10-5
W3H3 0.375 0 0.937 5 2 351.75 7.13×10-5
表选项
表 5 ug=0.04 m·s-1时压降和液相回流流量的方差分析结果 Table 5 Analysis of variance for Δp and F at ug=0.04 m·s-1
Source Δp/Pa F/(m3·s-1)
F-value p-value F-value p-value
Model 102.35 <0.000 1 157.91 <0.000 1
W* 146.74 <0.000 1 469.96 <0.000 1
H* 118.68 <0.000 1 3.04 0.115 4
W*H* 41.63 0.000 1 0.725 4 0.416 5
表选项
表 6 ug=0.08 m·s-1时不同隔板结构的反应器压降与液相回流流量的计算值 Table 6 The simulated values of Δp and F in the reactors with different partitions at ug=0.08 m·s-1
Guide vanes W* H* Δp/Pa F/(m3·s-1)
W1H1 0.250 0 0.312 5 2 099.86 6.79×10-4
W1H2 0.250 0 0.625 0 2 161.00 7.81×10-4
W1H3 0.250 0 0.937 5 2 205.59 8.13×10-4
W2H1 0.312 5 0.312 5 2 122.40 2.16×10-4
W2H2 0.312 5 0.625 0 2 200.30 2.56×10-4
W2H3 0.312 5 0.937 5 2 278.60 2.67×10-4
W3H1 0.375 0 0.312 5 2 168.47 4.82×10-5
W3H2 0.375 0 0.625 0 2 256.01 3.27×10-5
W3H3 0.375 0 0.937 5 2341.83 2.53×10-5
表选项
表 7 ug=0.08 m·s-1时压降和液相回流流量的方差分析结果 Table 7 Analysis of variance for Δp and F at ug=0.08 m·s-1
Source Δp/Pa F/(m3·s-1)
F-value p-value F-value p-value
Model 642.51 <0.000 1 34.76 <0.000 1
W* 605.52 <0.000 1 102.90 <0.000 1
H* 1 275.82 <0.000 1 0.570 6 0.469 3
W*H* 46.20 <0.000 1 0.810 8 0.391 3
表选项

对比表 3、表 5和表 7可知，低气速下隔板宽度是反应器压降的决定因素，当ug提高到0.04 m·s-1时，隔板宽度和高度对压降的影响相当，ug继续增大到0.08 m·s-1时，隔板高度对压降的影响较大。当隔板宽度一定时，其高度越高，第2级下降段的流体受到的导流作用越明显，其向中心区域运动的趋势越明显，与上升的气液两相发生“碰撞”，导致流动阻力变大。液相回流流量的最主要决定因素为隔板宽度。

当ug=0.04 m·s-1时，对数据进行拟合后得到的Δp和F的关联式为：

$\begin{gathered}\Delta p=2.170 \times 10^3-3.303 \times 10^2 W^*- \\ 5.121 \times 10^2 H^*+2.262 \times 10^3 W^* H^* \\ \left(R^2=0.9620\right)\end{gathered}$ (7)
$\begin{gathered}F=1.953 \times 10^{-3}-5.183 \times 10^{-3} W^*+ \\ 3.680 \times 10^{-4} H^*-8.830 \times 10^{-4} W^* H^* \\ \left(R^2=0.9751\right)\end{gathered}$ (8)

当ug=0.08 m·s-1时，对数据进行拟合后得到的Δp和F的关联式为：

$\begin{gathered}\Delta p=1.977 \times 10^3+2.586 \times 10^2 W^*- \\ 3.838 \times 10^1 H^*+8.657 \times 10^2 W^* H^* \\ \left(R^2=0.9860\right)\end{gathered}$ (9)
$\begin{gathered}F=1.678 \times 10^{-3}-4.521 \times 10^{-3} W^*+ \\ 7.140 \times 10^{-4} H^*-2.010 \times 10^{-3} W^* H^* \\ \left(R^2=0.8941\right)\end{gathered}$ (10)

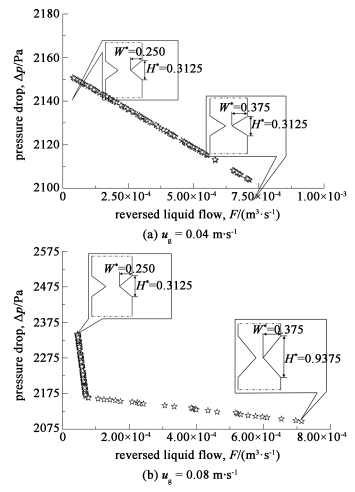
ug=0.04 m·s-1和ug=0.08 m·s-1时得到的Pareto前沿曲线分别如图 9所示。图 9(b)中，曲线的左侧区域压降改变很大才会改变液相回流流量，而曲线右侧压降改变很小就会造成液相回流流量变化很大。这可能是由于气速较大时，气体的惯性力较大，只能通过改变隔板的宽度和高度以形成较大的流动阻力，提高隔板最窄处的流速，减小液相回流流量。而当隔板产生的阻力已经较大时，稍微加大流动阻力，就会减小液相回流流量。

图 9 当ug=0.04 m·s-1和ug=0.08 m·s-1时Pareto前沿曲线 Fig.9 Pareto fronts at ug=0.04 m·s-1 and ug=0.08 m·s-1
图选项
2.5 不同优化目标下隔板最优Pareto解

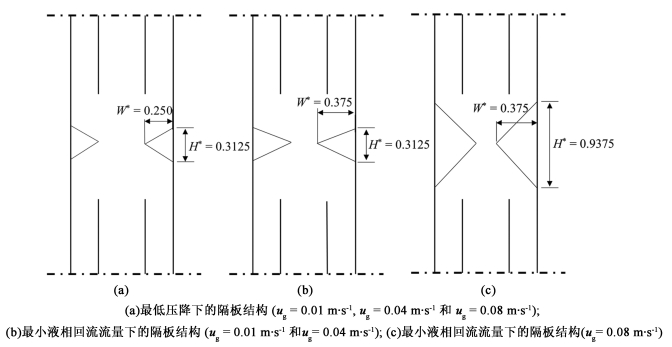
图 10所示为优化得到的隔板。其中图 10(a)为气速为0.01、0.04和0.08 m·s-1下，所有Pareto最优解中具有最小压降的隔板；图 10(b)为表观气速为0.01和0.04 m·s-1时，所有Pareto最优解中具有最小液相回流流量的隔板；图 10(c)为表观气速为0.08 m·s-1时，所有Pareto最优解中具有最小液相回流流量的隔板。从优化结果看，压降主要来源于隔板处流道改变所导致的流体流动方向改变。所有表观气速下具有最小压降的隔板的宽度和高度均保持一致，为变化范围中的最小值。液相回流流量随隔板宽度的增大而减小，因此图 10(b)和10(c)的隔板的宽度为变化范围中的最大值。而隔板高度对液相回流流量的影响较为复杂，主要有2方面，一方面随着高度的增加，在隔板的导流作用下，从第2级下降段流向第1级的液体具有向下的速度，有逐渐向第1级运动的趋势，因此液相回流流量会增大；另一方面，随着高度的增加，第2级下降段的液体在隔板的导流作用下有向反应器中心运动的趋势，可以与由第1级向上运动的流体进行动量传递，从而被带入到第2级上升段，故液相回流流量随高度的变化会因宽度以及表观气速的变化而变化。当气速较低，隔板高度较低时，其倾斜角度较小，可以减小第2级下降段中液体向下的速度分量，不利于液体向下运动进入第1级，因此图 10(b)中隔板的高度为变化范围内的最小值；而当气速较高时，较大的隔板倾斜角度可以提高第2级下降段中液体向中心区域运动的速度，从而与第1级中向上运动的气相发生动量传递，被带入到第2级上升段，起到抑制液体向下运动的效果，故图 10(c)中的隔板高度为变化范围的最大值。

图 10 具有最低压降和液相回流流量的Pareto最优隔板 Fig.10 Geometries of Pareto optimality partitions with lowest pressure drop and reversed liquid flow
图选项

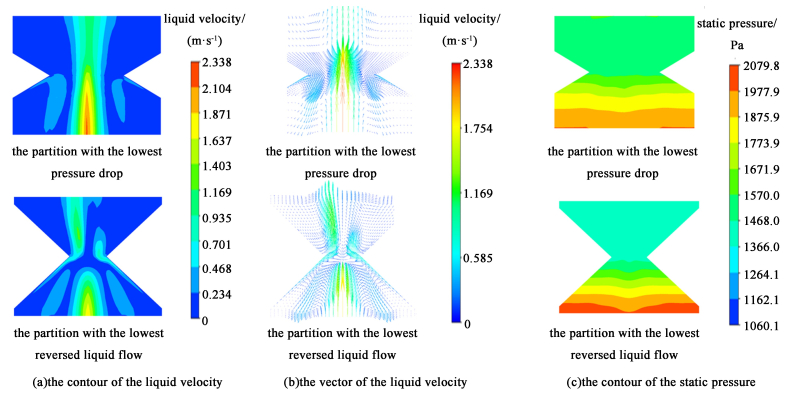
图 11所示为表观气速为0.08 m·s-1时安装隔板的反应器内的速度大小分布云图、速度矢量图以及静压力分布图。从图 11中可以明显看出，在左侧图中具有较小宽度的隔板结构流动阻力较小，但部分液体会经过第2级的下降段进入到第1级；而在右侧图中具有较大宽度的隔板流动阻力较大，但从第2级返回进入到第1级的液体也相应减少。

图 11 ug=0.08 m·s-1时隔板处的流动特性图(t=80 s) Fig.11 Flow characteristics of Pareto optimality partitions at ug=0.08 m·s-1 and t=80 s
图选项
3 结论

针对二级环流反应器在不同隔板宽度和高度下的流动阻力和级间液相交换进行了数值模拟研究，在不同的表观气速下得到了压降和液相回流流量随隔板宽度和高度的变化规律，并进行了多目标优化，得到了不同性能参数下的最优隔板，主要结论如下。

(1) 所有气速下，随着隔板宽度的增加，流道截面积变小，反应器压降增大，液相回流流量减小。隔板高度对压降以及液相回流流量的影响较为复杂，一方面随着高度的增加，在隔板的导流作用下，从第2级下降段流向第1级的液体速度方向逐渐向下，有逐渐向第1级运动的趋势，因此液相回流流量会增大；另一方面，随着高度的增加，第2级下降段的液体在隔板的导流作用下有向反应器中心运动的趋势，能与由第1级向上运动的流体进行动量传递，从而被带入到第2级上升段，故液相回流流量减小，而压降增大。总体上讲，液相回流流量以及压降随高度的变化会因宽度以及表观气速的不同而变化。

(2) 随着表观气速的增大，压降的主要影响因素从隔板宽度变为隔板高度，液相回流流量的最主要影响因素为隔板宽度，宽度越大，液相回流流量越小。

(3) 本研究的气速范围内，宽度和高度较小(W*=0.25，H*=0.3125)的隔板具有较小的压降；当气速较低时，宽度较大(W*=0.375)，高度较小(H*=0.3125)的隔板具有较小的液相回流流量，抑制级间液相交换较为明显；而当气速较大时，宽度较大(W*=0.375)，高度较大(H*=0.9375)的隔板具有较小的液相回流流量，抑制级间液相交换较为明显。

参考文献
[1]
HUANG Q, ZHANG W, YANG C. Modeling transport phenomena and reactions in a pilot slurry airlift loop reactor for direct coal liquefaction[J]. Chemical Engineering Science, 2015, 135: 441-451. DOI:10.1016/j.ces.2015.01.003
[2]
WANG T, WANG J, JIN Y. Slurry reactors for gas-to-liquid processes: A review[J]. Industrial & Engineering Chemistry Research, 2007, 46(18): 5824-5847.
[3]
VIOTTI P, LUCIANO A, MANCINI G, et al. A wastewater treatment using a biofilm airlift suspension reactor with biomass attached to supports: A numerical model[J]. International Journal of Environmental Science and Technology, 2014, 11(3): 571-588.
[4]
DE JESUS S S, MOREIRA N J, MACIEL F R. Hydrodynamics and mass transfer in bubble column, conventional airlift, stirred airlift and stirred tank bioreactors, using viscous fluid: A comparative study[J]. Biochemical Engineering Journal, 2017, 118: 70-81. DOI:10.1016/j.bej.2016.11.019
[5]
HOL A, VAN DER WEIJDEN R D, VAN WEERT G, et al. Bio-reduction of pyrite investigated in a gas lift loop reactor[J]. International Journal of Mineral Processing, 2010, 94(3/4): 140-146.
[6]
DAMODAR R A, YOU S, OU S. Coupling of membrane separation with photocatalytic slurry reactor for advanced dye wastewater treatment[J]. Separation and Purification Technology, 2010, 76(1): 64-71. DOI:10.1016/j.seppur.2010.09.021
[7]
RENGEL A, ZOUGHAIB A, DRON D, et al. Hydrodynamic study of an internal airlift reactor for microalgae culture[J]. Applied Microbiology and Biotechnology, 2012, 93(1): 117-129. DOI:10.1007/s00253-011-3398-9
[8]
AL-QODAH Z, LAFI W. Modeling of antibiotics production in magneto three-phase airlift fermenter[J]. Biochemical Engineering Journal, 2001, 7(1): 7-16.
[9]
GUETTEL R, KUNZ U, TUREK T. Reactors for Fischer-Tropsch synthesis[J]. Chemical Engineering & Technology, 2008, 31(5): 746-754.
[10]
HUANG Q, YAO L, LIU T, et al. Simulation of the light evolution in an annular photobioreactor for the cultivation of Porphyridium cruentum[J]. Chemical Engineering Science, 2012, 84: 718-726. DOI:10.1016/j.ces.2012.09.017
[11]
VAN BENTHUM W A J, VAN DER LANS R G J M, VAN LOOSDRECHT M C M, et al. The biofilm airlift suspension extension reactor-Ⅱ: Three-phase hydrodynamics[J]. Chemical Engineering Science, 2000, 55(3): 699-711. DOI:10.1016/S0009-2509(99)00035-4
[12]
MOHANTY K, DAS D, BISWAS M N. Treatment of phenolic wastewater in a novel multi-stage external loop airlift reactor using activated carbon[J]. Separation and Purification Technology, 2008, 58(3): 311-319. DOI:10.1016/j.seppur.2007.05.005
[13]
DE KEE D, CHHABRA R P. A photographic study of shapes of bubbles and coalescence in non-Newtonian polymer solutions[J]. Rheologica Acta, 1988, 27(6): 656-660.
[14]
LAU Y M, DEEN N G, KUIPERS J A M. Development of an image measurement technique for size distribution in dense bubbly flows[J]. Chemical Engineering Science, 2013, 94: 20-29. DOI:10.1016/j.ces.2013.02.043
[15]
BAI F, WANG L, HUANG H, et al. Oxygen mass-transfer performance of low viscosity gas-liquid-solid system in a split-cylinder airlift bioreactor[J]. Biotechnology Letters, 2001, 23(14): 1109-1113. DOI:10.1023/A:1010555715556
[16]
CERRI M O, FUTIWAKI L, JESUS C D F, et al. Average shear rate for non-Newtonian fluids in a concentric-tube airlift bioreactor[J]. Biochemical Engineering Journal, 2008, 39(1): 51-57. DOI:10.1016/j.bej.2007.08.009
[17]
RODRIGUEZ G Y, VALVERDE-RAMÍREZ M, MENDES C E, et al. Global performance parameters for different pneumatic bioreactors operating with water and glycerol solution: Experimental data and CFD simulation[J]. Bioprocess and Biosystems Engineering, 2015, 38(11): 2063-2075. DOI:10.1007/s00449-015-1446-z
[18]
KUMAR N, BANSAL A, GUPTA R. Shear rate and mass transfer coefficient in internal loop airlift reactors involving non-Newtonian fluids[J]. Chemical Engineering Research and Design, 2018, 136: 315-323. DOI:10.1016/j.cherd.2018.05.042
[19]
谷奎庆. 三相连续环流反应器液相传质及混合特性研究[D]. 北京: 北京化工大学, 2007
GU Kuiqing. Study on mass transfer and mixing characteristics of liquid phase in three-phase continuous loop reactor[D]. Beijing: Beijing University of Chemical Technology, 2007 (in Chinese)
[20]
杨辉. 双喷嘴连续气泡生成与聚并行为的数值模拟[D]. 天津: 天津大学, 2016
YANG Hui. Numerical simulation of continuous bubble formation and coalescence behavior with two nozzles[D]. Tianjin: Tianjin University, 2016(in Chinese)
[21]
GAVRILESCU M, TUDOSE R Z. Effects of downcomer-to-riser cross sectional area ratio on operation behaviour of external-loop airlift bioreactors[J]. Bioprocess Engineering, 1996, 15(2): 77-85.
[22]
冯加和. 硅油光-热老化气升式外环流反应器流动特性研究[D]. 天津: 天津大学, 2014
FENG Jiahe. Study on flow characteristics of air-lift external loop reactor with photo-thermal aging of silicone oil[D]. Tianjin: Tianjin University, 2014 (in Chinese)
[23]
徐斌. 气升式内环流生物反应器的Fluent模拟研究[D]. 长沙: 湖南大学, 2017
XU Bin. Fluent simulation of airlift internal loop bioreactor[D]. Changsha: Hunan University, 2017 (in Chinese)
[24]
杨志方, 杜峰, 于清江, 等. 78.5升气升式环流反应器内构件优化[J]. 化工进展, 2015, 34(3): 659-663.
YANG Zhifang, DU Feng, YU Qingjiang, et al. Internals optimization of 78.5L airlift loop reactor[J]. Chemical Industry and Engineering Progress, 2015, 34(3): 659-663. (in Chinese)
[25]
陶金亮, 黄建刚, 肖航, 等. 级间隙高度和表观气速对多级环流反应器混合和传质的影响[J]. 化工学报, 2018, 69(7): 2878-2889, 3301.
TAO Jinliang, HUANG Jiangang, XIAO Hang, et al. Influences of interstage height and superficial gas velocity in multistage internal airlift loop reactor on performance of mixing and mass transfer[J]. CIESC Journal, 2018, 69(7): 2878-2889, 3301. (in Chinese)
[26]
RUSSELL A B, THOMAS C R, LILLY M D. The influence of vessel height and top-section size on the hydrodynamic characteristics of airlift fermentors[J]. Biotechnology and Bioengineering, 1994, 43(1): 69-76. DOI:10.1002/bit.260430110
[27]
LUKIĆ N L, ŠIJAČKI I M, KOJIĆ P S, et al. Enhanced mass transfer in a novel external-loop airlift reactor with self-agitated impellers[J]. Biochemical Engineering Journal, 2017, 118: 53-63. DOI:10.1016/j.bej.2016.11.014
[28]
CHISTI Y, JAUREGUI-HAZA U J. Oxygen transfer and mixing in mechanically agitated airlift bioreactors[J]. Biochemical Engineering Journal, 2002, 10(2): 143-153. DOI:10.1016/S1369-703X(01)00174-7
[29]
ZHANG X, GUO K, QI W, et al. Gas holdup, bubble behaviour, and mass transfer characteristics in a two-stage internal loop airlift reactor with different screens[J]. The Canadian Journal of Chemical Engineering, 2017, 95(6): 1202-1212. DOI:10.1002/cjce.22767
[30]
RÄSÄNEN M, EERIKÄINEN T, OJAMO H. Characterization and hydrodynamics of a novel helix airlift reactor[J]. Chemical Engineering and Processing: Process Intensification, 2016, 108: 44-57. DOI:10.1016/j.cep.2016.07.006
[31]
ZHENG Z, CHEN Y, ZHAN X, et al. Mass transfer intensification in a novel airlift reactor assembly with helical sieve plates[J]. Chemical Engineering Journal, 2018, 342: 61-70.
[32]
LUO L, YUAN J, XIE P, et al. Hydrodynamics and mass transfer characteristics in an internal loop airlift reactor with sieve plates[J]. Chemical Engineering Research and Design, 2013, 91(12): 2377-2388. DOI:10.1016/j.cherd.2013.06.002
[33]
YU W, WANG T, LIU M, et al. Liquid backmixing and particle distribution in a novel multistage internal-loop airlift slurry reactor[J]. Industrial & Engineering Chemistry Research, 2008, 47(11): 3974-3982.
[34]
DREHER A J, KRISHNA R. Liquid-phase backmixing in bubble columns, structured by introduction of partition plates[J]. Catalysis Today, 2001, 69(1/2/3/4): 165-170.
[35]
ZHANG L, PAN Q, REMPEL G L. Liquid backmixing and phase holdup in a gas-liquid multistage agitated contactor[J]. Industrial & Engineering Chemistry Research, 2005, 44(14): 5304-5311.
[36]
SHI J, GUO K, WANG Z, et al. Computational fluid dynamics simulation of hydrodynamics in a two-stage internal loop airlift reactor with contraction-expansion guide vane[J]. ACS Omega, 2021, 6(10): 6981-6995.
[37]
谢承旺. 多目标群体智能优化算法[M]. 北京: 北京理工大学出版社, 2020.