2. 江南大学机械工程学院, 江苏 无锡 214122
2. School of Mechanical Engineering, Jiangnan University, Wuxi, Jiangsu 214122, China
微波连续流管式反应器是一种在微波加热环境下让物料连续均匀地从管中流入流出的反应器[1]。相比于常规加热,微波加热属于体积加热[2],加热速度更快、热损失更小、易于控制;相比于间歇式,连续流使得有机反应发生得更加充分[3]。因此微波连续流管式反应器已广泛应用于食品、医疗、化工等各个领域[4, 5]。但是,如何获得最佳微波加热效率和控制加热不均匀性[6]是微波连续流管式反应器应用过程中仍未被完全解决的问题。因此国内外许多专家针对改善微波加热效果的措施进行了一系列研究,Niu等[7]、Tuta等[8]以及Zhang等[9]验证了在微波连续流系统中螺旋管的使用相对于直管,可以提高加热效率和温度均匀性。郭帅等[10]和Dewanga等[11]设计的新型连续流螺旋管微波反应器对于制备生物柴油和加热液态食品都有显著效果。Wu等[12]建立了一个具有交叉结构的微波连续流反应管模型提高了微波加热的均匀性。吴雁泽[13]通过在微波连续流管式反应器中加入模式搅拌器改变电磁场分布从而提高微波加热效果。Yang等[14]和Li等[15]通过改变波导的数量和组合方式显著优化了微波连续流反应器管内物料的加热效果。Zhou等[16]通过优化微波腔形状尺寸来提高微波加热效率和加热均匀性。Huseyin等[17]对连续流微波反应器腔体几何形状和管道的分布进行优化研究,表明系统内的管道方向影响电场分布和温度均匀性。
上述研究表明,对于高效微波反应器的研发过程中,为获得最优微波加热效率的同时保持较好的均匀性,微波源波导在反应系统中的位置、微波腔中管道形状和空间位置等结构参数,微波功率和物料流速等工艺参数,已被证明对提高连续流微波加热的效率具有重要影响,但其影响规律尚不清晰。因此,本研究的目的是在2 450 MHz频率下,耦合多层流动元件,通过体平均温度、|S11|和电磁功率损耗等评价指标优化微波反应器结构,评估连续流动微波加热系统的改进工艺,以期获得最佳微波加热效率和控制加热不均匀性的高产能连续流微波反应器。
1 研究方法 1.1 研究对象及模型为了提高连续流矩形微波反应器节能增产的效果,以课题组前期所设计的反应器[1]为参照,提出一种耦合多层流动元件的新反应器。该反应器腔体沿Z轴均匀分成若干个区域并布置若干层物料,设定反应器内物料相对于反应器中心距离为h,波导相对于反应器中心距离为l,通过空腔内流动物料体积V、位置h和波导位置l的变化,研究微波加热对腔内物料的加热效果及影响因素,以期提高处理物料量和反应器微波能利用率,反应器结构如图 1所示。本课题中物料体积以ΔV等倍增加;物料间距变化范围[20 mm, 140 mm],波导位置变化范围[-60 mm,60 mm],移动步长分别为Δh=20 mm和Δl=10 mm。

|
| 图 1 微波连续流反应器示意图 Fig.1 Diagram of a microwave continuous flow reactor |
| |
连续流动微波反应系统数学模型建立过程中耦合了COMSOL Multiphysics 5.4软件中的电磁波、流体传热以及层流模块。首先,通过求解麦克斯韦方程得到电磁能量的分布,它的微分形式为[18]:
| $ \left\{\begin{array}{c} \nabla \times \vec{H}(\vec{r}, t)=\frac{\partial}{\partial t} \vec{D}(\vec{r}, t)+\vec{J}(\vec{r}, t) \\ \nabla \times \vec{E}(\vec{r}, t)=-\frac{\partial}{\partial t} \vec{B}(\vec{r}, t) \\ \nabla \times \vec{D}(\vec{r}, t)=\rho(\vec{r}, t) \\ \nabla \times \vec{B}(\vec{r}, t)=0 \end{array}\right. $ | (1) |
式(1)中:
电磁加热是微波电磁能转化为被加热物料中热量的过程,其中热源Qe主要来自于电阻损耗和电磁损耗,由式(2)计算得出:
| $ Q_{\mathrm{e}}=Q_{\mathrm{rh}}+Q_{\mathrm{ml}} $ | (2) |
式(2)中电阻损耗的表达式为:
| $ Q_{\mathrm{rh}}=\frac{1}{2} \operatorname{Re}\left(\vec{J} \cdot \vec{E}^*\right) $ | (3) |
电磁损耗的表达式为:
| $ Q_{\mathrm{ml}}=\frac{1}{2} \operatorname{Re}\left(i \omega \vec{B} \cdot \vec{H}^*\right) $ | (4) |
假设计算时微波连续流反应器中的物料处于流动状态;物料流动遵守质量守恒定律和动量守恒定律。
质量守恒方程:
| $ \frac{\partial \rho}{\partial t}+\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}+\frac{\partial(\rho w)}{\partial z}=0 $ | (5) |
动量守恒方程:
| $ \left\{\begin{array}{l} \frac{\partial(\rho u)}{\partial t}+\operatorname{div}(\rho u \boldsymbol{u})=\operatorname{div}(\mu \operatorname{grad} u)-\frac{\partial p}{\partial x}+S_{\mathrm{u}} \\ \frac{\partial(\rho v)}{\partial t}+\operatorname{div}(\rho v \boldsymbol{u})=\operatorname{div}(\mu \operatorname{grad} v)-\frac{\partial p}{\partial y}+S_{\mathrm{v}} \\ \frac{\partial(\rho w)}{\partial t}+\operatorname{div}(\rho w \boldsymbol{u})=\operatorname{div}(\mu \operatorname{grad} w)-\frac{\partial p}{\partial z}+S_{\mathrm{w}} \end{array}\right. $ | (6) |
式(6)中:ρ、u、u、v、w、p、t和μ分别指密度、速度矢量、速度矢量在x方向的分量、速度矢量在y方向的分量、速度矢量在z方向的分量、流体微元体上的压力、时间和动力黏度;Su、Sv和Sw是动量守恒方程的广义源项。
本研究物料流动状态为层流,层流状态下的流体传热控制方程为:
| $ \rho C_p \frac{\partial T}{\partial t}+\rho C_p \boldsymbol{u} \cdot \nabla T=\nabla \cdot(k \nabla T)+Q_{\mathrm{e}} $ | (7) |
式(7)中:u是速度矢量;t是时间;T是温度;ρ, CP和k分别是被加热材料的密度、恒压热容和导热系数。
1.3 边界条件与物性参数微波连续流反应器壁面材料为铜,设为阻抗边界,玻璃管壁为开放边界。选用BJ-22型波导,微波频率为2.45 GHz、微波功率为500~1 500 W,入口流速为0.01~0.06 m·s-1,端口激励为TE10。模拟过程中使用的物料为水,初始温度T=293.15 K,相关参数如表 1所示。
| 参数 | 参数值 | 参考 |
| 密度rho(T)/(kg·m-3) | 0.00001034T3-0.0134T2+4.9693T+432.257 | COMSOL |
| 动力黏度eta(T)/(Pa·s) | 1.38-0.021T+1.36E-4T2-4.65E-7T3+8.9E-10T4-9.1E-13T5+3.85E-16T6 | COMSOL |
| 导热系数K(T)/(W·m-1) | -0.87+0.0089T-1.58E-5T2+7.97E-9T3 | COMSOL |
| 恒压热容Cp(T)/(J·kg-1) | 12010.15-80.4T+0.31T2-5.38E-4T3+3.63E-5T4 | COMSOL |
| 比热率alpha_p | -1/rho(T)·d[rho(T), T] | COMSOL |
| 热膨胀系数gamma_w | 1+[T/Cp(T)]·[alpha_p(T)·cs(T)]2 | COMSOL |
| 相对介电常数 | 78.5-1.3j | [16] |
| 电导率/(S·m-1) | 5.5E-6 | [16] |
| 相对磁导率 | 1 | [16] |
网格划分使用COMSOL Multiphysics 5.4软件平台,划分结果如图 2(a)所示:对于流动管单独进行角细化,流动管壁面设为2层边界层网格,拉伸因子为1.2,厚度调节因子为5;其余壁面为非结构化自由四面体网格。研究网格单元数对加热100 s(后续不作特殊说明,加热时间均为100 s)物料出口处平均温度的影响,如图 2(b)所示:当网格数量达到433 282时,可以观察到反应器内物料的出口温度都基本达到稳定状态,此时网格数量再增加出口温升基本不再变化,所以在后续研究中,网格数量定为433 282。

|
| 图 2 网格及无关性分析 Fig.2 Mesh and independent analysis |
| |
为了验证微波连续流反应器内物料体积的变化对物料微波能量利用率、加热效率的影响,图 3给出了物料体积的变化时反应腔内电场和温度场分布的影响。图 3(a)可以观察到物料体积变化时反应腔内布置2层物料时电场强度最高;图 3(b)明显看出2层物料的反应器内管面上红色高温区域更明显。
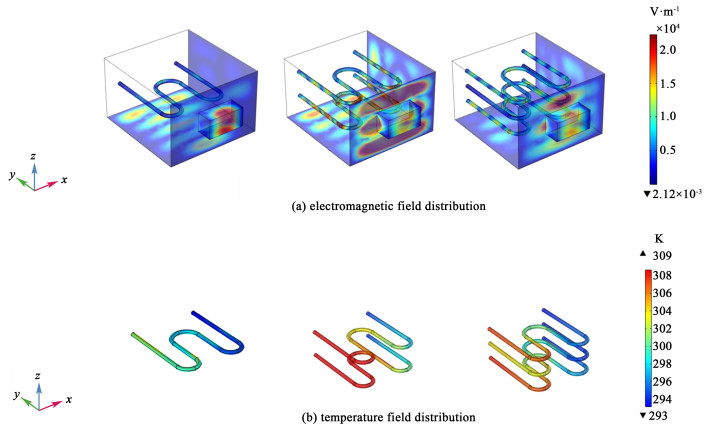
|
| 图 3 物料体积变化时的电磁场和温度场分布 Fig.3 Distribution of electromagnetic field and temperature field when material volume changes |
| |
为了研究物料体积的变化对物料微波能量利用率的影响,讨论了3组模型的体平均温升、电磁功率损耗密度(Qe)和|S11|[19]系数的变化,可以发现3种指标由低到高的趋势为:体平均温升:1层 < 3层 < 2层;Qe:1层 < 3层 < 2层;|S11|:1层 < 3层 < 2层。
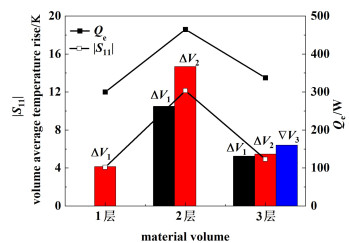
|
| 图 4 不同物料体积下的体平均温度,Qe和|S11|的变化 Fig.4 Variation of average volume temperature, Qe and |S11| at different material volumes |
| |
图 5讨论了物料体积变化时反应器腔内物料出口温升和COV[20](

|
| 图 5 不同物料体积的出口温度和COV的变化 Fig.5 Variation of outlet temperature and COV for different material volumes |
| |
如图 6所示,在2.4~2.5 GHz的频率范围内,随着物料体积的增加,微波连续流反应器内物料的最大体平均温度和|S11|最大值所在的频率位置由2.42 GHz迁移至2.45 GHz最后至2.46 GHz。其中当反应器内放置2层物料,在微波频率为2.45 GHz时有最好的加热效率和最大的|S11|,且此时腔内物料的温度分布也更加均匀。

|
| 图 6 频率变化时不同物料体积反应器体平均温度和|S11|的变化 Fig.6 The change of the volume average temperature of the reactor and |S11| with different material volumes when the frequency changes |
| |
在研究物料体积的影响时,可以发现在反应器内布置2层物料拥有较高的温升和微波能量利用率以及|S11|,但是2层物料的温度均匀性较差,因此在后续研究中,选择耦合2层流动元件的单波导微波连续流反应器作为研究对象,考察结构参数和工艺参数的变化以研究耦合多流动元件反应器分区域物料对微波能量的利用率和对加热效果的均匀控制。
2.2 结构参数对反应器微波能量利用效率的影响在本节首先讨论物料间距和波导位置对反应器内不同区域物料微波能量利用效率的影响。考虑流动元件直径、物料间距和波导位置分别以Δh=20 mm和Δl=10 mm增加,所有考察的模型参数如表 2所示。
 |
±10 (±1)Δl |
±20 (±2)Δl |
±30 (±3)Δl |
±40 (±4)Δl |
±50 (±5)Δl |
±60 (±6)Δl |
| 20(Δh) | A(20, ±10) | A(20, ±20) | A(20, ±30) | A(20, ±40) | A(20, ±50) | A(20, ±60) |
| 40(2Δh) | B(40, ±10) | B(40, ±20) | B(40, ±30) | B(40, ±40) | B(40, ±50) | B(40, ±60) |
| 60(3Δh) | C(60, ±10) | C(60, ±20) | C(60, ±30) | C(60, ±40) | C(20, ±50) | C(60, ±60) |
| 80(4Δh) | D(80, ±10) | D(80, ±20) | D(80, ±30) | D(80, ±40) | D(80, ±50) | D(80, ±60) |
| 100(5Δh) | E(100, ±10) | E(100, ±20) | E(100, ±30) | E(100, ±40) | E(100, ±50) | E(100, ±60) |
| 120(6Δh) | F(120, ±10) | F(120, ±20) | F(120, ±30) | F(120, ±40) | F(120, ±50) | F(120, ±60) |
| 140(7Δh) | G(140, ±10) | G(140, ±20) | G(140, ±30) | G(40, ±40) | G(140, ±50) | G(140, ±60) |
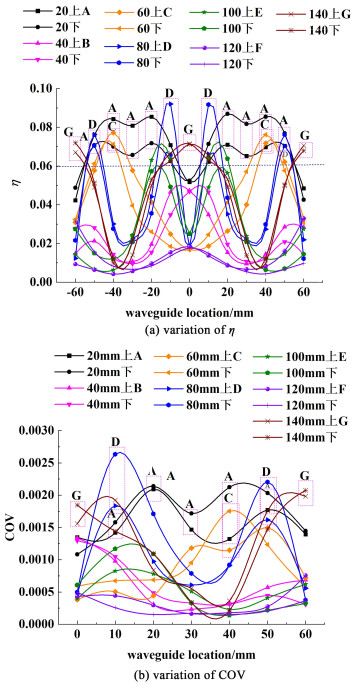
图 7绘制了模型内物料平均电场模(E)的分布。可以看出腔内不同区域物料内E随波导位置升高存在周期性变化,其中物料间距20 mm,波导位置-20 mm的反应器,即模型(20,-20)存在最大平均电场模(Emax)。对于物料间距为40和120 mm且任一波导位置下的反应器,其物料区域E值均低于7 000 V·m-1(即80%Emax),不利于微波能利用。而其它大部分物料间距的反应器在波导变化范围内,双层物料区域并不能同时达80%Emax以上的电磁场特征;仅当物料间距为20、80、100和140 mm时,一些波导位置下,如图 7中所示标记A\D\E\G组模型腔内双层物料区域E可达80%Emax及以上,其中物料间距为20 mm时的A模型组最多(9组)。意味着双层流动物料区域E值与结构参数h和l呈现出复杂的非线性关系。此外,除波导位于反应器中心高度l=0时,所有模型中2层流动元件内物料区域E值并不相同,存在一定的差值,这种差值亦随物料间距和波导位置变化而变化,h=60 mm时尤为显著,会引起2层物料加热效果的差异,需要进一步评估。

|
| 图 7 不同物料间距下波导位置变化时物料的平均电场模变化 Fig.7 Variation of the average electric field mode of the material when the waveguide position changes with different material spacing |
| |
图 8为结构参数变化时模型中物料电磁功率损耗(Qe)的变化。其中最大的电磁功率损耗值Qe,max(Δh,Δl)出现在反应器D(80, 10)处;当波导位置一定时,物料间距Δh为40、100和120 mm的模型的Qe始终低于400 W(即80%Qe,max),而其他物料间距的模型均存在高于80%Qe,max的波导位置;当波导位置在[0, 6Δl]范围内变化时,不同波导位置下Qe值从大到小为:Qe, D(80, 10)>Qe, D(20, 20)>Qe, D(20, 40)>Qe, D(80, 50)>Qe, D(60,40)>Qe, D(20, 50)>Qe, D(20, 30)>Qe, D(140, 60)。

|
| 图 8 不同物料间距下波导位置变化时物料的电磁功率损耗 Fig.8 Electromagnetic power loss of materials when the waveguide position changes with different material spacings |
| |
以上分析表明物料间距和波导位置对反应器内微波能量利用率影响呈复杂的非线性特征。其中模型A(20, 20)、A(20, 30)、A(20, 40)、D(80, 10)、G(140, 60)5组模型的E和Qe, 均达到了其最大值的80%以上,同时A组模型整体上呈现出较好的能量利用率。后续通过体平均温度、η和COV等参数进一步讨论结构参数对物料的加热效果的影响。
2.3 结构参数对反应器加热效果的影响模型内物料体平均温度随反应器结构参数的变化如图 9所示。从图 9中可以看出,除去波导位置l=0的情况,其余所有物料间距的条件下腔内双层物料体平均温度均有差异,当物料间距为20、60、80和140 mm时,如图中所示标记A/C/D/G组模型腔内双层物料区域内体平均温度都高于302 K(即70%最高温升)。结合2.2节得出微波能量利用率越高的模型腔内物料体平均温度也越高;但是模型腔内双层物料的体平均温度差距明显,当波导在[-6Δl, 6Δl]范围内变化时,模型腔内体平均温度均匀程度由大到小分别为:C(60, ±40)>A(140, ±60)>A(20, ±20)>A(20, ±30)>A(20, ±40)>D(80, ±10)。

|
| 图 9 不同物料间距下波导位置变化时物料的体平均温度变化 Fig.9 Changes of the volume average temperature of the material when the waveguide position changes under different material spacing |
| |
图 10讨论了物料间距和波导位置变化时腔内双层物料的温升比η(
|
| 图 10 不同物料间距下波导位置变化时物料的η和COV变化 Fig.10 The changes of η and COV of materials when the waveguide position changes with different material spacing |
| |
结合上节对于微波能量利用率的讨论,A(20, 20)、A(20, 30)、D(80, 10)3组模型都具有较高的微波能量利用率和加热效率,但是加热均匀性较差,并且腔内双层物料η的分布差异较大,并且D(80, 10)2组模型COV的分布差异也较大;而模型A(20, 0),C(60, 40)腔内双层物料的微波能量利用率和加热效率不高但是COV值较低,并且腔内双层物料的η和COV的分布差异较小。因此,后续通过A(20, 0)、A(20, 20)、A(20, 30)、C(60, 40)、D(80, 10)5组模型研究工艺参数的变化对双层物料加热效果和加热均匀性的影响。
2.4 功率变化对腔内物料加热效果的影响在研究工艺参数(微波功率,入口流速)对耦合多层流动元件的微波连续流反应器的加热效果和加热均匀性的影响时,选择的5组模型具体参数见表 3。
| 模型 | 电磁功率损耗/W | 体平均温度/K | η | COV (10-2) |
| A(20, 0) | 299.132 | 299.884 300.765 |
0.052 0.052 |
0.135 0.108 |
| A(20, 20) | 446.147 | 304.444 307.347 |
0.072 0.086 |
0.313 0.279 |
| A(20, 30) | 414.503 | 303.451 306.567 |
0.066 0.081 |
0.258 0.273 |
| C(60, 40) | 427.520 | 304.589 305.708 |
0.071 0.078 |
0.298 0.290 |
| D(80, 10) | 464.813 | 303.679 307.824 |
0.067 0.093 |
0.23 0.36 |
微波功率对反应器内物料体平均温度和上下层物料体积平均温差(ΔTv)的影响如图 11所示。随着功率的增加,反应器腔内物料温升增大,但上下层增幅并不一致,下层物料温升显著高于上层物料,但模型A(20, 0)除外。其中模型D(80, 10)下半区的物料体平均温度最高,即加热效果最好;模型A(20, 30)上半区的物料加热效果最差。从上下层物料体积平均温差分布可以看出,对于模型A(20, 0),功率增加腔内双层物料的体平均温度分布始终均匀,而其他模型随着功率的增加腔内物料体平均温度的差异增大,其中模型D(80, 10)中物料体积平均温差随功率增加增幅最大,而模型C(60, 40)温差增幅是除模型A(20, 0)外最小的,意味着功率的增加会使非对称结构参数模型腔内上下层物料区域加热差异性增加。

|
| 图 11 微波功率变化时不同模型的体平均温度和ΔTv的变化 Fig.11 Variation of volume average temperature and ΔTv in different models when microwave power changes |
| |
图 12为5组模型在微波功率变化时腔内双层物料Δη和ΔCOV(Δη=η1-η2, ΔCOV=COV1-COV2, η1-η2和COV1-COV2分别为模型腔内双层物料η和COV的差距)的变化。随着功率的增加物料的Δη和ΔCOV线性增加,其中模型A(20, 0)、A(20, 30)和C(60, 40)中Δη和ΔCOV都增幅缓慢且较小,说明此时腔内物料温升增加的同时加热均匀性较好;而模型D(80,10)中的物料Δη和ΔCOV增幅最大,说明虽然该模型物料温升比较高但同时加热不均匀性也显著增强。
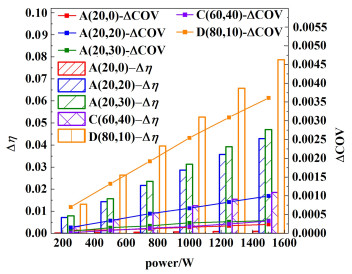
|
| 图 12 微波功率变化时不同模型的Δη和ΔCOV的变化 Fig.12 Variation of Δη and ΔCOV for different models with microwave power |
| |
为进一步探索上下层管物料加热差异性的原因,图 13(a)讨论了模型A(20, 20)在功率变化时腔内物料沿沿管长的温度变化率kt(
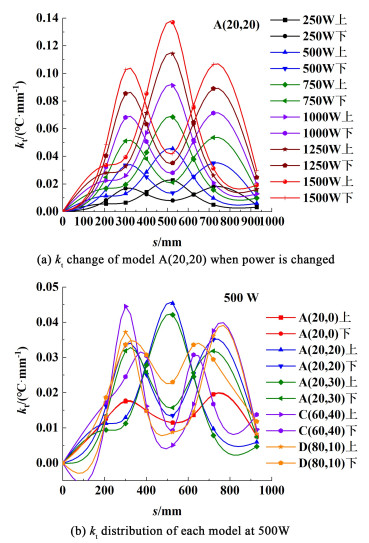
|
| 图 13 物料沿管长的温度变化速率 Fig.13 The change rate of temperature of the material along the length of the tube |
| |
从2.4节可以得出,随着功率的增加,除了模型A(20, 0),其余4组模型腔内双层物料的体平均温度差异、Δη、ΔCOV,kt均在增大,说明功率的增加使得反应器内双层物料的差异性变得更加显著,不利于控制反应器内物料的均匀加热。因此后续研究流速的变化对模型腔内物料加热效果的影响。
2.5 流速变化对腔内物料加热效果的影响图 14绘制了入口流速变化对反应器内物料体平均温度和上下层物料体积平均温差(ΔTv)的分布。随着流速的增加,反应器腔内物料温升下降,然而温升趋势与图 11相似:模型D(80,10)下半区的物料加热效果最好;模型A(20, 30)上半区的物料加热效果最差。对于上下层物料体积平均温差分布,模型A(20, 0)在流速增加时腔内双层物料的体平均温度分布始终均匀,而其他模型随着流速的增加腔内物料体平均温度的差异减小,意味着增加流速缩短物料停留时间,会削弱非对称结构参数模型腔内上下层物料区域加热差异性。
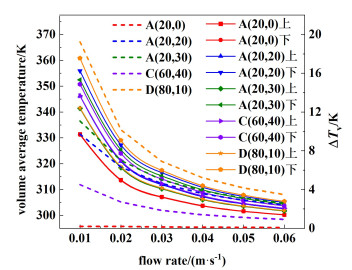
|
| 图 14 流速变化时不同物料的体平均温度和ΔTv的变化 Fig.14 Variation of volume average temperature and ΔTv of different materials when the flow rate changes |
| |
在入口流速变化时腔内不同区域物料Δη和ΔCOV的变化如图 15所示。与图 12中的Δη和ΔCOV趋势相反,随着流速的增加,4组模型物料的Δη和ΔCOV逐渐降低,说明此时上下层物料温升比差异变小,同时加热均匀性提高;其中模型D(80,10)中的物料Δη和ΔCOV减幅明显大于其它模型A(20, 0)、A(20, 30)和C(60, 40)中Δη和ΔCOV的减幅,说明提高流速可以显著缩减该模型上下层物料温升比差异、改善加热均匀性。
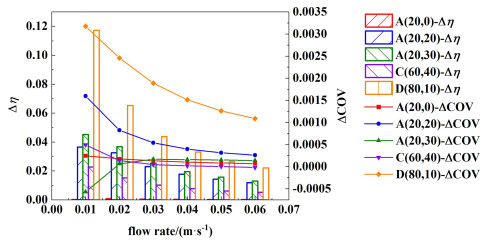
|
| 图 15 流速变化时不同模型的Δη和ΔCOV的变化 Fig.15 Variation of Δη and ΔCOV for different models when the flow rate changes |
| |
图 16为模型D(80, 10)在入口流速变化时物料体平均温度和kt的分布。从图 16(a)中可以看出随着流速增加,物料在管中停留时间减少,物料的体平均温度降低,当物料入口流速增加到0.06 m·s-1时,腔内双层物料达到稳定体平均温度所需的时间低于30 s;图 16(b)中得出模型腔内上下层物料温度梯度沿管长的变化随着流速的增加变化缓慢且不同步,并且上层物料温度变化率波动始终比下层大。

|
| 图 16 流速变化时D(80, 10)体平均温度的变化和沿管长的温度变化速率 Fig.16 Variation of D(80, 10) volume-averaged temperature and change rate of temperature along the length of the tube as the flow rate changes |
| |
随着流速的增加,除了模型A(20, 0),其余4组模型腔内双层物料的体平均温度、ΔTv、Δη、ΔCOV均减小;其中模型D(80, 10)中物料达到稳定体平均温度的时间缩短,kt波动减缓。说明流速的增加不利于反应器内物料的加热,但是提高流速削弱了反应器内双层物料温升的差异性,有利于控制反应器内不同区域物料的均匀加热。
3 结论设计了一种耦合多层流动元件的微波连续流反应器,研究了反应器物料体积、物料间距、波导位置、微波功率和入口流速的变化对物料的微波能量利用率和物料加热效率的影响,主要结论如下:(1)相比于在反应器内布置1层或3层物料,2层物料的条件下物料的微波能量利用率和温升效果更优越;(2)模型的结构参数对腔内物料的微波能量利用率和加热效果影响呈非线性变化,除波导位置为0的情况, 其余位置的不同物料间距下反应器腔内双层物料的微波能量利用率和加热效果呈现出不同幅度的差异;(3)当微波功率增加时,反应器腔内物料加热效果改善,但是腔内双层物料加热效果的差异性增大,说明功率的增加不利于模型腔内物料的加热效果的均匀控制;(4)入口流速的增加使得物料在反应器内停留时间缩短,使得物料加热效果变差,然而增加流速有助于改善反应器内双层物料的加热效果差异性。
| [1] |
吴雁泽, 金光远, 邹鹏程, 等. 基于响应面法对一种连续型矩形微波反应器加热效果的模拟优化[J]. 化学工业与工程, 2021, 38(4): 84-94. WU Yanze, JIN Guangyuan, ZOU Pengcheng, et al. Simulation and optimization of heating effect of a continuous rectangular microwave reactor by response surface method[J]. Chemical Industry and Engineering, 2021, 38(4): 84-94. (in Chinese) |
| [2] |
侯影飞, 游海鹏, 齐升东, 等. 微波反应器加热效率及均匀性仿真优化[J]. 化学工程, 2018, 46(6): 21-25. HOU Yingfei, YOU Haipeng, QI Shengdong, et al. Simulation and optimization of heating efficiency and uniformity on microwave reactor[J]. Chemical Engineering, 2018, 46(6): 21-25. DOI:10.3969/j.issn.1005-9954.2018.06.005 (in Chinese) |
| [3] |
KANT B S, KANT B R, JEON J M, et al. An overview on advancements in biobased transesterification methods for biodiesel production: Oil resources, extraction, biocatalysts, and process intensification technologies[J]. Fuel, 2021, 285: 119117. DOI:10.1016/j.fuel.2020.119117 |
| [4] |
YE J, XIA Y, YI Q, et al. Multiphysics modeling of microwave heating of solid samples in rotary lifting motion in a rectangular multi-mode cavity[J]. Innovative Food Science & Emerging Technologies, 2021, 73: 102767. |
| [5] |
王楠楠, 郑彤, 姜继平, 等. 一种应用于有机废水处理的微波强化管式系统: 基于COMSOL Multiphysics的初步设计、优化与验证[J]. 节能, 2020, 39(8): 98-102. WANG Nannan, ZHENG Tong, JIANG Jiping, et al. A microwave enhanced tubular system for organic wastewater treatment—Preliminary design, optimization and verification based on COMSOL Multiphysics[J]. Energy Conservation, 2020, 39(8): 98-102. (in Chinese) |
| [6] |
ZHU H, HE J, HONG T, et al. A rotary radiation structure for microwave heating uniformity improvement[J]. Applied Thermal Engineering, 2018, 141: 648-658. DOI:10.1016/j.applthermaleng.2018.05.122 |
| [7] |
NIU X, LUO S, FAN L, et al. Numerical simulation on the flow and heat transfer characteristics in the one-side heating helically coiled tubes[J]. Applied Thermal Engineering, 2016, 106: 579-587. DOI:10.1016/j.applthermaleng.2016.05.167 |
| [8] |
TUTA S, PALAZOǦLU T K. Finite element modeling of continuous-flow microwave heating of fluid foods and experimental validation[J]. Journal of Food Engineering, 2017, 192: 79-92. DOI:10.1016/j.jfoodeng.2016.08.003 |
| [9] |
ZHANG Y, YANG H, YAN B, et al. Continuous flow microwave system with helical tubes for liquid food heating[J]. Journal of Food Engineering, 2021, 294: 110409. DOI:10.1016/j.jfoodeng.2020.110409 |
| [10] |
郭帅, 朱铧丞, 黄卡玛. 一种新型连续流生物柴油微波反应器仿真与设计[J]. 太赫兹科学与电子信息学报, 2020, 18(4): 656-659. GUO Shuai, ZHU Huacheng, HUANG Kama. Simulation and design of a new continuous flow biodiesel microwave reactor[J]. Journal of Terahertz Science and Electronic Information Technology, 2020, 18(4): 656-659. (in Chinese) |
| [11] |
DEWANGAN S, KUMAR D. Numerical modeling of fluid flow and heat transfer through helical tube[J]. International Journal of Heat and Technology, 2020, 38(2): 541-552. DOI:10.18280/ijht.380232 |
| [12] |
WU Y, HONG T, TANG Z, et al. Dynamic model for a uniform microwave-assisted continuous flow process of ethyl acetate production[J]. Entropy, 2018, 20(4): 241. |
| [13] |
吴雁泽. 一种连续流微波反应器的设计与优化[D]. 江苏无锡: 江南大学, 2021 WU Yanze. Design and optimization of a continuous flow microwave reactor[D]. Jiangsu Wuxi: Jiangnan University, 2021(in Chinese) |
| [14] |
YANG H, YAN B, MENG L, et al. Mathematical modeling of continuous microwave heating of surimi paste[J]. Journal of Food Engineering, 2022, 315: 110797. DOI:10.1016/j.jfoodeng.2021.110797 |
| [15] |
LI M, WU X, HAN D, et al. A high-efficiency single-mode traveling wave reactor for continuous flow processing[J]. Processes, 2022, 10(7): 1261. DOI:10.3390/pr10071261 |
| [16] |
ZHOU J, WANG Y, YANG X. Shape optimization of microwave cavity using arbitrary Lagrangian-Euler method to improve the heating uniformity[J]. IEEE Transactions on Microwave Theory and Techniques, 2022, 70(3): 1932-1942. DOI:10.1109/TMTT.2021.3129774 |
| [17] |
TOPCAM H, ERDOGDU F. Designing system cavity geometry and optimizing process variables for continuous flow microwave processing[J]. Food and Bioproducts Processing, 2021, 127: 295-308. DOI:10.1016/j.fbp.2021.03.006 |
| [18] |
SOTO-REYES N, TEMIS-PÉREZ A L, LÓPEZ-MALO A, et al. Effects of shape and size of agar gels on heating uniformity during pulsed microwave treatment[J]. Journal of Food Science, 2015, 80(5): E1021-E1025. |
| [19] |
邹鹏程, 金光远, 崔政伟, 等. 一种具有搅拌桨的微波夹层反应釜内多物理场特性研究[J]. 化学工业与工程, 2022, 39(3): 98-106. ZOU Pengcheng, JIN Guangyuan, CUI Zhengwei, et al. Study of multi-physical field characteristics in a microwave reactor with an interlayer and a stirring blade[J]. Chemical Industry and Engineering, 2022, 39(3): 98-106. (in Chinese) |
| [20] |
TANGY A, PULIDINDI I N, PERKAS N, et al. Continuous flow through a microwave oven for the large-scale production of biodiesel from waste cooking oil[J]. Bioresource Technology, 2017, 224: 333-341. |
 2023, Vol. 40
2023, Vol. 40





