2. 北京市安全生产工程技术研究院, 北京 102617
2. Beijing Academy of Safety Engineering and Technology, Beijing 102617, China
N-甲基氧化吗啉(NMMO)是一种高级叔胺类氧化物,对纤维素有极强溶解性能且易于回收,在纺制Lyocell纤维方面具有重大用途[1-3]。作为氮氧化物,由于N O键具有强极性并且含能较高,因此NMMO具有强氧化性与热不稳定性[4]。近年来,氮氧化物造成多起事故,造成大量的人员伤亡与经济损失,例如2015年8月12日,天津市滨海新区发生危险品仓库特别重大火灾爆炸事故,硝化棉积热自燃导致硝酸铵等危化品发生爆炸,造成165人遇难、8人失踪、798人受伤[5];2017年12月9日,江苏省连云港市聚鑫生物公司二氯苯生产装置发生爆炸事故,由于氮氧化物尾气进入保温釜并与釜内物料发生化学反应,物料大量喷出,遇火源发生爆炸,造成10人死亡,1人受伤。因此,对含有氮氧键的化学物质开展热分解动力学研究,确定其危险等级对降低热分解引发的事故具有重要意义。
NMMO合成方法较多[6, 7],其中过氧化氢氧化法[8]因原料成本低、反应条件温和而被广泛应用。徐军辉等[9]利用红外光谱仪检测到过氧化氢氧化法合成的产物收率高达94%。但由于原料过氧化氢在高温、光照或碱性条件下会迅速水解并放出大量的热,具有热分解爆炸危险性[10, 11],该特性直接或间接导致了多起热分解爆炸事故。差示扫描量热仪(DSC)和绝热加速量热仪(ARC)作为主要的量热技术,主要测试分解反应的放热量并获得相关热动力学参数,进而对分解进行危险性评估[12-14]。Li等[15]利用DSC和热重(TG)研究了3, 3'-联(1, 2, 4-噁二唑)-5, 5'-二甲硝酸酯在非等温条件下的热动力学性能和热稳定性,得到其分解活化能与指前因子,并建立了动力学模型;同时使用动力学分析软件AKTS自带的Friedman模型、Flynn-Wall-Ozawa模型和ASTM E698模型获取分解反应的热力学参数,为热安全风险评估提供依据。Cong等[16]利用DSC、C600与ARC得到3-溴-1-(3,5-二氯吡啶-2-基)-4, 5-二氢-1H-吡唑-5-羧酸(BDPCA)的热分解参数,借助AKTS模拟软件得到绝热条件下最大反应速率到达时间(TMRad)为24 h时所对应的温度分别为110.2、107.3和104.9 ℃,并预测得到50 kg包装的BDPCA的自加速分解温度(SADT)分别为101和96 ℃。王建娜等[17]对O-3-氯-2-丙烯基羟胺的热危险性进行研究,DSC实验结果表明当样品质量超过1 mg时,热分解过程存在爆炸性放热,同时ARC实验表明其分解过程还会产生大量气体,有导致密闭容器超压爆炸的可能。Abrishami等[18]采用DSC和TG技术研究了BDNPF的热稳定性,并使用Flynn-Wall-Ozawa模型和ASTM E698模型求算其活化能和频率因子等动力学参数。NMMO作为一种强氧化剂,往往会在化学反应过程中大量放热,从而导致反应混合物发生爆炸、起火和完全炭化[19],但对于甲基氧化吗啉的热稳定性却鲜有研究。
本工作对NMMO的热分解动力学进行研究,首先利用DSC和ARC对NMMO进行非等温与绝热模式下的分解特性进行研究,并利用多种热动力学模型求得其反应活化能Ea、TMRad、最大反应速率到达时间为24 h所对应的温度(TD24)等参数,并对比不同加热模式对其动力学参数的影响。最后,基于风险矩阵法对NMMO热危险性进行评估。
1 实验部分 1.1 实验样品N-甲基氧化吗啉,50%(质量分数,下同),分析纯,上海阿拉丁试剂有限公司。
1.2 仪器与实验条件 1.2.1 绝热分解实验绝热加速量热仪由英国HEL公司制造,样品池材质为哈氏合金,质量为25.334 5 g,比热容为0.38 J ·g-1 ·K-1。实验温度范围为40~350 ℃,升温台阶为5 ℃,等待时间10 min,温升速率灵敏度为0.02 ℃ ·min-1,样品质量为2 g。
1.2.2 动态DSC实验实验仪器为差示扫描量热仪(DSC131Evo),法国赛特拉姆公司制造。实验过程采用氮气保护,温度范围30~350 ℃,升温速率分别为2、4、8和16 ℃ ·min-1,样品质量为2.5(±0.5) mg,坩埚为高压密闭不锈钢坩埚。
1.2.3 AKTS软件模拟分析AKTS(Advanced Kinetics and Technology Solutions)热动力学分析软件由法国Setaram公司开发,可对DSC、DTA、TGA和EGA (TG-MS、TG-FTIR)数据进行动力学分析,并且遵循国际热分析和量热联合会(ICTAC)动力学委员会关于支持动力学分析数据正确计算的基本原则的建议[20],准确获得相关热力学参数,从而开展热安全研究。将动态DSC实验数据导入至AKTS软件中,分别采用无模型Friedman法、Ozawa-Flynn-Wall法和ASTM E698计算反应活化能和指前因子并进行比对,进一步得出TMRad曲线与TD24。
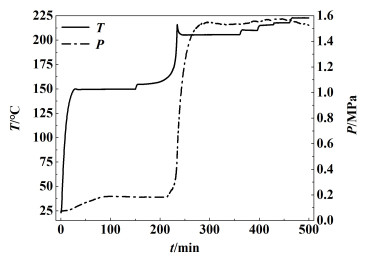
2 结果与讨论 2.1 绝热实验结果通过绝热分解实验,可以获得样品自分解过程的初始分解温度(T0)、分解终止温度(Tf)、自加热速率(βm)和绝热温升(ΔTad)。图 1为温度与压力随时间变化的曲线。
|
| 图 1 NMMO分解过程中温度、压力随时间变化曲线 Fig.1 Temperature and pressure vs. time curves in the adiabatic decomposition of NMMO |
| |
由图 1可知,经过若干次加热-等待-搜寻模式(H-W-S)后,在154.86 ℃检测到放热,同时压力与温度均由明显升高,表明NMMO在该温度下发生自分解反应,60 min左右后达到最大升温速率18.67 ℃ ·min-1,之后迅速下降,分解反应结束。具体绝热分解参数见表 1。
| 样品 | To/℃ | Tf/℃ | βm/(℃·min-1) | TMRad/min | ΔTad/℃ | ΔH/(J·g-1) |
| NMMO | 154.86 | 215.9 | 18.67 | 60.50 | 61.04 | -414.15 |
在绝热分解实验中,样品分解释放的热量会同时加热自身与样品池,被加热的样品池又会对样品进行加热从而导致分解特性参数出现误差。因此利用热惯性因子对TMRad、ΔTad等参数进行修正[12, 21]。修正公式见式(1)。
| $ \varPhi=1+\frac{M_{\mathrm{b}} C_{p, \mathrm{~b}}}{M_{\mathrm{s}} C_{p, \mathrm{~s}}} $ | (1) |
式(1)中:Mb为样品池质量,g;Cp,b为样品池比热容,J ·g-1 ·K-1;Ms为样品质量,g;Cp,s为样品比热容。
由式(1)得到热惯性因子Φ为3.43,修正后的分解特性参数见表 2。
| 样品 | Φ | βm, s/(℃·min-1) | TMRad, s/min | ΔTad, s/℃ | ΔH/(J·g-1) |
| NMMO | 3.43 | 64.03 | 17.64 | 209.37 | -1 420.53 |
利用NMMO初始分解温度、最大分解温度和最大自热速率可以对反应的活化能和指前因子进行推导。绝热条件下升温速率与温度的关系可用式(2)和(3)来描述[22, 23]。
| $ \frac{\mathrm{d} T}{\mathrm{~d} t}=A \exp \left(-\frac{E_{\mathrm{a}}}{R T}\right)\left(\frac{T_{\mathrm{f}}-T}{\Delta T_{\mathrm{ad}}}\right)^n \Delta T_{\mathrm{ad}} c_0^{n-1} $ | (2) |
| $ k=A \exp \left(\frac{E_{\mathrm{a}}}{R T}\right) c_0^{n-1}=\frac{\mathrm{d} T}{\mathrm{~d} t}\left(\frac{\Delta T_{\mathrm{ad}}}{T_{\mathrm{f}}-T}\right)^n \frac{1}{\Delta T_{\mathrm{ad}}} $ | (3) |
式(2)和(3)中:Tf为绝热分解最高温度,℃;ΔTad为绝热温升,℃;c0为样品初始浓度,mol ·L-1;A为指前因子, s-1;k为反应速率常数;Ea为反应活化能, kJ ·mol-1;R为气体常数, 8.314 J ·mol-1 ·K-1。
根据Arrhenius公式得到lnk-1000T-1曲线:
| $ \ln k=\ln \left(A c_0^{n-1}\right)-\frac{E_{\mathrm{a}}}{R T} $ | (4) |
TMRad作为热力学重要参数,被广泛应用到热危险性评估中[24, 25],如式(5)和(6)所示:
| $ \begin{gathered} \mathrm{TMR}_{\mathrm{ad}}=t_{\mathrm{m}}-t=\int\limits_t^{t_{\mathrm{m}}} \mathrm{d} t= \\ \int\limits_T^{T_{\mathrm{m}}} \frac{d T}{A \exp \left(-\frac{E_{\mathrm{a}}}{R T}\right)\left(\frac{T_{\mathrm{f}}-T}{\Delta T_{\mathrm{ad}}}\right)^n \Delta T c_0^{n-1}} \end{gathered} $ | (5) |
| $ \mathrm{TMR}_{\mathrm{ad}, \text { real }}=\frac{\mathrm{TMR}_{\mathrm{ad}}}{\varPhi} $ | (6) |
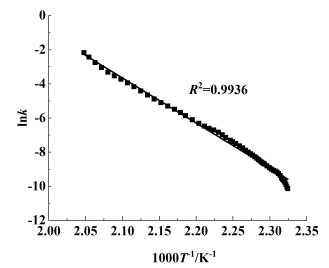
图 2为lnk与1000T-1的关系曲线,根据式(4)可以得到NMMO的反应级数为1,由图 2中的斜率与截距求得该反应的活化能与指前因子分别为219.7 kJ ·mol-1和3.25E+22(R2=0.9936)。将活化能与指前因子的数值代入式(5)和(6),得到NMMO绝热分解的TMRad曲线(图 3)以及TD24为85.5 ℃。
|
| 图 2 lnk与1000T-1关系曲线 Fig.2 lnk vs. 1000T-1 curve of NMMO |
| |

|
| 图 3 绝热条件下NMMO最大温升速率到达时间与温度关系曲线 Fig.3 TMRad vs. temperature curve of NMMO under adiabatic mode |
| |
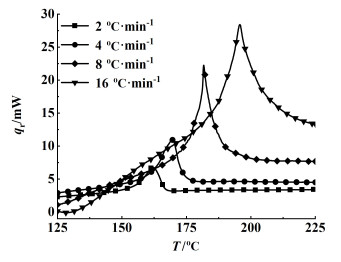
图 4为NMMO在2、4、8、16 ℃ ·min-1升温速率下的热流(qr)曲线,表 3为非等温实验下NMMO热分解参数。
|
| 图 4 不同升温速率下NMMO的DSC曲线 Fig.4 DSC curves of NMMO at different heating rates |
| |
| β/(℃·min-1) | Tonset/℃ | Tpeak/℃ | ΔH/(J·g-1) |
| 2 | 161.07 | 165.01 | -332.89 |
| 4 | 161.70 | 169.52 | -376.52 |
| 8 | 187.72 | 181.95 | -502.02 |
| 16 | 186.40 | 195.61 | -519.64 |
由图 4可知,在150~220 ℃之间存在明显的放热峰,并且随着升温速率的增加,出峰位置后移,初始分解温度升高。这是因为升温速率越快,传热时间越短,导致NMMO分解温度升高[26]。
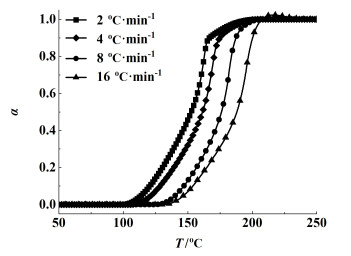
2.3 动力学分析利用AKTS软件对DSC数据进行模拟分析,得到了温度随转化率(α)变化的关系曲线,如图 5。从图 5中可以看出,在不同升温速率下,曲线具有很好的相关性。通过计算得到的相关系数R2为0.994 8,相关性较高,说明模拟结果能够准确反映实际分解过程。曲线变化趋势一致,说明升温速率对NMMO的分解影响不大。
|
| 图 5 反应进程与温度的关系曲线 Fig.5 Reaction process vs. temperature curve |
| |
Friedman法作为常用的动力学模型,在不选择机理函数的情况下可以得到动力学参数,用于初步确定活化能和指前因子。其计算公式如式(7):
| $ \ln \left(\beta \frac{\mathrm{d} \alpha}{\mathrm{d} T}\right)=\ln [A f(\alpha)]-\frac{E_{\mathrm{a}}}{R T} $ | (7) |
式(7)中:β为升温速率, ℃ ·min-1; α为转化率; T为t时刻系统温度, ℃。
由式(7)可得NMMO在4种升温速率下ln(dα/dt)和1000T-1的变化曲线,如图 6所示。将同一转化率处的点相连接,所得直线的斜率即为-Ea/R,根据斜率即可计算出该转化率下所对应的活化能,如图 7。

|
| 图 6 不同温升速率下ln(dα/dt)与1000T-1的关系 Fig.6 Relationship between ln(dα/dt) and 1000T-1 at different heating rates |
| |

|
| 图 7 NMMO活化能和线性回归相关系数随α的变化曲线 Fig.7 Ea and R2 vs. α of NMMO |
| |
由于反应初期与末期活化能受基线影响较大,因此主要关注0.1 < α < 0.9下的计算结果。该范围内活化能在81~134 kJ ·mol-1之间,相关系数R2相对接近于1 (0.987 5~0.998 7)。由于未选择机理函数,活化能波动较大,因此需要进一步对活化能进行计算。
2.3.2 Flynn-Wall-Ozawa法Flynn-Wall-Ozawa法[27]作为常用的热分析动力学方法,其优点在于当不确定反应机理函数时直接求取反应活化能,避免了因机理函数选取不当造成的误差,方程为:
| $ \lg \beta=\lg \left[\frac{A E_{\mathrm{a}}}{R G_{\mathrm{a}}}\right]-2.315-0.4567 \frac{E_{\mathrm{a}}}{R T} $ | (8) |
式(8)中G(α)为积分形势下动力学机理函数。
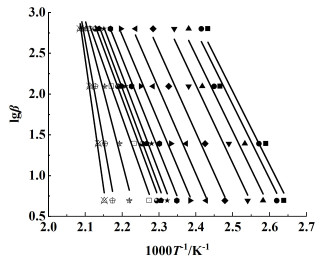
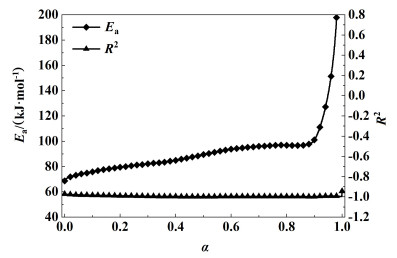
在不同升温速率下,选择相同的转化率,积分形式的机理函数G(α)都是1个恒定值,因此可以推算得到lgβ和1000T-1呈线性关系,如图 8。取不同转化率下曲线的斜率即可得到当前阶段反应活化能,如图 9。由图 9可知在0.1 < α < 0.9的范围内由Flynn-Wall-Ozawa法得到的反应活化能在75.81~100.34 kJ ·mol-1之间,R2接近于1 (0.983 4~0.996 7),变化趋势与Friedman法得到的较为一致,且波动范围更小,由于不涉及机理函数,因此所求活化能更加准确。
|
| 图 8 由Flynn-Wall-Ozawa模型得到的lgβ与1000T-1的关系曲线 Fig.8 Relationship of lgβ vs. 1000T-1 by Flynn-Wall-Ozawa method |
| |
|
| 图 9 活化能和线性回归相关系数随α的变化曲线 Fig.9 Ea and R2 vs. α of NMMO |
| |
ASTM E698法[28]是在Kissinger法的基础上得到的,假设每个单步反应的最大值(如DSC或DTG曲线上的)可以通过同样的转化速率得到,而与加热速率无关。该假定虽不能在任何情况下都成立,但造成的误差可以接受[29]。该方程为:
| $ \ln \frac{\beta}{T_{\mathrm{p}}^2}=\text { Const }-\frac{E_{\mathrm{a}}}{R T_{\mathrm{p}}} $ |
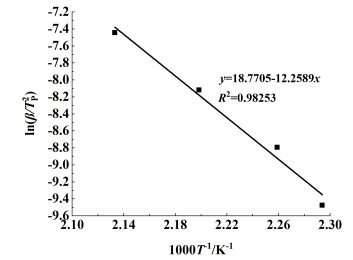
由式(9)得到ln(β/Tp2)与1000T-1的关系曲线,如图 10。经线性拟合后得到斜率为12.258 9,求得反应活化能为101.92 kJ ·mol-1,R2为0.982 5。
|
| 图 10 由ASTM E698模型得到的ln(β/Tp2)与1000T-1的关系曲线 Fig.10 Relationship of ln(β/Tp2) vs. 1000T-1 by ASTM E698 method |
| |
由Friedman法、Flynn-Wall-Ozawa法和ASTM E698法得到的反应活化能有所差异,具体数据见表 4。
| 动力学模型 | Ea/(kJ·mol-1) | R2 |
| Friedman | 81~134 | 0.987 5 |
| Flynn-Wall-Ozawa | 75.81~100.34 | 0.983 4 |
| ASTM E698 | 101.92 | 0.982 5 |
由表 4可知,Flynn-Wall-Ozawa法和ASTM E698法所求结果较为相似,由于Friedman法并未选取机理函数,造成活化能范围较大,存在一定误差。而ASTM E698法只能得到1个值,不能得到活化能随转化率变化的关系,因此在机理函数不确定的情况下,采用Flynn-Wall-Ozawa法求取活化能较为准确。
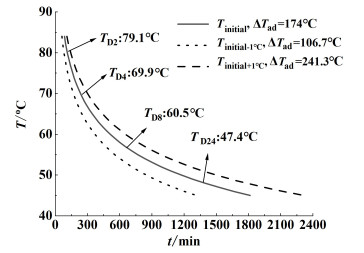
2.4 热危险性预测图 11为NMMO分解反应的TMRad曲线。由图 11可知分解反应的TD24为47.4 ℃,ΔTad为174 ℃,相较于ARC测量的结果较低,同时DSC实验获得的分解放热量ΔH也远低于绝热条件下的放热量。这是由于在绝热条件下提高了NMMO对热分解的敏感性,分解温度的提前导致了绝热条件下的放热量更高,这与Sivapirakasam等[30]的研究是相似的。ARC获得的Ea依赖于式(3)中的绝热温升速率,其随着Φ值的增加而增大[31],因此ARC计算得到的Ea比DSC所计算得到的Ea大。
|
| 图 11 绝热条件下NMMO最大温升速率到达时间与温度关系曲线 Fig.11 Curve of time to maximum rate vs. temperature of NMMO under adiabatic mode |
| |
根据AKTS与ARC实验的结果对NMMO热分解反应进行风险评估。反应失控的严重程度见表 5,反应失控的可能性见表 6,风险评估矩阵见图 12。
| 等级 | ΔTad/℃ | 失控后果 |
| 1 | ≤50且无压力影响 | 批量损失 |
| 2 | 50 < ΔTad < 200 | 工厂短期破坏 |
| 3 | 200≤ΔTad < 400 | 工厂严重损失 |
| 4 | ≥400 | 工厂毁灭性的损失 |
| 等级 | TMRad/h | 失控后果 |
| 1 | >24 | 很少发生 |
| 2 | 8~24 | 偶尔发生 |
| 3 | 1~8 | 很可能发生 |
| 4 | < 1 | 频繁发生 |

|
| 图 12 风险评价矩阵 Fig.12 The risk assessment matrix |
| |
由表 5可知,当ΔTad为174 ℃时,失控反应的严重程度为2级,后果为工厂遭到短期破坏;由绝热加速实验得到TMRad为17.64 min,小于1 h,根据表 6失控反应可归为4级,是频繁发生的事件。由风险评价矩阵得到NMMO分解反应的危险等级为Ⅲ级,属于不可接受风险,应当通过工艺优化、技术路线的改编,工程、管理上的控制措施,降低风险等级,或者采取必要的隔离方式,全面实现自动控制。具体结论见表 7。
因此在生产NMMO的过程中,应对合成工艺进行优化,实时监测记录生产过程中的工艺参数,并配置相应的自动控制系统,以保证工艺流程安全高效的运行。
3 结论(1) 利用绝热加速量热仪对NMMO进行绝热分解实验。实验结果显示NMMO分解过程中TMRad和ΔTad分别为17.64 min和209.37 ℃。由动力学模型计算得出反应活化能和指前因子分别为219.7 kJ ·mol-1和3.25E+22,TD24为85.5 ℃。
(2) 非等温DSC实验结果得到NMMO分解反应放热量平均值为432.78 J ·g-1。同时利用AKTS软件中Friedman法、Flynn-Wall-Ozawa法和ASTM E698法3种动力学模型得到的活化能分别为81~134、75.81~100.34和101.92 kJ ·mol-1,其中Flynn-Wall-Ozawa法所得结果较为准确,TD24为47.4 ℃为,ΔTad为174 ℃,均低于ARC所测结果。
(3) 根据风险矩阵法可知,NMMO分解反应失控的严重度为2级,可能性为4级,该反应风险为Ⅲ级,属于不可接受风险。在NMMO的生产、储存和运输过程中要采取相应的风险控制措施,避免因高温导致NMMO分解。
| [1] |
FINK H P, WEIGEL P, PURZ H J, et al. Structure formation of regenerated cellulose materials from NMMO-solutions[J]. Progress in Polymer Science, 2001, 26(9): 1473-1524. DOI:10.1016/S0079-6700(01)00025-9 |
| [2] |
JADHAV S, LIDHURE A, THAKRE S, et al. Modified Lyocell process to improve dissolution of cellulosic pulp and pulp blends in NMMO solvent[J]. Cellulose, 2021, 28(2): 973-990. DOI:10.1007/s10570-020-03580-1 |
| [3] |
PROTZ R, LEHMANN A, GANSTER J, et al. Solubility and spinnability of cellulose-lignin blends in aqueous NMMO[J]. Carbohydrate Polymers, 2021. DOI:10.1016/j.carbpol.2020.117027 |
| [4] |
吴翠玲, 李新平, 秦胜利, 等. 新型有机纤维素溶剂: NMMO的研究[J]. 兰州理工大学学报, 2005, 31(2): 73-76. WU Cuiling, LI Xinping, QIN Shengli, et al. Study of new organic cellulose solvent: N-methyl morpholine-N-oxide (NMMO)[J]. Journal of Lanzhou University of Technology, 2005, 31(2): 73-76. (in Chinese) |
| [5] |
周方越, 马云. 天津爆炸事故的分析、处理及启示[J]. 经贸实践, 2016(1): 329-329. ZHOU Fangyue, MA Yun. Analysis, treatment and enlightenment of Tianjin explosion accident[J]. Economic & Trade, 2016(1): 329-329. (in Chinese) |
| [6] |
CYMERMAN CRAIG J, PURUSHOTHAMAN K K. An improved preparation of tertiary amine N-oxides[J]. The Journal of Organic Chemistry, 1970, 35(5): 1721-1722. DOI:10.1021/jo00830a121 |
| [7] |
CORREA P E, HARDY G, RILEY D P. Selective autoxidation of electron-rich substrates under elevated oxygen pressures[J]. The Journal of Organic Chemistry, 1988, 53(8): 1695-1702. DOI:10.1021/jo00243a018 |
| [8] |
孟宇伯, 高殿明, 赵倩. N-甲基氧化吗啉的合成研究[J]. 精细化工, 1996, 13(3): 15-17. MENG Yubo, GAO Dianming, ZHAO Qian. The synthesis study of N-methyl morpholine oxide[J]. Fine Chemicals, 1996, 13(3): 15-17. (in Chinese) |
| [9] |
徐军辉, 刘羿君, 封云芳, 等. 氧化甲基吗啉的合成研究[J]. 浙江理工大学学报, 2008, 25(4): 402-405. XU Junhui, LIU Yinjun, FENG Yunfang, et al. The synthesis study of N-methylmorpholine-N-oxide[J]. Journal of Zhejiang Sci-Tech University, 2008, 25(4): 402-405. (in Chinese) |
| [10] |
ETO I, AKIYOSHI M, MATSUNAGA T, et al. Influenceof heavy metal ion on the thermal explosion of hydrogen peroxide[J]. Journal of Thermal Analysis and Calorimetry, 2006, 85(3): 623-627. DOI:10.1007/s10973-006-7636-9 |
| [11] |
KUMASAKI M. An explosion of a tank car carrying waste hydrogen peroxide[J]. Journal of Loss Prevention in the Process Industries, 2006, 19(4): 307-311. DOI:10.1016/j.jlp.2005.06.032 |
| [12] |
ZHANG J, MA Y, CHEN L, et al. Experimental and numerical simulation to identify the thermal hazards and hazardous scenarios of N-nitrodihydroxyethyl dinitrate[J]. Process Safety and Environmental Protection, 2021, 145: 211-221. DOI:10.1016/j.psep.2020.07.040 |
| [13] |
ZHANG Z, LIU S, ZHANG B, et al. Runaway reaction and thermal hazards simulation of 4-amino-1, 2, 4-triazole picrate by HP-DSC and ARC[J]. Journal of Thermal Analysis and Calorimetry, 2020, 139(2): 1367-1377. DOI:10.1007/s10973-019-08529-6 |
| [14] |
陈莹莹, 陈利平, 陈网桦, 等. 硝基胍溶液的热分解性能及动力学[J]. 含能材料, 2017, 25(3): 257-261. CHEN Yingying, CHEN Liping, CHEN Wanghua, et al. Thermal decomposition characteristic and kinetics of nitroguanidine solution[J]. Chinese Journal of Energetic Materials, 2017, 25(3): 257-261. (in Chinese) |
| [15] |
LI B, LUO Y, WANG H, et al. Thermal kinetic performance and thermal safety of 3, 3'-bis-oxadiazole-5, 5'-bis-methylene dinitrate[J]. Propellants, Explosives, Pyrotechnics, 2020, 45(12): 1870-1876. DOI:10.1002/prep.202000132 |
| [16] |
CONG Y, WEI Z, MA X, et al. Determination of SADT and TMRad of 3-bromo-1-(3, 5-dichloropyridin-2-yl)-4, 5-dihydro-1H-pyrazole-5-carboxylic acid: Applying thermal decomposition kinetics[J]. Results in Chemistry, 2021. DOI:10.1016/j.rechem.2021.100112 |
| [17] |
王建娜, 韩蒙蒙, 宁艳霞, 等. O-3-氯-2-丙烯基羟胺热危险性及其淬灭研究[J]. 化学工业与工程, 2022, 39(1): 27-32. WANG Jianna, HAN Mengmeng, NING Yanxia, et al. Study on thermal hazard and quenching of O-(3-chloro-2-propenyl)-hydroxylamine[J]. Chemical Industry and Engineering, 2022, 39(1): 27-32. (in Chinese) |
| [18] |
ABRISHAMI F, CHIZARI M, ZOHARI N, et al. Study on thermal stability and decomposition kinetics of bis (2, 2-dinitropropyl) fumarate (BDNPF) as a melt cast explosive by model-free methods[J]. Propellants, Explosives, Pyrotechnics, 2019, 44(11): 1446-1449. |
| [19] |
BÖHMDORFER S, HOSOYA T, RÖDER T, et al. A cautionary note on thermal runaway reactions in mixtures of 1-alkyl-3-methylimidazolium ionic liquids and N-methylmorpholine-N-oxide[J]. Cellulose, 2017, 24(5): 1927-1932. |
| [20] |
VYAZOVKIN S, BURNHAM A K, CRIADO J M, et al. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data[J]. Thermochimica Acta, 2011, 520(1/2): 1-19. |
| [21] |
CAO C, LIU S. Thermal hazard characteristic evaluation of two low-temperature-reactive azo compounds under adiabatic process conditions[J]. Process Safety and Environmental Protection, 2019, 130: 231-237. |
| [22] |
SUN D, MIAO X, XIE C, et al. Study on thermal properties and kinetics of benzoyl peroxide by ARC and C80 methods[J]. Journal of Thermal Analysis and Calorimetry, 2012, 107(3): 943-948. |
| [23] |
何志伟, 颜事龙, 刘祖亮, 等. 加速量热仪研究2, 4, 6-三氨基-3, 5-二硝基吡啶-1-氧化物的热分解[J]. 含能材料, 2015, 23(5): 415-419. HE Zhiwei, YAN Shilong, LIU Zuliang, et al. Adiabatic decomposition properties of 2, 4, 6-triamino-3, 5-dinitropyridine-1-oxide by accelerating rate calorimeter[J]. Chinese Journal of Energetic Materials, 2015, 23(5): 415-419. (in Chinese) |
| [24] |
TOWNSEND D I, TOU J. Thermal hazard evaluation by an accelerating rate calorimeter[J]. Thermochimica Acta, 1980, 37(1): 1-30. |
| [25] |
PASTRÉ J, WÖRSDÖRFER U, KELLER A, et al. Comparison of different methods for estimating TMRad from dynamic DSC measurements with ADT 24 values obtained from adiabatic Dewar experiments[J]. Journal of Loss Prevention in the Process Industries, 2000, 13(1): 7-17. |
| [26] |
MUSUC A M, BIRZAN L, CRISTEA M, et al. A DSC study of new compounds based on (E)-3-(azulen-1-yldiazenyl)-1, 2, 5-oxadiazole[J]. Journal of Thermal Analysis and Calorimetry, 2021, 146(4): 1763-1772. |
| [27] |
OZAWA T. Estimation of activation energy by isoconversion methods[J]. Thermochimica Acta, 1992, 203: 159-165. |
| [28] |
ASTM E698. Standard test method for Arrhenius kinetic constants for thermally unstable materials using differential scanning calorimetry and the Flynn/Wall/Ozawa method[M]. West Conshohocken, PA: ASTM International, 1999.
|
| [29] |
DOYLE C. Study on lifetime of energetic materials under different storage conditions[J]. J Appl Polym Sci, 1962, 6: 639-645. |
| [30] |
SIVAPIRAKASAM S P, NALLA MOHAMED M, SURIANARAYANAN M, et al. Evaluation of thermal hazards and thermo-kinetic parameters of a matchhead composition by DSC and ARC[J]. Thermochimica Acta, 2013, 557: 13-19. |
| [31] |
WU X, CHEN L, RAO G, et al. Impacts of thermal inertia factor on adiabatic decomposition of 40% mass content DCP in ethyl benzene[J]. Journal of Chemistry, 2020, 2020(2): 1-8. |
 2023, Vol. 40
2023, Vol. 40





