蛋氨酸(C5H11NO2S, CAS:59-51-8),又称甲硫氨酸,英文名称Methionine(MET),是一种重要的非极性氨基酸[1],在畜牧饲料、水产养殖、生物医药、食品工业和化妆品等多行业中有广泛的应用[2-4]。自工业化生产开始,蛋氨酸在供需端均保持高速增长,具有广阔的市场前景[5]。
工业生产中主要通过海因法合成蛋氨酸,先利用甲硫基丙醛(TMPA)与氰化钠或氢氰酸进行缩合反应得到甲硫基乙基乙内酰脲(海因),海因继续在氢氧化钠、碳酸钾等存在下水解生成相应的蛋氨酸钠/钾盐,再进一步用硫酸、盐酸、CO2等酸化反应结晶得到DL-蛋氨酸固体[6]。使用盐酸、硫酸会增加水解液中的无机盐浓度,溶液中蛋氨酸局部浓度可能过大,从而引发爆发成核、晶体聚结包裹无机盐溶液等问题[7]。在CO2酸化反应结晶工艺中,CO2可以循环利用,且酸化条件较温和,酸化结晶母液可以循环套用,因此,可以降低物料成本,工艺更为高效环保。目前CO2酸化反应结晶工艺的研究多见于专利[8-10],缺乏相关结晶动力学研究的报道。
本论文以蛋氨酸钾(METK)为原料,利用间歇动态法[11],在可视结晶器中对蛋氨酸CO2酸化反应结晶动力学进行了研究,测定了蛋氨酸在反应区间的溶解度数据,确定了成核、生长、聚结动力学模型及其动力学参数。
1 实验部分 1.1 实验试剂蛋氨酸,山东新和成氨基酸有限公司,质量分数≥99%;氢氧化钾,MACKLIN公司,质量分数≥95%;碳酸氢钾,上海展云化工有限公司,质量分数≥99.5%;二氧化碳,浙江欧特森气体有限公司,质量分数≥99.5%;氮气,林德气体(宁波)有限公司,质量分数为99.99%;去离子水,杭州娃哈哈集团有限公司。
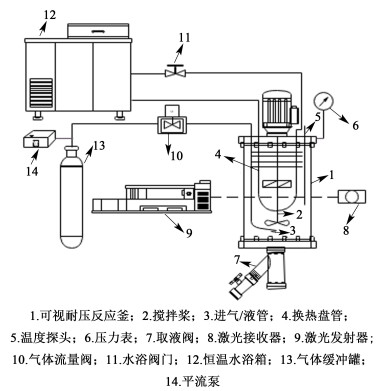
1.2 实验仪器与装置本研究所使用的主要实验仪器如表 1所示。CO2酸化间歇反应结晶制备蛋氨酸及测定该体系过程中蛋氨酸溶解度的实验装置如图 1所示,主要由结晶器、恒温装置、激光监测装置与进液/气装置组成,其中结晶器两侧为可视玻璃窗口,有效体积为3 L,配有釜内换热盘管,温度测量精度为0.1 ℃。
| 仪器名称 | 型号 | 生产厂家 |
| 可视结晶器 | WBF-3L | 威海自控反应釜有限公司 |
| 平流泵 | MP0506C | 上海三为科学仪器有限公司 |
| 激光功率计 | HNL020LB | 索雷博光电科技有限公司 |
| 加热制冷循环水浴 | CF31 | 优莱博技术(北京)有限公司 |
| 气体流量阀 | AST10-DLC | 阿斯尔特测控技术有限公司 |
| 激光粒度分析仪 | LS13320 | 美国贝克曼库尔特有限公司 |
| 元素分析仪 | Vario Micro | 德国分析元素有限公司 |
| 电子天平 | MS104TS/02 | 梅特勒托利多科技有限公司 |
| pH计 | PHSJ-4F | 上海仪电科学仪器有限公司 |
|
| 图 1 蛋氨酸CO2酸化半间歇反应结晶实验装置 Fig.1 Experimental device for semi-batch reaction crystallization of methionine under CO2 condition |
| |
本实验中,采用激光动态法[12]测定蛋氨酸钾与CO2反应结晶过程中蛋氨酸的溶解度,实验装置与图 1相似,气体缓冲罐替换为平流泵,进气口改为进液口。蛋氨酸钾由蛋氨酸与氢氧化钾1∶1物质的量之比混合反应制取[13],以不同物质的量之比碳酸氢钾与蛋氨酸钾混合溶液模拟蛋氨酸钾溶液与CO2反应过程中各阶段溶液组成。向釜内加入2 L混合
溶液与定量蛋氨酸(过量),开启水浴循环与搅拌至设定条件并维持超过3 h,用平流泵每次加入一定体积混合溶液(2~10 mL)直至激光信号强度达到最大值,记录溶液的加入体积与密度,重复3次,取平均值为实验记录值。记录加入溶液的体积与密度,重复3次,取平均值为实验记录值。蛋氨酸在混合溶液中的摩尔溶解度x1可以表示为:
| $ x_1=\frac{m_1 / M_1}{m_1 / M_1+m_2 / M_2+m_3 / M_3+m_4 / M_4} $ | (1) |
式(1)中:m1、m2、m3、m4分别表示为蛋氨酸、蛋氨酸钾、碳酸氢钾、水的质量;M1、M2、M3和M4分别表示为蛋氨酸、蛋氨酸钾、碳酸氢钾和水的摩尔质量。
1.3.2 反应结晶动力学实验在本实验中,实验装置如图 1所示,用氮气吹扫釜内排空二氧化碳后,向反应釜中加入2.5 kg浓度为1.8 mol ·kg-1的蛋氨酸钾溶液, 检查装置气密性,开启恒温循环水浴与搅拌至设定条件并维持超过1 h,以恒定速率通入CO2气体至釜底,经搅拌桨打散分散。为避免气泡对激光强度干扰,利用电导率法[14]辅助判断结晶起点并开始计时,在结晶过程中期每隔一段时间从釜底收集晶浆(10~20 mL),利用质量法[15]计算晶浆悬浮密度,并测定晶体粒度分布,改变转速、表观气速、温度条件重复实验,由式(2)计算各粒度区间晶体的粒数密度(ni):
| $ n_i=\frac{\Delta V_i M_{\mathrm{t}}}{\rho k_v \overline{L_i}^3 \Delta L_i} $ | (2) |
式(2)中:ΔVi为第i个粒度区间内晶粒所占体积分数;Mt为晶浆悬浮密度,kg ·m-3;ρ为晶体密度,kg ·m-3;kv为晶粒体积形状因子;Li为该区间粒度的平均值,m;ΔLi为该粒度区间宽度,m。蛋氨酸晶体密度为1 340 kg ·m-3,体积形状因子选取0.524[16]。
2 结果与讨论 2.1 反应过程对结晶过程的影响蛋氨酸固体在中性水溶液中以两性离子存在,解离平衡可以表示为:
| $ \begin{gathered} \mathrm{NH}_3^{+} \mathrm{CH}(\mathrm{R}) \mathrm{COOH} \stackrel{\mathrm{K}_1}{\rightleftharpoons} \mathrm{NH}_3^{+} \mathrm{C}(\mathrm{R}) \mathrm{COO}^{-}+\mathrm{H}^{+} \stackrel{\mathrm{K}_2}{\rightleftharpoons} \\ \mathrm{NH}_2 \mathrm{CH}(\mathrm{R}) \mathrm{COO}^{-}+2 \mathrm{H}^{+} \end{gathered} $ | (3) |
式(3)中:K1, K2为解离平衡常数;R指代[—CH2CH2SCH3]基团。
蛋氨酸在多种无机盐水溶液中解离常数变化规律一致,不同实验条件下的解离常数(pK2*)较接近,8.847 < pK2* < 9.369[17]。在本研究中实验条件与上述条件相似,蛋氨酸钾的pH值范围为10.729~11.065,可认为蛋氨酸钾在水溶液中完全解离为[K]+和[H2NCH(R)COO]-。
氨基酸离子、伯胺与CO2的反应机理类似[18],基于两性离子反应机理[19, 20]或三分子机理[21, 22]可以将蛋氨酸钾与CO2反应结晶归纳为以下几个过程。
CO2的吸收:
| $ \begin{gathered} \mathrm{NH}_2 \mathrm{CH}(\mathrm{R}) \mathrm{COO}^{-}+\mathrm{CO}_2 \rightleftharpoons \\ { }^{-} \mathrm{OOC}^{+} \mathrm{NH}_2 \mathrm{CH}(\mathrm{R}) \mathrm{COO}^{-} \end{gathered} $ | (4) |
| $ \begin{aligned} & { }^{-} \mathrm{OOC}^{+} \mathrm{NH}_2 \mathrm{C}(\mathrm{R}) \mathrm{COO}^{-}+\mathrm{A}_i \rightarrow \\ & { }^{-} \mathrm{OOCNH}-\mathrm{CH}(\mathrm{R}) \mathrm{COO}^{-}+\mathrm{A}_i \mathrm{H}^{+} \end{aligned} $ | (5) |
| $ \begin{gathered} ^{-}\mathrm{OOCNH}{-} \mathrm{C}(\mathrm{R}) \mathrm{COO}^{-}+\mathrm{H}_2 \mathrm{O} \rightarrow \\ \mathrm{H}_2 \mathrm{NCH}(\mathrm{R}) \mathrm{COO}^{-}+\mathrm{HCO}_3^{-} \end{gathered} $ | (6) |
蛋氨酸的生成:
| $ \begin{gathered} \mathrm{NH}_2 \mathrm{C}(\mathrm{R}) \mathrm{COO}^{-}+\mathrm{H}^{+} \rightleftharpoons \mathrm{NH}_3^{+} \mathrm{C}(\mathrm{R}) \mathrm{COO}^{-} \rightleftharpoons \\ \mathrm{NH}_2 \mathrm{C}(\mathrm{R}) \mathrm{COOH} \end{gathered} $ | (7) |
CO2的水合:
| $ \mathrm{CO}_2+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}^{+}+\mathrm{HCO}_3^{-} $ | (8) |
| $ \mathrm{HCO}_3^{-} \rightleftharpoons \mathrm{H}^{+}+\mathrm{CO}_3^{2-} $ | (9) |
水的解离:
| $ \mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}^{+}+\mathrm{OH}^{-} $ | (10) |
氨基酸钾盐对CO2的吸收能力可以用总拟一级反应速率常数(Kov)表示[13],定义为:
| $ K_{\mathrm{ov}}=K_{\mathrm{app}}+K_{\mathrm{OH}^{-}} c_{\mathrm{OH}^{-}} $ | (11) |
式(11)中:Kapp为拟一级反应速率常数;KOH-为CO2与溶液中氢氧根的反应速率常数;cOH-为溶液中OH-浓度。蛋氨酸钾、二乙醇胺(DEA)与CO2的反应机理类似,反应速率数据如表 2所示。
相比于DEA,蛋氨酸钾具有更强的CO2吸收能力,且在该条件下DEA的八田数Ha为28>3[23],可以判断反应是在液膜内进行的快速反应,为传质控制的反应结晶过程[24]。本研究中蛋氨酸钾溶液浓度远高于0.5 mol ·L-1,可推断CO2的吸收过程应同为快速反应过程。而CO2的水合过程过于缓慢[25],对结晶过程的影响可忽略不计。
基于上述推断,通过反应过程中物料衡算计算溶液浓度,根据溶液饱和浓度与悬浮密度计算得到过饱和度。
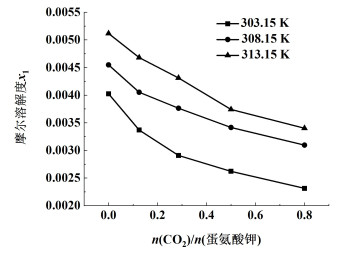
2.2 蛋氨酸在反应结晶过程中的溶解度CO2的吸收过程为快速反应,CO2消耗物质的量与碳酸氢钾生成物质的量比值近似为1,以通入二氧化碳物质的量与溶液中蛋氨酸钾物质的量比值为横坐标,在3个不同温度点,蛋氨酸在反应结晶过程中的溶解度曲线如图 2所示。
|
| 图 2 蛋氨酸在CO2酸化反应结晶过程中的溶解度 Fig.2 Solubility of methionine during reaction crystallization under CO2 acidification condition |
| |
当二氧化碳物质的量之比增加,溶液pH值也相应不断下降。在水溶液中蛋氨酸的溶解度随着溶液碱度降低而减小,溶解度变化速率随着pH值接近等电点而减慢[26]。本研究中溶解度变化规律与上述情况一致,可认为蛋氨酸溶解度受pH值影响,该变化规律可以较好地解释反应过程中过饱和度逐渐降低现象。
2.3 结晶动力学模型的建立 2.3.1 晶体成核一般认为反应结晶在初始过饱和度较高,且晶体粒度较小时,成核类型主要为初次成核[27],本研究选取结晶过程中期(1 350~6 750 s)进行研究,此时溶液过饱和度较小且晶体粒度较大,在后续搅拌的影响下,可认为二次成核作用占据主导。对CO2气液反应结晶的研究多集中在碳酸盐的结晶过程。Chen等[28, 29]研究了CO2-BaCl2-H2O体系中BaCO3的结晶过程,证明CO2进气速率影响二次成核速率,在鼓泡塔连续结晶器中得到成核动力学模型:
| $ B=K_{\mathrm{N}} Q_{\mathrm{g}}^a c_{\mathrm{g}}^b Q_{\mathrm{L}}^c c_{\mathrm{L}}^d \exp \left(-\frac{E_{\mathrm{b}}}{R T}\right) $ | (12) |
式(12)中:B为晶体成核速率;KN为二次成核速率常数;Qg为气体表观速率,m ·s-1;cg为气体浓度;QL为连续相溶液速率;cL为连续相溶液浓度;a、b、c、d为指数参数;Eb为成核活化能,kJ ·mol-1;R为理想气体常数,8.314 J ·mol-1 ·K-1;T为温度,K。
本研究为半间歇反应结晶,无连续相影响,CO2浓度固定不变,考虑反应在液膜处发生,结晶器内气含率变化会影响CO2气泡数量进而影响成核速率,式(13)为含盘管反应釜气含率ε表达式:
| $ \varepsilon=r Q_{\mathrm{g}}^e N_{\mathrm{P}}^f $ | (13) |
式(13)中:r为气含率系数;NP为搅拌转速,r ·min-1;e、f为指数参数。
结合经典二次成核经验公式[30],成核动力学模型最终表示为:
| $ B=K_{\mathrm{N}} G^{\mathrm{g}} Q_{\mathrm{g}}^a N_{\mathrm{P}}^h M_{\mathrm{t}}^l $ | (14) |
式(14)中:G为晶体生长速率;Mt为悬浮密度,kg ·m-3;g、h、l为指数参数。
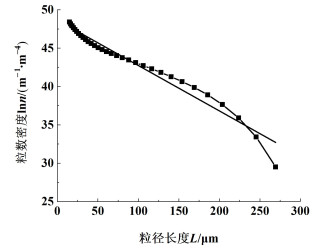
2.3.2 晶体生长根据生长速率与粒度的相关性,可以将晶体生长类型分为粒度无关生长、粒度相关生长与生长分散。图 3是反应结晶前期蛋氨酸的粒数密度分布图,在0.375~257 μm粒径范围内lnn-L具有良好的线性关系,可以认为本研究晶体生长类型为粒度无关生长,与蛋氨酸冷却结晶生长类型一致[31]。结合工业结晶一般经验方程[32],得到晶体生长动力学模型,可表示为:
| $ G=K_{\mathrm{G}} \exp \left(-\frac{E_{\mathrm{g}}}{R T}\right) \Delta C^m $ | (15) |
|
| 图 3 蛋氨酸在反应结晶初期的粒数密度分布图 Fig.3 Particle number density distribution of methionine at the initial stage of reaction crystallization |
| |
式(15)中:KG为晶体生长速率常数;Eg为晶体生长活化能,kJ ·mol-1;ΔC为过饱和度,kg ·m-3;m为指数参数。
与冷却结晶不同,随着反应结晶过程持续,初次成核与二次成核并存,在粒径较大时,线性关系出现偏差,主要原因是晶体开始出现聚结现象。
2.3.3 晶体聚结与破碎图 4为反应结晶中期(1 350 s)蛋氨酸晶体的电镜照片,可以看到晶体粒度均出现了明显的聚结现象,在动力学模型中需要考虑晶体聚结的影响,通常采用生死函数进行表征[33],表达式为:
| $ \begin{gathered} B_a(v)=\frac{1}{2} \int\limits_0^v \beta(u, v-u) n(u, t) n(v-u, t) \mathrm{d} u \\ D_a(v)=n(v, t) \int\limits_0^{\infty} \beta(u, v) n(u, t) \mathrm{d} u \end{gathered} $ | (16) |

|
| 图 4 蛋氨酸反应结晶晶体SEM图 Fig.4 SEM image of methionine crystals from reaction crystallization |
| |
式(16)中:Ba(v)、Da(v)分别表示为单位体积晶浆单位粒度范围内由于聚结作用粒径为v的粒子生成与消亡的速率,(μm3 ·m3 ·s)-1;β(x, y)为聚结核,表示粒径为x和y的粒子的聚结速率;n(x, t)为x粒径的粒子在t时刻的粒数密度,(μm3 ·m3)-1。
结合混合悬浮混合排料(MSMPR)连续结晶器聚结动力学模型[34, 35],考虑生长速率、表观气速、悬浮密度、结晶时间和搅拌速率的影响,本研究聚结动力学模型可以表示为:
| $ \beta=K_\beta G^p N_{\mathrm{P}}^w Q_{\mathrm{g}}^x M_{\mathrm{t}}^y t^z $ | (17) |
式(17)中:β为晶体聚结速率;Kβ为聚结速率常数;t为结晶时间,s;p、w、x、y、z为指数参数。
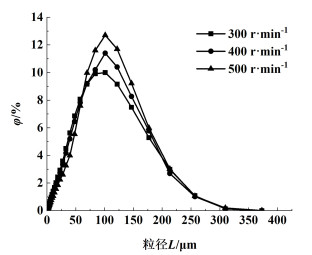
本研究考察了晶体破碎对结晶过程的影响,图 5为温度303.15 K、结晶时间1 800 s、搅拌转速分别为300、400和500 r ·min-1条件下蛋氨酸的晶体粒度分布。
|
| 图 5 不同搅拌转速对蛋氨酸晶体粒度分布的影响 Fig.5 Effects of stirring speeds on the particle size distribution of methionine |
| |
由图 5可知,搅拌转速的增加没有改变粒径的正态分布情况,粒径没有双峰出现,搅拌转速没有显著影响晶体的破碎,图 4电镜图片中聚结的晶体保持较为完整的片状结构,因此忽略晶体破碎对动力学模型的影响。
2.3.4 模型求解以粒数衡算方程为基础,假设(1)结晶器内物料均匀混合;(2)晶体粒度无关生长;(3)晶体聚结对结晶的影响不可忽略;(4)晶体在粒径L=0处开始成核;(5)忽略取样时溶液的体积变化,方程可以简化为:
| $ \frac{\partial n}{\partial t}+\frac{\partial(G n)}{\partial L}=B_a(L)-D_a(L) $ | (18) |
定义粒数密度分布关于粒度对原点的阶矩mj:
| $ m_j=\int\limits_0^{\infty} n(L, t) L^j \mathrm{~d} L(j=0, 1, 2) $ | (19) |
将式(16)代入式(18),求解式(19)各阶矩量对时间的积分,并利用矩量变换法[36]对方程两边进行处理,在取样时间间隔Δt较短的情况下,可认为阶矩与时间呈线性关系,得到如下方程组:
| $ \begin{aligned} & \frac{\Delta m_0}{\Delta t}=B-\frac{1}{2} \beta \overline{m_0^2} \\ & \frac{\Delta m_1}{\Delta t}=m_0 G \\ & \frac{\Delta m_2}{\Delta t}=2 \overline{m_1} G+\overline{m_1^2} \beta \end{aligned} $ | (20) |
式(20)中:
将不同实验条件下,各取样时刻晶体的粒数密度代入式(19)中得到对应各阶矩量mj,根据式(20)求解相应的成核速率B、生长速率G与聚结速率β。
2.4 结晶动力学参数拟合 2.4.1 结晶动力学数据动力学实验与计算结果如表 3所示。
| 温度 T/K |
结晶时间 t/s |
转速Np/(r·min-1) | 气速Qg/(m·s-1) | 过饱和度ΔC×102/(mol·L-3) | 悬浮密度Mt/(kg·m-3) | B×1011/(m-3·s-1) | G×10-10/(m-3·s-1) | β×10-19/(m-3·s-1) |
| 313.15 | 1 350 | 400 | 0.4 | 2.76 | 25.54 | 2.59 | 4.15 | 37.48 |
| 2 025 | 400 | 0.4 | 2.36 | 37.96 | 3.13 | 3.24 | 18.34 | |
| 2 700 | 400 | 0.4 | 2.04 | 50.43 | 3.43 | 2.59 | 7.88 | |
| 3 375 | 400 | 0.4 | 1.82 | 62.85 | 4.00 | 2.20 | 4.40 | |
| 308.15 | 1 350 | 400 | 0.4 | 2.88 | 24.36 | 2.84 | 3.76 | 30.60 |
| 2 025 | 400 | 0.4 | 2.49 | 36.38 | 3.47 | 3.04 | 15.87 | |
| 2 700 | 400 | 0.4 | 2.23 | 48.35 | 3.40 | 2.55 | 6.41 | |
| 3 375 | 400 | 0.4 | 2.03 | 60.20 | 4.27 | 2.17 | 3.91 | |
| 303.15 | 1 350 | 400 | 0.4 | 3.52 | 20.64 | 2.92 | 4.69 | 68.16 |
| 2 025 | 400 | 0.4 | 3.07 | 32.88 | 2.62 | 3.73 | 32.56 | |
| 2 700 | 400 | 0.4 | 2.74 | 44.85 | 3.26 | 2.96 | 19.24 | |
| 3 375 | 400 | 0.4 | 2.51 | 56.51 | 3.56 | 2.54 | 9.66 | |
| 1 800 | 400 | 0.3 | 2.98 | 20.64 | 2.11 | 3.47 | 36.04 | |
| 2 700 | 400 | 0.3 | 2.58 | 32.88 | 2.22 | 3.10 | 22.37 | |
| 3 600 | 400 | 0.3 | 2.31 | 44.85 | 2.50 | 2.40 | 6.35 | |
| 4 500 | 400 | 0.3 | 2.11 | 56.51 | 2.79 | 2.09 | 3.62 | |
| 2 700 | 400 | 0.2 | 3.66 | 21.55 | 1.69 | 4.83 | 32.06 | |
| 4 050 | 400 | 0.2 | 3.11 | 33.76 | 2.38 | 3.90 | 9.91 | |
| 5 400 | 400 | 0.2 | 2.66 | 45.59 | 2.44 | 2.75 | 6.50 | |
| 6 750 | 400 | 0.2 | 2.31 | 57.18 | 2.25 | 2.03 | 3.06 | |
| 1 800 | 300 | 0.3 | 3.54 | 20.52 | 1.44 | 4.66 | 56.21 | |
| 2 700 | 300 | 0.3 | 2.99 | 32.87 | 1.49 | 3.50 | 23.36 | |
| 3 600 | 300 | 0.3 | 2.58 | 44.85 | 2.08 | 2.74 | 11.59 | |
| 4 500 | 300 | 0.3 | 2.32 | 56.50 | 2.30 | 2.39 | 8.92 | |
| 1 800 | 500 | 0.3 | 2.64 | 21.86 | 2.32 | 3.17 | 31.57 | |
| 2 700 | 500 | 0.3 | 2.33 | 33.85 | 2.87 | 2.53 | 14.08 | |
| 3 600 | 500 | 0.3 | 2.05 | 45.65 | 3.18 | 2.00 | 8.58 | |
| 4 500 | 500 | 0.3 | 1.84 | 57.22 | 3.63 | 1.89 | 4.61 |
根据式(15)利用最小二乘法多元线性回归得到生长速率方程为:
| $ \begin{gathered} G=3.07 \times 10^{-4} \exp \left(-\frac{21006.21}{R T}\right) \Delta C^{1.52} ; \\ R^2=0.96 \end{gathered} $ | (21) |
图 6是303.15 K下过饱和度对生长速率的影响。

|
| 图 6 303.15 K过饱和度对生长速率的影响 Fig.6 Effect of supersaturation on growth rate at 303.15 K |
| |
由图 6可知,生长速率随着过饱和度的增加而增加,过饱和度相对于生长速率的指数为1.52,介于1~2之间,这说明了晶体生长同时受表面反应过程与扩散过程控制。
蛋氨酸在水溶液中冷却结晶的生长活化能为86.31 kJ ·mol-1[37],本研究中蛋氨酸反应晶体生长活化能为21.01 kJ ·mol-1。在反应结晶条件下,晶体平均粒径较小,晶体聚结与搅拌的存在,使得聚集体表面缺陷较多,晶格生长不够完整,为晶体生长提供了更多的活性位点,减少了生长阻力,从而降低了生长活化能。式(21)实验值与计算值均方差为5.89%。
2.4.3 成核速率拟合根据式(14)将成核速率与生长速率、悬浮密度、气速和搅拌速度进行关联,利用Origin软件对数据进行多元线性回归得到成核速率方程为:
| $ \begin{gathered} B=2.86 \times 10^{11} G^{0.41} M_{\mathrm{t}}^{0.64} Q_{\mathrm{g}}^{0.59} N_{\mathrm{P}}^{1.22} ; \\ R^2=0.88 \end{gathered} $ | (22) |
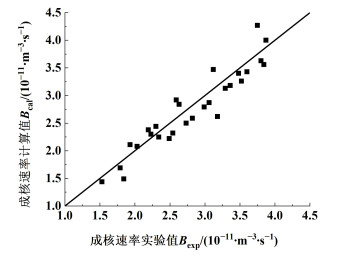
成核速率的计算值与实验值对比如图 7所示。将过饱和度与成核速率进行关联,过饱和度相对于成核速率的指数为0.62,过饱和度的增加对晶体的成核与生长都有促进作用,而生长速率增加更为迅速,在工业生产中可以适当增加过饱和度以提升晶体平均粒度,式(22)实验值与计算值均方差为8.46%。
|
| 图 7 成核速率关联对比图 Fig.7 Correlation for nucleation rate of methionine |
| |
典型二次成核速率方程中,悬浮密度关于成核速率的指数应接近于1[38],本研究中指数为0.64,说明本研究所选定的结晶时间内初次成核方式仍然存在。搅拌转速对成核速率的影响最为显著,转速增加一方面会增大结晶器中晶浆的扰动与碰撞,有利于接触成核;另一方面表观气速不变的条件下,会增加结晶器中气泡的数量,增大液膜面积,促进晶体成核。
2.4.4 聚结速率拟合根据式(17)将聚结速率、生长速率、表观气速、结晶时间、进行关联,得到聚结速率方程为:
| $ \begin{gathered} \beta=5.91 \times 10^{-11} G^{0.63} N_{\mathrm{P}}^{-0.45} Q_{\mathrm{g}}^{3.00} M_{\mathrm{t}}^{-3.48} t^{1.88} ; \\ R^2=0.92 \end{gathered} $ | (23) |
图 8是聚结速率计算模拟值与实验数据对比图,由图 8可见,在实验条件范围内,模拟值与实验数据比较一致,但式(23)实验值与计算值均方差为22.1%,与成核与生长速率方程相比,误差波动较大,误差主要集中在低聚结速率区间。

|
| 图 8 聚结速率关联对比图 Fig.8 Correlation for agglomeration rate of methionine |
| |
生长速率关于聚结速率的指数为0.63,关联后过饱和度关于聚结的系数为0.96,接近于线性关系,随着过饱和度的增大,结晶推动力增加,晶体聚结速率也有所增大。结晶时间关于聚结的系数为1.88,说明随着结晶时间的继续,晶体碰撞几率增加,有更多的小晶体黏结在大晶体表面,从而形成更多的生长中心,晶体的聚结因此程度增加。气速的增加会增加晶浆中的液膜面积,初级成核更为剧烈,聚结也更容易形成。搅拌转速、悬浮密度关于聚结是负指数关系,原因可能是二者的增加提高了晶浆中晶粒的碰撞几率与碰撞强度,在快速搅拌和高悬浮密度条件下反而不利于聚结的生成。在结晶反应后期,高悬浮密度的出现伴随着结晶器中CO2分压不断上升,这说明了CO2吸收反应速率不断下降,过高的悬浮的密度阻碍了气液接触,结晶推动力下降,对晶体的生长与聚结都产生了不利影响,在工业生产中应尽量避免。
3 结论在蛋氨酸CO2酸化半间歇反应结晶过程中,初次成核与二次成核方式同时存在,结晶的生长类型为粒度无关生长,晶体的聚结对晶体粒度分布具有一定影响。
利用间歇动态法与矩量变换法得到各结晶时刻的成核、生长与聚结速率,利用最小二乘法多元线性回归得到结晶动力学方程为:
| $ \begin{gathered} G=3.07 \times 10^{-4} \exp \left(-\frac{21006.21}{R T}\right) \Delta C^{1.52} \\ B=2.86 \times 10^{11} G^{0.41} M_{\mathrm{t}}^{0.64} Q_{\mathrm{g}}^{0.59} N_{\mathrm{P}}^{1.22} \\ \beta=5.91 \times 10^{-11} G^{0.63} N_{\mathrm{P}}^{-0.45} Q_{\mathrm{g}}^{3.00} M_{\mathrm{t}}^{-3.48} t^{1.88} \end{gathered} $ |
晶体生长过程受扩散过程与表面反应过程共同控制,晶体生长活化能为21.01 kJ ·mol-1。表观气速与搅拌转速对晶体成核与聚结均有不同程度的影响,过饱和度的增加同时有利于晶体的成核与生长,高过饱和度与高转速有利于晶体成核,但不利于晶体聚结和晶体平均粒径的增加。
| [1] |
WILLKE T. Methionine production—A critical review[J]. Applied Microbiology and Biotechnology, 2014, 98(24): 9893-9914. DOI:10.1007/s00253-014-6156-y |
| [2] |
JANKOWSKI J, KUBIŃSKA M, ZDUŃCZYK Z. Nutritional and immunomodulatory function of methionine in poultry diets-a review[J]. Annals of Animal Science, 2014, 14(1): 17-32. DOI:10.2478/aoas-2013-0081 |
| [3] |
MARTÍNEZ Y, LI X, LIU G, et al. The role of methionine on metabolism, oxidative stress, and diseases[J]. Amino Acids, 2017, 49(12): 2091-2098. DOI:10.1007/s00726-017-2494-2 |
| [4] |
王欣宇, 魏月, 李宁. 蛋氨酸在畜牧业和水产养殖业的应用进展[J]. 饲料研究, 2021, 44(12): 126-129. WANG Xinyu, WEI Yue, LI Ning. Advances in application of methionine in animal husbandry and aquaculture[J]. Feed Research, 2021, 44(12): 126-129. (in Chinese) |
| [5] |
赵辰. 蛋氨酸为何能逆势上涨?[J]. 中国石油和化工, 2020(5): 26-29. ZHAO Chen. Why can methionine rise against the trend?[J]. China Petroleum and Chemical Industry, 2020(5): 26-29. (in Chinese) |
| [6] |
高文亮, 李林凤, 张静静, 等. 蛋氨酸生产工艺及核心制备技术研究进展[J]. 化工进展, 2012, 31(4): 866-872, 888. GAO Wenliang, LI Linfeng, ZHANG Jingjing, et al. Advance in production process and key manufacture technology for methionine[J]. Chemical Industry and Engineering Progress, 2012, 31(4): 866-872, 888. (in Chinese) |
| [7] |
王建华, 刘海智, 田东平. 5-(β-甲硫基乙基)海因水解制备蛋氨酸的研究[J]. 西北药学杂志, 1986, 1(2): 18-21. WANG Jianhua, LIU Haizhi, TIAN Dongping. Preparation of methionine by hydrolysis of 5-(β-methylthioethyl) hydantion[J]. Northwest Pharmaceutical Journal, 1986, 1(2): 18-21. (in Chinese) |
| [8] |
FISCHER D, STENNER P, BERNHARDT S, et al. Process for preparing methionine: US20200157045[P]. 2020-05-21
|
| [9] |
THOMA J A, GREGOIRE J H C M A. Process for the recovery of methionine and potassium bicarbonate: US4303621[P]. 1981-12-01
|
| [10] |
YOSHIKAWA M, NAKASUJI T. Method for producing methionine: US20110319659[P]. 2011-12-29
|
| [11] |
金鑫, 徐志高, 池汝安, 等. 亚磷酸钠的生产工艺及结晶动力学研究[J]. 武汉工程大学学报, 2017, 39(4): 307-312. JIN Xin, XU Zhigao, CHI Ruan, et al. Manufacturing technique and crystallization kinetics of sodium phosphite[J]. Journal of Wuhan Institute of Technology, 2017, 39(4): 307-312. (in Chinese) |
| [12] |
李群生, 冯召东, 赵宇, 等. 激光动态法测定DL-酒石酸有机溶剂中的溶解度[J]. 北京化工大学学报(自然科学版), 2012, 39(5): 6-10. LI Qunsheng, FENG Zhaodong, ZHAO Yu, et al. Measurement and correlation of the solubility of DL-tartaric acid in selected solvents using a laser monitoring technique[J]. Journal of Beijing University of Chemical Technology (Natural Science Edition), 2012, 39(5): 6-10. (in Chinese) |
| [13] |
HOLST J V, VERSTEEG G F, BRILMAN D W F, et al. Kinetic study of CO2[J]. Chemical Engineering Science, 2009, 64(1): 59-68. DOI:10.1016/j.ces.2008.09.015 |
| [14] |
梁玺, 赵改菊, 路春美, 等. 葡萄糖酸钙结晶的热力学特性[J]. 化学工程, 2021, 49(3): 22-27. LIANG Xi, ZHAO Gaiju, LU Chunmei, et al. Thermodynamic properties of calcium gluconate crystallization[J]. Chemical Engineering (China), 2021, 49(3): 22-27. (in Chinese) |
| [15] |
党乐平, 王占忠, 刘朋标, 等. 苊冷却结晶动力学的间歇动态法研究[J]. 化学工程, 2010, 38(4): 17-20. DANG Leping, WANG Zhanzhong, LIU Pengbiao, et al. Cooling crystallization kinetics of acenaphthene by using a batch dynamic method[J]. Chemical Engineering (China), 2010, 38(4): 17-20. (in Chinese) |
| [16] |
WANTHA L, FLOOD A E. Population balance modeling of the solution-mediated transformation of DL-methionine polymorphs[J]. Chemical Engineering & Technology, 2013, 36(8): 1313-1319. |
| [17] |
陈志荣, 童云, 袁慎峰, 等. 蛋氨酸在KCl溶液中的解离常数与活度系数[J]. 化工学报, 2021, 72(9): 4469-4478. CHEN Zhirong, TONG Yun, YUAN Shenfeng, et al. Dissociation constants and activity coefficients of methionine in KCl aqueous solutions[J]. CIESC Journal, 2021, 72(9): 4469-4478. (in Chinese) |
| [18] |
KUMAR P S, HOGENDOORN J A, VERSTEEG G F, et al. Kinetics of the reaction of CO2 with aqueous potassium salt of taurine and glycine[J]. AIChE Journal, 2003, 49(1): 203-213. |
| [19] |
CAPLOW M. Kinetics of carbamate formation and breakdown[J]. Journal of the American Chemical Society, 1968, 90(24): 6795-6803. |
| [20] |
DANCKWERTS P V. The reaction of CO2 with ethanolamines[J]. Chemical Engineering Science, 1979, 34(4): 443-446. |
| [21] |
CROOKS J E, DONNELLAN J P. Kinetics and mechanism of the reaction between carbon dioxide and amines in aqueous solution[J]. Journal of the Chemical Society, Perkin Transactions 2, 1989(4): 331. |
| [22] |
DA SILVA E F, SVENDSEN H F. Ab initio study of the reaction of carbamate formation from CO2 and alkanolamines[J]. Industrial & Engineering Chemistry Research, 2004, 43(13): 3413-3418. |
| [23] |
BLAUWHOFF P M M, VERSTEEG G F, VAN SWAAIJ W P M. A study on the reaction between CO2 and alkanolamines in aqueous solutions[J]. Chemical Engineering Science, 1983, 38(9): 1411-1429. |
| [24] |
KALE C, GÓRAK A, SCHOENMAKERS H. Modelling of the reactive absorption of CO2 using mono-ethanolamine[J]. International Journal of Greenhouse Gas Control, 2013, 17: 294-308. |
| [25] |
沈丽. 新型相变吸收剂AEP/正丙醇水溶液捕集二氧化碳传质—反应动力学[D]. 杭州: 浙江大学, 2021 SHEN Li. Kinetics of mass transfer with chemical reaction of CO2 capture into novel AEP/1-propanol/H2O biphasic solvent[D]. Hangzhou: Zhejiang University, 2021 (in Chinese) |
| [26] |
CHEN Z, ZHOU R, YIN H, et al. Determination and correlation of temperature and pH value dependent solubility of dl-methionine[J]. AIChE Journal, 2020. DOI:10.1002/aic.16270 |
| [27] |
陆杰, 王静康. 反应结晶过程研究(Ⅱ): 二次过程及机理分析[J]. 化学工业与工程, 1999, 16(1): 58-61, 66. LU Jie, WANG Jingkang. Study on reaction crystallization(Ⅱ)—Secondary process and mechanism[J]. Chemical Industry and Engineering, 1999, 16(1): 58-61, 66. (in Chinese) |
| [28] |
CHEN P, CHEN C, FUN M, et al. Mixing and crystallization kinetics in gas-liquid reactive crystallization[J]. Chemical Engineering & Technology, 2004, 27(5): 519-528. |
| [29] |
CHEN P, SHI W, DU R, et al. Crystallization kinetics of Barium carbonate crystals in a lab-scale bubble-column scrubber[J]. Journal of the Taiwan Institute of Chemical Engineers, 2014, 45(5): 2418-2426. |
| [30] |
VAN DER HEIJDEN A E D M, VAN DER EERDEN J P, VAN ROSMALEN G M. The secondary nucleation rate: A physical model[J]. Chemical Engineering Science, 1994, 49(18): 3103-3113. |
| [31] |
WANTHA L, FLOOD A E. Crystal growth rates and secondary nucleation threshold for γ-DL-methionine in aqueous solution[J]. Journal of Crystal Growth, 2011, 318(1): 117-121. |
| [32] |
MULLIN J W. Crystallization[M]. London: Butterworths, 1961.
|
| [33] |
陆杰, 王静康. 普鲁卡因青霉素的结晶动力学[J]. 高校化学工程学报, 1999, 13(5): 403-407. LU Jie, WANG Jingkang. Crystallization kinetics of procaine benzylpenicillium[J]. Journal of Chemical Engineering of Chinese Universities, 1999, 13(5): 403-407. (in Chinese) |
| [34] |
GARSIDE J, SHAH M B. Crystallization kinetics from MSMPR crystallizers[J]. Industrial & Engineering Chemistry Process Design and Development, 1980, 19(4): 509-514. |
| [35] |
TAVARE N S, PATWARDHAN V. Agglomeration in a continuous MSMPR crystallizer[J]. AIChE Journal, 1992, 38(3): 377-384. |
| [36] |
HULBURT H M, KATZ S. Some problems in particle technology[J]. Chemical Engineering Science, 1964, 19(8): 555-574. |
| [37] |
周容帆. 蛋氨酸结晶过程研究[D]. 杭州: 浙江大学, 2021 ZHOU Rongfan. Crystallization process of D, L-methionine[D]. Hangzhou: Zhejiang University, 2021 (in Chinese) |
| [38] |
WANG D, LI Z. Gas-liquid reactive crystallization kinetics of hydromagnesite in the MgCl2-CO2-NH3-H2O system: Its potential in CO2 sequestration[J]. Industrial & Engineering Chemistry Research, 2012, 51(50): 16299-16310. |
 2023, Vol. 40
2023, Vol. 40





