蒸汽在过冷液体喷雾上直接接触冷凝传热是指,在传热空间内液体以一定流动形式喷洒至饱和汽相中(如图 1所示),汽相与液相直接接触换热,使汽相部分或完全冷凝的过程。该传热过程不需管壁或填料等设备构件为流体的流动和换热提供界面,与传统热交换装置相比,其主要优点是设备结构简单、没有设备污垢问题、压降极小、换热界面面积大、冷热流股间的最小换热温差不受限制[1, 2]等。汽相与液相直接接触换热过程传热效率高,在现代工业中具有广阔应用前景,倍受研究领域和工业界的关注,已在闪蒸、脱气、真空冷却和核反应堆冷却等工业过程中应用[3-8]。

|
| 图 1 饱和蒸汽空间内的过冷液体喷雾 Fig.1 Subcooled liquid spray in saturated vapor space |
| |
虽然蒸汽-过冷液体的直接接触换热过程已有一些领域的工业应用,但由于该冷凝换热过程受到液体分散相流动形式、液膜/液滴分布、液相组成变化等因素的影响,传热过程机制十分复杂,尚未形成系统的理论方法,过程和设备的设计仍基于经验。
蒸汽-过冷液体的直接接触冷凝一般通过压力旋流式喷嘴将产生的过冷液体喷雾[9]喷射至饱和蒸汽空间中实现。过冷液体经由压力旋流式喷嘴后获得轴向、径向和切向的速度,形成空心圆锥状液膜,在不稳定力的影响下破碎为带状,最后成为液滴[10]。已经有实验和理论分析研究了液膜区和液滴区的流体力学特性和传热机理。Lekic等[11],Sundararayan等[12, 13]以及Chung等[14]研究了蒸汽在单个运动液滴上的冷凝。Lee等[15]对喷雾液膜的形成进行了研究。Hasson等[16]通过理论分析研究了蒸汽与液膜直接接触冷凝的传热行为。Weinberg[17]通过实验和理论分析研究了液膜和液滴2个区域的传热行为,指出液膜区的温升较快,大多数的传热都发生在液膜区,液膜区的换热能力远大于液滴区。Mayinger等[18]利用脉冲全息技术实验揭示了液膜和液滴区域的传热行为,指出传热系数随液相质量流量的增大而增大,在一定压力范围内传热系数随蒸汽压力的增大而增大,超过此范围后传热系数反而有所下降,最终给出了液膜区的局部传热系数在19~256 kW ·(m2 ·K)-1,液滴区局部传热系数在5~325 kW ·(m2 ·K)-1,并认为液膜区和液滴区的换热能力相当。Celata等[19]通过实验和理论分析针对饱和蒸汽在过冷水喷雾上的直接接触冷凝,研究了水和蒸汽的温度、喷嘴的直径和长度对传热的影响,在假设液体喷雾径向无速度梯度条件下,基于轴向热传导提出了传热系数与轴向距离的关联式。Takahashi等[20]对蒸汽在过冷水喷雾上直接接触冷凝传热进行了实验研究。通过对液膜温度的测量,指出液膜区的换热量远大于液滴区的换热量,计算得到液膜区的局部传热系数为200~2 000 kW ·(m2 ·K)-1,液滴区的局部传热系数为20~150 kW ·(m2 ·K)-1,并且传热系数沿流动方向递减。
尽管上述研究已取得了一定进展,但对喷雾轴向、径向温度分布及液膜局部传热系数的研究还不充分,对于液膜区和液滴区哪一个承担主要的换热作用这一点,不同研究给出了不同的结论,由此可见喷雾冷凝传热的规律尚未明确,为了得到更加可信的实验数据和了解蒸汽喷雾相界面的传热现象,有必要对直接接触冷凝进行进一步的研究。本工作通过实验的方法研究过冷液体喷雾与蒸汽直接接触冷凝的传热规律,考察流场分布和形态变化与传热匹配的规律,研究液相初始温度等条件变化对液膜温度分布以及局部传热系数的影响,获得换热过程的总换热系数,从而对汽液直接接触冷凝传热设备的工程化设计和优化改造提供理论指导。
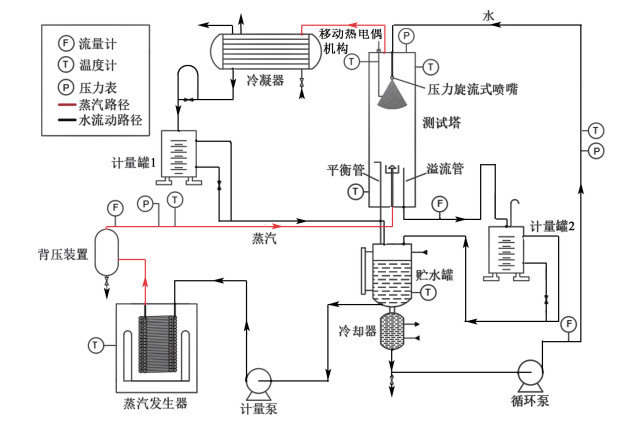
1 实验研究 1.1 实验装置及流程图 2是实验装置示意图。实验采用的工质为水。实验装置包括测试塔、水循环回路和蒸汽供应系统。测试塔尺寸为DN300 mm×700 mm,材质为玻璃,塔的外表面覆盖保温材料。塔内的平衡管用于平衡整个装置和测试塔的压力,并使测试塔保持在101.3 kPa。压力旋流式喷嘴(Spraying Systems Co.,型号:B1/4GG-SS3030HC)安装在测试塔的顶部,过冷水经过喷嘴在测试塔中形成空心锥膜状喷雾。喷嘴的结构如图 3所示,喷嘴入口段的内径6.80 mm,扩张段出口的内径5.16 mm,喷嘴总长度20.96 mm。
|
| 图 2 实验装置示意图 Fig.2 Schematic diagram of experimental device |
| |

|
| 图 3 压力旋流式喷嘴 Fig.3 Hollow-cone pressure-swirl nozzle |
| |
水从测试塔下面的贮水罐经过冷却器、流量计以规定的温度和流量从顶部进入测试塔内,通过压力旋流式喷嘴形成空心锥状喷雾,与在该喷雾上冷凝的蒸汽经溢流口流至计量罐2,最后流入贮水罐。蒸汽是由水从贮水罐经计量泵进入蒸汽发生器产生,经背压装置、涡街流量计后由塔底进入测试塔与过冷水喷雾逆流接触换热。未冷凝的蒸汽从测试塔塔顶流出经冷凝器冷凝后进入计量罐1回到贮水罐。
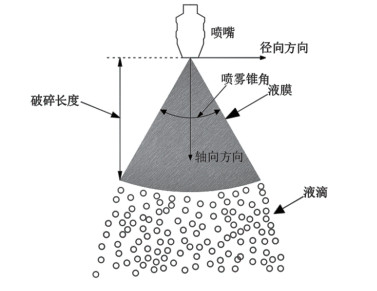
1.2 实验内容蒸汽-过冷水直接接触冷凝过程在具有保温的玻璃圆柱形测试塔内进行。实验过程中过冷水经喷嘴内部的螺旋流道,沿切线方向进入旋流室,经过收缩段和扩张段流出喷嘴,由于具有切向、径向和轴向的动量,液体在喷嘴出口处形成空心圆锥状液膜,经过一段距离后,在不稳定力的作用下,液膜断裂成带状,最后破碎成液滴。图 4是喷雾从压力旋流式喷嘴喷出后的形态示意图,喷雾离开喷嘴后的流动可以粗略地分为液膜区和液滴区2个区域。从实验中观察可以发现当液膜破碎时受到重力影响呈现近乎垂直状态的下落现象,与锥形的空心锥状液膜形成转折,该转折处即为液膜破碎点,破碎位置上方为液膜区,下方即为液滴区。本实验主要研究液膜区的换热情况,主要考察液膜轴向及径向方向上的温度分布。
|
| 图 4 喷雾示意图 Fig.4 Hollow-cone spray |
| |
液膜温度由k型铠装热电偶(WRNK-161 φ1×100~1 500)测量,精度1级,如图 5所示,热电偶连接1个可以在垂直方向移动、水平旋转的测温机构,测温机构由步进电机控制,在水平方向上移动1步相当于旋转0.018°,垂直方向上移动1步的距离为0.002 mm,由此可实现测量液膜轴向及径向方向上的温度分布。

|
| 图 5 移动热电偶测温示意图 Fig.5 Schematic diagram of temperature measurement with mobile thermocouple |
| |
设喷嘴出口处为轴向和径向的原点,方向如图 4所示,此处轴向距离为0 mm,实验选取轴向距离5、10、15、20、25和30 mm轴向位置测量液膜沿径向方向温度的变化。不同轴向位置的液膜温度由可移动测温机构完成,以测量轴向距离5 mm位置处的液膜径向方向温度分布为例,测温机构从喷嘴出口位置,沿轴向方向向下移动2 500步到达轴向距离5 mm位置,测温装置水平旋转至接近液膜处,每旋转一定角度记录1个温度,记录测温探头从开始进入液膜至离开液膜的各点温度。
2 实验结果与讨论本实验考察液相入口温度分别为76.5和84.0 ℃条件下液膜温度分布及液膜局部传热系数的变化规律。实验中液相质量流率0.061 0 kg ·s-1,测试塔内蒸汽温度100 ℃,塔内压力为常压。需要说明的是,由于液膜的不稳定性(如图 1所示),在蒸汽和液体相界面,热电偶有时会接触到蒸汽,此时会输出蒸汽温度信号。同样,在液滴区域(轴向位置35 mm附近及以下的区域),由于液滴流动是不连续的,热电偶的输出温度既包含蒸汽温度也包含液滴温度。因此,为了确定任一位置处的液膜或液滴温度,需要把蒸汽温度从热电偶的输出信号中去掉,并且由于液体会在热电偶装置上迸溅,可能会影响温度测量信号,因此对温度取时间平均值作为测定温度。
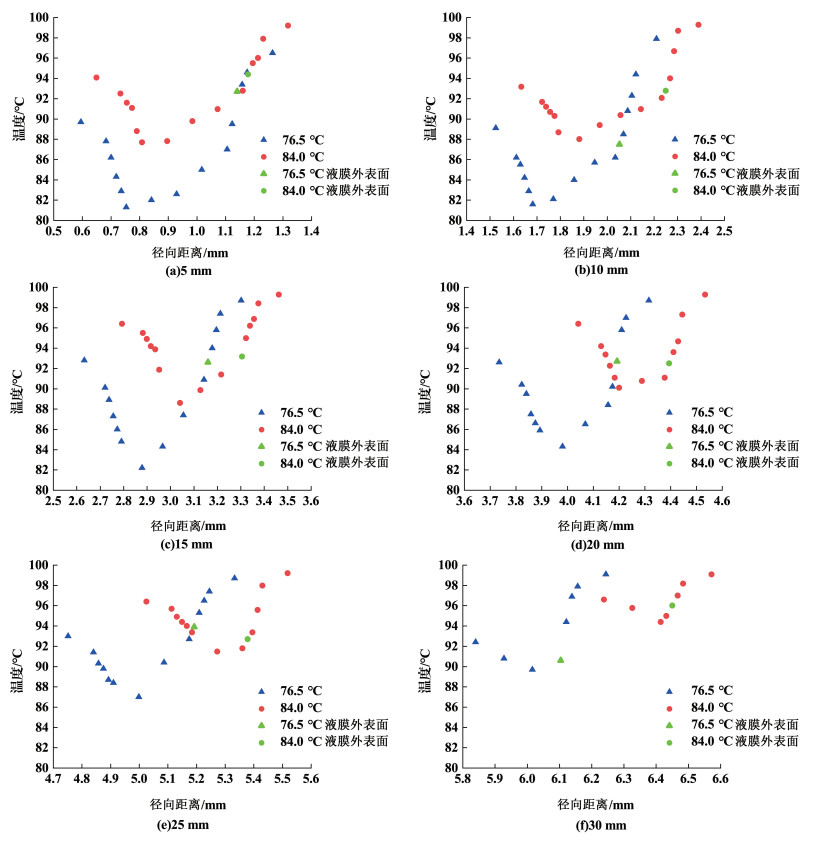
2.1 不同轴向距离液膜径向方向温度分布图 6是入口液相温度在76.5和84.0 ℃时,轴向距离5、10、15、20、25和30 mm处液膜区域径向方向温度分布。从图 6中可以看出在任一轴向位置处液膜的径向温度分布趋势相似,都呈现两侧高、中间低的趋势,液膜中存在1个最低温度,从液膜的外侧到液膜中心的温度逐渐减小,从液膜中心到液膜内侧的温度逐渐升高,这是由于液膜内外两侧表面都与蒸汽接触进行了换热。以轴向距离15 mm处液膜温度分布[图 6(c) 76.5 ℃条件下]测定结果为例说明温度变化过程,测温装置的热电偶从液膜外侧某一空间位置(图 6中径向距离3.301 mm)向液膜外侧表面移动并开始计量温度变化,在接触液膜表面(图 6中径向距离3.160 mm)之前,温度由98.7 ℃降低至92.6 ℃,这是由于蒸汽与液膜存在温差使蒸汽侧形成温度梯度边界层造成的。在径向距离3.160 mm处,热电偶开始接触液膜外表面,随着热电偶从液膜外表面移动到近似液膜中心(图 6中径向距离2.879 mm),温度从92.6 ℃下降到82.2 ℃,随着热电偶继续移动到液膜内侧已被划破的位置(图 6中径向距离2.632 mm),温度由82.2 ℃上升至92.8 ℃。液膜的表面由于与蒸汽直接接触温度最高,而蒸汽在液膜表面冷凝时释放的冷凝潜热须经过液膜热传导才能到达液膜中心,此时从液膜表面到液膜中心的这段液膜成为换热的主要热阻,因此从液膜中心到液膜的内外表面都有一定的温度梯度。
|
| 图 6 轴向位置的径向温度分布 Fig.6 Radial temperature profile at axial distance |
| |
由实验结果还发现,相比于入口液相温度76.5 ℃的条件,在入口液相温度84.0 ℃下,同一轴向位置液膜内部径向方向上的各点温度更高,但液膜中心最低温度与入口液相温度的差较小。还是以轴向距离15 mm处液膜温度分布[图 6 (c)]测定结果为例,入口液相温度76.5 ℃时液膜中心的最低温度为82.2 ℃,与入口温度相差5.7 ℃;而入口液相温度84.0 ℃时液膜中心的最低温度为88.6 ℃,与入口温度相差4.6 ℃。这是因为入口温度的高低已经决定了温度整体的大小趋势,因此高入口液相温度下液膜中心的最低温度也较高。但是低入口液相温度时的传热推动力更大,液膜温升会更高。
此外,图 6中可以看出2种入口液相温度下液膜能够达到最远的径向距离不同。以轴向距离30 mm液膜温度分布为例[即图 6(f)],入口液相温度76.5 ℃时液膜最远能运动到径向距离6.244 mm处,而入口液相温度84.0 ℃时液膜最远能运动到径向距离6.572 mm处。这是因为84.0 ℃入口液相温度的条件下液膜的喷雾锥角比76.5 ℃时的略大一些,使得液膜能够运动到径向距离更远的位置。
在实验中容易通过观察确定热电偶接触到液膜外表面的位置,但由于液膜的遮挡,内表面的位置很难准确观察到。为确定相对准确的液膜厚度,本研究假设液膜内部径向方向上的温度分布是近似对称的,且液膜的中心的温度最低,则液膜厚度可近似为液膜外表面到液膜中心的2倍,通过记录热电偶从接触液膜外表面到获得液膜的中心最低温度的步进距离,可估算出不同轴向位置的液膜厚度。根据上述计算方式得到液膜厚度变化范围在176~774 μm。图 7是液膜厚度随轴向距离的变化规律。图 7中可以看到随着轴向距离的增大,液膜厚度逐渐减小,这是由于液膜形态是锥形的,根据能量守恒,下游的液膜需要运动到更远的径向位置,因此液膜厚度逐渐变薄。此外,当入口液相温度较低时,液膜的厚度会更大,这可能是因为较低液相温度时的气液相间温差更大,冷凝传热的推动力更强,将会有更多的气相分子进入到液相中,因此液膜厚度增大。

|
| 图 7 轴向方向上液膜厚度的变化 Fig.7 Variation of the liquid sheet thickness in the axial direction |
| |
图 8是入口液相温度76.5和84.0 ℃下,轴向距离5、10、15、20、25和30 mm及液膜破碎时液膜内径向的最低温度。从图 8中可以看出随着喷雾向下游流动,液膜内径向的最低温度逐渐升高,并接近蒸汽的温度。该温度的变化规律也能够代表液膜轴向上平均温度的变化规律。由于传热从液体离开喷嘴出口时就已经开始,随着液体沿轴向流动,换热一直在持续,并且冷凝是1个放热过程,因此液膜的温度随轴向距离的增大而升高。此外,图 8中可以发现入口液相温度较低时液膜的破碎长度更大。原因是入口液相温度较低时水的表面张力更大,更大的表面张力可以维持液膜的形态,使其更不容易破碎,因此破碎长度更大。

|
| 图 8 轴向距离上液膜最低温度的变化规律 Fig.8 Variation of the minimum temperature of the liquid sheet along the axial direction |
| |
图 9为基于液膜破碎温度的液膜温升的变化规律。基于液膜破碎温度的液膜温升定义式为式(1):
| $ \Delta T_1=\frac{T-T_{\mathrm{i}}}{T_{\mathrm{break}}-T_{\mathrm{i}}} $ | (1) |

|
| 图 9 基于液膜破碎温度的液膜温升 Fig.9 Temperature rise of liquid sheet based on breaking temperature |
| |
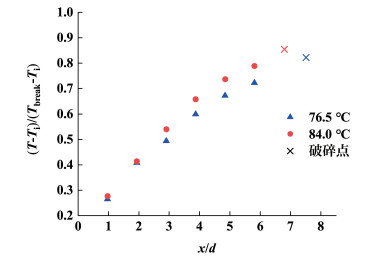
式(1)中:T为液膜在某轴向位置时的径向平均温度,Ti为入口液相温度,Tbreak为液膜发生破碎处的温度,取破碎位置附近仍为连续液相的液膜测温近似为破碎点的温度。该定义式表示了不同轴向位置处液膜的温升占液膜破碎时的温升的比率,通过测该式可以探究液膜区中的温升规律。图 9中横坐标为轴向距离与喷嘴出口直径的比值。由图 9可看到在距喷嘴出口轴向距离10 mm(即x/d=1.938)处液膜温升已占到破碎时的总温升的50%,说明喷嘴出口处的液膜换热较剧烈,在液膜区的换热中起到主要作用。此外,在图 9中能看出喷雾的上游区域温升速度较快,下游的温升速度变缓,这是因为喷雾上游距离喷嘴出口较近,液膜的湍流程度高,传热速率更高。
图 10是基于蒸汽温度的液膜温升的变化规律。基于蒸汽温度的液膜温升定义式为式(2):
| $ \Delta T_2=\frac{T-T_{\mathrm{i}}}{T_{\mathrm{sat}}-T_{\mathrm{i}}} $ | (2) |
|
| 图 10 基于蒸汽温度的液膜温升 Fig.10 Temperature rise of liquid sheet based on steam temperature |
| |
式(2)中:Tsat为蒸汽的饱和温度,该无量纲常数表示了不同轴向位置处液膜的温升占喷雾(液膜和液滴)温升的比值。从图 10中可以看出沿着轴向方向发展,液膜温升占比不断升高,到破碎时的液膜温升占喷雾换热总温升的80%~85%,说明在喷雾冷凝换热的2个区域中,液膜区的冷凝换热起到主要作用。
2.4 入口液相温度对传热系数的影响当液膜轴向上2个位置距离十分接近,假设2个位置间蒸汽冷凝引起液膜质量的变化可忽略不计,则局部平均换热系数可从2个测量位置的局部传热量和这2个位置的温差计算得到,如式(3)所示:
| $ Q=c_{\mathrm{pc}} m_{\mathrm{c}}\left(T_2-T_1\right)=h A\left(T_{\mathrm{sat}}-T_{12}\right) $ | (3) |
式(3)中:cpc为局部位置温度下的恒压比热容;mc为喷雾的质量流率;T1为位置1的平均温度;T2为位置2的平均温度;A为局部传热面积;T12为环状液膜的平均温度。如图 11所示,蓝色线框内代表计算局部传热系数的环状液膜。

|
| 图 11 局部传热系数计算示意图 Fig.11 Schematic diagram of local heat transfer coefficient calculation |
| |
由于液膜的形状为空心锥状液膜,且液膜的厚度相对于液膜的轴向和径向距离小很多,因此假设液膜内外侧表面积相等,并按锥形计算。
| $ A=2 \pi\left(r_1+r_2\right) \frac{\Delta x}{\cos (\theta / 2)} $ | (4) |
式(4)中:r1为位置1下的液膜距离中心轴的径向距离,即液膜在位置1下的半径;r2为液膜在位置2下的半径;Δx为位置1和位置2间的轴向距离;θ为喷雾锥角。图 12是计算得到的局部传热系数随轴向距离的变化情况。从图 12中可以看出不同的液相入口温度下,都呈现喷嘴出口处的局部传热系数最大,随着轴向距离的增大,局部传热系数逐渐减小的规律,这是由于喷嘴出口处的湍流程度最大,最大程度上强化了喷雾与蒸汽之间的传热,同时也说明喷嘴出口处的换热起到主要作用。此外,尽管2个温度下局部传热系数随着轴向距离的增大都有较快减小,但相比入口液相温度76.5 ℃,入口液相温度为84.0 ℃时喷嘴出口的局部传热系数较高,这是因为入口液相温度高时,液膜的表面张力小,维持液膜形态的能力更弱,使得液膜湍流程度较高,而湍流程度大小是影响传热系数的高低的重要因素。此外液膜与蒸汽的换热过程是受对流传热和热传导共同作用的,入口液相温度高水的热导率更大,有利于传热。通过曲线拟合给出了局部传热系数随轴向距离的变化关系。

|
| 图 12 入口液相温度对传热系数的影响 Fig.12 Effect of inlet liquid temperature on the heat transfer coefficient along the axial direction |
| |
当入口液相温度为76.5 ℃时,
| $ \begin{gathered} h(x)=1471.0273 \times 0.8841^x+57.7252 \\ 0 \leqslant x \leqslant 38.75 \end{gathered} $ | (5) |
当入口液相温度为84.0 ℃时,
| $ \begin{gathered} h(x)=1419.6953 \times 0.8974^x+73.8201 \\ 0 \leqslant x \leqslant 35.09 \end{gathered} $ | (6) |
式(5)和(6)中:x代表轴向距离,单位mm。拟合的决定系数R2分别为0.988 3和0.974 9 7。
本研究所获得的局部传热系数随轴向距离的变化规律与Takahashi[20]研究一致,但从所得的液膜区的传热系数大小看,本研究获取的传热系数小于Takahashi所获得的200~2 000 kW ·(m2 ·K)-1。由于实验条件、蒸汽与喷雾的流动方向不同,Takahashi实验中的蒸汽是由测试室的侧面进入的,侧面的空间较小,且蒸汽有一定的速度,在接触喷雾时可能会导致液膜的湍动程度加大,所得的传热系数值较大。
尽管目前获得了液膜局部传热系数的数值及其随轴向距离的变化规律,但是局部传热系数不能直接用于换热装置设计,而总传热系数用来描述考虑蒸汽-过冷水直接接触冷凝过程时,可更方便和直观反映传热过程的强度,是设计和衡量换热器工作效率的重要参数。
定义液膜的总传热系数为喷嘴出口位置到液膜破碎位置的传热系数。总传热系数可对局部传热系数取积分平均得到:
| $ K=\frac{1}{x_{\text {break }}-x_{0_{\operatorname{mm}}}} \int_{x_{\text {omm }}}^{x_{\text {break }}} h(x) \mathrm{d} x $ | (7) |
式(7)中:K为总传热系数;xbreak为液膜的破碎时的轴向位置;x0mm为距喷嘴出口轴向和径向距离为0的位置。最终计算得到入口液相温度76.5和84.0 ℃时的总传热系数分别为355.17和432.40 kW ·(m2 ·K)-1。相比于液相流量大小差异不大的水平管内膜状冷凝[21]的传热系数,板式塔内膜状冷凝[22]的传热系数,填料塔内膜状冷凝[23]传热系数都在100 kW ·(m2 ·K)-1以下,蒸汽与过冷水喷雾的直接接触冷凝传热有较高的传热系数,该系数在工业设备的设计中非常重要,对蒸汽-过冷液体直接接触传热设备中喷嘴的合理布置有重要意义,能够对工业设计起到一定的指导作用。
3 结论通过实验研究了饱和蒸汽与过冷水的逆流直接接触冷凝传热过程。考察了不同入口液相温度下液膜厚度及破碎长度变化;获取了常压下液膜在轴向和径向的温度分布,基于实验数据计算出了液膜局部传热系数及总传热系数。
1) 换热过程中液膜在径向方向上存在温度梯度。液膜表面温度较高,且液膜中存在最低温度,表明液膜中心两侧到液膜的表面都有1层由液膜厚度形成的热阻,使得液膜内部的温度分布呈现梯度变化。
2) 低入口液相温度时,由于气液相温差更大使得冷凝速率增大,导致液膜厚度增大。液膜厚度随着轴向距离的增大而减小。
3) 喷嘴出口处液膜温升最快,并随轴向距离的增大而减小。喷嘴出口液膜的局部传热系数最大,该系数随喷雾往下游流动逐渐减小。此外,入口液相温度较高时局部传热系数更大。实验表明在整个喷雾的冷凝传热过程中,相比于液滴区的传热,液膜区的传热起到了主要作用。
4) 通过计算获得了液膜总传热系数,蒸汽-过冷水喷雾直接接触冷凝的传热系数约为400 kW ·(m2 ·K)-1,是传统的膜状冷凝传热系数的4倍以上,体现了直接接触换热的优势。该系数可用于蒸汽-过冷水直接接触冷凝过程的评价及设计。
5) 由于实验装置容量的局限,本实验只研究了入口液相温度的影响。在改进实验装置后,后续的研究可进一步研究蒸汽的流量、温度以及入口液相的质量流量变化对传热过程的影响。从测量手段的角度出发,由于液膜的稳定性对传热过程有一定影响,可以考虑使用非侵入式设备获取液膜的温度。
| [1] |
章学来, 卢家才, 李瑞阳, 等. 直接接触式换热技术的研究进展[J]. 能源技术, 2001, 22(1): 2-6. ZHANG Xuelai, LU Jiacai, LI Ruiyang, et al. The research advancement of direct contact heat transfer technology[J]. Energy Technology, 2001, 22(1): 2-6. DOI:10.3969/j.issn.1005-7439.2001.01.002 (in Chinese) |
| [2] |
章学来, 卢家才, 李瑞阳, 等. 直接接触式换热技术的研究进展(续)[J]. 能源技术, 2001, 22(2): 53-55, 58. ZHANG Xuelai, LU Jiacai, LI Ruiyang, et al. The research advancement of direct contact heat transfer technology[J]. Energy Technology, 2001, 22(2): 53-55, 58. DOI:10.3969/j.issn.1005-7439.2001.02.003 (in Chinese) |
| [3] |
DEENDARLIANTO, HÖHNE T, LUCAS D, et al. CFD studies on the phenomena around counter-current flow limitations of gas/liquid two-phase flow in a model of a PWR hot leg[J]. Nuclear Engineering and Design, 2011, 241(12): 5138-5148. DOI:10.1016/j.nucengdes.2011.08.071 |
| [4] |
APANASEVICH P, LUCAS D, BEYER M, et al. CFD based approach for modeling direct contact condensation heat transfer in two-phase turbulent stratified flows[J]. International Journal of Thermal Sciences, 2015, 95: 123-135. DOI:10.1016/j.ijthermalsci.2014.11.015 |
| [5] |
DEENDARLIANTO, HÖHNE T, APANASEVICH P, et al. Application of a new drag coefficient model at CFD-simulations on free surface flows relevant for the nuclear reactor safety analysis[J]. Annals of Nuclear Energy, 2012, 39(1): 70-82. DOI:10.1016/j.anucene.2011.09.010 |
| [6] |
AYA I, NARIAI H. Evaluation of heat-transfer coefficient at direct-contact condensation of cold water and steam[J]. Nuclear Engineering and Design, 1991, 131(1): 17-24. DOI:10.1016/0029-5493(91)90314-8 |
| [7] |
KANG Y, KIM N J, HUR B K, et al. A numerical study on heat transfer characteristics in a spray column direct contact heat exchanger[J]. KSME International Journal, 2002, 16(3): 344-353. DOI:10.1007/BF03185232 |
| [8] |
陈建民, 杨娜, 罗铭芳, 等. 常减压装置减压深拔技术研究进展[J]. 现代化工, 2010, 30(6): 20-24. CHEN Jianmin, YANG Na, LUO Mingfang, et al. Research progress in deep-cut technology in crude oil distillation unit[J]. Modern Chemical Industry, 2010, 30(6): 20-24. (in Chinese) |
| [9] |
潘阳敏, 罗祎青, 王丽雯, 等. 压力旋流式喷嘴喷淋液膜区换热过程的数值模拟[J]. 化工学报, 2017, 68(2): 575-583. PAN Yangmin, LUO Yiqing, WANG Liwen, et al. Numerical simulations on sheet region of spray cooling process of pressure-swirl nozzle[J]. CIESC Journal, 2017, 68(2): 575-583. (in Chinese) |
| [10] |
曹建明. 液体喷雾学[M]. 北京: 北京大学出版社, 2013.
|
| [11] |
LEKIC A, FORD J D. Direct contact condensation of vapour on a spray of subcooled liquid droplets[J]. International Journal of Heat and Mass Transfer, 1980, 23(11): 1531-1537. DOI:10.1016/0017-9310(80)90156-8 |
| [12] |
SUNDARARAJAN T, AYYASWAMY P S. Heat and mass transfer associated with condensation on a moving drop: Solutions for intermediate Reynolds numbers by a boundary layer formulation[J]. Journal of Heat Transfer, 1985, 107(2): 409-416. DOI:10.1115/1.3247430 |
| [13] |
SUNDARARAJAN T, AYYASWAMY P S. Hydrodynamics and heat transfer associated with condensation on a moving drop: Solutions for intermediate Reynolds numbers[J]. Journal of Fluid Mechanics, 1984, 149(-1): 33-58. DOI:10.1017/S0022112084002524 |
| [14] |
CHUNG J N, CHANG T H. A mathematical model of condensation heat and mass transfer to a moving droplet in its own vapor[J]. Journal of Heat Transfer, 1984, 106(2): 417-424. DOI:10.1115/1.3246688 |
| [15] |
LEE S Y, TANKIN R S. Study of liquid spray (water) in a condensable environment (steam)[J]. International Journal of Heat and Mass Transfer, 1984, 27(3): 363-374. DOI:10.1016/0017-9310(84)90283-7 |
| [16] |
HASSON D, LUSS D, PECK R. Theoretical analyses of vapour condensation on laminar liquid jets[J]. International Journal of Heat and Mass Transfer, 1964, 7(9): 969-981. DOI:10.1016/0017-9310(64)90040-7 |
| [17] |
WEINBERG S. Heat transfer to low pressure sprays of water in a steam atmosphere[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Management and Engineering Manufacture, 1953, 1(1/2/3/4/5/6/7/8/9/10/11/12): 240-258. |
| [18] |
MAYINGER F, CHÁVEZ A. Measurement of direct-contact condensation of pure saturated vapour on an injection spray by applying pulsed laser holography[J]. International Journal of Heat and Mass Transfer, 1992, 35(3): 691-702. |
| [19] |
CELATA G P, CUMO M, FARELLO G E, et al. A comprehensive analysis of direct contact condensation of saturated steam on subcooled liquid jets[J]. International Journal of Heat and Mass Transfer, 1989, 32(4): 639-654. |
| [20] |
TAKAHASHI M, NAYAK A K, KITAGAWA S I, et al. Heat transfer in direct contact condensation of steam to subcooled water spray[J]. Journal of Heat Transfer, 2001, 123(4): 703-710. |
| [21] |
AKERS W W, DEANS H A, CROSSOR O K. Condensing heat transfer within horizontal tubes[J]. Chemical Engineering and Progress, 1959, 55(13): 171-176. |
| [22] |
GENIĆ S B, JAĆIMOVIĆ B M, VLADIĆ L A. Heat transfer rate of direct-contact condensation on baffle trays[J]. International Journal of Heat and Mass Transfer, 2008, 51(25/26): 5772-5776. |
| [23] |
LI X, LIU S, CUI X, et al. Experimental study of direct contact steam condensation in structured packing[J]. Asia-Pacific Journal of Chemical Engineering, 2013, 8(5): 657-664. |
 2023, Vol. 40
2023, Vol. 40





