2. 江南大学机械工程学院, 江苏 无锡 214122
2. School of Mechanical Engineering, Jiangnan University, Jiangsu Wuxi 214122, China
目前,制备生物柴油采用的反应器有釜式反应器、管式反应器、固定床反应器和环流反应器等,其中釜式反应器应用比较广泛[1]。搅拌混合是釜式反应器内实现液体混合的最常见方式,搅拌将机械能转化为动能,改变反应器内的流场和混合性能[2]。但是传统搅拌反应器的结构特点使其内部易产生稳定的流场结构,影响流体之间的混合效率[3]。
近年来,随着非线性理论的发展,国内外学者使用非定常手段破坏间歇式搅拌反应器内的稳定流场结构,使反应器内的流动变得更加复杂、无序,从而强化流体之间的混合。刘作华等[4]提出了一种长短叶片复合型的刚柔桨,发现当柔性叶片数量为3片时,柔性桨叶的形变和振动作用能破坏反应器内的对称流场结构,提高了流体混合效率。Ameur[5]研究了叶轮转向和叶轮偏心率对于三维流场和功耗的影响,发现相对于顺时针搅拌,逆时针方向可以降低功耗。此外,偏心率在容器直径的24%~48%之间时可以获得最佳混合效果。
现有的文献大多停留在间歇操作的层面上,针对连续式搅拌反应器(CSTR)内流场特性的研究较少。连续式搅拌反应器采用连续化工艺,可以提高生产过程中产物的连续性,克服传统间歇式搅拌反应器内产物品质不稳定、能耗高、难以大规模生产的弊端,有很高的实际应用价值[6, 7]。
与间歇式搅拌反应器相比,连续式搅拌反应器内的流动情况变得更为复杂[8]。Busciglio等[9]的研究发现,在连续式搅拌反应器中,搅拌转速越小,入口射流对于反应器内的流场特征影响越大,而且在较小的输入功率下,喷射射流可以大大缩短混合时间。Liu[10]进一步发展了均龄理论用来描述CSTR反应器中的空间不均匀性,量化分析了进出口位置、流量的不同对于混合效果的影响,并且定义了一种新的混合程度评价方法,能正确地反映多种情况下反应器内的短流和平推流特征。Patel等[11]采用电阻层析成像技术(ERT),测量连续式搅拌反应器中的非理想流动,探索了不同叶轮类型、进料速度、进出口位置等对反应器内混合性能的影响,发现进出口位置对于混合过程有显著影响。Rasouli等[12]针对卧式CSTR反应器进行了仿真计算,发现在卧式平推流反应器中进行径向搅拌可以有效避免反应过程中的固体颗粒沉降。
因此,本工作旨在进一步研究入口射流对于反应器性能的影响,使用计算流体力学(CFD)技术,考察非理想型连续流搅拌反应器中不同的入口射流位置、射流与搅拌之间的相对方向等因素对于反应器内的流动特性、混合特性以及停留时间分布特性的影响。研究结果可以为连续式搅拌反应器的优化设计提供参考和依据。
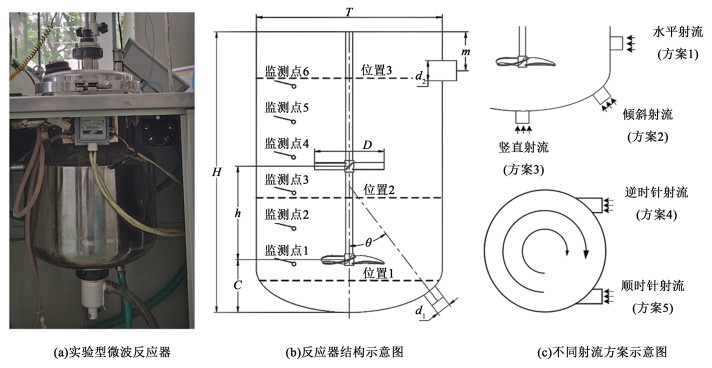
1 计算模型 1.1 连续式反应器结构计算采用的连续式反应器主体部分是1个搅拌釜,如图 1(a)和图 1(b)所示,反应器直径T为260 mm;反应器高度H为390 mm。采用Lightnin公司生产的2种轴流式叶轮作为搅拌桨,由A200型叶轮和A100型叶轮组合而成。叶轮直径D=98 mm, 下层叶轮距反应器底部高度C=60 mm,双层叶轮间距h=130 mm。底部进料口直径d1=20 mm,顶部出料口直径d2=28 mm,出料口轴心距反应器顶部的距离m=55 mm,倾斜射流时进料口轴线与搅拌桨轴线之间的夹角θ=37°。根据进料位置的不同,对比分析了5种射流方案对于反应器内流动特性及混合特性的影响,详细布置及结构参数见图 1。其中,方案1是水平射流,方案2是倾斜射流,方案3是竖直射流,方案4是逆时针射流,方案5是顺时针射流。
|
| 图 1 反应器结构和射流方案示意图 Fig.1 Schematic diagram of reactor structure and jet solution |
| |
搅拌混合液为物质的量之比为6∶1的甲醇和菜籽油混合液,经测定密度ρ=876kg·m-3,黏度μ=0.016Pa·s,反应器内射流速度为0.9~1.5m·s-1,搅拌转速为280~600r·min-1;根据雷诺数公式(1),计算最低转速(280 r·min-1)条件下雷诺数Re=2428, 大于2 000,属于湍流状态。
| $ R e=\frac{\rho N D^2}{60 \mu} $ | (1) |
本研究主要对象是连续式反应器内的流动特性和停留时间分布,需遵守流体力学物理守恒方程,即满足连续性方程和动量方程。
连续性方程:
| $ \frac{\partial \rho}{\partial t}+\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}+\frac{\partial(\rho w)}{\partial z}=0 $ | (2) |
式(2)中:u、v、w为速度矢量V在x、y、z方向的分量。
动量方程:
| $ \frac{\partial(\rho u)}{\partial t}+\nabla \cdot(\rho u \boldsymbol{V})=-\frac{\partial p}{\partial x}+\frac{\partial \tau_{x x}}{\partial x}+\frac{\partial \tau_{y x}}{\partial y}+\frac{\partial \tau_{z x}}{\partial z}+\rho f_x $ | (3) |
| $ \frac{\partial(\rho v)}{\partial t}+\nabla \cdot(\rho v \boldsymbol{V})=-\frac{\partial p}{\partial y}+\frac{\partial \tau_{x y}}{\partial x}+\frac{\partial \tau_{y y}}{\partial y}+\frac{\partial \tau_{z y}}{\partial z}+\rho f_y $ | (4) |
| $ \frac{\partial(\rho w)}{\partial t}+\nabla \cdot(\rho w \boldsymbol{V})=-\frac{\partial p}{\partial z}+\frac{\partial \tau_{x z}}{\partial x}+\frac{\partial \tau_{y z}}{\partial y}+\frac{\partial \tau_{z z}}{\partial z}+\rho f_z $ | (5) |
式(3)~式(5)中:p为流体微元上的压力;τij为j方向的黏性应力作用在垂直于i轴的平面上的分量;fx、fy和fz为单位质量体积力在x、y和z方向的分量。
由雷诺数计算结果,可以判断流体处于湍流状态,所以系统要附加湍流输运方程Standard k-ε湍流模型[13],关于湍流动能方程k和扩散方程ε分别为:
| $ \begin{gathered} \frac{\partial}{\partial t}(\rho k)+\frac{\partial}{\partial x_i}\left(\rho k u_i\right)=\frac{\partial}{\partial x_i}\left[\left(\mu+\frac{\mu_{\mathrm{t}}}{\sigma_{\mathrm{k}}}\right) \frac{\partial k}{\partial x_j}\right]+ \\ G_{\mathrm{k}}+G_{\mathrm{b}}-\rho \varepsilon-Y_{\mathrm{M}}+S_{\mathrm{k}} \end{gathered} $ | (6) |
| $ \begin{gathered} \frac{\partial}{\partial t}(\rho \varepsilon)+\frac{\partial}{\partial x_i}\left(\rho \varepsilon u_i\right)=\frac{\partial}{\partial x_j}\left[\left(\mu+\frac{\mu_{\mathrm{t}}}{\sigma_{\varepsilon}}\right) \frac{\partial \varepsilon}{\partial x_j}\right]+ \\ G_{1 \varepsilon} \frac{\varepsilon}{k}\left(G_{\mathrm{k}}+G_{3 \varepsilon} G_{\mathrm{b}}\right)-C_{2 \varepsilon} \rho \frac{\varepsilon^2}{k}+S_{\varepsilon} \end{gathered} $ | (7) |
在模拟示踪剂的扩散过程中,需要开启组分方程:
| $ \begin{gathered} \frac{\partial\left(\rho c_{\mathrm{s}}\right)}{\partial t}+\nabla\left(\rho c_{\mathrm{s}} V\right)=\frac{\partial}{\partial x}\left[D_{\mathrm{s}} \frac{\partial\left(\rho c_{\mathrm{s}}\right)}{\partial x}\right]+ \\ \frac{\partial}{\partial y}\left[D_{\mathrm{s}} \frac{\partial\left(\rho c_{\mathrm{s}}\right)}{\partial y}\right]+\frac{\partial}{\partial z}\left[D_{\mathrm{s}} \frac{\partial\left(\rho c_{\mathrm{s}}\right)}{\partial z}\right]+S_{\mathrm{s}} \end{gathered} $ | (8) |
式(8)中:cs为组分s的体积浓度,%;ρcs为组分s的质量浓度,kg·m-3;Ds为组分s的扩散系数,m2·s-1;Ss为系统内部单位时间内单位体积通过化学反应产生的组分s的质量,即生产率,kg。
2.2 边界条件运用CFD中多重参考系模型(MRF)将反应釜分为2个计算域:转子计算域与静止计算域。转子计算域包括桨和搅拌轴;静止计算域包括壁面、进料口等在内的区域,2者用交界面(interface)进行数据交换。将转子计算域设为旋转运动条件;静止计算域为静止条件;反应器入口为速度入口,出口为压力出口,搅拌桨相对于转子计算域的速度为0,为旋转无滑移壁面边界条件;其余设置为静止无滑移壁面边界条件。
2.3 计算方法因反应器内处于湍流状态,故选择标准k-ε湍流模型;考虑重力影响;速度压力耦合采用SIMPLE算法;压力离散选用Standard格式;动量离散选择二阶迎风格式,松弛因子保持不变;计算过程中,需要共同考虑残差和其他变量的变化,以避免计算结果出现伪收敛的情况,设置收敛残差为10-6,同时监测上层搅拌桨附近的流速,当残差以及搅拌桨附近速度达到收敛且稳定的情况下,认为计算收敛,获得稳态流场。
将稳态计算收敛的流场作为初始条件进行示踪剂扩散过程仿真。选择同组分的醇油混合液作为示踪剂,启动组分传输模型,激活组分扩散方程,不打开化学反应选项,确保反应器内单相多组分间只进行单纯的物料混合。在射流入口处脉冲注入示踪剂,通过控制进料时间来控制示踪剂的剂量。浓度收敛残差设定为10-6,以搅拌桨每转过1°所需时间确定初始计算时间步长为0.000 5 s,开始迭代运算。同时在反应器内创建6个不同高度处的监测点,位置如图 1(b)所示。
2.4 网格划分以及网格收敛性指数(GCI)分析在Space Claim (SCDM)中建立连续式搅拌反应器的几何模型,导入Ansys Mesh中进行网格划分。由于非结构化四面体网格在处理弯曲曲面时具有优良的适应性,因此选用非结构化四面体网格对反应釜模型进行网格划分,并对桨表面及进出口区域做加密处理。采用Roache在1977年提出的网格收敛指数[14](Grid Convergence Index, GCI)对6套网格进行网格无关性验证,以尽可能提高仿真结果的准确性[15, 16]。
在反应器内竖直方向拉1根直线,提取不同高度位置处的合速度V进行网格无关性评估,不同网格数量的计算结果如图 2(b)所示。将直线上的平均速度Vave作为关键参数,用来衡量网格计算结果的准确性。GCI的计算过程如式(9):
| $ p=\frac{\ln \left(\frac{f_3-f_2}{f_2-f_1}\right)}{\ln r} $ | (9) |

|
| 图 2 网格划分及无关性分析 Fig.2 Meshing grid and independence check |
| |
式(9)中:p是收敛阶;f1、f2和f3(f1对应最细化的网格)是仿真过程中获得的关键参数,在本研究中为平均速度Vave;r是网格细化过程中的细化率,为1.11。
网格收敛指数(GCI)的定义为:
| $ \mathrm{GCI}=F_{\mathrm{s}} \frac{\left|\varepsilon_1\right|}{r^p-1} $ | (10) |
式(10)中:Fs是安全因子,当使用2套网格来估算GCI时,Fs取值为3;当使用3套或3套以上网格来估算GCI时,Fs取值为1.25。ε1是网格收敛误差,定义[17, 18]为:
| $ \varepsilon_1=\frac{f_2-f_1}{f_1} $ | (11) |
如果计算结果在收敛的渐近范围之内,则满足:
| $ \mathrm{GCI}_{23} \approx r^p \mathrm{GCI}_{12} $ | (12) |
因此,如果满足:
| $ \frac{\mathrm{GCI}_{23}}{r^p \mathrm{GCI}_{12}} \approx 1 $ | (13) |
则认为达到网格独立[15]。
使用6套疏密程度不同的网格计算得到的平均速度Vave如图 2(b)所示。参照Rasouli等[12]的研究,选用平均速度差异最小的3套网格(269万、467万和690万)进行分析,计算过程如式(9)到式(13)所示。根据式(13)进行计算,结果如式(14):
| $ \frac{\mathrm{GCI}_{23}}{r^p \mathrm{GCI}_{12}}=1.007 \approx 1 $ | (14) |
而且467万与690万2套网格之间的平均速度误差小于1%,认为网格数量467万时计算结果已经达到网格无关。
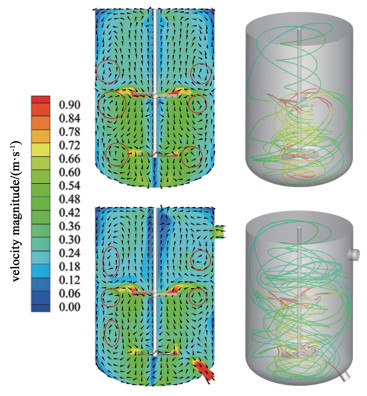
3 结果与讨论 3.1 射流结合机械搅拌对于反应器内流动特性的影响为了分析射流对具有搅拌桨的反应器内流动特性的影响,对有射流和无射流反应器内部的流场进行了对比分析,如图 3所示。
|
| 图 3 射流引入前后反应器内流场对比 Fig.3 Comparison of the flow before and after the jet is introduced |
| |
由图 3可知,连续式搅拌反应器相比于传统搅拌反应器,入口处射流使其反应器内的流体在局部径向产生了更高的速度,打破了被叶轮分为上、中、下3个循环区的流动流型,改变了关于搅拌轴的对称流动结构,反应器内对称的漩涡发生偏移,流动扩展至反应器的大部分区域,使得流动的发展更加充分,形成了射流-搅拌耦合场,这种射流与搅拌流动的强烈干涉,有利于反应器内的流体传质和混合。
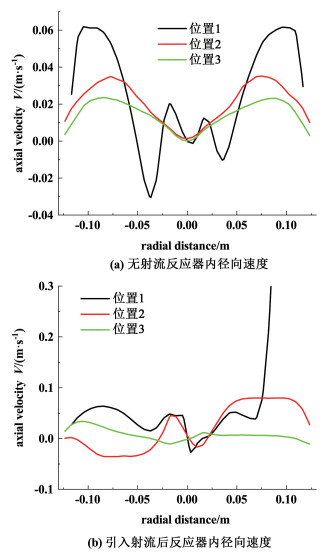
为了进一步对比分析射流的引入对于反应器内流场的影响,在反应器高度方向上0.1、0.4和0.8H(位置1~3)处取3条直线上的径向速度进行比较,3条线位置如图 1(b)所示。径向速度以指向搅拌轴为正,指向反应器壁面为负。由图 4对比引入射流前后的径向速度分布,可以发现射流破坏了反应器内的对称流型。结合图 3,可以看出射流的加入一方面直接影响射流区的流场,另一方面可以通过改变反应器内原有的循环涡流的位置影响反应器内的全局流动,以此强化反应器内的不对称性和不稳定性。
|
| 图 4 射流引入前后反应器内不同高度处径向速度对比 Fig.4 Comparison of radial velocity at different heights in the reactor before and after the jet is introduced |
| |
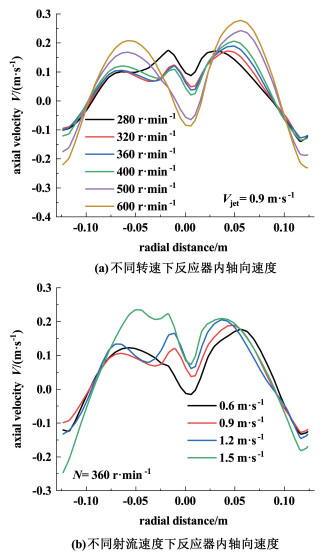
搅拌转速N和射流速度Vjet对于反应器内的流场有着重要的影响,取反应器中位置2处不同转速和射流速度下的轴向速度作对比,如图 5所示。由图 5(a)可以看出,射流速度一定时,反应器内轴向速度随着搅拌转速的提高而提高,且搅拌桨的2侧轴向速度峰值不等。当转速达到500 r·min-1时,反应器内轴向速度呈现关于搅拌桨对称的趋势,说明搅拌转速过高会导致射流的效果减弱。同时,转速过低会使得反应器内流动区域变小,不利于混合。由图 5(b)可以看出,搅拌转速一定时,射流速度提高会增大反应器内的轴向速度,但同时也会增大入口流量,降低物料在反应器中的理想停留时间。所以,综合考虑,选择转速为360 r·min-1,射流速度为0.9 m·s-1进行后续研究。
|
| 图 5 不同工况条件下反应器内的轴向速度分布 Fig.5 Axial velocity distribution in the reactor under different working conditions |
| |
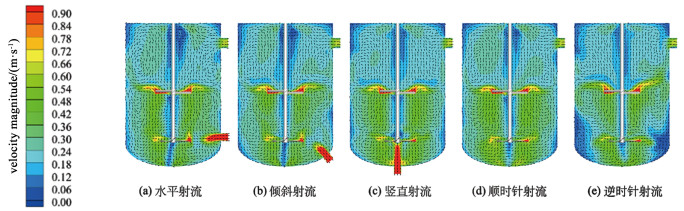
反应器轴向纵截面内的速度特征主导反应器内流特性,通过分析该截面的速度分布,以揭示不同射流角度及射流方向对流动特性的影响。图 6为不同射流方案下反应器内纵向截面内的速度矢量图,可以看出,射流的引入一定程度上破坏了原有的对称结构。在加入射流之后,在射流方向正对轴心时,发现射流角度的不同对于反应器内的流动特性有着不同的影响。当水平和倾斜射流时,由图 6(a)和6(b)可以看出,射流的液体进入反应器后在搅拌桨剪切力的作用下分成2个分流,1股分流直接汇入向上的总流,另1股流体流向反应器底部,在搅拌桨的卷吸作用下再汇入向上的总流。当采用竖直射流方案时,由图 6(c)可以看出,反应器内的对称流型几乎不变,与水平射流和倾斜射流相比,底部区域的涡心位置更低,有利于搅动底部流体。
|
| 图 6 不同射流方案时反应器内纵向截面处的速度云图和平均速度矢量图 Fig.6 Mean velocity vector plot superimposed to the velocity magnitude of different jet solutions at the vertical interface |
| |
以倾斜射流为基础,发现射流方向的不同对于反应器内的流型及速度分布影响较大。由图 6(d)可以看出,当顺时针射流时,反应器内流动发展充分,流速分布均匀,反应器底部出现了3个尺寸较小的漩涡。当逆时针射流时,由图 6(e)可以看出,反应器内速度梯度大,流体受到的剪切力大,反应器中部流动发展充分,有利于该区域进行分散和混合。而反应器底部速度相对较低,这是由于射流与原先反应器中的旋转流体撞击产生动能耗散,流速急剧降低,加剧了流体之间的相互剪切作用。
3.3 停留时间分布和混合效果反应器内的物料混合是化工行业普遍存在的操作,对于化学反应的进行有着重要的意义。对于连续式搅拌反应器,反应器内物料按照均匀的速度连续进出,如果反应器内的搅拌混合效率特别高,即原料加入反应器后瞬间与反应器内物质混合均匀达到一致,视为理想连续式反应器或者全混流反应器。对不同射流方案下反应器内的停留时间进行数值模拟,绘制停留时间分布曲线,并与理想连续式反应器进行对比。
停留时间的分布密度函数E(t)定义为:
| $ E(t)=\frac{C(t)}{\int_0^{\infty} C(t) \mathrm{d} t}=\frac{C\left(t_i\right)}{\sum_0^{\infty} C\left(t_i\right) \Delta t_i} $ | (15) |
式(15)中:C(t)为出口监测到的浓度随时间变化的函数。
平均停留时间tm表达式为:
| $ t_{\mathrm{m}}=\frac{\int_0^{\infty} t E(t) \mathrm{d} t}{\int_0^{\infty} E(t) \mathrm{d} t}=\frac{\sum_0^{\infty} t E\left(t_i\right) \Delta t_i}{\sum_0^{\infty} E\left(t_i\right) \Delta t_i} $ | (16) |
为了比较不同射流方案之间的差异,通常对停留时间进行无因次化处理,得到无因次停留时间θ和无因次停留时间分布密度函数E(θ):
| $ \theta=\frac{t}{t_{\mathrm{m}}} $ | (17) |
| $ E(\theta)=t_{\mathrm{m}} E(t) $ | (18) |
无因次停留时间方差σθ2:
| $ \sigma_\theta^2=\frac{\sigma_{\mathrm{t}}^2}{t_{\mathrm{m}}^2} $ | (19) |
| $ \sigma_{\mathrm{t}}^2=\frac{\sum_0^{\infty}\left(t-t_{\mathrm{m}}\right)^2 E\left(t_i\right) \Delta t_i}{\sum_0^{\infty} E\left(t_i\right) \Delta t_i}=\sum\limits_0^{\infty} t_i^2 E\left(t_i\right) \Delta t_i-t_{\mathrm{m}}^2 $ | (20) |
方差σθ2越大,表示对均值的离散程度越大,则分布越宽,停留时间分布的时间长短参差不齐的程度越大[19]。
从如图 7可以看出,5种射流方案的停留时间分布比较接近,E(θ)曲线出峰时间早、拖尾长,说明反应器内循环比大,物料的反混程度强。通过对比可以看出,水平、逆时针以及竖直射流时的E(θ)曲线与全混流曲线更加接近,反应器内的混合效果更好。

|
| 图 7 射流方案对于停留时间分布的影响 Fig.7 Influence of jet solutions on residence time distribution |
| |
为了比较与理想流型曲线之间的偏差程度,引入均方差MSE作为指标评价偏差程度,定义如式(21):
| $ \operatorname{MSE}=\frac{1}{n} \sum\limits_1^n\left(y_i-y_i^*\right)^2 $ | (21) |
式(21)中:yi为实际值;yi*为理想值;n为样本数量。
表 1为不同射流方案时反应器内停留时间分布的特征值及与理想流型的均方差,从表 1中可以得到与前文相似的结论。均方差(MSE)越小,则与理想流型之间的偏差越小,所以根据均方差可以看出逆时针射流时停留时间分布曲线最接近理想流型曲线,即此时反应器内的流型最接近理想连续式反应器内的流型。同时可以看出不同射流方案下反应器内的平均停留时间tm差异较小,竖直射流时反应器内的方差σθ2最大,为0.85,说明此方案时反应器内停留时间分布差异最大,其次是逆时针射流,为0.84。
| 射流方案 | tm/s | σθ2 | MSE×10-3 | 混合时间/s |
| 传统搅拌 | 11.43 | |||
| 水平射流 | 68.35 | 0.83 | 7.21 | 7.88 |
| 倾斜射流 | 69.48 | 0.78 | 9.22 | 8.92 |
| 竖直射流 | 68.37 | 0.85 | 7.08 | 8.48 |
| 逆时针射流 | 68.63 | 0.84 | 5.41 | 7.62 |
| 顺时针射流 | 68.56 | 0.77 | 11.84 | 11.80 |
综合考虑不同射流方案时的停留时间分布曲线与理想流型曲线之间的均方差、停留时间方差以及平均停留时间等因素,得出逆时针射流时混合效果最佳。
反应器内物料从开始到达到最终稳定浓度的(±5)%所需要的时间为混合时间[20],是用于衡量反应器内混合性能的重要参数,为比较最适宜射流条件下反应器内混合效率的提升情况,在注入示踪剂后,令反应器出入口处示踪剂质量浓度相等,并在反应器内不同高度处创建6个示踪剂浓度的监测点,如图 1(b)所示。表 1中可以看到不同射流方案下的混合时间。从表 1中可以看出,相较于传统的搅拌式反应器,在逆时针射流的情况下,反应器内达到混合均匀所需的时间缩短了33%,混合效率显著提升。
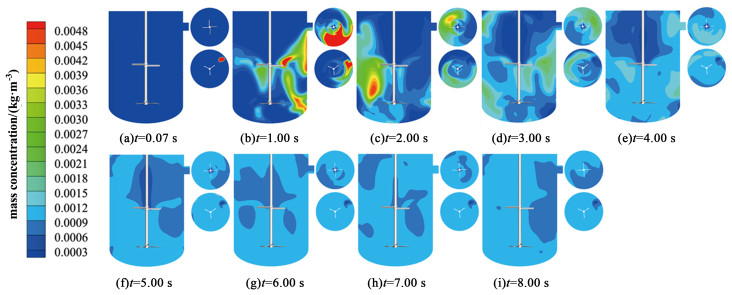
3.4 示踪剂扩散过程以及监测点处浓度响应为了便于后续对反应器的结构进行进一步改善,针对反应器内示踪剂的扩散过程进行研究,并且在反应器内不同高度处创建6个监测点,如图 1(b)所示。图 8显示了反应器内纵向平面以及2个搅拌桨所在平面上示踪剂浓度随时间变化的分布图,即示踪剂的扩散过程。选取每1 s为1个时间间隔,同时加入t=0.07 s时间点,用于展示示踪剂在混合开始之前的状态,由于篇幅限制,仅选取逆时针射流时的反应器内的扩散过程进行展示。其他射流角度及方向时反应器内的混合过程通过监测点浓度响应曲线体现。
|
| 图 8 反应器内示踪剂的扩散过程 Fig.8 The diffusion process of the tracer in the reactor |
| |
如图 8可以看出,示踪剂进入反应器后,由于射流与反应器内旋转物料发生撞击,使得示踪剂在进入反应器后1 s内便到达反应器中部,并在搅拌桨的带动下周向运动,同时出现了第1波短流。t=3 s时,反应器内各位置之间的浓度差异开始缩小,示踪剂主要分成3部分在反应器的上中下3块区域进行扩散。当反应进行到t=6 s以后,由于上层循环涡流的携带扩散,示踪剂沿着反应器壁面到达反应器顶部,并向转轴附近扩散,反应器内各处示踪剂的浓度差异逐渐变小,逐渐趋于均匀。
为了探究不同射流角度时反应器内各水平高度处的示踪剂浓度扩散响应历程,以监测点处的浓度作为纵坐标值,绘制反应器内监测点浓度的时间响应曲线,如图 9所示。由图 9可以看出,监测点的响应顺序与位置密切相关。

|
| 图 9 不同射流方案时反应器内示踪剂浓度响应曲线 Fig.9 Tracer concentration response curve at different jet solutions in reactor |
| |
根据监测点的响应顺序以及峰值出现的位置,可以看出当入射角度为水平和竖直时,示踪剂进入反应器后均是先汇入向上的总流,到达反应器中部后分成2股流动,被循环涡流夹带到达反应器的底部和顶部。由监测点的浓度峰值可以看出,倾斜和顺时针射流时,示踪剂进入反应器后主要在反应器的底部运动,在轴向的扩散效果较差,因此监测点1、2的浓度响应峰值出现早且远超均匀混合时的浓度。当逆时针射流时,各监测点浓度响应曲线形态和峰值的差异小,代表搅拌过程中示踪剂扩散过程更均衡[21],混合效率高。
4 结论为提高连续式搅拌反应器的生产效率,本研究进一步研究入口射流对于反应器性能的影响,通过数值仿真,研究了机械搅拌和射流的耦合对于反应器内流场、混合特性的影响,主要结论如下。
1) 通过对比反应器内的流场,发现射流通过直接影响射流区的流场,以及改变反应器内循环涡流的位置来间接影响全局流动;通过控制变量法对影响流场的各因素进行对比,考虑到射流效果和理想停留时间,选定工况为转速360 r·min-1、射流速度0.9 m·s-1。
2) 对不同射流方案下反应器内的流场进行分析,发现改变射流方向对于反应器内流型影响更大,逆时针射流时反应器内的速度梯度大,流体之间的剪切作用更强。
3) 利用组分扩散模型模拟了反应器内示踪剂的扩散过程,综合考虑反应器内的停留时间分布特征、监测点浓度响应特征和与理想曲线之间的均方差,得到逆时针射流时反应器内的混合性能最佳。
| [1] |
张家仁, 雪晶, 孙洪磊. 生物柴油新反应器及其应用[J]. 化工进展, 2015, 34(4): 911-920. ZHANG Jiaren, XUE Jing, SUN Honglei. Novel biodiesel reactor and its application[J]. Chemical Industry and Engineering Progress, 2015, 34(4): 911-920. (in Chinese) |
| [2] |
刘作华, 孙伟, 熊黠, 等. 脉冲射流-刚柔组合桨强化流体混沌混合及传质性能研究[J]. 化工学报, 2020, 71(10): 4632-4641. LIU Zuohua, SUN Wei, XIONG Xia, et al. Chaotic mixing performance and mass transfer enhanced by rigid-flexible impeller with pulse jet[J]. CIESC Journal, 2020, 71(10): 4632-4641. (in Chinese) |
| [3] |
MAKINO T, OHMURA N, KATAOKA K. Observation of isolated mixing regions in a stirred vessel[J]. Journal of Chemical Engineering of Japan, 2001, 34(5): 574-578. DOI:10.1252/jcej.34.574 |
| [4] |
刘作华, 魏红军, 熊黠, 等. 长短叶片复合型刚柔桨强化搅拌槽内流体混沌混合行为[J]. 化工学报, 2020, 71(11): 5080-5089. LIU Zuohua, WEI Hongjun, XIONG Xia, et al. Chaotic mixing performance enhanced by rigid-flexible impeller with long-short blades in stirred tank[J]. CIESC Journal, 2020, 71(11): 5080-5089. (in Chinese) |
| [5] |
AMEUR H. Effect of the shaft eccentricity and rotational direction on the mixing characteristics in cylindrical tank reactors[J]. Chinese Journal of Chemical Engineering, 2016, 24(12): 1647-1654. DOI:10.1016/j.cjche.2016.05.011 |
| [6] |
王宝琴, 范慧, 何爱山, 等. 连续化生产生物柴油的反应器与工艺的研究进展[J]. 化工进展, 2010, 29(4): 606-610. WANG Baoqin, FAN Hui, HE Aishan, et al. Progress in reactors for continuous biodiesel production processes[J]. Chemical Industry and Engineering Progress, 2010, 29(4): 606-610. (in Chinese) |
| [7] |
WONGJAIKHAM W, WONGSAWAENG D, RATNITSAI V, et al. Low-cost alternative biodiesel production apparatus based on household food blender for continuous biodiesel production for small communities[J]. Sci Rep, 2021. DOI:10.21203/rs.3.rs-289076/v1 |
| [8] |
ROUSSINOVA V, KRESTA S M. Comparison of continuous blend time and residence time distribution models for a stirred tank[J]. Industrial & Engineering Chemistry Research, 2008, 47(10): 3532-3539. |
| [9] |
BUSCIGLIO A, MONTANTE G, PAGLIANTI A. Flow field and homogenization time assessment in continuously-fed stirred tanks[J]. Chemical Engineering Research and Design, 2015, 102: 42-56. DOI:10.1016/j.cherd.2015.06.017 |
| [10] |
LIU M. Age distribution and the degree of mixing in continuous flow stirred tank reactors[J]. Chemical Engineering Science, 2012, 69(1): 382-393. DOI:10.1016/j.ces.2011.10.062 |
| [11] |
PATEL D, EIN-MOZAFFARI F, MEHRVAR M. Using tomography to visualize the continuous-flow mixing of biopolymer solutions inside a stirred tank reactor[J]. Chemical Engineering Journal, 2014, 239: 257-273. |
| [12] |
RASOULI M, MOUSAVI S M, AZARGOSHASB H, et al. CFD simulation of fluid flow in a novel prototype radial mixed plug-flow reactor[J]. Journal of Industrial and Engineering Chemistry, 2018, 64: 124-133. |
| [13] |
马泽文, 刘涛, 孙旭东. 基于CFD的结晶搅拌反应釜流场分析与改进[J]. 系统仿真学报, 2018, 30(5): 1900-1907. MA Zewen, LIU Tao, SUN Xudong. CFD based analysis and improvement of the flow field of stirred tank reactor for crystallization[J]. Journal of System Simulation, 2018, 30(5): 1900-1907. (in Chinese) |
| [14] |
ROACHE P. Error bars for CFD[C]//41st Aerospace Sciences Meeting and Exhibit. Reno, Nevada. Reston, Virginia: AIAA, 2003: 1-21
|
| [15] |
CRAIG K J, NIEUWOUDT M N, NIEMAND L J. CFD simulation of anaerobic digester with variable sewage sludge rheology[J]. Water Research, 2013, 47(13): 4485-4497. |
| [16] |
TRUCANO T, POST D. Verification and validation in computational science and engineering[J]. Computing in Science & Engineering, 2004, 6(5): 8-9. |
| [17] |
FREITAS C J. The issue of numerical uncertainty[J]. Applied Mathematical Modelling, 2002, 26(2): 237-248. |
| [18] |
MANNA P, DHARAVATH M, SINHA P K, et al. Optimization of a flight-worthy scramjet combustor through CFD[J]. Aerospace Science and Technology, 2013, 27(1): 138-146. |
| [19] |
李绍芬. 反应工程[M]. 3版. 北京: 化学工业出版社, 2013.
|
| [20] |
RAKOCZY R, PRZYBYŁ A, KORDAS M, et al. The study of influence of a rotating magnetic field on mixing efficiency[J]. Chemical Engineering and Processing: Process Intensification, 2017, 112: 1-8. |
| [21] |
梁瑛娜, 高殿荣, 拜亮. 偏心组合桨搅拌槽内层流混合过程的数值模拟[J]. 化工进展, 2014, 33(12): 3203-3209. LIANG Yingna, GAO Dianrong, BAI Liang. Numerical simulation of laminar flow and mixing process in eccentrically stirred tank with combined impeller[J]. Chemical Industry and Engineering Progress, 2014, 33(12): 3203-3209. (in Chinese) |
 2023, Vol. 40
2023, Vol. 40





