2. 天津化学化工协同创新中心, 天津 300072
2. Collaborative Innovation Center of Chemical Science and Engineering, Tianjin 300072, China
晶体的微观结构信息是了解和掌握固体材料物理化学性质的关键[1]。然而,研究晶体结构的结晶学自诞生之日起,便以实验为主导;同时,由于物质结构的形成常常受化学(分子结构、原子性质等)、热力学、动力学等因素的影响,使得晶体结构的理论预测成为凝聚态和化学科学长期以来面临的挑战[2]。近年来,得益于先进的计算工具和理论方法的开发,晶体结构的理论预测为许多新型和复杂晶体材料的发现做出了重大贡献[3-5]。此外,使用第一性原理方法的晶体结构搜索,不仅仅局限于三维结构,还可以搜索获得点缺陷结构、(纳米)团簇结构、固体表面及界面结构等[6]。晶体结构预测正日益成为发现新功能材料的最有效方法之一,通过枚举法、启发式知识或最新的基于深度学习的生成式机器学习模型可以轻松获得新成分[7]。
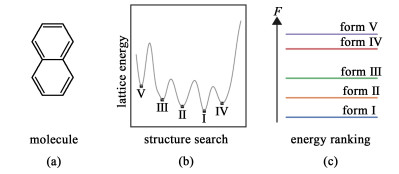
1 晶体结构预测理论上,通过求解在原子坐标空间定义的势能面的局部优化问题,便可以找到由原子或分子组装形成的稳定或亚稳结构[8]。目前,晶体结构预测(Crystal Structure Prediction, CSP)主要是寻找最具热力学稳定性的晶体结构,在不输入任何实验信息的情况下确定固体中在能量上最有利的晶体排列[1]。几乎所有的CSP方法都是基于在高维势能面上搜索局部极小值,并将能量表示为描述晶体结构变量的函数[9]。这些方法通常假设势能表面上的全局最小值对应于最有可能观察到的晶体结构[10]。然而,热力学并不是决定物质固态形式的唯一因素,高能量的晶体结构或能量非常接近的其他晶体结构,有时并不是热力学上的最稳定结构[11]。这在现实世界中极为常见,如常常受结晶动力学或结晶条件影响而产生的多晶型现象。亚稳态多晶型的鉴定在CSP的许多应用中也十分重要,其高能结构有时会表现出最吸引人的特性[12, 13]。因此,CSP的研究可以作为一种固体形态和结构实验筛选的补充,以确定与结晶动力学无关的热力学晶体结构堆积的范围[14]。
标准CSP问题,即为在给定的压力-温度条件下,为给定的化学成分寻找到具有最低自由能的晶体结构[15]。一般而言,一个成功的CSP计算涉及2方面内容(图 1)[16]:(1)生成所有潜在的低能量结构的搜索;(2)计算获得一系列候选结构相对稳定性的能量排序。但随着研究系统变大,计算资源消耗也会随之飞速增加。此外,由于大多数CSP方法主要依赖于第一性原理势能面的计算,使得在进行CSP研究时,必须慎重考虑“对势能面的可靠全局搜索”和“对势能面的准确描述”这2个主要问题[17, 18]。
为实现晶体结构预测,提出了全局优化(Global Optimization Methods,基于强大的探索性计算机算法)和数据挖掘(Data Mining,基于现有知识和晶体结构数据库)这2种互补的CSP方法[6, 16],同时解决了势能面的全局搜索问题。其中,全局优化策略能够在几乎没有任何先验知识和数据存在的情况下,实现全局预测。依赖强大的搜索算法,全局优化能够产生全新的晶体结构和化合物,包括那些与最初的理想网(Ideal Nets,由实际晶体结构中抽象出来的结构)不相关的结构。但其往往采用计算成本高昂的从头算法(Ab initio),对于小体系化合物更为合适[7]。数据挖掘是基于现有知识和晶体结构数据库的内容而开发的一种非全局优化的预测手段,可以非常快速地预测稳定的晶体结构,并且在搜索具有最佳性能的材料方面十分有效,如基于元素替代的模板法[7, 8, 19, 20]。然而,与晶体材料的巨大化学空间相比,目前可用的数据库中已知的晶体结构非常有限[21, 22],因此,该方法无法预测数据库中不存在的全新晶体结构。与数据挖掘方法相比,发现全新结构的可能性是结构预测的关键优势[6],然而,在现有的计算机技术水平及优化方法下和有限的计算时间内,还没有哪种方法可以真正找到全局最小值[16]。目前,比较流行的全局优化方法有随机搜索、模拟退火、进化算法和粒子群算法等。
2 晶体结构预测理论方法 2.1 不基于全局优化的方法(Methods Not Based on Global Optimization)属于该情况的几种重要的方法是数据挖掘(Data Mining)[23, 24]、团簇扩展(Cluster Expansion)[25]以及模板法或元素替换法[7, 8, 19, 20],均需要大量预先存在的晶体结构信息,才能完成结构预测。常用的晶体材料数据库有ICSD(~200 000个结构数据)[21, 26]、CCDC[27]、Materials Project[28]、OQMD(~1 023 000种材料及其属性)[29]、Landolt-Börnstein(~6 836个结构和多种性质数据)[30]等。
数据挖掘:利用现有晶体数据库信息,可以非常快速地预测稳定的晶体结构,但却无法预测全新的晶体结构[6]。然而,随着理论计算发现的新结构不断输入数据库,数据挖掘方法的能力也正在不断增强。
团簇扩展:团簇扩展是在n-体簇(与n个Bravais格点相关)和有效簇的相互作用中的基集展开,并指定了构型能量,是一种基于DFT电子结构能量的多尺度方法。从潜在的晶体结构知识开始,并允许预测的原子和/或磁矩的顺序作为温度的函数。
模板法或元素替换法:旨在通过替换已知模板晶体中的元素来预测稳定的晶体结构,此时需要该模板晶体对要预测的目标结构具有很高的化学可替代性。除非需要通过局部优化来替换晶体,这种基于取代的方法不需要耗时的势能计算,可以显著降低计算成本[31, 32]。严格来讲,元素替换法也属于数据挖掘的一种。
2.2 全局优化方法(Global Optimization Methods)全局优化是应用数学中一个非常大的研究领域,许多优化算法也在不断发展完善。按照是否依赖初始给定结构,可进一步将全局优化方法划分为2大类,即基于初始结构进行演化的跃迁势垒方法,如盆地跳跃、模拟退火、元动力学和极小值跳跃法;以及不依赖初始结构的群体搜索法,如随机结构搜索、进化算法和粒子群算法等。下面介绍几种在CSP领域中较为流行的方法。
2.2.1 随机结构搜索(Random Structure Searching)对势能面进行随机搜索采样为结构搜索提供了一种简单、无偏的方法[14],其中最简单的搜索策略是准随机抽样结构[33],它随机对结构进行采样以最大化探索,但通常由人类直觉约束(如对称性和协调数)引导至更真实的结构[34]。如从头算随机结构搜索(ab initio Random Structure Searching,AIRSS)[33],该方法具有在某些规则(如对称性、体积和协调性)的准随机结构生成中的简单性,以及在高度并行运算中找到全局最小值的有效性[21]。然而,在实践中,在保持结构多样性的同时,引导搜索朝着寻找现实结构的方向发展更为重要,通常需要通过对对称性、原子间距离、配位数、化学计量、维度和结构单元等施加约束来实现[6]。
2.2.2 模拟退火(Simulated Annealing)模拟退火是一种受物理中固体物质的退火过程启发的策略,是一个简单而稳健的过程,具有渐进收敛性。在该策略中,通过加热来越过能垒,再经由逐渐冷却最终达到能量最低的稳定态,获得平衡晶体结构。如果温度下降过快(淬火)或初始温度太低,则系统可能会冻结成玻璃态或含有空穴和位错等缺陷的晶体系统。在模拟退火的过程中,使用分子动力学或Monte Carlo方法连续扰动每个温度下的候选结构,其中移动算子(Move Class Operators)用于扰动当前候选结构内的随机数量的粒子,并使用Metropolis准则来确定是否接受或拒绝Monte Carlo移动。温度的下降,会获得具有较低势能的结构,并可降低局部极小值间跳跃的概率。理论上,如果这种退火过程一直进行下去且进行的足够缓慢,那么最终结构便很有可能是全局最小值[35]。需要注意的是,该方法仅在结果分析时进行结构弛豫。涉及该方法的晶体结构预测实现程序如GULP[36],已在辅助结构解析和无机物固体预测研究中发挥了巨大作用。
另一种包括模拟退火的成功方法是由Mellot-Draznieks等[37]开发的次级构筑单元自动组装法(The Automated Assembly of Secondary Building Units (AASBU) Method),该方法的关键是黏性原子对,该原子对可以促进或阻碍次级构筑单元(SBUs)在模拟退火或最小化阶段连接在一起,其中SBUs可以是无机碎片,也可以由有机分子或碎片组成。
2.2.3 盆地跳跃(Basin Hopping)盆地跳跃是一种基于超表面变形的无偏随机全局优化方法[38],结合了局部能量最小化和Monte Carlo采样[39, 40]。主要包含以下过程:(1)对初始结构进行结构优化以获得能量极小值;(2)在随机扰动后产生新的结构,并立即进行结构弛豫,得到新的能量极小值;(3)使用Monte Carlo方法中的Metropolis准则来判断是否接受或拒绝产生的新结构;(4)循环上述过程,以探索势能面的其他区域。通常,盆地跳跃的计算温度被固定在3 000 K,在搜索过程中,步长也不是固定的,因此Monte Carlo移动的平均接受率为50%[41],实现程序有GMIN等[42]。
然而,模拟退火法和盆地跳跃法均存在一明显缺陷,它们对能量景观图的探索必须从一个点开始,而且可能无法获得所有低能量区域。因此,为了避免这种情况的发生,必须对具有不同初始配置的结构进行多次运算[35]。
2.2.4 元动力学或巨动力学(Metadynamics)元动力学[43]是一类通过引入额外的偏置势(或力)作用于某些自由度上来提高采样效率的方法。在晶体结构预测中,需要1组集合变量来区分系统的状态(对于CSP,晶胞矢量目前被用作一种虽不完美但很实用的选择),并通过历史相关势扭曲实际能量景观图的方式,来扫描能量景观的低能量部分,以此来阻止系统对已经采样的状态进行重复采样。该方法的实现程序有PLUMED等[44]。
2.2.5 最小值跳跃(Minima Hopping)最小值跳跃法[6]能够通过改变势垒跃迁能力来进行势能面搜索。与盆地跳跃法类似,该方法同样引入了局部极小化方法以获得局部能量极小值,但却不依赖于体系的热力学性质,主要依靠分子动力学过程来产生新结构的演化迭代。在进行分子动力学获得新结构后,对其进行结构弛豫,若弛豫后获得的是已经访问过的结构,则在更高的温度下开始新的分子动力学计算,并继续该过程直到发现新的结构。
2.2.6 进化算法(Evolutionary Algorithms)进化算法是当前使用最为广泛的全局优化算法之一[21],通过构建结构群来避免以一个点为开始的相关问题。由于众多的进化算法都是基于群体的,因此可以通过合适的初猜找到各种全局和局部最优解,并且通常表现出更稳健的搜索结果,而不被困于局部最优解中。虽然存在不同的进化策略,但不同的进化策略一般都涉及2个关键步骤[45, 46]:首先,针对给定的特定化学成分,初始化结构库(即群体);其次,使用DFT计算评估每个晶体结构的目标特性(如形成焓)后更新群体。研究者普遍认为,在低能量结构的自然选择的驱动下,结构群体得以进化,这些低能量结构将成为新一代结构的父母。从父母那里产生后代的方法(基因交叉和突变)是非常重要的。
2.2.6.1 遗传算法(Genetic Algorithm,GAs)遗传算法是受生物进化过程启发的基于群体的搜索算法[47]。当应用于结构预测时,生物体只是一种结构或候选结构。在“繁殖”过程中,通过应用2个算子生成新的候选结构:对候选结构对进行“交叉”,从而将当前的结构特征结合到新的个体中。对单个候选结构进行“突变”,从而可能将新的结构特征引入到种群中。通常,突变是一种Monte Carlo移动[35]。与其他启发式搜索算法相比,GA已被证明适用于大规模全局优化问题,主要用于自由能最小化。主要的超参数包括种群大小(Population Size)、交叉率(Crossover Rate)和突变率(Mutation Rate)。
2.2.6.2 差分进化算法(Differential Evolution,DE)差分进化[31, 48]是一种随机的、基于群体的进化优化算法,旨在优化实参数(Real-parameter)、实值函数(Real-valued Functions)。不同于遗传算法更多地关注交叉算子,DE主要利用自身特殊的突变算子,通过将2个群体成员之间的加权差添加到第3个成员来生成新的候选结构。这种突变算子具有固有的自适应特征,当种群接近全局或局部最优时,可以产生较小的突变。因此,它通常是稳健的,并且可以实现快速收敛。它有3个主要参数:种群大小(Population Size,通常是变量数量的5~10倍)、比例因子F(Scaling Factor,F)和交叉率(Crossover Rate)。
2.2.6.3 协方差矩阵自适应-进化策略(Covariance Matrix Adaptation-Evolution Strategy,CMA-ES)协方差矩阵自适应-进化策略[49]是一种随机、快速、稳健的局部搜索算法,不需要计算梯度。它从其均值的多元正态分布中采样新的候选解,并在每次迭代后进行调整。CMA-ES主要用于求解非线性和非凸优化问题,具有随机性。与大多数其他进化算法相比,它是一种准无参数算法(Quasiparameterless Algorithm)。CMA-ES是处理复杂数值优化问题的最有效的方法之一,已广泛应用于实际问题。
2.2.7 粒子群优化算法(Particle Swarm Optimization, PSO)粒子群优化[49, 50]是一种基于种群的随机优化算法,用于解决非线性全局优化问题,其灵感来自一些动物的社会行为,如鸟群或鱼群。通过在群体中搜索个体之间的协作和信息共享来寻求最优解,每个个体根据过去经验和群体行为进行机率式的搜寻策略调整,来更新其在搜索空间中的移动。随机产生初始粒子群(均匀分布),其中每个粒子都是一个求解问题的候选解,粒子群会参考个体及群体的最佳经验,选择修正方式,经过不断的修正,粒子群会逐渐接近最优解。虽然PSO对于复杂的问题可能会陷入局部最优,但其搜索速度快、效率高、算法简单。
2.2.8 贝叶斯优化算法(Bayesian Optimization, BO)贝叶斯优化[51]是一种用于优化需要很长时间才能做出评估的、昂贵目标函数的算法,适用于小于20维的连续域的优化。贝叶斯优化是函数评估数量方面最有效的优化方法之一,通过结合对问题的问题信念(Problem Belief about the Problem)来帮助指导采样,并采用自动化机制来权衡基于其依赖的采集函数(Acquisition Function)的采样的搜索空间的探索和开发/利用。常见的采集函数包括预期改进(Expected Improvement)、熵搜索(Entropy Search)和知识梯度(Knowledge Gradient)。它通常使用高斯过程回归器或深度神经网络,为昂贵的目标函数构建代理模型[52],并使用贝叶斯估计来计算每个采样点的预测不确定性。
2.2.9 基于RBF模型的优化(RBF Model-Based Optimization,RBFOpt)RBFOpt[53]是一种基于径向基函数法的连续优化算法,它构建并迭代优化未知目标函数的代理模型,并利用有噪声但成本较低的代理模型来加速收敛到精确预言的最佳值。在这方面,它与贝叶斯优化方法共享一些原则。它还在优化过程中引入了自动模型选择阶段,其关键思想之一是使用RBF插值来构建代理模型并定义“颠簸度(Bumpiness)”的度量。给定采样点的目标函数值,它的颠簸度便可根据插值点来度量该目标函数值在该采样点上出现的可能性。假设未知函数不会振荡太多,便可以找到能够解释数据并最小化颠簸度的模型。先前的基准研究表明,该算法在评估次数和稳健性方面具有较高的效率。
3 相关程序与典型应用一些公开可用的结构预测代码包括:AIRSS、CALYPSO、CrySPY、DMACRYS、GASP、GAtor、GRACE、MAISE、Molpak、UPack、USPEX、和Xtalopt等。这里着重介绍以下4种。
3.1 CALYPSOCALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization)[45]是一种基于粒子群算法的高效结构预测方法和软件,由吉林大学马琰铭教授团队研究开发。只需给定化合物的化学组分,就可预测在给定外部条件(如压力)下的稳定或亚稳结构,可用于预测或确定团簇、二维层结构、二维表面和三维晶体结构并设计多功能材料。目前,CALYPSO在预测纳米颗粒、纳米团簇、二维层(单层/多层、弯曲层)、表面、界面等体系的能量稳定的结构方面具有广泛的应用[54]。但由于CALYPSO结构预测方法基于第一性原理,受目前计算资源的限制,只能处理小尺寸体系。
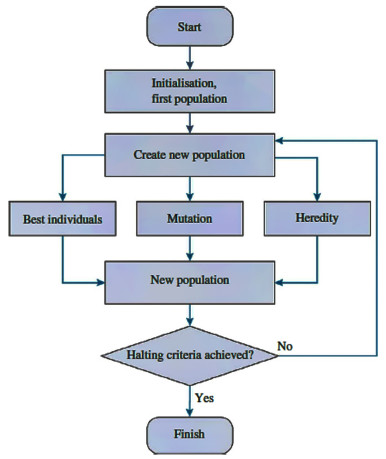
CALYPSO的搜索过程如图 2所示[1]。首先,在适当的物理约束(如最小原子间距离、晶体对称规则等)下随机生成初始群体中的结构;然后通过使用结构表征技术去除重复或类似的结构。在生成每个种群的所有结构之后,执行局部优化以确定局部极小值。最后,通过PSO或人工蜂群(Artificial Bee Colony)等群智能算法进行结构进化,为下一代生成新的结构[55]。重复以上步骤,直到达到终止标准(如规定的阈值或固定的迭代次数)。为了避免结构演化过程中的过早收敛,在每代结构中均纳入了一定比列的新随机结构,以增强结构的多样性。
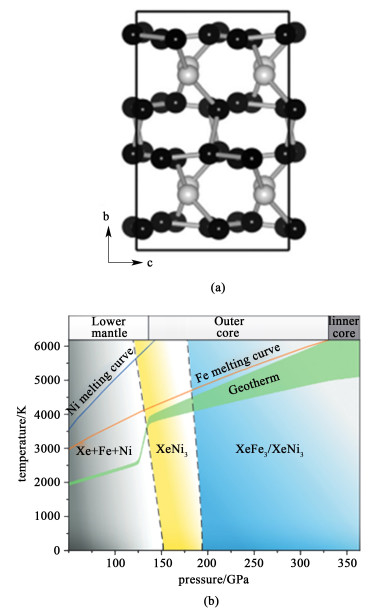
研究者利用CALYPSO法对锂金属高压下的半导体结构进行探索,理论预测了1种晶胞中含有40个原子的复杂底心正交Aba2-40结构[图 3(a)],该结构的能量远低于其他算法所获得的结构[56],并被爱丁堡大学Guillaume等报道的高压单晶X射线结果证实,从而破解了单质锂高压半导体相的结构难题[57]。Zhu等[58]利用CALYPSO法,预测并提出了一种全新的地核环境下铁/镍-氙化合物的晶体结构(XeFe3、XeNi3),并进一步构筑了铁/镍-氙化合物的高温-高压相图[图 3(b)],首次给出了在地核环境下氙气与铁/镍等发生化学反应的证据。Wang等[59]采用CALYPSO方法探索固体氮的高压相,发现了意想不到的笼状金刚石状聚合物氮结构。聚合氮的类金刚石结构采用高度对称的体心立方结构,晶格位点由类金刚石占据,每个晶格由10个氮原子组成,形成N10四环笼。这一预测为理解固体氮和其他氮相关材料在极端条件下的行为迈出了重要一步。此外,在CALYPSO预测的指导下,发现了一系列由轻元素形成的超硬材料,如氮化碳、氮化硼、B4C4、SiCN等。Tong等[60, 61]将机器学习技术引入CALYPSO来精确构建势能面,从而避免了第一性原理方法中昂贵的能量和力的评估。然而,该方法目前尚无法应用于大型系统及有机物的理论预测。
USPEX(Universal Structure Predictor: Evolutionary Xtallography)[46]是由Oganov实验室开发的一款基于进化算法的晶体结构预测方法和程序,特别适用于高温、高压等极限条件下晶体结构和分子结构的预测。在不需要输入经验参数只输入化学元素时,便可实现最稳定的化学组分和对应的晶体结构的预测,广泛应用于零维纳米粒子、一维聚合物、二维表界面、二维晶体及三维晶体的结构预测。该方法还可以高效地处理分子晶体(包括柔性分子和非常复杂的分子),也可以预测亚稳结构,搜索获得具有目标理化性质(如力学性质、光电性质等)的材料结构。同时,在结构预测过程中,USPEX可以使用多种第一性原理或分子力场计算程序(如VASP、LAMMPS、CASTEP、CP2K等)来进行能量和结构的局部优化计算。典型USPEX的搜索过程如图 4所示[62]。USPEX的代码使用2类变异运算符:(1)突变算子(Mutation Operators),1种只有1个父代参与产生1个子代的算子,突变可以是随机的,如晶格突变、原子突变、置换算子、旋转变异算子及协同变异算子等多种不同类型的突变;(2)遗传算子(Heredity Operators),通过利用和精炼晶体结构所拥有的物化性质信息,在空间连贯性的帮助下,从上一代那里延续下来。
Zhang等[63]利用可变成分USPEX理论预测出高压下会出现具有不同化学计量的新材料,如Na3Cl、Na2Cl、Na3Cl2、NaCl3、NaCl7等理论上可稳定存在的结构(图 5),随后又通过实验合成了呈现立方和正交晶系的NaCl3及具有二维金属的四方晶系Na3Cl,他们均表现不同寻常的键合能力和电子性质。其研究说明对于非环境条件下的简单系统,违反化学直觉的化合物也可以是热力学稳定的。Zhou等[64]利用USPEX发现了高压下Mg(BH4)2的更稳定晶型,解决了δ-Mg(BH4)2晶型不稳定及转晶问题。张晓铮[65]采用USPEX对TaB3的晶体结构进行预测,得到了非常稳定的新相oC16-TaB3,通过与已合成的TaB3的晶体进行对比,发现当压强高于75 GPa时,预测得到的oC16-TaB3成为最稳定的相,证明oC16-TaB3成为硬质材料或者潜在的超硬材料的可能。

|
| 图 5 不同化学计量的钠-氯化合物结构[63]:(a) Pm3-NaCl7; (b)Pnma-NaCl3; (c) Pm3n-NaCl3; (d) P4/mmm-Na3Cl; (e) P4/m-Na3Cl2; (f) Cmmm-Na3Cl2; (g) P4/mmm-Na2Cl; (h)Cmmm-Na2Cl; (i) Imma-Na2Cl (紫色:钠原子;绿色:氯原子) Fig.5 Crystal structures of Na chlorides[63]. (a) Pm3-NaCl7; (b) Pnma-NaCl3; (c) Pm3n-NaCl3; (d) P4/mmm-Na3Cl; (e) P4/m-Na3Cl2; (f) Cmmm-Na3Cl2; (g) P4/mmm-Na2Cl; (h) Cmmm-Na2Cl; (i) Imma-Na2Cl (Purple and green spheres denote Na and Cl atoms, respectively) |
| |
AIRSS(Ab initio Random Structure Searching)[66]是一款非常简单、功能强大且可高度并行的结构预测软件,基于随机结构搜索原理,可以对结构空间进行广泛且无偏采样。随机结构产生后被进一步弛豫到就近的局部极小点,再采用密度泛函理论对其能量进行评估。这些随机结构是由合理的密度和原子分离标准构造而成,考虑到搜索效率问题,通常进行的是有约束限制的“随机感性结构”搜索。该方法已广泛应用于预测分子/团簇、固体缺陷、界面、表面及三维晶体结构。
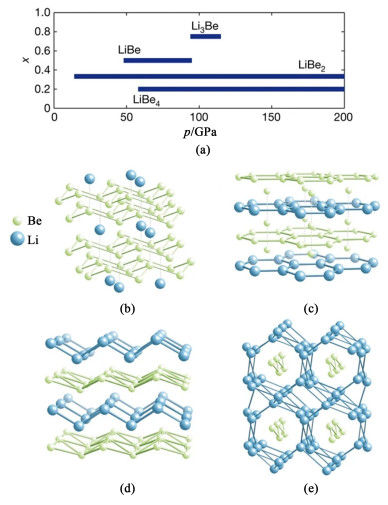
AIRSS在有机分子的晶体结构中使用较为广泛,在多次的晶体结构盲测中表现良好。此外,Pickard等[67]利用AIRSS发现并合成了一种高压(20 GPa)下存在的新的亚稳态H2O,该结构几乎完全由弱键H2O、H3O、H2O2、H2OH…OH、H2和O2组成。Feng等[68]采用AIRSS探索了Li-Be合金在承压状态下的结构(图 6),发现当体系压力高于25 GPa时,LiBe2结构的合金比2金属单独存在时更稳定,而Li3Be、LiBe和LiBe4则在更高的压力下具有稳定性,其中最稳定的是LiBe。进一步研究发现,LiBe化合物的电子结构呈现二维特征,且在价带底部具有典型的阶梯状特征。
相比于无机物,有机分子晶胞中通常包含数百个原子[6],且常常依赖于强度较弱且方向性较差的分子间相互作用[69],造成分子晶体结构预测更加困难。此外,由于分子晶体含有多个独立的自由度,如晶胞参数、不对称单元中分子的质心位置与方向、分子构象自由度等,使得分子晶体结构预测需要搜索高维构型空间。对于晶格能相差较小(≦2 kJ ·mol-1)[70]的多晶型体系,则需要更高精度水平的计算方法进行评估。因此,对于分子晶体结构预测需要高效精准的搜索方法。最近,Nikhar和Szalewicz[71]提出一种基于第一性原理的廉价分子晶体预测方法,通过分子二聚体的量子力学计算结果,构建了精确的双体刚性单体从头算力场(An Accurate Two-Body, Rigid-Monomer Ab Initio-Based Force Field,aiFF),耗时与经验力场相当,但计算精度却是经验力场所无法达到的。
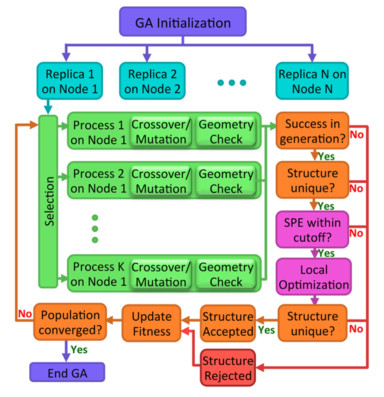
3.4 GATorGAtor[72, 73]是由Curtis和Marom等开发的一款基于遗传算法的分子晶体结构预测软件,适用于没有内部旋转自由度的(半)刚性分子,其中通过遗传算法模仿进化过程来执行全局优化,使用具有色散校正的密度泛函理论执行局部优化和能量评估。GAtor可提供各种适应度评估、选择、交叉和突变方案。通过使用机器学习对动态更新的种群进行结构相似性聚类,然后采用基于聚类的适应度函数,在GAtor中实现进化小生境(Evolutionary Niching)。进化小生境通过进化几个亚群体来促进势能表面的均匀采样,克服初始池偏差和选择偏差(遗传漂移),其搜索流程如图 7所示[72]。初始化后,主进程在N个节点上生成用户定义数量的GA副本,每个独立副本在读取和写入动态更新的结构池时独立地执行核心遗传算法任务。GAtor同样采用交叉和突变这2类遗传算子,当子代无法通过几何查验时,则执行新的选择;若通过几何查验,则其将继续进行唯一性检查。如果候选结构成功的通过了几何查验、唯一性检查和单点能截断,那么它将被添加到种群中。
Curtis等[73]使用GAtor对1, 3-二溴-2-氯-5-氟苯分子进行晶体结构预测,经过采用不同的设置多次运行GA的方式,找到该物质的实验结构和几个额外的低能量结构,这些结构在使用传统的基于能量的适应度函数时很难发现,因为传统能量的适应度函数无法准确描述卤键的静电作用和色散作用。Bier等[74]将GAtor应用于含能材料(2, 4, 6-三硝基苯-1, 3, 5-三胺(TATB)和2, 4, 6-三硝基苯-1, 3-二胺(DATB))的晶体结构预测,不仅成功预测出已有的实验结构,还在已知多晶型晶格能量差异的上限范围内发现了几种比实验结构密度更高的结构,并可以在高压下稳定存在。图 7中,N个独立的GA副本运行在N个计算节点上,每个节点有K个核心处理单元。
3.5 由数据驱动的CSP数据驱动CSP研究的关键是学习适当的结构-功能关系,当更先进的机器学习技术(ML)应用于CSP过程时,可获得更精确的结构-功能关系[75]。Behler和Parrinello[76]用所有原子位置表示晶体系统,建立神经网络模型来学习DFT势能曲面。Meredig等[77]开发了一种基于集成树的地层能量预测模型,该模型以组成元素的原子性质为输入,在某些情况下将计算成本降低了6个数量级。Isayev等[78]提出了以属性标记的材料碎片作为无机晶体材料的表示,用最少的结构输入,获得较高的预测精度。Xie和Grossman[79]在其晶体图卷积神经网络(CGCNN)框架中提出利用晶体原子间的连接(即连接矩阵)作为晶体材料可解释的通用表示,并对包括形成能在内的各种性质进行了有前景的预测。Zhu等[69]采用“同构取代”的类比方法,将已知多孔结构中的分子替换为理论上能够采用相同晶体排列的相关分子,发现了一种罕见的低密度(0.54 g ·cm-3)介孔氢键骨架(HOF) 3D-CageHOF-1。Richard等[32]采用数据驱动的拓扑映射方法,准确预测了3种药物(马钱子碱、盐酸帕罗西汀和酒石酸西格列汀)的稳定结晶水合物。Deringer等[34]将基于机器学习的原子间势加入了AIRSS代码中,显著降低了计算成本。近年来,生成式机器学习体系结构作为CSP的一种新方法引起了研究者的兴趣。用于CSP的生成模型(GMs)是无监督的ML模型,它从高维结构设计空间学习低维表示,并使用嵌入在潜在空间中的知识生成新的结构。生成模型的CSP的关键是晶体设计空间的有效和可逆表示,最好是能够表示和结构设计空间之间的一对一映射关系。Nouira等[80]首次将生成对抗网络(GAN)架构应用于CSP,并开发了CrystalGAN代码,该代码从观察到的二元结构生成三元稳定晶体结构。Kim等[21]基于晶胞和原子分数坐标,构建晶体结构生成对抗网络,用于Mg-Mn-O三元材料的高通量虚拟筛选,预测了23种具有合理计算稳定性和带隙的新晶体结构。Noh等[81]提出了一种基于变分自动编码器(VAE)的晶体结构生成器,具有基于3D图像的可逆输入表示。Yang等[22]将物理原理整合到机器学习模型中,通过优化接触图匹配精度、个体年龄和配位数3个目标,提出了一种基于接触图的晶体结构预测的多目标遗传算法,用于配合物的晶体结构预测,该方法可以以更高的质量重建晶体结构,也能缓解过早收敛的问题。Cheng等[2]利用图形网络技术在给定的数据库中通过机器学习建立了晶体结构和生成焓之间的关联模型,并利用优化算法加速寻找到生成焓最低的典型光伏半导体GaAs、CdTe和CsPbI3等的晶体结构,准确率高达86.2%。
然而,目前使用机器学习进行CSP的成功案例大部分局限于无机材料和化学复杂性不高的有机分子体系,缺乏向复杂的、更高相对分子质量的分子的推广;在晶体形成能计算方面,虽然机器学习可以从DFT计算中学习到很高的精度,并加速计算,但其计算精度不可能超越DFT,其相对稳定性可能也没有那么准确[82]。
4 总结与展望在原子水平上预测晶体结构是凝聚态科学领域的最基本挑战。尽管目前开发了各种各样的晶体结构预测方法,并已经广泛应用于地球学、天文学、材料学等多个领域,解决了很多科学难题,但由CSP预测得到的稳定晶体结构并不一定能保证成功实验合成,晶体结构预测仍然面临着许多挑战。
(1) 大型系统的晶体结构预测:在大多数CSP过程中,通常需要通过第一性原理对势能面进行精确评估,而势能面的复杂程度随着体系中原子数目的增加而迅速增加,其维度线性增加,能量极小值数量则呈指数增长,因此现有预测方法在处理复杂体系势能面时均面临采样效率严重下降的问题。此外,大型、复杂体系结构预测往往需要对大量候选结构进行能量评估,当采用精度较高的第一性原理处理时,计算成本则极为昂贵。
(2) 极端环境下的晶体结构预测:目前,大多数CSP方法未考虑温度效应,导致预测结构与实验结果不同。这是由于不同于压力仅是一个简单的热力学参数,温度的正确计算需要对每一个相进行典型的103~107种构型的采样,这使得自由能的计算变得十分昂贵。然而,自由能的局部极小值的数量随着温度的升高迅速减少,这为理论预测极端环境下的晶体结构,提供了可能。
(3) 高Z′问题的处理:高Z′结构的出现意味着要对任何有机分子的所有观察到的晶体结构进行完整的搜索,然而,这实际上是不可能的。对于单组分有机晶体,目前通常是将搜索限制在Z′=1,并将搜索变量的数量减少到空间组所需的数量。虽然一些Z′>1多晶型与更简单的Z′=1结构密切相关,可以被视为“途中晶体”或不完全结晶,或者可能是较低温度的多晶型,但这些结构本质上仍含有不止一种分子构象。
(4) 外部环境及结晶动力学因素:能量景观图上的晶体结构,在热力学上是合理的。然而,对于由结晶动力学控制及外部环境影响(如溶剂、添加剂、杂质等)的晶体结构的形成,当前CSP还不能准确预测。此外,对于配合物,如果忽略晶胞外的化学环境,则有可能导致不合理的配位。
尽管当前CSP方法还存在许多困难和挑战,但其在预测大量具有非凡性能材料方面取得了巨大进步。相信随着优化方法的不断发展改进、计算机技术及计算能力的提升以及基础物理化学理论的逐步完善,晶体结构预测将会在更广阔的领域里发挥更重要作用。
| [1] |
WANG Y, LV J, GAO P, et al. Crystal structure prediction via efficient sampling of the potential energy surface[J]. Accounts of Chemical Research, 2022, 55(15): 2068-2076. DOI:10.1021/acs.accounts.2c00243 |
| [2] |
CHENG G, GONG X, YIN W. Crystal structure prediction by combining graph network and optimization algorithm[J]. Nature Communications, 2022. DOI:10.1038/s41467-022-29241-4 |
| [3] |
FRATINI S, CIUCHI S, MAYOU D, et al. A map of high-mobility molecular semiconductors[J]. Nature Materials, 2017, 16(10): 998-1002. DOI:10.1038/nmat4970 |
| [4] |
NEMATIARAM T, PADULA D, TROISI A. Bright Frenkel excitons in molecular crystals: A survey[J]. Chemistry of Materials: A Publication of the American Chemical Society, 2021, 33(9): 3368-3378. |
| [5] |
KUNKEL C, SCHOBER C, MARGRAF J T, et al. Finding the right bricks for molecular legos: A data mining approach to organic semiconductor design[J]. Chemistry of Materials, 2019, 31(3): 969-978. DOI:10.1021/acs.chemmater.8b04436 |
| [6] |
OGANOV A R, PICKARD C J, ZHU Q, et al. Structure prediction drives materials discovery[J]. Nature Reviews Materials, 2019, 4(5): 331-348. DOI:10.1038/s41578-019-0101-8 |
| [7] |
WEI L, FU N, SIRIWARDANE E M D, et al. TCSP: A template-based crystal structure prediction algorithm for materials discovery[J]. Inorganic Chemistry, 2022, 61(22): 8431-8439. DOI:10.1021/acs.inorgchem.1c03879 |
| [8] |
KUSABA M, LIU C, YOSHIDA R., et al. Crystal structure prediction with machine learning-based element substitution[J]. Computational Materials Science, 2022. DOI:10.1016/j.commatsci.2022.111496 |
| [9] |
WOODLEY S M, DAY G M, CATLOW R. Structure prediction of crystals, surfaces and nanoparticles[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2020. DOI:10.1098/rsta.2019.0600 |
| [10] |
YANG S, DAY G M. Exploration and optimization in crystal structure prediction: Combining Basin hopping with quasi-random sampling[J]. Journal of Chemical Theory and Computation, 2021, 17(3): 1988-1999. DOI:10.1021/acs.jctc.0c01101 |
| [11] |
CRUZ-CABEZA A J, REUTZEL-EDENS S M, BERNSTEIN J. Facts and fictions about polymorphism[J]. Chemical Society Reviews, 2015, 44(23): 8619-8635. DOI:10.1039/C5CS00227C |
| [12] |
PULIDO A, CHEN L, KACZOROWSKI T, et al. Functional materials discovery using energy-structure-function maps[J]. Nature, 2017, 543(7647): 657-664. DOI:10.1038/nature21419 |
| [13] |
AITCHISON C M, KANE C M, MCMAHON D P, et al. Photocatalytic proton reduction by a computationally identified, molecular hydrogen-bonded framework[J]. Journal of Materials Chemistry A, 2020, 8(15): 7158-7170. DOI:10.1039/D0TA00219D |
| [14] |
PRICE S L. Predicting crystal structures of organic compounds[J]. Chemical Society Reviews, 2014, 43(7): 2098-2111. DOI:10.1039/C3CS60279F |
| [15] |
ZHU Q, OGANOV A R, SALVADO M A, et al. Denser than diamond: Ab initio search for superdense carbon allotropes[J]. Physical Review B, 2011. DOI:10.1103/PhysRevB.83.193410 |
| [16] |
ZHU Q, HATTORI S. Organic crystal structure prediction and its application to materials design[J]. Journal of Materials Research, 2022, 1-18. |
| [17] |
OGANOV A R. Crystal structure prediction: Reflections on present status and challenges[J]. Faraday Discussions, 2018, 211(0): 643-660. |
| [18] |
DEMIR S, TEKIN A. FFCASP: A massively parallel crystal structure prediction algorithm[J]. Journal of Chemical Theory and Computation, 2021, 17(4): 2586-2598. DOI:10.1021/acs.jctc.0c01197 |
| [19] |
HAUTIER G, FISCHER C, EHRLACHER V, et al. Data mined ionic substitutions for the discovery of new compounds[J]. Inorganic Chemistry, 2011, 50(2): 656-663. DOI:10.1021/ic102031h |
| [20] |
WANG H, BOTTI S, MARQUES M A L. Predicting stable crystalline compounds using chemical similarity[J]. Npj Computational Materials, 2021. DOI:10.1038/s41524-020-00481-6 |
| [21] |
KIM S, NOH J, GU G, et al. Generative adversarial networks for crystal structure prediction[J]. ACS Central Science, 2020, 6(8): 1412-1420. DOI:10.1021/acscentsci.0c00426 |
| [22] |
YANG W, DILANGA SIRIWARDANE E M, HU J. Crystal structure prediction using an age-fitness multiobjective genetic algorithm and coordination number constraints[J]. The Journal of Physical Chemistry A, 2022, 126(4): 640-647. DOI:10.1021/acs.jpca.1c07170 |
| [23] |
NOSENGO N, CEDER G. Can artificial intelligence create the next wonder material?[J]. Nature, 2016, 533(7601): 22-25. DOI:10.1038/533022a |
| [24] |
CURTAROLO S, HART G L W, NARDELLI M B, et al. The high-throughput highway to computational materials design[J]. Nature Materials, 2013, 12(3): 191-201. DOI:10.1038/nmat3568 |
| [25] |
ZARKEVICH N A, JOHNSON D D. Reliable first-principles alloy thermodynamics via truncated cluster expansions[J]. Physical Review Letters, 2004. DOI:10.1103/PhysRevLett.92.255702 |
| [26] |
FIZ Karlsruhe-Leibniz Institute for Information Infrastructure. Inorganic crystal structure database[DB/OL]. http://icsd.fiz-karlsruhe.de
|
| [27] |
The Cambridge Crystallographic Data Centre. Cambridge crystallographic data centre[DB/OL]. https://www.ccdc.cam.ac.uk/
|
| [28] |
Materials Project. Materials Project[DB/OL]. https://materialsproject.org/
|
| [29] |
Chris Wolverton's group at Northwestern University. Open Quantum Materials Database[DB]. https://www.oqmd.org/
|
| [30] |
Springer Materials. The Landolt-B rnstein-Database[DB/OL]. https://materials.springer.com/
|
| [31] |
HU J, YANG W, DONG R, et al. Contact map based crystal structure prediction using global optimization[J]. CrystEngComm, 2021, 23(8): 1765-1776. DOI:10.1039/D0CE01714K |
| [32] |
HONG R, MATTEI A, SHEIKH A Y, et al. A data-driven and topological mapping approach for the a priori prediction of stable molecular crystalline hydrates[J]. PNAS, 2022. DOI:10.1073/pnas.2204414119 |
| [33] |
PICKARD C J, NEEDS R J. Ab initio random structure searching[J]. Journal of Physics: Condensed Matter, 2011. DOI:10.1103/PhysRevB.90.035424 |
| [34] |
DERINGER V L, PICKARD C J, CSÁNYI G. Data-driven learning of total and local energies in elemental boron[J]. Physical Review Letters, 2018. DOI:10.1103/PhysRevLett.120.156001 |
| [35] |
WOODLEY S M, CATLOW R. Crystal structure prediction from first principles[J]. Nature Materials, 2008, 7(12): 937-946. DOI:10.1038/nmat2321 |
| [36] |
Curtin Institute for Computation at Curtin University. GULP[CP]. https://gulp.curtin.edu.au/gulp
|
| [37] |
MELLOT DRAZNIEKS C, NEWSAM J M, GORMAN A M, et al. De novo prediction of inorganic structures developed through automated assembly of secondary building units (AASBU method)[J]. Angewandte Chemie International Edition, 2000, 39(13): 2270-2275. DOI:10.1002/1521-3773(20000703)39:13<2270::AID-ANIE2270>3.0.CO;2-A |
| [38] |
BANERJEE A, JASRASARIA D, NIBLETT S P, et al. Crystal structure prediction for benzene using basin-hopping global optimization[J]. The Journal of Physical Chemistry A, 2021, 125(17): 3776-3784. DOI:10.1021/acs.jpca.1c00903 |
| [39] |
WALES D J, DOYE J P K. Global optimization by basin-hopping and the lowest energy structures of lennard-Jones clusters containing up to 110 atoms[J]. The Journal of Physical Chemistry A, 1997, 101(28): 5111-5116. DOI:10.1021/jp970984n |
| [40] |
LI Z, SCHERAGA H A. Monte Carlo-minimization approach to the multiple-minima problem in protein folding[J]. Proceedings of the National Academy of Sciences of the United States of America, 1987, 84(19): 6611-6615. DOI:10.1073/pnas.84.19.6611 |
| [41] |
WALES D J, SCHERAGA H A. Global optimization of clusters, crystals, and biomolecules[J]. Science, 1999, 285(5432): 1368-1372. DOI:10.1126/science.285.5432.1368 |
| [42] |
University of Cambridge. GMIN[CP]. http://www-wales.ch.cam.ac.uk/GMIN/
|
| [43] |
RAITERI P, MARTONÁK R, PARRINELLO M. Exploring polymorphism: The case of benzene[J]. Angewandte Chemie (International Ed in English), 2005, 44(24): 3769-3773. DOI:10.1002/anie.200462760 |
| [44] |
PLUMED consortium. PLUMED[CP]. https://www.plumed.org/
|
| [45] |
WANG Y, LV J, ZHU L, et al. CALYPSO: A method for crystal structure prediction[J]. Computer Physics Communications, 2012, 183(10): 2063-2070. DOI:10.1016/j.cpc.2012.05.008 |
| [46] |
GLASS C W. USPEX-Evolutionary crystal structure prediction[J]. Computer Physics Communications, 2006, 175(11/12): 713-720. |
| [47] |
GOLDBERG D E, HOLLAND J H. Genetic algorithms and machine learning[J]. Machine Learning, 1988, 3(2/3): 95-99. DOI:10.1023/A:1022602019183 |
| [48] |
STORN R, PRICE K. Differential Evolution-A simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 |
| [49] |
HANSEN N. The CMA evolution strategy: A comparing review[M]//Towards a New Evolutionary Computation. Berlin, Heidelberg: Springer Berlin Heidelberg, 2007: 75-102
|
| [50] |
POLI R, KENNEDY J, BLACKWELL T. Particle swarm optimization[J]. Swarm Intelligence, 2007, 1(1): 33-57. DOI:10.1007/s11721-007-0002-0 |
| [51] |
MOCKUS J. Application of Bayesian approach to numerical methods of global and stochastic optimization[J]. Journal of Global Optimization, 1994, 4(4): 347-365. DOI:10.1007/BF01099263 |
| [52] |
VU K K, D'AMBROSIO C, HAMADI Y, et al. Surrogate-based methods for black-box optimization[J]. International Transactions in Operational Research, 2017, 24(3): 393-424. DOI:10.1111/itor.12292 |
| [53] |
COSTA A, NANNICINI G. RBFOpt: An open-source library for black-box optimization with costly function evaluations[J]. Mathematical Programming Computation, 2018, 10(4): 597-629. DOI:10.1007/s12532-018-0144-7 |
| [54] |
WANG Y, LV J, ZHU L, et al. Materials discovery via CALYPSO methodology[J]. Journal of Physics Condensed Matter: An Institute of Physics Journal, 2015. DOI:10.1088/0953-8984/27/20/203203 |
| [55] |
高朋越, 吕健, 王彦超, 等. 基于智能全局优化算法的理论结构预测[J]. 物理, 2017, 46(9): 582-589. GAO Pengyue, LV Jian, WANG Yanchao, et al. Structure prediction via intelligent global optimization algorithms[J]. Physics, 2017, 46(9): 582-589. (in Chinese) |
| [56] |
LV J, WANG Y, ZHU L, et al. Predicted novel high-pressure phases of lithium[J]. Physical Review Letters, 2011. DOI:10.1103/PhysRevLett.106.015503 |
| [57] |
GUILLAUME C L, GREGORYANZ E, DEGTYAREVA O, et al. Cold melting and solid structures of dense lithium[J]. Nature Physics, 2011, 7(3): 211-214. DOI:10.1038/nphys1864 |
| [58] |
ZHU L, LIU H, PICKARD C J, et al. Reactions of xenon with iron and nickel are predicted in the earth's inner core[J]. Nature Chemistry, 2014, 6(7): 644-648. DOI:10.1038/nchem.1925 |
| [59] |
WANG H, WA NG, Y, LV J, et al. CALYPSO structure prediction method and its wide application[J]. Computational Materials Science, 2016, 112: 406-415. DOI:10.1016/j.commatsci.2015.09.037 |
| [60] |
TONG Q, XUE L, LV J, et al. Accelerating CALYPSO structure prediction by data-driven learning of a potential energy surface[J]. Faraday Discussions, 2018, 211(0): 31-43. |
| [61] |
魏晓辉, 周长宝, 沈笑先, 等. 机器学习加速CALYPSO结构预测的可行性[J]. 吉林大学学报(工学版), 2021, 51(2): 667-676. WEI Xiaohui, ZHOU Changbao, SHEN Xiaoxian, et al. Accelerating CALYPSO structure prediction with machine learning[J]. Journal of Jilin University (Engineering and Technology Edition), 2021, 51(2): 667-676. DOI:10.13229/j.cnki.jdxbgxb20191070 (in Chinese) |
| [62] |
LYAKHOV A O, Oganov A R, Stokes H T. New developments in evolutionary structure prediction algorithm USPEX[J]. Computer Physics Communications, 2013, 184(4): 1172-1182. DOI:10.1016/j.cpc.2012.12.009 |
| [63] |
ZHANG W, OGANOV A R, GONCHAROV A F, et al. Unexpected stable stoichiometries of sodium chlorides[J]. Science, 2013, 342(6165): 1502-1505. DOI:10.1126/science.1244989 |
| [64] |
ZHOU X, OGANOV A R, QIAN G, et al. First-principles determination of the structure of magnesium borohydride[J]. Physical Review Letters, 2012. DOI:10.1103/PhysRevLett.109.245503 |
| [65] |
张晓铮. 过渡金属硼化物的物理性能的第一性原理研究[D]. 呼和浩特: 内蒙古工业大学, 2015 ZHANG Xiaozheng. First-principle calculations of physical properties of transitional metal borides[D]. Hohhot: Inner Mongolia University of Tehchnology, 2015 (in Chinese) |
| [66] |
PICKARD C J, NEEDS R J. Ab initio random structure searching[J]. Journal of Physics Condensed Matter, 2011. DOI:10.1088/0953-8984/23/5/053201 |
| [67] |
PICKARD C J, NEEDS R J. When is H2O not water?[J]. The Journal of Chemical Physics, 2007. DOI:10.1063/1.2812268 |
| [68] |
FENG J, HENNIG R G, ASHCROFT N W, et al. Emergent reduction of electronic state dimensionality in dense ordered Li-Be alloys[J]. Nature, 2008, 451(7177): 445-448. DOI:10.1038/nature06442 |
| [69] |
ZHU Q, JOHAL J, WIDDOWSON D E, et al. Analogy powered by prediction and structural invariants: Computationally led discovery of a mesoporous hydrogen-bonded organic cage crystal[J]. Journal of the American Chemical Society, 2022, 144(22): 9893-9901. DOI:10.1021/jacs.2c02653 |
| [70] |
BERAN G J O. Modeling polymorphic molecular crystals with electronic structure theory[J]. Chemical Reviews, 2016, 116(9): 5567-5613. DOI:10.1021/acs.chemrev.5b00648 |
| [71] |
NIKHAR R, SZALEWICZ K. Reliable crystal structure predictions from first principles[J]. Nature Communications, 2022. DOI:10.1038/s41467-022-30692-y |
| [72] |
CURTIS F, LI X Y, ROSE T, et al. GAtor: A first-principles genetic algorithm for molecular crystal structure prediction[J]. Journal of Chemical Theory and Computation, 2018, 14(4): 2246-2264. DOI:10.1021/acs.jctc.7b01152 |
| [73] |
CURTIS F, ROSE T, MAROM N. Evolutionary niching in the GAtor genetic algorithm for molecular crystal structure prediction[J]. Faraday Discussions, 2018, 211(0): 61-77. |
| [74] |
BIER I, O'CONNOR D, HSIEH Y T, et al. Crystal structure prediction of energetic materials and a twisted arene with Genarris and GAtor[J]. CrystEngComm, 2021, 23(35): 6023-6038. DOI:10.1039/D1CE00745A |
| [75] |
YIN X, GOUNARIS C E. Search methods for inorganic materials crystal structure prediction[J]. Current Opinion in Chemical Engineering, 2022. DOI:10.1016/j.coche.2021.100726 |
| [76] |
BEHLER J, PARRINELLO M. Generalized neural-network representation of high-dimensional potential-energy surfaces[J]. Physical Review Letters, 2007. DOI:10.1103/PhysRevLett.98.146401 |
| [77] |
MEREDIG B, AGRAWAL A, KIRKLIN S, et al. Combinatorial screening for new materials in unconstrained composition space with machine learning[J]. Physical Review B, 2014. DOI:10.1103/PhysRevB.89.094104 |
| [78] |
ISAYEV O, OSES C, TOHER C, et al. Universal fragment descriptors for predicting properties of inorganic crystals[J]. Nature Communications, 2017. DOI:10.1038/ncomms15679 |
| [79] |
XIE T, GROSSMAN J C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties[J]. Physical Review Letters, 2018. DOI:10.1103/PhysRevLett.120.145301 |
| [80] |
NOUIRA A, SOKOLOVSKA N, CRIVELLO J C. CrystalGAN: Learning to discover crystallographic structures with generative adversarial networks[EB/OL]. 2018: arXiv: 1810.11203. https://arxiv.org/abs/1810.11203
|
| [81] |
NOH J, KIM J, STEIN, H S, et al. Inverse design of solid-state materials via a continuous representation[J]. Matter, 2019, 1(5): 1370-1384. DOI:10.1016/j.matt.2019.08.017 |
| [82] |
XIOURAS C, CAMELI F, QUILLÓ G L, et al. Applications of artificial intelligence and machine learning algorithms to crystallization[J]. Chemical Reviews, 2022, 122(15): 13006-13042. DOI:10.1021/acs.chemrev.2c00141 |
 2023, Vol. 40
2023, Vol. 40