随着最优化方法的发展,为了避免算法陷入局部最优,更好的探索空间,相关学者提出了很多元启发式算法,从原理上大致可分为3类[1]:进化启发式算法、群体启发式算法和物理启发式算法。进化启发式算法顾名思义是一种受到生物进化过程和机制的启发,如进化、突变、迁移和繁殖等,而诞生的模拟算法。1975年,Hollod等提出了最经典的进化算法——遗传算法[2](Genetic algorithm,GA),而受到GA的启发,后续研究不断有新的进化启发式算法被提出,如鲸鱼算法[3]、灰狼算法[4]和萤火虫算法[5]等;群体启发算法是模拟群体智能而诞生的一种算法,群体依靠一定机制变化位置,进行空间搜索。代表性的群体启发算法有蚁群算法[6](Ant colony optimization,ACO)以及粒子群算法[7](Particle swarm optimization,PSO)[8]。物理启发式算法简单来说就是模拟宇宙中的物理定律,最具代表性的是模拟退火算法[9](Simulated annealing arith metic,SAA),近年来,越来越多的物理启发式算法被提出,例如雷电附着优化算法[10]、多元宇宙优化算法[11]、热传导搜索算法[12]以及本论文要介绍的原子搜索优化算法(Atom search optimization,ASO)[13]。
GA算法编码较复杂,局部搜索能力不足且存在随机游走现象[14],依靠经验选择的参数(例如交叉率、变异率)对最优解的影响较大,算法的收敛性和搜索效率差[15];ACO算法采用正反馈机制提高收敛速度,但其缺点在于一旦初期蚂蚁在次优解留下更多信息激素,正反馈机制导致次优解作为最优解迅速占据优势,引导整个系统陷入局部最优,且难以跳出局部最优[16];对于SAA算法,如果温降较慢,得到解的性能也会较好,但与此相对的是收敛速度更慢,反之,追求快速的收敛过程,提高降温速度,很可能难以找到最优解[17];ASO算法中原子间的引力促使原子更广泛的探索空间,而斥力使其更有效的开发潜在区域,其收敛速度快、寻优能力强的优势和特点,可以显著提高对复杂问题的求解效率,考虑到ASO算法的诸多优势,本工作将优化思想引入到BP(Back propagation)神经网络,构建了ASO-BP神经网络用以海底管道腐蚀速率的预测。
据统计,约有20%的海底管道事故的主要原因都是油气管线腐蚀[18],海底油气管道事故不仅会导致生产中断造成经济损失[19],更严重的是油气对海洋环境的污染[20],在倡导环境保护,绿色发展的大环境下,海底油气管道的安全必须得到保证[21],严防环境污染[22]。由于自然环境的限制,海底管道内检测成本高风险高,这就导致难以判断其腐蚀速率;另一方面,随着我国智慧管网的发展与建设,管道数据采集量随之增大,优秀的预测模型可以应对大量数据,准确预测管道腐蚀速率,对保障管道安全健康运行具有重大意义。凌晓等[23]利用Logistics混沌映射优化的萤火虫算法,建立了IFA-BPNN预测模型,用于长输管道外腐蚀速率预测时平均相对误差5.94%;李海涛等[24]采用GA优化的BP神经网络建立了金属材料在海洋环境中的腐蚀速率模型,但未能解决GA容易早熟以及其随机性问题;骆正山等[25]建立了以灰色径向基函数(RBF)为基础的神经网络预测模型,用以预测海管腐蚀速率,相对误差6.37%;El-Abbasy等[26]基于人工神经网络,建立油气管道失效预测模型;印翔等[27]将粒子群优化算法引入GM(1, 1)模型中,预测精度较高;宋莹莹[28]采用随机森林算法预测海管腐蚀速率,平均相对误差5.89%;陈永红等[29]采用遗传算法优化的最小二乘支向量机方法(GA-LSSVM)预测管道腐蚀速率,精度高于传统模型;张新生等[30]通过GM(1, 1)模型的改进,对海管进行了腐蚀深度预测,优化后的模型平均相对误差从5.96%降低至3.77%;张新生等[31]后续的研究结合主成分分析法、蚁狮优化算法、加权最小二乘支持向量机(KPCA-ALO-WLSSVM)建立的埋地管道腐蚀速率预测模型,平均误差4.39%,相较于陈永红的研究,张新生通过LSSVM算法改进后的WLSSVM算法,使得模型的学习性能和鲁棒性得到加强,提高了模型精度。
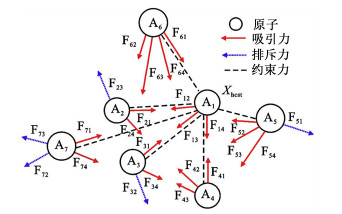
1 ASO算法原理Zhao[13]于2018年提出了ASO算法,其基本思想是:基于分子动力学模型,模拟分子系统中相邻原子之间的吸引力和排斥力,以及全局最优原子对其他原子的约束力,使原子产生位移的现象。其中吸引力促使原子广泛地探索整个搜索空间,而排斥力使它们能够有效地开发潜在区域,因此具有寻优能力强、收敛快的特点。图 1为ASO算法中原子群相互作用示意图。
|
| 图 1 原子群相互作用示意图(i=6) Fig.1 Schematic diagram of the interaction of atomic groups (i=6) |
| |
原子运动现象遵循经典力学规律,受到原子间的相互作用力Fi和最优原子对其的几何约束力Gi共同作用产生[32],原子加速度与其质量成反比,第i个原子的加速度可以表示为:
| $ a_i=\frac{F_i+G_i}{m_i} $ | (1) |
式(1)中:Fi为第i个原子所受的相互作用力;Gi第i个原子所受的共价键约束力;mi为第i个原子的质量。
1.1 相互作用力Fid相互作用力Fid表示第i个原子周围的原子对其作用力之和,可以表示为:
| $ F_i^d(t)=\sum_{j \in K_{\text {best }}(t)} \operatorname{rand}_j F_{i j}^d(t) $ | (2) |
式(2)中:d表示原子所在的维数;t表示当前迭代次数;randj为[0, 1]上的随机数;Fijd(t)表示第t次迭代中,第j个原子对原子i的Lennard-Jones势作用力。
Lennard-Jones势作用力可以表示为:
| $ F_{i j}^d(t)=-\eta(t)\left\{2\left[h_{i j}(t)\right]^{13}-\left[h_{i j}(t)\right]^7\right\} $ | (3) |
式(3)中:η(t)为深度函数,用于调整排斥区域和吸引区域;hij为2个原子之间的距离,可以定义为:
| $ \eta(t)=-\alpha\left(1-\frac{t-1}{T}\right)^3 \mathrm{e}^{-\frac{20 t}{T}} $ | (4) |
| $ h_{i j}=\frac{r_{i j}(t)}{\sigma(t)} $ | (5) |
| $ r_{i j}(t)=\left\|x_i(t), x_j(t)\right\|_2 $ | (6) |
| $ \sigma(t)=\left\|x_i(t), \frac{\sum_{j \in K_{\text {best }}(t)} x_j(t)}{K_{\text {best }}(t)}\right\| $ | (7) |
式(4)~式(7)中:α为深度权重;xi,xj分别表示原子i,j的位置;r为原子间的欧几里距离;σ表示碰撞尺度。
每个原子与多个具有较好适应度的原子产生相互作用,增强了算法跳出局部最优解和在迭代初期进行全局搜索的能力。在迭代后期,原子与邻近较少的适应度较好的原子相互作用,这种交互增强了算法的局部开发能力,保证了算法的收敛性。适应度较好的临近原子数量用K表示[32],式(2)中Kbest表示K个适应度函数值较好的原子集合,可以定义为:
| $ K_{\text {best }}(t)=N-(N-2) \times \sqrt{\frac{t}{T}} $ | (8) |
式(8)中:N为原子总数;T为总迭代次数。
1.2 几何约束力Gi| $ G_i^d(t)=\beta \mathrm{e}^{-\frac{20 t}{T}}\left[x_{\text {best }}^d(t)-x_i^d(t)\right] $ | (9) |
式(9)中:β为系数因子;xbestd(t)和xid(t)分别为第t次迭代时,种群中最佳原子位置和原子i的位置。
1.3 原子加速度将定义式(2)和(9)代入式(1),可以得到t时d维上第i个原子的加速度式:
| $ \begin{array}{c} a_i=\frac{F_i+G_i}{m}=-\alpha\left(1-\frac{t-1}{T}\right)^3 \mathrm{e}^{-\frac{20 t}{T}} \\ \sum_{j \in K_{\text {best }}(t)} \frac{\operatorname{rand}_j\left[2 h_{i j}(t)-h_{i j}(t)\right]}{m(t)}+ \\ \beta \mathrm{e}^{-\frac{20 t}{T}} \frac{x_{\text {best }}^d(t)-x_i^d(t)}{m} \end{array} $ | (10) |
此时原子质量mi(t)由当前种群个体的适应度值大小决定,可以定义为:
| $ M_i(t)=\mathrm{e}^{\frac{f_i(t)-f_{\min }(t)}{f_{\max }(t)-f_{\min }(t)}} $ | (11) |
| $ m_i(t)=\frac{M_i(t)}{\sum_{j=1}^N M_i(t)} $ | (12) |
| $ v_i^d(t+1)=\operatorname{rand}_i^d v_i^d(t)+a_i^d(t) $ | (13) |
| $ x_i^d(t+1)=x_i^d(t)+v_i^d(t+1) $ | (14) |
式(13)~式(14)中:vid和xid分别为原子速度和位置;randid为[0, 1]上的随机数。
2 ASO-BP神经网络的构建BP神经网络的结构如图 2所示,通常由输入层、隐藏层和输出层组成[33], 是一种建立在最速梯度下降法的基础上,误差反向传播,不断调整和优化神经网络的权值和阈值[34],以寻找网络最小误差平方和的方法。

|
| 图 2 BP神经网络结构示意图 Fig.2 Schematic diagram of BP neural network structure |
| |
设定BP神经网络学习的训练次数为1 000,学习速率为0.01,训练目标最小误差为10-5,动量因子0.01,最小性能梯度10-6,最高失败次数6次;ASO算法初代种群规模为30,最大进化次数为50,通过迭代计算,不断优化BP神经网络的权值和阀值。本模型建立输入层为9个影响因素,输出层为腐蚀速率,故设置输出层为1。
2.2 隐含层的确定一般来说,隐含层的节点数不唯一,而是在一个区间内。本研究根据经验公式(15)确定该区间[35],通过试值的方式确立最优节点数。
| $ m=\sqrt{n+1}+\alpha $ | (15) |
式(15)中:m为隐含层节点数,n为输入层节点数,l为输出层节点数,α为调节常数,取1~10。经计算,m的取值为4~13,分别代入预测模型,进行计算可得表 1。
| m取值 | 均方误差 | m取值 | 均方误差 | |
| 4 | 0.334 66 | 9 | 0.464 88 | |
| 5 | 0.256 60 | 10 | 0.798 73 | |
| 6 | 1.089 90 | 11 | 0.235 04 | |
| 7 | 0.258 32 | 12 | 0.575 35 | |
| 8 | 0.332 29 | 13 | 0.778 14 |
从表 1中可以看出,最佳的隐含层节点数为11,相应的均方误差为:0.235 04。
ASO-BP模型在训练中的迭代进化过程如图 3所示。

|
| 图 3 ASO-BP迭代过程 Fig.3 ASO-BP iterative process |
| |
依据中海油某管道段内腐蚀情况检查数据,以50组现场数据建立腐蚀速率预测模型,如表 2所示。
| 序号 | X0 | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 |
| 1 | 2.606 3 | 66.4 | 2.31 | 0.031 7 | 4.20 | 0.511 | 8 280 | 20.6 | 59.8 | 141 |
| 2 | 2.954 0 | 61.3 | 2.66 | 0.033 1 | 6.10 | 0.639 | 6 340 | 18.1 | 62.1 | 155 |
| 3 | 2.728 6 | 64.5 | 2.14 | 0.034 8 | 5.96 | 0.506 | 5 740 | 22.7 | 63.5 | 172 |
| 4 | 2.552 3 | 64.2 | 1.52 | 0.032 8 | 5.89 | 0.469 | 5 780 | 25.2 | 56.2 | 152 |
| 5 | 2.612 9 | 64.5 | 2.03 | 0.033 0 | 5.83 | 0.458 | 6 620 | 24.5 | 52.9 | 154 |
| 6 | 2.961 5 | 65.8 | 2.30 | 0.032 9 | 6.00 | 0.443 | 6 800 | 21.1 | 57.1 | 153 |
| 7 | 3.105 4 | 65.5 | 2.78 | 0.032 9 | 6.01 | 0.552 | 6 900 | 20.8 | 61.9 | 153 |
| 8 | 2.664 7 | 65.5 | 3.23 | 0.032 8 | 5.93 | 0.564 | 6 180 | 20.9 | 59.4 | 152 |
| 9 | 2.628 5 | 64.0 | 2.54 | 0.031 1 | 6.04 | 0.493 | 4 620 | 23.6 | 61.7 | 153 |
| 10 | 2.610 5 | 49.7 | 2.08 | 0.030 2 | 5.88 | 0.545 | 6 420 | 27.4 | 63.1 | 154 |
| ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 41 | 2.286 5 | 47.5 | 2.5 | 0.034 0 | 6.1 | 0.605 | 5 700 | 18.6 | 55.3 | 154 |
| 42 | 2.838 5 | 65.9 | 2.27 | 0.031 7 | 5.10 | 0.640 | 7 560 | 26.8 | 58.5 | 141 |
| 43 | 2.621 8 | 69.4 | 2.09 | 0.032 0 | 4.30 | 0.690 | 8 000 | 23.4 | 60.3 | 134 |
| 44 | 2.718 6 | 67.9 | 2.11 | 0.032 5 | 5.00 | 0.557 | 7 260 | 23.1 | 57.8 | 149 |
| 45 | 2.692 4 | 64.0 | 2.65 | 0.031 7 | 6.10 | 0.365 | 6 480 | 23.2 | 60.1 | 141 |
| 46 | 2.953 3 | 68.0 | 1.78 | 0.032 4 | 4.20 | 0.524 | 4 800 | 25.9 | 61.5 | 148 |
| 47 | 2.955 5 | 64.3 | 2.22 | 0.031 2 | 6.20 | 0.491 | 5 620 | 29.7 | 54.2 | 136 |
| 48 | 2.717 5 | 64.9 | 2.23 | 0.032 6 | 5.20 | 0.406 | 7 120 | 24.5 | 50.9 | 150 |
| 49 | 2.621 5 | 65.3 | 2.35 | 0.030 5 | 4.60 | 0.547 | 7 680 | 20.3 | 57.5 | 129 |
| 50 | 2.599 7 | 67.7 | 2.41 | 0.032 6 | 4.50 | 0.628 | 8 020 | 19.8 | 62.3 | 150 |
| 注:X1为温度,℃;X2为系统压力,MPa;X3为CO2分压,MPa;X4为pH值;X5为介质流速,m ·s-1;X6为Cl-浓度,mg ·L-1;X7为CO2浓度,mg ·L-1;X8为含水率,%;X9为HCO3-浓度,mg ·L-1。 | ||||||||||
为了检验ASO-BP模型的预测精度,本研究分别用经典算法GA和ACO,输出最优权值和阈值并赋值给BP神经网络,以传统的BP模型以及构建的GA-BP、ACO-BP、ASO-BP 3种预测模型进行对比。构建流程如图 4所示,结果如图 5所示。

|
| 图 4 混合模型预测流程图 Fig.4 Flow chart of mixed model prediction |
| |

|
| 图 5 预测结果对比图 Fig.5 Comparison of prediction results |
| |
为进一步评价模型的预测性能,本研究将采用平均绝对误差(MAE)、均方误差根(RSME)以及平均绝对百分比误差(MAPE)[36]作为指标对模型进行评价,结果列于表 3和表 4。
| 序号 | 腐蚀速率 | BP | GA-BP | ACO-BP | ASO-BP | |||||||
| 预测值 | MAPE/% | 预测值 | MAPE/% | 预测值 | MAPE/% | 预测值 | MAPE/% | |||||
| 1 | 2.286 5 | 2.325 2 | 1.69 | 2.28 80 | 0.07 | 2.679 4 | 17.18 | 2.420 7 | 5.87 | |||
| 2 | 2.838 5 | 2.260 6 | 20.36 | 2.932 3 | 3.30 | 2.660 6 | 6.27 | 2.826 6 | 0.42 | |||
| 3 | 2.621 8 | 2.134 7 | 18.58 | 3.410 7 | 30.09 | 2.855 9 | 8.93 | 2.658 5 | 1.40 | |||
| 4 | 2.718 6 | 2.303 7 | 15.26 | 2.436 9 | 10.36 | 2.776 7 | 2.14 | 2.810 2 | 3.37 | |||
| 5 | 2.692 4 | 2.943 7 | 9.33 | 3.123 7 | 16.02 | 2.716 7 | 0.90 | 2.437 4 | 9.47 | |||
| 6 | 2.953 3 | 1.798 4 | 39.11 | 2.177 9 | 26.25 | 2.812 0 | 4.78 | 3.022 7 | 2.35 | |||
| 7 | 2.955 5 | 2.540 2 | 14.05 | 2.918 9 | 1.24 | 3.007 5 | 1.76 | 2.997 7 | 1.43 | |||
| 8 | 2.717 5 | 2.487 7 | 8.46 | 2.344 9 | 13.71 | 3.017 2 | 11.03 | 2.697 3 | 0.74 | |||
| 9 | 2.621 5 | 2.619 9 | 0.06 | 2.628 3 | 0.26 | 2.854 2 | 8.88 | 2.657 7 | 1.38 | |||
| 10 | 2.599 7 | 2.554 8 | 1.73 | 2.513 5 | 3.32 | 2.695 6 | 3.69 | 2.733 2 | 5.14 | |||
| 模型 | MAE | RSME | MAPE/% |
| BP | 0.361 7 | 0.486 7 | 12.86 |
| GA-BP | 0.287 5 | 0.405 6 | 10.46 |
| ACO-BP | 0.170 9 | 0.205 1 | 6.56 |
| ASO-BP | 0.083 1 | 0.109 1 | 3.16 |
结果表明,本研究模型预测精度较传统的BP和GA-BP,ACO-BP模型有了显著提高,进一步表明ASO算法优化BP可以有效提高其精确度。且相对于油气管道腐蚀速率相关预测模型,其精度较高,说明本研究建立的预测模型能较好的应用于油气管道腐蚀速率的预测。
4 结论1) ASO算法作为一种新颖的智能算法,具有收敛速度快、简单易实现、寻优能力强等突出优点,本研究将ASO引入BP神经网络进行优化,从某种意义上弥补了BP收敛速度慢,容易陷入局部极值的固有缺点;2)分别使用BP、GA-BP、ACO-BP和ASO-BP神经网络对海底油气管道腐蚀速率数据训练和预测,本研究建立的ASO-BP模型MAPE为3.16%,预测结果优于BP、GA-BP和ACO-BP,验证了其可靠性以及良好的预测性能,为海底管道腐蚀速率预测研究提供了新的方法和思路;3)由于海洋环境复杂,存在的影响因素众多,且工程上难以获得其完整影响数据,后续研究可在编码中加入噪音数据。
| [1] |
王国顺. 基于改进鲸群算法的置换流水车间调度问题的应用研究[D]. 辽宁鞍山: 辽宁科技大学, 2019 WANG Guoshun. Application research of permutation flow shop scheduling problem based on improved whale algorithm[D]. Liaoning Anshan: University of Science and Technology Liaoning, 2019 (in Chinese) |
| [2] |
HOLLAND J B, HOLLAND J, HOLLAND J H, et al. Adaption in natural and artificial systems[J]. Ann Arbor, 1975, 6(2): 126-137. |
| [3] |
MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. DOI:10.1016/j.advengsoft.2016.01.008 |
| [4] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. DOI:10.1016/j.advengsoft.2013.12.007 |
| [5] |
YANG X, DEB S. Eagle strategy using Lévy walk and firefly algorithms for stochastic optimization nature inspired cooperative strategies for optimization[M]. Berlin Heidelberg: Springer, 2010
|
| [6] |
DORIGO M, MANIEZZO V, COLORNI A. Ant system: Optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 1996, 26(1): 29-41. DOI:10.1109/3477.484436 |
| [7] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of ICNN'95-International Conference on Neural Networks. Perth, WA, Australia. IEEE, 1995: 1942-1948
|
| [8] |
秦煜森, 胡凌, 青志明, 等. 基于萤火虫算法的电网节点编号优化[J]. 重庆理工大学学报(自然科学), 2017, 31(11): 198-203. QIN Yusen, HU Ling, QING Zhiming, et al. Researches on the grid node numbering optimization based on the firefly algorithm[J]. Journal of Chongqing University of Technology (Natural Science), 2017, 31(11): 198-203. (in Chinese) |
| [9] |
KIRKPATRICK S, VECCHI M P. Optimization by simulated annealing[M]//MEZARD M, PARISI G, VIRASORO M A. Spin glass theory and beyond: An introduction to the replica method and its applications. Singapore, 1987
|
| [10] |
NEMATOLLAHI A F, RAHIMINEJAD A, VAHIDI B. A novel physical based meta-heuristic optimization method known as lightning attachment procedure optimization[J]. Applied Soft Computing, 2017, 59: 596-621. DOI:10.1016/j.asoc.2017.06.033 |
| [11] |
MIRJALILI S, MIRJALILI S M, HATAMLOU A. Multi-Verse optimizer: A nature-inspired algorithm for global optimization[J]. Neural Computing and Applications, 2016, 27(2): 495-513. DOI:10.1007/s00521-015-1870-7 |
| [12] |
PATEL V K, SAVSANI V J. Heat transfer search (HTS): A novel optimization algorithm[J]. Information Sciences, 2015, 324: 217-246. DOI:10.1016/j.ins.2015.06.044 |
| [13] |
ZHAO W, WANG L, ZHANG Z. A novel atom search optimization for dispersion coefficient estimation in groundwater[J]. Future Generation Computer Systems, 2019, 91: 601-610. DOI:10.1016/j.future.2018.05.037 |
| [14] |
魏良霄, 张婷, 党乐平, 等. 一种改进的遗传算法在间歇化工过程设计中的应用[J]. 化学工业与工程, 2020, 37(4): 58-65. WEI Liangxiao, ZHANG Ting, DANG Leping, et al. Application of an improved genetic algorithm in the design of batch chemical process[J]. Chemical Industry and Engineering, 2020, 37(4): 58-65. (in Chinese) |
| [15] |
贾思奇, 郄彦辉, 李煜彤, 等. 基于遗传-神经网络算法的含均匀腐蚀缺陷油气管线爆破压力预测研究[J]. 中国安全生产科学技术, 2020, 16(12): 105-110. JIA Siqi, QIE Yanhui, LI Yutong, et al. Research on burst pressure prediction of oil and gas pipelines with uniform corrosion defects based on GA-BPNNs algorithm[J]. Journal of Safety Science and Technology, 2020, 16(12): 105-110. (in Chinese) |
| [16] |
张松灿, 普杰信, 司彦娜, 等. 蚁群算法在移动机器人路径规划中的应用综述[J]. 计算机工程与应用, 2020, 56(8): 10-19. ZHANG Songcan, PU Jiexin, SI Yanna, et al. Survey on application of ant colony algorithm in path planning of mobile robot[J]. Computer Engineering and Applications, 2020, 56(8): 10-19. (in Chinese) |
| [17] |
朱炜, 刘斌, 侯海云, 等. 4种智能算法在相平衡数据拟合中的应用[J]. 化学工业与工程, 2019, 36(4): 42-50. ZHU Wei, LIU Bin, HOU Haiyun, et al. Application of four intelligent algorithms in phase equilibrium data fitting[J]. Chemical Industry and Engineering, 2019, 36(4): 42-50. (in Chinese) |
| [18] |
詹燕红. 海底油气集输管道的腐蚀问题分析及防治措施研究[J]. 清洗世界, 2021, 37(3): 98-99. ZHAN Yanhong. Analysis of corrosion problem of submarine oil and gas gathering and transportation pipeline and research on prevention measures[J]. Cleaning World, 2021, 37(3): 98-99. (in Chinese) |
| [19] |
周晶晶. 油气管道的腐蚀与防护技术研究[J]. 中国科技博览, 2014(36): 30-30. ZHOU Jingjing. Research on corrosion and protection technology of oil and gas pipelines[J]. China Science and Technology Expo, 2014(36): 30-30. (in Chinese) |
| [20] |
崔铭伟. 多相流海管CO2内腐蚀及剩余强度研究[D]. 山东东营: 中国石油大学(华东), 2014 CUI Mingwei. Study on CO2 internal corrosion and residual strength of multiphase offshore pipeline[D]. Shandong Dongying: China University of Petroleum (Huadong), 2014 (in Chinese) |
| [21] |
丁鹏. 海底管线安全可靠性及风险评价技术研究[D]. 北京: 中国石油大学, 2008 DING Peng. Research on safety reliability and risk assessment of submarine pipeline[D]. Beijing: China University of Petroleum, 2008 (in Chinese) |
| [22] |
段继周, 刘超, 刘会莲, 等. 海洋水下设施生物污损及其控制技术研究进展[J]. 海洋科学, 2020, 44(8): 162-177. DUAN Jizhou, LIU Chao, LIU Huilian, et al. Research progress of biofouling and its control technology in marine underwater facilities[J]. Marine Sciences, 2020, 44(8): 162-177. (in Chinese) |
| [23] |
凌晓, 徐鲁帅, 高甲程, 等. 基于IFA-BPNN的长输管道外腐蚀速率预测[J]. 表面技术, 2021, 50(4): 285-293. LING Xiao, XU Lushuai, GAO Jiacheng, et al. Prediction of external corrosion rate of oil pipeline based on improved IFA-BPNN[J]. Surface Technology, 2021, 50(4): 285-293. (in Chinese) |
| [24] |
李海涛, 袁森. 基于遗传算法和BP神经网络的海洋工程材料腐蚀预测研究[J]. 海洋科学, 2020, 44(10): 33-38. LI Haitao, YUAN Sen. Corrosion prediction of marine engineering materials based on genetic algorithm and BP neural network[J]. Marine Sciences, 2020, 44(10): 33-38. (in Chinese) |
| [25] |
骆正山, 袁宏伟. 基于误差补偿的GM-RBF海底管道腐蚀预测模型[J]. 中国安全科学学报, 2018, 28(3): 96-101. LUO Zhengshan, YUAN Hongwei. GM-RBF model based error compensation for prediction of submarine pipeline corrosion[J]. China Safety Science Journal, 2018, 28(3): 96-101. (in Chinese) |
| [26] |
EL-ABBASY M S, SENOUCI A, ZAYED T, et al. Artificial neural network models for predicting condition of offshore oil and gas pipelines[J]. Automation in Construction, 2014, 45: 50-65. |
| [27] |
印翔, 黄一, 李恺强, 等. 基于粒子群优化算法的腐蚀预测灰色动态模型[J]. 腐蚀与防护, 2020, 41(1): 18-22. YIN Xiang, HUANG Yi, LI Kaiqiang, et al. A dynamic grey model of corrosion prediction based on PSO arithemetic[J]. Corrosion & Protection, 2020, 41(1): 18-22. (in Chinese) |
| [28] |
宋莹莹. 在役海底油气管道内腐蚀速率预测研究[D]. 西安: 西安建筑科技大学, 2020 SONG Yingying. Research for internal corrosion rate prediction of submarine oil and gas pipelines in service[D]. Xi'an: Xi'an University of Architecture and Technology, 2020 (in Chinese) |
| [29] |
陈永红, 苏永生, 胡平. 基于GA-LSSVM模型的管道腐蚀速率预测研究[J]. 材料保护, 2021, 54(1): 63-67. CHEN Yonghong, SU Yongsheng, HU Ping. Research on the prediction of pipelines corrosion rate based on GA-LSSVM[J]. Materials Protection, 2021, 54(1): 63-67. (in Chinese) |
| [30] |
张新生, 曹昕, 韩文超, 等. 基于参数优化GM-Markov模型的海底管道腐蚀预测[J]. 油气储运, 2020, 39(8): 953-960. ZHANG Xinsheng, CAO Xin, HAN Wenchao, et al. Prediction of submarine pipeline corrosion based on parameter optimized GM-Markov model[J]. Oil & Gas Storage and Transportation, 2020, 39(8): 953-960. (in Chinese) |
| [31] |
张新生, 张莹莹. 基于KPCA-ALO-WLSSVM的埋地管道外腐蚀速率预测[J]. 安全与环境学报, 2021. ZHANG Xinsheng, ZHANG Yingying. Prediction of external corrosion rate of buried pipeline[J]. Journal of Safety and Environment, 2021. DOI:10.13637/j.issn.1009-6094.2021.0275 (in Chinese) |
| [32] |
肖子雅, 刘升. 黄金正弦混合原子优化算法[J]. 微电子学与计算机, 2019, 36(6): 21-25, 30. XIAO Ziya, LIU Sheng. Atom search optimization based on golden-sine algorithm[J]. Microelectronics & Computer, 2019, 36(6): 21-25, 30. (in Chinese) |
| [33] |
李增刚, 王正彦, 孙敬成. 基于FPGA的手写数字BP神经网络研究与设计[J]. 计算机工程与应用, 2020, 56(17): 251-257. LI Zenggang, WANG Zhengyan, SUN Jingcheng. Research and design of handwritten digital BP neural network based on FPGA[J]. Computer Engineering and Applications, 2020, 56(17): 251-257. (in Chinese) |
| [34] |
李波, 张文泉, 马兰. 厚松散层薄基岩条件下矿井顶板涌水致灾因素分析及预测研究[J]. 山东科技大学学报(自然科学版), 2017, 36(6): 39-46. LI Bo, ZHANG Wenquan, MA Lan. Influencing factors and prediction of mine water inrush disaster under thick unconsolidated layers and thin bedrock[J]. Journal of Shandong University of Science and Technology (Natural Science), 2017, 36(6): 39-46. (in Chinese) |
| [35] |
董志贵, 王福林, 宋庆凤, 等. 基于BP神经网络的无约束优化方法[J]. 统计与决策, 2019, 35(1): 79-82. DONG Zhigui, WANG Fulin, SONG Qingfeng, et al. An unconstrained optimization method based on BP neural network[J]. Statistics & Decision, 2019, 35(1): 79-82. (in Chinese) |
| [36] |
朱广宇, 毕军, 钱大琳, 等. 一种多维度评价向量的排序模型及一致性证明[J]. 北京交通大学学报, 2007, 31(3): 35-37, 49. ZHU Guangyu, BI Jun, QIAN Dalin, et al. A sequencing model to multi-dimensional evaluation vectors and its consistency proving[J]. Journal of Beijing Jiaotong University, 2007, 31(3): 35-37, 49. (in Chinese) |
 2022, Vol. 39
2022, Vol. 39





