微波加热速度快、效率高[1],因此微波反应器被应用于辅助化工生产中[2-4]。然而,微波加热过程中会出现不可控的冷热点,具有明显的加热不均匀性[5, 6],限制了微波加热化学反应的高效性[7]。
国内外许多学者都在研究方案改善微波加热效果,钟汝能等[8]利用有限元法验证了微波反应器腔体内壁设置脊形凹槽能改善加热均匀性;Geedipalli等[9]采用有限元软件仿真发现转盘能提高微波炉内加热均匀性约40%;Meng等[10]利用COMSOL仿真计算微波炉内搅拌器旋转的加热过程。除了通过改进微波反应器的结构和加入搅拌器等辅助元件,还可以利用流体搅拌技术进一步加强微波加热效果,Peiter等[11]通过实验发现较高的搅拌速度可以在反应的第一分钟内获得较高的生物柴油产量;Louhasakul等[12]设计了一个带有搅拌桨的2 L反应槽生产生物柴油,发现当搅拌速度为1 000 r·min-1时获得最高的生物柴油产量;郭智君等[13]通过多物理场耦合计算验证了锚式搅拌桨可以改善去离子水的微波加热均匀性。
为提高微波加热化学反应的转化率和改善加热效果,研究在前期试验设计的一种微波夹层反应釜内引入流体搅拌桨[14],对釜内物料使用COMSOL仿真软件进行电磁场、温度场和流场的多物理场耦合计算,探究物料介电特性、微波功率和搅拌桨参数对微波加热特性的影响,为未来微波化学反应器的制备提供理论依据。
1 研究方法 1.1 计算模型对实验室微波反应釜[图 1(a)]进行结构优化,优化后的微波夹层反应釜的仿真模型如图 1 (b)所示。微波腔体是一个具有椭圆形底部且最外层由金属壁封闭的圆柱体,波导位于反应釜的侧面;在夹层和物料之间用一种无介电损耗的非极性材料隔开,使微波在夹层内无阻碍自由传播。搅拌桨叶与杆的材料均为聚四氟乙烯且其釜内位置和形状如图 1 (b)所示,叶轮直径为D,叶轮距离反应釜底部间隙为C,选择A100叶轮[15, 16]作为研究对象,反应釜的结构参数在表 1中。为了方便以不同的规模复制此反应釜结构,结果以无量纲数字表示,底部间隙C可用腔室高度H (H=H0+c0)归一化,写成λC (λC=C/H);叶轮直径D可用反应釜腔体直径T归一化,写成λD(λD=D/T)。

|
| 图 1 微波夹层反应釜示意图 Fig.1 Diagram of a microwave reactor with an interlayer |
| |
| Parameter | Value/mm |
| Cavity height H0 | 390 |
| Oval bottom height c0 | 60 |
| H1 | 210 |
| Reactor diameter T | 260 |
| Waveguide height h0 | 344 |
| Air interlayer thickness d | 20 |
通过耦合电磁场、传热、流动方程求解釜内微波加热特性。求解麦克斯韦方程,得到电磁加热模型中加热物料的电场E分布[17]:
| $ \left\{ {\begin{array}{*{20}{l}} {\nabla \times \mathit{\boldsymbol{H}}(\mathit{\boldsymbol{r}}, t) = \frac{\partial }{{\partial \mathit{\boldsymbol{t}}}}\mathit{\boldsymbol{D}}(\mathit{\boldsymbol{r}}, t) + \mathit{\boldsymbol{J}}(\mathit{\boldsymbol{r}}, t)}\\ {\nabla \times \mathit{\boldsymbol{E}}(\mathit{\boldsymbol{r}}, t) = - \frac{\partial }{{\partial \mathit{\boldsymbol{t}}}}\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{r}}, t)}\\ {\nabla \times \mathit{\boldsymbol{D}}(\mathit{\boldsymbol{r}}, t) = \rho (\mathit{\boldsymbol{r}}, t)}\\ {\nabla \times \mathit{\boldsymbol{B}}(\mathit{\boldsymbol{r}}, t) = 0} \end{array}} \right. $ | (1) |
式(1)中:D是电通量密度, B是磁通密度, H是磁场矢量, J是电流密度, E是电场矢量, ρ是密度, (r, t) 是时间t和空间r的函数。加热物料吸收的电磁功率Qe作为热源,由(2)计算得出[18, 19]:
| $ {Q_e} = \frac{1}{2}\omega {\varepsilon _0}{\varepsilon ^{\prime \prime }}|E{|^2} $ | (2) |
式(2)中:ε″为物料相对介电常数的虚部,|E|是电场。
釜内流动处于湍流状态,采用k-ε模型计算湍流流动与换热问题,控制方程主要包括流动连续方程、Naveir-Stokes方程[20],最后耦合求解热传递方程来描述电磁热及流动中的热传递。仿真使用COMSOL Multiphysics,并采用冷冻转子法模拟釜内搅拌流动。
连续性方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho u)}}{{\partial x}} + \frac{{\partial (\rho v)}}{{\partial y}} + \frac{{\partial (\rho w)}}{{\partial z}} = 0 $ | (3) |
Navier-Stokes方程:
| $ \begin{array}{l} \frac{{\partial (\rho u)}}{{\partial t}} + {\mathop{\rm div}\nolimits} (\rho u\mathit{\boldsymbol{u}}) = {\mathop{\rm div}\nolimits} (\mu {\mathop{\rm grad}\nolimits} u) - \frac{{\partial p}}{{\partial x}} + {S_u}\\ \frac{{\partial (\rho v)}}{{\partial t}} + {\mathop{\rm div}\nolimits} (\rho v\mathit{\boldsymbol{u}}) = {\mathop{\rm div}\nolimits} (\mu {\mathop{\rm grad}\nolimits} v) - \frac{{\partial p}}{{\partial y}} + {S_v}\\ \frac{{\partial (\rho w)}}{{\partial t}} + {\mathop{\rm div}\nolimits} (\rho w\mathit{\boldsymbol{u}}) = {\mathop{\rm div}\nolimits} (\mu {\mathop{\rm grad}\nolimits} w) - \frac{{\partial p}}{{\partial z}} + {S_w} \end{array} $ | (4) |
式(4)中:ρ是流体密度,u是速度矢量,u、v、w是x、y、z方向上的速度分量,p是压力,Su、Sv、Sw是源项,μ是动态黏度。
求解热传递方程来描述流体中的热传递:
| $ \rho {C_p}\frac{{\partial T}}{{\partial t}} + \rho {C_p}\mathit{\boldsymbol{u}} \cdot \nabla T = \nabla \cdot (k\nabla T) + {Q_{\rm{e}}} $ | (5) |
式(5)中:T为温度,u是速度向量,ρ、CP和k分别是物料的密度、热容和热导率。
1.3 边界条件与物性参数反应釜金属壁的边界条件为完美电导体,不考虑物料与外界的能量交换,物料的外表面设定为绝热边界条件。选用BJ-26波导,微波频率为2.45 GHz、功率为1 000 W,端口为横电TE10模。仿真使用的酯化反应物料为植物油,参数如表 2所示。
| Parameter | Value |
| Density/(kg·m-3) | 965 |
| Dynamic viscosity/(Pa·s) | 0.065 |
| Relative permeability | 1 |
| Thermal conductivity/[W·(m·K)-1] | 0.15 |
| Atmospheric heat capacity/[J·(kg·K)-1] | 3 000 |
| Specific heat rate | 1 |
| Relative permittivity | 2.73-0.13j[14] |
| Conductivity/(S·m-1) | 0 |
不含搅拌桨的反应釜是静态电磁加热模型,根据最佳网格尺寸公式(9)[21],将最小网格尺寸设置为4 mm,最大尺寸在10~25 mm之间,使用COMSOL非结构化自由四面体网格划分模型;模拟含搅拌桨的湍流模型,流体动力学与电磁加热耦合计算需要更细化的网格,因此对图 2物料区域的网格细化,图 3使用不同的网格划分方案探讨网格数量对转矩的影响,当网格数量为50×104时,相邻转矩之间的偏差小于1%,此时的网格数量满足网格独立性的要求。
| $ h = \frac{\lambda }{{6\sqrt {{\varepsilon ^\prime }} }} $ | (6) |

|
| 图 2 物料域网格划分图 Fig.2 Grid division diagram of material area |
| |

|
| 图 3 网格独立性分析 Fig.3 Grid independence analysis |
| |
式(6)中:h是网格尺寸,λ是自由空间波长,ε′是介电常数。
1.5 加热均匀性的量化量化加热均匀性的最有效方法之一是评估温度的变异系数(COV)[10, 22]。微波加热均匀性越好,
COV的计算值越低[23],计算公式为:
| $ {\rm{COV}} = {\sigma _1}/{\mu _1} $ | (7) |
式(7)中:σ1、μ1分别是物料的温度标准差和平均温度。由于没有考虑加热过程中模型与外界的传热,时间越长,计算结果越不准确,后文不加特殊说明COV取60 s时的仿真结果。
2 结果与讨论 2.1 物料介电特性对微波加热特性的影响实验发现物料的介电特性随着酯化反应中醇油混合物的成分比例的变化而改变,因此在无搅拌条件下,选用不同反应时间下物料的相对介电常数:14.57-9.81j (化学反应时间10 min)、3.32-0.86j (15 min)、2.73-0.13j (25 min)、2.16-0.28j (40 min)和1.81-0.07j (60 min)探究物料介电特性对微波加热的影响[24]。
不同介电常数下加热物料的电场、温度分布如图 4所示。当物料的相对介电常数较大时,图 4(a)中物料电场云图颜色范围低,场强弱,图 4(b)中物料上部温度高,下部温度低,加热均匀性差;随着反应的进行,相对介电常数降低,物料对微波的吸收作用减弱,电场云图颜色范围增大,场强升高,温度云图颜色分布变均匀,微波加热均匀性得到改善。

|
| 图 4 不同介电常数下物料电场、温度场的分布 Fig.4 Distribution of material electric and temperature field under different dielectric constants |
| |
图 5绘制了不同反应时间下不同介电特性的物料微波加热后平均温度和COV的变化,在反应初期,物料相对介电常数较大,平均温度和COV的值高,加热均匀性差;随着反应的进行,相对介电常数下降,平均温度和COV的值减小,加热均匀性改善。当物料的相对介电常数处于(2.16-0.28j)~(2.73-0.13j),微波的加热均匀性较好,因此想要反应过程中不同介电常数下微波加热效果均较佳,可以动态调整反应过程中的微波频率大小[25]。

|
| 图 5 不同介电特性物料平均温度与COV的变化 Fig.5 Variation of material COV and average temperature with different dielectric properties |
| |
取直径λD=0.38、离底间隙λC=0.15、转速N=120 r·min-1的叶轮研究搅拌时间对微波加热的影响,图 6分析了5 s内有搅拌与无搅拌物料的COV随时间的变化。

|
| 图 6 搅拌与未搅拌物料的COV随时间的变化 Fig.6 Variation of stirred and unstirred material COV over time |
| |
图 6 (a)中,无搅拌时COV随时间线性增加,加搅拌后,COV随时间增加的速度变慢。图 6 (b)绘制了物料COV下降比例
| $ \begin{array}{*{20}{c}} {y = 0.0012{x^4} - 0.017{x^3} + 0.085{x^2} - }\\ {0.0147x + 0.2494}\\ {{R^2} = 0.9999} \end{array} $ | (8) |
式(8)中:y为COV的下降比例,x为加热时间,R2为可决系数。发现当计算时间达到2 s,搅拌与无搅拌的物料COV都表现出明显的规律性,表明此时的微波加热均匀性分析具有很大的可靠性。另外,计算机很难长时间模拟微波加热搅拌流体,因此只仿真计算2 s内流体搅拌对微波加热特性的影响。
2.3 微波功率对微波加热特性的影响以叶轮直径λD=0.38、离底间隙λC=0.15、转速N=120 r·min-1为例探究微波功率对加热特性的影响,图 7 (XY截面距离反应釜底部80 mm)绘制了不同功率下物料内的电场分布,微波功率越大,物料中的电场云图颜色范围越大,电场分布效果越佳。

|
| 图 7 不同微波功率下物料内的电场分布 Fig.7 Material electric field distribution under different microwave powers |
| |
不同功率下搅拌与无搅拌2种情况下加热物料的温度分布如图 8所示,随着功率的增加,温度云图的颜色变亮,物料在单位时间内的温升增加,但热点的位置没有发生变化;对比有搅拌和无搅拌2种加热情况,有搅拌时的热点区域明显模糊化且整体云图颜色变化范围减少,因此搅拌可以有效削弱热点效应,改善加热均匀性。

|
| 图 8 不同微波功率下物料的温度分布 Fig.8 Material temperature distribution under different microwave powers |
| |
图 9计算不同功率下搅拌和无搅拌两种情况下物料的COV,图 9(a)中,2种情况下COV随功率的增加均呈线性增加,但有搅拌时的COV低于无搅拌的;图 9(b)中,随着功率的增加,2种情况下COV的差值线性增加,但COV下降比例

|
| 图 9 不同微波功率下物料温度均匀性的变化 Fig.9 Variation of material COV under different microwave powers |
| |

|
| 图 10 不同叶轮直径下的速度分布图 Fig.10 The velocity distribution under different impeller diameters |
| |
以转速N=120 r·min-1和离底间隙λC=0.15为例,探究直径λD对微波加热特性的影响,图 10中物料经叶轮搅拌后,倾斜向上移动,同时叶轮底部的物料向叶轮移动,反应釜内壁附近的物料向反应釜底部移动,从而形成循环涡流;随着直径λD的增加,涡流也越大,搅拌效果越好。
图 11绘制了不同叶轮直径下的搅拌功耗与COV,直径λD增加,叶轮旋转克服的阻力增大,功耗增加,直径λD越大,功耗增加的速度越快;图 11中COV随着直径λD的增加不断减小,加热均匀性得到改善。分析图 11中功耗与COV的斜率,直径λD较小时,功耗增加的速度低于COV减少的速度,随着直径λD增大,功耗增加的速度逐渐超过COV减小的速度,即当直径λD达到一定值后,增大直径λD对微波加热均匀性改善效果的提升速度变慢,但功耗却急剧增加。

|
| 图 11 不同叶轮直径下的搅拌功耗与COV Fig.11 Stirring power consumption and COV under different impeller diameters |
| |
以直径λD=0.5、转速N=120 r·min-1为例探讨离底间隙λC对微波加热特性的影响,图 12绘制了不同离底间隙下的流场分布,当λC=0.09时,涡流辐射范围到达反应釜底部,但搅拌对物料上部区域无效果;当λC=0.23时,物料的上部区域有明显的速度分布,但反应釜底部的流速很低。

|
| 图 12 不同底部间隙的流场分布 Fig.12 Flow field distribution of different bottom clearances |
| |
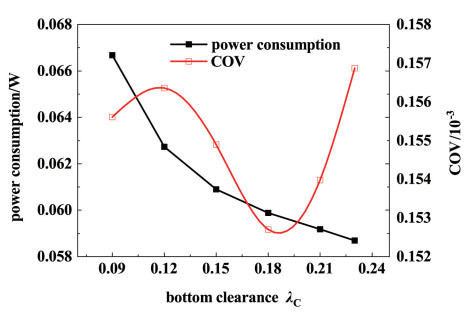
图 13计算了不同离底间隙下搅拌功耗与COV的变化,λC越大,叶轮转动克服的阻力越小,因此功耗随着λC的增大而减小;图 13中COV随着λC的增加上下波动,当λC=0.18时,COV的值最小,与流场的分析结果相符。对比功耗以及COV的曲线,离底间隙对搅拌功耗和COV影响的显著性小于叶轮直径。
|
| 图 13 不同底部间隙下的搅拌功耗与COV Fig.13 Stirring power consumption and COV under different bottom clearances |
| |
以直径λD=0.5、间隙λC=0.18为例探究搅拌转速对微波加热特性的影响,图 14绘制了不同转速下物料中流场情况,转速N=120 r·min-1时,仅叶轮附近的物料有流动迹象,随着转速增大,高流速区域急剧扩大;当N =600 r·min-1时,叶轮的搅拌作用已经扩散到整个物料区域。

|
| 图 14 不同转速下物料内的速度分布 Fig.14 Velocity distribution in the material at different stirring speeds |
| |
图 15绘制不同转速下搅拌功耗与COV的变化,随着转速N的增加,叶轮转动的阻力变大,因此功耗增加的速度越来越快;图 15中COV与搅拌转速近似呈反比关系,转速越大,搅拌混合的效果越好,物料不同区域间的温差越小,COV值越小,微波加热均匀性越好。对比功耗与COV的曲线,搅拌转速对功耗和COV的影响显著性大于离底间隙和叶轮直径。

|
| 图 15 不同转速下的搅拌功耗与COV Fig.15 Variation of stirring power consumption and COV at different stirring speeds |
| |
在这项研究中,基于前期试验结构优化后的微波夹层反应釜,将流体搅拌桨引入反应釜内,并使用COMSOL对电场、温度场、流场进行多物理场耦合计算,探究物料的相对介电常数、微波功率和搅拌桨参数对微波加热特性的影响,研究发现:1)当物料的相对介电常数在(2.16-0.28j)~(2.73-0.13j)时,微波加热均匀性较好;2)微波加热的均匀性在加热2 s后呈现出规律性的变化;3)随着微波功率的增大,相同加热时间下物料温升变快,但搅拌对物料温度均匀性的改善效果不受影响;4)叶轮直径越大、搅拌转速越高,物料的温度变异系数越低,微波加热均匀性越好,但搅拌功耗也越高;变异系数随着叶轮离底间隙的增大先减小后增大,功耗随着离底间隙的增大线性减小;5)搅拌桨参数对功耗和变异系数影响的显著性为:搅拌转速>叶轮直径>离底间隙。
| [1] |
廖雪峰, 刘钱钱, 陈晋, 等. 微波加热在干燥过程中的研究现状[J]. 矿产综合利用, 2016(4): 1-5. LIAO Xuefeng, LIU Qianqian, CHEN Jin, et al. Research status of microwave heating in drying[J]. Multipurpose Utilization of Mineral Resources, 2016(4): 1-5. DOI:10.3969/j.issn.1000-6532.2016.04.001 (in Chinese) |
| [2] |
ADAM D. Out of the kitchen[J]. Nature, 2003, 421(6923): 571-572. DOI:10.1038/421571a |
| [3] |
MOTASEMI F, ANI F N. A review on microwave-assisted production of biodiesel[J]. Renewable and Sustainable Energy Reviews, 2012, 16(7): 4719-4733. DOI:10.1016/j.rser.2012.03.069 |
| [4] |
ARPIA A A, CHEN W, LAM S S, et al. Sustainable biofuel and bioenergy production from biomass waste residues using microwave-assisted heating: A comprehensive review[J]. Chemical Engineering Journal, 2021. DOI:10.1016/j.cej.2020.126233 |
| [5] |
HORIKOSHI S, OSAWA A, ABE M, et al. On the generation of hot-spots by microwave electric and magnetic fields and their impact on a microwave-assisted heterogeneous reaction in the presence of metallic Pd nanoparticles on an activated carbon support[J]. The Journal of Physical Chemistry C, 2011, 115(46): 23030-23035. DOI:10.1021/jp2076269 |
| [6] |
VADIVAMBAL R, JAYAS D S. Non-uniform temperature distribution during microwave heating of food materials—A review[J]. Food and Bioprocess Technology, 2010, 3(2): 161-171. DOI:10.1007/s11947-008-0136-0 |
| [7] |
BARHAM J P, KOYAMA E, NORIKANE Y, et al. Microwave flow: A perspective on reactor and microwave configurations and the emergence of tunable single-mode heating toward large-scale applications[J]. The Chemical Record, 2019, 19(1): 188-203. DOI:10.1002/tcr.201800104 |
| [8] |
钟汝能, 姚斌, 向泰, 等. 腔体内壁脊形凹槽对微波反应器加热效率及均匀性的影响[J]. 食品与机械, 2017, 33(4): 81-85. ZHONG Runeng, YAO Bin, XIANG Tai, et al. Influence of ridge groove structure of the inner walls on heating efficiency and uniformity of microwave reactor[J]. Food & Machinery, 2017, 33(4): 81-85. (in Chinese) |
| [9] |
GEEDIPALLI S S R, RAKESH V, DATTA A K. Modeling the heating uniformity contributed by a rotating turntable in microwave ovens[J]. Journal of Food Engineering, 2007, 82(3): 359-368. DOI:10.1016/j.jfoodeng.2007.02.050 |
| [10] |
MENG Q, LAN J, HONG T, et al. Effect of the rotating metal patch on microwave heating uniformity[J]. Journal of Microwave Power and Electromagnetic Energy, 2018, 52(2): 94-108. DOI:10.1080/08327823.2018.1440341 |
| [11] |
PEITER A S, LINS P V S, MEILI L, et al. Stirring and mixing in ethylic biodiesel production[J]. Journal of King Saud University-Science, 2020, 32(1): 54-59. DOI:10.1016/j.jksus.2018.01.010 |
| [12] |
LOUHASAKUL Y, CHEIRSILP B, MANEERAT S, et al. Direct transesterification of oleaginous yeast lipids into biodiesel: Development of vigorously stirred tank reactor and process optimization[J]. Biochemical Engineering Journal, 2018, 137: 232-238. DOI:10.1016/j.bej.2018.06.009 |
| [13] |
郭智君, 田文艳, 刘晓华, 等. 基于多物理场计算的微波加热均匀性研究[J]. 太原科技大学学报, 2019, 40(4): 323-329. GUO Zhijun, TIAN Wenyan, LIU Xiaohua, et al. Study of uniformity of microwave heating based on multi-physics calculation[J]. Journal of Taiyuan University of Science and Technology, 2019, 40(4): 323-329. DOI:10.3969/j.issn.1673-2057.2019.04.012 (in Chinese) |
| [14] |
聂国宇, 金光远, 吴雁泽, 等. 一种带夹层釜式微波反应器加热效果模拟分析[J]. 化学工业与工程, 2020, 37(4): 49-57. NIE Guoyu, JIN Guangyuan, WU Yanze, et al. Simulation analysis of heating effect of a microwave reactor with interlayer tank[J]. Chemical Industry and Engineering, 2020, 37(4): 49-57. (in Chinese) |
| [15] |
HOSSEINI S, PATEL D, EIN-MOZAFFARI F, et al. Study of solid-liquid mixing in agitated tanks through electrical resistance tomography[J]. Chemical Engineering Science, 2010, 65(4): 1374-1384. DOI:10.1016/j.ces.2009.10.007 |
| [16] |
HOSSEINI S, PATEL D, EIN-MOZAFFARI F, et al. Study of solid-liquid mixing in agitated tanks through computational fluid dynamics modeling[J]. Industrial & Engineering Chemistry Research, 2010, 49(9): 4426-4435. |
| [17] |
HONG Y, LIN B, LI H, et al. Three-dimensional simulation of microwave heating coal sample with varying parameters[J]. Applied Thermal Engineering, 2016, 93: 1145-1154. DOI:10.1016/j.applthermaleng.2015.10.041 |
| [18] |
GOLDBLITH S A, WANG D I C. Effect of microwaves on Escherichia coli and Bacillus subtilis[J]. Applied Microbiology, 1967, 15(6): 1371-1375. DOI:10.1128/am.15.6.1371-1375.1967 |
| [19] |
HUANG K, LIAO Y. Transient power loss density of electromagnetic pulse in Debye media[J]. IEEE Transactions on Microwave Theory and Techniques, 2015, 63(1): 135-140. DOI:10.1109/TMTT.2014.2374158 |
| [20] |
SALOMATOV V V. Computational modeling of turbulent flows[J]. Journal of Engineering Thermophysics, 2020, 156-69. |
| [21] |
LIU S, FUKUOKA M, SAKAI N. A finite element model for simulating temperature distributions in rotating food during microwave heating[J]. Journal of Food Engineering, 2013, 115(1): 49-62. DOI:10.1016/j.jfoodeng.2012.09.019 |
| [22] |
HE J, YANG Y, ZHU H, et al. Microwave heating based on two rotary waveguides to improve efficiency and uniformity by gradient descent method[J]. Applied Thermal Engineering, 2020. DOI:10.1016/j.applthermaleng.2020.115594 |
| [23] |
TANG Z, HONG T, LIAO Y, et al. Frequency-selected method to improve microwave heating performance[J]. Applied Thermal Engineering, 2018, 131: 642-648. DOI:10.1016/j.applthermaleng.2017.12.008 |
| [24] |
宋睿, 金光远, 崔政伟, 等. 酯交换反应体系混合物料的介电特性[J]. 化工学报, 2018, 69(8): 3670-3677. SONG Rui, JIN Guangyuan, CUI Zhengwei, et al. Dielectric properties of mixed materials in transesterification reaction system[J]. CIESC Journal, 2018, 69(8): 3670-3677. (in Chinese) |
| [25] |
姚伟, 朱铧丞, 杨阳, 等. 基于选频技术的高效高均匀性微波加热[J]. 太赫兹科学与电子信息学报, 2020, 18(2): 269-272. YAO Wei, ZHU Huacheng, YANG Yang, et al. Microwave heating with high efficiency and uniformity based on frequency-selected technology[J]. Journal of Terahertz Science and Electronic Information Technology, 2020, 18(2): 269-272. (in Chinese) |
 2022, Vol. 39
2022, Vol. 39





