2. 河北冀衡集团有限公司, 河北 衡水 053000
2. Hebei Jiheng Group Co., Ltd., Hebei Hengshui 053000, China
过硫酸铵((NH4)2S2O8,CAS:7727-54-0),又称高硫酸铵、过二硫酸铵,英文名称Ammonium Persulfate (APS)[1, 2]是一种大宗化工产品,白色单斜结晶或粉末状晶体,易溶于水(0 ℃时溶解度为56.2 g),潮湿空气中易受潮结块[3, 4]。过硫酸铵吸湿后发生水解反应;受热或在银盐等物质的催化作用下,能发生氧化分解,并放出大量热量。过硫酸铵属于危险品,自身或与某些还原性较强的有机物混合,可引起着火或爆炸[5, 6]。过硫酸铵在较低温度下可分离成自由基,具有强氧化性和腐蚀性; 主要用于制造过硫酸盐和双氧水,在有机合成、电子、纺织印染等领域也具有广泛的用途[7-9]。
目前工业生产的过硫酸铵产品普遍存在晶体粒度分布宽、细碎晶体多、产品结块严重等问题。结块导致过硫酸铵在使用前需要进行破碎处理,给产品的使用带来诸多不便[10-12],限制了过硫酸铵产品的应用,降低了产品的使用价值,因此优化从硫酸铵电解液中结晶过硫酸铵的工艺具有重要的工程实践意义。过硫酸铵水溶液高温易分解,故工业生产中多采用冷却结晶生产过硫酸铵[13, 14]。但是由于其结晶热力学和动力学等理论研究的缺失,工业化生产中缺乏有力的支持与指导。基于上述过硫酸铵工业化生产现状,对硫酸铵电解液中过硫酸铵结晶过程的热力学和动力学行为进行了的研究。
1 实验 1.1 实验试剂与仪器| 名称 | w | 等级 | 来源 |
| (NH4)2SO4 | ≥0.995 | GR | 天津科密欧化学试剂有限公司 |
| (NH4)2S2O8 | ≥0.990 | AR | 天津科密欧化学试剂有限公司 |
| I2 | ≥0.998 | AR | 天津煜翔科技有限公司 |
| KI | ≥0.990 | AR | 上海麦克林生化科技有限公司 |
| 去离子水 | 18.2 MΩ·cm | UP | 天津大学结晶中心纯水仪自制 |
| 仪器名称 | 型号/规格 | 生产厂家 |
| 冰机 | CF41 | 优莱博实验室技术有限公司 |
| 加热磁力搅拌器 | EMS-9A | 天津市欧诺仪器仪表有限公司 |
| 机械搅拌器 | HD2015W | 上海司乐仪器有限公司 |
| 微机自动电位滴定仪 | WDDY-2008 | 泰州大唐分析仪器有限公司 |
| 离子色谱仪 | ICS-5000 | 美国赛默飞世尔科技公司 |
| 分析天平 | AL104 | 瑞士梅特勒托莱多仪器有限公司 |
| X射线粉末衍射仪 | D/max-2500 | 日本理学电机株式会社 |
本工作中(NH4)2S2O8-(NH4)2SO4-H2O体系的三元相图研究采用的是等温溶解平衡法[15-17]。在实验温度下,将一种盐分批少量加入到另一种盐的饱和溶液中,当达到平衡后,分析液相的组成[18],实验装置图如图 1所示。

|
| 图 1 测定三元相图的实验装置图 Fig.1 The experimental equipment in measuring the ternary phase diagram |
| |
具体实验步骤如下:1)将定量的去离子水倒入放有磁子的结晶器中,确保结晶器的密封性;2)将与结晶器连接的冰机设置为实验目标温度,待温度恒定;3)加入过量的一种盐,确保搅拌开启后溶液中有未溶解的盐;4)加入另一种盐,并根据实验计划设置不同的配比,搅拌20 h,以保证体系达到固液平衡;5)停止磁力搅拌,体系静置2 h使上层液体澄清。用注射器取1~2 mL上层清液,透过滤膜(0.22 μm)注入100 mL容量瓶中,确定取样的质量后稀释定容;6)稀释后的平衡液相用淀粉碘化钾滴定法确定S2O82-的浓度(参考HG/T 3818-2006《工业过硫酸铵》);7)用离子色谱建立SO42-的浓度标准曲线,测定稀释后的平衡液相用中SO42-的浓度;8)改变实验温度,重新配置实验体系,重复以上步骤。
1.2.2 介稳区及诱导期实验方法介稳区的测定:1)根据测定温度下的(NH4)2S2O8在纯水中的溶解度数据,配制该温度下的饱和溶液;2)固定机械搅拌速率,设置冰机温度至配制溶液的饱和温度以上5 K,完全溶解后恒温30 min;3)开启激光发射器,按预定降温速率(6、18、30和48 K·h-1)开始降温。当接收屏上的光线透光率开始变化时,迅速读取此时溶液中温度计的示数,即为对应的过饱和温度;4)改变机械搅拌速率和降温速率,重复上述实验操作,即可得到不同条件下的超溶解度曲线,对照溶解度曲线即可得到(NH4)2S2O8在不同条件下的介稳区。
诱导期的测定:1)根据测定的(NH4)2S2O8在纯水中的溶解度数据和实验所需的过饱和度S,称量一定量的(NH4)2S2O8和去离子水,加入到结晶器中;2)固定磁力搅拌速率,设定冰机温度为高于溶解温度5 K;3)待固体完全溶解后,将体系恒温30 min,并开启激光发射器;4)关闭恒温槽,重新接入温度为目标过饱和度所需温度的恒温水浴;5)从转换恒温水浴完成后开始计时,此时为诱导期起点;6)观察激光接收屏上光线的变化,当光的透过率发生变化,表示体系已经发生初级成核现象,此时刻为诱导期终点,起点与终点的间隔为诱导期记做tind;7)改变实验中(NH4)2S2O8的浓度或温度设定值,重复上述实验操作,测量不同条件下的诱导期。
2 结果与讨论 2.1 三元相图测定结果根据实验测得的相平衡数据(表 3、表 4、表 5和表 6)绘制所得三元相图,如图 2、图 3和图 4所示。
| 编号 | w(水) | w[(NH4)2SO4] | w[(NH4)2S2O8] |
| 1 | 0.582 1 | 0.371 3 | 0.046 6 |
| 2 | 0.580 0 | 0.350 4 | 0.069 6 |
| 3 | 0.580 2 | 0.326 8 | 0.093 0 |
| 4 | 0.671 5 | 0.027 0 | 0.301 5 |
| 5 | 0.683 8 | 0.055 2 | 0.261 1 |
| 6 | 0.680 0 | 0.082 1 | 0.237 9 |
| 7 | 0.665 6 | 0.106 6 | 0.227 9 |
| 8 | 0.657 8 | 0.132 1 | 0.210 2 |
| 9 | 0.664 9 | 0 | 0.335 1 |
| 10 | 0.595 9 | 0.404 1 | 0 |
| 11 | 0.579 4 | 0.304 4 | 0.116 2 |
| 编号 | w(水) | w[(NH4)2SO4] | w[(NH4)2S2O8] |
| 1 | 0.565 1 | 0.379 2 | 0.055 7 |
| 2 | 0.548 3 | 0.338 6 | 0.113 1 |
| 3 | 0.571 7 | 0.063 1 | 0.365 2 |
| 4 | 0.563 6 | 0.143 6 | 0.292 8 |
| 5 | 0.552 4 | 0.197 2 | 0.250 5 |
| 6 | 0.531 2 | 0.307 9 | 0.160 9 |
| 7 | 0.577 0 | 0 | 0.423 0 |
| 8 | 0.574 4 | 0.425 6 | 0 |
| 9 | 0.516 8 | 0.290 7 | 0.192 6 |
| 10 | 0.565 1 | 0.379 2 | 0.055 7 |
| 编号 | w(水) | w[(NH4)2SO4] | w[(NH4)2S2O8] |
| 1 | 0.545 8 | 0.389 3 | 0.064 9 |
| 2 | 0.524 1 | 0.347 2 | 0.128 7 |
| 3 | 0.508 6 | 0.300 5 | 0.190 9 |
| 4 | 0.524 8 | 0.086 3 | 0.388 8 |
| 5 | 0.518 4 | 0.137 8 | 0.343 8 |
| 6 | 0.511 4 | 0.213 9 | 0.274 7 |
| 7 | 0.519 8 | 0 | 0.480 2 |
| 8 | 0.561 5 | 0.438 6 | 0 |
| 9 | 0.502 4 | 0.247 5 | 0.250 1 |
| 10 | 0.500 0 | 0.301 5 | 0.198 5 |
| 温度/K | m(水) | m(硫酸铵) | m(过硫酸铵) | w(硫酸铵) | w(过硫酸铵) | w(硫酸铵)/w(水) | w(过硫酸铵)/w(水) |
| 303.15 | 0.469 2 | 0.275 3 | 0.217 6 | 0.287 6 | 0.226 1 | 0.586 9 | 0.463 8 |
| 288.15 | 0.360 4 | 0.202 7 | 0.134 3 | 0.290 6 | 0.192 6 | 0.562 5 | 0.372 6 |
| 267.15 | 0.427 2 | 0.224 4 | 0.085 6 | 0.304 3 | 0.116 2 | 0.525 3 | 0.200 6 |

|
| 图 2 267.15 K下(NH4)2S2O8-(NH4)2SO4-H2O的三元相图 Fig.2 Ternary phase diagram of (NH4)2S2O8-(NH4)2SO4-H2O at 267.15 K |
| |

|
| 图 3 288.15 K下(NH4)2S2O8-(NH4)2SO4-H2O的三元相图 Fig.3 Ternary phase diagram of (NH4)2S2O8-(NH4)2SO4-H2O at 288.15 K |
| |

|
| 图 4 303.15 K下(NH4)2S2O8-(NH4)2SO4-H2O的三元相图 Fig.4 Ternary phase diagram of (NH4)2S2Ο8-(NH4)2SO4-H2O at 303.15 K |
| |
结果表明,在267.15、288.15和303.15 K 3个温度下的(NH4)2S2O8-(NH4)2SO4-H2O三元相图都有1个共饱和点,2条溶解度曲线,点A、B和C分别代表纯(NH4)2SO4、纯(NH4)2S2O8和H2O。点M和N分别代表对应温度下(NH4)2S2O8和(NH4)2SO4在纯水中的溶解度。
点O是(NH4)2S2O8和(NH4)2SO4共同存在下的共饱和点。由此可以看出,曲线OM和曲线ON分别是(NH4)2S2O8和(NH4)2S2O8和(NH4)2SO4在溶有另外一种固体的水中的溶解度曲线。
从图(2)~图(4)数据可以看出,按照303.15、288.15和267.15 K降温次序,共饱和点逐渐向右上方移动,单(NH4)2S2O8固体存在的固液相区逐渐变大,单(NH4)2SO4固体存在的固液相区逐渐变小。需要关注的是,(NH4)2S2O8在共饱和点中所占的质量百分比越来越低,303.15 K的共饱和点中质量占比w(过硫酸铵)为22.62%;288.15 K时,这一数值变为19.26%;267.15 K时降低为11.62%。而(NH4)2SO4在共饱和点中所占的质量百分比是逐步增加的,主要是由(NH4)2S2O8在体系中所占质量百分比迅速减少导致的,实际上,303.15、288.15和267.15 K 3个温度下的共饱和点中,(NH4)2S2O8和(NH4)2SO4与溶剂水的质量比值是逐步降低的,w(过硫酸铵)/w(水)依次为0.463 8、0.372 6和0.200 6。(NH4)2S2O8-(NH4)2SO4-H2O相平衡数据和相图通过冷却结晶将(NH4)2S2O8从三元体系中分离的过程提供了热力学依据。
2.2 过硫酸铵结晶动力学结晶动力学是分析、设计与优化结晶过程的重要基础数据。通过测量(NH4)2S2O8的介稳区性质及结晶诱导期,对(NH4)2S2O8结晶动力学进行了研究。
2.2.1 不同温度不同降温速率下的介稳区变化搅拌速率为300 r·min-1的条件下,研究了不同的降温速率(6、18、30和48 K·h-1)对不同温度下(NH4)2S2O8饱和溶液介稳区宽度的影响。可以得到不同温度下(NH4)2S2O8饱和溶液的介稳区宽度与降温速率的变化关系图如图 5所示。

|
| 图 5 降温速率对介稳区宽度的影响 Fig.5 The influence of cooling rate on the metastable zone |
| |
当固定搅拌速率为300 r·min-1,降温速率为6 K·h-1时,(NH4)2S2O8在纯水中的介稳区宽度随温度的升高变窄。随着温度的升高,离子的布朗运动加快,离子的碰撞频率增大,有利于晶体成核。从而导致介稳区宽度随着温度的升高变窄。
当搅拌速率一定、且(NH4)2S2O8饱和温度一定时,(NH4)2S2O8在纯水中的介稳区宽度会随着降温速率的增大而增大。这主要是因为晶核的形成需要一定的时间,增加降温速率,达到相同的温度时间缩短,(NH4)2S2O8在较短的时间内没有形成稳定的晶核,这也就造成了介稳区宽度的增加。
更进一步,本研究利用实验测定的介稳区宽度数据,用Self-consistent Nývlt-like方程确定了(NH4)2S2O8在纯水中的成核动力学相关参数[19, 20]。
Nývlt方程由Nývlt在1968年推导提出,研究了介稳区宽度与溶液的结晶动力学关系,可以表示为:
| $ \ln \Delta T_{\max }=\frac{1-m}{m} \ln \left(\frac{\mathrm{d} c}{\mathrm{~d} T}\right)-\frac{1}{m} \ln k+\frac{1}{m} \ln R $ | (1) |
式(1)中:ΔTmax是介稳区宽度;T为温度,K;c表示摩尔分数溶解度;m,k和R分别为表观成核级数、成核常数以及降温速率。
Sangwal对Nývlt方程方程进行了修正,提出了Self-consistent Nývlt-like方程,用式(2)表示:
| $ \ln \frac{\Delta T_{\max }}{T_{0}}=\frac{1-m}{m} \ln \left(\frac{\Delta H_{\mathrm{S}}}{R_{\mathrm{G}} T_{\mathrm{lim}}}\right)+\frac{1}{m} \ln \left(\frac{f}{K T_{0}}\right)+\frac{1}{m} \ln R $ | (2) |
式(2)中:T0为饱和温度;ΔHS和RG分别为溶解焓和理想气体常数8.314 J·mol-1·K-1;Tlim为出晶温度;f为比例常数;K为成核速率常数;其他参数与式(1)中一致。
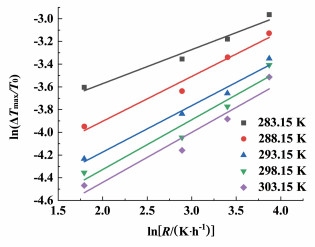
图 6中,ln(ΔTmax/T0)与lnR有较好的线性关系,温度从低到高R2值依次为:0.955 3、0.961 5、0.971 5、0.909 6和0.907 5。公式(2)中,ln(ΔTmax/T0)与lnR之间可以表示为系数1/m的线性关系,ΔHS/RG的值可以利用溶解度数据求解得出。利用以上两式求出的成核级数m与成核常数k如表 7所示。
|
| 图 6 不同饱和温度下ln (ΔTmax/T0) 与lnR的关系图 Fig.6 The relationship of ln (ΔTmax/T0) versus lnR at different saturation temperatures |
| |
| 饱和温度T0/K | 成核级数m | 成核速率常数k/(m-3·s-1) |
| 283.15 | 3.340 0 | 5 123.387 2 |
| 288.15 | 2.534 2 | 5 057.436 4 |
| 293.15 | 2.445 5 | 5 011.310 2 |
| 298.15 | 2.283 1 | 3 347.955 9 |
| 303.15 | 2.272 7 | 3 943.018 7 |
经计算发现模型对介稳区的拟合效果较好。拟合得到的成核级数m、成核常数k如表 7所示。
2.2.2 搅拌速率对介稳区的影响本实验测定了在固定的降温速率为6 K·h-1的条件下,3个不同的搅拌速率(400、300和200 r·min-1)对介稳区宽度的影响,根据实验数据可以得到不同搅拌速率(400、300和200 r·min-1)下的超溶解度曲线与溶解度曲线的关系图,如图 7所示。可以看出,随着搅拌速率的增大,(NH4)2S2O8在纯水中的介稳区宽度逐渐变窄。这是因为介稳区本质上就是一个不稳定的动力学性质,很容易受到外界波动的影响,搅拌的加入,人为破坏了溶液体系的的亚稳状态,搅拌速率的提高,加速了由热力学亚稳状态向热力学稳定状态转变的过程。

|
| 图 7 搅拌速率对介稳区宽度的影响 Fig.7 The influence of stirring rate on the metastable zone |
| |
采用激光法研究了在固定温度和搅拌速度300 r·min-1条件下,过饱和度S对(NH4)2S2O8在纯水中诱导期的影响,并且将其做了进一步的研究。不同温度下(NH4)2S2O8在纯水中的诱导期随过饱和度的变化趋势,如图 8所示。

|
| 图 8 不同温度下过饱和度对诱导期的影响 Fig.8 The influence of supersaturation on the induction time at different temperature |
| |
根据经典成核理论可以得出过饱和度越大,聚集形成的晶簇浓度随着过饱和度的增大而升高,有利于成核,即有更短的诱导期。宏观表现为,在一定温度下诱导期tind随着过饱和度S的增大而逐渐减小。另外,在过饱和度相同的条件下,溶液处于较高温度时的诱导期明显低于较低温度时的诱导期。这是因为较高温度的溶液内部分子运动速率快,能量高。
在所考察的3个温度下,当过饱和度S超过1.23以后,诱导期的变化逐渐趋于平缓,即温度对诱导期的影响不再明显。其原因为,当过饱和度增大到一定程度时,溶质分子之间相互碰撞的频率极大地增加了,成核受到分子运动速率的影响较弱。
将lntind随ln-2S的变化数据作图,如图 9所示。从图 9中可以看出,当出晶温度一定时,每个温度下的lntind与ln-2S都可以认为是由2条斜率不同的直线构成,2条直线有1个交点,交点分布在S≈1.23左右。这是因为,在对应的过饱和度左右两侧,其主要成核方式不一致。3个出晶温度下的交点的横坐标基本一致,交点对应的过饱和度是(S≈1.23)。lntind与ln-2S关系如式(3)~(8):

|
| 图 9 不同温度下lntind与ln-2S的关系图 Fig.9 The diagram of lntind versus ln-2S at different temperatures |
| |
在278.15 K下的关系式:
| $ S<1.23, \ln t_{\text {ind }}=0.0684 \ln ^{-2} S+5.9849, R^{2}=0.9834 $ | (3) |
| $ S>1.23, \ln t_{\text {ind }}=0.4912^{-2} S-3.0157, R^{2}=0.9673 $ | (4) |
在278.15 K下的关系式:
| $ S<1.23, \ln t_{\text {ind }}=0.0707 \ln ^{-2} S+6.4734, R^{2}=0.9842 $ | (5) |
| $ S>1.23, \ln t_{\text {ind }}=0.4406 \ln ^{-2} S-1.2096, R^{2}=0.9862 $ | (6) |
在283.15 K下的关系式:
| $ S<1.23, \ln t_{\text {ind }}=0.0619 \ln ^{-2} S+7.2951, R^{2}=0.9762 $ | (7) |
| $ S>1.23, \ln t_{\text {ind }}=0.4681 \ln ^{-2} S-1.1549, R^{2}=0.9898 $ | (8) |
相同温度下,出现2条斜率不同的直线的原因是:当过饱和度小于1.23时,非均相成核为其主要的成核方式;当过饱和度大于1.23时,均相成核为其主要的成核方式[21, 22]。
根据成核速率方程变形得到和诱导期相关的公式:
| $ \ln t_{\mathrm{ind}}=Y+\frac{16 {\mathtt{π}} \gamma^{3} V_{\mathrm{S}}^{2}}{3 k_{\mathrm{B}}^{3} T_{\mathrm{lim}}^{3} \ln ^{2} S} $ | (9) |
式(9)中:Y为常数。在一定温度范围内,lntind与1/ln2S呈线性关系。可以通过测量诱导期数据得斜率,记绘制曲线斜率为α,表达式如式(10):
| $ \alpha=\frac{16 {\mathtt{π}} \gamma^{3} V_{\mathrm{S}}^{2}}{3 k_{\mathrm{B}}^{3} T_{\mathrm{lim}}^{3}} $ | (10) |
变形得到固液表面张力γ表达式,如式(11)所示:
| $ \gamma=\left(\frac{3 \alpha k_{\mathrm{B}}^{3} T_{\mathrm{lim}}^{3}}{16 {\mathtt{π}} V_{\mathrm{S}}^{2}}\right)^{1 / 3} $ | (11) |
式(9)~式(11)中:VS表示分子体积,Tlim为出晶温度,kB=1.3806×10-23 J·K-1,表示玻尔兹曼常数,S表示过饱和度比,γ表示表面张力。根据lntind与1/ln2S呈线性关系的拟合结果,代入式(9)~式(11),分别计算得到273.15、278.15和283.15 K 3个不同温度下的固液表面张力γ分别为:0.085 01、0.083 49及0.086 72 J·m-2。
根据经典成核理论得到晶胚的吉布斯自由能ΔG(r)的表达式:
| $ \Delta G(r)=-\left(\frac{k_{\mathrm{v}} r^{3}}{V_{\mathrm{S}}}\right) k_{\mathrm{B}} T \ln S+k_{\mathrm{a}} r^{2} \gamma $ | (12) |
对其求导变形可得
| $ \Delta G_{\text {crit }}=\frac{k_{\mathrm{a}} r_{\text {crit }}{ }^{2} \gamma}{3}=\frac{16 {\mathtt{π}} \gamma^{3} V_{\mathrm{S}}^{2}}{3\left(k_{\mathrm{B}} T \ln S\right)^{2}} $ | (13) |
| $ i_{\text {crit }}=\frac{4 {\mathtt{π}} r_{\text {crit}}{}^{3}}{3 V_{\mathrm{S}}} $ | (14) |
式(12)~式(14)中kv、ka分别表示的晶胚的体积和面积形状因子,在这里可以近似的将粒子当做球形的处理,其值分别为4π/3和4π。VS表示分子体积,kB=1.380 6×10-23 J·K-1,表示玻尔兹曼常数,S表示过饱和度比,γ表示表面张力。将固液表面张力γ的数值分别带入式(12)~式(14),即可得到对应条件下,初级均相成核的临界晶核粒径rcrit、临界成核自由能ΔGcrit、临界分子数icrit以及初级成核速率J的表达式。
在273.15 K下的相关表达式:
| $ \gamma_{\text {crit }}=\frac{2 V_{\mathrm{s}} \gamma}{k_{\mathrm{B}} T \ln S}=\frac{7.21 \times 10^{-11}}{\ln S} $ | (15) |
| $ \Delta G_{\text {crit }}=\frac{16 {\mathtt{π}} \gamma^{3} V_{\mathrm{S}}^{2}}{3\left(k_{\mathrm{B}} T \ln S\right)^{2}}=\frac{1.8522 \times 10^{-21}}{\ln ^{2} S} $ | (16) |
| $ i_{\text {crit }}=\frac{4 {\mathtt{π}}\left(r_{\text {crit }}\right)^{3}}{3 V_{\mathrm{S}}}=\frac{90.23}{\ln ^{3} S} $ | (17) |
| $ J=A \exp \left(-\frac{\Delta G_{\text {crit }}}{k_{\mathrm{B}} T}\right)=A \exp \left(-\frac{49.115}{\ln ^{2} S}\right) $ | (18) |
在278.15 K下的相关表达式:
| $ r_{\text {crit }}=\frac{2 V_{\mathrm{S}} \gamma}{k_{\mathrm{B}} T \ln S}=\frac{6.95743 \times 10^{-11}}{\ln S} $ | (19) |
| $ \Delta G_{\text {crit }}=\frac{16 {\mathtt{π}} \gamma^{3} V_{\mathrm{S}}^{2}}{3\left(k_{\mathrm{B}} T \ln S\right)^{2}}=\frac{1.692 \times 10^{-21}}{\ln ^{2} S} $ | (20) |
| $ i_{\text {crit }}=\frac{4 {\mathtt{π}}\left(r_{\text {crit }}\right)^{3}}{3 V_{\mathrm{S}}}=\frac{88.12}{\ln ^{3} S} $ | (21) |
| $ J=A \exp \left(-\frac{\Delta G_{\text {crit }}}{k_{\mathrm{B}} T}\right)=A \exp \left(-\frac{44.062}{\ln ^{2} S}\right) $ | (22) |
在283.15 K下的相关表达式:
| $ r_{\text {crit }}=\frac{2 V_{\mathrm{s}} \gamma}{k_{\mathrm{B}} T \ln S}=\frac{7.09916 \times 10^{-11}}{\ln S} $ | (23) |
| $ \Delta G_{\text {crit }}=\frac{16 {\mathtt{π}} \gamma^{3} V_{\mathrm{S}}^{2}}{3\left(k_{\mathrm{B}} T \ln S\right)^{2}}=\frac{1.8299 \times 10^{-21}}{\ln ^{2} S} $ | (24) |
| $ i_{\text {crit }}=\frac{4 {\mathtt{π}}\left(r_{\text {crit }}\right)^{3}}{3 V_{\mathrm{S}}}=\frac{93.62}{\ln ^{3} S} $ | (25) |
| $ J=A \exp \left(-\frac{\Delta G_{\text {crit }}}{k_{\mathrm{B}} T}\right)=A \exp \left(-\frac{46.81}{\ln ^{2} S}\right) $ | (26) |
对(NH4)2S2O8冷却结晶的结晶过程热力学和动力学进行研究和讨论,为开发新的结晶工艺提供理论基础。
首先采用等温溶解度法测定了303.15、288.15和267.15 K 3个温度下(NH4)2S2O8-(NH4)2SO4-H2O的相平衡数据,分析了相图和共饱和点随温度变化而变化的规律,得出温度从303.15 K变为267.15 K时共饱和点中w(过硫酸铵)从22.62%大幅度降低为11.62%,而与之相对的w(硫酸铵)/w(水)仅仅是从0.586 9降低为0.525 2,基本没有变化。温度降低,w(过硫酸铵)大幅降低,表明通过冷却结晶手段将(NH4)2S2O8从三元体系中分离从热力学上是可行的。w(水)/w(硫酸铵)随温度降低只产生微幅波动的特点表明在降温过程中,三元体系中的(NH4)2S2O8只有微小量的析出。利用这一点,工业生产中在降温开始前可以通过添加过(NH4)2SO4,使体系中的(NH4)2SO4接近267.15 K共饱和点中(NH4)2SO4的含量。这一操作在保证(NH4)2S2O8的纯度的前提下,可以提高(NH4)2S2O8的单程收率。(NH4)2S2O8-(NH4)2SO4-H2O的相平衡数据为工业生产提供了热力学可行性分析和提升生产效益的手段。
利用激光法测定了不同温度下(NH4)2S2O8在纯水中的超溶解度和诱导期数据,绘制出了(NH4)2S2O8在纯水中的介稳区和诱导期相关图表。研究了降温速率、搅拌速率对(NH4)2S2O8介稳区宽度的影响;利用成核理论、介稳区数据和Self-consistent Nývlt-like方程计算得到了成核级数和成核常数随温度的降低而升高,即在实验温度范围内温度越低成核越困难,相关数据已在表 7中列出。解释了(NH4)2S2O8介稳区随温度降低、降温速率增加和搅拌速率降低而增加的原因。利用诱导期数据拟合出以过饱和度1.23为分界点的3个温度下的lntind与ln-2S关系、计算得到了273.15、278.15和283.15 K温度下的固液表面张力γ为:0.085 01、0.083 49及0.086 72 J·m-2。初级均相成核的临界晶核粒径rcrit、临界成核自由能ΔGcrit、临界分子数icrit以及初级成核速率J的表达式。工业产品存在严重的结块问题,动力学参数的确定,可以指导生产过程中的工艺优化。生产出晶体形貌完整、粒度分布均一产品,解决工业产品结块严重的问题。
| [1] |
华和维. 过硫酸铵连续结晶工艺与设备研究[D]. 西安: 西安石油大学, 2013 HUA Hewei. Research on the ammonium persulfate's continuous technology and equipment[D]. Xi'an: Xi'an Shiyou University, 2013 (in Chinese) |
| [2] |
魏婷. 过硫酸铵连续结晶器流场模拟[D]. 西安: 西安石油大学, 2015 Wei Ting, Flow field simulation of ammonium persulfate continuous crystallizer[D]. Xi'an: Xi'an Shiyou University, 2015(in Chinese) |
| [3] |
高毅颖, 郭强, 王洋洋, 等. 一种过硫酸铵结晶体的制备方法: CN109665498B[P]. 2020-04-03
|
| [4] |
樊玉光, 魏婷, 华和维. 降温速率对过硫酸铵结晶介稳区影响的研究[J]. 无机盐工业, 2014, 46(10): 23-25. FAN Yuguang, WEI Ting, HUA Hewei. Study on effects of cooling rate on ammonium persulfate's crystallization metastable zone[J]. Inorganic Chemicals Industry, 2014, 46(10): 23-25. DOI:10.3969/j.issn.1006-4990.2014.10.005 (in Chinese) |
| [5] |
陈迎春, 经建生, 田亮, 等. 过硫酸铵的热不稳定性分析[J]. 消防科学与技术, 2005, 24(4): 408-411. CHEN Yingchun, JING Jiansheng, TIAN Liang, et al. Heat instability analysis of Annonium sulfate[J]. Fire Science and Technology, 2005, 24(4): 408-411. DOI:10.3969/j.issn.1009-0029.2005.04.002 (in Chinese) |
| [6] |
李冠男, 蒋慧灵, 杨守生. 过硫酸铵的热稳定性研究[J]. 安全与环境学报, 2011, 11(3): 191-195. LI Guannan, JIANG Huiling, YANG Shousheng. Study on the thermal stability of ammonium persulfate[J]. Journal of Safety and Environment, 2011, 11(3): 191-195. DOI:10.3969/j.issn.1009-6094.2011.03.047 (in Chinese) |
| [7] |
任玉荣, 贾树勇, 于庆勇, 等. 过硫酸铵催化合成乙酸正丁酯的研究[J]. 应用化工, 2005, 34(1): 38-39. REN Yurong, JIA Shuyong, YU Qingyong, et al. Study on the synthesis of n-butyl acetate catalyzed by ammonium peroxydisulfate[J]. Shaanxi Chemical Industry, 2005, 34(1): 38-39. (in Chinese) |
| [8] |
贝利平. 过硫酸铵引发壳聚糖与AM及DMAEMA的接枝共聚合成与应用[D]. 山东青岛: 中国海洋大学, 2009 BEI Liping. Synthesis and application of graft copolymerization of AM and DMAEMA onto CTS using ammonium persulfate[D]. Shandong Qingdao: Ocean University of China, 2009 (in Chinese) |
| [9] |
张天峰, 傅瑞芳. 过硫酸盐生产装置DCS控制系统: CN207992803U[P]. 2018-10-19
|
| [10] |
赵美敬, 李霞, 李光明. 工业过硫酸铵国家标准现状分析[J]. 中国石油和化工标准与质量, 2010, 30(5): 24-27. |
| [11] |
周邦荣. 我国过硫酸盐生产消费现状[J]. 化工生产与技术, 2005(3): 38-39. |
| [12] |
解涛, 高英敏. 过硫酸铵防结块的研究[J]. 无机盐工业, 1997, 29(5): 30-32, 4. XIE Tao, GAO Yingmin. Study on anticaking of ammonium persulfate[J]. Inorganic Chemicals Industry, 1997, 29(5): 30-32, 4. (in Chinese) |
| [13] |
赵建宏, 孙培永, 王留成, 等. 电解法生产过硫酸铵的研究[J]. 郑州大学学报(工学版), 2006, 27(1): 109-112. ZHAO Jianhong, SUN Peiyong, WANG Liucheng, et al. Study on the process for electrosynthesis of ammonium persulfate[J]. Journal of Zhengzhou University (Engineering Science), 2006, 27(1): 109-112. (in Chinese) |
| [14] |
乐爱山. 过硫酸铵的防结块技术研究[J]. 陕西化工, 2000, 29(1): 25-26. YUE Aishan. Research on anti-lump technology of ammonium persulfate[J]. Shaanxi Chemical Industry, 2000, 29(1): 25-26. (in Chinese) |
| [15] |
GUO L, HAN H, OUYANG D, et al. Thermodynamics and phase equilibrium of the high concentration solid solution-aqueous solution system KCl-RbCl-H2O from T=298.15 K to T=323.15 K[J]. The Journal of Chemical Thermodynamics, 2017, 106: 285-294. |
| [16] |
YIN J, SHI X, ZHOU H, et al. Solid-liquid phase equilibria of (Ca(H2PO2)2+H2O), (Ca(H2PO2)2+CaCl2+H2O), and (Ca(H2PO2)2+NaH2PO2+H2O) systems[J]. Journal of Chemical & Engineering Data, 2017, 62(2): 744-751. |
| [17] |
NIU Z, CHENG F. The phase diagram of salt-water system and its application[M]. 第2版. 天津: 天津大学出版社, 2002.
|
| [18] |
SONG L, XU Y, SI T, et al. Measurement and application of a solid-liquid equilibrium for the ternary NaCl+Na2S2O3+H2O system[J]. Industrial & Engineering Chemistry Research, 2015, 54(15): 3976-3980. |
| [19] |
SANGWAL K. A novel self-consistent Nývlt-like equation for metastable zone width determined by the polythermal method[J]. Crystal Research and Technology, 2009, 44(3): 231-247. |
| [20] |
ZÖLLNER J P, VBENSEE H, PAASCH G, et al. A novel self-consistent theory of the electronic structure of inversion layers in InSb MIS structures[J]. Physica Status Solidi (b), 1986, 134(2): 837-845. |
| [21] |
HUANG J, HOU B, GUO N, et al. Solid-liquid phase equilibria of ternary system Na2S2O3-Na2SO4-H2O in a wide range of temperatures: Measurement and application[J]. The Journal of Chemical Thermodynamics, 2018, 125: 1-10. |
| [22] |
GAO X, ZHANG F, YU Y, et al. Solid-liquid phase equilibria of the ternary system (2-naphthaldehyde+4-methylphthalic anhydride+ethyl acetate) at (288.15, 298.15, and 308.15) K[J]. Journal of Chemical & Engineering Data, 2018, 63(8): 2848-2855. |
 2022, Vol. 39
2022, Vol. 39





