间歇过程是工业过程的一种重要的生产方式,常用于生物化学、制药、食品加工和精细化工等领域[1]。间歇过程操作难度高,产品质量容易受到环境条件和设备因素影响。这些因素在过程中的异常变化轻则会影响产品质量,重则将危及生产安全。因此需要对间歇过程进行实时的监测,及时地发现过程中的异常变化,并指导操作人员消除异常或者提前终止反应。
与连续过程不同,间歇过程具有动态特性,间歇操作没有稳定的工作点,物料浓度和反应速率等关键变量随时间变化,即操作的正常工况是一个随时间变化的轨迹[2]。另外间歇过程具有非连续性的特点,产品分批次生产并输出,每个批次可以根据要求设置不同的初始条件和操作条件,且不同的条件下反应速率不同,各批次具有一定程度的差异性和不等长性。以上特点为间歇过程的监测带来了巨大挑战。为了解决多批次和批次不等长问题,多项主成分分析被提出并应用于间歇过程的监测[3]。该方法将多个批次的数据进行轨迹同步化,将每个批次的数据处理成相同长度,并展开为二维矩阵,再利用传统的主元分析法监测。但是这种基于数据展开的线性方法不仅计算复杂,且无法提取间歇过程多阶段下的动态特性。在数据展开的基础上,有许多学者提出了改进方法,如自适应阶段识别算法[4]、非线性特征提取算法[5]和基于动态模型的方法[6]等。但是这些方法都没有能够同时考虑过程的非线性和动态特性,因此无法及时地识别出故障的发生。
本论文提出了一种基于长短时记忆神经网络和支持向量数据描述的间歇过程监测方法。该方法无需对多批次数据进行展开处理,且不用对批次的不等长特性进行特殊处理,可以说实现了间歇过程监测问题的连续化处理,不仅减少了计算的复杂度,而且能够有效提取过程变量的动态性和非线性,实时地检测到过程故障的发生。
首先,多个批次的正常运行状态下的历史数据被用来建立长短时记忆神经网络回归模型。然后用支持向量数据描述对正常工况下得到的残差进行超球体描述,测试集样本点到超球体中心的距离作为监测统计量,对故障样本进行检测。本方法被应用于青霉素发酵仿真过程,结果表明该方法能够对间歇过程的故障进行早期报警。
1 基于神经网络和支持向量数据描述的监测方法结合了长短时记忆神经网络和支持向量数据描述算法,提出一种基于残差的间歇过程监测模型,具体算法及监测策略在本节中进行介绍。
1.1 长短时记忆神经网络长短时记忆神经网络是由Hochreiter和Schmidhuber提出的一种循环神经网络的变体[7]。该网络在循环神经网络的基础上引入了记忆的思想,构造了遗忘门、输入门和输出门。遗忘门用来决定要保留或舍弃哪些信息,如式(1)所示,遗忘门将之前状态信息ht-1和当前状态xt输入到激活函数σ中,其中:Wf是遗忘门的权重;bf是偏置;ft是遗忘门的输出,输出值在0与1之间,0表示完全遗忘,1表示全部保留。
| $ f_{t}=\sigma\left(W_{\mathrm{f}} \times\left[h_{t-1}, x_{t}\right]+b_{\mathrm{f}}\right) $ | (1) |
输入门决定单元中更新的信息,式(2)可以用来决定需要更新的新信息,其中:ht-1表示上一历史状态;xt表示当前状态;Wi表示权重;bi表示偏置;σ是Sigmoid激活函数。
式(3)用1个tanh激活函数决定用于更新状态的候选新信息,其中:ht-1表示上一历史状态;xt表示当前状态;WC表示权重;bC表示偏置。将式(2)相乘得到要加入该单元的更新信息。式(4)为单元状态值的更新。
| $ i_{t}=\sigma\left(W_{i} \times\left[h_{t-1}, x_{t}\right]+b_{i}\right) $ | (2) |
| $ \tilde{C}_{t}=\tan h\left(W_{C} \times\left[h_{t-1}, x_{t}\right]+b_{\mathrm{C}}\right) $ | (3) |
| $ C_{t}=f_{t} \times C_{t-1}+i_{t} \times \tilde{C}_{t} $ | (4) |
输出门决定输出的信息,式(5)决定需要输出多少当前状态的信息,其中:ht-1表示上一历史状态;xt表示当前状态;Wo表示权重;bo表示偏置;σ是Sigmoid激活函数。然后式(6)将式(5)与激活后的当前单元状态相乘得到神经网络的输出。
| $ o_{t}=\sigma\left(W_{0} \times\left[h_{t-1}, x_{t}\right]+b_{\mathrm{o}}\right) $ | (5) |
| $ h_{t}=o_{t} \cdot \tan h\left(C_{t}\right) $ | (6) |
由于长短时记忆神经网络能够同时考虑当前值和历史值的信息,因此能够提取过程的动态和非线性特征,适用于建立间歇过程时间序列的回归模型。
1.2 支持向量数据描述支持向量数据描述是一种常用的异常值检测算法,它的原理可以转化为式(7)中的优化问题[8]。
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {\min }\limits_{a, R, \xi } {R^2} + C\sum\limits_{i = 1}^n {{\xi _i}} \\ s.t.{\left\| {\mathit{\Phi }\left( {{x_i}} \right) - a} \right\|^2} \le {R^2} + {\xi _i}, {\xi _i} \ge 0 \end{array} $ | (7) |
将训练数据x通过变换函数映射到特征空间, 在特征空间寻找一个最小体积的超球体。其中:R是超球体的半径;a是球心;ξ是松弛因子;C是惩罚项。引入式(8)所示的核函数,结合拉格朗日乘子法,超球体的半径R可以由任意支持向量xk用式(9)求得。
| $ K\left( {{x_i}, {x_j}} \right) = \mathit{\Phi }\left( {{x_i}} \right) \cdot \mathit{\Phi }\left( {{x_j}} \right) $ | (8) |
| $ R = \sqrt {1 - 2\sum\nolimits_{i = 1}^n {{\alpha _i}K\left( {{x_i}, {x_k}} \right)} - \sum\nolimits_{i = 1}^n {\sum\nolimits_{j = 1}^n {{\alpha _i}{\alpha _j}K\left( {{x_i}, {x_j}} \right)} } } $ | (9) |
其中:αi是样本xi对应的拉格朗日系数,对于测试样本xtest,用式(10)计算其与球心a的距离作为统计量,如果距离超过超球体的半径,则说明该样本为异常样本。
| $ \begin{array}{*{20}{c}} {{\rm{Dis}} = }\\ {\sqrt {1 - 2\sum\nolimits_{i = 1}^n {{\alpha _i}K\left( {{x_i},{x_{{\rm{test}}}}} \right)} - \sum\nolimits_{i = 1}^n {\sum\nolimits_{j = 1}^n {{\alpha _i}{\alpha _j}K\left( {{x_i},{x_j}} \right)} } } } \end{array} $ | (10) |
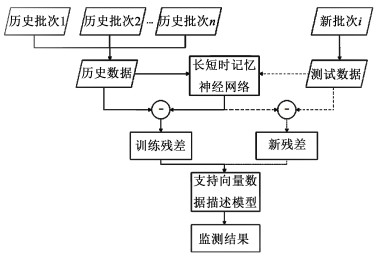
将以上2种方法相结合,提出了一种新的间歇过程监测方法,将残差作为监测对象,将复杂的间歇过程监测转化为连续过程监测问题来处理。具体的实现策略如图 1所示,首先将包含不同初始条件的多个正常批次数据作为训练数据,训练长短时记忆神经网络回归模型,迭代至模型的损失不再明显下降为止。然后将从回归模型获取的残差数据用支持向量数据描述模型从原始空间投影到特征空间,寻找最小超球体来确定正常残差数据的范围。至此,监测模型建立完成。当新的批次生产时,将实时数据带入建立好的神经网络回归模型得到实时的残差数据,再计算残差数据到超球体球心的距离并与超球体的半径进行比较,若该距离小于半径,过程处于正常运行状态,否则,说明过程出现了异常,监测模型开始报警。
|
| 图 1 本研究过程监测方法流程图 Fig.1 The flow chart of the proposed monitoring method |
| |
本节将1.3所提出的监测方法应用于青霉素发酵仿真过程,对该方法的有效性进行验证。
2.1 青霉素发酵过程青霉素发酵过程是一种典型的间歇操作过程,发酵初期为间歇操作,产生大量菌体,菌体消耗掉葡萄糖底物后,进入半间歇补料阶段,再向发酵罐中连续加入葡萄糖。发酵期间,无论是环境条件、培养基初始条件还是操作变量的波动都会影响最终得到的青霉素浓度,青霉素浓度难以在线测量[9],因此需要对过程中涉及到的测量变量与操作变量进行实时监测,以便能够及时消除故障,保证过程按照正常工况的发酵轨迹运行。该过程具有很强的动态时变性和非线性,监测难度大。本论文采用Cinar教授团队[10]开发的Pensim软件来对该过程进行模拟并获取数据。
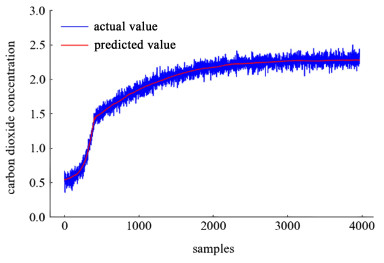
2.2 数据描述和模型构建首先模拟10个批次不同初始条件的正常工况数据作为训练数据,过程变量信息如表 1所示。反应时间395 h到405 h不等,采样频率为0.1 h,以窗口的形式输入到长短时记忆神经网络进行训练,根据过程数据的复杂度,模型层数选为2层,隐藏单元个数设为64个。当训练的损失不再有明显下降后,停止迭代,确定回归模型。并生成1组随机初始条件和批次长度的正常工况数据测试回归模型的效果。以图 2所示的CO2浓度的回归效果为例,可以看出该模型对青霉素发酵过程的不同阶段都是良好的回归效果,通过计算评价回归效果的指标得到R2为0.983,均方根误差为0.060 6,说明该模型可以满足回归要求。
| 变量 | 单位 |
| 通气速率 | L·h-1 |
| 搅拌机功率 | W |
| 底物进料速率 | L·h-1 |
| 底物进料温度 | K |
| 溶解氧浓度 | g·L-1 |
| 培养基体积 | L |
| CO2浓度 | g·L-1 |
| 发酵罐温度 | K |
| 生成热 | kcal |
| 冷却水流率 | L·h-1 |
| 注:1 kcal=4.186 kJ。 | |
|
| 图 2 CO2浓度的回归结果 Fig.2 Regression result for carbon dioxide concentration |
| |
确定回归模型后,计算正常工况数据的残差作为监测模型的训练数据,为了验证本方法的监测效果,通过Pensim仿真平台设定3个常见的故障,分别在反应进行到100 h时分别引入于3个不同批次中,故障信息如表 2所示,故障引入于操作变量,且有阶跃和斜坡2种故障方式。同时补充1个不引入故障的正常批次数据来测试模型对正常工况的监测效果。
| 故障序号 | 故障类型 | 故障开始时间/h |
| 1 | 通气速率阶跃下降 | 100 |
| 2 | 搅拌机功率斜坡下降 | 100 |
| 3 | 底物进料速率斜坡下降 | 100 |
将这1个批次的正常数据和3个批次的故障测试数据分别带入建立好的回归模型,得到残差,即通过模型得到的回归值与真实值之间的差值,再将残差带入监测模型计算距离统计量与控制限进行比较来判断当前样本所处的运行状态。
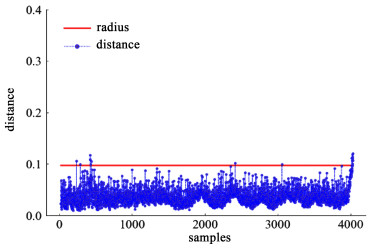
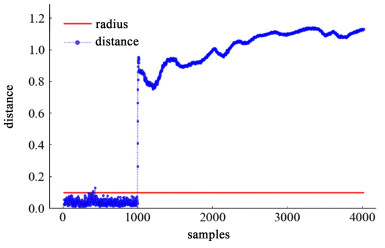
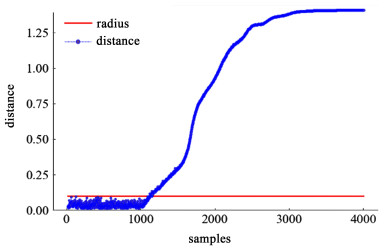
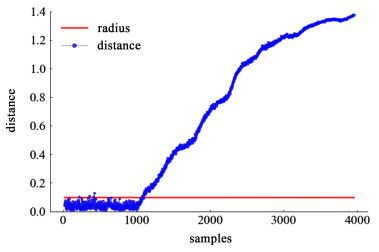
监测结果如图 3、图 4、图 5和图 6所示,可以看出,针对正常工况的测试数据,监测统计量保持在控制限以下,说明模型具有极低的误报率。对于阶跃故障,该模型能够在故障发生的第1个时间点进行实时报警,对于故障2和3的斜坡故障,即使故障幅度较小,也能够在1 100样本点之前进行及时的报警。结果表明,本研究提出的监测方法能够有效地提取间歇过程中复杂的动态及非线性特征,并实时地检测到故障的发生。同时,本方法还可以免去传统方法对变量展开和批次轨迹同步化的复杂运算
|
| 图 3 正常数据的监测结果 Fig.3 Monitoring result under normal condition |
| |
|
| 图 4 故障1的监测结果 Fig.4 Monitoring result of fault 1 |
| |
|
| 图 5 故障2的监测结果 Fig.5 Monitoring result of fault 2 |
| |
|
| 图 6 故障3的监测结果 Fig.6 Monitoring result of fault 3 |
| |
提出了一种基于神经网络和支持向量描述的间歇过程监测方法,通过提取过程的动态和非线性特征建立回归模型,并以残差为监测对象,可以避免数据展开和批次不等长处理等复杂计算,以连续过程监测的处理方式解决了间歇过程监测的问题,并应用于青霉素发酵过程,结果表明该方法能够实现对该过程中的异常偏离的实时监测,本方法的监测思想为间歇过程的监测提供了一种新的思路。
| [1] |
卢静宜, 曹志兴, 高福荣. 批次过程控制——回顾与展望[J]. 自动化学报, 2017, 43(6): 933-943. LU Jingyi, CAO Zhixing, GAO Furong. Batch process control—Overview and outlook[J]. Acta Automatica Sinica, 2017, 43(6): 933-943. (in Chinese) |
| [2] |
赵春晖, 余万科, 高福荣. 非平稳间歇过程数据解析与状态监控: 回顾与展望[J]. 自动化学报, 2020, 46(10): 2072-2091. ZHAO Chunhui, YU Wanke, GAO Furong. Data analytics and condition monitoring methods for nonstationary batch processes—Current status and future[J]. Acta Automatica Sinica, 2020, 46(10): 2072-2091. (in Chinese) |
| [3] |
NOMIKOS P, MACGREGOR J F. Monitoring batch processes using multiway principal component analysis[J]. AIChE Journal, 1994, 40(8): 1361-1375. DOI:10.1002/aic.690400809 |
| [4] |
SUN W, MENG Y, PALAZOGLU A, et al. A method for multiphase batch process monitoring based on auto phase identification[J]. Journal of Process Control, 2011, 21(4): 627-638. DOI:10.1016/j.jprocont.2010.12.003 |
| [5] |
ZHAO C, GAO F, WANG F. Nonlinear batch process monitoring using phase-based kernel-independent component analysis-principal component analysis (KICA-PCA)[J]. Industrial & Engineering Chemistry Research, 2009, 48(20): 9163-9174. |
| [6] |
CHOI S W, MORRIS J, LEE I B. Dynamic model-based batch process monitoring[J]. Chemical Engineering Science, 2008, 63(3): 622-636. DOI:10.1016/j.ces.2007.09.046 |
| [7] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [8] |
TAX D M J, DUIN R P W. Support vector domain description[J]. Pattern Recognition Letters, 1999, 20(11/12/13): 1191-1199. |
| [9] |
刘世成, 高彦臣, 王海清, 等. 特征空间递归更新的ICA算法及发酵过程监测应用[J]. 化工学报, 2008, 59(11): 2830-2836. LIU Shicheng, GAO Yanchen, WANG Haiqing, et al. ICA algorithm based on recursively updating of feature space and application to fermentation process monitoring[J]. Journal of Chemical Industry and Engineering (China), 2008, 59(11): 2830-2836. DOI:10.3321/j.issn:0438-1157.2008.11.022 (in Chinese) |
| [10] |
BIROL G, ÜNDEY C, ÇINAR A. A modular simulation package for fed-batch fermentation: Penicillin production[J]. Computers & Chemical Engineering, 2002, 26(11): 1553-1565. |
 2022, Vol. 39
2022, Vol. 39





