2. 中国石油大学(北京)自动化系, 北京 102249
2. Department of Automation, China University of Petroleum, Beijing 102249, China
石油和天然气资源是国家发展的血液。石油和天然气生产在促进工业发展和社会进步方面发挥着极其重要的作用。近年来,中国的原油对外依存度不断提高,对国家能源安全构成了严重威胁。为了缓解中国油气资源短缺的问题,一方面,中国积极采取节能减排措施,提出了绿色、低碳、经济发展的目标。另一方面,美国地质调查局(USGS)的调查报告指出,全球深水石油资源具有巨大的勘探和开发潜力。勘探表明,中国的深水区有丰富的石油和天然气资源。南海广大深水区具有形成大中型油气田的基本地质条件,具有良好的油气勘探前景和资源潜力。近10年来,我国新发现的油气田大多位于海上,深海油气田的比例不断增加。政策的支持和引导加快了深水油气勘探开发的进程。随着海洋工程装备的快速发展,也大大增强了深水油气勘探开发的能力。深海油气田的油气资源一般通过海底管道和管汇系统向上运输到浮式生产装置(FPS)和浮式生产储油装置(FPSO),之后利用穿梭油轮将经过FPSO初次处理的石油转移到石油存储基地,此油气资源运输过程被称为海上原油采集运输系统或者石油外输系统。在这个运输过程中穿梭油轮扮演着极其重要的角色,是衔接海上石油钻井平台、浮式生产储油卸油装置(FPSO)以及陆地石油储油基地的关键。
海上石油钻井平台和FPSO由于油井压力改变、储油装置容量大小等原因,有时会导致本身产出的原油超过容量限制,为了保障生产安全必须采取停产措施。这样会导致生产成本上升且生产效率下降,如果对石油外输系统中的生产环节进行生产调度优化则可以合理地避免这种情况。与此同时高效率的穿梭油轮运输可以在运输环节中明显地缩短原油运输周期,降低原油运输成本。因此,生产调度优化与穿梭油轮路径的协同调度具有重要的研究意义。
本论文研究的穿梭油轮船队设计及路径规划问题可归类为船舶调度优化问题。目前对该问题相关的研究大致分为如下3类。
1) 船舶调度优化研究: 焦宁泊提出了沿海支线集装箱运输网络基本理论,并建立了一种沿海支线集装箱运输网络优化模型,使整个运输网络总成本最小化为目标,并使用粒子群算法求解该模型[1]。唐磊等根据船速的变化建立了以最大化运营收益为目标的船舶的调度模型[2]。杨立乾考虑船舶储存量和班轮时间限制,建立以最小化运输成本为目标的调度模型,并使用粒子群算法求解该模型[3]。王泉慧为应对需求波动和潮汐影响,提出了多船型船舶调度优化问题,建立了以运输成本最小为目标的多船型船舶调度模型,并用改进遗传算法求解了该模型[4]。唐丽敏等针对持续低迷的航运市场背景,提出了以航速为优化变量的最小班轮航线配船模型[5]。由近年来发表的文献看,船速的变化越来越成为学者关注的重点。
2) 港口船舶调度优化研究: 孙有才等建立了2阶段的双边匹配优化模型,考虑了供需之间的匹配,提出了合理的船舶运输调度方案[6]。张新宇等建立了以船舶在港口等候总时间最短为目标的调度模型,并提出了模拟退火、多种群遗传算法进行求解[7]。何淑芬等建立了一个以优化进出港口的船舶密度的多目标船舶调度优化模型并进行求解,为港口船舶调度优化提供了新思路[8]。随着研究的深入,学者们研究的内容更加细化,旨在为实际的生产提供指导。
3) 车辆路径调度优化研究: 自1959年Dantzig和Ramser[9]提出卡车分配问题以来,车辆的路径选择以及交货时间安排已经成了研究热点。近年来,为了减少二氧化碳排放和燃料的使用,绿色调度问题成了研究热点[10-12]。由于许多公司在配送过程中需要考虑多个仓库的事实,在当今竞争激烈的环境中,企业经常在配送过程中进行协作与合作以降低巨额成本。自2013年以来,具有二维和三维载荷约束的车辆路径调度问题引起了人们越来越大的兴趣[13-16],这种变体受到计算机科学的发展青睐,并为研究人员提供了同时考虑2个复杂问题的机会,即:车辆的路线和包装[17]。动态规划问题提供实时数据[18, 19],可大大提高规划人员的工作效率。
具体地,部分学者对穿梭油轮船队设计及路径优化问题也做出了深入研究。在2018年陈子根将穿梭油轮船队的设计与调度问题抽象为考虑硬时间窗约束的多车型车辆路径问题,建立穿梭油轮船队设计与调度优化模型。基于列生成思想设计精确求解算法并进行数值实验,最终证明了所提出的模型和算法可有效解决穿梭油轮船队设计与船舶调度的协同优化问题[20]。在2019年辛旭实现了穿梭油轮车队的绿色运营成本最小化,建立了用于穿梭油轮车队绿色调度的整数规划模型,并用列生成算法求解了该问题,有效地提高了求解效率[21]。
基于前人的研究内容,在以效率、和谐、持续为目标的绿色调度优化的要求下,本论文提出一种基于连续时间表达的穿梭油轮路径绿色调度优化模型。该模型以降低穿梭油轮航行总成本为目标,同时优化穿梭油轮船队设计、油轮航行路线规划以及航行速度选择。本论文提出的调度优化方法属于高效的优化调度方法,可以有效提高企业经济效益,实现油轮航行的节能减排、降耗、降低航运总成本的目标,减少航行时废气排放对环境的影响,实现经济指标和绿色指标的协同优化。绿色油轮路径调度比传统的路径调度更复杂、更难解决,研究也更具有现实意义和应用价值。
1 问题描述海上平台开采原油后,通过输油管道输送到浮式生产储存卸货装置(FPSO)进行脱水、砂滤等初步处理,经过初步处理的原油储存在FPSO货仓中以待转移。被称作“海上输油管”、“浮动管道”的穿梭油轮,如同往返于航站楼和飞机之间的摆渡车,把FPSO中的原油及时地输送到陆地储油基地,以供内陆原油加工生产的需要。在现代原油供应系统中,使用更为合理的船队组织,以更低的能源和绿色运营成本完成原油转移成为决策者竞相追逐的目标。油气资源开发从陆地转向海洋、浅海转向深海已成必然。随着FPSO与穿梭油轮的装备升级,传统的小批量和高频的“点对点”式外输方式正在向“多点停靠、协同运输”的方式转变。中型乃至大型穿梭油轮连续停泊多个FPSO以收集原油转移到陆地储油基地已成新趋势。
现代原油供应系统分为2个子系统。一个是以FPSO为中心的原油储存子系统,在该系统中需要考虑的主要约束为各个FPSO货仓的储油上限。另一个是以原油外输船队为中心的原油收集和分配子系统,该系统的决策变量决定了穿梭油轮的调度方案。相较于之前学者的研究,本论文侧重于对穿梭油轮路径的绿色调度优化。在考虑碳排放的大背景下,穿梭油轮路径的调度优化决策更为复杂。在原油外输子系统中,小型穿梭油轮可能会造成更高的运营成本,而大型穿梭油轮可能会增加碳排放量以造成污染。除此之外,穿梭油轮速度直接决定油耗,而油耗又决定着碳排放量,从而影响绿色运营成本。这就迫使决策者在对穿梭油轮船队设计时,同时兼并考虑穿梭油轮的类型以及穿梭油轮的航行速度。
本论文在考虑碳排放的大背景下,针对穿梭油轮路径绿色调度面临的船队设计、航线规划以及航速选择三大挑战进行研究。旨在保障FPSO生产稳定的前提下,以最小化绿色运营成本为目标,决策出穿梭油轮的类型、数量、停靠顺序以及航行速度。
2 模型建立本论文考虑FPSO库存限制,以最小化绿色运营成本为目标,建立基于连续时间表达的穿梭油轮路径绿色调度优化模型,实现对穿梭油轮船队优化设计、油轮航行路线规划以及航行速度选择。
2.1 问题的假设为构建穿梭油轮路径绿色调度优化模型,做出了如下假设:1)穿梭油轮在每次取油任务开始之前均由陆地石油储存基地出发,在所服务的FPSO处取油结束之后,返回到陆地储存基地;2)每个穿梭油轮可服务多个FPSO,但是每次每个FPSO均由一艘穿梭油轮服务;3)只考虑运输一种类型的石油产品;4)陆地储存基地的石油储存能力无限制,即不考虑基地的石油储存能力;5)在系统成本上,穿梭油轮、FPSO、陆地储存基地的维护保养成本不计算在内;6)每个FPSO中的原油量在装载过程中随时间线性增加;7)油轮在陆地储存基地的卸油时间与排放的油量成线性关系;8)拥有多种类型且足够数量的穿梭油轮构成一支舰队;9)在某一段航线上的速度选定后即保持不变;10)穿梭油轮取油操作的开始和结束时间可发生在时间轴的任意点上,由模型求解结果确定,取油时间的长度由FPSO卸油时间决定;11)穿梭油轮在FPSO取油后,FPSO中的原油全部排空。
已知信息包括:1)各个FPSO的产油速率和容量限制;2)给定不同类型的穿梭油轮与FPSO之间的石油传输速率;3)各FPSO之间的航行距离;4)给定各个穿梭油轮的容量限制;5)各类穿梭油轮航行的固定成本与可变成本。
决策方案:1)石油外输系统的穿梭油轮船队组成、取油路径以及航行速度选择结果;2)各穿梭油轮的调度时刻表。
2.2 数学模型本论文的目标函数为最小化绿色运营成本,如公式(1)所示。该部分由穿梭油轮航行的固定成本cvsF与因航行速度不同而产生的可变成本cvsV 2部分组成,不考虑穿梭油轮、FPSO与陆地基地等设备的维护保养成本。
| $ \min : \sum\limits_{i \in I, j \in I, n \in N, s \in S, v \in V}\left(c_{v s}^{F}+c_{v s}^{V}\right) t_{i j s} X_{i j p s n} $ | (1) |
约束条件如下。
1) 时间顺序约束。
| $ T f_{v n-1} \leqslant T s_{v n}, \forall v \in V n \in N, n \geqslant 2 $ | (2) |
| $ T s_{v n} \leqslant H, \forall v \in V, n \in N $ | (3) |
| $ T f_{v n} \leqslant H, \forall v \in V, n \in N $ | (4) |
该约束表示为对于任意穿梭油轮,前一事件点的结束时间Tfvn-1要晚于后一事件点的开始时间Tsvn,并且所有调度均在调度期H内。
2) 事件点持续时间约束。
| $ t_{i v}=\frac{T s_{v n} R_{i}^{u}}{w_{i}}, \forall i \in F, v \in V, n \in N $ | (5) |
| $ \begin{gathered} 0 \leqslant T f_{v n}-T s_{v n}-t_{i j s} X_{i j v s n} \leqslant 0 \\ \forall i, j \in F, v \in V, n \in N_{1}, s \in S \end{gathered} $ | (6) |
| $ \begin{gathered} 0 \leqslant T f_{v n}-T s_{v n}-t_{i v} X S_{i v n} \leqslant 0 \\ \forall i \in F, v \in V, n \in N_{2}, s \in S \end{gathered} $ | (7) |
公式(5)表示对于任意穿梭油轮在FPSO的取油作业时间。公式(6)和公式(7)分别表示对穿梭油轮航行与取油作业的持续时间约束。
公式(7)存在连续时间变量与整数变量相乘项,属于难以求解的非线性项,对该约束进行线性化处理,使其变成易求解的线性约束[22],处理如式(8)~式(13)所示。
| $ \begin{gathered} 0 \leqslant T f_{v n}-T s_{v n}-A X_{i v n}^{6} \leqslant 0 \\ \forall i \in F, v \in V, n \in N_{2} \end{gathered} $ | (8) |
| $ \begin{gathered} A X_{i v n}^{6}+A X_{i v n}^{7}=t_{i v} \\ \forall i \in F, v \in V, n \in N_{2} \end{gathered} $ | (9) |
| $ \begin{gathered} A X_{i v n}^{6} \leqslant X S_{i v n} H \\ \forall i \in F, v \in V, n \in N_{2} \end{gathered} $ | (10) |
| $ \begin{gathered} A X_{i v n}^{7} \leqslant\left(1-X S_{i v n}\right) H \\ \forall i \in F, v \in V, n \in N_{2} \end{gathered} $ | (11) |
| $ A X_{i v n}^{6} \geqslant 0, \forall i \in F, v \in V, n \in N_{2} $ | (12) |
| $ A X_{i v n}^{7} \geqslant 0, \forall i \in F, v \in V, n \in N_{2} $ | (13) |
3) 穿梭油轮的起始与终点约束。
| $ \sum\limits_{n \in N_{1}} \sum\limits_{j \in F} \sum\limits_{s \in S} X_{0 j v s n}=1 \forall v \in V $ | (14) |
| $ \sum\limits_{n \in N_{1}} \sum\limits_{i \in F} \sum\limits_{s \in S} X_{i 0 v s n}=1 \forall v \in V $ | (15) |
公式(14)与公式(15)表示穿梭油轮必须从陆地储油基地出发,取油之后回到陆地储油基地。
4) 连贯性约束。
| $ \begin{gathered} \sum\limits_{n \in N_{1}} \sum\limits_{i \in N_{3}} \sum\limits_{s \in S} X_{i j v s n}=\sum\limits_{i \in N_{3}}\sum\limits_{i \in N_{3}} \sum\limits_{S \in S} X_{j i v s n} \\ \forall j \in F, v \in V \end{gathered} $ | (16) |
该公式用来确保任意穿梭油轮的连贯性,即表示在节点j处服务的穿梭油轮,来自上一节点i,且服务之后去下一节点i。
5) 生产连续性约束。
| $ \sum\limits_{n \in N_{2}} \sum\limits_{v \in V} X S_{i v n} \geqslant 1 \forall i \in F $ | (17) |
公式(17)表示每个FPSO均被某艘穿梭油轮访问,以保证FPSO生产的连续性,即不能出现因穿梭油轮取油不及时而造成FPSO溢罐的停产现象。
6) 航线访问唯一性约束。
| $ \sum\limits_{s \in S} \sum\limits_{v \in V} X_{i j v s n} \leqslant 1 \forall i, j \in F, n \in N_{1} $ | (18) |
为了避免穿梭油轮相撞,公式(18)约束在每个事件点航线(i, j)仅被一艘穿梭油轮航行。
7) 事件与时间段匹配约束。
| $ \begin{gathered} X S_{i v n}\left(X S_{i v n}-X S_{i v n+1}\right)=\sum\limits_{s \in S} \sum\limits_{j \in F} X_{i j v s n+1} \\ \forall i \in F, \forall v \in V, \forall n \in N, n \leqslant N_{\max } \end{gathered} $ | (19) |
| $ \begin{gathered} \sum\limits_{s \in S} \sum\limits_{i \in F} X_{i j v s n-1}=X S_{j v n}\left(X S_{j v n}-X S_{j v n-1}\right) \\ \forall j \in F, \forall v \in V, \forall n \in N, n \geqslant 2 \end{gathered} $ | (20) |
对于任意穿梭油轮,在调度期内仅包含两类事件,即:在FPSO间航行的转移事件以及在FPSO上的取油事件。两类事件在同一时间轴上交替出现,公式(19)和公式(20)确保了同一时间轴上相邻的事件点的决策变量取值只能为{0, 1}或者{1, 0}。上述约束属于2个整数变量相乘的非线性约束,对其进行如下线性化处理如公式(21)到公式(25)所示:
| $ \begin{gathered} X S_{i v n}-A X_{i v n}^{1}=\sum\limits_{s \in S} \sum\limits_{j \in F} X_{i j v s n+1} \\ \forall i \in F, \forall v \in V, \forall n \in N, n \leqslant N_{\max } \end{gathered} $ | (21) |
| $ \begin{gathered} \sum\limits_{s \in S} \sum\limits_{i \in F} X_{i j v s n-1}=X S_{j v n}-A X_{j v n-1}^{1} \\ \forall j \in F, \forall v \in V, \forall n \in N, n \geqslant 2 \end{gathered} $ | (22) |
| $ \begin{gathered} A X_{i v n}^{1} \leqslant X S_{i v n} \\ \forall i \in F, \forall v \in V, \forall n \in N \end{gathered} $ | (23) |
| $ \begin{gathered} A X_{i v n}^{1} \leqslant X S_{i v n+1} \\ \forall i \in F, \forall v \in V, \forall n \in N, n \leqslant N_{\max } \end{gathered} $ | (24) |
| $ \begin{gathered} A X_{i v n}^{1} \geqslant X S_{i v n}+X S_{i v n+1}-1 \\ \forall i \in F, \forall v \in V, \forall n \in N, n \leqslant N_{\max } \end{gathered} $ | (25) |
8) 穿梭油轮的容量约束。
| $ \begin{gathered} \sum\limits_{i \in F} \sum\limits_{n \in N_{2}}\left(T s_{v n} R_{i}^{u}+b_{i}\right) X S_{i v n}<q_{v} \\ \forall v \in V \end{gathered} $ | (26) |
| $ \begin{gathered} \sum\limits_{i \in F} \sum\limits_{n \in N_{2}} T s_{v n} R_{i}^{u} X S_{i v n}+\sum\limits_{i \in F} \sum\limits_{n \in N_{2}} b_{i} X S_{i v n}<q_{v} \\ \forall v \in V \end{gathered} $ | (27) |
公式(26)表示,在整个调度期内,任意穿梭油轮的取油量都不能超过其容量限制qv。公式(27)为公式(26)的展开式,公式的第1项存在连续变量与整数变量乘积的非线性项,对其进行如下线性化处理如公式(28)~公式(33)所示。
| $ \sum\limits_{i \in F} \sum\limits_{n \in N_{2}} R_{i}^{u} A X_{i v n}^{2}+\sum\limits_{i \in F} \sum\limits_{n \in N_{2}} b_{i} X S_{i v n}<q_{v} \forall v \in V $ | (28) |
| $ A X_{i v n}^{2}+A X_{i v n}^{3}=T s_{v n} \forall i \in F, v \in V, n \in N_{2} $ | (29) |
| $ A X_{i v n}^{2} \leqslant X S_{i v n} H \forall i \in F, v \in V, n \in N_{2} $ | (30) |
| $ A X_{i v n}^{3} \leqslant\left(1-X S_{i v n}\right) H \forall i \in F, v \in V, n \in N_{2} $ | (31) |
| $ A X_{i v n}^{2} \geqslant 0 \forall i \in F, v \in V, n \in N_{2} $ | (32) |
| $ A X_{i v n}^{3} \geqslant 0 \forall i \in F, v \in V, n \in N_{2} $ | (33) |
9) FPSO的容量约束。
| $ \begin{gathered} \sum\limits_{v \in V} \sum\limits_{n \in N_{2}} T s_{v n}\left(1-X S_{i v n}\right) R_{i}^{u}+b_{i}<q f_{i} \\ \forall i \in F \end{gathered} $ | (34) |
| $ \begin{gathered} \sum\limits_{v \in V} \sum\limits_{n \in N_{2}} T s_{v n} R_{i}^{u}- \sum\limits_{v \in V} \sum\limits_{n \in N_{2}} T s_{v n} R_{i}^{u} X S_{i v n}<q f_{i} \\ \forall i \in F \end{gathered} $ | (35) |
公式(34)表示FPSO的储油量不能超过其储油量上限qfi,以保证生产的连续性。公式(35)为公式(34)的展开式,第2项存在连续变量与整数变量相乘的非线性项,对其线性化处理如公式(36)到公式(41)所示。
| $ \begin{gathered} \sum\limits_{v \in V} \sum\limits_{n \in N_{2}} T s_{v n} R_{i}^{u}-\sum\limits_{v \in V} \sum\limits_{n \in N_{2}} A X_{i v n}^{4} R_{i}^{u}<q f_{i} \\ \forall i \in F \end{gathered} $ | (36) |
| $ A X_{i v n}^{4}+A X_{i v n}^{5}=T s_{v n} \forall i \in F, v \in V, n \in N_{2} $ | (37) |
| $ A X_{i v n}^{4} \leqslant X S_{i v n} H \forall i \in F, v \in V, n \in N_{2} $ | (38) |
| $ A X_{i v n}^{5} \leqslant\left(1-X S_{i v n}\right) H \forall i \in F, v \in V, n \in N_{2} $ | (39) |
| $ A X_{i v n}^{4} \geqslant 0 \forall i \in F, v \in V, n \in N_{2} $ | (40) |
| $ A X_{i v n}^{5} \geqslant 0 \forall i \in F, v \in V, n \in N_{2} $ | (41) |
由于船舶租赁市场的繁荣,大量的船舶信息是公开透明的。因此,从网上直接查询FPSO信息,原油生产速度以及每艘穿梭油轮的容量、速度、运营成本和租金等信息。本论文选自渤海某石油开采公司数据作案例分析,以验证模型的有效性。
3.1 仿真数据该案例包含1个陆地储油基地和7个FPSO平台,陆地储油基地与各FPSO之间的航行距离取欧式距离,忽略不可抗力因素,航行距离如表 1所示。
| 平台 | FPSO 1 | FPSO 2 | FPSO 3 | FPSO 4 | FPSO 5 | FPSO 6 | FPSO 7 | 基地 |
| FPSO 1 | 0 | 12 | 17 | 30 | 47 | 59 | 21 | 79 |
| FPSO 2 | 0 | 24 | 23 | 37 | 54 | 24 | 69 | |
| FPSO 3 | 0 | 46 | 61 | 48 | 8 | 77 | ||
| FPSO 4 | 0 | 20 | 72 | 46 | 75 | |||
| FPSO 5 | 0 | 75 | 59 | 67 | ||||
| FPSO 6 | 0 | 40 | 43 | |||||
| FPSO 7 | 0 | 70 | ||||||
| 基地 | 0 | |||||||
| 注:1海里=1.852 km。 | ||||||||
各FPSO的储油量、生产速率和外输速率等数据如表 2所示。
| 平台 | FPSO的载重量/t | 石油生产速率/ (m3·h-1) | 石油外输速率/ (m3·h-1) |
| FPSO 1 | 52 000 | 367.0 | 3 000 |
| FPSO 2 | 5 2000 | 396.0 | 2 400 |
| FPSO 3 | 150 000 | 317.5 | 6 000 |
| FPSO 4 | 58 000 | 962.5 | 2 700 |
| FPSO 5 | 300 000 | 630.4 | 8 000 |
| FPSO 6 | 160 000 | 295.0 | 6 000 |
| FPSO 7 | 165 000 | 295.6 | 6 000 |
给定每种类型的油轮有5种不同的航行速度。穿梭油轮的主要参数如表 3所示。
| 油轮类型 | 容量约束/ m3 | 航行固定成本/ (kRMB·h-1) | 可变成本/(kRMB·h-1) | ||||
| 5 kn | 8 kn | 11 kn | 13 kn | 16 kn | |||
| A | 60 000 | 2.4 | 2.8 | 4.1 | 5.6 | 6.9 | 7.9 |
| B | 120 000 | 2.7 | 3.0 | 4.6 | 6.3 | 7.6 | 9.3 |
| C | 170 000 | 3.0 | 3.5 | 5.4 | 7.0 | 8.6 | 10.5 |
| D | 180 000 | 3.0 | 3.5 | 5.4 | 7.0 | 8.6 | 10.5 |
| E | 220 000 | 3.3 | 3.9 | 6.0 | 7.7 | 9.4 | 12.0 |
| 注: 1 kn=1.852 km·h-1。 | |||||||
该调度优化模型利用GAMS win 32 24.0.2平台中的CPLEX求解。电脑配置为Intel core i5-7500 CPU,3.41 GHz,内存8 GB。模型统计结果如表 4所示。
根据优化结果,穿梭油轮路径航行的绿色运营的优化成本为48.4万元,船队优化、路径规划以及速度选择的调度方案结果如下表 5所示。
| 穿梭油轮选择 | 路径选择 | 速度选择/kn |
| A | 0—2—1—4—0 | 16—13—16—16 |
| B | 0—3—7—0 | 16—11—16 |
| C | 0—6—0 | 16—11 |
| D | 0—5—0 | 16—16 |
| 注: 1 kn=1.852 km·h-1。 | ||
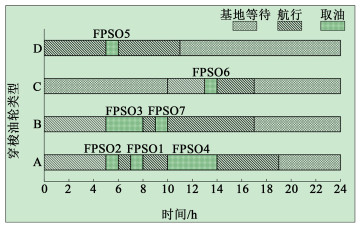
各穿梭油轮的调度期间的时刻安排如图 1所示。由图 1可以看出,在调度期内,A类型油轮先后完成了对FPSO 2、FPSO 1和FPSO 4的取油任务;B类型油轮先后完成了对FPSO 3和FPSO 7的取油任务;C类型油轮完成了对FPSO 6的取油任务;D类型油轮完成了对FPSO 5的取油任务。通过案例表明,在调度期内,所有FPSO均被取油,且在调度期结束时,所有油轮均回到基地等待,不存在取油超时的情况。
|
| 图 1 穿梭油轮时刻表 Fig.1 Schedule of shuttle tanker |
| |
在调度期内,各FPSO的储油量变化如图 2所示。结合表 2及图 2可以得出,在调度期内,所有的FPSO储油量均未超过其容量上限,保障了FPSO生产的连续性。

|
| 图 2 FPSO储油变化量 Fig.2 Change of FPSO oil storage |
| |
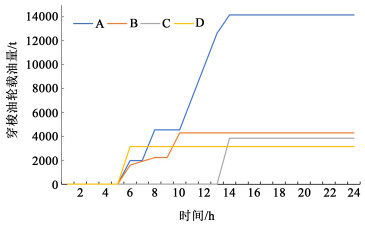
在调度期内,各穿梭油轮载油量变化如图 3所示。结合表 3及图 3可以得出,在调度期内,所有类型的穿梭油轮载重量均未超过其容量上限,取油方案合理。
|
| 图 3 穿梭油轮载油量 Fig.3 Fuel load of shuttle tanker |
| |
综上,在调度期间,各FPSO均被访问,保障了FPSO生产的连续性,同时在调度过程中,原油运载量均未超过调度穿梭油轮的容量上限,证明了该模型的有效性。
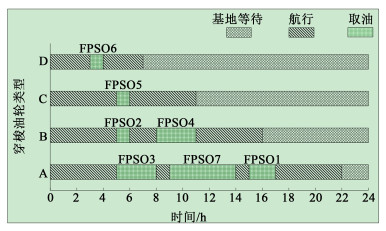
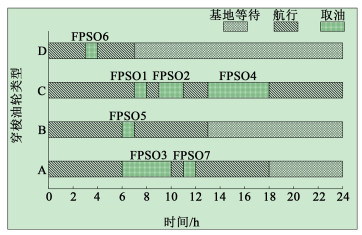
为了验证速度选择对调度方案绿色运营成本的影响,进行了定速案例的调度测试。调度方案以及各穿梭油轮的时刻表如图 4~图 6所示。图 4~图 6依次是油轮航行速度为定值16、13和11 kn(1 kn=1.852 km·h-1,下同)的调度方案。在各航行速度下的船队优化、路径规划调度方案结果汇总如下表 6所示。通过案例表明,在调度期内,所有FPSO均被取油,且在调度期结束时,所有油轮均回到基地等待,不存在取油超时情况。
|
| 图 4 穿梭油轮时刻表(速度:16 kn) Fig.4 Schedule of shuttle tanker (speed: 16 kn) |
| |
|
| 图 5 穿梭油轮时刻表(速度:13 kn) Fig.5 Shuttle tanker schedule (speed: 13 kn) |
| |

|
| 图 6 穿梭油轮时刻表(速度:11 kn) Fig.6 Schedule of shuttle tanker (speed: 11 kn) |
| |
| 穿梭油轮选择 | 路径选择 | ||
| 速度=16 kn | 速度=13 kn | 速度=11 kn | |
| A | 0—3—7—1—0 | 0—3—7—0 | 0—1—7—0 |
| B | 0—2—4—0 | 0—5—0 | 0—4—2—0 |
| C | 0—5—0 | 0—1—2—4—0 | 0—3—0 |
| D | 0—6—0 | 0—6—0 | 0—5—0 |
| E | 0—5—0 | ||
在同等条件下,当油轮航行速度减小至5 kn和8 kn已经无法满足调度要求。
表 7为各方案的成本对比情况,可见考虑航行速度选择对降低穿梭油轮路径调度的绿色运营成本有着极其重要的影响。
| 速度 | 速度组合 | 16 kn | 13 kn | 11 kn | 8 kn | 5 kn |
| 成本/万元 | 48.4 | 50.9 | 53.6 | 67.7 | +INF | +INF |
| 注:1 kn=1.852 km·h-1。 | ||||||
本论文所解决的是一个生产调度与穿梭油轮路径调度协同优化的问题。生产调度体现在FPSO在调度期内不停地储油,必须在储油量达到上限值之前对FPSO中的原油进行及时地运走,否则一经停产,则造成巨大的经济损失。穿梭油轮路径调度体现在如何在穿梭油轮容量限制内以经济最优的取油路线完成取油作业。本论文针对此问题提出了一种基于连续时间表达的穿梭油轮路径绿色调度优化模型,该模型对船队设计、路径规划以及穿梭油轮速度选择进行了最优调度,并用案例验证了模型的有效性。
符号说明:
0—陆地储存基地;
F—所有FPSO集合,F={1, 2, …, n};
I—所有节点集合,I={0, 1, 2, …, n};
N—事件点集合N={n|n=0, 1, 2, …, Nmax};
N1—穿梭油轮航行事件集;
N2—穿梭油轮取油事件集;
Nmax—最大事件点;
V—穿梭油轮的类型集合;
v—v表示穿梭油轮所选类型,v∈V;
S—穿梭油轮可选的速度集合;
s—s表示穿梭油轮所选速度,s∈S;
i, j—i, j表示不同的FPSO节点;
(i, j)—穿梭油轮的路径选择;
CVSF—穿梭油轮v以速度s航线的单位固定成本;
CVSV—穿梭油轮v以速度s航线的单位可变成本;
H—调度周期;
Riu—在节点i处的单位时间产油量;
bi—调度开始时,在节点i处的储油量;
qv—穿梭油轮v的储油能力;
qfi—FPSO i的储油能力;
tijs—油轮以速度s从节点i到节点j的航行时间;
wi—在节点i的石油外输速率;
tiv—穿梭油轮v在节点i的取油时间;
AXivnt—辅助变量,其中t=1, 2, …, 7;
Tsvn—决策变量,穿梭油轮v在时间段n的开始时间;
Tfvn—决策变量,穿梭油轮v在时间段n的结束时间;
XSivn—决策变量,若穿梭油轮v在事件点n在节点i处取油,则取1,否则为0;
Xijvsn—决策变量,若穿梭油轮v在事件点n以速度s从节点i向节点j,则取1,否则为0。
| [1] |
焦宁泊. 沿海支线集装箱运输网络优化研究[D]. 辽宁大连: 大连海事大学, 2008 JIAO Ningbo. Study on coastal container feeder network optimization[D]. Liaoning Dalian, China: Dalian Maritime University, 2008 (in Chinese) |
| [2] |
唐磊, 谢新连, 王成武. 基于集合划分的航速可变不定期船舶调度模型[J]. 上海交通大学学报, 2013, 47(6): 909-915. TANG Lei, XIE Xinlian, WANG Chengwu. Model of tramp ship scheduling with variable speed based on set partition approach[J]. Journal of Shanghai Jiao Tong University, 2013, 47(6): 909-915. (in Chinese) |
| [3] |
杨立乾. 基于轴辐式网络的集装箱支线运输多船型船舶调度模型[J]. 中国管理科学, 2015, 23(S1): 860-864. YANG Liqian. Scheduling model of feeder line multi-hull container ships based on hub-and-spoke network[J]. Chinese Journal of Management Science, 2015, 23(S1): 860-864. (in Chinese) |
| [4] |
王泉慧. 考虑潮汐影响的班轮多船型船舶调度优化研究[D]. 辽宁大连: 大连海事大学, 2019 WANG Quanhui. Research on multi-ship scheduling of liners considering tidal effects[D]. Liaoning Dalian, China: Dalian Maritime University, 2019 (in Chinese) |
| [5] |
唐丽敏, 赵伟, 曹艺欣. 考虑航速的集装箱班轮航线配船优化研究[J]. 武汉理工大学学报(交通科学与工程版), 2019, 43(1): 41-46. TANG Limin, ZHAO Wei, CAO Yixin. Optimization of container liner route allocation considering speed[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2019, 43(1): 41-46. DOI:10.3963/j.issn.2095-3844.2019.01.009 (in Chinese) |
| [6] |
孙有才, 孙卓, 林国顺, 等. 基于双边匹配优化模型的电厂煤炭采购及船舶运输调度[J]. 物流科技, 2015, 38(9): 32-35. SUN Youcai, SUN Zhuo, LIN Guoshun, et al. Coal purchase and shipping scheduling for power plants based on two-sided matching[J]. Logistics Sci-Tech, 2015, 38(9): 32-35. DOI:10.3969/j.issn.1002-3100.2015.09.009 (in Chinese) |
| [7] |
张新宇, 林俊, 郭子坚, 等. 基于模拟退火多种群遗传算法的港口船舶调度优化[J]. 中国航海, 2016, 39(1): 26-30. ZHANG Xinyu, LIN Jun, GUO Zijian, et al. Vessel scheduling optimization based on simulated annealing and multiple population genetic algorithm[J]. Navigation of China, 2016, 39(1): 26-30. DOI:10.3969/j.issn.1000-4653.2016.01.007 (in Chinese) |
| [8] |
何淑芬. 集装箱运输船舶调度的多目标优化模型建模[J]. 舰船科学技术, 2018, 40(2): 22-24. HE Shufen. Modeling of multi objective optimization model for container ship scheduling[J]. Ship Science and Technology, 2018, 40(2): 22-24. DOI:10.3404/j.issn.1672-7649.2018.02.004 (in Chinese) |
| [9] |
DANTZIG G B, RAMSER J H. The truck dispatching problem[J]. Management Science, 1959, 6(1): 80-91. DOI:10.1287/mnsc.6.1.80 |
| [10] |
LIN C, CHOY K L, HO G T S, et al. Survey of green vehicle routing problem: Past and future trends[J]. Expert Systems With Applications, 2014, 41(4): 1118-1138. DOI:10.1016/j.eswa.2013.07.107 |
| [11] |
文笑雨, 孙海强, 李浩, 等. 基于改进NSGA-Ⅱ的多目标绿色作业车间调度问题研究[J]. 河南理工大学学报(自然科学版), 2020, 39(5): 120-129. WEN Xiaoyu, SUN Haiqiang, LI Hao, et al. Research on multi-objective green job shop scheduling problem based on improved NSGA-Ⅱ[J]. Journal of Henan Polytechnic University (Natural Science), 2020, 39(5): 120-129. (in Chinese) |
| [12] |
马艳芳, 应斌, 康凯, 等. 模糊需求下绿色同时取送货问题与算法研究[J]. 计算机工程与应用, 2020, 56(16): 248-257. MA Yanfang, YING Bin, KANG Kai, et al. Algorithms for green simultaneous pickup and delivery problem with fuzzy demand[J]. Computer Engineering and Applications, 2020, 56(16): 248-257. DOI:10.3778/j.issn.1002-8331.1905-0264 (in Chinese) |
| [13] |
FUELLERER G, DOERNER K F, HARTL R F, et al. Metaheuristics for vehicle routing problems with three-dimensional loading constraints[J]. European Journal of Operational Research, 2010, 201(3): 751-759. DOI:10.1016/j.ejor.2009.03.046 |
| [14] |
LEUNG S C H, ZHANG Z, ZHANG D, et al. A meta-heuristic algorithm for heterogeneous fleet vehicle routing problems with two-dimensional loading constraints[J]. European Journal of Operational Research, 2013, 225(2): 199-210. DOI:10.1016/j.ejor.2012.09.023 |
| [15] |
王征, 胡祥培, 王旭坪. 带二维装箱约束的物流配送车辆路径问题[J]. 系统工程理论与实践, 2011, 31(12): 2328-2341. WANG Zheng, HU Xiangpei, WANG Xuping. Vehicle routing problem in distribution with two-dimensional loading constraint[J]. Systems Engineering-Theory & Practice, 2011, 31(12): 2328-2341. DOI:10.12011/1000-6788(2011)12-2328 (in Chinese) |
| [16] |
刘阿宁. 二维装载限制的车辆路径问题的研究[D]. 南宁: 广西师范学院, 2012 LIU A'ning. The research on the two-dimensional loading capacitated vehicle routing problem[D]. Nanning: Guangxi Teachers Education University, 2012 (in Chinese) |
| [17] |
蔡淇森. 带二维装箱约束的异构车辆路由问题的混合启发式算法研究[D]. 福建厦门: 厦门大学, 2013 CAI Qisen. A hybrid meta-heuristic for the heterogeneous fleet capacitated vehicle routing problem with two-dimensional loading constraints[D]. Fujian Xiamen, China: Xiamen University, 2013 (in Chinese) |
| [18] |
李晓玲. 基于动态规划算法的散货港口船舶调度优化[J]. 计算机仿真, 2020, 37(11): 393-397. LI Xiaoling. Ship scheduling optimization of bulk port based on dynamic programming algorithm[J]. Computer Simulation, 2020, 37(11): 393-397. DOI:10.3969/j.issn.1006-9348.2020.11.083 (in Chinese) |
| [19] |
朱贵冬, 尹文宾, 刘圣阳, 等. 基于视觉路况和路径规划的辅助驾驶神经网络模型动态调度框架[C]//第十二届中国卫星导航年会论文集. 南昌, 2021
|
| [20] |
陈子根, 辛旭, 陈康, 等. 考虑硬时间窗的多船型海上穿梭油轮船队设计与调度同步优化模型[J]. 大连海事大学学报, 2018, 44(3): 49-55. CHEN Zigen, XIN Xu, CHEN Kang, et al. A collaborative optimization model for design and scheduling of multi-ship tanker fleet considering hard time windows[J]. Journal of Dalian Maritime University, 2018, 44(3): 49-55. (in Chinese) |
| [21] |
XIN X, WANG X, TIAN X, et al. Green scheduling model of shuttle tanker fleet considering carbon tax and variable speed factor[J]. Journal of Cleaner Production, 2019, 234: 1134-1143. DOI:10.1016/j.jclepro.2019.06.275 |
| [22] |
YOU F, GROSSMANN I E. Integrated multi-echelon supply chain design with inventories under uncertainty: MINLP models, computational strategies[J]. AIChE Journal, 2010, 56(2): 419-440. |
 2022, Vol. 39
2022, Vol. 39





