气液两相体系在化学工业中有着广泛的应用,反应、分离和纯化等化工过程大多涉及到气液两相流的传递过程[1-5]。由于传统设备效率偏低, 气液两相流的传递过程强化受到广泛关注[6-9]。因此,微化工技术作为化工过程强化的有效手段之一,自20世纪90年代起得到了快速发展和应用[10]。
微化工技术的基础设备是微通道,与传统设备相比,微通道是微尺度下的受限空间,其特征尺寸在数十到数百微米之间,具有传递效率高、可操控性强、操作灵活等优点。但微通道的处理量小,是微化工技术工业化的一大瓶颈。比较而言,微通道的尺寸放大会导致较强的放大效应,随着特征尺寸的放大,通道内的传质性能有所降低[11-12]。而并行放大则可以较好地保持单通道优良传递特性[13]。但并行放大不可避免地会对流体分布产生不利影响。实际上,正是流体分布的不均匀性严重限制了并行微通道的应用。因此,如何对微通道进行并行放大,并将其应用于工业生产中成为了国内外研究者的主要关注点。本论文针对微通道内气液两相体系的流动和传质、微通道的并行放大研究进行综述,并对微化工技术的未来发展进行展望。
1 微通道内的气液两相流 1.1 气液两相流的流型微通道内气液两相流的流型直接影响着停留时间、比表面积和传递性能[14-15]。目前已知的两相流常见流型有泡状流、弹状流(泰勒流)、搅拌流和环状流,如图 1所示。
图 1中,弹状流由于其较高的稳定性、较大的操作范围和良好的可控性,成为了两相流进行传递过程的最适宜流型[17]。
伴有传质的气液两相流在弹状流下的流动情况如图 2中Yin等[18]的研究所示,弹状气泡在向下游流动的过程中,由于液相对气泡的持续不断的吸收作用,其长度不断减小,形成弹状-泡状流或弹状流。而在流动过程中,一方面由于气泡的表面积逐渐缩小,另一方面由于液相中的吸收剂逐渐饱和,因此在通道下游的气泡缩短趋势逐渐减缓。
在水平放置的微通道中,气液两相流流型主要由惯性力、黏性力和表面张力共同控制,因此气液相流量、物理性质和通道结构均会对其产生影响。相较于传统宏观设备,气液两相流在微通道内受到惯性力的作用相对较小,黏性力和表面张力在受限空间内占据主导作用[19]。目前,已有文献对微通道内气液两相流的流型转换线进行了预测。
研究初期,由于对微通道内气液两相流的流动机理缺乏理解,流型转换线的预测式大多以气液相流量为划分标准。Triplett等[20]采用空气-水的气液两相流体系,分别在圆形微通道和三角形微通道中进行实验探究。以气相和液相的表观速度为坐标将所有的流型转换线绘出,发现不同微通道内的流型转换线具有一定的相似性。
这种简单的流型划分方式十分清晰直观,为后续对流型的深入研究奠定了基础。但此类预测式忽略了流体物性和通道结构的影响,仅适用于文献所采用的操作条件,其适用性十分有限。随着对微通道内气液两相流的流动机理的不断深入研究,各种流型的形成机理及其在形成过程中受到的作用力逐渐被科研工作者所认知。通过分析惯性力、黏性力和表面张力对流型的影响,以一系列无量纲准数作为流型转换的衡量标准,做出了流型转换线的准数关联预测式。这类预测式具有更普遍的适用性。
Akbar等[21]分析了微尺度下惯性力和表面张力对气泡生成和流动过程的影响,并采用Weber准数表示惯性力和表面张力之比,将气液两相流流型划分为表面张力控制区、共同控制区和惯性力控制区3个区域。Yue等[22]考虑到微通道结构对气液两相流流型的影响,在不同水力直径的微通道内对气液两相流流型进行了研究。其研究结果发现Akbar等提出的预测模型针对不同水力直径的微通道均具有较好的适用性。而Wang等[23]在研究中发现,微通道气液两相流流型的不仅受到惯性力和表面张力的影响,还受到液相的黏性力的作用。因此,在微通道内采用Capillary准数来表示流体受到黏性力与表面张力的作用,对实验得到的流型进行了更加精确的预测。
此外,Dang等[24]利用CLSVOF和VOF 2种方法对微通道内气泡的生成过程进行了模拟研究,对接触角、表面张力和黏度对流型的影响进行了分析。结果证明,数值模拟作为研究微通道两相流的重要手段,在研究多变量的操作条件时具有其独特的优势。
迄今为止,众多研究者已经对微通道内的两相流的流型进行了大量的研究,但由于微通道内的流动机理十分复杂,普适的流型转换机理仍未能建立。同时,目前的研究主要集中于无相间传质的气液两相流,对伴有传质的气液两相的研究仍不充分。在伴有传质的气液两相流在微通道内流动过程中,由于液相对气泡的持续吸收作用,其气泡长度会沿通道持续减小,使得伴有传质的气液两相流在微通道内的流动机理更为复杂,其流型的转换也受到更多控制因素的影响[25]。深入地研究伴有传质的气液两相流在微通道内的流型及流型转换规律是目前研究的主要聚焦点。
1.2 气液两相流的相间传质目前在微通道内研究气液传质的方法主要为在线分析法。采用高速摄像机对伴有传质的气液两相流在微通道内的流动过程进行拍摄,通过对气泡体积减小速率进行计算,得到气液两相流在微通道内的传质特性。
1.2.1 泡状流在泡状流流型下,生成的气泡为球状,其初始长度小于或等于微通道的宽度,且其相邻的液弹长度较长,2个相邻气泡间的距离较远。
Lu等[26]在研究中发现,在泡状流流型下,气泡在生成过程中的传质量可以占到总传质量的50%~60%,是通道内传质的主要贡献者。Pennemann和Hessel[27]的研究则指出,泡状流下的气泡在流动过程中体积不断减小,其尺寸将远小于通道宽度,此时,气泡受到流场轴向的推动力逐渐减弱,受到的径向作用逐渐占据主导。因此气泡在下游聚集和停滞,不利于传质过程的进行。也因此,下游微通道内的气泡在流动过程中的传质速率较低。研究表明,若微通道具有足够长的长度,通道下游处的气泡尺寸几乎不发生变化,传质的主要贡献区域为生成部分和通道上游。
一般来说,气泡的尺寸越小,其比表面积越大,越有利于传质系数的提高。但当泡状流形成时,其对应的微通道内的气相流量往往比较小,气相在气泡的生成过程中需要经过一段时间的积压才能进入主通道中,因此微通道内的泡状气泡生成频率较低,无法形成密集的泡状流。因此,微通道内的气液两相总接触面积并不大,总体积传质系数也并不高。
1.2.2 弹状流弹状流下生成的气泡长度大于微通道的宽度,相邻气泡之间存在较短的液弹。在此流型下,其返混程度较小,近似于平推流[28]。
Yao等[29]在研究中发现,弹状流下的液弹中存在较强的液弹内循环,这种流动模式对提升传质效率具有促进作用。此外,Yao等[30]还发现,矩形微通道内存在角区泄漏流,角区泄露流对传质过程具有抑制作用。而角区的大小由流体的物理性质和操作条件共同决定。在弹状气泡向下游流动的过程中,其气泡体积逐渐减小,因此其气液两相接触面积持续下降。同时,气泡体积的减小也会导致气泡流动速度的逐渐减缓,这会造成液弹内循环的减弱。这2方面的原因共同决定了气液传质效率随弹状气泡的流动而减弱。弹状流下的液弹内循环和泄漏流示意图已在Yao等[30]的研究中给出,如图 3所示。
Zhang等[31]在对弹状流下吸收过程的三维模拟研究中,发现液弹内的浓度场和速度场均存在旋涡,这也证明了泄漏流的存在。同时,气泡流动状态的变化导致了液弹内循环的减弱。此外,他们还定量分析了液膜厚度对传质的影响,结果表明,在气泡的流动过程中,其周围的液膜逐渐增厚,略微地提升了传质系数。Ye等[32]考察了微通道内气液两相流的传质系数和体积传质系数随气泡在通道内位置的演变规律,并研究了传质推动力随流动过程的变化。研究表明传质系数kL和体积传质系数kLa随流动的变化存在临界位置。在临界位置之前,液弹内循环对传质系数的影响占主导作用,而临界位置之后角区泄漏流对传质系数的影响占主导作用。Guo等[33]研究了弹状流下非水溶液对CO2的吸收过程,结果表明,在高黏的非水溶液体系下,微通道仍能保持较高的比表面积和较好的传质性能,其液侧体积传质系数远高于宏观设备。
弹状流下的气泡生成频率较快,排列较为紧密,因此通道内的气液接触面积较大。同时,弹状流具有良好的可控性和较好的稳定性,因此一般将气液反应控制在此流型下进行。
1.2.3 环状流环状流流型下,气相和液相均会连续地流过微通道,不再出现交替排布的气泡和液弹。Yue等[34]在研究中发现,环状流流型下的气液接触面积较弹状流有所下降,并且不随气液两相流量的改变而改变。Sobieszuk等[35]认为,环状流会削弱对流传质,导致微通道内的传质系数下降。同时,由于环状流的不稳定性以及伴随而来的高压力降,一般不将此流型作为气液两相反应的主要流型。
微通道内气液两相流的传质特性是对微通道性能的最直接的判断依据。气液两相流在微通道内的传质系数是在微通道内进行两相流反应的基础数据。液相对气相的吸收会改变气泡在通道内的运动规律,同时,气泡运动状态的改变也会影响气液两相的相间传质过程。大量研究表明,气液两相流在微通道内的比表面积和体积传质系数可比传统宏观设备高2~4个数量级[36]。
1.2.4 传质系数预测式微通道内气液两相流的各种已知流型中,弹状流作为一种操作范围较宽、流体流动稳定、气液接触面积的流型,其传质模型得到了研究者们的广泛研究。弹状流流型下的体积传质系数预测模型从最初简单的纯经验关联式发展为目前半理论半经验的无量纲准数模型。
Bercic和Pintar[37]研究了圆形微通道内气液两相流的传质过程,发现其体积传质系数主要由气液两相流量决定,通过实验中得到的流体表观流速、空隙率和气液单元长度拟合得到了关于体积传质系数的经验关联式:
| ${k_{\rm{L}}}a = 0.111\frac{{{{({u_{\rm{B}}} + {u_{\rm{L}}})}^{1.19}}}}{{{{[(1 - \varepsilon ){l_{{\rm{UC}}}}]}^{0.57}}}} $ | (1) |
式(1)中:uB代表气泡在通道内的流动速度;uL代表液弹在通道内的流动速度;ε代表微通道内的空隙率;lUC代表一个气液单元的长度。
而van Baten和Krishna[38]引入了渗透理论,通过引入扩散系数对体积传质系数预测模型进行了修正。他们在研究中指出,微通道内弹状流的体积传质系数为气泡主体部分和气泡球帽部分,而这2部分的传质机理有着明显的不同,应当分别进行计算。
| $\begin{array}{l} {k_{\rm{L}}}a = {k_{{\rm{L, cap}}}}{a_{{\rm{cap}}}} + {k_{{\rm{L, body}}}}{a_{{\rm{body}}}} = \\ 2\frac{{\sqrt 2 }}{{\rm{ \mathsf{ π} }}}\sqrt {\frac{{D{u_{\rm{B}}}}}{{{d_{\rm{H}}}}}} \frac{4}{{{l_{{\rm{UC}}}}}} + \frac{2}{{\sqrt {\rm{ \mathsf{ π} }} }}\sqrt {\frac{{D{u_{\rm{B}}}}}{{\varepsilon {l_{\rm{UC}}}}}} \frac{{4\varepsilon }}{{{d_{\rm{H}}}}} \end{array} $ | (2) |
式(2)中:kL, cap和kL, body分别代表气泡球帽和主体的液侧传质系数;acap和abody分别代表气泡球帽和主体的比表面积;D表示气相在液相中的扩散系数;dH表示通道的水力直径。
基于流动状态的模型是对体积传质系数预测的初步探索。通过对微通道内气液两相流流动状态的观察,可以对应地预测其体积传质系数,但这也表示此类预测模型的普适性较差。
Jepsen[39]认为微通道内的气液两相流压力降是气液两相流在通道内的流动状态的具体体现。因此可以将压力降作为衡量流体运动状态的指标,并将其作为预测体积传质系数的主要参数。
| ${k_{\rm{L}}}a = \frac{{\Delta P}}{L}({u_{\rm{G}}} + {u_{\rm{L}}}) $ | (3) |
式(3)中:ΔP表示微通道内的气液两相流压力降;L表示微通道的总长度;uG和uL分别表示气相和液相的表观流速。
随后,Yue等[34]对其进行了修正,将压力降作为预测体积传质系数的唯一参数,研究了气液两相流的压力降与体积传质系数的对应关系,并建立了能量耗散模型。
| ${k_{\rm{L}}}a = 0.863{\left( {\frac{{\Delta P}}{L}} \right)^{0.881}} $ | (4) |
相较于基于流动状态的预测模型,能量耗散模型更加简练,其预测所需的数据也更容易获取。但能量耗散模型对体积传质系数的预测仍不够准确。
Yue等[22]认为,不同操作条件会改变微通道内的惯性力和黏性力,进而对微通道内的气液两相流流动状态产生影响。他们指出,采用无量纲准数可以准确地描述微通道内气液两相流的流动状态,进而对体积传质系数进行准确地预测:
| $S{h_{\rm{L}}}a{d_{\rm{H}}} = {a_1}Re_{\rm{G}}^{{a_2}}Re_{\rm{L}}^{{a_3}}Sc_{\rm{L}}^{{a_4}} $ | (5) |
式(5)中:Sh为舍伍德数,是反映包含有待定传质系数的无因次数群;Re是雷诺数,用来表征流体的流动情况;Sc为施密特数,可以用来描述同时有动量扩散及质量扩散的流体,与流体动力学层和质量传递边界层的相对厚度有关;下标L和G分别代表液相和气相。
而Ji等[40]在研究中发现,除惯性力和黏性力之外,表面张力也对微通道内的传质有着显著的影响。他们在无量纲准数预测模型中引入毛细数Ca来表示表面张力的作用,对体积传质系数进行了关联:
| $S{h_{\rm{L}}}a{d_{\rm{H}}} = {a_1}Re_{\rm{G}}^{{a_2}}Re_{\rm{L}}^{{a_3}}Sc_{\rm{L}}^{{a_4}}Ca_{\rm{L}}^{{a_5}} $ | (6) |
此后,大量的学者对不同操作条件下的无量纲准数模型进行了修正。Niu等[41]针对圆形截面微通道提出了一个相似的无量纲准数预测模型。Yao等[29]则利用无量纲准数模型对微通道内非水溶液吸收CO2的过程进行了研究。研究结果均表明,此类预测模型具有较好的预测性能。
但是,目前对于微通道内伴有化学吸收的气液两相流的研究还不充分,对不同微通道及不同气液两相流体系下的化学增强因子的研究还有待继续开展。
2 微通道的应用现状由于微通道具有传递效率高和安全性能好的优势,并且可以将间歇工艺改进为连续工艺,研究者逐渐将微通道应用于不同的多相流反应中,如快速的强放热反应、快速均匀混合的反应和涉及不稳定中间产物的反应等,均取得了令人满意的效果。因此,科研工作者开始探索如何建立大规模的高度集成的微反应工厂。由于微通道处理量小,可以通过将微通道反应器进行并联的方式来增大微通道反应器的处理量[42]。
Adamo等[43]介绍了一种即插即用的可重构药物合成系统,此系统具有高效、灵活的特点,其体积(1.0 m×0.7 m×1.8 m)仅与冰箱相当。在这个冰箱大小的系统中,可以对药物进行连续合成,并大大减少反应时间。这种灵活的即插即用方法的基础是微通道设备、连续流合成和并行放大。在此基础上,Bedard等[44]通过硬件、软件和分析的集成,解决了自动化生产的问题。通过软件可以对试剂和单元操作进行控制选择,并进行自动优化,如图 4所示。该系统的性能在C—C和C—N交联、烯烃化、还原胺化和光氧化还原催化等过程中得到了证明。
清华大学将微化工技术应用于聚合物产品的制备,开发出30 000 t/a卤化丁基橡胶合成微反应技术与装备,获得了良好效果[45]。该技术对提高我国高端橡胶产品的产量具有重要意义。
中国科学院化学物理研究所在微反应通道中进行硝酸异辛酯的合成,其转化率高于99.9%,产品质量分数大于99.5%,实现了产物的大规模连续生产[45]。
Su等[46]采用微反应器组件并行放大的方式来实现大规模的光催化反应,其结果证明,采用并行放大的方法可以在保证转化率的前提下提高处理量,其产率与单微通道基本相当。该并行微反应器如图 5所示。
Yasuhiro等[47]在并行多通道微反应器中利用臭氧的分解对有机试剂进行氧化,其产率和效率都达到较高水平。分别研究了亚硝酸盐、胺和烯烃的臭氧氧化过程,结果显示,在不到1 s的接触时间内,其转化率和选择性均可达100%。Ahn等[48]采用3 D打印技术制造了并行放大的金属微反应器,在其中分别进行了药物和特殊化学品的催化反应,实现了高通量合成,证明该反应器具有商业化的潜力。Kuijpers等[49]发现,利用并行微反应器可以有效地提高光化学反应的效率,并克服处理量的限制。但同时,并行微反应器内的流体分布不均会导致反应效率的下降,甚至使反应器堵塞,这会极大地限制并行微反应器的应用。
可以看到,通过并联集成的方式对微通道进行放大,可以达到提高产量的效果,但其收率相较于单微通道仍会略有下降。原因在于,简单地对微通道进行并行放大会造成流体分布不均的问题,进而对传质产生负面影响。因此,对微通道的并行放大进行基础理论研究对于微化工技术的发展具有举足轻重的意义。
3 微通道的并行放大在并行放大的过程中,需要解决的关键问题是并行微通道内流体分布的均匀性。根据流体在微通道的入口和出口的相对位置,Chein等[50]将并行微通道分为3种:U型、Z型和I型,如图 6所示。其中,U型和Z型属于非对称结构,I型属于对称结构[50-51]。Manoj等[51]对3种结构中的流体分布均匀性进行了定量分析。U型、Z型和I型微通道的流体分布不均匀因子分别约为55%、28%和15%。Xia等[52]研究了4种不同结构的并行微通道内流体分布的均匀性。结果同样表明,I型结构的流体分布均匀性优于其他构型,但随着雷诺数的增大,各构型的微通道的流体分布均匀性都有所下降。可以看到,I型结构的流体分布均匀性最好,U型结构的流体分布不均匀性最大,而Z型结构介于2者之间。对于Z型结构的并行微通道,流体从入口流向出口的每条路径的长度均相等,但由于其结构的不对称性,每条支通道内的压力降并不相等。尽管I型微通道是对称结构,但流体从入口流向出口的每条路径的长度不一定完全相同,这也会导致各支通道内的压力降出现差异。
此外,Chein等[50]利用数值模拟方法,对各构型内的流体分布和温度分布进行了研究。结果表明,在并行微通道内,构型对流体分布的影响十分显著,I型通道的分布均匀性明显优于其他构型。同时,当进料方向为垂直方向时,通道内的分布均匀性更好。
通过优化Z型和I型微通道的结构,可以抑制2种并行微通道的流体分布不均匀性。Amador等[53]提出一种基于电阻网络的分析方法,研究了不同构型微通道下的流体分布,并根据微通道反应器中停留时间的分布,制定了优化方案。他们建立的分析模型既适用于圆形微通道,也适用于矩形微通道。目前已有大量文献对这2种并行放大方式进行了报道。
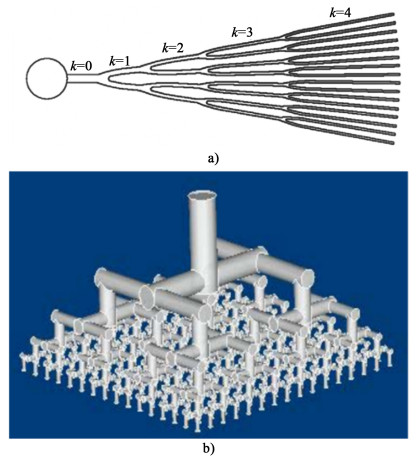
3.1 对称并行放大受哺乳动物呼吸系统的启发,研究者们提出一种基于I型结构的微通道树状并行放大方式。树状并行微通道的每一级支通道都具有完全的自相似性,即流体在通道内的不同支通道内移动的距离完全相等,如图 7所示。
Bejan的研究证实了树状并行微通道内流体分布的均匀性,并对支通道的尺寸进行了分析和优化[56-58]。随后,根据Bejan的建构理论,Fan等[59]设计了一个有1个进口、16个出口的树状流体分布器。该分布器可以实现单相流的均匀分布,并且具有较小的压力降和较短的停留时间。Hoang等[60]分析了树状并行微通道内流体分布不均匀的原因,确定了导致不均匀的3个主要来源:气泡尺寸的不均匀、气泡的非对称破裂,以及由于制造不准确造成的误差。基于以上原因,他们提出,在T型分岔口周围加入旁路通道可以降低流体分布的不均匀性。而Tondeur和Luo[55]则将树状并行微通道由二维结构拓展为三维结构,三维结构的树状并行微通道具有更均匀的流体分布,但随着支通道的逐渐增多,其流体分布的均匀性有所下降。因此,树状并行多通道的流体分布性能仍有待改善。
相较于单相流,气液两相流在树状并行微通道内的流动行为更加复杂。Kwak等[54]研究了树状并行微通道的各支通道内的气液两相流流型,并建立了流型转换的预测模型。他们得到的流型与Chung等[61]的实验结果非常吻合,各支通道内得到的流型并非固定的,而是随时间具有一定的周期变化性。Xu等[62]对并行通道内各支通道流型的变化做出了解释,他们认为,各支通道内的流型形成是具有一定周期性的,且各支通道间的流型转换周期并不相同,这是由于各支通道内压降的变化造成的。树状并行微通道内的流型比单微通道内更为复杂,各支通道内出现的流型也不尽相同。
为了分析支通道间的相互作用,Zhang等[63]定量描述了树状并行双通道中弹状流的均匀性。结果表明,气液流速的增加会增大气泡在各支通道内的长度和频率差异,进而破坏支通道间的平衡。通过分析双通道间的压力降差,研究了支通道间的相互作用。这些研究结果将有助于微通道的进一步放大。Guo等[64]在树状并行双通道中对气液两相流进行了初步探索,得到了不同于单通道的交替分配流和破裂流等流型。研究结果表明,流体分配均匀性由分岔口处的气泡长度和通道内流体动力学反馈共同控制。同时,均匀的流体分布可以促进传质性能。
Yue等[65]对多级树状并行微通道内气液两相流的流动和传质特性进行了研究。结果表明,只有在一定操作范围内,并行微通道反应器才可以保持单通道的优良传质性能。由于大流量条件下惯性力起主导作用,流动不均匀性随着流量的增加而不断加剧。而在流量较低的树状并行微通道中,其流体分布的均匀性相对较好。这一结论在Wang等[66]的模拟研究中得到了验证。此外,流体的分布还受到液相黏度的影响。液相的黏度越大,流体分布越均匀。随后,Guo等[67]对气液两相流在多级树状并行微通道中的流体动力学及传质进行了研究。实验得到了紧密弹状流这一新流型。实验结果表明,流体在树状并行微通道中的分配均匀性由T型分岔口的Ca和通道下游的反馈效应控制。存在1个临界气液流量比使并行通道内的分配均匀性达到最佳。
在实际应用中,树状分布器的几何结构也会影响树状并行微通道内流体的分布规律。Liu等[68]对树状分布器的结构进行了模拟研究,探究了树状分布器的分岔角度对流体分布的影响。结果表明,树状分布器的分岔角度对流体分布的均匀性具有较大影响,当分岔角度为180°时(即T型分岔口),其流体分布的均匀性最佳。这一结论与Wang等[69]的研究一致。此外,Liu等[70]还发现树状分布器的弯曲壁面相较于直角壁面更容易得到均匀的流体分布。而Sun等[71]通过实验研究了不同支通道宽度对并行微通道内两相流分布行为的影响。结合实验结果和可视化数据,分析了气液两相流在T型分岔口处的受力机理,并通过破裂因子来评价气泡的破裂均匀性。结果表明,随着支通道宽度的减小,流体分布的均匀性得到了很好的改善。同时,支通道宽度对弹状流的影响程度大于环状流。Guo等[72]针对树状并行微通道的2种典型结构(半宽通道和恒宽通道)进行了研究,如图 8所示。结果表明,半宽通道具有更高的效能比。相比较而言,在半宽通道中,由于通道尾部反馈效应更加明显,其操作范围明显较恒宽通道更窄。同时,由于不同宽深比对气泡生成和尾部反馈效应的综合影响,半宽通道的流体分配均匀性随气液比的增大逐渐变差。
对微通道进行树状并行放大可以得到较为均匀的流体分布,但目前对气液两相流的流体动力学仍处于探索阶段。Guo等[73]通过在线分析法建立了气液两相流在树状并行微通道内的压力降预测模型,这可以为更深入地理解树状并行微通道中的气液两相流动力学奠定理论基础。但对于树状结构,并行放大的基本原则仍未完全建立。如何实现不同操作条件下流体分布和能量利用的最优化,仍是基础理论研究的重点。
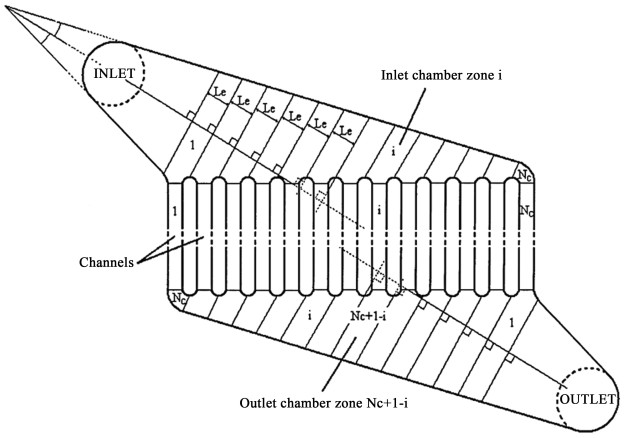
3.2 非对称并行放大尽管对称并行放大已取得了较为理想的效果,但树状并行放大也有无法克服的缺陷,其支通道数量只能是2n条,空间排布具有一定的局限性。因此,为了使微化工技术得到更广泛的应用,研究微通道的非对称并行放大十分必要。目前对非对称并行放大的研究主要集中于基于Z型结构的梳状并行微通道。
Choi等[74]从机理上解释了气泡在非对称并行微通道中的运动行为,为研究梳状并行微通道提供了理论依据。他们认为,气泡在并行通道中流动时,会将自己分散在所有可能的支通道中,以使通道的压力降最小。也就是说,流体的分布取决于各支通道内的阻力。单个气泡在分岔口处会出现破裂和不破裂2种运动状态,并在随后的流动过程中根据各支通道压力降的不同选择流动路径。气泡群的流动状态就构成了非对称并行通道的流体分布规律。
Pistoresi等[75]通过数值模拟的方法对多级梳状并行微通道进行了研究,分析了梳状结构对流体分布的影响。结果表明,在极低的流体流量下,微通道可以达到相对均匀的流体分布。但在大流量下,随着支通道数量的增多,流体分布的均匀性逐渐变差。随后,Commenge等[76]提出可以采用斜Z型结构来优化梳状并行微通道的流体分配性能,其结构如图 9所示。结果表明,倾斜的角度可以调节各支通道的阻力,从而使并行微通道在较大的流量下仍能保持均匀的流体分布。但在高流量下,大部分流体将被推入通道的下游,从而导致了流体分布的不均匀性。为解决这一问题,Delsman等[77]提出了一种优化的斜Z型结构,将其拐角由直角改为圆角,从而降低系统的压力降,在高流量下也可以得到较为均匀的流体分布。同时,增大入口和出口的宽度可进一步降低大流量时的压力降,进而改善流体分布的均匀性。
一般来说,梳状并行微通道内的流体分布很大程度上取决于封头。通过合理优化封头的形状和尺寸,可以大大降低流体分布的不均匀性,进而提高传质性能。
Anbumeenakshi等[78]对不同流量下封头形状对流动不均匀性的影响进行了探究。研究发现,梯形和三角形封头的并行微通道在小流量时流体分布更均匀,而矩形封头的并行微通道在大流量时流体分布更均匀。随后,Zoljalali等[79]发现封头的曲率对流体分布也具有较大的影响。研究表明,由于曲线结构比直线结构具有更低的压力降,因此弯曲壁面相较于直角壁面更容易得到均匀的流体分布。在此基础上,进一步得出了凹曲线结构比凸曲线结构的流体分布更均匀这一结论。而Kumaran等[80-81]的研究表明,流体分布的不均匀性随封头宽度的增大而减小。在三角封头中,当封头的宽度为48.5 mm时,其流体分布的均匀性远不如封头宽度为55.5 mm时。
除封头之外,支通道的间距也对梳状并行微通道内的流体分布具有一定的影响。Liu和Wang[82]采用高速摄像仪对梳状并行微通道中的流体动力学进行了观察。研究发现,梳状并行微通道内的流体分布特性受到支通道间距的影响。在低流量下,增大支通道间距不利于流体的均匀分布,而在高流量,增大支通道间距有利于流体的均匀分布。
此外,操作条件也会对并行微通道内的流体分布产生巨大影响。Liu等[83]通过实验研究了进料方向对并行微通道内两相流分布的影响,并观察到了3种流动状态。结果表明,对于弹状流,垂直向下的进料方向可以实现流体的均匀分布。而对于环状流,垂直向上的进料方向可以改善流体分布的均匀性。Liu等[84]的研究表明,梳状并行微通道内两相流的分布均匀性与入口处的气泡长度和速度有很大的关系,并且上游通道会对下游通道的流体分布产生影响。在高流速、短气泡的情况下,支通道可实现均匀的流体分布。而Al-Rawashdeh等[85]发现,并行通道内的流体分布均匀性还与进料压力有关。他们在两相空腔与多通道之间建立了增压通道,如图 10所示。这种设计保证了流体的均匀性,有效避免了窜流现象。
通过对结构进行优化并选择合适的操作条件,可以有效地提高流体在非对称并行微通道内的分布均匀性[86],进而可以提高反应的选择性并降低通道的整体压力降[87]。在实际应用中,非对称并行微通道的空间排布更为灵活,但其流体分布均匀性仍劣于对称并行微通道。
4 结语综上所述,微化工技术具有高效、灵活、安全的优点,是一项极具应用前景的过程强化技术。近年来,微通道内的气液两相流及微通道的并行放大得到了广泛的研究,相关的研究成果既丰富了微化学工程学科的基础理论,又为微化工技术在气-液两相体系中的大规模工业化应用奠定了基础。
微化工技术是21世纪化学工程领域的关键技术,未来将会有大量的工业应用和示范运行。但目前,仍有许多研究亟待开展。
1) 气液两相流在微通道内的流动以二维图像居多,缺乏三维流动信息。随着表征手段和计算模拟的发展,应获取通道内的三维流动信息,以便更加客观地分析通道内气液两相流的流动与传质。
2) 在矩形微通道中,角区的泄漏流和液膜对气液两相流的流动和传质具有重要影响,但其过程机理还缺乏深入地研究。同时,对液弹内循环对传质的作用规律尚不充分了解,对传质过程的认识仍有待提高。
3) 微通道并行放大的过程中存在多尺度结构,应着重解决由并行放大引入的宏观尺度和微尺度间的相互作用机制,优化流体在并行通道中的分布均匀性及整体传质性能。
4) 目前对微通道的并行放大还处于初步探索阶段,应基于高度集成化和压降最小化的约束条件,对并行微通道反应器进行结构优化,建立较为普适的并行放大准则,为微化工技术的工业化应用奠定理论基础。
5) 目前在实验室中所用的微通道反应器造价昂贵,尽管其已表现出令人满意的性能,但并行放大带来的设备成本成为了其推广应用的一大障碍。因此,应研发高效、廉价的加工技术,降低微化工设备的应用成本。
| [1] |
Yuan Y, Han M, Wang L, et al. Mass transfer coefficient for two-phase countercurrent flow in a packed column with a novel internal[J]. Chemical Engineering Journal, 2004, 99(3): 273-277. DOI:10.1016/j.cej.2003.12.002 |
| [2] |
Wibisono Y, Cornelissen E R, Kemperman A J B, et al. Two-phase flow in membrane processes: A technology with a future[J]. Journal of Membrane Science, 2014, 453: 566-602. DOI:10.1016/j.memsci.2013.10.072 |
| [3] |
Li X, Wei T, Wang D, et al. Study of gas-liquid two-phase flow patterns of self-excited dust scrubbers[J]. Chemical Engineering Science, 2016, 151: 79-92. DOI:10.1016/j.ces.2016.05.010 |
| [4] |
Dries H W, Hoffmann A C. A correlation giving improved description of the capacity and efficiency of vane-type gas-liquid separators[J]. AIChE Journal, 2019. DOI:10.1002/aic.16566 |
| [5] |
Iliuta I, Iliuta M C. Modeling of SO2 seawater scrubbing in countercurrent packed-bed columns with high performance packings[J]. Separation and Purification Technology, 2019, 226: 162-180. DOI:10.1016/j.seppur.2019.05.078 |
| [6] |
Bauer T, Schubert M, Lange R. Prozessintensivierung heterogen katalysierter gas/flüssig-reaktionen mit monolithreaktoren[J]. Chemie Ingenieur Technik, 2005, 77(11): 1683-1692. DOI:10.1002/cite.200500143 |
| [7] |
Zheng Z, Chen Y, Zhan X, et al. Mass transfer intensification in a novel airlift reactor assembly with helical sieve plates[J]. Chemical Engineering Journal, 2018, 342: 61-70. DOI:10.1016/j.cej.2018.01.039 |
| [8] |
Han S, Kashfipour M A, Ramezani M, et al. Accelerating gas-liquid chemical reactions in flow[J]. Chemical Communications, 2020, 56(73): 10593-10606. DOI:10.1039/D0CC03511D |
| [9] |
Chang Y, Xu L, Li J, et al. Gas-liquid swirling-sparger configured along a toroidal distributor for the intensification of gas-liquid contacting[J]. Industrial & Engineering Chemistry Research, 2021, 60(3): 1423-1433. |
| [10] |
陈光文, 赵玉潮, 乐军, 等. 微化工过程中的传递现象[J]. 化工学报, 2013, 64(1): 63-75. Chen Guangwen, Zhao Yuchao, Yue Jun, et al. Transport phenomena in micro-chemical engineering[J]. CIESC Journal, 2013, 64(1): 63-75. DOI:10.3969/j.issn.0438-1157.2013.01.009 (in Chinese) |
| [11] |
Plouffe P, Bittel M, Sieber J, et al. On the scale-up of micro-reactors for liquid-liquid reactions[J]. Chemical Engineering Science, 2016, 143: 216-225. DOI:10.1016/j.ces.2015.12.009 |
| [12] |
Sattari-Najafabadi M, Nasr Esfahany M, Wu Z, et al. The effect of the size of square microchannels on hydrodynamics and mass transfer during liquid-liquid slug flow[J]. AIChE Journal, 2017, 63(11): 5019-5028. DOI:10.1002/aic.15822 |
| [13] |
Kashid M N, Gupta A, Renken A, et al. Numbering-up and mass transfer studies of liquid-liquid two-phase microstructured reactors[J]. Chemical Engineering Journal, 2010, 158(2): 233-240. DOI:10.1016/j.cej.2010.01.020 |
| [14] |
Liu Y, Yue J, Xu C, et al. Hydrodynamics and local mass transfer characterization under gas-liquid-liquid slug flow in a rectangular microchannel[J]. AIChE Journal, 2020. DOI:10.1002/aic.16805 |
| [15] |
Yao C, Zhao Y, Zheng J, et al. The effect of liquid viscosity and modeling of mass transfer in gas-liquid slug flow in a rectangular microchannel[J]. AIChE Journal, 2020. DOI:10.1002/aic.16934 |
| [16] |
Zhang T, Cao B, Fan Y, et al. Gas-liquid flow in circular microchannel. Part I: Influence of liquid physical properties and channel diameter on flow patterns[J]. Chemical Engineering Science, 2011, 66(23): 5791-5803. DOI:10.1016/j.ces.2011.07.035 |
| [17] |
Bordbar A, Taassob A, Zarnaghsh A, et al. Slug flow in microchannels: Numerical simulation and applications[J]. Journal of Industrial and Engineering Chemistry, 2018, 62: 26-39. DOI:10.1016/j.jiec.2018.01.021 |
| [18] |
Yin Y, Zhu C, Guo R, et al. Gas-liquid two-phase flow in a square microchannel with chemical mass transfer: Flow pattern, void fraction and frictional pressure drop[J]. International Journal of Heat and Mass Transfer, 2018, 127: 484-496. DOI:10.1016/j.ijheatmasstransfer.2018.07.113 |
| [19] |
Fu T, Ma Y. Bubble formation and breakup dynamics in microfluidic devices: A review[J]. Chemical Engineering Science, 2015, 135: 343-372. DOI:10.1016/j.ces.2015.02.016 |
| [20] |
Triplett K A, Ghiaasiaan S M, Abdel-Khalik S I, et al. Gas-liquid two-phase flow in microchannels Part I: Two-phase flow patterns[J]. International Journal of Multiphase Flow, 1999, 25(3): 377-394. DOI:10.1016/S0301-9322(98)00054-8 |
| [21] |
Akbar M K, Plummer D A, Ghiaasiaan S M. On gas-liquid two-phase flow regimes in microchannels[J]. International Journal of Multiphase Flow, 2003, 29(5): 855-865. DOI:10.1016/S0301-9322(03)00043-0 |
| [22] |
Yue J, Luo L, Gonthier Y, et al. An experimental investigation of gas-liquid two-phase flow in single microchannel contactors[J]. Chemical Engineering Science, 2008, 63(16): 4189-4202. DOI:10.1016/j.ces.2008.05.032 |
| [23] |
Wang X, Yong Y, Fan P, et al. Flow regime transition for cocurrent gas-liquid flow in micro-channels[J]. Chemical Engineering Science, 2012, 69(1): 578-586. DOI:10.1016/j.ces.2011.11.012 |
| [24] |
Dang M, Yue J, Chen G. Numerical simulation of Taylor bubble formation in a microchannel with a converging shape mixing junction[J]. Chemical Engineering Journal, 2015, 262: 616-627. DOI:10.1016/j.cej.2014.10.017 |
| [25] |
谭璟, 赵菁菁, 徐建鸿, 等. 微通道中气体/离子液体两相流动与分散性能[J]. 化工学报, 2014, 65(1): 55-60. Tan Jing, Zhao Jingjing, Xu Jianhong, et al. Flow and dispersion performance of gas/ionic liquid systems in microchannels[J]. CIESC Journal, 2014, 65(1): 55-60. DOI:10.3969/j.issn.0438-1157.2014.01.007 (in Chinese) |
| [26] |
Yang L, Tan J, Wang K, et al. Mass transfer characteristics of bubbly flow in microchannels[J]. Chemical Engineering Science, 2014, 109: 306-314. DOI:10.1016/j.ces.2014.02.004 |
| [27] |
Pennemann H, Hessel V, Kost H J, et al. Investigations on pulse broadening for catalyst screening in gas/liquid systems[J]. AIChE Journal, 2004, 50(8): 1814-1823. DOI:10.1002/aic.10150 |
| [28] |
尧超群, 乐军, 赵玉潮, 等. 微通道内气-液弹状流动及传质特性研究进展[J]. 化工学报, 2015, 66(8): 2759-2766. Yao Chaoqun, Yue Jun, Zhao Yuchao, et al. Review on flow and mass transfer characteristics of gas-liquid slug flow in microchannels[J]. CIESC Journal, 2015, 66(8): 2759-2766. (in Chinese) |
| [29] |
Yao C, Dong Z, Zhao Y, et al. An online method to measure mass transfer of slug flow in a microchannel[J]. Chemical Engineering Science, 2014, 112: 15-24. DOI:10.1016/j.ces.2014.03.016 |
| [30] |
Yao C, Dong Z, Zhang Y, et al. On the leakage flow around gas bubbles in slug flow in a microchannel[J]. AIChE Journal, 2015, 61(11): 3964-3972. DOI:10.1002/aic.14895 |
| [31] |
Jia H, Zhang P. Investigation of the Taylor bubble under the effect of dissolution in microchannel[J]. Chemical Engineering Journal, 2016, 285: 252-263. DOI:10.1016/j.cej.2015.09.102 |
| [32] |
Ye C, Chen G, Yuan Q. Process characteristics of CO2 absorption by aqueous monoethanolamine in a microchannel reactor[J]. Chinese Journal of Chemical Engineering, 2012, 20(1): 111-119. DOI:10.1016/S1004-9541(12)60370-X |
| [33] |
Guo R, Zhu C, Yin Y, et al. Mass transfer characteristics of CO2 absorption into 2-amino-2-methyl-1-propanol non-aqueous solution in a microchannel[J]. Journal of Industrial and Engineering Chemistry, 2019, 75: 194-201. DOI:10.1016/j.jiec.2019.03.024 |
| [34] |
Yue J, Chen G, Yuan Q, et al. Hydrodynamics and mass transfer characteristics in gas-liquid flow through a rectangular microchannel[J]. Chemical Engineering Science, 2007, 62(7): 2096-2108. DOI:10.1016/j.ces.2006.12.057 |
| [35] |
Sobieszuk P, Pohorecki R, Cygański P, et al. Determination of the interfacial area and mass transfer coefficients in the Taylor gas-liquid flow in a microchannel[J]. Chemical Engineering Science, 2011, 66(23): 6048-6056. DOI:10.1016/j.ces.2011.08.029 |
| [36] |
Ganapathy H, Shooshtari A, Dessiatoun S, et al. Hydrodynamics and mass transfer performance of a microreactor for enhanced gas separation processes[J]. Chemical Engineering Journal, 2015, 266: 258-270. DOI:10.1016/j.cej.2014.12.028 |
| [37] |
Bercic G, Pintar A. The role of gas bubbles and liquid slug lengths on mass transport in the Taylor flow through capillaries[J]. Chemical Engineering Science, 1997, 52(21/22): 3709-3719. |
| [38] |
van Baten J M, Krishna R. CFD simulations of mass transfer from Taylor bubbles rising in circular capillaries[J]. Chemical Engineering Science, 2004, 59(12): 2535-2545. DOI:10.1016/j.ces.2004.03.010 |
| [39] |
Jepsen J C. Mass transfer in two-phase flow in horizontal pipelines[J]. AIChE Journal, 1970, 16(5): 705-711. DOI:10.1002/aic.690160504 |
| [40] |
Ji X, Ma Y, Fu T, et al. Experimental investigation of the liquid volumetric mass transfer coefficient for upward gas-liquid two-phase flow in rectangular microchannels[J]. Brazilian Journal of Chemical Engineering, 2010, 27(4): 573-582. DOI:10.1590/S0104-66322010000400009 |
| [41] |
Niu H, Pan L, Su H, et al. Flow pattern, pressure drop, and mass transfer in a gas-liquid concurrent two-phase flow microchannel reactor[J]. Industrial & Engineering Chemistry Research, 2009, 48(3): 1621-1628. |
| [42] |
Kockmann N, Roberge D M. Scale-up concept for modular microstructured reactors based on mixing, heat transfer, and reactor safety[J]. Chemical Engineering and Processing: Process Intensification, 2011, 50(10): 1017-1026. DOI:10.1016/j.cep.2011.05.021 |
| [43] |
Adamo A, Beingessner R L, Behnam M, et al. On-demand continuous-flow production of pharmaceuticals in a compact, reconfigurable system[J]. Science, 2016, 352(6281): 61-67. DOI:10.1126/science.aaf1337 |
| [44] |
Bédard A C, Adamo A, Aroh K C, et al. Reconfigurable system for automated optimization of diverse chemical reactions[J]. Science, 2018, 361(6408): 1220-1225. DOI:10.1126/science.aat0650 |
| [45] |
辛靖, 朱元宝, 胡淼, 等. 微化工技术的研究与应用进展[J]. 石油化工高等学校学报, 2020, 33(5): 8-13. Xin Jing, Zhu Yuanbao, Hu Miao, et al. Research and application progress of microchemical technology[J]. Journal of Petrochemical Universities, 2020, 33(5): 8-13. DOI:10.3969/j.issn.1006-396X.2020.05.002 (in Chinese) |
| [46] |
Su Y, Kuijpers K, Hessel V, et al. A convenient numbering-up strategy for the scale-up of gas-liquid photoredox catalysis in flow[J]. Reaction Chemistry & Engineering, 2016, 1(1): 73-81. |
| [47] |
Wada Y, Schmidt M A, Jensen K F. Flow distribution and ozonolysis in gas-liquid multichannel microreactors[J]. Industrial & Engineering Chemistry Research, 2006, 45(24): 8036-8042. |
| [48] |
Ahn G N, Yu T, Lee H J, et al. A numbering-up metal microreactor for the high-throughput production of a commercial drug by copper catalysis[J]. Lab on a Chip, 2019, 19(20): 3535-3542. DOI:10.1039/C9LC00764D |
| [49] |
Kuijpers K P L, van Dijk M A H, Rumeur Q G, et al. A sensitivity analysis of a numbered-up photomicroreactor system[J]. Reaction Chemistry & Engineering, 2017, 2(2): 109-115. |
| [50] |
Chein R, Chen J. Numerical study of the inlet/outlet arrangement effect on microchannel heat sink performance[J]. International Journal of Thermal Sciences, 2009, 48(8): 1627-1638. DOI:10.1016/j.ijthermalsci.2008.12.019 |
| [51] |
Manoj S V, Pattamatta A, Das S K. Investigation on flow maldistribution in parallel microchannel systems for integrated microelectronic device cooling[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2014, 4(3): 438-450. DOI:10.1109/TCPMT.2013.2284291 |
| [52] |
Xia G, Jiang J, Wang J, et al. Effects of different geometric structures on fluid flow and heat transfer performance in microchannel heat sinks[J]. International Journal of Heat and Mass Transfer, 2015, 80: 439-447. DOI:10.1016/j.ijheatmasstransfer.2014.08.095 |
| [53] |
Amador C, Gavriilidis A, Angeli P. Flow distribution in different microreactor scale-out geometries and the effect of manufacturing tolerances and channel blockage[J]. Chemical Engineering Journal, 2004, 101(1/2/3): 379-390. |
| [54] |
Kwak Y, Pence D, Liburdy J, et al. Gas-liquid flows in a microscale fractal-like branching flow network[J]. International Journal of Heat and Fluid Flow, 2009, 30(5): 868-876. DOI:10.1016/j.ijheatfluidflow.2009.03.014 |
| [55] |
Tondeur D, Luo L. Design and scaling laws of ramified fluid distributors by the constructal approach[J]. Chemical Engineering Science, 2004, 59(8/9): 1799-1813. |
| [56] |
Lorente S, Wechsatol W, Bejan A. Optimization of tree-shaped flow distribution structures over a disc-shaped area[J]. International Journal of Energy Research, 2003, 27(8): 715-723. DOI:10.1002/er.907 |
| [57] |
Lewins J. Bejan's constructal theory of equal potential distribution[J]. International Journal of Heat and Mass Transfer, 2003, 46(9): 1541-1543. DOI:10.1016/S0017-9310(02)00441-6 |
| [58] |
Wechsatol W, Lorente S, Bejan A. Tree-shaped networks with loops[J]. International Journal of Heat and Mass Transfer, 2005, 48(3/4): 573-583. |
| [59] |
Fan Z, Zhou X, Luo L, et al. Experimental investigation of the flow distribution of a 2-dimensional constructal distributor[J]. Experimental Thermal and Fluid Science, 2008, 33(1): 77-83. DOI:10.1016/j.expthermflusci.2008.07.003 |
| [60] |
Hoang D A, Haringa C, Portela L M, et al. Design and characterization of bubble-splitting distributor for scaled-out multiphase microreactors[J]. Chemical Engineering Journal, 2014, 236: 545-554. DOI:10.1016/j.cej.2013.08.066 |
| [61] |
Chung P M Y, Kawaji M. The effect of channel diameter on adiabatic two-phase flow characteristics in microchannels[J]. International Journal of Multiphase Flow, 2004, 30(7/8): 735-761. |
| [62] |
Xu J, Feng Y, Cen J. Transient flow patterns and bubble slug lengths in parallel microchannels with oxygen gas bubbles produced by catalytic chemical reactions[J]. International Journal of Heat and Mass Transfer, 2007, 50(5/6): 857-871. |
| [63] |
Zhang L, Peng D, Lyu W, et al. Uniformity of gas and liquid two phases flowing through two microchannels in parallel[J]. Chemical Engineering Journal, 2015, 263: 452-460. DOI:10.1016/j.cej.2014.11.004 |
| [64] |
Guo R, Fu T, Zhu C, et al. The effect of flow distribution on mass transfer of gas-liquid two-phase flow in two parallelized microchannels in a microfluidic loop[J]. International Journal of Heat and Mass Transfer, 2019, 130: 266-273. DOI:10.1016/j.ijheatmasstransfer.2018.10.078 |
| [65] |
Yue J, Boichot R, Luo L, et al. Flow distribution and mass transfer in a parallel microchannel contactor integrated with constructal distributors[J]. AIChE Journal, 2010, 56(2): 298-317. |
| [66] |
Wang L, Wu W, Li X. Numerical and experimental investigation of mixing characteristics in the constructal tree-shaped microchannel[J]. International Journal of Heat and Mass Transfer, 2013, 67: 1014-1023. DOI:10.1016/j.ijheatmasstransfer.2013.08.077 |
| [67] |
Guo R, Fu T, Zhu C, et al. Hydrodynamics and mass transfer of gas-liquid flow in a tree-shaped parallel microchannel with T-type bifurcations[J]. Chemical Engineering Journal, 2019, 373: 1203-1211. DOI:10.1016/j.cej.2019.05.124 |
| [68] |
Liu H, Li P. Even distribution/dividing of single-phase fluids by symmetric bifurcation of flow channels[J]. International Journal of Heat and Fluid Flow, 2013, 40: 165-179. DOI:10.1016/j.ijheatfluidflow.2013.01.011 |
| [69] |
Wang X, Mujumdar A S, Yap C. Effect of bifurcation angle in tree-shaped microchannel networks[J]. Journal of Applied Physics, 2007. DOI:10.1063/1.2794379 |
| [70] |
Liu H, Li P, Lew J V, et al. Experimental study of the flow distribution uniformity in flow distributors having novel flow channel bifurcation structures[J]. Experimental Thermal and Fluid Science, 2012, 37: 142-153. DOI:10.1016/j.expthermflusci.2011.10.015 |
| [71] |
Sun W, Liu Y, He K, et al. The phase distribution of gas-liquid two-phase flow in microimpacting T-junctions with different branch channel diameters[J]. Chemical Engineering Journal, 2018, 333: 34-42. DOI:10.1016/j.cej.2017.09.136 |
| [72] |
Guo R, Fu T, Zhu C, et al. Flow distribution and mass transfer of gas-liquid flow in parallel microchannels with different tree-shaped distributors: Halving-width versus constant-width[J]. Industrial & Engineering Chemistry Research, 2020, 59(3): 1327-1335. |
| [73] |
Guo R, Fu T, Zhu C, et al. Pressure drop model of gas-liquid flow with mass transfer in tree-typed microchannels[J]. Chemical Engineering Journal, 2020. DOI:10.1016/j.icheatmasstransfer.2011.08.020 |
| [74] |
Choi W, Hashimoto M, Ellerbee A K, et al. Bubbles navigating through networks of microchannels[J]. Lab on a Chip, 2011, 11(23): 3970-3978. DOI:10.1039/c1lc20444k |
| [75] |
Pistoresi C, Fan Y, Luo L. Numerical study on the improvement of flow distribution uniformity among parallel mini-channels[J]. Chemical Engineering and Processing: Process Intensification, 2015, 95: 63-71. DOI:10.1016/j.cep.2015.05.014 |
| [76] |
Commenge J M, Falk L, Corriou J P, et al. Optimal design for flow uniformity in microchannel reactors[J]. AIChE Journal, 2002, 48(2): 345-358. DOI:10.1002/aic.690480218 |
| [77] |
Delsman E R, Pierik A, de Croon M H J M, et al. Microchannel plate geometry optimization for even flow distribution at high flow rates[J]. Chemical Engineering Research and Design, 2004, 82(2): 267-273. DOI:10.1205/026387604772992864 |
| [78] |
Anbumeenakshi C, Thansekhar M R. Experimental investigation of header shape and inlet configuration on flow maldistribution in microchannel[J]. Experimental Thermal and Fluid Science, 2016, 75: 156-161. DOI:10.1016/j.expthermflusci.2016.02.004 |
| [79] |
Zoljalali M A, Omidbakhsh A E. Study of the flow distribution in parallel micro-channels with a triangular manifold[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2019, 42(1): 1-9. DOI:10.1007%2Fs40430-019-2140-x |
| [80] |
Kumaraguruparan G, Kumaran R M, Sornakumar T, et al. A numerical and experimental investigation of flow maldistribution in a micro-channel heat sink[J]. International Communications in Heat and Mass Transfer, 2011, 38(10): 1349-1353. DOI:10.1016/j.icheatmasstransfer.2011.08.020 |
| [81] |
Kumaran R M, Kumaraguruparan G, Sornakumar T. Experimental and numerical studies of header design and inlet/outlet configurations on flow mal-distribution in parallel micro-channels[J]. Applied Thermal Engineering, 2013, 58(1/2): 205-216. |
| [82] |
Liu Y, Wang S. Distribution of gas-liquid two-phase slug flow in parallel micro-channels with different branch spacing[J]. International Journal of Heat and Mass Transfer, 2019, 132: 606-617. DOI:10.1016/j.ijheatmasstransfer.2018.12.040 |
| [83] |
Liu Y, Sun W, Wu W, et al. Gas-liquid two-phase flow distribution in parallel micro-channels with different header and channels' orientations[J]. International Journal of Heat and Mass Transfer, 2017, 112: 767-778. DOI:10.1016/j.ijheatmasstransfer.2017.05.029 |
| [84] |
Liu Y, Sun W, Wang S. Experimental investigation of two-phase slug flow distribution in horizontal multi-parallel micro-channels[J]. Chemical Engineering Science, 2017, 158: 267-276. DOI:10.1016/j.ces.2016.10.021 |
| [85] |
Al-Rawashdeh M, Fluitsma L J M, Nijhuis T A, et al. Design criteria for a barrier-based gas-liquid flow distributor for parallel microchannels[J]. Chemical Engineering Journal, 2012, 181/182: 549-556. DOI:10.1016/j.cej.2011.11.086 |
| [86] |
Madane K, Kulkarni A A. Pressure equalization approach for flow uniformity in microreactor with parallel channels[J]. Chemical Engineering Science, 2018, 176: 96-106. DOI:10.1016/j.ces.2017.10.021 |
| [87] |
Saber M, Commenge J M, Falk L. Microreactor numbering-up in multi-scale networks for industrial-scale applications: Impact of flow maldistribution on the reactor performances[J]. Chemical Engineering Science, 2010, 65(1): 372-379. DOI:10.1016/j.ces.2009.06.010 |
 2021, Vol. 38
2021, Vol. 38