为了在全球市场上保持竞争力,优化生产流程的设计和管理是重中之重。间歇化工过程以其技术密集性、动态性、多样性、灵活性和不确定性等特点在化工及相关行业中发挥着重要作用[1]。虽然在间歇过程的设计和优化方面均有了很大的进展,但由于这是一个离散变量和连续变量共存的混合整数非线性规划MINLP(Mixed-Integer Nonlinear Programming)问题[2],求解过程中目标函数的复杂度随着变量的数量变化呈指数增长趋势。所以对问题进行建模和求解仍然相当困难[3]。
差分运算是间歇过程设计中最早使用的方法[4],但解决方案的复杂性使得该方法很快被分支定界法[5-6]、数学规划法和其他启发式方法所取代[7-8]。然而,这些方法即使是在解决简单问题的过程中就非常麻烦,显然不适合解决大规模问题。人工智能算法或通过多种方法相结合的方式来解决上述问题获得了成功的应用。Loonkar和Robinson[9]使用迭代方法来最小化设备投资。Yeh等[10]使用启发式算法讨论单一产品化学过程的综合问题。郑国文等[11]基于Yeh的研究通过添加中间存储单元,进一步研究了这一过程。Kirkpatrick等[12]提出了模拟退火算法(SAA),Yuan等[13]在间歇过程的设计和调度中使用了该算法。杨志才等[14]提出了一种分解策略,然后引入了基于该策略和随机算法的组合算法来解决间歇过程优化的MINLP问题。正如Moniz等[15]所指出的,我们仍然需要新的方法,它应该对启发式方法和智能优化算法进行整合,以解决现实中更加复杂的问题。
本研究提出了一种基于遗传算法(GA)的MINLP模型,并用回溯法对该模型进行了补充。该算法在保持遗传算法优点的前提下结合回溯法指导搜索过程,消除劣质基因;并且在建模过程中,考虑了设备利用率最大化问题。最后通过实例与利用枚举法和回溯法相结合的方法建立的模型进行了比较。
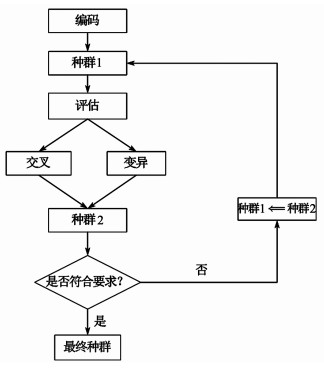
1 遗传算法的基本原理遗传算法是由美国密歇根大学的Holland[16]提出的。它是解决复杂系统问题的框架,具有良好的适用性和鲁棒性。一个典型的遗传算法的基本要求是:1)解域的遗传表示。2)用于评估解域的适应度函数。
每个候选解决方案的标准表示形式是位数组。其他类型和结构的数组基本上可以以相同的方式使用。如图 1所示,遗传算法的过程包括以下步骤[17]:1)创建一组编码方案。2)使用适应度函数评估不同的字符串。3)字符串根据其评估的适应度大小进行排序。4)然后创建2个子节点,对2个字符串进行交叉和编译操作,然后替换上一代的2个字符串。5)最后重复该循环,直到达到停止标准。
|
| 图 1 遗传算法典型流程图 Fig.1 Typical structure of genetic algorithm |
| |
为降低模型建立时的复杂程度,我们做如下假设:1)生产工艺和配方已知;2)总生产时间和生产需求已经明确;3)有充足的原料供应;4)设备在整个时间段内无故障;5)设备为非标设备;6)设备数量不加以限制;7)处理时间已经确定,不会改变;8)处理时间包括进料时间、出料时间、反应时间和清洗时间。
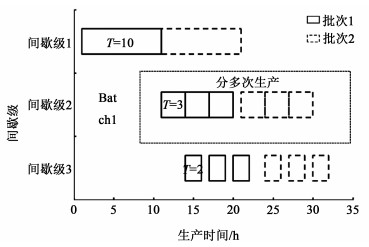
2.2 约束方程为了提高设备的利用率,规定可以将前一间歇级的产品分为xi次生产,即设置中间存储,如图 2间歇级2所示。很明显如果间歇级1中的物料尚未被间歇级2处理完,间歇级1是不能接受新的物料的投入的,否则会造成中间存储中物料的积压。于是可以将这个分次生产过程等效为一个处理时间较长的过程,因此有:
| $ t_i^\prime \ge {t_i}\prod\limits_1^i {{x_i}} \quad {x_i} \ge 1\quad \forall i $ | (1) |
|
| 图 2 分段生产示意图 Fig.2 Schematic diagram of sectional production |
| |
式(1)中:ti为产品在间歇级i的处理时间,h;t′i为产品在间歇级i的等效处理时间,h;xi为上一级产品在在下一级的分批生产次数。
间歇化工过程通常包含1个或多个瓶颈阶段。通常这些阶段涉及到更长的处理时间或者资本密集型设备[18]。将与瓶颈阶段相对应的时间称为循环时间:
| $ T \ge {\rm{max}}\left( {\frac{{t_i^\prime }}{{{n_i}}}} \right) $ | (2) |
式(2)中:ni为间歇级i的异步平行单元数;T为限制循环时间,h。
在1台设备上每批应完成的产品量为:
| $ {B_i} \ge \frac{{{Q_i}}}{{\prod\limits_1^i {{x_i}} (H/T){m_i}}} $ | (3) |
式(3)中:mi为间歇级i的同步平行单元数;Bi为间歇级i每1批完成的产品量,kg;Qi为间歇级i的生产总量,kg;H为年生产时间,h。
设备的体积与设备加工的产品量之间的关系为:
| $ {V_i} \ge {B_i}/{S_i} $ | (4) |
式(4)中:Si为间歇级i的尺寸因子,kg/m3;Vi为设备体积,m3。
并且有:
| $ {V_{i,{\rm{min}}}} \le {V_i} \le {V_{i,{\rm{max}}}} $ | (5) |
引入平行单元以降低这些瓶颈阶段的主导地位[19]。同步平行单元的最大数值被指定为在非覆盖式下操作时需要设置的同步平行单元的数。
| $ {m_i} \le {Q_i}{S_i}/\frac{{{V_{{\rm{max}}}}H}}{{\sum\nolimits_i {{t_i}} }} $ | (6) |
式(6)中:Vmax为设备最大体积,m3。
反应设备总数为:
| $ {N = \sum\limits_{i = 1} {({m_i}{n_i})} } $ | (7) |
| $ {1 \le {n_i} \le {n_{{\rm{max}}}}} $ | (8) |
式(8)中:nmax为间歇级的最大异步平行单元数。
2.3 目标函数该模型以设备投资最低为目标函数[20],在计算过程中设备成本的估算通常以体积的指数函数表示[21]:
| $ {\rm{cost}}{ _i} = {\alpha _i}V_i^{{\beta _i}} $ | (9) |
式(9)中:αi为间歇级i的成本系数;βi为间歇级i的成本指数。
故总投资为:
| $ {\rm{obj}} = {[\sum\limits_i {({m_i}{n_i}{\alpha _i}V_i^{{\beta _i}})} ]_{{\rm{min}}}} $ | (10) |
以实际项目为例,该项目包含7个间歇级,每个间歇级的出料都是固体,包含过滤和干燥2种操作。因此,我们可以将每个间歇级的设备等效为1个具有过滤和干燥功能的反应器。为了确保转化率不受较大影响,将设备最大体积设为5 m3。年生产时间为330 d,每天24 h不间断生产,故总生产时间为7 920 h。其他所有输入数据在表 1中给出。
| 操作时间/h | 总投料量/103 kg | 尺寸因子Si | 费用系数α | 费用指数β | |
| 间歇级1 | 120 | 100.0 | 22.5 | 250 | 0.68 |
| 间歇级2 | 24 | 70.0 | 29.0 | 700 | 0.45 |
| 间歇级3 | 24 | 46.0 | 9.1 | 250 | 0.68 |
| 间歇级4 | 24 | 27.0 | 14.7 | 780 | 0.68 |
| 间歇级5 | 24 | 27.0 | 18.8 | 250 | 0.60 |
| 间歇级6 | 24 | 31.3 | 8.9 | 780 | 0.68 |
| 间歇级7 | 24 | 30.7 | 11.5 | 700 | 0.45 |
该模型的主体为遗传算法,有3组变量:同步平行单元数、异步平行单元数和连续生产数。其中连续生产是指在2个连续批次的同一间歇级生产时间间隔可能较大的情况下前一间歇级中该步骤的产物分为几次投入到此间歇级中进行生产,以减少设备的体积,提高设备的利用率。
由于变量较多,生成的染色体较为复杂。我们决定直接以十进制数生成染色体,并且取消编码和解码过程。该模型的每个染色体由14个基因组成。分为2部分,前7个基因代表每个间歇级的同步平行单元数,后7个基因代表每个间歇级的异步平行单元数。在突变过程中,应根据基因所处的位置使用相应的函数进行突变,否则极大可能会产生劣质基因。
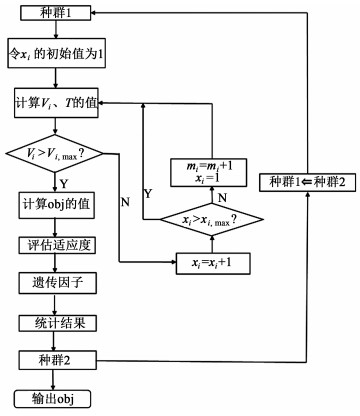
异步平行单元数最大值由经验指定,在本模型中指定为4。然而当使用这些基因计算反应器的体积时,发现反应器的体积超过了最大体积的极限。于是采用惩罚操作对进化过程进行优化,简单的流程如图 3所示。
|
| 图 3 初始模型流程图 Fig.3 Flow chart of initial model |
| |
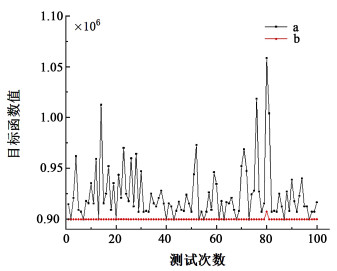
程序运行后最优值为9.146×105,但是在重新运行模型后发现最优值发生了变化,图 4a是模型运行100次后最优值的波动情况。从图 4a中可以看出,最优值一直在变化,其中最低值为8.998×105,最高值为10.580×105,增加了17.6%。
|
| 图 4 最优值波动曲线 Fig.4 Fluctuation curve of optimal solution after optimization |
| |
经过计算,发现随机种群生成后,许多染色体不仅不能满足限制条件的约束,甚至出现严重错误。比如在这些染色体的指导下会出现上一批物料尚未加工完毕便又投入新的物料的现象,这明显不符合实际情况。并且这些染色体在种群中占很高的比例,这使得在种群在进化过程中很难获得更优秀的基因,并且覆盖范围变得狭窄,这使得GA的特性无法正常发挥。图 5a显示了100代种群进化过程中每一代中有缺陷基因的比例。从图 5a中我们可以看出,在几乎每一代中,有缺陷基因的比例都超过80%甚至接近100%。

|
| 图 5 每一代中有缺陷基因的比例 Fig.5 The proportion of faulty genes in each generation |
| |
因此,在计算适应度前必须对基因进行优化。于是建立了一种自寻优机制,每次形成新的种群时都对染色体进行判断,并在出现错误时对染色体进行优化。简单的流程如图 6所示。

|
| 图 6 自优化机制流程图 Fig.6 Flow chart of self-optimization mechanism |
| |
再次运行模型100次后发现最优值几乎稳定在8.998×105,如图 4b所示。即使在最优值发生变化的地方,最大值也只有9.072×105,只比8.998×105高0.822 %。并且大部分错误基因出现的比例下降到了50%以下,如图 5b所示。当然自优化机制的作用不仅仅是这样,它真正的作用是在错误基因出现后对其进行优化,而错误基因出现的比例下降是由于上一代错误的基因减少造成的,这是一种额外效果。
3.3 结果该程序在MATLAB2017b中运行,运行时间为0.634 s。经过一定代数的繁衍后收敛到8.998 ×105这一值。限制循环时间为120 h,其他数据如表 2所示。
| 变量 | m | n | xi | V/m3 |
| 间歇级1 | 7 | 1 | 1 | 4.862 |
| 间歇级2 | 2 | 1 | 4 | 3.841 |
| 间歇级3 | 1 | 1 | 1 | 1.590 |
| 间歇级4 | 1 | 1 | 1 | 1.502 |
| 间歇级5 | 1 | 1 | 1 | 1.911 |
| 间歇级6 | 1 | 1 | 1 | 1.051 |
| 间歇级7 | 1 | 1 | 1 | 1.338 |
将计算结果绘制成甘特图如图 7所示。从图 7中可以看出,间歇级1有7个同步平行单元,间歇级2有2个同步平行单元,整个过程中没有异步平行单元。间歇级1是时间限制级。中间存储器设置在间歇级2中,并且调用间歇级2的2个批次生产时间间隔从原来的120 h变为当前的24 h。每个阶段反应器的利用率如图 8所示。

|
| 图 7 利用遗传算法得到的甘特图 Fig.7 Gantt chart obtained by genetic algorithm |
| |

|
| 图 8 利用遗传算法得到的设备利用率 Fig.8 Reactor utilization obtained by genetic algorithm |
| |
本模型参考郑国文等[11]所建立的模型,利用枚举法和回溯法进行建模。首先计算所有满足约束方程的x的值,然后将它们带入图 9所示的流程图中来搜索局部最优值。最后从所有局部最适宜值中选择最小的结果作为最优结果。
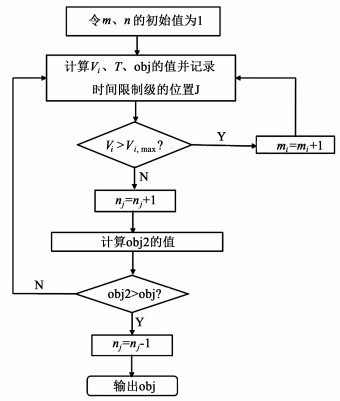
|
| 图 9 启发式算法流程图 Fig.9 Flow chart of heuristic method |
| |
该程序在MATLAB 2017b中运行并运行14 s。程序运行后,设备投资局部最优值分布折线如图 10所示,其中横坐标代表不同的中间存储方案,纵坐标代表确定存储方案后模型求得的最优解。从图 10中可以看出,设备投资成本的分布范围较大,最小值出现在3个位置。它们分别位于横坐标57、88和96上,所有与最优值相关的计算结果列在表 3中。

|
| 图 10 局部最优值分布曲线 Fig.10 Distribution curve of optimal solution |
| |
| 间歇级 | 60 h | 120 h | 180 h | |||||||||||
| m | n | xi | V/m3 | m | n | xi | V/m3 | m | n | xi | V/m3 | |||
| 间歇级1 | 4 | 2 | 1 | 4.254 | 4 | 2 | 2 | 4.254 | 4 | 2 | 3 | 4.254 | ||
| 间歇级2 | 2 | 1 | 2 | 3.849 | 2 | 1 | 4 | 3.849 | 2 | 1 | 6 | 3.849 | ||
| 间歇级3 | 1 | 1 | 1 | 1.590 | 1 | 1 | 1 | 1.590 | 1 | 1 | 1 | 1.590 | ||
| 间歇级4 | 1 | 1 | 1 | 1.502 | 1 | 1 | 1 | 1.502 | 1 | 1 | 1 | 1.502 | ||
| 间歇级5 | 1 | 1 | 1 | 1.911 | 1 | 1 | 1 | 1.911 | 1 | 1 | 1 | 1.911 | ||
| 间歇级6 | 1 | 1 | 1 | 1.051 | 1 | 1 | 1 | 1.051 | 1 | 1 | 1 | 1.051 | ||
| 间歇级7 | 1 | 1 | 1 | 1.338 | 1 | 1 | 1 | 1.338 | 1 | 1 | 1 | 1.338 | ||
从表 3中可以看出,3个结果的同步平行单元数和异步平行单元数相同,但是连续生产次数不同。显然,实际生产中在间歇级1前设置中间存储是没有意义的,因此我们只选取列表中x1=1的情况,即仅保留表 3中的第一种情况。
这种生产方法以甘特图的形式表示,见图 11。从图 11中可以看出,间歇级1为过程中的时间限制级,包含4个同步平行单元4个异步平行单元。异步平行单元使限制时间由原来的120 h减少到了60 h。在间歇级2中设置中间存储,使得上一间歇级的物料分两批加入此间歇级,从而减小后续阶段反应器的体积,增大反应器利用率。可以得出每个阶段的反应器利用率,如图 12所示。

|
| 图 11 利用一般启发式方法得到的甘特图 Fig.11 Gantt chart obtained using general heuristic method |
| |
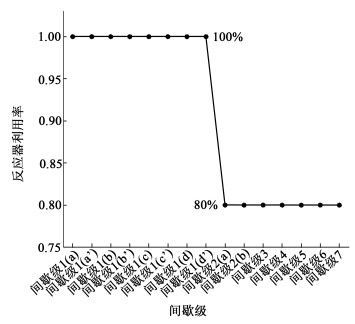
|
| 图 12 利用一般启发式方法得到的设备利用率 Fig.12 Reactor utilization obtained using general heuristic method |
| |
比较以上2个结果,可以看出,遗传算法获得的设备投资结果比启发式算法获得的结果低2.66%。这是因为同步平行单元数和异步平行单元数是随机生成的,并且在后续的交叉变异等操作过程中使得每个阶段的同步平行单元数和异步平行单元数更加具有多样性,因此优化过程中遗传算法的覆盖范围比一般启发式算法的覆盖范围更广。并且一般启发式算法的同步平行单元数和异步平行单元数都是按照一定的规律进行变化的,这使得在优化过程中易于陷入局部最优解。用遗传算法建立的模型在计算速度上是用一般启发式算法建立的模型的22倍。但是,当中间存储的容量变小时,2者之间的时间差距逐渐减小,这表明要解决的问题越复杂,遗传算法的优势越明显。但是,设备的利用率没有变化。这是因为用一般启发式算法建立的模型使用枚举法来优化设备的利用率,并且所有可能性都包含在指定范围内,因此无法进一步优化。
5 结论介绍了一种改进的遗传算法在解决单产品间歇化工过程设计问题中的应用。通过引入自我优化机制和惩罚操作在不影响遗传算法特性的前提下对基因进行人为干预,从而减少种群中劣质染色体的出现,使种群得以顺利稳定的繁衍下去。最后与一般启发式算法建立的模型进行比较。结果表明该模型在计算结果、收敛速度和计算速度上均优于一般启发式方法。
| [1] |
孔令启.基于内外圈协同优化策略的间歇化工过程不确定性调度研究[D].广州: 华南理工大学, 2010 Kong Lingqi. The study on scheduling of batch chemical processes with uncertainty based on inner-outer loop optimization strategies simultaneously[D]. Guangzhou: South Chine University of Technology, 2010(in Chinese) |
| [2] |
Grossmann I E, Sargent R W H. Optimum design of multipurpose chemical plants[J]. Industrial & Engineering Chemistry Process Design and Development, 1979, 18(2): 343-348. |
| [3] |
王凌, 王雄. 间歇化工工艺优化设计研究[J]. 清华大学学报:自然科学版, 2000, S2(40): 265-269. Wang Ling, Wang Xiong. Survey on optimal design of batch chemical process[J]. Journal of Tsinghua University:Science and Technology, 2000, S2(40): 265-269. (in Chinese) |
| [4] |
Kenter S E. Minimize batch equipment cost[J]. Chem Engineering, 1960, 22(6/7): 121-132. |
| [5] |
Kim M, Lee I B. Rule-Based reactive rescheduling system for multi-purpose batch processes[J]. Computers & Chemical Engineering, 1997, 21: S1197-S1202. |
| [6] |
Shah N, Pantelides C. Optimal long-term campaign planning and design of batch operations[J]. Industrial and Engineering Chemistry Research, 1991, 30(10): 2308-2321. DOI:10.1021/ie00058a010 |
| [7] |
Espuna A, Lazaro M, martinez J M, et al. Efficient and simplified solution to the predesign problem of multiproduct plants[J]. Comput Chem Eng, 1989, 13(1): 163-170. |
| [8] |
Ku H, Rajagopalan D, Karimi I A. Scheduling in batch processes[J]. Chem Eng Process, 1987, 83(8): 35-40. |
| [9] |
Loonkar Y R, Robinson J D. Minimization of capital investment for batch processes. Calculation of optimum equipment sizes[J]. Industrial & Engineering Chemistry Process Design and Development, 1970, 9(4): 625-629. |
| [10] |
Yeh N C, Reklaitis G V. Synthesis and sizing of batch/semicontinuous processes:Single product plants[J]. Computers & Chemical Engineering, 1987, 11(6): 639-654. |
| [11] |
郑国文, 许锡恩. 单产品间歇化工过程设计[J]. 高校化学工程学报, 1995, 9(3): 252-258. Zheng Guowen, Xu Xi'en. Design of single product batch chemical processes[J]. Journal of Chemical Engineering of Chinese Universities, 1995, 9(3): 252-258. (in Chinese) |
| [12] |
Kirkpatrick S, Gelatt J C D, Vecchi M P. Optimization by simulated annealing[J]. Science, 1983, 220(4598): 671-680. DOI:10.1126/science.220.4598.671 |
| [13] |
Yuan X, Chen Z. A hybrid global optimization method for design of batch chemical processes[J]. Comput Chem, 1997, S1(21): 685-690. |
| [14] |
杨志才. 化工生产中的间歇过程——原理、工艺及设备[M]. 2001, 北京: 化学工业出版社, 2001.
|
| [15] |
Moniz S, Barbosa-Povoa A P, deSousa J P. On the complexity of production planning and scheduling in the pharmaceutical industry: The delivery trade-offs matrix[R]//In: Gernaey K V, Huusom J K, Gani R. (Eds.), 12th International Symposium on Process Systems Engineering and 25th European Symposium on Computer Aided Process Engineering, Denmark Copenhagen, 2015: 1865-1870
|
| [16] |
Holland J H. Adaptation in natural and artificial systems[M]. MI: University of Michigan Press, 1975.
|
| [17] |
Bernal-Haro L, Azzaro-Pantel C, Pibouleau L, et al. Multiobjective batch plant design:A two-stage methodology. 2. Development of a genetic algorithm and result analysis[J]. Ind Eng Chem Res, 2002, 41: 5743-5758. DOI:10.1021/ie0106478 |
| [18] |
Verbiest F, Cornelissens T, Springael J. Design of a chemical batch plant: A study of dedicated parallel lines with intermediate storage and the plant performance[M]//Computer Aided Chemical Engineering, Elsevier, 2016: 739-744
|
| [19] |
Biegler L T, Grossmann I E, Westerberg A W. Systematic methods for chemical process design[M]. United States: Prentice Hall, 1997.
|
| [20] |
Barbosa-Póvoa A P. A critical review on the design and retrofit of batch plants[J]. Comp & Chem Eng, 2007, 31(7): 833-855. |
| [21] |
Himmelblau D M, Lasdon L S. Optimization of chemical processes[M]. 2nd ed. New York: The McGraw-Hill Companies, 2001.
|
 2020, Vol. 37
2020, Vol. 37





