2. 江南大学机械工程学院, 江苏 无锡 214122
2. School of Mechanical Engineering, Jiangnan University, Jiangsu Wuxi 214122, China
微波辐射可以强化化学反应中介质的活化能,加快反应速度,提高反应的转化率[1],而且与传统加热相比,微波加热速度快、效率高[2],因此微波技术被快速地应用于微波化学领域。微波化学的核心是微波反应设备,随着科技的发展,学者们虽然也设计研发了很多类型的微波反应器,但其应用仍然还存在着很多的问题[3],其中一个重要的问题就是微波加热过程中会出现不可控的冷热点,具有明显的加热不均匀性。目前国内外针对微波反应器的加热效率和加热均匀性的优化有很多,有通过改变微波反应器局部结构如在腔体壁上设置凹凸面[4-5]、在反应器内设计转盘或者搅拌器[6-10]等改善加热均匀性,有在能量馈入方面如功率[11]、频率[12]、馈口位置和数量设置[13]等改善加热均匀性,还有在被加热物体的位置、形状等[14]方面改善加热均匀性。
但以上研究的反应器被加热物体尺寸较小,仅限于实验室研究使用,而且被加热区域仅占微波腔体的一小部分。基于此,为满足酯化反应制备生物柴油的工艺要求,本研究在借鉴前人经验的基础上,将微波反应器周围的空间压缩为薄夹层,并与反应釜相结合设计了一种中试规模的带夹层釜式微波反应器。运用多物理场仿真的方法,通过改变波导位置和夹层厚度研究反应器加热效率和加热均匀性的变化规律,并根据仿真结果,得出一系列可用于提升釜式微波反应器加热效率和加热均匀性的结论,为反应器的最终搭建提供理论依据。
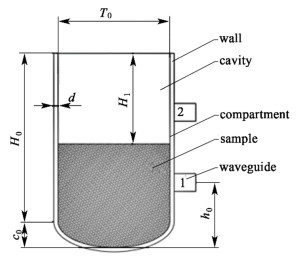
1 研究方法 1.1 模型描述本研究设计了一种单馈口圆柱形微波反应器,内层为传统的反应釜,外层为方便微波均匀分布的夹层,波导位置放置在反应器的侧面,并运用COMSOL Multiphysics软件中的电磁加热模块对模型进行仿真分析,模型具体尺寸见图 1。
|
| 图 1 微波反应釜模型的二维示意图 Fig.1 Two-Dimensional schematic diagram of microwave reactor model |
| |
如图 1所示,釜式微波反应器的腔体高度H0为390 mm;底部为椭圆底,高度c0为60 mm,取H1为210 mm,物料高度为240 mm。波导位于反应器侧面,主要分为液面之下(位置1)和液面之上(位置2)2种情况。波导中心距离反应器内壁底部的垂直距离为h0 ,通过改变h0大小改变波导的位置(图 1中位置1处h0=150 mm,位置2处h0=330 mm)。在反应器金属内壁和物料之间用一种无介电损耗的非极性材料隔开,本研究取理想情况,将材料的相对介电常数设置为1,夹层厚度为d。
1.2 控制方程微波腔体内电磁场的分布由麦克斯韦方程决定[15],频域中电场强度的控制方程可以写为:
| $ \left\{ {\begin{array}{*{20}{c}} {\nabla \times \mu _{\rm{r}}^{ - 1}\left( {\nabla \times \overrightarrow E } \right) - k_0^2\left( {{\varepsilon _{\rm{r}}} - \frac{{j\sigma }}{{\omega {\varepsilon _0}}}} \right)\overrightarrow E = 0}\\ {{k_0} = \omega \sqrt {{\varepsilon _0}{\mu _0}} = \frac{\omega }{{{c_0}}}} \end{array}} \right. $ | (1) |
式(1)中,▽为拉普拉斯算子;μr为相对磁导率(空气为1);
微波在通过有耗介质时会损失部分能量,由电磁能转化为材料中的热能,微波的耗散功率可以写为[16]:
| $ {P_{\rm{v}}} = 2{\rm{ \mathsf{ π} }}f{\varepsilon _0}\varepsilon ''{E^2} $ | (2) |
式(2)中:Pv为微波耗散功率;f为微波输入频率;ε″为腔体内材料的相对介电损耗。
微波电场的非均匀性分布导致不同位置物料的温度不同,因此必须考虑到物料内部的传热[17]:
| $ \rho {C_p}\frac{{\partial T}}{{\partial t}} = k{\nabla ^2}\theta + {P_{\rm{v}}}\left( {x, y, z} \right) $ | (3) |
式(3)中:ρ为物料密度,Cp为物料恒压热容,k为物料导热系数,θ为物料温度。
反应器金属壁的厚度尺寸远远小于腔体,由于集肤效应,电磁场穿透到釜壁深度可以忽略不计,因此把釜壁简化成没有厚度的面[18],通过阻抗边界条件描述金属壁和腔体内微波辐照度之间的相互作用:
| $ \sqrt {\frac{{{\mu _0}{\mu _{\rm{r}}}}}{{{\varepsilon _0}{\varepsilon _{\rm{r}}} - j\sigma /\omega }}} \overrightarrow n \times \overrightarrow H + \overrightarrow E - \left( {\overrightarrow n \cdot \overrightarrow E } \right)\overrightarrow n = \left( {\overrightarrow n \cdot {{\overrightarrow E }_{\rm{s}}}} \right)\overrightarrow n - {\overrightarrow E _{\rm{s}}} $ | (4) |
式(4)中,
模拟过程中对物料进行短时加热,使其整体温度在300 K以下。因此可以忽略加热后物料蒸发带来的多相加热和换热的问题,将模拟过程简化为单相微波加热的过程,并忽略其与外界的热交换,在瞬态计算过程中,将物料外表面设置为绝热边界条件:
| $ n\left( {k\nabla T} \right) = 0 $ | (5) |
模拟过程中使用的物料为某种植物油,具体仿真参数如表 1所示:
| 参数 | 单位 | 参数值 |
| 密度 | kg·m-3 | 965 |
| 动力黏度 | Pa·s | 0.065 |
| 相对磁导率 | 1 | |
| 导热系数 | W·(m·K)-1 | 0.15 |
| 常压热容 | J·(kg·K)-1 | 3 000 |
| 比热率 | 1 | |
| 相对介电常数 | 2.73-0.13j | |
| 电导率 | S·m-1 | 0 |
模型波导为BJ-26国家标准型波导,微波频率为2.45 GHz, 微波功率为1 000 W,端口为横电TE10模。
1.4 网格无关性分析本研究中在模拟过程中采用非结构化的自由四面体网格,分析时将加热时间设定为20 s,取物料中一点的温度作为考察对象,网格单元数对模拟结果的影响如图 2所示。

|
| 图 2 网格无关性 Fig.2 Grid independence |
| |
从图 2中可以看出,随着网格数量的增加,物料温度逐渐趋于稳定,当网格数达到8万以后,物料温度不再发生变化,认为网格单元数8万左右即可满足模拟准确性的要求,本研究模拟过程中采用的网格数均为8万个左右。
1.5 加热效率以及加热均匀性的计算方法由于本研究模拟中物料与外界没有热传导,因此加热效率的计算可以由式(6)给出:
| $ \eta = \frac{{\rho V{C_p}\Delta T}}{{Pt}} \times 100\% $ | (6) |
式(6)中:η为加热效率;ρ为物料密度;V为物料体积;Cp为物料恒压热容;ΔT为物料温升;P为微波输入功率;t为加热时间。
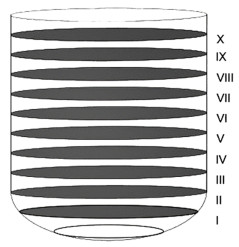
如图 3所示将物料在高度方向上分为12等份,从40 mm高度处向上取10个高度的截面,编号分别为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ、Ⅸ和Ⅹ,通过计算不同截面温度之间的变异系数评价不同条件下反应器的加热均匀性,变异系数越小则说明加热越均匀。变异系数的计算由式(7)给出:
|
| 图 3 物料区域选取的10个平面 Fig.3 10 planes selected in the material area |
| |
| $ {c_{\rm{v}}} = \sigma /\mu $ | (7) |
式(7)中:cv为变异系数;σ为物料不同截面平均温度的标准差;μ为物料不同截面的平均温度。
2 结果与分析 2.1 加热效率和加热均匀性随时间的变化情况取无夹层情况下,h0分别为90、210、270和390 mm的模型为研究对象,探究反应器加热效率(图 4)和加热均匀性(图 5)随时间的变化。

|
| 图 4 不同波导高度加热效率随时间的变化 Fig.4 Change of heating efficiency of different waveguide heights with time |
| |
|
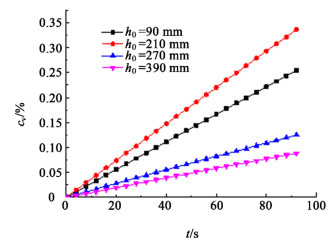
| 图 5 变异系数随时间的变化 Fig.5 Change of coefficient of variation (CV) with time |
| |
如图 4所示,绘制了4个波导位置加热效率随时间的变化的趋势图,其中h0=90和h0=210 mm时波导位置在物料的液面之下,h0=270和h0=390 mm时在物料的液面之上。从图 4中可以看出随着时间的变化加热效率在一定范围内上下浮动,时间越长浮动范围越小,15 s内加热效率的变化幅度在3%左右,加热时间达到30 s以后,变化幅度缩小到1%以内,60 s以后变化幅度缩小到0.5%以内,之后加热效率的变化幅度缩小得越来越慢。由于模型没有考虑到加热过程中模型与外界的传热,时间越长结果越不准确,因此后文不加特殊说明加热效率由60 s时的仿真结果计算所得。
如图 5所示,绘制了4个波导位置温度变异系数随时间变化的趋势。从图 5中可以看出,由于同一波导位置下电场的分布情况没有发生改变,因此随着时间的增加,热点区域的温度以高于其他区域的温升速度持续升温,变异系数持续增加,温度均匀性越来越差,而且在不考虑与外界换热的情况下,加热均匀性随时间的增加线性变差。为了方便计算,取60 s时的温度变异系数进行温度均匀性评价。
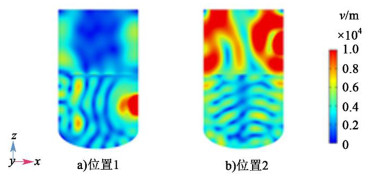
2.2 波导位置对加热效率和加热均匀性的影响取夹层厚度d=0 mm,对如图 1所示的2个波导位置分别进行仿真计算。不同波导位置下反应器内电场驻波形成的位置不同,从而导致加热后物料内的温度分布情况发生改变,计算得到的电场分布和温度场分布情况如图 6和图 7所示。
|
| 图 6 不同波导位置反应器内电场的分布 Fig.6 Distribution of the electric field in the reactor at different waveguide locations |
| |

|
| 图 7 不同波导位置物料内温度的分布 Fig.7 Distribution of temperature within the material at different waveguide locations |
| |
从图 6和图 7中可以看出,物料温度场的分布情况和物料内电场的分布基本一致。位置1的微波直接馈入物料之中,由于物料对微波传播的阻碍作用,致使高电场强度区域主要集中在微波馈入位置附近,从而使得波导处物料的温度远远高于反应器其他部分物料的温度,形成超级热点;而位置2中的微波先馈入空气,经过空气的传播以及金属壁的反射等,进入物料的位置和角度大大增加,物料内电场和温度场的颜色变化较小,中间颜色区域增多,均匀性明显有所改善。
为了进一步探究波导位置对加热效率和加热均匀性的影响,分别取h0为90、150、210、240、270、330和390 mm进行计算,其中h0=240 mm时,波导中心面高度与液面持平,计算结果如图 8和图 9所示。

|
| 图 8 波导位置对加热效率的影响 Fig.8 Effect of waveguide position on heating efficiency |
| |

|
| 图 9 波导位置对加热均匀性的影响 Fig.9 Effect of waveguide position on heating uniformity |
| |
如图 8所示,波导位于物料液面附近时加热效率较高,达到98.1%;波导在液面之下时加热效率基本在85%左右,变化幅度较小;而当波导位置在液面之上时,加热效率随着波导与液面距离的增加先升高后降低,最高达到94.1%,最低仅为74.9%,变化幅度达到20%。因此从加热效率角度考虑,波导位置处于物料液面附近或者在反应器上方的合适位置可以取得较好的效果,波导位于液面之下的适用性较强,但难以取得较高的加热效率。
如图 9所示,当波导位于物料液面之上时,变异系数明显降低,波导高度达到300 mm后,变异系数曲线逐渐稳定在1个较低的值;当波导中心与物料液面持平时,变异系数的值最大,温度均匀性最差。因此从加热均匀性角度考虑,波导位置应在反应器的300 mm高度以上的合适位置,并避免将波导放置在物料液面附近。
2.3 夹层厚度对加热效率和加热均匀性的影响通过2.2的分析发现,当微波经由空气传入物料时,可以显著改善微波加热的均匀性,并在某些情况下提高加热效率。因此本节以加热均匀性最差的h0=210 mm、加热效率最低的h0=330 mm模型为研究对象,探究夹层对釜式微波反应器加热效率和加热均匀性的影响。理论上在输入功率一定的情况下,因为被加热物料对微波的传播具有阻碍作用,适当厚度的夹层有利于微波从物料的更多位置和角度进入其内部,从而物料内平均电场强度增加,不同位置电场强度的差值减少,因此加热效率增加、加热均匀性提高,但是当夹层厚度过大时,被加热区域占微波腔体的比例下降,物料内的电场强度反而降低,加热效率下降。这种现象当波导位于液面之下(微波直接馈入物料)时应当更加显著。
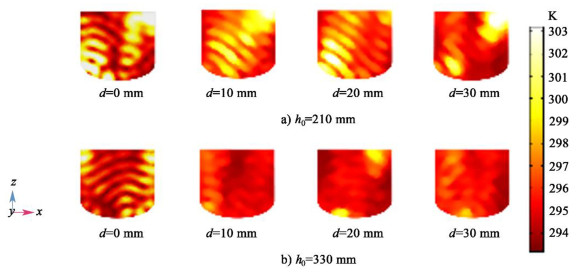
计算得到物料的温度分布如图 10所示。
|
| 图 10 不同夹层厚度物料内温度的分布 Fig.10 Distribution of temperature in materials with different interlayer thickness |
| |
从图 10中可以看出,波导位置不同,夹层对物料温度分布的影响不同,但相对于无夹层模型加热均匀性有显著改善,说明夹层可以有效改善反应器的加热均匀性。为了对加热效率和加热均匀性有更加准确和直观的评价,分别计算2个模型不同夹层厚度下的加热效率和变异系数,结果如图 11和图 12所示。

|
| 图 11 夹层厚度对加热效率的影响 Fig.11 Effect of interlayer thickness on heating efficiency |
| |
|
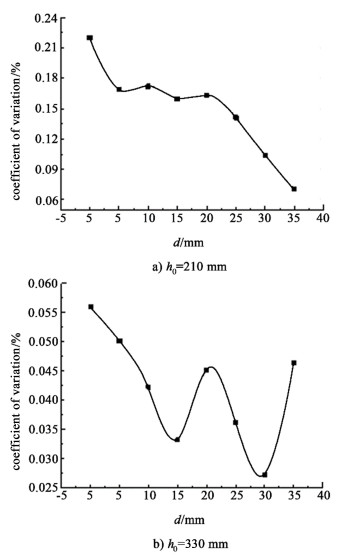
| 图 12 夹层厚度对加热均匀性的影响 Fig.12 Effect of interlayer thickness on heating uniformity |
| |
如图 11所示,对于h0=210 mm模型,加热效率随着夹层厚度的增加先升高后降低,当d=15 mm时,加热效率最大达到99.12%,比没有夹层时的加热效率高了12.4%,但若夹层厚度过大,比如达到35 mm时,加热效率反而相对于无夹层模型低了0.4%。对于h0=330 mm模型,随着夹层厚度的增加,加热效率的波动增加,但均高于无夹层时的加热效率10%以上,当d=20 mm时加热效率最高达到95.8%。
如图 12所示,对于h0=210 mm模型,随着夹层的添加以及增厚,变异系数逐渐降低,夹层对于加热均匀性的改善效果显著。但对于h0=330 mm模型来说,由于微波已经是经由空气传入物料,夹层的添加仅仅改善了物料侧面和底部的微波馈入,因此变异系数的值随夹层厚度的增加上下波动,夹层厚度对于加热均匀性的改善效果较差,但比较其变异系数,其加热的均匀性仍然优于波导在物料液面之下时的情况。
以上试验结果均与理论分析保持一致。
2.4 微波加热效率和加热均匀性的响应面分析通过以上分析可知,不同波导位置下夹层厚度对微波加热效率以及加热均匀性的影响规律不同,2.2和2.3节的分析仅仅只能反映出波导位置和夹层厚度对加热效率以及加热均匀性非常片面的影响规律,因此本节对反应器模型进行二因素多水平的仿真试验,并对试验结果进行响应面分析,以期得到更加全面的影响规律。仿真试验结果如表 2和表 3所示。
| h0/mm | d/mm | |||||||
| 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | |
| 90 | 86.225 | 96.932 | 98.059 | 98.623 | 98.059 | 96.932 | 92.987 | 87.352 |
| 150 | 83.407 | 94.678 | 96.369 | 96.932 | 96.932 | 94.678 | 90.733 | 85.098 |
| 210 | 86.788 | 91.860 | 95.805 | 99.187 | 98.623 | 95.242 | 91.297 | 86.225 |
| 240 | 98.059 | 98.750 | 98.750 | 96.932 | 92.424 | 91.860 | 91.860 | 89.606 |
| 270 | 94.115 | 98.623 | 89.606 | 82.843 | 74.953 | 81.716 | 89.606 | 96.369 |
| 330 | 74.953 | 82.843 | 91.297 | 85.661 | 95.805 | 90.733 | 89.042 | 89.606 |
| 390 | 87.915 | 65.373 | 93.551 | 73.263 | 88.479 | 74.390 | 64.246 | 61.992 |
| h0/mm | d/mm | |||||||
| 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | |
| 90 | 0.166 | 0.164 | 0.162 | 0.110 | 0.102 | 0.147 | 0.169 | 0.153 |
| 150 | 0.174 | 0.176 | 0.179 | 0.105 | 0.064 | 0.082 | 0.101 | 0.102 |
| 210 | 0.220 | 0.169 | 0.172 | 0.160 | 0.163 | 0.141 | 0.104 | 0.071 |
| 240 | 0.161 | 0.142 | 0.119 | 0.084 | 0.085 | 0.090 | 0.068 | 0.055 |
| 270 | 0.083 | 0.068 | 0.059 | 0.035 | 0.039 | 0.052 | 0.052 | 0.051 |
| 330 | 0.056 | 0.050 | 0.042 | 0.033 | 0.045 | 0.036 | 0.027 | 0.046 |
| 390 | 0.058 | 0.032 | 0.061 | 0.044 | 0.056 | 0.032 | 0.018 | 0.028 |
加热效率试验结果如表 2所示,响应面分析结果如图 13所示。在波导位置和夹层厚度的相互影响下,加热效率的表现规律性较差,其中加热效率高的部分主要集中在如图所示的3个区域,优化分析结果是当h0=230.19 mm,d=7.38 mm时,预测值最高达到101.32%。为检测优化结果的准确性,对其进行仿真检验,得到的加热效率为99.19%,与预测值的相对误差为2.1%,说明响应面分析对于加热效率的预测具有较大的参考价值。

|
| 图 13 加热效率响应面分析结果 Fig.13 RSM result of heating efficiency |
| |
对加热均匀性响的试验结果如表 3所示,响应面分析结果如图 14所示。从图 14中可以看出:当波导位于物料液面之下(h0 < 240 mm)时,夹层使得微波进入物料的角度和位置大大增加,随着夹层厚度的增加,变异系数在整体上逐渐变小,温度的分布越来越均匀,此时夹层对于改善加热均匀性具有十分积极效果;当波导位置位于物料液面之上(h0>240 mm)时,整体上变异系数的值远小于波导位置在液面之下,但夹层厚度变化对于变异系数的影响被削弱,对加热均匀性的影响较小。根据优化分析的结果,当h0=389.74 mm、d=30.09 mm时,预测值最低为0.018,同样对其进行仿真检验,得到的变异系数为0.013,比预测值低了0.005,说明响应面分析结果对于加热均匀性优化同样具有参考价值。

|
| 图 14 加热均匀性响应面分析结果 Fig.14 RSM result of heating uniformity |
| |
根据优化结果,发现很难在取得高加热效率的同时保证加热的均匀性,因此在实际应用中应根据侧重点的不同选择合适和波导位置和夹层厚度。
3 结论设计并成功建立了一种新型的带夹层釜式微波反应器模型,运用多物理场耦合计算的方式,从波导位置和夹层厚度2个方面对反应器的加热效率和加热均匀性进行了探究,得到如下结论:1)一般情况下,波导位置在物料液面之下的加热效率高于在物料液面之上,但加热均匀性相对于波导位置在物料液面之上较差。2)夹层具有改善加热效率和加热均匀性的效果,但不同波导位置下效果不同:波导位置在物料液面之下时,改善效果较好,但均匀性较差;波导在物料液面之上时,夹层厚度的改变对加热均匀性影响较小但具有良好的均匀性。3)验证了响应面分析法对反应器设计的有效性,并通过响应面分析优化得到:当h0=230.19 mm,d=7.38 mm时,可以获得最高加热效率为99.19%,当h0=389.74 mm、d=30.09 mm时变异系数最低达到0.013,可以获得最佳的加热均匀性。
以上结论阐述了波导位置和夹层厚度对加热效率和加热均匀性影响的一般规律,为实际的反应器设计提供了重要的理论参考。
| [1] |
Danks T N. Microwave assisted synthesis of pyrroles[J]. Tetrahedron Letters, 1999, 40(20): 3957-3960. DOI:10.1016/S0040-4039(99)00620-6 |
| [2] |
Orsat V, Raghavan G S V, Krishnaswamy K. Microwave technology for food processing[M]. USA: Elsevier, 2017.
|
| [3] |
Barham J P, Koyama E, Norikane Y, et al. Microwave flow:A perspective on reactor and microwave configurations and the emergence of tunable single-mode heating toward large-scale applications[J]. The Chemical Record, 2019, 19(1): 188-203. |
| [4] |
钟汝能, 姚斌, 向泰, 等. 腔体内壁脊形凹槽对微波反应器加热效率及均匀性的影响[J]. 食品与机械, 2017, 33(4): 81-85. Zhong Runeng, Yao Bin, Xiang Tai, et al. Influence of ridge groove structure of the inner walls on heating efficiency and uniformity of microwave reactor[J]. Food & Machinery, 2017, 33(4): 81-85. (in Chinese) |
| [5] |
钟汝能, 姚斌, 向泰, 等. 圆柱形凸槽结构对微波反应器加热效率及均匀性的影响[J]. 云南大学学报:自然科学版, 2017, 39(6): 981-987. Zhong Runeng, Yao Bin, Xiang Tai, et al. Influence of cylindrical convex groove structure on heating efficiency and uniformity of microwave reactor[J]. Journal of Yunnan University:Natural Sciences Edition, 2017, 39(6): 981-987. (in Chinese) |
| [6] |
Liu S, Fukuoka M, Sakai N. A finite element model for simulating temperature distributions in rotating food during microwave heating[J]. Journal of Food Engineering, 2013, 115(1): 49-62. |
| [7] |
Geedipalli S S R, Rakesh V, Datta A K. Modeling the heating uniformity contributed by a rotating turntable in microwave ovens[J]. Journal of Food Engineering, 2007, 82(3): 359-368. |
| [8] |
Meng Q, Lan J, Hong T, et al. Effect of the rotating metal patch on microwave heating uniformity[J]. Journal of Microwave Power and Electromagnetic Energy, 2018, 52(2): 94-108. DOI:10.1080/08327823.2018.1440341 |
| [9] |
Pitchai K, Chen J, Birla S, et al. Multiphysics modeling of microwave heating of a frozen heterogeneous meal rotating on a turntable[J]. Journal of Food Science, 2015, 80(12): E2803-E2814. DOI:10.1111/1750-3841.13136 |
| [10] |
Sebera V, Nasswettrová A, Nikl K. Finite element analysis of mode stirrer impact on electric field uniformity in a microwave applicator[J]. Drying Technology, 2012, 30(13): 1388-1396. DOI:10.1080/07373937.2012.664800 |
| [11] |
Romano V R, Marra F, Tammaro U. Modelling of microwave heating of foodstuff:Study on the influence of sample dimensions with a FEM approach[J]. Journal of Food Engineering, 2005, 71(3): 233-241. |
| [12] |
李涛, 张伟, 陈海龙, 等. 频率和功率对轮胎微波加热的影响[J]. 橡胶工业, 2016, 63(6): 365-368. Li Tao, Zhang Wei, Chen Hailong, et al. Influence of frequency and power on microwave heating for tire[J]. China Rubber Industry, 2016, 63(6): 365-368. DOI:10.3969/j.issn.1000-890X.2016.06.010 (in Chinese) |
| [13] |
Tortajada E D, Gonzalez P P, Morcillo A D, et al. Optimisation of electric field uniformity in microwave heating systems by means of multi-feeding and genetic algorithms[J]. International Journal of Materials and Product Technology, 2007, 29(1): 149-162. |
| [14] |
戴辉明, 郭雯, 程裕东, 等. 不同形状包装食品在微波加热过程中的三维温度分布[J]. 食品工业科技, 2015, 36(13): 82-86, 102. Dai Huiming, Guo Wen, Cheng Yudong, et al. Three-Dimensional temperature distribution of the packaged foods with different shapes during microwave heating[J]. Science and Technology of Food Industry, 2015, 36(13): 82-86, 102. (in Chinese) |
| [15] |
Meredith R. Engineers' handbook of industrial microwave heating[M]. UK: The Institution of Engineering and Technology, Michael Faraday House, 1998.
|
| [16] |
Curcio S, Aversa M, Calabrò V, et al. Simulation of food drying:FEM analysis and experimental validation[J]. Journal of Food Engineering, 2008, 87(4): 541-553. |
| [17] |
Pitchai K, Birla S L, Subbiah J, et al. Coupled electromagnetic and heat transfer model for microwave heating in domestic ovens[J]. Journal of Food Engineering, 2012, 112(1/2): 100-111. |
| [18] |
Yeong S P, Law M C, You K, et al. A coupled electromagnetic-thermal-fluid-kinetic model for microwave-assisted production of palm fatty acid distillate biodiesel[J]. Applied Energy, 2019, 237: 457-475. DOI:10.1016/j.apenergy.2019.01.052 |
 2020, Vol. 37
2020, Vol. 37





