异烟肼(C6H7N3O,CAS: 54-85-3)是一种抗结核杆菌药,用于治疗肺结核、皮肤结核等,其分子结构式如图 1所示[1-3]。目前异烟肼都是采用合成法制备[4],但是得到的产品纯度不高。为了提高产品纯度,可以通过结晶或者重结晶法进行提纯分离。溶液结晶法是一种制备药物晶体的手段,可以有效控制晶体产品的纯度、粒度和晶习等[5-7]。确定合适的结晶溶剂以及获取相应的溶解度数据是溶液结晶工艺开发的必要工作[8-10],但是目前关于异烟肼溶解度及其溶解热力学数据的文献较少[11-13],所以仍需对其溶解及热力学方面进行系统研究。

|
| 图 1 异烟肼分子结构 Fig.1 Molecular structure of isoniazid |
| |
对于药品来说,合理地控制晶体的生长以得到所需要的晶体形貌(也称之为晶习),不仅能够提高有效成份的含量,而且能使产品具备适宜的溶解速率,这在实际应用时非常重要[14-16]。晶习是晶体的内部结构和形成时物理化学条件的综合反映,它不仅取决于晶体的点阵结构和晶体的热力学性质,而且还受到晶体生长动力学以及热量和质量传递等过程的影响[17-18]。良好的晶习能使产品的分离、洗涤、包装、运输和贮藏得到不同程度的改善。所以,晶习的研究对异烟肼的生产及产品的性质有着极为重要的影响。但是目前并没有相关文献报道异烟肼晶习的研究。
为了系统地研究异烟肼的结晶过程,本研究首先测量了异烟肼在不同溶剂中的溶解度。使用在线浊度法测定了异烟肼在甲醇、乙醇、正丙醇、异丙醇、正丁醇、异丁醇、丙酮、乙腈、乙酸甲酯与乙酸丁酯中的溶解度。采用改进的Apelblat、Wilson与NRTL方程对溶解度数据进行了拟合,对异烟肼溶解焓、溶解熵与溶解吉布斯能进行了计算。基于溶解度数据,分析了甲醇、乙醇、正丙醇与丙酮对异烟肼冷却结晶晶习的影响规律,确定了乙醇为较适宜的结晶溶剂。
1 实验材料和方法 1.1 材料异烟肼(质量分数99.5%),购于阿拉丁试剂公司。甲醇、乙醇、正丙醇、异丙醇、正丁醇、异丁醇、丙酮、乙腈、乙酸甲酯与乙酸丁酯均为分析纯试剂,购于天津江天化工有限公司。
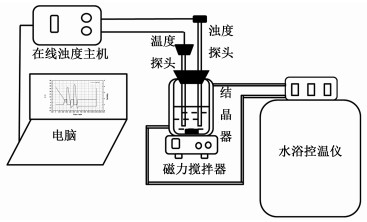
1.2 溶解度测量装置溶解度测量装置如图 2所示,它由结晶器、水浴控温仪、磁力搅拌器、温度探头、浊度探头、在线浊度主机与电脑等部分组成。
|
| 图 2 溶解度实验测量装置图 Fig.2 Schematic experimental apparatus of solubility measurement |
| |
X-射线衍射仪(XRD),D/MAX 2500型,日本Rigaku;差示扫描量热仪(DSC),DSC1/500,瑞士Mettler-Toledo;电子微量天平(精度为0.1 mg),ML204型,瑞士Mettler-Toledo;低温恒温槽(XOYS型),南京先欧仪器制造有限公司。
1.4 溶解度测量实验异烟肼在有机溶剂中的溶解度采用在线浊度仪测定,其实验装置如图 2所示,具体测定步骤参考文献[19]:1)调节水浴控温仪至某一特定温度,其中温度误差为0.05 K。在结晶器中加入一定有机溶剂,然后加入浊度探头与温度探头,以300 r/min转速进行磁力搅拌。2)称取一定量的异烟肼,加入到结晶器中,瞬间浊度示数上升,随着搅拌进行,晶体逐渐溶解,浊度示数开始下降,重复加入一定量的异烟肼至结晶器中,直至某次加入异烟肼浊度示数不再下降时,那么将该次以前所有加入到结晶器的晶体总量定义为该温度下的溶解度,然后在该温度下重复3次实验,取其平均值作为最终溶解度。3)改变水浴温度,待温度稳定后,依次重复步骤1)与2)进行下一个温度点晶体溶解度的测定,这样就能测定异烟肼在同种溶剂,不同温度条件下的溶解度。4)改变溶剂种类,重复步骤1)、2)与3),就可以测定异烟肼在不同溶剂与不同温度下的溶解度。本研究中的异烟肼溶解度采用摩尔分数进行计算,如式(1)所示:
| $ x = \frac{{{m_0}/{M_0}}}{{{m_0}/{M_0} + {m_1} + {M_1}}} $ | (1) |
式(1)中:x是异烟肼的溶解度(摩尔分数);m0与M0分别代表异烟肼质量与其相对分子质量;m1与M1分别代表溶剂质量与其相对分子质量。
1.5 异烟肼冷却结晶实验异烟肼冷却结晶实验装置与溶解度测量装置基本一致,如图 2所示,具体实验步骤如下:1)调节水浴控温仪至50 ℃,将一定量的原料异烟肼与有机溶剂加入到结晶器中,进行恒定速率300 r/min搅拌至溶解完全。2)开启降温程序,降温至终点温度10 ℃,在终点温度处养晶30 min。3)最后进行抽滤,将固体产品放于真空干燥箱进行干燥,对干燥后的异烟肼产品进行形态学分析。
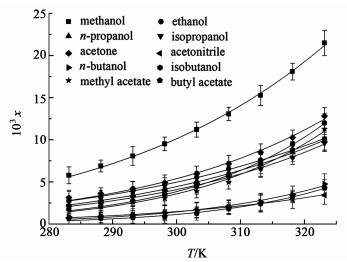
2 实验结果 2.1 异烟肼溶解度数据异烟肼在不同温度、不同溶剂中的溶解度数据如表 1与图 3所示。
| T/K | 103x | 103xcal | 103x | 103xcal | ||||
| Apelblat | Wilson | NRTL | Apelblat | Wilson | NRTL | |||
| methanol | ethanol | |||||||
| 283.15 | 5.776 3 | 5.615 4 | 5.312 6 | 4.971 8 | 2.731 5 | 2.738 1 | 2.278 6 | 2.219 9 |
| 288.15 | 6.878 4 | 6.721 2 | 6.452 4 | 6.113 2 | 3.197 8 | 3.291 2 | 2.828 4 | 2.768 9 |
| 293.15 | 8.072 2 | 8.010 4 | 7.786 3 | 7.464 5 | 3.904 2 | 3.931 0 | 3.487 7 | 3.429 9 |
| 298.15 | 9.504 4 | 9.508 0 | 9.339 4 | 9.056 0 | 4.680 6 | 4.666 8 | 4.271 6 | 4.219 2 |
| 303.15 | 11.206 0 | 11.241 0 | 11.139 0 | 10.920 0 | 5.555 6 | 5.508 7 | 5.198 7 | 5.156 2 |
| 308.15 | 13.064 0 | 13.241 0 | 13.213 0 | 13.091 0 | 6.513 1 | 6.467 1 | 6.288 9 | 6.262 0 |
| 313.15 | 15.255 0 | 15.540 0 | 15.595 0 | 15.610 0 | 7.600 9 | 7.552 8 | 7.565 0 | 7.560 9 |
| 318.15 | 18.084 0 | 18.176 0 | 18.323 0 | 18.524 0 | 8.795 7 | 8.777 3 | 9.051 0 | 9.078 4 |
| 323.15 | 21.484 0 | 21.188 0 | 21.437 0 | 21.881 0 | 10.083 0 | 10.152 0 | 10.773 0 | 10.842 0 |
| n-propanol | isopropanol | |||||||
| 283.15 | 2.231 5 | 2.269 3 | 2.073 5 | 2.074 0 | 2.113 1 | 2.088 2 | 1.928 9 | 1.934 0 |
| 288.15 | 2.697 8 | 2.792 1 | 2.589 5 | 2.590 1 | 2.582 8 | 2.562 9 | 2.412 9 | 2.418 4 |
| 293.15 | 3.404 2 | 3.411 0 | 3.211 9 | 3.212 5 | 3.178 4 | 3.130 3 | 2.996 6 | 3.002 3 |
| 298.15 | 4.176 2 | 4.138 9 | 3.956 3 | 3.956 6 | 3.847 9 | 3.805 6 | 3.695 8 | 3.701 1 |
| 303.15 | 5.055 6 | 4.989 9 | 4.841 4 | 4.841 1 | 4.609 6 | 4.606 0 | 4.528 1 | 4.532 6 |
| 308.15 | 6.013 1 | 5.979 3 | 5.887 7 | 5.886 3 | 5.518 2 | 5.551 0 | 5.514 3 | 5.517 1 |
| 313.15 | 7.100 9 | 7.123 2 | 7.118 5 | 7.115 6 | 6.547 1 | 6.662 5 | 6.676 0 | 6.676 2 |
| 318.15 | 8.495 7 | 8.439 1 | 8.563 5 | 8.558 3 | 7.879 4 | 7.965 2 | 8.042 2 | 8.038 5 |
| 323.15 | 9.883 2 | 9.945 2 | 10.244 0 | 10.236 0 | 9.611 2 | 9.486 7 | 9.644 7 | 9.635 3 |
| acetone | acetonitrile | |||||||
| 283.15 | 3.124 9 | 2.786 6 | 2.610 3 | 2.618 8 | 0.726 1 | 0.756 0 | 0.671 9 | 0.635 3 |
| 288.15 | 3.612 9 | 3.403 4 | 3.247 2 | 3.256 3 | 0.900 5 | 0.926 2 | 0.847 4 | 0.809 7 |
| 293.15 | 4.174 1 | 4.140 3 | 4.010 5 | 4.019 7 | 1.095 5 | 1.130 6 | 1.060 6 | 1.023 5 |
| 298.15 | 4.915 3 | 5.017 7 | 4.920 8 | 4.929 4 | 1.363 2 | 1.375 4 | 1.318 6 | 1.284 4 |
| 303.15 | 5.967 6 | 6.058 9 | 6.001 7 | 6.008 9 | 1.694 8 | 1.667 6 | 1.628 7 | 1.600 4 |
| 308.15 | 7.131 8 | 7.290 6 | 7.275 7 | 7.280 4 | 2.050 4 | 2.015 1 | 1.998 5 | 1.980 2 |
| 313.15 | 8.504 7 | 8.749 7 | 8.771 1 | 8.771 8 | 2.487 5 | 2.427 5 | 2.438 4 | 2.434 9 |
| 318.15 | 10.258 0 | 10.45 0 | 10.522 0 | 10.517 0 | 2.925 2 | 2.915 4 | 2.956 6 | 2.974 6 |
| 323.15 | 12.813 0 | 12.452 0 | 12.576 0 | 12.563 0 | 3.437 6 | 3.491 0 | 3.566 3 | 3.613 2 |
| n-butanol | isobutanol | |||||||
| 283.15 | 0.841 2 | 0.574 4 | 0.575 6 | 0.647 2 | 1.741 6 | 1.570 2 | 1.640 7 | 1.878 6 |
| 288.15 | 0.942 6 | 0.758 6 | 0.751 9 | 0.843 9 | 2.122 1 | 2.062 3 | 2.115 4 | 2.406 3 |
| 293.15 | 1.077 4 | 0.996 0 | 0.976 3 | 1.090 6 | 2.722 4 | 2.692 7 | 2.727 2 | 3.059 9 |
| 298.15 | 1.290 5 | 1.300 4 | 1.265 1 | 1.398 5 | 3.532 9 | 3.495 9 | 3.509 2 | 3.863 8 |
| 303.15 | 1.615 7 | 1.688 6 | 1.639 1 | 1.780 6 | 4.439 1 | 4.514 2 | 4.482 8 | 4.843 6 |
| 308.15 | 1.989 9 | 2.181 3 | 2.109 4 | 2.250 1 | 5.668 7 | 5.798 8 | 5.729 5 | 6.036 8 |
| 313.15 | 2.640 5 | 2.803 8 | 2.741 7 | 2.829 1 | 7.329 7 | 7.411 6 | 7.338 0 | 7.486 1 |
| 318.15 | 3.516 8 | 3.586 5 | 3.571 6 | 3.538 2 | 9.471 1 | 9.427 3 | 9.407 4 | 9.240 6 |
| 323.15 | 4.748 9 | 4.566 5 | 4.686 1 | 4.407 1 | 11.992 0 | 11.936 0 | 12.014 0 | 11.350 0 |
| methyl acetate | butyl acetate | |||||||
| 283.15 | 2.205 4 | 1.457 9 | 1.523 3 | 1.731 5 | 0.653 2 | 0.401 1 | 0.479 2 | 0.563 4 |
| 288.15 | 2.349 1 | 1.917 4 | 1.951 6 | 2.218 1 | 0.675 3 | 0.550 1 | 0.605 0 | 0.735 7 |
| 293.15 | 2.589 2 | 2.505 3 | 2.490 0 | 2.819 0 | 0.755 3 | 0.749 7 | 0.771 5 | 0.952 7 |
| 298.15 | 3.070 6 | 3.252 7 | 3.181 8 | 3.558 8 | 0.885 9 | 1.015 1 | 0.988 0 | 1.223 5 |
| 303.15 | 3.908 5 | 4.197 7 | 4.084 2 | 4.467 0 | 1.247 1 | 1.366 1 | 1.317 8 | 1.562 2 |
| 308.15 | 4.952 3 | 5.385 9 | 5.225 7 | 5.571 4 | 1.816 7 | 1.827 7 | 1.791 9 | 1.982 7 |
| 313.15 | 6.667 1 | 6.872 3 | 6.760 0 | 6.923 4 | 2.406 2 | 2.431 6 | 2.382 0 | 2.497 5 |
| 318.15 | 8.793 8 | 8.722 2 | 8.733 3 | 8.561 6 | 3.249 1 | 3.217 4 | 3.209 7 | 3.130 4 |
| 323.15 | 11.256 0 | 11.013 6 | 11.224 0 | 10.534 0 | 4.257 8 | 4.234 9 | 4.296 4 | 3.901 6 |
| a温度标准误差u (T)=0.05 K, 压力标准误差u (p)=0.3 kPa, 溶解度相对误差ur (x)=0.07。 | ||||||||
|
| 图 3 不同温度、不同溶剂中的实验溶解度与计算溶解度(实线是Apelblat模型计算的数据) Fig.3 Measured and calculated solubility x of isoniazid in different pure solvents at different temperatures (The solid lines are calculated values by using the modified Apelblat model) |
| |
表 1显示,异烟肼在所有溶剂中的溶解度随温度升高而增加,当温度低于303 K时,异烟肼的溶解度与溶剂关系符合如下顺序:甲醇>丙酮>乙醇>正丙醇>异丙醇>异丁醇>乙酸甲酯>乙腈>正丁醇>乙酸丁酯。当温度高于303 K时,异烟肼在异丁醇与乙酸甲酯中的溶解度升高更加明显,溶解度大小满足:甲醇>丙酮>异丁醇>乙酸甲酯>乙醇>正丙醇>异丙醇>正丁醇>乙酸丁酯>乙腈。该结果表明:异烟肼更容易与强极性的甲醇、丙酮形成氢键作用,从而促进异烟肼的溶解。对比文献[11]中异烟肼在乙醇与甲醇中的溶解度数据发现,本研究动态法测定的溶解度在对应的温度下与文献数值接近,其中乙醇与甲醇中的数据误差最大仅为6.5%,这说明动态法也可以作为一种测定溶解度的有效方式。为了确保溶解度测量过程中,异烟肼没有出现多晶型转化现象,在每组测量过程中,都取固体样品进行了XRD与DSC分析。XRD衍射角度范围为2°~50°,扫描速率为1 step/s,DSC的加热速率为10 K/min,结果如图 4与图 5所示。

|
| 图 4 不同溶剂中异烟肼的XRD图谱 Fig.4 XRD pattern of isoniazid in different solvents |
| |
|
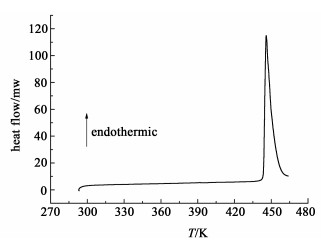
| 图 5 异烟肼的DSC曲线 Fig.5 DSC curve of isoniazid |
| |
从图 4可以看出,所有溶剂中的异烟肼固相具有相同的XRD图谱,所以并没有多晶型的形成。
图 5显示异烟肼的熔点为448 K,该数据也与文献报道的一致[2]。
2.2 异烟肼冷却结晶晶习基于溶解度数据,选择甲醇、丙酮、乙醇、正丙醇作为异烟肼冷却结晶时的溶剂。结晶起点温度为50 ℃,终点温度为10 ℃。异烟肼的晶习照片如图 6所示。

|
| 图 6 异烟肼在不同溶剂冷却结晶的晶习照片 Fig.6 Crystal habit photos of isoniazid after cooling crystallization in different solvents |
| |
从图 6中可以看出,异烟肼在3种醇溶剂中冷却结晶时的晶习均为长棒状,而在丙酮中冷却结晶时的晶习为棱块状,这表明不同类试剂对异烟肼的晶习影响较大。对比醇溶剂发现,异烟肼的尺寸大小满足:正丙醇>甲醇>乙醇,最大长度达到600 μm。照片中还发现,乙醇中的产品没有发生聚结现象,平均尺寸为200 μm,而其它溶剂中产品出现了不同程度的聚结。综合考虑,选择乙醇作为异烟肼的冷却结晶优化溶剂。
3 数据处理与讨论 3.1 溶解度数据拟合 3.1.1 改进的Apelblat方程固体溶质在有机溶剂中溶解度与温度关系可以用改进的Apelblat方程进行拟合,如式(2)所示[20]:
| $ {\rm{ln}}{x_1} = A + \frac{B}{T} + C{\rm{ln}}T $ | (2) |
式(2)中:x1是溶解度,T/K为温度,A、B、C为模型参数。
3.1.2 Wilson方程Wilson方程是一种常用的拟合固体溶质在有机溶剂中溶解度的方程,其方程如式(3)~式(5)所示[21]:
| $ {\rm{ln}}{\gamma _1} = - {\rm{ln}}({x_1} + {\varLambda _{12}}{x_2}) + {x_2}\left( {\frac{{{\varLambda _{12}}}}{{{x_1} + {\varLambda _{12}}{x_2}}} - \frac{{{\varLambda _{21}}}}{{{x_2} + {\varLambda _{21}}{x_1}}}} \right) $ | (3) |
| $ {{\varLambda _{12}} = \frac{{{V_2}}}{{{V_1}}}{\rm{exp}}\left( { - \frac{{{\lambda _{12}} - {\lambda _{11}}}}{{RT}}} \right) = \frac{{{V_2}}}{{{V_1}}}{\rm{exp}}\left( { - \frac{{\Delta {\lambda _{12}}}}{{RT}}} \right)} $ | (4) |
| $ {{\varLambda _{21}} = \frac{{{V_1}}}{{{V_2}}}{\rm{exp}}\left( { - \frac{{{\lambda _{11}} - {\lambda _{12}}}}{{RT}}} \right) = \frac{{{V_1}}}{{{V_2}}}{\rm{exp}}\left( { - \frac{{\Delta {\lambda _{21}}}}{{RT}}} \right)} $ | (5) |
式(3)~式(5)中:x1是溶解度,R为常数;T为温度,K;V1与V2分别为溶质与溶剂摩尔体积;γ1为活度;Δλ12与Δλ21为模型参数。
3.1.3 NRTL方程固体溶质在有机溶剂中的溶解度也可以采用NRTL方程进行拟合,如式(6)~式(8)所示[22]:
| $ {{\rm{ln}}{\gamma _1} = x_2^2\left[ {\frac{{{\tau _{21}}G_{21}^2}}{{{{({x_1} + {G_{21}}{x_2})}^2}}} + \frac{{{\tau _{12}}G_{12}^2}}{{{{({x_2} + {G_{12}}{x_1})}^2}}}} \right]} $ | (6) |
| $ {{G_{12}} = {\rm{exp}}( - {\alpha _{12}}{\tau _{12}});{G_{21}} = {\rm{exp}}( - {\alpha _{12}}{\tau _{21}})} $ | (7) |
| $ {{\tau _{12}} = \frac{{{g_{12}} - {g_{22}}}}{{RT}} = \frac{{\Delta {g_{12}}}}{{RT}};{\tau _{21}} = \frac{{{g_{21}} - {g_{11}}}}{{RT}} = \frac{{\Delta {g_{21}}}}{{RT}}} $ | (8) |
式(6)~式(8)中,x1是溶解度;R为常数;T为温度,K;γ1为活度;τ12与τ21为模型参数。
各方程的拟合精度用平均相对偏差(ARD)来表示,如式(9)所示[23]:
| $ {\rm{ARD}} = \frac{{100}}{N}\sum\limits_{i = 1}^N | \frac{{{x_i} - x_i^{{\rm{ cal }}}}}{{{x_i}}}| $ | (9) |
式(9)中:xi是实验测定的溶解度;xical是模型拟合计算溶解度;N为溶解度数据点。
改进的Apelblat、Wilson与NRTL方程的拟合结果如表 2所示,其中NRTL方程中α12取经验值0.3。从表 2中可以看出,改进的Apelblat模型拟合得到的ARD值最小,表明其拟合精度最高,更适用于异烟肼溶解度的拟合。从ARD值还可以看出,溶解度数据越大,拟合得到ARD值越小,表明精度越高。
| Solvents | Apelblat | Wilson | NRTL | |||||||||
| A | B | C | ARD | Δλ12/(J·mol-1) | Δλ21/(J·mol-1) | ARD | Δg12/(J·mol-1) | Δg21/(J·mol-1) | ARD | |||
| methanol | -36.597 0 | -1 140.2 | 6.277 3 | 1.255 7 | -2 889.0 | 23 773.0 | 2.778 0 | 12 030.0 | 2 470.0 | 6.893 1 | ||
| ethanol | 6.615 3 | -3 084.4 | -0.287 4 | 0.802 0 | -9.0 | 16 609.0 | 7.513 6 | 12 026.0 | 558.0 | 4.063 0 | ||
| n-propanol | 7.079 9 | -3 435.5 | -0.183 4 | 1.083 2 | 815.0 | 18 130.0 | 3.669 9 | 12 617.0 | 2 525.0 | 3.644 4 | ||
| isopropanol | -42.180 0 | -1 290.6 | 7.185 0 | 1.042 5 | 1 017.0 | 17 782.0 | 3.466 0 | 12 446.0 | 2 667.0 | 3.347 7 | ||
| n-butanol | -66.258 0 | 1 620.1 | 10.880 0 | 9.521 2 | 9 558.4 | -1 410.9 | 8.590 3 | -224.7 | 6 983.3 | 9.040 5 | ||
| isobutanol | -72.185 0 | 1 889.1 | 11.745 0 | 2.315 6 | 7 702.1 | -1 708.7 | 1.109 4 | -509.3 | 4 779.0 | 7.616 8 | ||
| acetone | -59.187 0 | -480.1 | 9.741 3 | 3.418 8 | 255.0 | 12 887.0 | 4.529 8 | 12 102.0 | 1 908.0 | 4.493 9 | ||
| acetonitrile | -69.827 0 | -122.9 | 11.171 0 | 2.078 0 | 2 105.0 | 25 840.0 | 3.671 5 | 12 678.0 | 5 315.0 | 5.873 3 | ||
| methyl acetate | -72.814 0 | -1 045.9 | 12.229 0 | 7.294 2 | 7 403.6 | -1 293.1 | 7.520 6 | -555.8 | 5 054.7 | 9.170 2 | ||
| butyl acetate | -67.252 0 | -1 164.8 | 11.497 0 | 9.064 9 | 13 010.0 | -3 005.0 | 6.763 7 | -227.4 | 7 309.5 | 9.240 3 | ||
通常溶解可以简化为4个步骤。首先,固体溶质从温度T被加热熔点温度Tm;然后在Tm进行融化;接着从温度Tm降温到温度T;最后在温度T下与溶剂混合形成溶液,如式(10)所示[24]:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Solute}}{{\rm{ }}_{{\rm{ solid }}}}(T)\mathop \to \limits^{{\rm{ heating }}} {\rm{ Solute}}{{\rm{ }}_{{\rm{ solid }}}}({T_m})\mathop \to \limits^{{\rm{ fusion }}} \\ {\rm{Solute}}{{\rm{ }}_{{\rm{ solid }}}}({T_m})\mathop \to \limits^{{\rm{ cooling }}} {\rm{ Solute}}{{\rm{ }}_{{\rm{ liquid }}}}(T)\mathop \to \limits^{{\rm{ mixing }}} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Solute}}{{\rm{ }}_{{\rm{Solution}}}}(T) \end{array} $ | (10) |
基于上面假设,溶解热力学可以采用式(11)计算[25]:
| $ {\Delta _{{\rm{ dis }}}}M = x({\Delta _{{\rm{ heat }}}}M + {\Delta _{{\rm{ fus }}}}M + {\Delta _{{\rm{ cool }}}}M) + {\Delta _{{\rm{ mix }}}}M $ | (11) |
式(11)中,M指溶解热力学性质,包括溶解吉布斯能G、溶解熵S和溶解焓H;x为溶解度;ΔheatM与ΔcoolM代表加热与冷却过程热力学性质;ΔfusM代表融化过程热力学性质;ΔmixM代表混合热力学性质。这些热力学性质可以采用式(12)~式(15)计算[26]:
| $ {{\Delta _{{\rm{ heat }}}}H = {C_{{\rm{p(s)}}}}({T_{\rm{m}}} - T)} $ | (12) |
| $ {{\Delta _{{\rm{ heat }}}}S = {C_{{\rm{p(s)}}}}{\rm{ln}}({T_{\rm{m}}}/T)} $ | (13) |
| $ {{\Delta _{{\rm{ cool }}}}H = {C_{{\rm{p(I)}}}}(T - {T_{\rm{m}}})} $ | (14) |
| $ {{\Delta _{{\rm{ cood }}}}S = {C_{{\rm{p(I)}}}}{\rm{ln}}(T/{T_{\rm{m}}})} $ | (15) |
式(12)~(15)中,Cp(s)与Cp(l)代表在一定压力下,固体溶质在固相与液相状态下的比热容,通常Cp(s)与Cp(l)大小接近,所以(ΔheatM+ΔcoolM)近似为0。平衡状态下,ΔfusG也为0,所以式(12)~式(15)可以简化为[27]:
| $ {{\Delta _{{\rm{ heat }}}}H + {\Delta _{{\rm{ fus }}}}H + {\Delta _{{\rm{ cool }}}}H = {\Delta _{{\rm{ fus }}}}H} $ | (16) |
| $ {{\Delta _{{\rm{ heat }}}}S + {\Delta _{{\rm{ fus }}}}S + {\Delta _{{\rm{ cool }}}}S = {\Delta _{{\rm{ tus }}}}S} $ | (17) |
| $ {{\Delta _{{\rm{ cool }}}}G + {\Delta _{{\rm{ fus }}}}G + {\Delta _{{\rm{ heat }}}}G = {\Delta _{{\rm{ fus }}}}H - T{\Delta _{{\rm{ tus }}}}S} $ | (18) |
混合热力学性质可以采用式(19)~式(21)表达:
| $ {{\Delta _{{\rm{ mix }}}}G = {G_{\rm{E}}} + \Delta {G_{{\rm{ id }}}}} $ | (19) |
| $ {{\Delta _{{\rm{ mix }}}}S = {S_{\rm{E}}} + \Delta {S_{{\rm{ id }}}}} $ | (20) |
| $ {{\Delta _{{\rm{ mix }}}}H = {H_{\rm{E}}} + \Delta {H_{{\rm{ id }}}}} $ | (21) |
式(19)~式(20)中,GE、SE与HE是过剩热力学性质,ΔGid、ΔSid与ΔHid是理想热力学性质[29]:
| $ {\Delta {G_{{\rm{id}}}} = RT({x_1}{\rm{ln}}{x_1} + {x_2}{\rm{ln}}{x_2})} $ | (22) |
| $ {\Delta {S_{{\rm{id}}}} = - R({x_1}{\rm{ln}}{x_1} + {x_2}{\rm{ln}}{x_2})} $ | (23) |
| $ {\Delta {H_{{\rm{id}}}} = 0} $ | (24) |
式(22)~式(23)中,x1与x2为溶液中溶质与溶剂的摩尔组成。
通常采用Wilson方程计算过剩热力学性质,如式(25)~式(28)所示[29-30]:
| $ {G_{\rm{E}}} = RT({x_1}{\rm{ln}}{\gamma _1} + {x_2}{\rm{ln}}{\gamma _2}) $ | (25) |
| $ {{G_{\rm{E}}} = - RT[{x_1}{\rm{ln}}({x_1} + {x_2}{\varLambda _{12}}) + {x_2}{\rm{ln}}({x_2} + {x_1}{\varLambda _{21}})]} $ | (26) |
| $ {{H^{\rm{E}}} = - {T^2}\left[ {\frac{{\partial ({G^{\rm{E}}}/T)}}{{\partial T}}} \right] = {x_1}{x_2}\left( {\frac{{\Delta {\lambda _{12}}{\varLambda _{12}}}}{{{x_1} + {\varLambda _{12}}{x_2}}} + \frac{{\Delta {\lambda _{21}}{\varLambda _{21}}}}{{{x_2} + {\varLambda _{21}}{x_1}}}} \right)} $ | (27) |
| $ {{S_{\rm{E}}} = ({H_{\rm{E}}} - {G_{\rm{E}}})/T} $ | (28) |
计算得到的溶解热力学数据(溶解吉布斯能、溶解焓、溶解熵)如表 3所示。
| T/K | ΔdisG/(J·mol-1) | ΔdisH/(J·mol-1) | ΔdisS/(J·mol-1·K-1) | ΔdisG/(J·mol-1) | ΔdisH/(J·mol-1) | ΔdisS/(J·mol-1·K-1) |
| methanol | ethanol | |||||
| 283.15 | -22.960 | 117.60 | 0.496 3 | -10.230 | 63.49 | 0.260 4 |
| 288.15 | -27.420 | 140.00 | 0.581 1 | -12.290 | 74.34 | 0.300 7 |
| 293.15 | -32.430 | 164.40 | 0.671 3 | -14.950 | 90.78 | 0.360 7 |
| 298.15 | -38.280 | 193.60 | 0.777 6 | -17.990 | 108.80 | 0.425 4 |
| 303.15 | -45.060 | 228.30 | 0.901 6 | -21.490 | 129.20 | 0.497 2 |
| 308.15 | -52.650 | 266.20 | 1.035 0 | -25.470 | 151.50 | 0.574 4 |
| 313.15 | -61.350 | 310.90 | 1.189 0 | -30.030 | 176.90 | 0.660 7 |
| 318.15 | -71.620 | 368.80 | 1.384 0 | -35.200 | 204.70 | 0.754 1 |
| 323.15 | -83.350 | 438.40 | 1.614 0 | -41.010 | 234.80 | 0.853 4 |
| n-propanol | isopropanol | |||||
| 283.15 | -8.924 | 53.67 | 0.221 0 | -8.363 | 51.25 | 0.210 5 |
| 288.15 | -10.900 | 64.88 | 0.263 0 | -10.270 | 62.64 | 0.253 0 |
| 293.15 | -13.490 | 81.88 | 0.325 3 | -12.590 | 77.09 | 0.305 9 |
| 298.15 | -16.440 | 100.40 | 0.392 0 | -15.280 | 93.33 | 0.364 3 |
| 303.15 | -19.850 | 121.60 | 0.466 6 | -18.400 | 111.80 | 0.429 5 |
| 308.15 | -23.730 | 144.60 | 0.546 4 | -22.070 | 133.80 | 0.506 0 |
| 313.15 | -28.190 | 170.80 | 0.635 5 | -26.290 | 158.80 | 0.591 1 |
| 318.15 | -33.530 | 204.40 | 0.747 8 | -31.360 | 191.10 | 0.699 4 |
| 323.15 | -39.370 | 237.80 | 0.857 6 | -37.440 | 233.10 | 0.837 3 |
| n-butanol | isobutanol | |||||
| 283.15 | -2.663 | 24.60 | 0.096 3 | -6.852 | 46.06 | 0.186 9 |
| 288.15 | -3.281 | 27.58 | 0.107 1 | -8.530 | 56.12 | 0.224 4 |
| 293.15 | -4.030 | 31.52 | 0.121 3 | -10.820 | 71.90 | 0.282 2 |
| 298.15 | -5.010 | 37.71 | 0.143 3 | -13.740 | 93.10 | 0.358 3 |
| 303.15 | -6.316 | 47.09 | 0.176 2 | -17.150 | 116.70 | 0.441 6 |
| 308.15 | -7.883 | 57.84 | 0.213 2 | -21.490 | 148.50 | 0.551 6 |
| 313.15 | -10.110 | 76.33 | 0.276 0 | -26.970 | 191.10 | 0.696 3 |
| 318.15 | -12.920 | 100.90 | 0.357 9 | -33.740 | 245.40 | 0.877 3 |
| 323.15 | -16.550 | 135.00 | 0.469 1 | -41.790 | 308.70 | 1.085 0 |
| acetone | acetonitrile | |||||
| 283.15 | -11.710 | 73.62 | 0.301 4 | -2.897 | 18.39 | 0.075 2 |
| 288.15 | -14.030 | 85.14 | 0.344 2 | -3.596 | 22.80 | 0.091 6 |
| 293.15 | -16.730 | 98.40 | 0.392 7 | -4.412 | 27.74 | 0.109 7 |
| 298.15 | -20.020 | 115.90 | 0.455 9 | -5.437 | 34.51 | 0.133 9 |
| 303.15 | -24.170 | 140.80 | 0.544 1 | -6.670 | 42.90 | 0.163 5 |
| 308.15 | -28.890 | 168.30 | 0.639 9 | -8.067 | 51.89 | 0.194 6 |
| 313.15 | -34.390 | 200.80 | 0.751 0 | -9.729 | 62.95 | 0.232 1 |
| 318.15 | -40.960 | 242.30 | 0.890 3 | -11.570 | 74.01 | 0.268 9 |
| 323.15 | -49.120 | 302.80 | 1.089 0 | -13.700 | 86.96 | 0.311 5 |
| methyl acetate | butyl acetate | |||||
| 283.15 | -7.000 | 59.93 | 0.236 4 | -2.079 | 16.93 | 0.067 1 |
| 288.15 | -8.380 | 63.89 | 0.250 8 | -2.449 | 17.68 | 0.069 9 |
| 293.15 | -10.040 | 70.45 | 0.274 6 | -2.948 | 19.90 | 0.077 9 |
| 298.15 | -12.320 | 83.45 | 0.321 2 | -3.605 | 23.41 | 0.090 6 |
| 303.15 | -15.510 | 105.90 | 0.400 6 | -4.777 | 32.69 | 0.123 6 |
| 308.15 | -19.430 | 133.70 | 0.497 1 | -6.391 | 46.94 | 0.173 1 |
| 313.15 | -24.860 | 178.90 | 0.650 8 | -8.197 | 61.51 | 0.222 6 |
| 318.15 | -31.420 | 234.40 | 0.835 6 | -10.590 | 81.82 | 0.290 4 |
| 323.15 | -39.180 | 297.90 | 1.043 0 | -13.510 | 105.60 | 0.368 7 |
从表 3可以看出,溶解吉布斯能均为负值,溶解焓与溶解熵均为正值,表明异烟肼在所选溶剂中的溶解过程为吸热熵增过程。同时可以看出,溶解吉布斯能的大小与溶解度存在一定关联,如图 7所示。

|
| 图 7 异烟肼在不同溶剂、不同温度下的溶解吉布斯能 Fig.7 Dissolution Gibbs energy of isoniazid vs. temperature in different solvents |
| |
从图 7中可以看出,吉布斯能绝对值越大,其溶解度越大,说明吉布斯能是影响溶解度的关键因素。
4 结论1) 异烟肼在所选有机溶剂中的溶解度均随温度升高而增加,在相同温度下,溶解度与溶剂关系符合如下顺序:甲醇>丙酮>乙醇>正丙醇>异丙醇>乙酸甲酯>异丁醇>正丁醇>乙腈>乙酸丁酯。
2) 改进的Apelblat、Wilson与NRTL方程对异烟肼溶解度数据有很好的拟合,其中改进的Apelblat方程对异烟肼溶解度拟合精度最高。
3) 异烟肼在所选有机溶剂中的溶解过程为吸热熵增过程,且其溶解度大小由Gibbs自由能大小决定,Gibbs自由能绝对值越大,溶解度越大。
4) 异烟肼在乙醇中冷却结晶晶习为长棒状,产品无聚结,平均尺寸为200 μm。
| [1] |
Swapna B, Maddileti D, Nangia A. Cocrystals of the tuberculosis drug isoniazid:polymorphism, isostructurality, and stability[J]. Crystal Growth & Design, 2014, 14(11): 5991-6005. |
| [2] |
Grobelny P, Mukherjee A, Desiraju G R. Drug-Drug co-crystals:Temperature-dependent proton mobility in the molecular complex of isoniazid with 4-aminosalicylic acid[J]. Cryst Eng Comm, 2011, 13: 4358-4364. DOI:10.1039/c0ce00842g |
| [3] |
Aitipamula S, Wong A, Chow P S, et al. Novel solid forms of the anti-tuberculosis drug, Isoniazid:Ternary and polymorphic cocrystals[J]. CrystEngComm, 2013, 15(29): 5877-5887. DOI:10.1039/c3ce40729b |
| [4] |
Jain S, Jain S K, Dixit V K. Magnetically guided rat erythrocytes bearing isoniazid:preparation, characterization, and evaluation[J]. Drug Dev Ind Pharm, 1997, 23(10): 999-1006. DOI:10.3109/03639049709149153 |
| [5] |
Chen J, Sarma B, Evans J M B, et al. Pharmaceutical crystallization[J]. Cryst Growth Des, 2011, 11(4): 887-895. DOI:10.1021/cg101556s |
| [6] |
赵绍磊, 王灵宇, 吴送姑. 药物多晶型的研究进展[J]. 化学工业与工程, 2018, 35(3): 12-21. Zhao Shaolei, Wang Lingyu, Wu Songgu. Progress in the research of pharmaceutical polymorph[J]. Chemical Industry and Engineering, 2018, 35(3): 12-21. DOI:10.3969/j.issn.1006-7906.2018.03.003 (in Chinese) |
| [7] |
Hsien H T, Edward L P, Michael M, et al. Crystallization of Organic Compounds[M]. New Jersey: John Wiley & Sons, Inc, 2009.
|
| [8] |
汤伟伟, 李斯, 龚俊波. 有机晶体成核分子机理研究进展[J]. 化学工业与工程, 2018, 35(3): 2-11. Tang Weiwei, Li Si, Gong Junbo. Research progress on molecular mechanism of nucleation of organic crystals[J]. Chemical Industry and Engineering, 2018, 35(3): 2-11. (in Chinese) |
| [9] |
Mullin J W. Crystallization[M]. Fourth edition. Oxford: Butterworth-Heinemann, 2001.
|
| [10] |
Xu R, Hou B, Wang N, et al. Thermodynamic properties of disodium sebacate in different binary solvent mixtures[J]. Journal of Molecular Liquids, 2018, 252: 194-202. DOI:10.1016/j.molliq.2017.12.104 |
| [11] |
Heryanto R Hasan M, Abdullah E C. Solubility of Isoniazid in Various Organic Solvents from (301 to 313) K[J]. Journal of Chemical & Engineering Data, 2008, 53: 1962-1964. |
| [12] |
Heryanto R D, Abdullah E C, Hasan M. Solubility of isoniazid in supercritical carbon dioxide[J]. Journal of Chemical & Engineering Data, 2010, 55(6): 2306-2309. |
| [13] |
Forte A, Melo C I, Bogel-Łukasik R, et al. A favourable solubility of isoniazid, an antitubercular antibiotic drug, in alternative solvents[J]. Fluid Phase Equilibria, 2012, 318: 89-95. DOI:10.1016/j.fluid.2012.01.022 |
| [14] |
Ouyang J B, Na B, Zhou L, et al. Crystal structures and phase transformation of two novel solvates of valnemulin hydrochloride[J]. CrystEngComm, 2017, 20(5): 563-569. |
| [15] |
Wang G, Ma Y, Wang Y, et al. Investigation of solution-mediated phase transformation of cefuroxime acid to its acetonitrile solvate[J]. Organic Process Research & Development, 2015, 19(12): 1820-1825. |
| [16] |
杨利强. 2, 3, 5-三甲基氢醌二酯结晶过程及晶体形态调控研究[D].天津: 天津大学, 2014 Yang Liqiang. Study on crystallization process and morphology regulation of 2, 3, 5-trimethyl-hydroquinone diester[D]. Tianjin: Tianjin University, 2014(in Chinese) |
| [17] |
Jat S K, Narayanasamy V, Krishna A, et al. Nucleation kinetics, growth, mechanical, thermal and optical characterization of sulphamic acid single crystal[J]. CrystEngComm, 2013, 15(46): 10034-10042. DOI:10.1039/c3ce41397g |
| [18] |
Suresh K, Nangia A. Lornoxicam salts:Crystal structures, conformations, and solubility[J]. Crystal Growth & Design, 2014, 14(6): 2945-2953. |
| [19] |
Ouyang J B, Na B, Liu Z, et al. Determination of solubility and nucleation kinetics of valnemulin hydrochloride solvate[J]. Journal of Solution Chemistry, 2019, 48(4): 413-426. DOI:10.1007/s10953-019-00861-7 |
| [20] |
Apelblat A, Manzurola E. Solubilities of o-acetylsalicylic, 4-aminosalicylic, 3, 5-dinitrosalicylic, and p-toluic acid, and magnesium-DL-aspartate in water from T=(278 to 348) K[J]. The Journal of Chemical Thermodynamics, 1999, 31(1): 85-91. DOI:10.1006/jcht.1998.0424 |
| [21] |
Wilson G M. Vapor-Liquid equilibrium. XI. A new expression for the excess free energy of mixing[J]. Journal of the American Chemical Society, 1964, 86(2): 127-130. DOI:10.1021/ja01056a002 |
| [22] |
Renon H, Prausnitz J M. Local compositions in thermodynamic excess functions for liquid mixtures[J]. AIChE Journal, 1968, 14(1): 135-144. DOI:10.1002/aic.690140124 |
| [23] |
Wu Y, Zhou L, Zhang X, et al. Determination and correlation of the solubility of acetylpyrazine in pure solvents and binary solvent mixtures[J]. Journal of Solution Chemistry, 2018, 47(5): 950-973. DOI:10.1007/s10953-018-0763-7 |
| [24] |
Ouyang J, Na B, Zhou L, et al. Determination and modeling of solubility of 4-aminobenzamide in different pure solvents[J]. J Chem Eng Data, 2019, 64: 1569-1576. DOI:10.1021/acs.jced.8b01144 |
| [25] |
Huang X, Wang J, Bairu A, et al. Solid-Liquid phase equilibrium and mixing thermodynamic analysis of coumarin in binary solvent mixtures[J]. Physics and Chemistry of Liquids, 2019, 57(2): 204-220. DOI:10.1080/00319104.2018.1437917 |
| [26] |
Han Z, Hao H, Wu H, et al. Solubility and thermodynamic properties of dirithromycin form A and form B in pure solvents and binary solvent mixture[J]. J Chem Thermodyn, 2019, 132: 240-249. DOI:10.1016/j.jct.2018.12.044 |
| [27] |
Li X, Huang X, Luan Y, et al. Solubility and thermodynamic properties of 5-nitrofurazone form γ in mono-solvents and binary solvent mixtures[J]. J Mol Liq, 2019, 275: 815-828. DOI:10.1016/j.molliq.2018.11.123 |
| [28] |
Halder G N. Introduction to chemical engineering thermodynamics[M]. 2nd Edition. India: PHI Learning Pvt Ltd, 2014.
|
| [29] |
Kondepudi D. Introduction to modern thermodynamics[M]. New Jersey: John Wiley & Sons, Inc, 2008.
|
| [30] |
Ouyang J B, Zhang Y, Na B, et al. Solubility determination of nicotinamide and its application for the cocrystallization with benzoic acid[J]. J Chem Eng Data, 2018, 63: 4157-4165. DOI:10.1021/acs.jced.8b00560 |
 2020, Vol. 37
2020, Vol. 37





