2. 天津市化学科学与工程协同创新中心, 天津 300072
2. Collaborative Innovation Center of Chemical Science and Engineering, Tianjin 300072, China
随着我国工业的蓬勃发展,环境问题也日益凸显,主要表现在水体污染[1]、大气污染[2]和土壤污染[3]等方面。近年来,水体污染正逐渐加重,危害着整个国民的安全和健康,如何处理水污染成为一个非常急迫的任务。染料对水体的污染是最严重的污染之一,极少量的染料就会使水体颜色变得糟糕不堪,并且部分染料具有极其严重的致癌性[4-5]。
阴离子染料有各种不同的结构,常见的有偶氮类、蒽醌类和芳甲烷类,一般相对分子质量较大,难以通过环境自身进行降解[6]。目前为止,各种技术被用于去除废水中的染料,如物理方法、生物降解、氧化和电解等。其中,吸附方法是一种普遍应用的处理方法,具有操作简单、处理能力高的优点[7]。因此,开发一种有效的吸附剂是很有必要的。
工业中,通常是在连续流动的条件下实现吸附剂对污水的处理,而实验室批量实验得到的结果很难预测实际的效果[8-9],但是许多对吸附剂性能的研究都忽略了实际应用的条件。因此,本研究将纤维吸附剂应用于动态流动吸附来模拟实际污水处理过程,并采用Thomas模型、Yoon-Nelson模型和BDST模型对实验结果进行分析以帮助我们更好地了解该纤维吸附剂的应用价值[10-11]。
1 实验部分 1.1 仪器与试剂紫外-可见光谱仪,北京普西通用仪器有限公司;pH计,Oakton WD-35634, 30 PH Tester 30;傅里叶红外光谱仪,AVATAR360 Thermo Nicolet。
腈纶纤维,中国抚顺石化公司;N, N-二甲基-1, 3-丙二胺,1-溴乙烷,甲基橙,乙醇,去离子水。
1.2 实验方法 1.2.1 吸附剂的制备步骤1:取3g干燥的腈纶纤维,50mL的N, N-二甲基-1, 3-丙二胺和50mL的水加入三口瓶中,加热回流4.5h后停止反应,冷却至室温。取出纤维用热水洗涤,烘干纤维,称质量,通过公式W=(W2-W1)/W1×100%计算增质量(28%)和公式F=(W2-W1)/W2M计算官能度(2.15 mmol·g-1), 其中W1和W2分别为原纤维和修饰后纤维的质量,M为增加的相对分子质量。
步骤2:取3g上步制备的纤维,5当量的1-溴乙烷和150mL的乙醇加入到三口瓶中,加热回流5h。反应结束后将溶液冷却至室温,取出纤维用乙醇洗涤,干燥称质量,计算增质量和官能度。
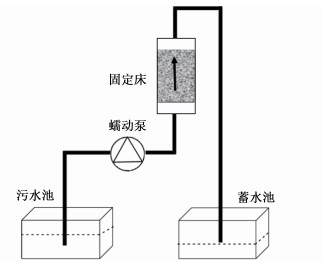
1.2.2 吸附试验流动实验在微型固定反应器中进行,该反应器长度为10cm,内径为0.64cm,如图 1所示。纤维吸附剂被紧密地填充在反应器中,使甲基橙溶液自下而上连续通过纤维吸附剂。使用紫外吸收光谱定时检测流出液中甲基橙溶液的浓度。整个吸附实验的甲基橙溶液的pH值为7。
|
| 图 1 动态流动过程的装置简图 Fig.1 The device diagram of dynamic flow process |
| |
本研究对腈纶纤维和修饰后的季铵离子化纤维进行红外测试,测试结果如图 2所示。

|
| 图 2 腈纶纤维和季铵离子化纤维的红外光谱 Fig.2 The Fourier-transfer infrared spectroscopy of origin fiber and quaternary ammonium ion fiber |
| |
原纤维的红外谱图在2244cm-1处出现CN的伸缩振动吸收峰。纤维修饰后,该吸收峰仍然存在,表明原纤维中只有部分的腈基进行了转化。在季铵离子化纤维的红外光谱中,3500~3 250cm-1处的吸收峰属于酰胺中N—H键的伸缩振动。与原纤维的红外光谱相比,季铵离子化纤维的红外光谱在1630cm-1处存在吸收峰,这归因于酰胺中CO的伸缩振动谱带。另外,其在1020cm-1处存在弱吸收峰,这是由于叔胺中C≡N单键的伸缩振动。以上讨论表明,季铵离子化纤维被成功合成。
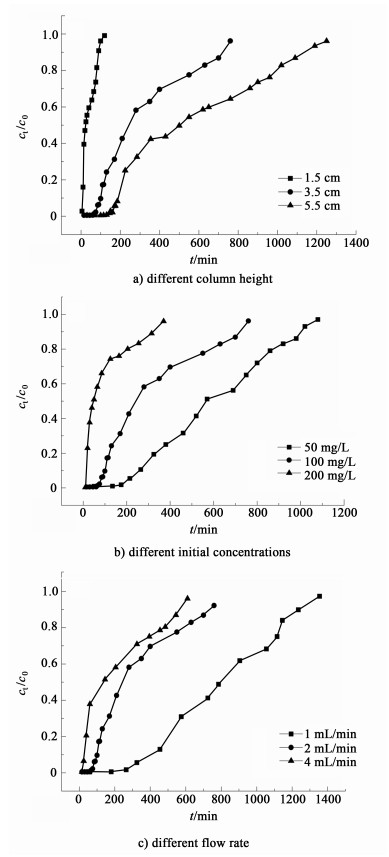
2.2 动态吸附 2.2.1 柱高对穿透曲线的影响在流速为2mL·min-1,初始浓度为100mg·L-1的条件下,考察了穿透曲线随柱高的变化情况,结果如图 3a)所示。随着柱高逐渐增加,穿透曲线的斜率逐渐减小。在柱高为1.5cm时,穿透时间需要110min;柱高为5.5cm时,穿透时间增加至1250min,而吸附量从60mg·g-1增加到355 mg·g-1(表 1,1~3)。显然,柱高的增高使吸附剂和甲基橙之间接触时间的增加,也增强了吸附剂对甲基橙的吸附效率。
|
| 图 3 不同的条件对穿透曲线的影响 Fig.3 The effect of different conditions on breakthrough curves |
| |
| 序号 | 质量 m/g |
柱高 h/cm |
初始浓度c0/ (mg·L-1) |
流速Q/ (mL·min-1) |
相关系数 R2 |
速率常数KTH/ (L·min-1·g-1) |
理论饱和吸附量(qe)cal/ (mg·g-1) |
实际饱和吸附量(qe)exp/ (mg·g-1) |
| 1 | 0.10 | 1.5 | 100 | 2 | 0.935 2 | 0.380 4 | 63.35 | 60 |
| 2 | 0.25 | 3.5 | 100 | 2 | 0.903 4 | 0.104 6 | 304.64 | 300 |
| 3 | 0.40 | 5.5 | 100 | 2 | 0.922 4 | 0.063 8 | 356.05 | 355 |
| 4 | 0.25 | 3.5 | 50 | 2 | 0.950 4 | 0.142 4 | 313.40 | 345 |
| 5 | 0.25 | 3.5 | 200 | 2 | 0.848 4 | 0.121 9 | 194.42 | 190 |
| 6 | 0.25 | 3.5 | 100 | 1 | 0.943 9 | 0.061 3 | 369.67 | 360 |
| 7 | 0.25 | 3.5 | 100 | 4 | 0.907 5 | 0.122 5 | 293.44 | 285 |
在2 mL·min-1的流速,柱高3.5cm的条件下,甲基橙的初始浓度不同,穿透曲线形状发生明显的变化,如图 3b)所示。随着甲基橙初始浓度的降低,穿透曲线的斜率逐渐减小。当初始浓度为200mg·L-1时,穿透时间为370min,初始浓度降低至50mg·L-1时,穿透时间增至1080min。由此可见,浓度的降低有利于纤维吸附剂的动态吸附过程。因为浓度增加,高的浓度梯度会提供大的传质驱动力,使吸附速率增加,纤维更快地达到饱和吸附。所以吸附剂与甲基橙之间短的接触时间会削弱吸附剂的吸附能力。
2.2.3 流速对穿透曲线的影响在100 mg·L-1的甲基橙初始浓度及3.5cm柱高条件下,考察了流速对穿透曲线的影响,如图 3c)所示。随着甲基橙流速的增加,穿透曲线的斜率逐渐增大。当流速从1 mL·min-1增加至4 mL·min-1时,穿透时间分别为1355min和610min。穿透时间的缩短是因为较高的流速导致吸附剂表面上低的外部膜质阻力并缩短了停留时间,纤维吸附剂对甲基橙的吸附能力降低。
2.3 动态吸附模型本研究分别采用Thomas、Yoon-Nelson和BDST 3种模型对不同柱高,不同初始浓度和不同流速条件下纤维吸附甲基橙的穿透曲线进行拟合。
2.3.1 Thomas模型首先采用Thomas模型对上述实验数据进行拟合分析,该模型假设当溶液流过固定床时没有轴向扩散并且吸附过程符合伪二级动力学模型。如公式(1):
| $ \ln \left( {\frac{{{c_0}}}{{{c_{\rm{t}}}}} - 1} \right) = \frac{{{K_{{\rm{TH}}}}{q_{\rm{e}}}m}}{Q} - {K_{{\rm{TH}}}}{c_0}t $ | (1) |
式(1)中:ct和c0分别为流出液浓度和初始浓度,mg·L-1;KTH为速率常数,mL·min-1·mg-1;qe为平衡时的吸附容量,mg·g-1;m为填充的质量,g;Q为流速,mL·min-1。
根据式(1)以

|
| 图 4 在不同条件下Thomas模型的拟合曲线 Fig.4 The fitting curves of Thomas model under different conditions |
| |
由表 1可知,不同的动态流动条件下,以Thomas模型对实验数据进行拟合的线性相关系数R2基本都在0.900 0以上,说明Thomas模型可以很好地描述动态吸附过程。随着柱高的增加,KTH值降低,而qe的值反而上升(表 1,1~3),这是因为较高的柱高导致较高的流动阻力并减弱了传质效应,使得KTH降低。同时,柱高越高会提供更多的活性吸附位点,因此吸附量增加。当流速和甲基橙的初始浓度增加,吸附量qe减小(表 1,2,4~7)。较大的流速使得吸附剂和甲基橙之间的接触时间大大缩短,因此饱和吸附量明显降低。综上讨论,较高的柱高,较低的吸附质初始浓度以及较小的流速有利于吸附。在实际应用中,可以采用Thomas模型对柱高,流速和溶液初始浓度进行调整,从而获得最佳吸附效果。
2.3.2 Yoon-Nelson模型另外,采用Yoon-Nelson模型对上述动态吸附的实验数据进行拟合分析,该模型不需要考虑吸附剂的种类和固定床的几何参数,主要是为了预测50%的穿透时间,如公式(2):
| $ \ln \frac{{{c_{\rm{t}}}}}{{{c_0} - {c_{\rm{t}}}}} = {K_{{\rm{YN}}}}t - {K_{{\rm{YN}}}}\tau $ | (2) |
式(2)中:ct和c0分别为流出液浓度和初始浓度,mg·L-1;KYN为速率常数,min-1;τ为50%穿透时间,min。根据式(2),以

|
| 图 5 不同条件下Yoon-Nelson模型的拟合曲线 Fig.5 The fitting curves of Yoon-Nelson model under different conditions |
| |
| 序号 | 质量 m/g |
柱高 h/cm |
初始浓度c0/ (mg·L-1) |
流速Q/ (mL·min-1) |
相关系数 R2 |
速率常数KYN/ min-1 |
理论50%穿透 时间τcal/min |
实际50%穿透 时间τexp/min |
| 1 | 0.10 | 1.5 | 100 | 2 | 0.935 2 | 0.038 04 | 31.67 | 33 |
| 2 | 0.25 | 3.5 | 100 | 2 | 0.903 4 | 0.010 46 | 380.80 | 345 |
| 3 | 0.40 | 5.5 | 100 | 2 | 0.922 4 | 0.006 38 | 712.10 | 720 |
| 4 | 0.25 | 3.5 | 50 | 2 | 0.950 4 | 0.007 12 | 635.73 | 640 |
| 5 | 0.25 | 3.5 | 200 | 2 | 0.848 4 | 0.024 38 | 121.51 | 135 |
| 6 | 0.25 | 3.5 | 100 | 1 | 0.943 9 | 0.006 13 | 866.68 | 870 |
| 7 | 0.25 | 3.5 | 100 | 4 | 0.907 5 | 0.012 25 | 230.90 | 205 |
由表 2可知,Yoon-Nelson模型对实验数据拟合的线性相关系数R2基本大于0.9,以及理论50%穿透时间τcal与实际50%穿透时间τexp之间误差较小,均说明该模型可以模拟纤维动态吸附甲基橙的过程。由于该模型简化实际条件而忽略了吸附剂的结构特点和固定床的几何参数,所以τcal普遍低于τexp。随着柱高的增高,50%穿透时间τ逐渐增加(表 2,序号1~3);随着初始浓度和流速的增加,50%穿透时间τ逐渐减小(表 2,序号2、4~7)。
2.3.3 BDST模型BDST模型假设吸附速率仅受吸附剂与甲基橙之间的表面反应控制,而不考虑内部扩散和传质阻力的影响。采用该模型描述柱高和穿透时间之间的关系,并预测在初始浓度和初始速率改变后的穿透时间。如公式(3):
| $ {t_{\rm{a}}} = \frac{{{N_0}}}{{{c_0}v}}h - \frac{1}{{{K_{\rm{a}}}{C_0}}}\ln \left( {\frac{{{c_0}}}{{{c_{\rm{t}}}}} - 1} \right) $ | (3) |
式(3)中:ta是穿透时间,min;N0是固定床的吸附容量,mg·L-1;Ka是BDST模型的吸附速率常数,L·(min·mg)-1;ct和c0分别是流出液浓度和初始浓度,mg·L-1;h为柱高,cm;v为线性流速(流速除以单位面积), cm·min-1。公式(3)也可以写为:
| $ {t_{\rm{a}}} = ah + b $ | (4) |
| $ a = \frac{{{N_0}}}{{{c_0}v}} $ | (5) |
| $ b = \frac{1}{{{K_{\rm{a}}}{C_0}}}\ln \left( {\frac{{{c_0}}}{{{c_{\rm{t}}}}} - 1} \right) $ | (6) |
当初始流速从Q变为Q′,线性流速从v变为v′,其他条件不变时,a变化而b不变,a值可以通过公式(7)计算:
| $ a' = a\frac{v}{{v'}} $ | (7) |
当初始浓度从c0变为c′0,a、b均发生变化,a、b值可以通过公式(8)和(9)计算:
| $ a' = a\frac{{{c_0}}}{{{{c'}_0}}} $ | (8) |
| $ b' = b\left( {\frac{{{c_0}}}{{{{c'}_0}}}} \right)\frac{{\ln \left( {\frac{{{{c'}_0}}}{{{{c'}_{\rm{t}}}}} - 1} \right)}}{{\ln \left( {\frac{{{c_0}}}{{{c_{\rm{t}}}}} - 1} \right)}} $ | (9) |
假定
| 序号 | 质量 m/g |
柱高 h/cm |
初始浓度c0/ (mg·L-1) |
流速Q/ (mL·min-1) |
线性流速v/ (cm·min-1) |
理论10%穿透时间 (ta)cal/min |
实际10%穿透时间 (ta)exp/min |
| 1 | 0.10 | 1.5 | 100 | 2 | 6.25 | 4.09 | 6 |
| 2 | 0.25 | 3.5 | 100 | 2 | 6.25 | 105.59 | 110 |
| 3 | 0.40 | 5.5 | 100 | 2 | 6.25 | 207.09 | 209 |
| 4 | 0.25 | 3.5 | 50 | 2 | 6.25 | 211.17 | 220 |
| 5 | 0.25 | 3.5 | 200 | 2 | 6.25 | 52.79 | 45 |
| 6 | 0.25 | 3.5 | 100 | 1 | 3.13 | 283.25 | 325 |
| 7 | 0.25 | 3.5 | 100 | 4 | 12.50 | 16.77 | 20 |
成功制备了季铵离子化纤维吸附剂,并将其应用于对阴离子染料甲基橙的动态吸附实验中。考察了甲基橙初始浓度、柱高和流速对穿透曲线的影响,并采用Thomas模型、Yoon-Nelson模型和BDST模型对这些实验数据进行拟合分析。Thomas模型拟合结果表明,较高的柱高、较低的吸附质初始浓度以及较小的流速有利于吸附;拟合曲线的相关系数R2均大于0.9,表明该模型可以很好地描述该动态吸附过程并预测吸附容量。Yoon-Nelson模型拟合曲线的相关系数R2均在0.9以上,说明该模型能够很好地预测50%的穿透时间。最后采用BDST模型成功预测初始浓度和初始速率改变后的穿透时间。
| [1] |
卢丽. 我国水环境污染现状及防治对策[J]. 产业与科技论坛, 2012, 11(6): 121-121. |
| [2] |
张黎. 我国大气环境污染现状及防治措施分析[J]. 山东工业技术, 2018(13): 208-208. |
| [3] |
韩倍雷. 我国农田土壤重金属污染现状及检测技术分析[J]. 环境与发展, 2018, 30(11): 160-162. Han Beilei. Analysis of present situation and detection technology of heavy metal pollution in farmland soils in China[J]. Environment and Development, 2018, 30(11): 160-162. (in Chinese) |
| [4] |
郭春香, 孔庆山, 高继贤, 等. 海藻酸纤维动态吸附废水中亚甲基蓝染料[J]. 环境工程学报, 2011, 5(2): 297-300. Guo Chunxiang, Kong Qingshan, Gao Jixian, et al. Dynamic adsorption of methylene blue dye from simulated wastewater by alginic acid fibers[J]. Chinese Journal of Environmental Engineering, 2011, 5(2): 297-300. (in Chinese) |
| [5] |
史月月, 单锐, 袁浩然. 改性稻壳生物炭对水溶液中甲基橙的吸附效果与机制[J]. 环境科学, 2019, 40(6): 2783-2792. Shi Yueyue, Shan Riu, Yuan Haoran. Effects and mechanisms of methyl orange removal from aqueous solutions by modified rice shell biochar[J]. Chinese Journal of Environmental Science, 2019, 40(6): 2783-2792. (in Chinese) |
| [6] |
Wong S, Tumari H H, Ngadi N, et al. Adsorption of anionic dyes on spent tea leaves modified with polyethyleneimine (PEI-STL)[J]. Journal of Cleaner Production, 2019, 206: 394-406. |
| [7] |
刘斌, 李孟斌, 王红华. 水中染料在活性炭上的动态吸附行为研究[J]. 工业水处理, 2018, 38(5): 21-24. Liu Bin, Li Mengbin, Wang Honghua, et al. Dynamic adsorption behavior of activated carbon on dyes in water[J]. Industrial Water Treatment, 2018, 38(5): 21-24. (in Chinese) |
| [8] |
Lim A P, Aris A Z. Continuous fixed-bed column study and adsorption modeling: Removal of cadmium (Ⅱ) and lead (Ⅱ) ions in aqueous solution by dead calcareous skeletons[J]. Biochemical Engineering Journal, 2014, 87: 50-61. |
| [9] |
Podder M S, Majumder C B. Fixed-Bed column study for As(Ⅲ) and As(V) removal and recovery by bacterial cells immobilized on Sawdust/MnFe2O4 composite[J]. Biochemical Engineering Journal, 2016, 105: 114-135. |
| [10] |
Hernandez-Eudave M T, Bonilla-Petriciolet A, Moreno-Virgen M R, et al. Design analysis of fixed-bed synergic adsorption of heavy metals and acid blue 25 on activated carbon[J]. Desalination and Water Treatment, 2016, 57(21): 9824-9836. |
| [11] |
邓国鸿, 罗学刚, 杨嘉怡, 等. 改性废弃皮革对U(Ⅵ)的动态吸附[J]. 环境工程学报, 2018, 12(9): 2602-2608. Deng Guohong, Luo Xuegang, Yang Jiayi, et al. Dynamic adsorption of U(Ⅵ) by modified leather waste[J]. Chinese Journal of Environmental Engineering, 2018, 12(9): 2602-2608. (in Chinese) |
 2020, Vol. 37
2020, Vol. 37





