2. 中国科学院大学化学工程学院, 北京 100049
2. School of Chemical Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
固-液搅拌槽广泛应用于化工冶金、生物制药和食品等工业过程。在固-液搅拌槽中,固体颗粒在搅拌槽内的悬浮状态直接决定了两相的有效接触面积,从而影响相际传质、传热以及化学反应进程[1]。目前,如何以最小的能耗获得生产所需要的悬浮效果是固-液搅拌槽研究的重点之一,而搅拌槽槽底的流动状况对固体颗粒的离底悬浮效果起决定性作用[2]。因此,研究不同桨型操作条件下槽底的流场情况具有重要的意义。
在实验室操作条件下,Zwietering等[3]对固体颗粒在搅拌槽内的悬浮进行了开创性研究,首次定义了固体颗粒在搅拌槽内的不同悬浮状态,并利用目测法测量了固体颗粒完全离底悬浮时的临界搅拌转速,提出了对应于不同搅拌桨的临界搅拌转速的经验关联式。Nienow等[4]将研究进一步深入,考察了搅拌桨安装位置对固体颗粒悬浮状态的影响,并定性研究了不同操作条件下固体颗粒在搅拌槽内容易堆积的位置,但研究仅针对Rushton桨。来永斌等[5]研究了搅拌桨离底间距和桨型(斜叶桨PBT和螺旋桨ZHX)对固相颗粒的悬浮状态、临界悬浮转速及功率消耗的影响,发现在相同工况下固相颗粒的悬浮效果PBT桨优于ZHX桨。Wu等[6]利用激光多普勒测速法研究了斜叶桨和圆盘涡轮桨几何参数(桨型、桨叶数目)对固-液搅拌槽湍流速度场和固-液悬浮状况的影响,发现流量准数与Zwietering[3]提出的临界悬浮转速公式中S的乘积为1个常数。Wang等[7]用目测法研究了桨型、搅拌桨几何参数等对颗粒悬浮效果的影响,发现在带挡板的搅拌槽中,轴流式桨比径流式桨能够更有效地悬浮固体颗粒。
对于在工业高压、高温等复杂条件下应用的大型反应器,实验室条件下无法得到工业放大情况下所需要的详细信息[8]。随着计算流体力学(CFD)的发展,运用数值模拟的方法预测搅拌槽内流体的流动状况显示出巨大的潜力。近年来对固-液搅拌槽内流体的数值模拟研究已取得较大进展。Micale等[9]使用标准k-ε湍流模型,模拟了Rushton桨操作下两相搅拌槽中的固体颗粒浓度分布,模拟结果与实验数据相差不大。Montante等[10]使用Eulerian-Eulerian多相流模型和k-ε湍流模型,研究了四叶45°斜叶桨搅拌槽内固体颗粒的轴向浓度分布,发现实验数据与模拟结果呈现良好的一致性。钟丽等[8]在不同转速条件下,模拟了标准六直叶涡轮桨操作时颗粒的临界悬浮转速,模拟结果与文献数据吻合度较高。王振松等[2]利用k-ε模型,分别在清水体系和玻璃珠-水体系中,使用CBYⅢ桨对搅拌槽槽底的流场分布趋势进行模拟,发现固体颗粒的加入会造成液相速度的衰减,槽底的悬浮状况与槽底流场分布状况相反。Gu等[11]采用经典的Eulerian-Eulerian方法与标准k-ε湍流模型,模拟了固-液搅拌槽内的颗粒悬浮状况,考察了搅拌桨桨型、几何尺寸和转速等对固-液体系均匀性的影响。
从以上研究可以发现,研究者们大多就搅拌容器的结构参数(如搅拌桨类型、尺寸、数量等)和操作条件与固体颗粒悬浮性能之间的关系进行实验和模拟研究,以期待能得到更好的固体颗粒悬浮效果。半折叶桨作为一种新型搅拌桨,通过折叶桨的倾斜部分和竖直部分的相互作用,能够有效带动颗粒离底悬浮[12],但尚未有研究者将该桨与其他桨型进行过对比。因此,本研究结合实验测量和数值模拟的方法,在固-液搅拌槽内考察了新型半折叶搅拌桨(HFT)的功耗、泵送能力和对固体颗粒的悬浮效果,并与传统径向流Rushton桨(RDT)和轴向流下推式45°六斜叶桨(PBTD)进行了对比,以便为半折叶桨的进一步优化设计和放大提供必要的理论依据。
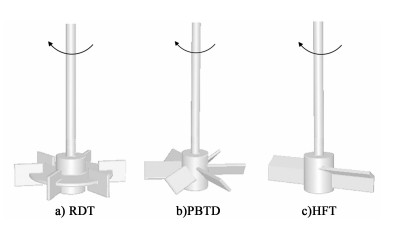
1 实验部分 1.1 实验装置实验装置图如图 1所示。实验在1个透明的平底圆柱形有机玻璃搅拌槽中进行,槽径T=240 mm。槽内设有4块挡板,挡板宽度为B=T/10,液面高度H=T,桨离底高度为C=T/4,以RDT桨为例,D为搅拌桨直径,l为搅拌桨桨叶长度,w为搅拌桨宽度,δ为搅拌桨叶片厚度,d为搅拌桨轮毂直径。搅拌桨由数显调速电机(RW 20 Digital, IKA)驱动,并通过扭矩传感器(型号SN-1050,北京森索中恒科技发展有限公司)测量扭矩。实验选用3种类型的搅拌桨,分别为Ruhston桨(RDT)、下推式45°六斜叶桨(PBTD)和新型半折叶桨(HFT)。图 2为各搅拌桨的示意图,搅拌轴径为8 mm,搅拌桨具体尺寸如表 1所示。其中,新型HFT桨的桨叶一半为垂直叶片,另一半为倾斜叶片,垂直叶片和倾斜叶片夹角为120°。实验选择常见的自来水(20 ℃)作为工作介质。固体采用红色玻璃珠,颗粒直径ds=2.00 mm,颗粒密度ρs=2 816.67 kg·m-3。搅拌桨转速为300、400和500 r/min,对应的雷诺数分别为43 882、58 510和73 137,表明实验在完全湍流状态下进行[13]。

|
| 图 1 实验装置图 Fig.1 Experimental setup |
| |
|
| 图 2 各搅拌桨示意图 Fig.2 Structure of the impellers |
| |
| 桨型 | 桨径D/mm | 桨长l/mm | 桨宽w/mm | 桨厚δ/mm | 轮毂直径d/mm |
| RDT | 94.0 | 23.5 | 18.8 | 3.0 | 25 |
| PBTD | 94.0 | 34.5 | 16.0 | 3.0 | 25 |
| HFT | 94.0 | 34.5 | 12.0 | 3.0 | 25 |
实验采用轴上扭矩法对功率进行测量。在某一转速下,通过安装在搅拌轴上的扭矩传感器测得扭矩值,待数据稳定后读取扭矩平均值。搅拌功率P的计算式如式(1):
| $ P{\rm{ = }}2{\rm{ \mathit{ π} }}MN $ | (1) |
式(1)中:M为扭矩,N·m;N为搅拌转速,r/s。
因电机、轴承、与轴传动中存在摩擦损耗,所以在测量扭矩之前,先让搅拌轴在无负载状态下空转,得到电机空载扭矩值;然后加入流体,得到相应转速下的负载扭矩值,减去空载值,即可得到对应的扭矩值。
1.3 搅拌桨性能参数功率准数Np表示机械搅拌过程中,施加于单位体积被搅拌液体的外力与液体惯性力之比,可反映搅拌桨功耗情况。当搅拌槽内流场处于完全湍流状态时,Np为一常数[13]。搅拌槽内Np的计算公式为:
| $ {N_{\rm{p}}} = \frac{p}{{{\rho _1}{N^3}{D^5}}} $ | (2) |
式(2)中:ρl为液相密度,kg·m-3。
搅拌桨的泵送能力对流体混合和传质也有较大影响,一般用流量准数Nq来衡量。径向流Rushton桨的流量准数通过径向液体流量Qrv计算,径向流量是指直径等于或略大于桨径、高度等于桨叶高度的圆环面单位时间内所通过的流体体积;而轴向流PBTD和HFT桨的流量准数通过轴向液体流量Qzv计算,轴向流量是指直径等于桨径、高度略低于桨叶下边缘的圆面单位时间内所通过的流体体积。计算公式分别如式(3)和式(4) [14]。
| $ {Q_{{\rm{rv}}}} = 2{\rm{ \mathit{ π} }}r\int_{{z_1}}^{{z_2}} {{u_{{\rm{lr}}}}} {\rm{d}}z $ | (3) |
| $ {Q_{{\rm{zv}}}} = \int_{{z_1}}^{{z_2}} {{u_{{\rm{lz}}}}} 2{\rm{ \mathit{ π} }}r{\rm{d}}z $ | (4) |
式(3)和式(4)中:r为径向距离,m;z为轴向高度,m;z1和z2分别为桨叶最低和最高点高度,m;ulr为径向速度,m·s-1;ulz为轴向速度,m·s-1。
搅拌桨的流量准数Nq计算公式为:
| $ {N_{\rm{q}}} = \frac{{{Q_{{\rm{zv}}}}}}{{N{D^3}}}或{N_{\rm{q}}} = \frac{{{Q_{{\rm{rv}}}}}}{{N{D^3}}} $ | (5) |
泵送效率η,即流量准数与功率准数的比值(Nq/Np),是表征搅拌桨性能的一个重要参数。泵送效率高,说明在相同的功率输入下,该桨的循环性能更强[13-14]。
2 数值模拟计算 2.1 数学模型使用Eulerian-Eulerian多相流模型来模拟固-液两相体系,分散相和连续相均被处理为相互贯穿的连续介质,共享同一压力场。每一相在流动过程中均遵守质量守恒方程、动量守恒方程以及能量守恒定律。
相m的质量守恒方程:
| $ \frac{{\partial \left( {{\alpha _m}{\rho _m}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\alpha _m}{\rho _m}\overrightarrow {{u_m}} } \right) = 0 $ | (6) |
式(6)中:αm为相m的体积分数,ρm为相m的密度,kg·m-3;
相m的动量守恒方程:
| $ \begin{array}{l} \frac{{\partial \left( {{\alpha _m}{\rho _m}\overrightarrow {{u_m}} } \right)}}{{\partial t}} + \nabla \cdot \left( {{\alpha _m}{\rho _m}\overrightarrow {{u_m}} \overrightarrow {{u_m}} } \right) = \\ - {\alpha _m}\nabla p + \nabla \cdot {\overline{\overline \tau } _{{\rm{eff, }}\mathit{m}}} + \overrightarrow F + {\alpha _m}{\rho _m}\overrightarrow g \end{array} $ | (7) |
式(7)中:p为两相共享的压力(Pa),
相间的滑移产生了相间曳力,对于固-液两相流相间曳力
| $ {\overrightarrow F _{{\rm{sl}}}} = - {\overrightarrow F _{{\rm{ls}}}} = \frac{3}{4}{\rho _1}{\alpha _1}{\alpha _{\rm{s}}}\frac{{{C_{{\rm{D}},{\rm{sl}}}}}}{{{d_{\rm{s}}}}}\left| {\overrightarrow {{u_{\rm{s}}}} - \overrightarrow {{u_{\rm{l}}}} } \right|\left( {\overrightarrow {{u_{\rm{s}}}} - {{\vec u}_{\rm{l}}}} \right) $ | (8) |
式(8)中:
| $ \frac{{{C_{{\rm{D, sl}}}} - {C_{{\rm{D, 0}}}}}}{{{C_{{\rm{D, 0}}}}}} = 8.671 \times {10^{ - 4}}{\left( {\frac{{{d_{\rm{s}}}}}{\lambda }} \right)^3} $ | (9) |
式(9)中:λ是Kolmogoroff微观尺度,m,其定义式为:
| $ \lambda = {\left( {\frac{{v_1^3}}{\varepsilon }} \right)^{0.25}} $ | (10) |
式(10)中:νl为液相运动黏度,m2·s-1;ε为能量耗散率,m2·s-3。
CD, 0为静止流体中的曳力系数,计算式为:
| $ {C_{{\rm{D, 0}}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{24}}{{\mathit{R}{\mathit{e}_s}}}\left( {1 + 0.15\mathit{Re}_s^{0.687}} \right), }&{\mathit{R}{\mathit{e}_s}\;\; < 1000}\\ {0.44, }&{\mathit{R}{\mathit{e}_s}\;\; \ge 1000} \end{array}} \right. $ | (11) |
式(11)中:Res为颗粒雷诺数,其定义式为:
| $ R{e_{\rm{s}}} = \frac{{{d_{\rm{s}}}\left| {\overrightarrow {{u_{\rm{s}}}} - \overrightarrow {{u_{\rm{l}}}} } \right|}}{{{v_1}}} $ | (12) |
采用CFD软件Ansys Fluent 15.0进行模拟,数值模拟时搅拌槽结构和操作条件与实验条件一致。搅拌桨的旋转采用多重参考系(MRF)实现。使用k-ε湍流模型进行稳态流场模拟,近壁区选择标准壁面函数。使用Eulerian-Eulerian多相流模型来模拟固-液两相体系,多相湍流的封闭模型选择Mixture模型,即使用混合物的特性来求解湍流动能和耗散的输运方程,压力速度的耦合采用相耦合的SIMPLE算法。
模拟中选取整个搅拌槽作为计算域,包含搅拌桨的旋转区域采用四面体网格划分,静止区域采用六面体网格划分。网格密度对计算结果影响较大,网格越精密,计算结果越精确,但是过高的网格密度所需计算时间较长,因此需要进行网格无关性测试,得到合适的网格精度。
本研究以HFT搅拌桨为例,考察了3种不同的网格数量对液相速度分量以及湍流动能的影响,grid1到grid3网格总数分别为498 759、1 191 282和1 908 156。图 3为网格总数为1 191 282(即grid 2)时,HFT搅拌桨操作下的平底圆柱形搅拌槽的网格划分示意图。由于桨叶区以外的区域可以较容易地实现网格无关性,因此这里仅对桨叶附近区域的网格无关性进行探讨。图 4比较了在不同网格密度下预测的液相径向速度分量和湍流动能的分布(N=400 r/min,r=0.054 m),其中utip为桨尖速度(utip=πDN)。从图 4可以看到,采用grid2和grid3的模拟结果几乎接近,因此选用grid2对HFT搅拌桨操作下的平底圆柱形搅拌槽进行模拟。由于搅拌桨构型的差异,对于不同的搅拌桨最终使用的网格数也存在差异。RDT桨使用的网格数为1 267 575,PBTD桨的网格数为1 237 590。此外,对于椭圆底结构的搅拌槽,网格总数也会随着槽底结构变化而变化。

|
| 图 3 网格划分示意图 Fig.3 Details of computational grids |
| |

|
| 图 4 流场网格无关性计算结果 Fig.4 Comparison of simulation results for three different grids |
| |
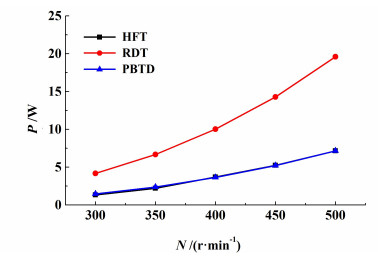
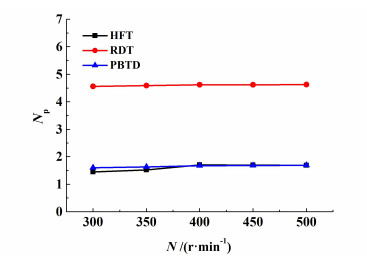
3种搅拌桨在不同转速下通过轴上扭矩法测量得到的功率如图 5所示。可以看出,3种桨的搅拌功率均随着搅拌转速的增加而增加。在相同搅拌转速下,PBTD桨和HFT桨功耗相近,RDT桨功耗最大,大约是PBTD桨和HFT桨搅拌功耗的3倍。图 6为3种桨分别在不同转速下计算得到的功率准数。从图 6中可以看到,当搅拌转速从300 r/min增加到500 r/min时,3种桨的功率准数都趋于平稳。RDT桨的功率准数趋近于4.7,与Nouri等[16]研究结果基本一致。PBTD桨的功率准数稳定在1.7左右,与Armenante等[17]研究结果一致。新型HFT桨的功率准数与PBTD桨的功率准数相近。
|
| 图 5 转速对功率的影响 Fig.5 Effect of impeller rotational speed on power consumption |
| |
|
| 图 6 转速对功率准数的影响 Fig.6 Effect of impeller rotational speed on power number |
| |
此外,对3种搅拌桨进行CFD数值模拟,得到各搅拌桨的功率准数和流量准数如表 2所示。从表 2的数值模拟结果可以看出,3种搅拌桨的功率准数模拟值与实验值基本一致。此外,RDT、PBTD和HFT桨的流量准数Nq和泵送效率η依次增大,表明HFT桨的泵送能力最强。
| 桨型 | 模拟结果 | 实验数据 | ||
| 功率准数Np | 流量准数Nq | η | 功率准数Np | |
| RDT | 4.55 | 0.68 | 0.15 | 4.7 |
| PBTD | 1.68 | 0.69 | 0.41 | 1.7 |
| HFT | 1.67 | 0.76 | 0.46 | 1.7 |
| 注:η为Nq/Np。 | ||||
为体现颗粒在搅拌槽内的分布状况,以红色固体颗粒(粒径ds=2.00 mm,密度ρs=2816.67 kg·m-3)作为固相,在搅拌槽中分别用3种桨进行固体颗粒悬浮状况的分析。固相体积分数αsv为0.01,桨离底高度C=T/4。图 7为不同转速条件下固体颗粒在搅拌槽内的悬浮状况。图 8为y=0平面上,数值模拟得到的连续相速度矢量图和速度分布云图。由于3种搅拌桨的安装位置较低,因此靠近液面附近的流体速度较低。

|
| 图 7 不同转速下固体颗粒悬浮状况 Fig.7 Distribution of solid particles at different rotational speeds |
| |

|
| 图 8 连续相速度矢量图和速度分布云图(m·s-1) Fig.8 Vector and contour plots of the continuous phase velocityes(m·s-1) |
| |
RDT桨为径向流搅拌桨,如图 8a)所示,其产生的径向流首先撞击壁面,然后向上或向下运动。向下运动后撞击搅拌槽底部,又重新回到中心处,与文献[18]描述一致。从图 7中可以看出,N=300 r/min时,颗粒在流体的推动下,被扫向槽底中心区域,并聚集在槽底桨叶下方区域;随着搅拌转速增加到N=500 r/min时,也只有少数固体颗粒实现离底悬浮。在固-液搅拌槽中,当所有固体颗粒均处于运动中,且没有任何颗粒在槽底停留超过1~2 s时的最小搅拌转速即为临界搅拌转速NJS[3]。Zwietering[3]用目测法得出了确定NJS的经验关联式:
| $ {N_{{\rm{JS}}}} = S\frac{{v_1^{0.1}d_{\rm{s}}^{0.2}{{\left( {g\Delta \rho /{\rho _1}} \right)}^{0.45}}{X^{0.13}}}}{{{D^{0.85}}}} $ | (13) |
式(13)中:S为与搅拌槽结构和搅拌桨型式有关的无因次常数,Δρ为固相与液相的密度差,kg·m-3,X为固相质量分数。
对于ds=2.00 mm的固体颗粒,按照公式(13)计算得到的临界离底悬浮搅拌转速高达1 089r/min。因此,在此固-液体系考察的转速范围内,RDT桨很难使固体颗粒实现离底悬浮。
PBTD为轴向流搅拌桨,其产生的流体先碰撞槽底,然后至槽壁并产生向上移动的液体壁射流,可将固体颗粒沿槽底边缘提升[19]。从图 7可看出,低转速N=300 r/min时,颗粒主要分散在槽底四周,桨叶下方基本无颗粒,极少数颗粒从四周提升;N=400 r/min时,边缘浮起粒子增多,且有一部分颗粒在流体推动下进入搅拌桨下方区域,难以实现离底悬浮;当转速增加到N=500 r/min时,挡板及槽底边缘处聚集的颗粒减少。对于HFT桨,从图 8b)和图 8c)可看出,其流型接近PBTD桨,流体从桨叶排出后,向下流动遇到槽底及釜壁会形成大循环区,此外,在搅拌桨与槽底之间还存在1个较小的二次诱导循环区,且该区域流动速度大于PBTD桨下方产生的二次诱导循环区内流体的流动速度。从图 7可看出,不同转速下,HFT桨操作下的固体颗粒悬浮状况与PBTD桨操作下的分布特征相似,在转速较低时,固体颗粒倾向于聚集在槽底四周,随着搅拌转速的增加,粒子不断沿搅拌槽壁面提升。但与PBTD桨相比,HFT桨操作下,有更多的固体颗粒在流体的带动下实现离底悬浮。
3.2.2 颗粒轴向速度分布王峰等[20]利用CFD研究RDT桨操作的固-液搅拌槽离底悬浮转速时指出,在搅拌槽底面附近,液流自槽壁至槽中心流动,因此,固体颗粒容易在RDT搅拌桨下方搅拌槽中央位置堆积。他还提出紧贴搅拌槽底面中央位置网格内分散相的轴向速度为正值时,即可认为固体颗粒完全悬浮。基于此,本研究也通过固-液搅拌槽内流体动力学特性的数值模拟,比较了3种搅拌桨在不同搅拌转速下搅拌槽底面附近网格内固体颗粒的轴向速度沿径向的分布特征。如图 9所示,对于直径2.00 mm的固体颗粒,搅拌转速从300 r/min增加到500 r/min时,RDT桨操作条件下固体颗粒的轴向速度几乎均为负值,说明在转速范围内,固体颗粒容易沉积在槽底;而对于HFT桨,300 r/min时,槽底附近较大范围内固体颗粒的轴向速度高于PBTD桨和RDT桨,且随着转速增加,搅拌桨正下方区域内轴向速度逐渐增加,表明其对颗粒的提升能力越强,即越容易使固体颗粒悬浮起来进入主体流区。

|
| 图 9 不同搅拌转速下分散相的轴向速度分布 Fig.9 Axial velocity distribution of the dispersed phase at different rotational speeds |
| |
此外,对于实验中使用的平底型固-液搅拌槽,使用PBTD桨和HFT桨时,固体颗粒均倾向于聚集在槽底四周。冯连芳等[13]指出槽底形状和桨叶的配合可以消除槽底与槽壁交接处的颗粒沉积死角。如图 8和图 9所示,由于HFT桨的正下方区域内流体湍动强于PBTD桨,有利于固体颗粒的提升,因此可将搅拌槽的平底改为标准椭圆底。图 10给出了标准椭圆底搅拌槽y=0平面上固相轴向速度以及相含率分布的数值模拟结果,从图 10中可以看到HFT搅拌桨在椭圆底搅拌槽内产生的流动可以有效带动固体颗粒实现离底悬浮,而PBTD桨操作下颗粒沉积在搅拌桨正下方,悬浮效率远差于HFT桨。

|
| 图 10 y=0平面上分散相轴向速度(usz)和无量纲固相体积分数(αs/αsv)分布图 Fig.10 Distribution of usz and αs/αsv at y=0 plane |
| |
因此,通过对图 7~图 10的实验和数值模拟结果分析表明,当搅拌桨离底高度C=T/4时,3种搅拌桨对颗粒的悬浮效果依次为:HFT>PBTD>RDT。
4 结论通过实验测量和数值模拟的方法,研究了固-液搅拌槽内不同搅拌桨(RDT桨、PBTD桨和HFT桨)的功耗、泵送能力和对固体颗粒的悬浮效果,得到结论:
1) 在相同转速下,HFT桨的功耗与PBTD桨的功耗接近,而RDT桨的功耗最大,大约是HFT和PBTD桨功耗的3倍。3种搅拌桨的功率准数Np的模拟值与实验值基本一致。其中,HFT桨的流量准数Nq和泵送效率η最大,表明HFT桨的泵送能力最强。
2) HFT桨的流型与PBTD桨接近,二者的共同点在于流体从桨叶排出后,向下流动遇到槽底及釜壁会形成大循环区。
3) 在考察的转速范围内,RDT桨操作下,颗粒聚集并堆积在桨的正下方区域,难以实现离底悬浮;相比于PBTD桨,HFT桨能带动更多的固体颗粒实现离底悬浮。此外,从颗粒的轴向速度分布数值模拟结果可以发现,HFT桨与标准椭圆底搅拌槽配合对颗粒的提升能力最强。综合实验和模拟结果,当离底高度C=T/4时,HFT桨对固体颗粒的悬浮效果最好。
符号说明:
B—挡板宽度,mm;
C—桨离底高度,mm;
CD, 0—静止流体中的曳力系数;
CD, sl—固-液相间曳力系数;
D—搅拌桨直径,mm;
d—搅拌桨轮毂直径,mm;
ds—颗粒直径,mm;
H—液面高度,mm;
k—湍流动能,m2·s-2;
l—搅拌桨桨叶长度,mm;
M—扭矩,N·m;
m—物相,m=s, l时分别代表固相和液相;
N—搅拌桨转速,r/min;
NJS—临界搅拌转速,r/s;
Np—功率准数;
Nq—流量准数;
P—搅拌桨消耗功率,W;
p—压力,Pa;
Qrv—径向液体流量,m3·s-1;
Qzv—轴向液体流量,m3·s-1;
Res—颗粒雷诺数;
r—径向距离,m;
S—与搅拌槽结构和搅拌桨型式有关的无因次常数;
T—搅拌槽直径,mm;
usz—固相轴向速度,m·s-1;
ulr—液相径向速度,m·s-1;
ulz—液相轴向速度,m·s-1;
ulθ—液相切向速度,m·s-1;
utip—搅拌桨桨尖速度,m·s-1;
w—搅拌桨桨叶宽度,mm;
X—固相质量分数;
z—轴向高度,m;
z1—桨叶最低点高度,m;
z2—桨叶最高点高度,m。
希腊字母:
αm—相m的体积分数;
αs—固相体积分数;
αsv—固相平均体积分数;
δ—搅拌桨叶片厚度,mm;
ε—能量耗散率,m2·s-3;
η—泵送效率,Nq/Np;
λ—Kolmogoroff微观尺度,m;
νl—液相运动黏度,m2·s-1;
ρl—液相密度,kg·m-3;
ρs—固相密度,kg·m-3;
Δρ—固相与液相的密度差(ρs-ρl),kg·m-3;
下角标:
l—液相;
s—固相;
0—流体静止状态;
1—测量最低点;
| [1] |
程荡, 程景才, 雍玉梅, 等. 多相搅拌槽内宏观混合研究进展[J]. 化学工程, 2011, 39(6): 59-64. Cheng Dang, Cheng Jingcai, Yong Yumei. Research progress of macromixing in multiphase stirred vessels[J]. Chemical Engineering(China), 2011, 39(6): 59-64. (in Chinese) |
| [2] |
王振松, 李良超, 黄雄斌. 固-液搅拌槽内槽底流场的CFD模拟[J]. 北京化工大学学报:自然科学版, 2005, 32(4): 5-9. Wang Zhensong, Li Liangchao, Huang Xiongbin. CFD modeling of liquid velocity in solid-liquid stirred tanks[J]. Journal of Beijing University of Chemical Technology, 2005, 32(4): 5-9. (in Chinese) |
| [3] |
Zwietering T N. Suspending of solid particles in liquid by agitators[J]. Chemical Engineering Science, 1958, 8(3/4): 244-253. |
| [4] |
Nienow A W. Suspension of solid particles in turbine agitated baffled vessels[J]. Chemical Engineering Science, 1968, 23(12): 1453-1459. |
| [5] |
来永斌, 杨敏官. 无挡板搅拌槽内固液悬浮的试验[J]. 江苏大学学报:自然科学版, 2010, 31(3): 309-313. Lai Yongbin, Yang Minguan. Experiment on solid-liquid suspension in unbaffled stirred tank[J]. Journal of Jiangsu University: Natural Science Edition, 2010, 31(3): 309-313. (in Chinese) |
| [6] |
Wu J, Zhu Y, Pullum L. Impeller geometry effect on velocity and solids suspension[J]. Chemical Engineering Research and Design, 2001, 79(8): 989-997. |
| [7] |
Wang S, Boger D V, Wu J. Energy efficient solids suspension in an agitated vessel-water slurry[J]. Chemical Engineering Science, 2012, 74: 233-243. |
| [8] |
钟丽, 黄雄斌, 贾志刚. 固-液搅拌槽内颗粒离底悬浮临界转速的CFD模拟[J]. 北京化工大学学报:自然科学版, 2003, 30(6): 18-22. Zhong Li, Huang Xiongbin, Jia Zhigang. CFD modeling of solids just-suspended impeller speed in stirred tanks[J]. Journal of Beijing University of Chemical Technology, 2003, 30(6): 18-22. (in Chinese) |
| [9] |
Micale G, Montante G, Grisafi F, et al. CFD simulation of particle distribution in stirred vessels[J]. Chemical Engineering Research and Design, 2000, 78(3): 435-444. |
| [10] |
Montante G, Micale G, Magelli F, et al. Experiments and CFD predictions of solid particle distribution in a vessel agitated with four pitched blade turbines[J]. Chemical Engineering Research and Design, 2001, 79(8): 1005-1010. |
| [11] |
Gu D Y, Liu Z, Xie Z, et al. Numerical simulation of solid-liquid suspension in a stirred tank with a dual punched rigid-flexible impeller[J]. Advanced Powder Technology, 2017, 28(10): 2723-2734. |
| [12] |
杨超, 段晓霞, 冯鑫, 等.一种折叶桨搅拌装置: CN, 108159951A[P].2018-06-15 Yang Chao, Duan Xiaoxia, Feng Xin, et al. A folded impeller mixing device: CN, 108159951A[P]. 2018-06-15(in Chinese) |
| [13] |
王凯, 冯连芳. 混合设备设计[M]. 北京: 机械工业出版社, 2000. Wang Kai, Feng Lianfang. Hybrid equipment design[M]. Beijing: Mechanical Industry Press, 2000. (in Chinese) |
| [14] |
孙东东, 郑志永, 李晶. 基于CFD模拟的新型径向流搅拌桨设计[J]. 过程工程学报, 2017, 17(4): 677-683. Sun Dongdong, Zheng Zhiyong, Li Jing, et al. Design of a novel radial flow impeller based on CFD simulation[J]. The Chinese Journal of Process Engineering, 2017, 17(4): 677-683. (in Chinese) |
| [15] |
Brucato A, Grisafi F, Montante G. Particle drag coefficients in turbulent fluids[J]. Chemical Engineering Science, 1998, 53(18): 3295-3314. |
| [16] |
Nouri J M, Hockey R M. Power number correlation between Newtonian and non-Newtonian fluids in a mixing vessel[J]. Journal of Chemical Engineering of Japan, 1998, 31(5): 848-852. |
| [17] |
Armenante P M, Mazzarotta B, Chang G M. Power consumption in stirred tanks provided with multiple pitched-blade turbines[J]. Industrial & Engineering Chemistry Research, 1999, 38(7): 2809-2816. |
| [18] |
Mollaabbasi R, Mohebbi Najmabad J. Experimental investigation and optimization of solid suspension in non-Newtonian liquids at high solid concentration[J]. Journal of Applied Fluid Mechanics, 2016, 9(6): 1907-1914. |
| [19] |
Kramers H, Baars G M, Knoll W H. A comparative study on the rate of mixing in stirred tanks[J]. Chemical Engineering Science, 1953, 2(1): 35-42. |
| [20] |
Wang F, Mao Z, Shen X. Numerical study of solid-liquid two-phase flow in stirred tanks with Rushton impel-ler-(Ⅱ) Prediction of critical impeller speed[J]. Chinese Journal of Chemical Engineering, 2004, 12(5): 610-614. |
 2020, Vol. 37
2020, Vol. 37





