2. 中国石油化工股份有限公司青岛安全工程研究院, 山东 青岛 266000
2. Sinopec Research Institute of Safety Engineering, Shandong Qingdao 266000, China
近年来,化学反应事故时常发生,造成的生命和财产损失不计其数,涉及的领域包括医药、涂料以及石油化工等,引起了国家对化工安全生产的高度重视。化学反应热失控是反应事故发生的主要原因,如何预防反应热失控、保证化工安全生产成为专家学者一直关注的问题。
预防反应事故发生有3道防线。第1道防线是设计阶段选择安全的操作条件;第2道防线是运行阶段采用响应灵敏的预警探测系统; 第3道防线是反应失控后能采取迅速有效的应急措施[1]。选择安全的操作条件一直是国内外研究的重点,这方面的研究包括参数敏感性研究[2-6]、本质安全操作条件[7-9]、安全界限图法[10]和失控情景分析法[11]等。相比于参数敏感性研究,安全界限图和失控情景分析法不需要获取动力学信息,能够节省获取大量准确动力学信息的时间和资金,突破参数敏感性发展的局限[1]。尽管发展了很多判据和方法帮助选择合适的操作条件,但是即使在安全反应条件下运行反应也不能完全避免反应事故的发生。当反应条件处于参数敏感区时,反应过程中的小小偏差,如果不及时采取措施纠正,都可能引起反应热失控,甚至演变成严重的反应事故[12]。如果有一套反应灵敏、预测准确的在线探测系统及时预警反应热失控,并针对偏差采取相应措施及时纠正,反应事故就能被避免,因此有必要发展响应灵敏的在线预警探测系统预判[1, 13]反应热失控。
在线预警检测系统有3部分构成:获取工艺数据的接口(监控)、区别危险情况和非危险情况的判据(检测)、诱发报警的程序(诊断和评估)。其中,能够及时准确区分危险和非危险情况的判据一直以来是在线检测预警系统发展的瓶颈[14]。本论文系统研究了在线预警探测系统反应热失控判据,包括限值检查判据、热平衡判据、基于模型的方法、散度判据和神经网络方法;同时,分析比较了各种方法的优缺点和应用情况,并对未来的发展提出了展望。
1 限值检查判据Hub[15]是第1个研究在线失控判据的学者,并且和Jones[16]描述了6种方法,分别是温度判据(T>Tlim)、温度对时间的一阶导数判据[dT/dt> (dT/dt)lim]、二阶导数判据[d2T/d2t>(d2T/d2t)lim]、“配方”检查、热平衡判据以及基于模型的方法。前3种判据是最简单的判据,其通过检测反应系统的参数——温度,并与设定值的大小比较来判断反应是否失控。除了温度参数,也可以通过检测其它的参数,例如压力、浓度等,来判断反应的失控情况。Marco等[17]通过探测2种过氧化物分解过程液相中的温度、气相压力以及利用在线质谱仪探测气相中分解产物的浓度,比较了温度测量、压力测量和气相产物浓度测量对于判断失控反应的灵敏性。
“配方”检查用的很少,该方法类似于危险与可操作性分析(Hazard and Operability Study,HAZOP),但较之简单。对于一个化学工艺,每次或每一阶段都可以指定一些可测量的变量、物理特性、设备各部分(如泵、阀门和电机)的状态或位置,这些参数构成了工艺的“配方”,可以用于设定报警的初始值;通过检查“配方”参数偏差,就能提前预防工艺危害。该方法操作比较繁琐,因此使用的较少。
2 热平衡判据热平衡判据在工业中使用的较广,这是因为限值的设定和初始变量的指定,需要对工艺十分了解以及专家的判断,适用于预测能够预知的危险,而对于工艺中常常发生的无法预知的危险却不适用[16]。依据热平衡发展的失控判据[14, 18]弥补了这个缺陷,其表达式如式(1):
| $ {q_{\rm{G}}} = \frac{{{\rm{d}}{Q_{\rm{R}}}}}{{{\rm{d}}t}} = \rho V{C_p}\frac{{{\rm{d}}T}}{{{\rm{d}}t}} + UA\left( {T - {T_{\rm{c}}}} \right) $ | (1) |
式(1)中qG为放热速率;QR为放热量;ρ为反应液密度;V为反应液体积;Cp为比热容;T为反应温度;t为反应时间;U为传热系数;A为传热面积;Tc为夹套温度。
当
| $ \begin{array}{l} 当\;\frac{{{\rm{d}}{Q_{\rm{R}}}}}{{{\rm{d}}t}} > 0\;时,则:\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{{\rm{d}}^2}T}}{{{{\rm{d}}^2}t}} > 0\;且\;\frac{{{\rm{d}}\left( {T - {T_{\rm{c}}}} \right)}}{{{\rm{d}}t}} > 0 \end{array} $ | (2) |
当反应温度T和夹套温度Tc满足上面的条件时,发生反应热失控。这种方法只要测定反应体系的温度就能预判反应热失控,不再依赖于人的知识和判断,并能预测未知的危险。该方法在使用时必须依赖于导数平滑的曲线,这是因为反应温度不可避免地会受到正常工艺状态和参数测量设备的波动以及随机误差等影响,很难判断结果是不是大于0,常常出现假报警[19]。因此,一方面要保证方法的可靠性,避免发生假报警;另一方面又要保证方法的灵敏度,能够及时预测反应失控的发生。敏感性和可靠性折中问题常常是失控判据发展的一个难题。为了保证可靠性,降噪是研究人员首先想到的方法。降噪的方法有低采样速率下求导、平均导数值和使用自适应滤波器。Spence等[19]利用绝热失控数据分析了这3种降噪方法,证实了热平衡判据预判反应热失控的可行性,结果同时表明使用滤波器的方法在降噪和敏感性方面都优于其它2种降噪方法,但这3种降噪方法仍然依赖于噪声的水平。
3 基于模型的判据基于模型的方法不同于以上所述的方法。上述的方法是通过测量工艺中的单一或多个参数,例如温度、压力或者浓度,只能表征工艺的部分状态,而反应器的行为是对整个工艺状态非线性敏感的,当有小小的波动发生时,如果只依赖于这几个测量的参数,当出现反应失控前兆时,预警可能为时已晚。如果建立出工艺的数学模型,就能通过测量的参数来重构工艺的整个状态。卡尔曼滤波器满足了这个需求。
卡尔曼滤波器是由Kalman 60年[20-21]代提出,是一种最优化自回归数据处理算法。卡尔曼滤波器由5个方程构成,分为时间更新公式和测量更新公式(如图 1所示)。时间更新公式负责根据前一时刻的状态预测当前的状态和协方差以获得下一时刻状态的先验估计值;测量更新公式负责反馈,是将测量值合并到先验估计值以获得改进的后验估计值[22]。卡尔曼滤波器通过不断预测、修正系统状态,获得最小偏差逼近未来真实状态函数的估计值。

|
| 图 1 Kalman滤波器模型 Fig.1 The model of Kalman filtering |
| |
King等[23]使用多个滤波器来求解状态空间模型;这些模型包括正常模式和故障模式,故障模式包括反应失控、冷却失效等。通过计算属于某个模式的最大概率来预测系统状态属于正常状态或故障状态。一般状态空间模型结构如式(3)
| $ {M^i}:\left\{ {\begin{array}{*{20}{l}} {{x^i}\left( t \right) = {f^i}\left[ {{x^i}\left( t \right),u\left( t \right),{\theta ^i},t} \right] + {G^i}\left[ {{x^i}\left( t \right),{\theta ^i},t} \right]{w^i}\left( t \right)}\\ {{y^i}\left( {{t_k}} \right) = {h^i}\left[ {{x^i}\left( {{t_k}} \right),{\theta ^i},{t_k}} \right] + v_k^i} \end{array}} \right. $ | (3) |
式(3)中,xi(t)为状态变量;yi(tk)为测量变量;u(t)为操作变量;θi为参数变量;t为时间;tk表示k时刻;wi(t)和vki为噪声。
令:操作变量Uk=(uk, uk-1, …, u1),测量值Yk=(yk, yk-1, …, y1),则:在给定操作变量和测量值的情况下,属于模型Mi的条件概率为:
| $ p\left( {{M^i}|{Y_k},{U_k}} \right) = p\left( {M = {M^i}|{Y_k},{U_k}} \right) $ | (4) |
令uk=g(yk,yk-1,…,y1),则:
| $ p\left( {{M^i}|{Y_k}} \right) = p\left( {M = {M^i}|{Y_k},{U_k}} \right) $ | (5) |
该方法具有很好的预测能力和选择性,但这取决于所建模型的质量;基于模型的判据既是优点,也是缺点,因为需要发展高质量的数学模型往往需要大量的研究[16]。该方法自发展以来得到了广泛的应用,King[24]将此方法用于芳香族化合物的磺化工艺,Chetouan等[25]将扩展卡尔曼滤波器用于冷却温度、搅拌速率以及进料速率突变造成的故障模式识别。李少远等[26]利用卡尔曼滤波器跟踪控制间歇反应过程中的温度并估计出干扰对于系统状态的影响。郑勇[27]将滤波器应用于锂离子电池过充及过放电故障诊断的研究。
4 散度判据 4.1 相空间重构散度判据在简单的单一实验变量和复杂的基于模型的状态空间法之间开辟了一条新的途径。其通过重构系统的相空间,实现了只需要测量单一变量的时间序列来获取整个反应系统的信息[28],这是因为系统的任意一个分量的演化是与之相互作用的其它分量所决定的。混沌系统分析的第一步是相空间重构,并在这个重构的相空间中进行混沌序列的判断、分析与预测。相空间重构方法有导数重构法和坐标延迟法,其中使用最普遍的是坐标延迟法,其关键步骤是确定嵌入维数m和延迟时间τ。确定嵌入维数常用的方法是G-P算法;延迟时间的确定常用的有平均位移法、互信息法和自相关函数法[29]。
4.2 Lyapunov指数判断参数敏感性化学反应器的动态行为具有很高的参数敏感性,系统参数小小的改变也会对反应器的动态行为产生巨大的改变[30]。Strozzil等[31]利用Lyapunov指数来表征间歇反应器的参数敏感性,定义t时刻的Lyapunov指数公式为:
| $ {\lambda _j}\left( t \right) = \frac{1}{t}{\log _2}\frac{{{p_j}\left( t \right)}}{{{p_j}\left( 0 \right)}},j = 1, \cdots ,m $ | (6) |
式(6)中pj(t)表征t时刻第j个椭圆的轴长。
因此t时刻高维相空间椭球体的体积为:
| $ v\left( t \right) = v\left( 0 \right){2^\mu },\mu = \sum\limits_j {{\lambda _j}\left( t \right)t} $ | (7) |
当v(0)=1,则v(t)=2μ,μ是系统参数的函数。
随着相空间椭球体体积的增加,相空间中相邻2点的轨迹会发生分离,由此基于局部Lyapunov指数定义的敏感性如式(8):
| $ {S_\mathit{\Phi }} = \frac{{{\rm{d}}\left( {\max {2^{\left[ {{\lambda _1}\left( t \right) + {\lambda _2}\left( t \right) + \cdots + {\lambda _d}\left( t \right)} \right]t}}} \right)}}{{{\rm{d}}\mathit{\Phi }}} $ | (8) |
式(8)中Φ是与系统敏感性有关的参数。
Strozzil等[32]通过硫酸催化的2-丁醇和丙酸酐酯化反应,证明了Lyapunov指数能够评估间歇反应的稳定性,并且该方法通过重构相空间可以利用直接测量的数据来计算Lyapunov指数,从而实现在线敏感性计算。
4.3 散度和Lyapunov指数的关系对于一个恒温间歇反应器,当t→∞,反应已经结束,反应物的温度等于夹套的温度。此时,相空间的轨迹会到达一个固定点,也就是说对于2个开始临近的点,最终会结束于1个固定点[14]。然而在到达固定点之前,2个点的轨迹可能发生偏离;这就是混沌理论中经常遇到的轨迹散度问题[33]。散度是1个标量,用来描述相空间矢量场的发散程度,其定义式如式(9)[34]:
| $ {\rm div} = \frac{{\delta \left( {\frac{{{\rm{d}}T}}{{{\rm{d}}t}}} \right)}}{{\delta T}} + \sum\limits_i {\frac{{\delta \left( {\frac{{{\rm{d}}{z_i}}}{{{\rm{d}}t}}} \right)}}{{\delta {z_i}}}} $ | (9) |
设能量和质量守恒的常微分方程为:
| $ \frac{{{\rm{d}}x\left( t \right)}}{{{\rm{d}}t}} = F\left[ {x\left( t \right)} \right] $ | (10) |
则:
| $ \begin{array}{*{20}{c}} {{\rm div}F\left[ {x\left( t \right)} \right] = \frac{{\delta {F_1}\left[ {x\left( t \right)} \right]}}{{\delta {x_1}\left( t \right)}} + \frac{{\delta {F_2}\left[ {x\left( t \right)} \right]}}{{\delta {x_2}\left( t \right)}} + }\\ { \cdots + \frac{{\delta {F_d}\left[ {x\left( t \right)} \right]}}{{\delta {x_d}\left( t \right)}}} \end{array} $ | (11) |
式(11)中x(t)=[x1(t), x2(t), x3(t)…, xd(t)],表示d维的相空间;且F=[F1, …, Fd],F[x(t)]表示Jacobian矩阵的迹,是1条平滑的非线性函数曲线,也就是说函数F[x(t)]对于x存在唯一性。x的初始值为x(0),经过t(t>0)时间之后变为x(t);同样,假定所有的初始条件处于一个特定的领域Г(0),经过t时间之后变为Г(t),根据Liouville定理[14]:
| $ \frac{{{\rm{d}}V\left( t \right)}}{{{\rm{d}}t}} = \int_{\mathit{\Gamma }\left( t \right)} {{\rm div}F\left[ {x\left( t \right)} \right]{\rm{d}}{x_1}\left( t \right) \cdots {\rm{d}}{x_d}\left( t \right)} $ | (12) |
式(12)中V(t)表示Г(t)的体积。
假设d维的体积足够小以至于散度divF(x)相对于V(t)来说是一个常数,那么:
| $ \frac{{{\rm{d}}V\left( t \right)}}{{{\rm{d}}t}} = V\left( t \right){\rm div}F\left[ {x\left( t \right)} \right] $ | (13) |
因此:
| $ \int_0^t {\frac{{{\rm{d}}V\left( \tau \right)}}{{V\left( \tau \right)}}} = \int_0^t {{\rm div}F\left[ {x\left( \tau \right)} \right]{\rm{d}}\tau } $ | (14) |
即:
| $ V\left( t \right) = V\left( 0 \right){e^{\int_0^t {{\rm div}F\left[ {x\left( \tau \right)} \right]{\rm{d}}\tau } }} $ | (15) |
根据式(7)和式(15)得:
| $ \sum\nolimits_j {{\lambda _j}\left( t \right)} = \frac{1}{{\ln 2}} \cdot \frac{1}{t}\int_0^t {{\rm div}F\left[ {x\left( \tau \right)} \right]{\rm{d}}\tau } $ | (16) |
通过重构相空间的散度的计算,就能得到Lyapunov指数的和,并应用到敏感性公式分析,在线判断反应的热失控。即在反应过程中,当div>0,相空间的体积膨胀;
Zaldívar等[35]证实了散度判据的有效性,结果表明散度判据不仅适用于多种类型的反应,如连续、平行、平衡和混合动力学反应,还适用于多种反应类型,如间歇、半间歇和连续反应器;同时也可用于等温、恒温等反应条件判断反应失控。由于散度判据广泛的适用性,其被使用的最多。Bosch等[36]只利用温度参数的测量数据,通过相空间重构技术计算散度判据,预测绝热间歇与半间歇反应热失控;当嵌入2维系统时,能够解决热平衡判据中假报警的情况。之后,Bosch等[37]又比较了测量系统温度和压力参数在线预测反应失控的情况,结果表明相比于测量压力而言,通过测量温度,散度判据能够更好地预测反应失控。只通过温度和压力等参数的测量是假设在所测量的参数分布能够代表整个系统的状态,因此这就牵涉到探测位置对于预测结果的影响。Milewska等[38-39]利用CFD模拟间歇搅拌反应釜搅拌失效引起反应失控的状况,对散度判据进行了修正。郭子超等[40]扩展了散度判据的应用,发展了一种适用任何反应级数的绝热判据。Ampelli等[41]和Alessandra等[42]利用散度判据调查甲基丙烯酸甲酯聚合工艺反应失控时,加入抑制剂对苯二酚和1, 4-苯醌对反应速率的影响。
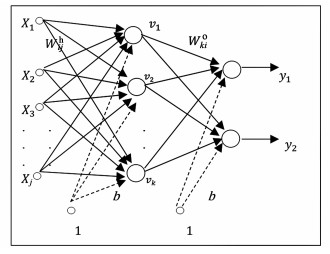
5 神经网络方法(ANNs)非线性现象是化学反应工程的一个普遍特征,为了解决非线性过程的建模和控制问题,特别是面向化学过程的非线性过程建模和控制问题,以及基于模型的控制方案,例如模型预测控制(MPC),人们进行了大量的工作[43]。20世纪70年代以来,研究人员发现了很多可用的工具,其中人工智能领域提出了一种新的方法——神经网络。神经网络可以分为生物神经网络和人工神经网络(ANNs)。本论文所说的是人工神经网络,它是一种大规模并行分布处理器,具有储存经验知识并应用于未来的本能[44];它能够近似任何连续非线性函数,并用于建立非线性过程的数据库经验模型[45];因此,它可以应用于模拟化学反应器的动态行为。其基本结构,如图 2所示。
|
| 图 2 神经网络结构 Fig.2 The structure of neural network |
| |
模型公式为:
| $ y = \delta \left( {\sum\nolimits_{j = 1}^N {{W_j}{x_j}} + b} \right) = \delta \left( {\sum\nolimits_{j = 1}^N {{W_j}{x_j}} } \right) $ | (17) |
式(17)中,xj表示输入量,Wj表示权重,b代表偏置单元为1的权重。δ常指sigmoid函数[46],如式(18)所示;其它的函数很少被用到,如:bipolar sigmoid函数,symmetric logarithmic函数。
| $ \delta \left( z \right) = \frac{1}{{1 + {{\rm{e}}^{ - z}}}} $ | (18) |
式(18)中z表示任意变量。
神经网络的训练:前馈神经网络是一个逼近器,最重要的是通过学习程序优化一套权重数W=(W1, W2, …, Wj),其优化方法是对于1组输入变量X=(x1, x2, …, xj),通过最小化输出结果Y=(y1, y2, …, yj)和实验学习数据D=(d1,d2, …, dj)的残差平方和,其方程如式(19)。
| $ E\left( W \right) = \frac{1}{2}\sum\nolimits_{j = 1}^P {\sum\nolimits_{k = 1}^M {{{\left( {y_k^j - d_k^j} \right)}^2}} } $ | (19) |
式(19)中P是当前学习数据集的个数,M是当前输出神经的数量。
反应失控的判断:以1个二级水解反应为例[44-45]:A+B→2D,其物料守恒公式如式(20)~(22):
| $ \begin{array}{*{20}{l}} {{\rm{A:}}}\\ {\;\;\;\;\;\;\frac{{{\rm{d}}{n_{\rm{A}}}}}{{{\rm{d}}t}} = {\mathit{\Phi }_{{\rm{V}},{\rm{A}}}}{C_{{\rm{A}},{\rm{dos}}}} - rV} \end{array} $ | (20) |
| $ \begin{array}{*{20}{l}} {{\rm{B}}:}\\ {\;\;\;\;\;\;\frac{{{\rm{d}}{n_{\rm{B}}}}}{{{\rm{d}}t}} = - rV} \end{array} $ | (21) |
能量守恒:
| $ \begin{array}{*{20}{c}} {{{\left( {\rho V{C_p}} \right)}_{{\rm{rm}}}}\frac{{{\rm{d}}T}}{{{\rm{d}}t}} = \left( { - \Delta {H_{\rm{B}}}} \right)rV - }\\ {{{\left( {\rho {\mathit{\Phi }_{{\rm{V}},{\rm{A}}}}{C_p}} \right)}_{{\rm{dos}}}}\left( {T - {T_{{\rm{dos}}}}} \right) - \left( {UA} \right)\left( {T - {T_{\rm{c}}}} \right)} \end{array} $ | (22) |
式(22)中:nA、nB为A、B的物质的量;ΦV, A为A的进料速率;CA, dos为A的进料浓度;r为反应速率;V为体积;ρ为密度;Cp为比热容;T为反应温度;Tdos为进料温度;ΔHB为摩尔反应焓;U为传热系数;A为传热面积;Tc为夹套温度。
目标温度:
| $ {T_{{\rm{ta}}}} = {T_{\rm{c}}} + \frac{{1.05\Delta {T_{{\rm{ad}}.{\rm{o}}}}}}{{\varepsilon \left[ {Wt\left( {1 + \varepsilon \theta } \right) + {R_{\rm{H}}}} \right]}} $ | (23) |
式(23)中ΔTad.o为绝热温升;ε为反应物体积比;Wt为Westerterp数;θ为无量纲时间;RH为热熔比。
定义F(t)=[T(t)-Tta(t)],F(t)用来量化真实反应器温度轨迹与失控状态的距离;当F(t) < 0, 反应处于安全状态; 当F(t)>0,反应失控。
令输入信号I如下:
| $ \begin{array}{*{20}{c}} {I = \left[ {T\left( {k - \Delta t{K_{\rm{T}}}} \right), \cdots ,T\left( {k - \Delta t} \right),T\left( k \right),} \right.}\\ {{T_{\rm{c}}}\left( {k - \Delta t{K_{\rm{T}}}} \right), \cdots ,{T_{\rm{c}}}\left( {k - \Delta t} \right),{T_{\rm{c}}}\left( k \right),}\\ {{T_{{\rm{dos}}}}\left( {k - \Delta t{K_{\rm{T}}}} \right), \cdots ,{T_{{\rm{dos}}}}\left( {k - \Delta t} \right),{T_{{\rm{dos}}}}\left( k \right),}\\ {\left. {{\mathit{\Phi }_{{\rm{V}},{\rm{A}}}}\left( {k - \Delta t{K_{\rm{T}}}} \right), \cdots ,{\mathit{\Phi }_{{\rm{V}},{\rm{A}}}}\left( {k - \Delta t} \right),{\mathit{\Phi }_{{\rm{V}},{\rm{A}}}}\left( k \right)} \right]} \end{array} $ | (24) |
式(24)中,k为迭代数;KT为步长。
监测热失控的神经网络就能够近似量化真实反应器温度和热失控状态温度轨迹距离函数,即:
| $ \begin{array}{*{20}{c}} {F\left( t \right) = \left[ {T\left( t \right) - {T_{{\rm{ta}}}}\left( t \right)} \right] = }\\ {\psi \left[ {k,E,\left( { - \Delta {H_{\rm{A}}}} \right),{{\left( {UA} \right)}_0},{V_{{\rm{B}}0}},{\mathit{\Phi }_{{\rm{V}},{\rm{A}}}},{T_{\rm{c}}},{T_{{\rm{dos}}}},t} \right]} \end{array} $ | (25) |
对于已知反应反应釜和反应体系,k、活化能E、(-ΔHB)和(UA)0是常数,所以:
| $ F\left( t \right) = \left[ {T\left( t \right) - {T_{{\rm{ta}}}}\left( t \right)} \right] = = \psi \left( {{\mathit{\Phi }_{{\rm{V}},{\rm{A}}}},{T_{\rm{c}}},{T_{{\rm{dos}}}},t} \right) $ | (26) |
其输出结果为:
| $ O = \left[ {F\left( {k + \Delta t} \right),F\left( {k + 2\Delta t} \right), \cdots ,F\left( {k + {K_{\rm{F}}}\Delta t} \right)} \right] $ | (27) |
在已知过去和现在T、Tc、Tdos和ΦV, A的情况下,神经网络根据输出变量来预测反应器真实温度轨迹与失控状态的距离来判断反应失控。
Molga[47-48]利用模拟实验证实了神经网络方法的有效性,并比较了热平衡判据、散度判据和神经网络方法,结果表明散度判据是最有效的方法,神经网络判据的敏感性还有待提高。目前神经网络还只应用于模拟,其适用范围还有待开发。
6 结论在线预警探测系统是预防反应失控的第2道防线,本论文对几类在线预警探测系统反应失控判据进行了系统的概述与比较,得出以下结论:
1) 限值检测方法和热平衡判据,只需要测量系统的单个和多个状态函数来预判反应热失控;尽管方法简单,但是他们共同存在无法表征整个系统状态的局限。系统整个真实状态的表征是发展失控判据的关键基础,也是未来发展热失控判据的方向。基于模型的方法、散度判据和神经网络方法分别通过状态空间重构、相空间重构以及神经网络模型来重构整个反应器的状态,能够更加准确的表征反应器的真实状态,具有更大的发展应用前景。
2) 敏感性和可靠性的权衡是这些方法共同面临的难题。发展更有效的降噪方法,在保证不发生假报警的基础上,提高方法的敏感性,更加提前的预测反应热失控是未来发展的方向。
3) 在线预警探测系统是假设在具有相应偏差纠正措施的基础之上,因此针对系统的偏差采取何种措施以及第3道防线的发展也尤为重要。
| [1] |
Westerterp K R, Molga E J. Safety and runaway prevention in batch and semibatch reactors:A review[J]. Chemical Engineering Research and Design, 2006, 84(7): 543-552. DOI:10.1205/cherd.05221 |
| [2] |
刘秀玉, 蒋军成. 连续搅拌釜式反应器放热反应失控事故预防[J]. 中国安全科学学报, 2006, 16(11): 140-144. Liu Xiuyu, Jiang Juncheng. Prevention runaway reaction in a CSTR with exothermic reaction[J]. China Safety Science Journal(CSSJ), 2006, 16(11): 140-144. DOI:10.3969/j.issn.1003-3033.2006.11.027 (in Chinese) |
| [3] |
刘秀玉, 蒋军成, 王彦富. 间歇放热反应系统热失控参数敏感性研究[J]. 化学工程, 2008, 36(3): 13-16, 30. Liu Xiuyu, Jiang Juncheng, Wang Yanfu. On parameter sensitivity for thermal runaway in batch reactors[J]. Chemical Engineering(China), 2008, 36(3): 13-16, 30. (in Chinese) |
| [4] |
吕家育, 陈网桦, 陈利平. 某恒温间歇反应的热失控研究[J]. 中国安全科学学报, 2011, 21(4): 121-127. Lv Jiayu, Chen Wanghua, Chen Liping. Research on thermal runaway of certain isoperibolic reaction in batch reactor[J]. China Safety Science Journal, 2011, 21(4): 121-127. DOI:10.3969/j.issn.1003-3033.2011.04.021 (in Chinese) |
| [5] |
江佳佳, 蒋军成, 潘勇. 间歇式放热反应热失控临界参数及热安全性[J]. 南京工业大学学报:自然科学版, 2012, 34(3): 36-40. Jiang Jiajia, Jiang Juncheng, Pan Yong. Thermal runaway critical parameters and thermal safety in batch exothermic reaction[J]. Journal of Nanjing University of Technology:Natural Science Edition, 2012, 34(3): 36-40. (in Chinese) |
| [6] |
江佳佳, 杨建洲, 蒋军成, 等. 间歇式反应系统参数敏感性与热失控临界判据[J]. 中国安全科学学报, 2017, 27(5): 117-121. Jiang Jiajia, Yang Jianzhou, Jiang Juncheng, et al. Parameter sensitivity and critical criterion thermal runaway of batch reaction system[J]. China Safety Science Journal, 2017, 27(5): 117-121. (in Chinese) |
| [7] |
Bai W, Hao L, Guo Z, et al. A new criterion to identify safe operating conditions for isoperibolic homogeneous semi-batch reactions[J]. Chemical Engineering Journal, 2017, 308: 8-17. DOI:10.1016/j.cej.2016.09.041 |
| [8] |
Guo Z, Chen L, Chen W. Development of adiabatic criterion for runaway detection and safe operating condition designing in semibatch reactors[J]. Industrial & Engineering Chemistry Research, 2017, 56(50): 14771-14780. |
| [9] |
Bai W, Hao L, Sun Y, et al. Identification of modified QFS region by a new generalized criterion for isoperibolic homogeneous semi-batch reactions[J]. Chemical Engineering Journal, 2017, 322: 488-497. DOI:10.1016/j.cej.2017.04.042 |
| [10] |
Westerterp K R, Lewak M, Molga E J. Boundary diagrams safety criterion for liquid phase homogeneous semibatch reactors[J]. Industrial & Engineering Chemistry Research, 2014, 53(14): 5778-5791. |
| [11] |
陈利平, 陈网桦, 彭金华, 等. 间歇与半间歇反应热失控危险性评估方法[J]. 化工学报, 2008, 59(12): 2963-2970. Chen Liping, Chen Wanghua, Peng Jinhua, et al. Thermal runaway assessment methods of chemical reactions in batch and semi-batch reactors[J]. Journal of Chemical Industry and Engineering(China), 2008, 59(12): 2963-2970. DOI:10.3321/j.issn:0438-1157.2008.12.001 (in Chinese) |
| [12] |
蒋军成, 江佳佳, 潘勇. 化学放热系统热失控临界判据的研究进展[J]. 化工进展, 2009, 28(11): 1890-1895. Jiang Juncheng, Jiang Jiajia, Pan Yong. Research progress of thermal runaway critical criteria in chemical exothermic system[J]. Chemical Industry and Engineering Progress, 2009, 28(11): 1890-1895. (in Chinese) |
| [13] |
Zaldívar J, Bosch J, Strozzi F, et al. Early warning detection of runaway initiation using non-linear approaches[J]. Communications in Nonlinear Science and Numerical Simulation, 2005, 10(3): 299-311. DOI:10.1016/j.cnsns.2003.08.001 |
| [14] |
Strozzi F, Zaldívar J M, Kronberg A E, et al. On-Line runaway detection in batch reactors using chaos theory techniques[J]. AIChE Journal, 1999, 45(11): 2429-2443. DOI:10.1002/aic.690451116 |
| [15] |
Svensson S. RACKETman, proactive risk identification and assessment methodology for organisational change[M]//Loss Prevention and Safety Promotion in the Process Industries. Elsevier, 2001: 1439-1446
|
| [16] |
Hub L, Jones J D. Early on-line detection of exothermic reactions[J]. Operations Progress, 1986, 5(4): 221-224. DOI:10.1002/prsb.720050408 |
| [17] |
Marco E, Peña J A, Santamaría J. Early detection of runaway reactions in systems with gas evolution using on-line mass spectrometry[J]. Chemical Engineering Science, 1997, 52(18): 3107-3115. DOI:10.1016/S0009-2509(97)00120-6 |
| [18] |
Ni L, Mebarki A, Jiang J, et al. Thermal risk in batch reactors:Theoretical framework for runaway and accident[J]. Journal of Loss Prevention in the Process Industries, 2016, 43: 75-82. DOI:10.1016/j.jlp.2016.04.004 |
| [19] |
Spence J P, Noronha J A. Reliable detection of runaway reaction precursors in liquid phase reactions[J]. Operations Progress, 1988, 7(4): 231-235. DOI:10.1002/prsb.720070407 |
| [20] |
彭丁聪. 卡尔曼滤波的基本原理及应用[J]. 软件导刊, 2009, 8(11): 32-34. Peng Dingcong. Basic principle and application of Kalman filter[J]. Software Guide, 2009, 8(11): 32-34. (in Chinese) |
| [21] |
黄小平. 卡尔曼滤波原理及应用--MATLAB仿真[M]. 北京: 电子工业出版社, 2015.
|
| [22] |
Bishop G, Welch G. An introduction to the Kalman filter[J]. Proc of SIGGRAPH, Course, 2001, 8(27599/23175): 19-33. |
| [23] |
King R, Gilles E D. Multiple filter methods for detection of hazardous states in an industrial plant[J]. AIChE Journal, 1990, 36(11): 1697-1706. DOI:10.1002/aic.690361110 |
| [24] |
King R. Early detection of hazardous states in chemical reactors[M]//Dynamics and Control of Chemical Reactors and Distillation Columns. Elsevier, 1988
|
| [25] |
Chetouani Y, Mouhab N, Cosmao J M, et al. Application of extended Kalman filtering to chemical reactor fault detection[J]. Chemical Engineering Communications, 2002, 189(9): 1222-1241. DOI:10.1080/00986440213877 |
| [26] |
李少远, 崔远. 基于卡尔曼滤波器的间歇反应预测控制[J]. 控制工程, 2009, 16(4): 394-397. Li Shaoyuan, Cui Yuan. Kalman filter based model predictive control for batch reactor[J]. Control Engineering of China, 2009, 16(4): 394-397. DOI:10.3969/j.issn.1671-7848.2009.04.004 (in Chinese) |
| [27] |
郑勇.锂离子电池过充及过放电故障诊断研究[D].西安: 长安大学, 2016 Zheng Yong. Fault diagnosis of overcharge and overdischarge of lithium-ion battery[D]. Xi'an: Changan University, 2016(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10710-1016920839.htm |
| [28] |
韩敏. 混沌时间序列预测理论与方法[M]. 北京: 水利水电出版社, 2007.
|
| [29] |
陈铿, 韩伯棠. 混沌时间序列分析中的相空间重构技术综述[J]. 计算机科学, 2005, 32(4): 67-70. Chen Keng, Han Botang. A survey of state space reconstruction of chaotic time series analysis[J]. Computer Science, 2005, 32(4): 67-70. DOI:10.3969/j.issn.1002-137X.2005.04.021 (in Chinese) |
| [30] |
Bekiaroglou P, Spanomitsios S. Parametric sensitivity in chemical systems[J]. Chemical Engineering and Processing:Process Intensification, 2000, 39(3): 287-288. DOI:10.1016/S0255-2701(99)00081-1 |
| [31] |
Strozzi F, Zaldívar J M. A general method for assessing the thermal stability of batch chemical reactors by sensitivity calculation based on Lyapunov exponents[J]. Chemical Engineering Science, 1994, 49(16): 2681-2688. DOI:10.1016/0009-2509(94)E0067-Z |
| [32] |
Strozzi F, Alo's M A, Zaldi'var J M. A method for assessing thermal stability of batch reactors by sensitivity calculation based on Lyapunov exponents:Experimental verification[J]. Chemical Engineering Science, 1994, 49(24): 5549-5561. DOI:10.1016/0009-2509(94)00302-5 |
| [33] |
Stine R A. Analysis of observed chaotic data[J]. Technometrics, 1997, 39(3): 334-335. DOI:10.1080/00401706.1997.10485127 |
| [34] |
邵辉, 杨亮.基于相空间重构方法的间歇反应器热失控判据研究[C]//石必明, 吕品, 彭伟.第22届全国高校安全工程学术年会论文集.北京: 中国职业安全健康协会, 2010: 37-40
|
| [35] |
Zaldívar J M, Cano J, Alós M A, et al. A general criterion to define runaway limits in chemical reactors[J]. Journal of Loss Prevention in the Process Industries, 2003, 16(3): 187-200. DOI:10.1016/S0950-4230(03)00003-2 |
| [36] |
Bosch J, Strozzi F, Zbilut J P, et al. On-Line runaway detection in isoperibolic batch and semibatch reactors using the divergence criterion[J]. Computers & Chemical Engineering, 2004, 28(4): 527-544. |
| [37] |
Bosch J, Strozzi F, Snee T J, et al. A comparative analysis between temperature and pressure measurements for early detection of runaway initiation[J]. Journal of Loss Prevention in the Process Industries, 2004, 17(6): 389-395. DOI:10.1016/j.jlp.2004.07.003 |
| [38] |
Milewska A, Rudniak L, Molga E. CFD modelling and divergence criterion for safety of chemical reactors[M]//Computer Aided Chemical Engineering. Elsevier, 2005: 259-264
|
| [39] |
Milewska A, Molga E J. CFD simulation of accidents in industrial batch stirred tank reactors[J]. Chemical Engineering Science, 2007, 62(18/19/20): 4920-4925. |
| [40] |
Guo Z C, Bai W S, Chen Y J, et al. An adiabatic criterion for runaway detection in semibatch reactors[J]. Chemical Engineering Journal, 2016, 288: 50-58. DOI:10.1016/j.cej.2015.11.065 |
| [41] |
Ampelli C, Di Bella D, Maschio G, et al. Calorimetric study of the inhibition of runaway reactions during methylmethacrylate polymerization processes[J]. Journal of Loss Prevention in the Process Industries, 2006, 19(5): 419-424. DOI:10.1016/j.jlp.2005.10.003 |
| [42] |
Russo A, Maschio G, Ampelli C. Reaction inhibition as a method for preventing thermal runaway in industrial processes[J]. Macromolecular Symposia, 2007, 259(1): 365-370. DOI:10.1002/masy.200751341 |
| [43] |
Noor R A M, Ahmad Z, Don M M, et al. Modelling and control of different types of polymerization processes using neural networks technique:A review[J]. The Canadian Journal of Chemical Engineering, 2010, 88(6): 1065-1084. DOI:10.1002/cjce.20364 |
| [44] |
Haykin S. Neural networks:A comprehensive founda-tion[M]. NJ: Prentice Hall PTR, 1994.
|
| [45] |
Hertz J, Krogh A, Palmer R G. Introduction to the theory of neural computation[M]. Boca Raton FL: CRC Press, 2018. DOI:10.1201/9780429499661
|
| [46] |
Saxén B, Saxén H. NNDT-A neural network development Tool[M]. Vienna: Springer Vienna, 1995: 325-328.
|
| [47] |
Molga E, Lewak M. Numerical and experimental compari-son of on-line methods for detection of thermal runaway events in batch and semi-batch chemical reactors[C]//Cora Bezuidenhout. 9th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics. Malta: HEFAT, 2012: 1022-1027
|
| [48] |
Molga E. Neural networks for thermal runaway detection in batch and semibatch reactors[C]//Ian David Lockhart Bogle and Michael Fairweather. Proceedings of the 22nd European Symposium on Computer Aided Process Engineering. London: Symposium on Computer Aided Process Engineering, 2012: 1-5
|
 2019, Vol. 36
2019, Vol. 36





