降膜蒸发冷却技术有换热效率高、传热温差小、节约水资源等优点,广泛应用于换热领域中[1-2]。针对平板上的降膜流动,刘梅等[3]通过计算模拟研究了不同因素对波纹板表面降膜流动的影响,指出流体黏度影响液膜厚度和流体速度,表面张力影响液膜的均匀性;Gu等[4]对倾斜波纹板进行了二维模拟计算,计算结果表明小的接触角可以有效提高壁面的润湿程度;Ishikawa等[5]对含有微结构的平板表面降膜流动做了实验和数值分析,提出挡板过高时,液膜容易发生破断,此时可提高雷诺数来控制液膜的连续,因为挡板的存在,液膜表面发生波动,波动的产生有提高液膜传质的可能。为提高降膜流动的换热效率,Fu等[6]通过数值模拟研究了水平振动的圆柱外对流换热效果,振动存在时,换热系数最大可提高13%;申江等[7]通过在吸收式制冷机的底部加装电动振动机,研究了振动频率和振幅对机组性能的强化效果,研究发现,在频率20~30 Hz内,提高传热效果达8%~20%,制冷量提高12%~18%。
对制冷机组加装的振动效果,实际是作用在换热设备上,本研究设想在平板降膜过程中运用振动技术来强化降膜换热效果,并寻求最适宜的振动参数来提高换热。
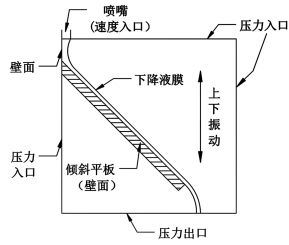
1 数学物理模型 1.1 物理模型液体从喷嘴处(2 mm)流出,并在重力、表面张力和壁面接触角的作用下沿板长方向流动,同时倾斜平板(40 mm)按正弦规律上下振动。
|
| 图 1 物理模型 Fig.1 Physical model |
| |
作如下假设:1)流体为连续不可压缩牛顿流体;2)忽略相变、热辐射和自然对流,仅考虑从壁面到气液界面之间的传热;3)流体物性参数恒定为常数。
体积分数方程:
| $ \frac{{\partial {\alpha _i}}}{{\partial t}} + u \cdot \nabla {\alpha _i} = 0 $ | (1) |
| $ \sum\limits_{i = 1}^2 {{\alpha _i}} = 1 $ | (2) |
式(1)和(2)中αi为第i相的体积分数;u为第i相的速度,m/s。
气液两相系统中密度ρ和黏度μ表示为:
| $ \rho = {\alpha _{\rm{L}}}{\rho _{\rm{L}}} + \left( {1 - {\alpha _{\rm{L}}}} \right){\rho _{\rm{G}}} $ | (3) |
| $ \mu = {\alpha _{\rm{L}}}{\mu _{\rm{L}}} + \left( {1 - {\mu _{\rm{L}}}} \right){\mu _{\rm{G}}} $ | (4) |
质量守恒方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho u) = 0 $ | (5) |
式(5)中ρ由式(3)计算得到。
动量方程:
动量方程通过物性参数ρ和u与体积分数相联系:
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial t}}(\rho u) + \nabla \cdot (\rho uu) = - \nabla p + }\\ {\nabla \left[ {\mu \left( {\nabla u + \nabla {u^{\rm{T}}}} \right)} \right] + \rho g + F} \end{array} $ | (6) |
能量方程:
| $ \frac{\partial }{{\partial t}}(\rho E) + \nabla \cdot [u(\rho E + p)] = \nabla \cdot \left( {{k_{{\rm{eff}}}}\nabla T} \right) + {S_{\rm{e}}} $ | (7) |
其中keff为有效热传导率,W·(m·K)-1,Se为能量方程源项,W·m-2。
振动正弦方程:
| $ S = A\sin (2{\rm{ \mathsf{ π} }}ft) $ | (8) |
式(8)中A为振幅,mm;f为频率,Hz;t为时间,s;S为平板振动的位移,mm,以向上为正;当S=0时,代表平板在平衡位置;当S=A时,代表平板在正方向最大位置;当S=-A时,代表平板在负方向最大位置(负号代表与正方向相反),振动方程由UDF导入计算。
1.3 计算方法与参数设置采用VOF模型,液体区域对边界层网格加密处理,湍流模型为RNG k-ε模型,压力项采用Body Force Weighted算法;压力-速度耦合方程的求解采用PISO算法;动量项采用QUICK格式;体积分数项采用Geo-Reconstruct格式;时间步长在10-6~10-5之间选取;平板倾斜角度为45°,饱和蒸汽压力为0.2 MPa,壁面接触角为21°;表面张力为0.066 2 N·m-1;为了研究振动参数对降膜换热的影响,需要在计算中排除液膜与蒸汽之间的换热对整个换热的影响,在参数设定时,蒸汽为特定温度压力下的饱和蒸汽,水为饱和水,视作液膜与蒸汽无热质交换。
计算参数见表 1。
| 模型 | 温度/ K |
密度/ (kg·m-3) |
黏度/ kg·(m·s)-1 |
| 平板壁面 | 336 | 8 979.0 | |
| 饱和水 | 333 | 983.1 | 4.699×10-4 |
| 饱和水蒸气 | 333 | 0.130 2 | 1.042×10-5 |
为验证计算结果对网格的无关性,对模型进行了3种不同密度的网格划分,网格数量分别为20 579、36 210和48 857,并在相同条件下进行数值模拟。计算结果表明3种网格划分条件下其平板表面平均热流密度分别为15 052、15 007和14 901,相差1%,充分考虑计算精度和迭代时间,文中计算模型采用网格数量为36 210的网格划分方式。
2 结果与分析引入特征长度(υl2/g)1/3[8],局部努塞尔数Nul定义如下:
| $ N{u_1} = \frac{{{h_1}{{\left( {\mathit{\boldsymbol{v}}_1^2/g} \right)}^{1/3}}}}{{{\lambda _1}}} = \frac{{{q_w}{{\left( {\mathit{\boldsymbol{v}}_1^2/g} \right)}^{1/3}}}}{{{\lambda _1}\left( {{T_w} - {T_{{\rm{in}}}}} \right)}} $ | (9) |
定义平均努塞尔数Nu:
| $ Nu = \frac{1}{L}\int_0^L N {u_1}{\rm{d}}x $ | (10) |
式(9)中:hl为壁面到液膜的换热系数,W·(m2·K)-1;λl为液相导热系数,W·(m·K)-1;υl为液相运动黏度,m2·s-1;g为重力加速度,m·s-2;qw为壁面热流密度,W·m-2;Tw和Tin分别是壁面温度和液相进口温度,K;L为平板长度,m;文中所有数据均出自S=0,即平板在平衡位置时。
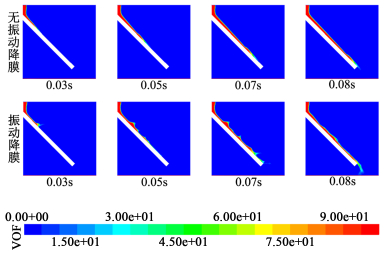
2.1 振动与无振动时液膜对比图 2为流量为0.000 6 m3/s时,不同状态(振动:f=50 Hz,A=2.4 mm或无振动发生),不同时刻的液膜分布情况。
|
| 图 2 不同时刻、不同状态下液膜流动分布 Fig.2 The distribution of liquid film at different time and state |
| |
由图 2可以看出,平板无振动发生时,其表面的液体沿倾斜的平板平滑稳定下降,而当平板振动时,其板面上的液膜发生剧烈的波动,液膜表面波动势必会强化液膜与其他相间的传热传质效果,这与文献[9]中的表述一致;同时对比不同时刻的液膜流动位置可以发现,振动平板上的液体比无振动状态下的液体更早到达平板尾部,即平板的振动效果加速了液膜的下降,这意味着低温液体将以更快的流动速度带走平板上的热量。
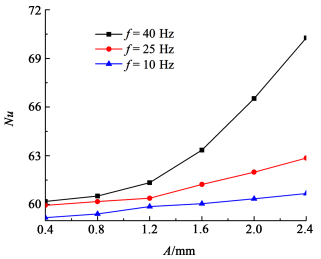
2.2 振幅对降膜换热的影响图 3展示了在3种频率状态,流量为0.000 6 m3/s时不同振幅下平板表面的平均Nu。
|
| 图 3 不同振幅下的平均Nu Fig.3 Average Nu number under different amplitudes |
| |
从图 3中可以看出,随着振幅的增加,Nu逐渐增大;且在不同频率状态下,振幅对换热的影响程度不同,频率变大,振幅对Nu的影响逐渐增大,在f=10和 f=25 Hz时,Nu随着振幅的增加缓慢增长,而频率f=40 Hz时,随着振幅从0.4 mm增长到2.4 mm,Nu迅速从60.18增长到70.26。而平板无振动发生时,平板表面液膜的平均Nu为58.40,动对比平板无振动时,振幅为2.4 mm,3种频率状态下的Nu分别提高了20%、7%和3%。
2.3 振幅对降膜换热的影响图 4为流量为0.000 6 m3/s,当振幅分别为0.4、1.2和2.0 mm时,不同频率状态对降膜换热的影响。

|
| 图 4 不同频率下的Nu Fig.4 Average Nu number at different frequencies |
| |
由图 4可以看出,当振幅A=0.4 mm,随着频率的增加此时Nu在60.00附近波动,相较于无振动时的换热效果,换热效果提高不明显;当A=1.2 mm时,随着频率的增加,换热先在一定幅度内迅速增加后又逐渐降低,而后又增加,呈现波动状,但均高于无振动条件下的换热效果;当A=2.0 mm时,频率的增加,给平板降膜换热效果带来了非常明显的提升,Nu从59.00迅速增加到74.80;在f=50 Hz,振幅为0.4、1.2和2.0 mm的状态下,平板降膜换热效果相较于无振动时分别提高了2.6%、7.1%和27%。
3 结论通过VOF模型、动网格技术和UDF函数,建立了可靠的平板降膜换热数值模型,分析结果表明:1)振动平板上液膜表面剧烈波动,强化了液膜表面传热传质效果;振动加快了下降液膜流速,使得液体以更快的速度带走平板热量。2)振动的振幅和频率均影响降膜换热效果,单独的因素(大振幅低频率、高频率小振幅)并不能带来明显强化的效果,但当2个因素结合时(高频率大振幅),换热效果随着频率增加或者振幅增加而迅速增强。3)在研究范围内,当f=50,A=2.0 mm时,相比于平板无振动时,降膜换热效果提高27%。
| [1] |
Wunder F, Enders S, Semiat R. Numerical simulation of heat transfer in a horizontal falling film evaporator of multiple-effect distillation[J]. Desalination, 2017, 401: 206-229. DOI:10.1016/j.desal.2016.09.020 |
| [2] |
Huang X, Yang Y, Hu P. Experimental study of falling film evaporation in large scale rectangular channel[J]. Annals of Nuclear Energy, 2015, 76: 237-242. DOI:10.1016/j.anucene.2014.09.053 |
| [3] |
刘梅, 宋朝匣, 吴正人, 等. 非平整倾斜表面上流动液膜的影响因素分析[J]. 化工进展, 2015, 34(1): 75-79, 112. Liu Mei, Song Zhaoxia, Wu Zhengren, et al. Analysis on flow film over uneven and inclined wall[J]. Chemical Industry and Engineering Progress, 2015, 34(1): 75-79, 112. (in Chinese) |
| [4] |
Gu F, Liu C, Yuan X, et al. CFD simulation of liquid film flow on inclined plates[J]. Chemical Engineering & Technology, 2004, 27(10): 1099-1104. |
| [5] |
Ishikawa H, Ookawara S, Yoshikawa S. A study of wavy falling film flow on micro-baffled plate[J]. Chemical Engineering Science, 2016, 149: 104-116. DOI:10.1016/j.ces.2016.04.021 |
| [6] |
Fu W, Tong B. Numerical investigation of heat transfer from a heated oscillating cylinder in a cross flow[J]. International Journal of Heat and Mass Transfer, 2002, 45(14): 3033-3043. DOI:10.1016/S0017-9310(02)00016-9 |
| [7] |
申江, 邹国文, 王建民, 等. 机械振动强化吸收式制冷传热传质的实验研究[J]. 制冷学报, 2016, 37(2): 46-52. Shen Jiang, Zou Guowen, Wang Jianmin, et al. Experimental study of heat and mass transfer enhancement of absorption refrigeration by mechanical vibration[J]. Journal of Refrigeration, 2016, 37(2): 46-52. DOI:10.3969/j.issn.0253-4339.2016.02.046 (in Chinese) |
| [8] |
Chun K R, A Seban R. Heat transfer to evaporating liquid film[J]. International Journal of Heat Mass Transfer, 1971, 93(3): 391-396. |
| [9] |
叶学民.壁面薄膜流的热质传递和稳定性研究[D].北京: 华北电力大学, 2002 Ye Xuemin. Investigation on heat and mass transfer and low stability of a thin liquid film draining down a wall[D]. Beijing: North China Electric Power University, 2002(in Chinese) |
 2019, Vol. 36
2019, Vol. 36





