化学工业与工程  2019, Vol. 36 Issue (4): 42-50
   Abstract               PDF                Figures                Tables
引用本文 0
朱炜, 刘斌, 侯海云, 李庆, 王新元, 樊增禄. 4种智能算法在相平衡数据拟合中的应用[J]. 化学工业与工程, 2019, 36(4): 42-50.
Zhu Wei, Liu bin, Hou Haiyun, Li Qing, Wang Xinyuan, Fan Zenglu. Application of Four Intelligent Algorithms inPhase Equilibrium Data Fitting[J]. Chemical Industry and Engineering, 2019, 36(4): 42-50.
4种智能算法在相平衡数据拟合中的应用
朱炜1 , 刘斌1 , 侯海云1 , 李庆1 , 王新元1 , 樊增禄2     
1. 西安工程大学环境与化学工程学院, 西安 710048;
2. 西安工程大学纺织与材料工程学院, 西安 710048
收稿日期: 2018-03-10
基金项目: 陕西省教育厅科学研究项目（17JK0348）；西安工程大学创新创业训练计划项目（2017086）；国家自然科学青年科学基金项目（2160030548）；陕西科技厅国际科技合作与交流计划项目（2017KW-026）
作者简介: 朱炜(1982-), 男, 博士, 讲师, 现从事分子热力学, 量化计算和分子模拟方面的研究.
通信作者: 樊增禄, E-mail:362284029@qq.com.
摘要：针对Marquardt-Levenberg法应用于多元物系相平衡数据拟合时，模型参数剧增，初值难以设定的难题，将4种智能算法，即遗传算法、神经网络，退火算法及粒子群算法，应用于相平衡数据的拟合。以正丙醇（1）+乙腈（2）二元物系汽液相平衡数据的Wilson拟合和甲醇（1）+乙腈（2）+1-乙基-3-甲基咪唑四氟硼酸盐（3）三元物系汽液相平衡数据的NRTL拟合为例，系统讨论了4种算法在应用时的主要影响因素，并将所得结果进行了分析和比较。结果表明遗传算法和粒子群算法可以较好地解决初值难设的问题，并且给出了每种算法的适用范围和使用建议。
关键词：相平衡    参数估值    遗传算法    神经网络    退火算法    粒子群算法    
Application of Four Intelligent Algorithms inPhase Equilibrium Data Fitting
Zhu Wei1 , Liu bin1 , Hou Haiyun1 , Li Qing1 , Wang Xinyuan1 , Fan Zenglu2     
1. School of Environmental and Chemical Engineering, Xi'an Polytechnic University, Xi'an 710048, Shanxi, China;
2. School of Textiles and Materials, Xi'an Polytechnic University, Xi'an 710048, Shanxi, China
Abstract: The Marquardt-Levenberg(ML) algorithm is the most commonly used algorithm for phase equilibrium data fitting. However, this algorithm belongs to the local optimization algorithm. When ML algorithm was applied to multi-component system phase equilibrium data fitting, it is difficult to find the appropriate initial values for the general thermodynamic researchers owing to model parameters increasing sharply. In this paper, four kinds of intelligent algorithms, namely, genetic algorithm, neural network, annealing algorithm and particle swarm algorithm were applied to fitting the vapor-liquid equilibrium data of n-propanol (1)+acetonitrile (2) binary system by Wilson model and fitting the vapor-liquid equilibrium data of methanol (1)+acetonitrile (2)+1-ethyl-3-methylimidazolium tetrafluoroborate (3) ([EMIM] [BF4]) ternary system by NRTL model, respectively. The mainly influencing factors of four algorithms on the phase equilibrium data fitting application were discussed. The results were also analyzed and compared. On the basis of above work, the scope of the application and the use of recommendations of each method were proposed.
Keywords: phase equilibria    parameter estimation    genetic algorithm    neural networks    annealing algorithm    particle swarm algorithm    

相平衡研究中一项很重要的任务是将所获的有限相平衡实验数据选择合适的热力学模型关联起来，即所谓的相平衡数据拟合。这样在实际工程应用中就可直接应用拟合模型来计算[1]。通常相平衡数据拟合使用最多的方法是Marquardt-Levenberg(ML)法[2-10]。ML法属于局部优化算法，当用其进行多元物系相平衡数据拟合时，由于模型参数剧增，初值的选取极其重要。合适的初值不但结果好，而且计算量小。但对一般热力学研究人员而言，初值只能凭经验获取或随机猜测，因而所得结果往往都不理想。

人工智能(Artificial Intelligence，AI)[11]最早提出于1956年，它是自然科学与社会科学的交叉。AI简单来说就是“让计算机能像人一样的去思考和解决问题”。AI领域中常用到的算法有遗传算法(Genetic Algorithm, GA)[12]，人工神经网络(Artificial Neural Network, ANN)[13]，退火算法(Simulate Anneal Arithmetic, SA)[14]和粒子群算法(Particle Swarm Optimization, PSO)[15]等。由于以上所提到的4种人工智能算法理论上均可进行全局优化，因此可将其应用于相平衡数据拟合中。郭宁等用BP(Back Propagation，反向传播) ANN计算了乙醇-环己烷-水体系的汽液平衡[16]和脂肪酸酯与超临界CO2体系的相平衡[17]；何学忠等[18]使用改进的BP ANN对大分子体系的相平衡进行预测；林金清等[19]将GA用于含化学反应体系的相平衡计算; 安维中等[20]将遗传算法用于多相多组分化学反应平衡和相平衡的计算; Senol[21]等采用遗传算法对水+甲酸+酯/醇三元物系进行了UNIFAC，SERLAS，NRTL，改进NRTL，三参数Margules模型关联；Khansary等[22]将GA和PSO用于多元体系液液相平衡作用相互参数的估计; Mirarab等[23]将基于GA的ANN用于CO2在乙醇+[EMIM][Tf2N]离子液体溶解度的预测; Li等[24]将基于自适应PSO和混沌理论的ANN用于聚合物中气体溶解度的预测。

相平衡研究中的热力学模型包括经验型[25](如Margules，Van Laar, Wohl)、半经验型[25](如Wilson，NRTL，UNIQUAC)和预测型(如UNIFAC[25]，COSMO-RS[26]，COSMO-SAC[27])3大类。其中，经验型只适合于二元物系，不能用于多元物系；基于基团贡献的UNIFAC虽然预测效果较好，但必须要有相关物系的基团参数；基于量子力学和统计力学的COSMO-RS，COSMO-SAC一般只能给出定性结果，而且对于大分子或复杂分子，其准确的量化计算极其耗时[28-29]。因此，本研究选用半经验模型来进行相平衡数据拟合。

为了探讨智能算法能否解决多元物系相平衡数据拟合难的问题，本研究将正丙醇(1)+乙腈(2)二元物系和甲醇(1)+乙腈(2)+1-乙基-3-甲基四氟硼酸盐([EMIM][BF4])(3)三元物系汽液相平衡数据，分别利用ML法，遗传算法、神经网络、退火算法和粒子群算法进行了数据拟合，对4者的拟合效果进行了全面的分析和比较, 并给出了每种算法的使用建议。

1 计算细节 1.1 相平衡数据

相平衡类型及对应的相平衡数据有多种，但不论哪种相平衡一旦选中某种半经验型模型，除了相平衡数据预处理过程不同，用该模型拟合的核心过程都是相同的。所以，本研究用汽液相平衡数据拟合代表所有相平衡数据的拟合，用二元汽液相平衡数据拟合代表少参数半经验模型的拟合，用三元汽液相平衡数据拟合代表多参数半经验模型的拟合。其中二元和三元汽液相平衡数据分别来自于文献[30]和[31]。二元物系共有15个实验数据点，使用Wilson半经验模型进行拟合，该模型含2个参数Λ12和Λ21(Λij为Wilson二元交互作用能量参数)；三元物系共有30个实验数据点，使用NRTL半经验模型进行拟合，模型中含6个参数，分别是α31, α23(αij为系统混合非随机特征参数), Δg13, Δg31, Δg23, Δg32(Δgij为NRTL二元交互作用能量参数)。

1.2 计算平台及编程环境

Windows7，64位；CPU: Intel i7-4790, 3.60 GHz, RAM: 16 GB，8核；Matlab R2010b。

1.3 目标函数

二元物系及三元物系相平衡数据拟合时采用式(1)所定义的目标函数(ARD)。

$ {\rm{ARD}} = \frac{1}{n}\sum\limits_n {\left| {\frac{{\gamma _i^{{\rm{exp}}} - \gamma _i^{{\rm{cal}}}}}{{\gamma _i^{{\rm{exp}}}}}} \right|} \times 100\% $ (1)

式(1)中γiexp和γical分别是组分i的实验测定活度系数和计算活度系数，n是实验数据点数。

1.4 比较标准

以ML法计算结果作为不同智能算法间比较的标准，详情见表 1。

表 1 ML法拟合时的目标函数值及耗时 Table 1 ARDs and time consuming obtained by ML method
物系(模型) ARD 时间/s
二元物系(Wilson) 0.190 0.2
三元物系(NRTL) 3.300 3 600.0
表选项
1.5 默认参数 1.5.1 遗传算法

种群初始化方法为带约束的随机产生，选择方法为随机均匀分布，再生方法的精英数目和交叉分数分别为2%和80%，变异方法为均匀变异，交叉方法为散点交叉，迁移方法为向前，其分数和间隔值分别是20%和20，停止准则为种群最大代数(5 000)或最小允许误差(1e-6)。

1.5.2 神经网络

使用具有S型隐形神经元和线性输出神经元的双层前馈神经网络，采用LM反向传播算法对网络进行训练，隐形神经元数目有10个，输入参数是液相组成和温度，输出为汽相组成，训练集的选择采用随机方式。网络结构如图 1所示。

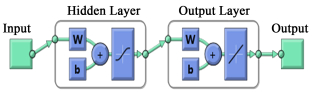
图 1 双层前馈神经网络 Fig.1 The two-layer feed-forward network
图选项
1.5.3 退火算法

最大允许误差设为1e-6，每次迭代的最大函数个数为(变量数×3000)，初始温度设为100，再退火间隔设为100，退火函数选择annealingFast，温度函数选择temperatureExp，变量类型采用双精度型。

1.5.4 粒子群算法

最大迭代次数为2 000，初始化种子数为24，局部最适宜加速度参数和全局最优加速度参数均为2，初始时刻加权值和收敛时刻加权值分别为0.9和0.4，算法终值阀值设为1e-25，终止算法的阈值为250，种子为随机产生。

2 结果与讨论 2.1 遗传算法

将遗传算法分别应用于二元和三元物系的汽液相平衡数据拟合，所得结果如表 1和表 2所示。

表 2 自定义种群数和种群数对于拟合的影响 Table 2 Effects of initial population and population size on the fitting results
No. 自定义种群数 种群数 ARD 时间/s
1 103 1.112 186.0
2 441 103 1.113 23.3
3 104 1.112 1 602.0
4 1 681 104 1.112 132.0
5 6 561 104 1.111 33.9
6 105 1.112 7 560.0
7 41 209 105 1.112 246.0
8 106 1.112 2 088.0
9 167 281 106 1.112 2 304.0
表选项
2.1.1 二元物系的拟合结果

对于二元物系的拟合，由表 2可知：自定义种群的存在可极大减少计算量(见编号2, 4, 5和7)，但当种群数很大时，自定义种群的这种影响就不再明显(见编号8和9)；所得结果均优于ML法，但是耗时要比ML法多，尤其是种群数很大时。

2.1.2 三元物系的拟合结果

对于三元物系的拟合，由表 3可知：随种群数增加，ARD值减小很快，相应计算时间却急剧增加(见编号5~8)；自定义种群在种群数较小时对ARD值的影响很大，随着种群数的增加，自定义种群的这种影响减弱(见编号9~14)；当种群数为106时才能取得与ML法相近的结果，而且计算时间要比ML法长。

表 3 自定义种群数和种群数对于拟合的影响 Table 3 Effects of initial population and population size on the fitting results
No. 自定义种群数 种群数 ARD 时间/s
1 105 7.093 2 100.0
2 105 6.916 1 182.0
3 105 4.737 492.0
4 105 4.730 462.0
5 103 9.505 48.0
6 104 9.510 48.0
7 105 6.990 450.0
8 106 4.410 4 380.0
9 104 9.447 52.8
10 2 304 104 4.620 50.2
11 105 4.916 504.0
12 15 625 105 4.384 503.3
13 106 4.526 5 172.0
14 117 649 106 4.143 4 938.0
表选项

此外，也对遗传算法的重现性和相关算法函数的影响进行了考察，详见表 4和表 5。

表 4 遗传算法的重现性 Table 4 The reproducibility of genetic algorithm
No. CPUs Population size ARD Time/min
1 4 105 4.737 8.2
2 4 105 4.741 7.8
3 4 105 4.710 7.3
4 6 105 7.302 12.8
5 6 105 5.066 9.1
6 6 105 5.864 7.3
表选项
表 5 交叉函数、选择函数、变异函数和迁移方向对于拟合的影响 Table 5 The effects of crossover function, selection function, mutation function and migration direction on the fitting results
No. 函数 ARD 时间/s
1 crossoverheuristic 4.173 516
2 crossoverintermediate 4.371 522
3 crossoversinglepoint 4.340 534
4 crossovertwopoint 4.602 660
5 crossoverarithmetic 4.497 432
6 selectionremainder 4.177 5 760
7 selectionuniform 5.053 468
8 selectionroulette 4.169 3 960
9 selectiontournament 4.607 522
10 mutationadaptfeasible 4.343 504
11 both 4.178 732
表选项

由表 4可知，由于算法中引入随机数的缘故，遗传算法的重现性不太稳定。

将表 5的结果与表 3中编号11相比可见：不同交叉函数对ARD值和耗时影响较小(见编号1~5)，其中crossoverheuristic结果最好；选择函数对ARD值有一定影响，虽然selectionremainder和selectionroulette结果较好，但耗时都较多(见编号6~9)；变异函数对ARD和耗时也影响较小(见编号10)；选择函数的both方向可减小ARD值，且耗时短。

2.1.3 建议

要增加遗传算法的拟合效果，增加种群数比增加代数更有效，但计算时间会相应增加；若粗略知道初值的可能范围，可使用自定义种群来提高计算效率；遗传算法使用时最好多算几次再取最优值；遗传算法的交叉函数，选择函数等对ARD值的影响不大，计算时不必过于计较。

2.2 神经网络

由于神经网络对二元物系和三元物系的拟合过程和结论相似，因此只选三元物系的结果进行讨论。该算法的每个结果都是进行了6次训练筛选而得。

2.2.1 三元物系的拟合结果

首先，采用27个数据点对神经网络进行训练，验证和预测，结果见图 2。图 2中短线之上数字表示该次计算的ARD值，短线之下数字表示计算耗时，下同。

图 2 27个数据点时神经元数和训练比例(训练分数，验证分数，预测分数)对于拟合的影响 Fig.2 Effect of number of neurons and training proportion (training, validation, testing) on the fitting results using 27 data points
图选项

由图 2可知，当输入数据为3×27，神经元数为10，预测分数为20%时，所得结果与ML法相近；在训练分数为70%，验证分数和预测分数均为15%时，3个神经元即可得到比ML法更好的结果。但此时预测分数只有15%~20%。

接着，采用51个数据点对神经网络进行训练、验证和预测，结果见图 3。

图 3 51个数据点时神经元数和训练比例(训练分数，验证分数，预测分数)对于拟合的影响 Fig.3 Effect of number of neurons and training proportion (training, validation, testing) on the fitting results using 51 data points
图选项

由图 3可知，当输入数据为3×51，神经元数为5，预测分数为35%时，所得结果与ML法相近；在训练分数为40%，验证分数和预测分数均为30%时，2个神经元即可得到比ML法更好的结果。此时预测分数已提高到30%~35%。为进一步提高网络的预测能力，继续尝试增加数据点。

最后，采用123个数据点对神经网络进行训练，验证和预测，结果见图 4。

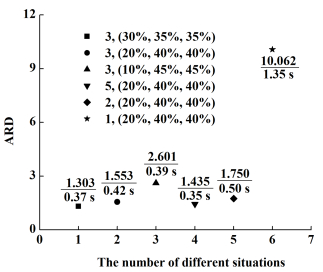
图 4 123个数据点时神经元数和训练比例(训练分数，验证分数，预测分数)对于拟合的影响 Fig.4 Effect of number of neurons and training proportion (training, validation, testing) on the fitting results using 123 data points
图选项

由图 4可知，当输入数据为3×123，神经元数为3，预测分数为45%时，所得结果已优于ML法；甚至在训练分数为20%，验证分数和预测分数均为40%时，2个神经元便可得到比ML法更好的结果。此时神经网络只需要非常少的训练集(10%~20%)和神经元(2或3)就能拥有很强的预测能力(40%~45%)。

对神经网络重现性的考察结果见图 5。图 5中图例的数字分别表示输入数据数，神经元数和训练比例(训练分数，验证分数，预测分数)。

图 5 神经网络的重现性 Fig.5 The reproducibility of neural network
图选项

由图 5可知，神经网络的重现性很差。这也是2.2.1节每个结果都是从6次训练中进行筛选的原因。

2.2.2 建议

神经网络输入数据越多，训练所得网络预测能力越强；数据点有限时，若要达到好的预测效果，训练集中必须包含相图中尽可能多的拐点；训练集精度越高，网络预测性能并非越高，其关键取决于训练集中拐点的多少；神经网络若要重现性好，训练集的选择就不可采用随机的方式。

2.3 退火算法

将退火算法分别应用于二元和三元物系的汽液相平衡数据拟合，结果如下。

2.3.1 二元物系的拟合结果

由表 6可知，对于二元物系拟合采用同样的初始值，ML法要比退火算法效率高很多。

表 6 ML法和退火算法对于两参数拟合的比较 Table 6 Comparison of ML and annealing algorithms for two-parameter fitting
序号 算法 初值 次数 ARD 时间/s
1 SA [1, 1] 5 914 0.194 3.2
2 ML 42 0.194 0.2
3 SA [10 000, 10 000] 5 912 5.819 2.7
4 ML 14 0.194 0.2
5 SA [-10 000, -10 000] 5 914 43.522 2.8
6 ML 16 0.194 0.2
表选项
2.3.2 三元物系的拟合结果

对于三元物系拟合由表 7可知，采用相同初始值，ML法的确比退火算法的效率高很多，而且初始值的适用范围更宽泛，但结果偶尔会稍差一点。

表 7 ML法和退火算法拟合的比较 Table 7 Comparison of ML and annealing algorithms for six-parameter fitting
初值 算法 次数 ARD 时间/s
[1, 1, 1, 1, 0.5, 0.5] SA 5 567 9.704 4.2
ML 401 10.039 1.2
[-30 000, 30 000, -1 000, 1 000, 0.3, 0.8] SA 5 067 34.073 3.8
ML 26 3.307 0.4
[-10 000, 10 000, -10 000, 10 000, 0.5, 0.5] SA 16 060 13.179 12.3
ML 401 12.494 1.0
[10 000, 10 000, 10 000, 10 000, 0.5, 0.5] SA 5 544 82.256 3.5
ML 44 15.218 0.3
[-30 000, 30 000, -1 000, 1 000, 0.3, 0.8] SA 8 040 137.746 6.4
ML 23 63.124 0.3
[1 000, 1 000, 1 000, 1 000, 0.9, 0.1] SA 3 055 47.514 2.1
ML 74 3.307 0.3
[100 000, -1 000, 10 000, -10 000, 0.9, 0.1] SA 7 836 5.148 5.2
ML 96 4.052 0.4
表选项

同时，也对退火算法的重现性和相关算法函数的影响进行了考察，结果见表 8~表 10。

表 8 初始温度对于拟合的影响及退火算法的重现性 Table 8 Effect of initial temperature on the fitting results and the reproducibility of annealing algorithm
序号 初值 初始温度 ARD 时间/ s
1 [-30 000, 30 000, -1 000, 1 000, 0.3, 0.8] 102 34.073 3.8
2 103 27.289 10.6
3 104 15.135 9.4
4 105 12.588 2.9
5 106 10.363 2.0
6 108 9.821 2.9
7 [100 000, -1 000, 10 000, -10 000, 0.9, 0.1] 102 6.132 2.9
8 103 5.181 2.9
9 104 4.782 3.1
10 105 10.470 2.7
11 105 46.603 2.1
12 105 11.384 4.9
13 105 9.526 2.3
14 106 12.707 2.1
15 108 10.666 2.3
表选项
表 9 最大函数个数对于拟合的影响 Table 9 Effect of max function evaluations on the fitting results
序号 初值 最大函数个数 ARD 时间/ s
1 [100 000, 0, 10 000, -10 000, 0.9, 0.1] 5×104 4.756 5.1
2 105 4.728 5.2
3 5×105 4.703 5.9
4 106 4.821 2.3
5 106 4.565 10.0
6 106 4.844 6.4
7 107 4.770 2.2
8 107 4.730 6.6
9 107 4.689 6.6
10 108 4.965 2.9
11 108 4.835 4.1
12 108 4.856 4.0
表选项
表 10 退火函数和温度函数对于拟合的影响 Table 10 Effect of annealing and temperature functions on the fitting results
序号 函数 迭代次数 ARD 时间/s
1 annealingboltz 3 432 5.699 2.2
7 998 5.104 5.6
6 349 6.144 4.5
2 temperatureboltz 3 773 9.641 2.6
4 422 8.928 3.1
7 204 5.290 5.4
3 temperaturefast 3 196 7.782 2.2
6 352 5.253 4.4
6 045 11.963 4.1
表选项

由表 8可知，初始温度对ARD值影响很大，通常初始温度越高结果越好(见编号1~6)，但也有例外(见编号7~15)，而且不同初始值对应不同的最适宜初始温度；由编号10~13可知，退火算法的重现性很差。

由表 9可知，最大函数个数对结果和重现性几乎无影响，因此无需设置大的最大函数个数。

由表 10可知，退火函数对结果影响不大；温度函数对结果影响较大，但是好是坏不能确定，其原因是退火算法重现性较差(见编号2和3)。

2.3.3 建议

退火算法可看作半全局优化，因为初值对结果影响很大。理论上初始温度越高，结果越趋近于全局最优，但实践中该说法不一定正确。要得到好结果，初始值和最适宜初始温度都必须慢慢尝试，而实现该过程最好的方式是编程。

2.4 粒子群算法

将粒子群算法分别应用于二元和三元物系的汽液相平衡数据拟合，并讨论结果。

2.4.1 二元物系的拟合结果

二元物系的拟合结果见表 11。表 11中第3列括号中数字表示实际需要的进化次数，括号外数字表示计算时设定的进化次数，下同。

表 11 种子数对拟合的影响 Table 11 Effect of population size on the fitting results
序号 种子数 进化次数 ARD 时间/s
1 20 2 000(1 147) 0.194 5.1
2 40 2 000(1 220) 0.194 6.9
3 80 300 0.194 4.5
4 160 300 0.194 5.1
5 1 000 300 0.194 25.4
6 10 000 300 0.194 192.0
表选项

由表 11可知，通过少种子数多进化次数或多种子数少进化次数，粒子群算法均可取得与ML法相同的结果，但耗时要比ML法多。

2.4.2 三元物系的拟合结果

三元物系的拟合结果见表 12。

表 12 种子数、进化次数对拟合的影响及粒子群算法的重现性 Table 12 Effect of population size and epochs and the reproducibility of particle swarm algorithm
序号 种子数 进化次数 ARD 时间/s
1 20 104 (3 542) 9.558 29.5
2 20 104 (1 680) 14.129 13.9
3 20 105 (2 071) 8.959 16.9
4 20 105 (1 652) 9.028 13.5
5 20 105 (1 741) 9.023 14.4
6 40 104 (2 933) 8.959 36.6
7 80 102 9.003 2.8
8 80 103 8.959 21.6
9 80 104 (1 427) 9.515 30.4
10 160 102 9.010 4.2
11 160 103 8.974 41.0
12 160 104 (1 524) 8.959 61.3
13 320 103 8.959 77.3
14 640 103 8.959 150.0
15 1 280 103 8.959 288.0
16 105 103 4.124 27 360.0
表选项

由表 12可知：增加种子数和进化次数均可优化结果(见编号1~16)，且采用大幅增加种子数的方式结果更好，但耗时增加严重(见编号16)；粒子群算法的重现性较好(见编号3~5)；当种子数为105时，可达到与ML法相近的结果，但耗时却是ML法的7.6倍。

2.4.3 建议

使用粒子群算法进行多参数拟合若要取得好结果，最好在参数限制条件内设置尽量大的种子数，并以运算时间剧增为代价。

2.5 4种算法的比较 2.5.1 效率

4种智能算法用于相平衡数据拟合时的效率比较见表 13。

表 13 4种智能算法效率的比较 Table 13 Comparison of efficiencies of four intelligent algorithms
二元物系每种算法的最优结果 三元物系每种算法的最优结果
标准 GA ANN PSO SA ML 标准 GA ANN PSO SA ML
ARD 1.111 0.181 0.194 0.194 0.190 ARD 4.169 0.435 4.124 4.501 3.300
时间/s 33.9 0.3 5.1 3.2 0.2 时间 1.1 h 0.4 s 7.6 h 2.2 d 1.0 h
表选项

由表 13可见，对于二元物系4种算法的效率排序为：ANN>SA>PSO>GA；对于三元物系4种算法的效率排序为：ANN>GA>PSO>SA。

2.5.2 相同点

1) 智能算法中随机数的引入，一方面使算法有可能得到全局最优，另一方面也导致每次计算结果有差异。因而智能算法应用时必须多算几次，再选其中最优者。

2) 智能算法的优势：第一，容易实现，不涉及梯度矩阵的计算，不会出现不收敛等情况；第二，并行计算可极大提高计算速度(除神经网络)；第三，拟合时初值的选择在智能算法中不是难题，因为每种算法都有其专属的初值函数用以产生满足限定条件的初值(除神经网络)。

2.5.3 不同点

1)粒子群算法没有交叉、选择和变异过程，比遗传算法更容易实现，但效率不如遗传算法。

2)神经网络效率最高(耗时少，精度高)，但所得模型参数较多且物理意义不明确，可将其用于各种热力学模型都难以描述或拟合效果很差的场合。

3 结论

本研究将4种智能算法引入相平衡数据拟合，通过对各算法具体应用时的分析和讨论，可得出以下几点结论：

1)少参数拟合使用ML法经济；多参数拟合推荐使用GA和PSO；若ML、GA、PSO和SA拟合效果均不理想，可尝试采用ANN进行拟合。

2)理论上智能算法均可实现全局优化，但实践中只能趋近于全局最优。若采用智能算法+局部优化的方式可获得更优结果。

3)拟合时将ARD的允许误差设置为10-4为宜，否则会因精度太高而浪费大量时间。

4)智能算法为多元相平衡数据拟合难问题提供了一种可行的解决方案。

参考文献
[1]
Walas S M. Phase equilibria in chemical engineering[M]. Oxford: Butterworth Publishers, 1985.
[2]
Soujanya J, Satyavathi B, Sankarshana T. Isobaric ternary vapour-liquid equilibrium of methanol (1)+diisopropyl ether(2)+isopropyl alcohol(3) along with methanol+isopropyl alcohol binary data at atmospheric and sub-atmospheric pressures[J]. Fluid Phase Equilibr, 2015, 405: 31-36. DOI:10.1016/j.fluid.2015.07.023
[3]
Kamiński W, Górak A, Kubiczek A. Modeling of liquid-liquid equilibrium in the quinary system of water, acetone, n-butanol, ethanol, and ionic liquid[J]. Fluid Phase Equilibr, 2014, 384: 114-121. DOI:10.1016/j.fluid.2014.10.017
[4]
Lei Z, Xi X, Dai C, et al. Extractive distillation with the mixture of ionic liquid and solid inorganic salt as entrainers[J]. AIChE J, 2014, 60(8): 2994-3004. DOI:10.1002/aic.v60.8
[5]
Lei Z, Dai C, Liu X, et al. Extension of the UNIFAC model for ionic liquids[J]. Ind Eng Chem Res, 2012, 51(37): 2135-2144.
[6]
Shao X, Ge H, Li Z, et al. Solubility of methylphosphonic acid in selected organic solvents[J]. Fluid Phase Equilibr, 2015, 390: 7-13. DOI:10.1016/j.fluid.2015.01.009
[7]
Pirouzi A, Nosrati M, Haghtalab A, et al. Experiment and correlation of osmotic coefficient for aqueous solution of carboxylic acids using NRTL nonrandom factor model[J]. Fluid Phase Equilibr, 2012, 327: 38-44. DOI:10.1016/j.fluid.2012.05.002
[8]
Ricardo F P, Moilton R F. Solubility of salicylic acid in water+salt (NaCl, KCl, NaBr, Na2SO4 and K2SO4) at 293.5~313.3 K[J]. Fluid Phase Equilibr, 2012, 330: 48-51. DOI:10.1016/j.fluid.2012.06.024
[9]
Paduszyński K, Okuniewski M, Domańska U. Solid-Liquid phase equilibria in binary mixtures of functionalized ionic liquids with sugar alcohols:New experimental data and modeling[J]. Fluid Phase Equilibr, 2015, 403: 167-175. DOI:10.1016/j.fluid.2015.06.002
[10]
Rogošić M, Sander A, Kojić V, et al. Liquid-Liquid equilibria in the ternary and multicomponent systems involving hydrocarbons, thiophene or pyridine and ionic liquid (1-benzyl-3-metylimidazolium bis(trifluorometyl sulfonyl)imide)[J]. Fluid Phase Equilibr, 2016, 412: 39-50. DOI:10.1016/j.fluid.2015.12.025
[11]
温正. 精通MATLAB智能算法[M]. 北京: 清华大学出版社, 2015.
Wen Zheng. Proficient in MATLAB intelligent algorithm[M]. Beijing: Tsinghua University Press, 2015. (in Chinese)
[12]
雷英杰, 张善文. MATLAB遗传算法工具箱及应用(第二版)[M]. 西安: 西安电子科技大学出版社, 2014.
Lei Yingjie, Zhang Shanwen. MATLAB genetic algorithm toolbox and its application (2nd)[M]. Xi'an: Xi'an University of Electronic Science and Technology Press, 2014. (in Chinese)
[13]
飞思科技产品研发中心. 神经网络理论与MATLAB7实现[M]. 北京: 电子工业出版社, 2005.
Feisi Technology Product R&D Center. Neural network theory and MATLAB7 implementation[M]. Beijing: Electronic Industry Press, 2005. (in Chinese)
[14]
康立山, 谢云, 尤矢勇, 等. 非数值并行算法(第一册):模拟退火算法[M]. 北京: 科学出版社, 1994.
Kang Lishan, Xie Yun, You Shiyong, et al. Non-Numerical parallel algorithm (Volume 1):Simulated annealing algorithm[M]. Beijing: Science Press, 1994. (in Chinese)
[15]
钱锋. 粒子群算法及其工业应用[M]. 北京: 科学出版社, 2013.
Qian F. Particle swarm algorithm and its industrial application[M]. Beijing: Science Press, 2013. (in Chinese)
[16]
郭宁, 崔志芹, 云志, 等. BP神经网络计算乙醇-环己烷-水体系汽-液平衡[J]. 南京工业大学学报, 2002, 24(4): 91-93.
Guo Ning, Cui Zhingqing, Yun Zhi, et al. Vapor-Liquid equilibrium data of ethanol-cyclohexane-water using BP artificial neural network[J]. Journal of Nanjing university of technology, 2002, 24(4): 91-93. DOI:10.3969/j.issn.1671-7627.2002.04.021 (in Chinese)
[17]
郭宁, 云志, 邵荣, 等. 神经网络计算脂肪酸酯与超临界CO2体系相平衡[J]. 南京工业大学学报, 2003, 25(3): 56-61.
Guo Ning, Yun Zhi, Shao Rong, et al. Calculation of phase equilibrium of systems containing supercritical carbon dioxide and fatty acid esters using artificial neural networks[J]. Journal of Nanjing University of technology, 2003, 25(3): 56-61. DOI:10.3969/j.issn.1671-7627.2003.03.012 (in Chinese)
[18]
何雪忠, 张香平, 张锁江, 等. 改进的L-M算法用于大分子体系相平衡的神经网络预测[J]. 化工学报, 2005, 56(3): 392-399.
He Xuezhong, Zhang Xiangping, Zhang Suojiang, et al. Improved L-M algorithm for ANNs prediction of phase equilibrium in macromolecule system[J]. CIESC Journal, 2005, 56(3): 392-399. DOI:10.3321/j.issn:0438-1157.2005.03.004 (in Chinese)
[19]
林金清, 李浩然, 韩世钧. 应用遗传算法求解含化学反应体系的相平衡[J]. 化工学报, 2002, 53(6): 616-620.
Lin Jinqing, Li Haoran, Han Shijun. Computation algorithm for simultaneous chemical and phase equilibrium by using genetic algorithm[J]. CIESC Journal, 2002, 53(6): 616-620. DOI:10.3321/j.issn:0438-1157.2002.06.012 (in Chinese)
[20]
安维中, 胡仰栋, 袁希钢. 多相多组分化学反应平衡和相平衡计算的遗传算法[J]. 化工学报, 2003, 54(5): 691-694.
An Weizhong, Hu Yangdun, Yuan Xigang. Calculation of multiphase and multicomponent chemical equilibrium using genetic algorithm[J]. CIESC Journal, 2003, 54(5): 691-694. DOI:10.3321/j.issn:0438-1157.2003.05.020 (in Chinese)
[21]
Senol A, Bilgin M, Baslioglu B, et al. Modeling phase equilibria of ternary systems (water+formic acid+ester or alcohol) through UNIFAC-original, SERLAS, NRTL, NRTL-modified, and three-suffix Margules:Parameter estimation using genetic algorithm[J]. Fluid Phase Equilibr, 2016, 429: 254-265. DOI:10.1016/j.fluid.2016.08.041
[22]
Khansary M A, Sani A H. Using genetic algorithm (GA) and particle swarm optimization (PSO) methods for determination of interaction parameters in multicomponent systems of liquid-liquid equilibria[J]. Fluid Phase Equilibr, 2014, 365: 141-145. DOI:10.1016/j.fluid.2014.01.016
[23]
Mirarab M, Sharifi M, Ghayyem M, et al. Prediction of solubility of CO2 in ethanol-[EMIM] [Tf2N] ionic liquid mixtures using artificial neural networks based on genetic algorithm[J]. Fluid Phase Equilibr, 2014, 371: 6-14. DOI:10.1016/j.fluid.2014.02.030
[24]
Li M, Huang X, Liu H, et al. Prediction of gas solubility in polymers by back propagation artificial neural network based on self-adaptive particle swarm optimization algorithm and chaos theory[J]. Fluid Phase Equilibr, 2013, 356: 11-17. DOI:10.1016/j.fluid.2013.07.017
[25]
Smith J M, Van Ness H C, Abbott M M. Introduction to chemical engineering thermodynamics (7th)[M]. New York: McGraw Hill Higher Education, 2005.
[26]
Klamt A. Conductor-Like screening model for real solvents:A new approach to the quantitative calculation of solvation phenomena[J]. J Phys Chem, 1995, 99(7): 2224-2235. DOI:10.1021/j100007a062
[27]
Lin S, Sandler S I. COSMO-SAC:A priori phase equilibrium prediction from a segment contribution solvation model[J]. Ind Eng Chem Res, 2002, 41(5): 899-913. DOI:10.1021/ie001047w
[28]
Lei Z, Chen B, Li C, et al. Predictive molecular thermodynamic models for liquid solvents, solid salts, polymers, and ionic liquids[J]. Chem Rev, 2008, 108(4): 1419-1455. DOI:10.1021/cr068441+
[29]
Xue Z, Mu T, Gmehling J. Comparison of a priori COSMO-RS models and group contribution methods:Original UNIFAC, modified UNIFAC (Do), and modified UNIFAC (Do) consortium[J]. Ind Eng Chem Res, 2012, 51(36): 11809-11817. DOI:10.1021/ie301611w
[30]
Zhu W, Qing L, Liu B, et al. Effect of imidazolium-based ionic liquid on vapor-liquid equilibria of 2-propanol+acetonitrile binary system at 101.3 kPa[J]. Fluid Phase Equilibr, 2016, 409: 383-387. DOI:10.1016/j.fluid.2015.10.035
[31]
Li Q, Zhu W, Liu B, et al. Measurement and correlation of the vapor-liquid equilibrium for methanol+acetonitrile+imidazolium-based ionic liquids at 101.3 kPa[J]. J Chem Thermodyn, 2016, 101: 25-30. DOI:10.1016/j.jct.2016.05.011