2. 哈尔滨工业大学能源科学与工程学院, 哈尔滨 150001
2. School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
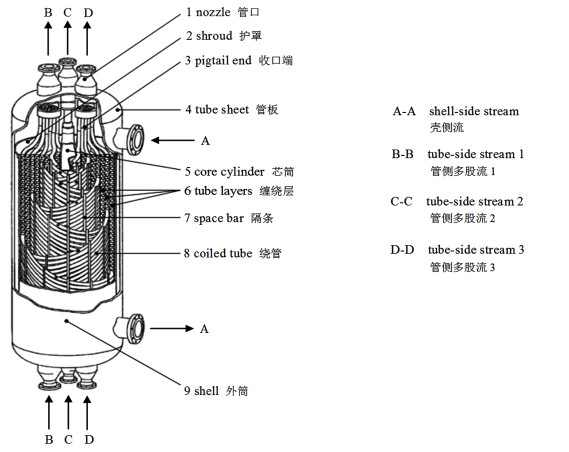
绕管式换热器(SWHE)作为低温换热首选设备在天然气液化(LNG)工艺中被普遍使用,其特点是适用于超低温环境、能承受介质高压、管侧可实现多股流放热。大量的小口径换热管以螺旋线的方式分层缠绕在芯筒上,从而制成该类换热器。相邻2层换热管的缠绕方向不同,层间使用隔条控制间隙[1-2],绕管式换热器构造见图 1[3]。
绕管式换热器用于天然气液化流程时,汽相天然气以多股流的形式自下而上地流过换热管内部,与此同时烷烃制冷剂以液态形式自上向下流过换热器壳侧。由于管和壳两侧存在换热温差,所以壳侧制冷剂吸收管侧天然气的热量而汽化,并在流动过程中先后经历两相和过热2种流态。
针对绕管式换热器换热性能研究内容而言,目前可找到的相关文献并不多见。Neeraas[4]设计出LNG绕管式换热器管侧实验台,通过实验测试出烷烃工质在管侧流动时的压降、换热数据,并给出了管侧流动适用的换热关联式。Aunan[5]搭建了LNG绕管式换热器壳侧实验装置,对烷烃制冷剂在壳侧的流动与换热性能展开了研究,同时给出了壳侧适用的关联式。Moawed[6]通过实验掌握了缠绕管曲率比、扭曲比与壳侧换热系数之间的变化规律,指出缠绕管曲率比、扭曲比与壳侧单相换热系数呈同向变化。Yang等[7]实验研究了高压氮气、氦气及其混合气流过绕管壳侧的换热特性,以实验数据说明了壳侧气相换热系数与气体压力、气体种类、绕管径向间距密切相关。Jamshidi等[8]通过实验研究了常温水流过单层绕管换热器时的换热性能,指出当换热管管径、螺距变大时将有利于增强壳侧换热,并且相应地给出了增强换热的优化方案。Shokouhmand等[9]研究了壳侧流速以及不同结构参数对壳侧换热系数的影响,认为增大换热管螺距、减小缠绕比有利于提高换热性能,同时指出逆流换热效果比顺流换热提升0~40%。
在绕管式换热器计算机仿真研究领域,贾金才[10]在壳侧气相流动的条件下研究了换热管管径、缠绕角、径向比、轴向比对壳侧换热系数的影响,指出减小换热管直径和径向比以及增大轴向比有利于换热。Zhang等[11]对绕管式换热器进行了三维整体建模,以高压烷烃气体作为流动工质,数值研究对象及方法同文献[10]相类似,但因几何参数控制手段不同,故所得结论与文献[10]差别较大。Lu等[12]就绕管式换热器壳侧单相换热进行了数值模拟研究,通过与Xin[13]的实验数据对比之后发现多层绕管换热性能优于单层绕管换热性能。
通过对上述文献分析后可以发现,绕管式换热器流动与换热性能研究主要是以实验方式来进行的,研究侧重于换热性能的影响因素分析及关联式的建立。即使存在少量的数值模拟研究文献,其研究内容也是针对换热器单相流动来进行的,而两相流动研究内容尚未展开。本研究则对LNG绕管式换热器壳侧降膜沸腾流动进行数值模拟研究,不仅可以节省超低温实验台的搭建费用,而且能够从微观细节上掌握该类换热器的流动与换热特性。
1 LNG绕管式换热器壳侧模型的建立 1.1 壳侧几何模型由于LNG绕管式换热器外观尺寸庞大、内部构造复杂,所以很难对换热器实体进行直接地仿真计算研究。本研究所建壳侧几何模型与文献[5]中的实验装置相同,并以文献[5]中的实验数据作为模拟计算检验标准。
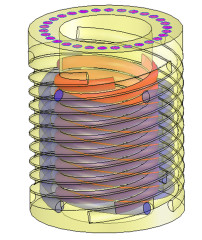
文献[5]中的实验设备是LNG绕管式换热器的简化模型,由3层换热管缠绕而成,并且相邻2层换热管的螺旋方向相反。对于内层、中间层和外层换热管,其并行同步缠绕的数目分别为3、4和5。中间缠绕层采用形状完整的换热管,而内、外缠绕层使用断面为半圆形的换热管,内、外2层半圆形换热管作为壳侧流动区域边界,换热器模型见图 2。文献[5]以恒定热流密度方式研究壳侧换热特性,在中间缠绕层底部并行的4根换热管内设置电加热丝,使其成为受热壁面,而其余壁面均设置成绝热壁面。制冷剂由顶部30个直径为10 mm的分流孔进入壳侧,经过上部多排换热管速度缓冲后流至换热测量段。测量段的加热壁面温度及流道截面温度均可通过多点实测而获得,壳侧沸腾换热温差由加热壁面平均温度与流过测量段的上、下流道截面平均温度的差值来计算。
|
| 图 2 换热器简化模型 Fig.2 SWHE simplified model |
| |
参照文献[5]中的换热器简化模型,本研究使用UG NX 6.0建立了壳侧模型,其几何参数见表 1。鉴于该模型具有轴对称性,因此将模型沿轴向切割36°作为模拟研究对象,其目的是使网格数量控制在100万左右,进而减少计算耗时。切割下来的壳侧36°几何模型见图 3。
| 几何参数 | 参数值 |
| 换热管外径Dtu/mm | 12.00 |
| 换热管轴向间距Pl/mm | 13.94 |
| 换热管径向间距Pr/mm | 15.91 |
| 换热管缠绕角θ/(°) | 7.938 |
| 换热管缠绕层数Nlayer/层 | 3 |
| 缠绕层并管数目Ni/根 | 3,4,5 |
| 缠绕直径Di/mm | 96.00,127.82,159.63 |
| 模型高度/mm | 160 |
| 分流孔直径/mm | 10 |
| 分流孔数目/个 | 30 |
制冷剂以液态流入壳侧时,换热管管束被液膜覆盖,形成降膜流动,沸腾产生的气泡及时从壁面脱离,沿流道缝隙流动,此时汽、液相间滑速比接近于1,相间作用力并不强烈,适宜采用两相流VOF模型进行模拟。ANSYS FLUENT软件中内置的VOF模型具有捕捉相界面清晰、求解方程数量少、计算速度快等优势,在求解壳侧降膜流动时的控制方程组如下[14]:
连续方程:
| $ \frac{{\partial {\beta _{\rm{g}}}}}{{\partial \tau }} + \nabla \cdot \left( {{\beta _{\rm{g}}}\vec v} \right) = \frac{{{\mathit{\Gamma }_{\rm{m}}}}}{{{\rho _{\rm{g}}}}} $ | (1) |
| $ \frac{{\partial {\beta _1}}}{{\partial \tau }} + \nabla \cdot \left( {{\beta _1}\vec v} \right) = - \frac{{{\mathit{\Gamma }_{\rm{m}}}}}{{{\rho _1}}} $ | (2) |
动量方程:
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial \tau }}(\rho \vec v) + \nabla \cdot (\rho \vec v\vec v) = - \nabla p + }\\ {\nabla \cdot \left[ {\mu \left( {\nabla \vec v + \nabla {{\vec v}^T}} \right)} \right] + \rho \vec g} \end{array} $ | (3) |
能量方程:
| $ \frac{\partial }{{\partial \tau }}(\rho E) + \nabla \cdot [\vec v(\rho E + p)] = \nabla \cdot (\lambda \nabla T) + {\mathit{\Gamma }_{\rm{e}}} $ | (4) |
其中,
| $ {\beta _{\rm{g}}} + {\beta _1} = 1 $ | (5) |
| $ \rho = {\beta _{\rm{g}}}{\rho _{\rm{g}}} + {\beta _1}{\rho _1} $ | (6) |
| $ \mu = {\beta _{\rm{g}}}{\mu _{\rm{g}}} + {\alpha _1}{\mu _1} $ | (7) |
| $ E = \frac{{{\beta _{\rm{g}}}{\rho _{\rm{g}}}{E_{\rm{g}}} + {\beta _1}{\rho _1}{E_1}}}{{{\beta _{\rm{s}}}{\rho _{\rm{g}}} + {\beta _{\rm{l}}}{\rho _1}}} $ | (8) |
式(5)~式(8)中,βg和βl分别为汽、液相体积分数;
壳侧降膜沸腾时连续方程和能量方程的源项可由下列模型给出。
1.2.1 相变传质模型根据Lee[15]的相变模型,当流体温度高于汽化温度时,即T≥Tsat条件下,单位控制单元内的汽化量Γm由式(9)计算:
| $ {\mathit{\Gamma }_{\rm{m}}} = {\beta ^{\rm{m}}}{\beta _{\rm{g}}}{\rho _{\rm{g}}}\frac{{T - {T_{{\rm{sat}}}}}}{{{T_{{\rm{sat}}}}}} $ | (9) |
类似地,在T < Tsat条件下,单位控制单元内的冷凝量由式(10)计算:
| $ {\mathit{\Gamma }_{\rm{m}}} = {\beta ^{\rm{m}}}{\beta _{\rm{g}}}{\rho _{\rm{g}}}\frac{{{\rm{T - }}{{\rm{T}}_{{\rm{sat}}}}}}{{{{\rm{T}}_{{\rm{sat}}}}}} $ | (10) |
此时,相对于汽化量为正而言,冷凝量为负值。式中,βm是计算相变传质所用的时间松弛参数,参考文献[16]的推荐值,本研究选取βm=3.0 s-1。
1.2.2 能量传输模型在质量源相Γm确定之后,能量源项Γe可按式(11)计算:
| $ {\mathit{\Gamma }_{\rm{e}}} = - {h_{{\rm{LH}}}}{\mathit{\Gamma }_{\rm{m}}} $ | (11) |
式(11)中,hLH为流体汽化潜热,J/kg,负号表示外界须向控制单元输入热量。
另外,湍流状态下应用VOF模型时,本研究推荐使用RNG k-ε湍流应力模型作为求解补充方程,其湍动能与耗散率方程参见文献[17]。
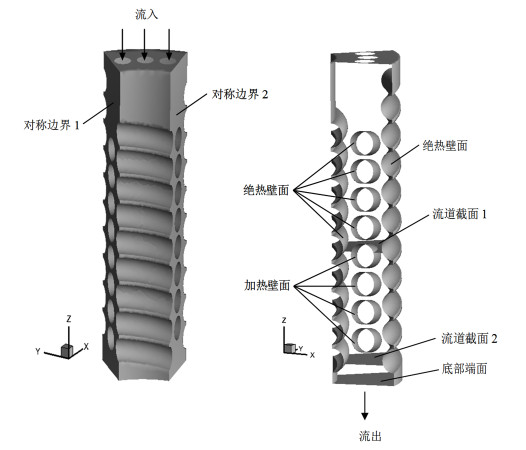
1.3 边界条件对于壳侧36°几何模型,流体从模型上部的3个分流孔流进,从模型底部流出,两侧切割断面均可视为对称边界,中间缠绕层下部4排换热管属于定热流受热壁面,其余壁面则均为绝热壁面,边界条件设置见表 2和图 3。
| 模型部位 | 边界条件类型 |
| 顶部3个分流孔 | 质量流量入口 |
| 底部端面 | 自由出流 |
| 两侧剖面 | 对称边界1和2 |
| 中间缠绕层 | 定热流密度,壁面无滑移 |
| 底部4排管壁 | 定热流密度,壁面无滑移 |
| 其余壁面 | 绝热且无滑移 |
|
| 图 3 壳侧36°几何模型 Fig.3 Shell side model with 36° |
| |
壳侧降膜沸腾所用的VOF模型检验是以文献[5]中乙烷实验数据为依据来进行的,工况参数变化范围是:压力0.2~0.6 MPa,质量流率29.96~93.84 kg/(m2·s),入口干度0~0.16,热流密度1 178~4 744 W/m2。
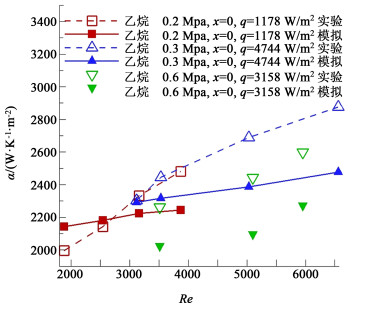
图 4显示了乙烷在入口干度为0时,于不同压力和热流密度条件下的换热系数模拟结果,其中乙烷在0.2 MPa下的质量流率变化范围是29.96~61.62 kg/(m2·s),在0.3 MPa下的质量流率变化范围是44.66~93.84 kg/(m2·s),在0.6 MPa下的质量流率变化范围是40.70~68.97 kg/(m2·s)。图 4中横坐标变量液相雷诺数Re表征了壳侧液相质量流率的变化情况,其表达式定义如式(12):
| $ Re = \frac{{4G(1 - x)A}}{{{\mu _1}\pi \left( {{D_{{\rm{ cree }}}} + {D_{{\rm{ shell }}}}} \right){N_{{\rm{ lay }}}}}} $ | (12) |
|
| 图 4 乙烷变质量流率时的换热模拟结果 Fig.4 Ethane's simulation of heat transfer under varying mass flow rate condition |
| |
式(12)中,G为壳侧质量流率,kg/(m2·s);x为壳侧入口干度,即壳侧入口处汽相质量流量与气液总质量流量的比值;A为壳侧流道平均截面积,m2;μl为液相动力黏度,Pa·s;Dcore、Dshell分别为芯筒、外筒直径,m;Nlay为换热管缠绕层数。
从图 4可以看出,无论是实验数据还是模拟结果,壳侧沸腾换热系数与液相Re呈同向变化,而压力和热流密度对换热系数影响没有液相Re强烈,即液相Re是壳侧换热的首要影响因素。
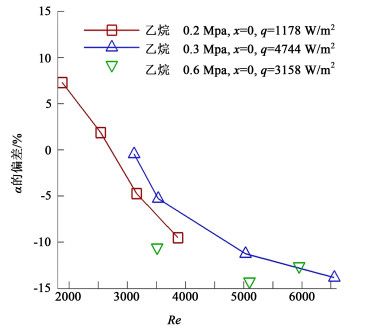
对应于图 4,图 5则显示了乙烷在变质量流率下的换热模拟偏差,可以看出模拟值普遍低于实验值,且换热系数偏差随Re增大有扩大化趋势,但在壳侧常规质量流率40~80 kg/(m2·s)条件下计算偏差在-20%~10%范围内,表明VOF模型的数值模拟结果比较理想。
|
| 图 5 乙烷变质量流率时的换热模拟偏差 Fig.5 Ethane's simulation deviation of heat transfer under varying mass flow rate condition |
| |
表 3显示了乙烷在壳侧入口干度分别为0.05、0.10和0.16时,在不同压力、质量流率及热流密度下的换热系数模拟结果及其偏差。由式(12)可知,在质量流率一定条件下,壳侧入口干度增大,则壳侧液相Re将逐步下降。
| 压力/ MPa | 质量流率/ (kg·m-2·s-1) | 热流密度/ (W·m-2) | 入口干度 | Re | 实验结果/ (W·m-2·K-1) | 模拟结果/ (W·m-2·K-1) | 模拟偏差/ % |
| 0.2 | 50 | 3 158 | 0.05 | 2 729 | 2 200.45 | 1 846.58 | -16.08 |
| 0.10 | 2 585 | 2 139.47 | 1 788.38 | -16.41 | |||
| 0.16 | 2 382 | 2 330.37 | 1 768.00 | -24.13 | |||
| 0.4 | 69 | 1 257 | 0.05 | 4 460 | 2 393.86 | 2 027.06 | -15.32 |
| 0.10 | 4 205 | 2 356.87 | 1 992.50 | -15.46 | |||
| 0.16 | 3 907 | 2 454.64 | 1 881.40 | -23.35 |
由表 3中的实验值可以看到,在定质量流率条件下入口干度小于0.10时换热系数与干度反向变化,而入口干度大于0.10时两者呈同向变化。这表明:随着入口干度增大,壳侧汽相质量增多,其流速也在不断增大,汽相吹扫加热壁面液膜的效果增强,两相流态由降膜流开始向剪切流转换,即干度对换热的促进作用愈加明显,液相Re的作用逐渐削弱。
从表 3还会发现,在入口干度为0.16时,模拟结果变化趋势与实验结果相异,表明VOF模型用于入口干度大于0.10时将无法体现汽相对沸腾换热的促进作用,这一点也可以通过表 3中的模拟偏差剧增得以证实。
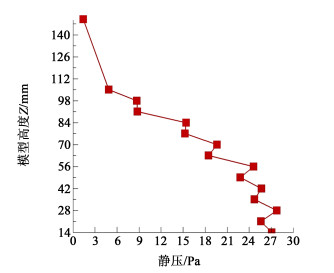
3 降膜沸腾换热特性分析乙烷在p=0.3 MPa,G=40 kg/(m2·s),入口干度x=0.04,q=4 445 W/m2下的降膜沸腾模拟结果见图 6~图 12。图 6和图 8是壳侧降膜流静压变化情况。同过热气相比[2],不同之处是沿流动方向静压总体呈上升趋势,但变化幅度小,其原因是汽、液两相流速低,摩擦压降小,由于位压作用使得静压有所增加。

|
| 图 6 降膜流轴向剖面静压分布 Fig.6 Static pressure distribution of falling flim flow in longitudinal section |
| |
|
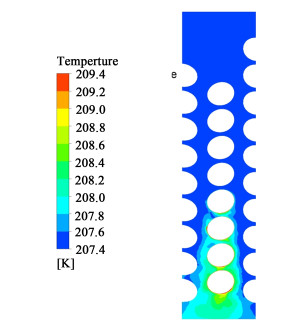
| 图 7 降膜流轴向剖面温度分布 Fig.7 Temperature distribution of falling flim flow in longitudinal section |
| |
|
| 图 8 降膜流流道静压变化 Fig.8 Static pressure change of falling flim flow in passageway |
| |
|
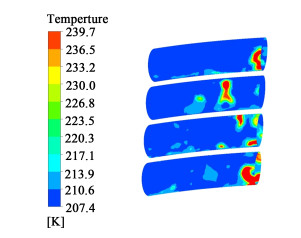
| 图 9 加热管壁面温度分布 Fig.9 Temperature distribution on wall of heat exchanger tube |
| |
|
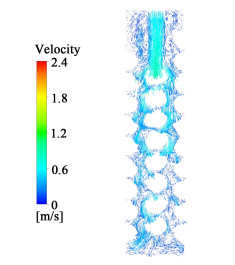
| 图 10 降膜流轴向剖面速度矢量分布 Fig.10 Velocity distribution of falling film flow in longitudinal section |
| |

|
| 图 11 轴向剖面汽相体积分数分布 Fig.11 Vapor volume fraction distribution in longitudinal section |
| |

|
| 图 12 加热管壁面汽相体积分数分布 Fig.12 Vapor volume fraction distribution on wall of heat exchanger tube |
| |
图 7和图 9是乙烷降膜流时的温度分布变化,沿轴向剖面温度变化较小,但是在加热壁面有温度较高的局部区域。结合图 9和图 12可知,这些高温区域正是汽相所处位置,因此当加热壁面存在大量汽体时,即剪切流状态下,使用VOF模型必然会使换热系数严重下降。
图 10展示了乙烷降膜流时在轴向剖面上的速度矢量分布情况。与过热气相比[2],汽和液两相流速显得较低,流道中的流速同样高于管缝处的流速,且沿换热管缠绕方向存在着螺旋向下的低速分量,因此换热器壳侧既有竖直向下的主流运动,又有较为微弱的螺旋环流。另外,结合壳侧轴向剖面上的汽相分布情况(参见图 11)可知,在壳侧顶部存在汽相涡流区域,因此在流进入壳侧后必将受到阻碍作用。
图 11和图 12分别显示了壳侧轴向剖面、加热管壁面处的汽相体积分数分布情况,加热管壁面基本被液膜覆盖,管间液膜呈连续状,流道内以汽相为主,在壳侧顶部集结了较多的汽相。
4 结论1) 对于LNG绕管式换热器壳侧数值研究,当入口干度x≤0.10时,VOF模型能够较好地模拟壳侧沸腾换热现象,可较为准确地预测出沸腾换热系数与冷剂质量流率间的关系。当入口干度x>0.10时,沸腾换热模拟开始失真,沸腾换热系数与入口干度间的正确关系无法得出。模拟失真的原因是壳侧入口干度增大后,汽和液相间滑速比变大,汽相对加热壁面上的液膜扰动、吹扫作用增强,这与VOF模型中的相间汽、液速度一致的假设相悖离,由此导致沸腾换热系数模拟值严重下降。
2) 壳侧降膜沸腾时,液相Re对换热性能起决定性作用,压力、热流密度对换热的影响并不显著。当壳侧入口干度增大后,换热管壁面液膜减少,流态由降膜流转变为剪切流,干度对换热的作用将超越液相Re对换热的影响。
3) 壳侧降膜流状态下,由于汽、液相流速较低,所以摩擦压降损失不大,甚至冷剂的位压减少量就可以平衡摩擦压降。换热管壁面基本被液膜覆盖,管间液膜呈连续状,流道内的流动以汽相为主。壳侧既有竖直向下的主流运动,又有较为微弱的螺旋环流,此外在壳侧顶部将集结较多的汽相。
| [1] |
吴志勇, 陈杰, 浦晖, 等. LNG绕管式换热器结构与流通参数计算方法[J]. 煤气与热力, 2014, 34(3): A34-A39. Wu Zhiyong, Chen Jie, Pu Hui, et al. Calculation of structure and circulation parameters of LNG spiral wound heat exchanger[J]. Gas and Heat, 2014, 34(3): A34-A39. (in Chinese) |
| [2] |
吴志勇, 陈杰, 浦晖, 等. LNG绕管式换热器壳侧过热流动的数值模拟[J]. 煤气与热力, 2014, 34(8): B6-B11. Wu Zhiyong, Chen Jie, Pu Hui, et al. Numerical simulation of superheated flow of refrigerant at shell side of LNG spiral wound heat exchanger[J]. Gas and Heat, 2014, 34(8): B6-B11. (in Chinese) |
| [3] |
Steffen H. Near-Optimal operation of LNG liquefaction processes by means of regulation[D]. Berlin: Berlin Institute of Technology, 2011
|
| [4] |
Neeraas B O. Condensation of hydrocarbon mixtures in coil-wound LNG heat exchangers tube-side heat transfer and pressure drop[D]. Trondheim: Norwegian Institute of Technology, 1993
|
| [5] |
Aunan B. Shell-Side heat transfer and pressure drop in coil-wound LNG heat exchanger[D]. Trondheim: Norwegian University of Science and Technology, 2000
|
| [6] |
Moawed M. Experimental study of forced convection from helical coiled tubes with different parameters[J]. Energy Conversion and Management, 2011, 52(2): 1150-1156. |
| [7] |
Yang Z, Zhao Z, Liu Y, et al. Convective heat transfer characteristics of high-pressure gas in heat exchanger with membrane helical coils and membrane serpentine tubes[J]. Experimental Thermal and Fluid Science, 2011, 35(7): 1427-1434. DOI:10.1016/j.expthermflusci.2011.06.001 |
| [8] |
Jamshidi N, Farhadi M, Ganji D D., et al. Experimental analysis of heat transfer enhancement in shell and helical tube heat exchangers[J]. Applied Thermal Engineering, 2013, 51(2): 644-652. |
| [9] |
Shokouhmand H, Salimpour M R, Akhavan M A. Experimental investigation of shell and coil tube heat exchangers using Wilson plots[J]. International Communications in Heat and Mass Transfer, 2008, 35(1): 84-92. DOI:10.1016/j.icheatmasstransfer.2007.06.001 |
| [10] |
贾金才. 几何参数对绕管式换热器传热特性影响的数值研究[J]. 流体机械, 2011, 39(8): 33-37. Jia Jincai. Numerical analysis geometry parameters on heat transfer for spiral wound heat exchanger[J]. Fluid Machinery, 2011, 39(8): 33-37. DOI:10.3969/j.issn.1005-0329.2011.08.008 (in Chinese) |
| [11] |
Zhang G, Zeng M, Li Y, et al. Numerical study on the thermo-hydraulic performance in the shell side of spiral-wound heat exchanger[C]//ASME 2013 Heat Transfer Summer Conference, New York: American Society of Mechanical Engineers, 2013
|
| [12] |
Lu X, Du X, Zeng M, et al. Experimental and numerical investigation on shell-side performance of multilayer spiral-wound heat exchangers[J]. Chemical Engineering Transactions, 2013, 35: 445-450. |
| [13] |
Xin R C, Ebadian M A. The effects of Prandtl numbers on local and average convective heat transfer characteristics in helical pipes[J]. Journal of Heat Transfer, 1997, 119(3): 467-473. DOI:10.1115/1.2824120 |
| [14] |
Yang Z, Peng X, Ye P. Numerical and experimental investigation of two phase flow during boiling in a coiled tube[J]. International Journal of Heat and Mass Transfer, 2008, 51(5): 1003-1016. |
| [15] |
Lee W H. A pressure iteration scheme for two-phase flow modeling[J]. Multiphase Transport Fundamentals, Reactor Safety, Applications, 1980, 1: 407-431. |
| [16] |
Wu Z, Cai W, Qiu G, et al. Prediction of mass transfer time relaxation parameter for boiling simulation on the shell-side of LNG spiral wound heat exchanger[C]//Advances in Mechanical Engineering, New York: Hindawi Publishing Corporation, 2014
|
| [17] |
Orszag S A, Yakhot V, Flannery W S, et al. Renormalization group modeling and turbulence simulations[C]//Proceedings of the International Conference on Near-Wall Turbulent Flows. Arizona: Elsevier Science Publishers BV, 1993
|
 2019, Vol. 36
2019, Vol. 36