2. 东方电气(广州)重型机器有限公司 广州 511455;
3. 天津大学化工学院, 天津 300072
2. DongFang(Guangzhou) Heavy Machinery Corporation Limited, Guangzhou 511455, China;
3. School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China
管壳式换热器是化工行业应用最广泛的一种换热器,具有结构简单、制造技术成熟、标准规范体系完善及操作弹性大等优点,适用于各种复杂操作工况[1]。但由于其结构优化手段有限,且冷热流体在管壳程操作条件下物理性质复杂,导致管壳式换热器常在较低的传热系数下进行工作,需求传热面积较大,占地面积大,换热器的成本较高[2]。因此,选择正确的计算方法,对管壳式换热器传热系数进行准确设计具有重要的意义。
在管壳式换热器的传热设计中,管侧的传热系数计算已相对成熟,而由于管束、折流板的存在,壳侧工质的流动情况非常复杂,故壳侧传热系数的计算一直是管壳式换热器传热设计中的难点[3-4]。管壳式换热器传热设计需要考虑管子节径比、折流板间距、折流板与壳体内壁间隙以及管束外缘与壳体内壁间隙等结构参数,这些参数均对壳侧的传热性能有较大影响[5-6]。几十年来,人们不断地深入研究,提出了多种计算方法,这些计算方法可分为3类[7-11]:
1) 整体法。整体法是指在计算壳侧流速以及分析其他问题时都是以壳侧总流率为基准,只是在考虑管束几何形状以及折流板的圆缺高度时才引进一些简单的修正系数。这类方法以Donohue法及Kern法为代表[2]。
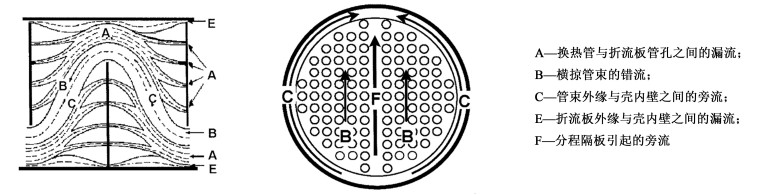
2) 半分析法。Bell-Delaware法是半分析法的代表。Tinker于1947年提出了壳侧流路的概念和模型,即将壳侧流体的流动分为5个部分(如图 1所示):横掠管束的错流;折流板和壳体内壁之间的漏流;折流板管孔与换热管之间的漏流;管束外围和壳内壁之间的旁流;分程隔板引起的旁流。Bell-Delaware法以Tinker模型为基础,同时考虑了各流路的影响,引进若干个独立的修正系数来对计算结果进行修正,但是其不足是各修正系数之间是相互孤立的,不能反映出各流路之间的相互关系,故称之为半分析法。
|
| 图 1 Tinker流路分布图 Fig.1 Tinker flow distribution |
| |
3) 流路分析法。流路分析法同样是以Tinker流路模型为基础,但与Bell-Delaware法不同的是,流路分析法从壳侧流体在各流路的实际分布出发,能够定量地计算出各流路的流量分布,能客观地反映出客观存在的真实情况。流路分析法以美国传热研究公司开发的HTRI软件(V7.2版)以及美国AspenTech公司的HTFS软件(V9.1版)为代表。
本论文分别采用上述3种方法对7台管壳式换热器的壳侧传热系数进行了计算,并通过对计算结果的对比和分析,研究管壳式换热器壳侧传热系数的影响因素,分析3种方法各自的适用性与准确性,以期对工程中此类问题的计算提供参考和建议。
1 换热器结构参数的影响分析本论文选取了7台典型的管壳式换热器,其性能参数及结构参数分别如表 1和表 2所示。从表 2中可以看到,所选取的7台换热器的壳体内径的范围:97~1 880 mm;管程数:单管程1~6管程;壳程数:单壳程、双壳程及分流的壳体形式;换热管的节径比:1.25~1.386;换热管根数:31~2 380根;换热管的排列方式涵盖了正三角形排布及正方形排布;换热管类型涵盖了直管和U形管2种;折流板间距:102~815 mm;折流板圆缺率:13.6%~32.6%,这个范围既涵盖了小缺口折流板到大缺口折流板情况,也包括了折流板缺口区无管子及折流板缺口区有多排管子的情况,分析的结果将更具有代表性和普遍性。
| 序号 | 设备名称 | 管侧 介质 | 壳侧 介质 | 管侧流量/ (kg·s-1) | 壳侧流量/ (kg·s-1) | 管侧介质 进口温度/ ℃ | 管侧介质 出口温度/ ℃ | 壳侧介质 进口温度/ ℃ | 管侧介质 出口温度/ ℃ | 管侧运行 压力/MPa | 壳侧运行 压力/ MPa |
| Ⅰ | 余热排出热交换器 | 放射性水 | 水 | 249.60 | 275.80 | 60.0 | 50.0 | 35.0 | 44.0 | 3.65 | 0.70 |
| Ⅱ | 再生式换热器 | 放射性水 | 放射性水 | 2.35 | 2.35 | 310.0 | 159.0 | 110.0 | 240.0 | 15.50 | 15.50 |
| Ⅲ | 除气冷却器 | 重水 | 水 | 22.70 | 121.00 | 204.0 | 66.0 | 35.0 | 61.2 | 1.62 | 0.69 |
| Ⅳ | 中间净化热交换器 | 重水 | 重水 | 70.56 | 68.46 | 266.0 | 107.0 | 65.0 | 233.3 | 11.08 | 9.74 |
| Ⅴ | 净化冷却器 | 重水 | 水 | 70.56 | 226.60 | 107.0 | 56.6 | 35.0 | 50.6 | 11.00 | 0.69 |
| Ⅵ | 慢化热交换器 | 重水 | 水 | 512.00 | 1 233.00 | 69.0 | 45.1 | 35.0 | 45.0 | 0.69 | 0.69 |
| Ⅶ | 关闭冷却器 | 重水 | 水 | 165.80 | 303.20 | 54.0 | 38.1 | 30.0 | 38.8 | 5.74 | 0.69 |
| 序号 | 设备名称 | 管侧 程数 | 壳侧 程数 | 壳体 内径/ mm | 换热管 规格/ mm | 管子 节距/ 节径比 | 换热管 根数 | 换热管 类型 | 管子排列 方式 | 折流板 间距/ mm | 折流板 圆缺率/ % |
| Ⅰ | 余热排出热交换器 | 2 | 1 | 1 030 | Φ16×1.00 | 22.000/1.375 | 572 | U形管 | 正三角形 | 815 | 18.8 |
| Ⅱ | 再生式换热器 | 1 | 1 | 97 | Φ10×1.50 | 13.000/1.300 | 31 | 直管 | 正三角形 | 102 | 32.6 |
| Ⅲ | 除气冷却器 | 2 | 1 | 750 | Φ15.87×1.13 | 22.000/1.386 | 238 | U形管 | 正方形 | 510 | 16.4 |
| Ⅳ | 中间净化热交换器 | 2 | 2 | 940 | Φ13×1.13 | 16.250/1.250 | 1 120 | U形管 | 正三角形 | 376 | 28.0 |
| Ⅴ | 净化冷却器 | 6 | 1 | 1 100 | Φ15.87×1.13 | 22.000/1.386 | 574 | U形管 | 正三角形 | 369 | 13.6 |
| Ⅵ | 慢化热交换器 | 4 | 分流 | 1 880 | Φ15.87×1.13 | 22.000/1.386 | 2 380 | U形管 | 正三角形 | 504 | 21.1 |
| Ⅶ | 关闭冷却器 | 4 | 1 | 1 397 | Φ15.87×1.13 | 22.000/1.386 | 1 128 | U形管 | 正三角形 | 381 | 17.6 |
壳侧流路中的B流路,即横向冲刷管束的错流的流通路径就是换热管之间的间隙,故换热管的节径比将直接影响B流路的流速,进而影响B流路的传热性能,而B流路是壳侧流体主流,故B流路的传热性能将直接决定整个壳侧的传热性能。
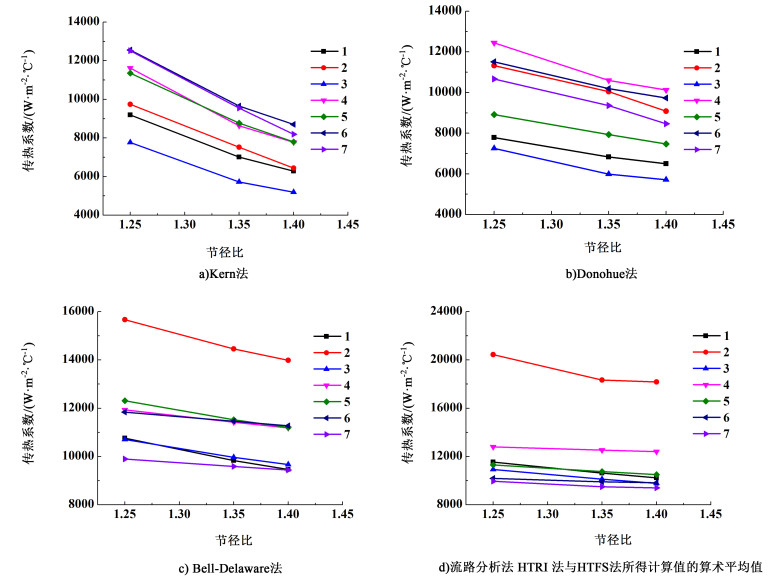
从提高传热性能方面考虑,希望换热管节径比尽可能小,但考虑加工制造的难度,换热管的节径比不能过小,GB/T 151-2014《热交换器》及TEMA-2007《管式交换器制造商协会标准》中均要求节径比不能小于1.25,本论文选取1.25、1.35和1.40 3个节径比进行计算,计算结果如图 2所示。从图 2中可以看出,各种计算方法的计算结果均表明随着节径比的减小,传热系数会增大。其中Kern法对于节径比最为敏感,不同节径比之间的传热系数差异最大,这是由于Kern法中当量直径的公式中关联了管间距,所以节径比的变化既会导致流速的变化,也会导致当量直径的变化,这2种效应的叠加就造成了节径比对于Kern法的影响最大。
|
| 图 2 不同节径比壳侧传热系数计算结果 Fig.2 Calculation results of heat transfer coefficient of different section diameter ratio shell side |
| |
表 3给出了不同节径比壳侧各流路流量百分比,从表 3中可以看到当节径比减小到1.25时,中间净化热交换器,净化冷却器,慢化热交换器以及关闭冷却器的传热系数变化较为明显,甚至比流路分析法的计算结果更大,这是由于当节径比变小时,压缩了B流路的流通面积,使得更多的流体经A流路(即管子与折流板管孔之间的漏流)流走。
| 设备名称 | 节径比 | 流量/% | ||||
| A流路 | B流路 | C流路 | E流路 | F流路 | ||
| 中间净化热交换器 | 1.25 | 37.5 | 38.7 | 8.6 | 15.2 | 0 |
| 1.35 | 32.7 | 44.5 | 9.3 | 13.4 | 0 | |
| 1.40 | 31.0 | 46.7 | 9.6 | 12.7 | 0 | |
| 净化冷却器 | 1.25 | 31.0 | 33.8 | 4.7 | 20.1 | 10.5 |
| 1.35 | 27.8 | 40.2 | 4.0 | 18.1 | 9.9 | |
| 1.40 | 26.6 | 42.6 | 4.0 | 17.3 | 9.5 | |
| 慢化热交换器 | 1.25 | 41.5 | 28.3 | 3.1 | 21.9 | 5.1 |
| 1.35 | 36.7 | 33.5 | 5.5 | 19.5 | 4.8 | |
| 1.40 | 34.5 | 36.2 | 6.4 | 18.4 | 4.5 | |
| 关闭冷却器 | 1.25 | 41.0 | 29.2 | 5.6 | 24.1 | 0 |
| 1.35 | 36.3 | 34.4 | 7.9 | 21.4 | 0 | |
| 1.40 | 34.5 | 37.1 | 8.0 | 20.3 | 0 | |
从表 3中还可以看到,当节径比为1.25时,中间净化热交换器与净化冷却器的A流路流量与B流路流量已经非常接近,而在慢化热交换器及关闭冷却器中出现了A流路流量大于B流路流量的情况。在流路分析法中,B流路是主流,是对传热贡献最大的流路,大量流体经A流路漏流势必影响传热性能,但由于节径比压缩了B流路流通面积使得B流路流速增大,从而传热增强,这个效应要大于A流路漏流的影响,故整体而言,壳侧传热系数会随着节径比的减小而增大。但从图 1可以看到,增大的趋势并不明显,且是以牺牲压降为代价的。反之,对于整体法而言,其并不考虑漏流的影响,只是单纯地考虑由于流通面积的减少导致的流速增加进而传热增强,所以会出现Kern法计算结果比流路分析法的结果更大的情况。
同时,对比表 3与图 2可以看到,整体法计算结果大于流路分析法的现象均出现在管数较多的设备中,这是由于管子根数多,特别是对于U形管形式的管子,其折流板上的管孔数较多,故相同情况下A流路漏流量也更大。但其中的例外是余热排出热交换器,其管数为572根,与净化冷却器的管数很接近,但其整体法的计算结果仍远小于流路分析法,这是由于其折流板间距较大。
1.2 折流板间距折流板间距会影响壳侧的流通面积,进而影响壳侧流速及传热性能,同时折流板间距也是影响壳侧压降以及管束流致振动的重要因素,故折流板间距的选取需要综合考虑。
图 3给出了节径比为1.25时不同折流板间距壳侧传热系数,折流板间距如表 4所示。

|
| 图 3 节径比为1.25时不同折流板间距壳侧传热系数 Fig.3 Shell side heat transfer coefficient of different baffle spacing when pitch diameter ratio is 1.25 |
| |
| 设备名称 | 折流板间距/ mm | 传热系数1a/ [W/(m2·℃)] | 传热系数2b/ [W/(m2·℃)] | 流量/% | ||||
| A流路 | B流路 | C流路 | E流路 | F流路 | ||||
| 余热排出热交换器 | 815 | 9 189 | 11 538 | 11.0 | 62.1 | 12.2 | 14.7 | 0 |
| 500 | 12 019 | 13 500 | 15.2 | 54.1 | 10.8 | 20.0 | 0 | |
| 中间净化热交换器 | 376 | 11 616 | 12 794 | 37.5 | 38.7 | 8.6 | 15.2 | 0 |
| 650 | 8 525 | 11 422 | 28.6 | 48.4 | 10.7 | 12.3 | 0 | |
| 净化冷却器 | 369 | 11 356 | 11 298 | 31.0 | 33.8 | 4.7 | 20.1 | 10.5 |
| 650 | 8 324 | 9 681 | 21.8 | 43.5 | 6.0 | 14.8 | 13.9 | |
| 慢化热交换器 | 504 | 12 557 | 12 557 | 41.5 | 28.3 | 3.1 | 21.9 | 5.1 |
| 850 | 9 404 | 9 404 | 32.9 | 37.6 | 4.2 | 18.1 | 7.1 | |
| 关闭冷却器 | 381 | 12 517 | 12 517 | 41.0 | 29.2 | 5.6 | 24.1 | 0 |
| 700 | 8 948 | 8 948 | 30.9 | 41.6 | 8.0 | 19.5 | 0 | |
| 注:a为Kern法所得计算值;b为流路分析法,即HTRI法与HTFS法所得计算值的算术平均值,下同。 | ||||||||
从图 3中可以看出,随着折流板间距的减小,传热系数增大,但流路分析法的结果增大的趋势较小,而Kern法则较为明显。其原因是折流板间距的缩小使得折流板两侧的压差增大,从而使得A流路的漏流量增大,而Kern法并不考虑漏流的修正,故其对于折流板间距的变化较为敏感。
从表 4中还可以看到,当折流板间距减小时,B流路流量减小,C、F流路流量变化不明显,而A、E流路流量明显增大,可见此时主流方向的B流路流量的一部分变为漏流。而E流路是对传热贡献最小的流路,应尽可能减小其流量,当E流路的流量超过15%时,应考虑增大折流板间距。但折流板间距的增大可能会带来管束流致振动的问题,此时可通过在折流板之间设置支撑板来解决。而对于慢化热交换器及关闭冷却器而言,折流板间距增大后,其E流路流量仍然较大,此时可通过减小折流板与壳体内壁的间隙来解决。
1.3 折流板与壳体内壁间隙折流板与壳体内壁的间隙大小会直接决定E流路流量的大小,如图 4和表 5所示。当折流板与壳体内壁间隙变小时,E流路的流量明显减小,满足E流路流量低于15%的限值。但壳侧传热系数的增大并不明显,这是因为当折流板与壳体内壁间隙变小时,E流路减小的流量并非全部转换成B流路的流量,而是部分转换成A流路流量。但是由于E流路的流量高并不仅仅影响壳侧传热系数,同时也会引起壳侧温度剖面的变形,影响有效平均温差,故当制造和装配精度足够高时,应尽可能减小折流板与壳体内壁的间隙。

|
| 图 4 不同折流板与壳体内壁间隙的壳侧传热系数 Fig.4 Shell side heat transfer coefficient at different gap betweenbaffle plate and inner wall of shell |
| |
| 设备名称 | 折流板与壳体内 壁间隙/mm | 流量/% | ||||
| A流路 | B流路 | C流路 | E流路 | F流路 | ||
| 慢化热交换器 | 6 | 35.6 | 40.9 | 4.6 | 11.3 | 7.7 |
| 10 | 32.9 | 37.6 | 4.2 | 18.1 | 7.1 | |
| 关闭冷却器 | 5 | 33.4 | 45.2 | 8.7 | 12.7 | 0 |
| 8 | 30.9 | 41.6 | 8.0 | 19.5 | 0 | |
管束外缘与壳体内壁之间的间隙是影响C流路流量的关键参数,选取C流路流量较大的2台换热器做对比分析,计算结果如图 5和表 6所示。

|
| 图 5 不同管束外缘与壳体内壁间隙壳侧传热系数 Fig.5 Shell side heat transfer coefficient at different gapbetween tube edge and shell inner wall gap |
| |
| 设备名称 | 管束外缘与壳体 内壁间隙/mm | 流量/% | ||||
| A流路 | B流路 | C流路 | E流路 | F流路 | ||
| 余热排出 热交换器 | 26 | 8.8 | 69.9 | 9.1 | 12.1 | 0 |
| 16 | 9.0 | 73.1 | 5.4 | 12.4 | 0 | |
| 再生式 换热器 | 8 | 9.8 | 56.3 | 21.8 | 12.1 | 0 |
| 6 | 10.3 | 60.0 | 17.4 | 12.6 | 0 | |
可以看出,当管束外缘与壳体内壁间隙减小时,不管是Bell-Delaware法还是流路分析法给出的传热系数均增大。这是因为当间隙减小时,C流路流量减小,而B流路流量增大,故传热性能提高,对比余热排出热交换器和再生式换热器,可以看到当间隙减小时,再生式换热器的传热系数提高更为显著,这是因为其C流路流量减小量及B流路流量的增加量更为明显。而造成这种现象的原因在于再生式换热器的壳体内径只有97 mm,换热管数也仅为31根,即管束外缘与壳体内壁的间隙所占整个流道的份额更大,故相对小的减小量也能产生明显的变化。另外,C流路的流量份额较小时,Bell-Delaware法的结果与流路分析法比较接近,误差较小,而当C流路流量份额较大时,则偏差较大,这是由于2种算法中对于C流路对传热的贡献程度的评价不一致,显然Bell-Delaware法认为C流路对于传热的贡献值较低。
但是管束外缘与壳体内壁的间隙受制造和装配条件的限制,不能过小,一种有效的替代方法是在间隙处设置旁流挡板,如表 7所示。
| 设备名称 | 管束外缘与壳体 内壁间隙/mm | 旁流挡板 对数 | 传热系数2/ [W/(m2·℃)] | 流量/% | ||||
| A流路 | B流路 | C流路 | E流路 | F流路 | ||||
| 余热排出热交换器 | 26 | 0 | 10 442 | 8.8 | 69.9 | 9.1 | 12.1 | 0 |
| 26 | 5 | 11 014 | 9.0 | 71.7 | 7.0 | 12.4 | 0 | |
| 再生式换热器 | 8 | 0 | 16 953 | 9.8 | 56.3 | 21.8 | 12.1 | 0 |
| 8 | 2 | 19 088 | 10.1 | 62.7 | 14.7 | 12.5 | 0 | |
从表 7中可以看出,设置旁流挡板能有效地减小C流路流量并使得B流路流量增加,从而有效地提高壳侧传热性能。
2 不同计算方法的对比分析表 8给出了采用3种方法计算7台管壳式换热器换热系数的计算结果,考虑到HTRI及HTFS在实际工程中均得到了广泛的应用,并取得了良好的效果,其计算结果是相对可靠的,故本论文以HTRI及HTFS的计算结果的算术平均值为基准,将3种计算结果进行了对比,偏差为2个软件计算得到的壳侧传热系数的平均值的偏差。
| 序号 | Kern法 | Donohue法 | Bell-Delaware法 | HTRI | HTFS | |||||||
| 传热系数/ [W/(m2·℃)] | 误差/ % | 传热系数/ [W/(m2·℃)] | 误差/ % | 传热系数/ [W/(m2·℃)] | 误差/ % | 传热系数/ [W/(m2·℃)] | 传热系数/ [W/(m2·℃)] | |||||
| Ⅰ | 6 661 | -36.2 | 6 699 | -35.8 | 9 643 | -7.6 | 10 563 | 10 320 | ||||
| Ⅱ | 7 551 | -51.1 | 9 377 | -39.3 | 9 866 | -41.8 | 18 377 | 15 529 | ||||
| Ⅲ | 5 333 | -46 | 5 798 | -41.3 | 9 739 | -1.4 | 10 164 | 9 592 | ||||
| Ⅳ | 11 616 | -9.2 | 12 444 | -2.7 | 11 916 | -6.9 | 12 995 | 12 593 | ||||
| Ⅴ | 8 060 | -23.7 | 7 613 | -27.9 | 11 281 | 6.8 | 10 304 | 10 812 | ||||
| Ⅵ | 8 863 | -9.9 | 9 764 | -0.8 | 11 322 | 15.1 | 10 146 | 9 532 | ||||
| Ⅶ | 8 318 | -11.9 | 8 466 | -10.3 | 9 481 | 0.4 | 9 142 | 9 737 | ||||
从表 8中可以看出,HTRI与HTFS虽然都采用了流路分析法,但由于一些经验系数的选取上每个公司都有自己的取值,故其结果略有区别。以Kern法及Donohue法为代表的整体法由于其理论模型的缺陷,计算精度较差,偏差均在20%以上,且其计算结果均趋于保守。但对于中间净化热交换器,慢化热交换器以及关闭冷却器这3台换热器而言,Kern法与Donohue法的精度都明显提高,其原因已在1.1中具体分析。Bell-Delaware法作为半分析法,与流路析法一样是以Tinker模型为基础,故其计算精度相对较高,平均误差仅为11.4%,但对于换热器Ⅱ,其计算结果误差较大,达到41.8%,其原因已在1.4中具体分析。
3 结论采用了多种计算方法分别对7台典型的管壳式换热器的壳侧传热系数进行计算,并研究了结构参数对壳侧传热性能的影响规律,得到了如下结论:
1) 管子节径比对于壳侧传热性能影响较大,主要体现在其对于A流路的流量影响较大。管子节径比小,则A流路流量增大,B流路流量减小,传热系数增大,但是壳侧压降将增大;由于Kern法本身物理模型的缺陷,当节径比较小时,Kern法的计算结果明显变大,甚至趋于激进;2)折流板间距除了对A流路有影响,还对E流路影响较大,适当增大折流板间距,有利于减小E流路流量,使得壳侧流体分布更为合理;3)折流板与壳体内壁间隙及管束外缘与壳体内壁间隙分别对于E流路和C流路有较大的影响。减小间隙传热系数增大,反之减小,因此,对于管束外缘与壳体内壁间隙可以采用设置旁流挡板的方式来替代;4)以Kern法和Donohue法为代表的整体法与流路分析法相比偏差较大,结果明显趋于保守。但当换热器管数较多,且管子节径比较小或折流板间距较小时,可能出现整体法计算结果精度高于流路分析法的情况。
Bell-Delaware法因其所采用的计算模型与流路分析法相同,故其计算结果相对于整体法有明显提高,接近流路分析法。但Bell-Delaware法作为半分析法,不能定量求取各流路的流量,仅靠经验系数修正,往往对某些影响因素估计不准,例如当C流路旁流量较大时,其计算偏差较大。
以HTRI和HTFS为代表的流路分析法结合大量实验及工程运行数据对计算模型进行修正,计算结果与工程实际符合的更好。
本论文为了获得在工业中广泛应用的管壳式换热器的结构参数对壳侧传热性能的影响规律,采用Kern法、Donohue法、Bell-Delaware法,以及流路分析法HTRI和HTFS软件包等换热器计算方法,对7台典型的管壳式换热器的壳侧换热系数进行了设计计算和分析,分析计算结果对于该类换热器的设计和应用具有一定借鉴意义。本论文仅研究了不同结构参数对于管壳式换热器壳侧传热系数的影响,并比较了不同计算方法的优劣,下一步将继续研究上述计算方法和关键结构参数对于该类换热器壳侧压降的影响。
| [1] |
刘永贞. 管壳式换热器传热系数影响因素分析[J]. 科技经济导刊, 2016(13): 48-50. Liu Yongzhen. Analysis of influence factors on heat transfer coefficient of shell and tube heat exchanger[J]. Technology and Economic Guide, 2016(13): 48-50. (in Chinese) |
| [2] |
Ahmed S M, Kazi S N, Khan G, et al. Correction to:Effect of various refining processes for Kenaf Bast non-wood pulp fibers suspensions on heat transfer coefficient in circular pipe heat exchanger[J]. Heat and Mass Transfer, 2018, 54(3): 875-882. DOI:10.1007/s00231-017-2176-3 |
| [3] |
Kang H, Chang S. The correlation of heat transfer coefficients for the laminar natural convection in a circular finned-tube heat exchanger[J]. Journal of Heat Transfer, 2018, 140(3): 031801. DOI:10.1115/AJK2011-35012 |
| [4] |
王岳衡. 氟塑料列管换热器的传热系数[J]. 化学工业与工程, 1986, 3(4): 49-53. Wang Yueheng. Heat transfer coefficient of a fluoroplastic tube heat exchanger[J]. Chemical Industry and Engineering, 1986, 3(4): 49-53. (in Chinese) |
| [5] |
冯惠生, 徐菲菲, 刘叶凤, 等. 工业过程余热回收利用技术研究进展[J]. 化学工业与工程, 2012, 29(1): 57-64. Feng Huisheng, Xu Feifei, Liu Yefeng, et al. Review of waste heat utilization technologies for industry processes[J]. Chemical Industry and Engineering, 2012, 29(1): 57-64. DOI:10.3969/j.issn.1004-9533.2012.01.013 (in Chinese) |
| [6] |
邓先和, 蒋夫花. 换热器壳程流路分析及折流与逆流的换热偏差[J]. 华南理工大学学报:自然科学版, 2010, 38(8): 12-16, 22. Deng Xianhe, Jiang Fuhua. Analyses of flow path in shell side of heat exchangers and heat transfer deviation of baffling flow from counter flow[J]. Journal of South China University of Technology:Natural Science Edition, 2010, 38(8): 12-16, 22. (in Chinese) |
| [7] |
刘巍, 邓方义, 刘云哲, 等. 冷换设备工艺计算手册[M]. 北京: 中国石化出版社, 2008. Liu Wei, Deng Fangyi, Liu Yunzhe, et al. Process manual for cold exchange equipment[M]. Beijing: Press of Petroleum Refinery Engineering, 2008. (in Chinese) |
| [8] |
齐福来. 无相变管壳式换热器壳程传热计算方法的进展[J]. 医药工程设计, 2002, 23(3): 29-36. Qi Fulai. Progress in shell side heat transfer calculation methods for phase change shell and tube heat exchangers[J]. Pharmaceutical Engineering Design, 2002, 23(3): 29-36. DOI:10.3969/j.issn.1008-455X.2002.03.010 (in Chinese) |
| [9] |
陈海峰, 石磊. 管壳式换热器的工艺设计方法[J]. 天津职业院校联合学报, 2014, 16(2): 38-41, 55. Chen Haifeng, Shi Lei. Design method of shell-and-tube heat exchanger[J]. Journal of Tianjin Vocational Institutes, 2014, 16(2): 38-41, 55. DOI:10.3969/j.issn.1673-582X.2014.02.010 (in Chinese) |
| [10] |
高晓东, 冯霄. 管壳式换热器壳程强化传热评价方法分析[J]. 华北电力大学学报, 2007, 34(2): 95-97. Gao Xiaodong, Feng Xiao. Evaluation methods to heat transfer enhancement performance in shell of shell and tube heat exchanger[J]. Journal of North China Electric Power University, 2007, 34(2): 95-97. DOI:10.3969/j.issn.1007-2691.2007.02.024 (in Chinese) |
| [11] |
赵志强. TEMA-E型管壳式换热器壳侧流路分析法的改进[J]. 通用机械, 2017(4): 70-73. Zhao Zhiqiang. Improvement of flow path analysis in shell side of TEMA-E heat exchanger[J]. General Machinery, 2017(4): 70-73. (in Chinese) |
 2019, Vol. 36
2019, Vol. 36





