翅片管式换热器高效的传热特性使其广泛地应用于化工制冷、供热、通风等行业中,优化翅片管换热器设计,提高其效率和紧凑性也成为了工程设计和理论研究人员不断追求的目标[1]。
空气侧的热阻是影响换热器换热效率的主要因素,因此提高换热器效率就要提高空气侧的传热系数。研究人员从改变翅片排列方式或改变翅片的形状,对翅片进行开缝或开孔等角度进行研究,设计出了波纹翅片管换热器和开缝,开孔型翅片管换热器。
国内外的学者们对不同翅片类型在不同工况下,对传热的影响因素做了诸多的研究。Lozza等[2]对不同翅片形状换热器的换热能力在实验台上进行了实验,研究对象是有相同的管径与翅片几何尺寸,形状分别为平直翅片、波纹翅片和百叶窗形翅片的翅片管换热器。结果表明翅片类型的不同明显影响着换热性能。2009年,Naphon[3]采用数值模拟,研究波纹片结构参数对温度和流动分布的影响。得出在热流条件一定情况下,波纹夹角的大小影响换热。秦萌等[4]研究了波纹翅片穿圆孔对翅片管换热器换热特性的影响。结果表明穿孔可以提高换热器的换热能力。
目前大多数研究主要集中在化工工业中应用的平直翅片和均匀倾角波纹翅片,对于正弦波纹翅片和平直开缝翅片研究的文献却很少。而且研究主要集中在实验研究方面,数值模拟工作开展比较少[5]。实验只能在一定范围内对换热及阻力进行研究,与之相比数值模拟具有很大的优势。本研究通过数值模拟方法研究了空气在均匀倾角波纹翅片,正弦波纹翅片和平直开缝翅片表面流动的换热特性,并与在相同边界条件下平直翅片表面流动的换热特性的模拟结果进行了对比。分析了翅片波纹形状以及开缝对换热器换热的影响,以及努塞尔数、阻力因子等与雷诺数的关系。
1 翅片管模型与数学问题分析 1.1 结构模型本研究模拟的4种类型的翅片管换热器基管管材料为铜,翅片材料为铝。
模拟的平直翅片管换热器结构简图如图 1所示,平直开缝翅片是在其基础上在翅片上开缝处理。开缝为2 mm×1 mm的矩形,在翅片表面呈百叶窗形状排列[6],如图 2所示。均匀倾角波纹翅片和正弦波纹翅片是在制造过程中将翅片设计成均匀倾角波纹形状和正弦波纹形状。4种类型的翅片管换热器的结构尺寸如表 1所示。

|
| 图 1 平直翅片管换热器结构示意图 Fig.1 The structure diagram of plain fin-and-tube heat exchanger |
| |
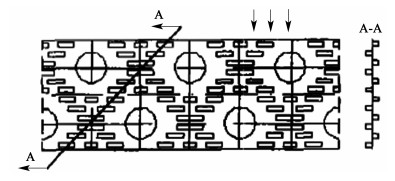
|
| 图 2 平直开缝翅片条缝布置 Fig.2 Schematic diagram of plain slitted fin-and-tube heat exchanger |
| |
| 项目规格 | 平直翅片 | 均匀倾角波纹翅片 | 正弦波纹翅片 | 平直开缝翅片 |
| 管外径D/mm | 7.2 | 7.2 | 7.2 | 7.2 |
| 管壁厚δ1/mm | 0.3 | 0.3 | 0.3 | 0.3 |
| 翅片间距S/mm | 1.5 | 1.5 | 1.5 | 1.5 |
| 翅片厚度δ/mm | 0.105 | 0.105 | 0.105 | 0.105 |
| 横向管间距P1/mm | 14.4 | 14.4 | 14.4 | 14.4 |
| 纵向管间距P2/mm | 12.7 | 12.7 | 12.7 | 12.7 |
| 波纹倾角θ/(°) | 20.86 | |||
| 正弦波纹幅值/mm | 0.75 | |||
| 正弦波纹周期/mm | 10.8 | |||
| 开缝尺寸/(mm×mm) | 2×1 |
换热管采用叉排方式并且竖直安放,根据翅片和换热管排列分布以及流体流动和换热的对称性, 建立周期性单元流道作为简化后的计算模型[1]。图 3所示的为模拟的4种翅片管换热器的俯视图和主视图,选取上下各一半厚度的空气通道以及空气通道之间的翅片板作为单元流道。研究单元为28.8 mm×12.7 mm,空气从左侧横掠换热器。为保证出口无回流,模拟时沿流动方向上入口延长1倍管径,出口延长2倍管径。
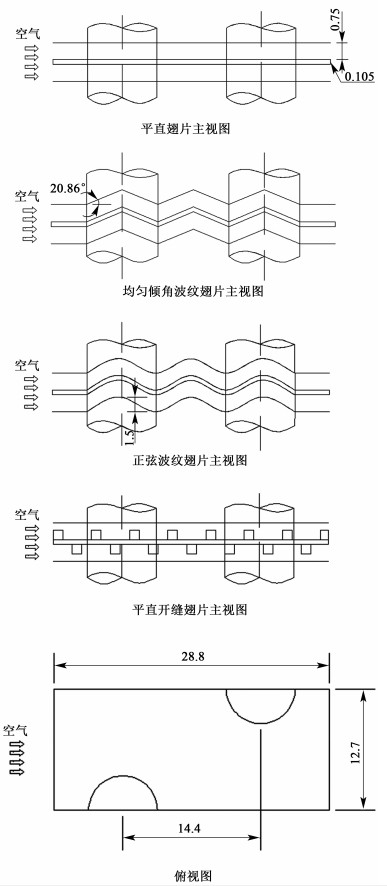
|
| 图 3 三维计算区域选取示意图 Fig.3 Diagram of tube banks for numerical simulation |
| |
在本数值模拟中由于翅片厚度0.105 mm,翅片和管外壁的接触热阻以及其本身的导热温差可被忽略,设定管壁的温度恒定为常数318 K。空气进口速度和温度均匀,速度为1~5 m/s,进口温度设为308 K,出口设为自由压力出口,换热器上下面为周期性边界条件,左右面为对称边界条件,如图 4所示。

|
| 图 4 计算区域的边界条件设置图 Fig.4 The boundary conditions of calculation area |
| |
计算在三维直角坐标系中进行,则换热的控制方程如下:
质量守恒方程:
| $ \frac{{\partial (\rho {u_i})}}{{\partial {x_i}}} = 0\;\;\;\;\left( {i = 1, 2, 3} \right) $ | (1) |
动量守恒方程:
| $ \frac{{\partial (\rho {u_i}{u_j})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left( {\mu \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)-\frac{{\partial P}}{{\partial {x_j}}}\;\;\;\;\left( {i = 1, 2, 3} \right) $ | (2) |
能量守恒方程:
| $ \frac{\partial }{{\partial {x_i}}}(\rho {u_i}T) = \frac{\partial }{{\partial {x_i}}}\left( {\frac{\lambda }{{Cp}}\;\cdot\;\frac{{\partial T}}{{\partial {x_i}}}} \right)\;\;\;\;\left( {i = 1, 2, 3} \right) $ | (3) |
式(1)~(3)中:ρ为密度,kg/m3;u为速度,m/s;P为静压,Pa;CP为定压比热容,kJ/(kg·K);T为温度,K;μ为动力黏度系数,kg/(m·s);λ为导热系数,W/(m·K)。
2 计算过程及计算结果处理方法 2.1 计算方法首先使用GAMBIT三维制图工具制作出平直片、均匀倾角波纹翅片、正弦波纹翅片平直开缝翅片4种形式的翅片管换热器模型,进行网格划分。把得到的MESH文件导入数值模拟软件FLUENT中。
在FLUENT进行模型计算时以稳态格式求解,流体为不可压缩流动。采用层流模型计算;为了得到精确解,动量方程和能量方程均用二阶迎风差分格式;压力和速度耦合的问题采用SIMPLE方法,最终得到4种类型的翅片管换热器空气流道中心面上的流场分布。进行数据处理得到在进口风速1~5 m/s的不同工况下,4种翅片形式的翅片管换热器的换热量Q、压降ΔP、努塞尔数Nu、阻力因子f等与进口风速u和雷诺数Re的关系。
2.2 计算结果处理方法1) 雷诺数定义如下:
| $ Re = \frac{{\rho {u_{\rm{m}}}{D_{\rm{h}}}}}{\mu } $ | (4) |
式(4)中:um为流体侧最小流通截面处的平均速度,m/s;Dh为流体侧最小流通截面处当量直径,m。
2) 对流换热系数定义[9]:
| $ h = \frac{q}{{{T_{{\rm{wall}}}}-{T_{{\rm{ref}}}}}} $ | (5) |
式(5)中:q为热流密度,W/m2;Twall为壁面温度,K;Tref为流体参考温度,K。
3) 努塞尔数定义如下:
| $ Nu = h{D_{\rm{h}}}/\lambda $ | (6) |
4) 总换热量定义:
| $ Q = m{c_p}({T_{{\rm{out}}}}-{T_{{\rm{in}}}}) $ | (7) |
式(7)中:m为流体质量流率,kg/s;Tout为流体入口平均温度, K;Tin为流体入口平均, K。
5) 阻力因子定义:
| $ f = \frac{{2\Delta P{D_{\rm{h}}}}}{{\rho {u^2}L}} $ | (8) |
式(8)中:ΔP为流体进出口平均压降, Pa。
3 计算结果与分析 3.1 不同翅片形式的换热流动情况分析1) 通过模拟,得到空气进口流速为3 m/s时,4种形式翅片的空气通道中心面温度分布如图 5所示。

|
| 图 5 翅片空气通道中心面上的温度分布图 Fig.5 The temperature distribution of air channel center face |
| |
由图 5可知,在空气进口流速为3 m/s时,4种不同形状翅片的空气进口中心面上的温度分布有明显的差别。气体掠过平直翅片时,由于翅片表面光滑平坦,空气受到较少的扰动,所以换热过程平稳的进行,得到的温度等值线也是均匀分布,呈波纹状。当采用均匀倾角波纹翅片和正弦波纹翅片时,由于翅片表面高低起伏,空气流过波纹的波峰和波谷时,空气流动速度的大小和方向都会受到影响,进而影响到传热的过程。这2种翅片类型呈现的温度等值线没有均匀分布,呈狭长条带状。当采用平直开缝翅片时,由于开缝的存在,空气扰动更加剧烈,传热效果也显著增强[7],相同位置的温度比以上3种翅片类型都高。
从整体看,4种翅片结构呈现出共同的特点:在管前区域,温度场均匀递增,换热效果显著,空气掠过换热管,在管后尾迹区,由于空气发生绕流产生了强烈的回流和涡流扰动,这个区域换热效果最好,温度差不多和管壁温度相当[1]。
2) 空气进口流速为3 m/s时4种不同翅片形式的压力等值线分布如图 6所示。
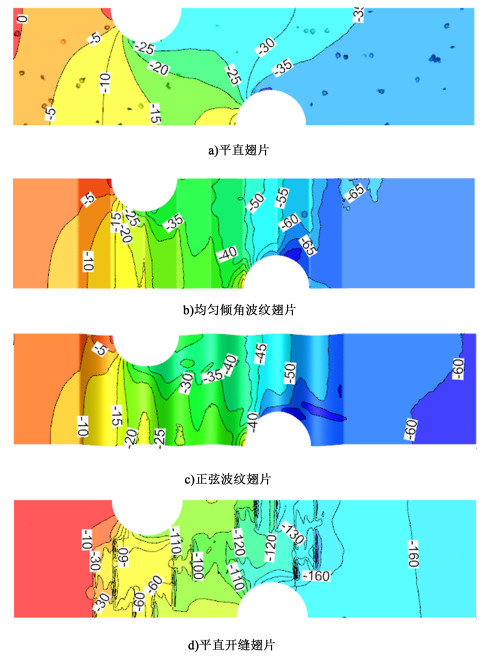
|
| 图 6 翅片空气通道中心面上的压力等值线分布图 Fig.6 The pressure contour distribution of air channel center face |
| |
由图 6可知,空气流过平直翅片,受到较少扰动,压力场分布均匀。均匀倾角波纹翅片和正弦波纹翅片,由于翅片表面的高低起伏,空气流过时受到剧烈的扰动,进而也产生了一定的能量损失,也即压力损失,因而呈现的压力场分布比较紊乱,在波纹的波峰和波谷处有明显的变化。空气流过翅片表面时,在2个换热管之间的最窄流通面两侧,压力是先降低然后增加,有时还会出现相对负压区。这有可能是因为空气在掠过换热管时,由于流通面的变化,空气流速会先增加后减少,然后气体的压力先减小后增大。
3.2 进口速度对换热的影响进口速度与换热量和压力损失之间的关系曲线如图 7和图 8所示。

|
| 图 7 换热量与进口速度之间关系曲线 Fig.7 Curve of the relationship between heat transfer and inlet velocity |
| |
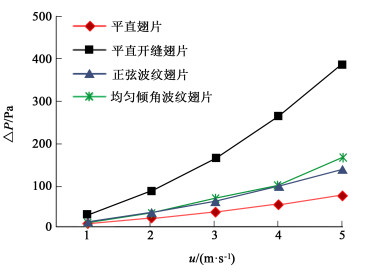
|
| 图 8 压降与进口速度之间关系曲线 Fig.8 Curve of the relationship between pressure drop and inlet velocity |
| |
由图 7可知,在空气进口速度u由1 m/s增加到5 m/s的过程中,4种翅片结构的换热量Q随u的增加而增大。在速度较小的情况下,换热量与进口速度之间呈近似线性关系。在相同工况下,平直开缝翅片换热效果最好,正弦波纹翅片的换热量略高于均匀倾角波纹翅片,平直翅片换热能力最差。当空气流速是3 m/s时,平直开缝翅片、正弦波纹翅片、均匀倾角波纹翅片的换热量分别比平板翅片增加19.8%、11.3%和11.2%, 强化传热效果显著。
随着空气进口速度u的提高,压力损失也随之增大,如图 8所示。当进口气速超过2 m/s后,压力损失增加的幅度渐趋陡峭[1]。平直开缝翅片的压力损失最高,其次是正弦波纹翅片和均匀倾角波纹翅片,平直翅片的压力损失最低。因此,平直开缝翅片管换热器在提高换热能力的同时也造成能量损失的提高。
3.3 雷诺数、阻力因子与努塞尔数之间的关系曲线图 9为努谢尔数Nu与雷诺数Re的变化关系曲线,Nu高则表示换热器换热效果显著。

|
| 图 9 努塞尔数与雷诺数之间关系曲线 Fig.9 Curve of relationship between Nu and Re |
| |
由图 9可知:在相同Re情况下,平直开缝翅片空气侧的换热效果明显优于平直翅片,Nu高出11%。在相同的工况下,空气流过平直开缝翅片时,由于开缝的存在,增加了对空气的扰动作用,空气的边界层被间断,使其无法在流动方向上持续增厚,因而边界层间断再重生,减薄了边界层的厚度,达到了增强换热的目的[8]。
图 10为其阻力因子f随Re变化的关系曲线,可知随着进口风速的增加,即雷诺数Re增大,压力损失ΔP不断增加,阻力因子f在逐渐减少。在同一工况下,平直开缝翅片阻力因子最大,2种形式的波纹翅片阻力因子大致相等,介于平直开缝和平直未开缝翅片之间。由于开缝的作用,使空气受到较大的干扰,产生了较大的阻力,使得平直开缝翅片的空气侧压力损失比平直翅片平均高出11.2%,阻力因子平均增加13.5%[9]。而均匀倾角波纹翅片和正弦波纹翅片表面的起伏,空气流动也受到扰动,空气侧压力损失和阻力因子都高于平直翅片。

|
| 图 10 阻力因子与雷诺数之间关系曲线 Fig.10 Curve of relationship between resistance factor and Re |
| |
对4种形式翅片管换热器空气侧的流动和传热特性进行了数值模拟,比较了在进口风速为1~5 m/s,Re范围为492.9~2 464.5时,换热量Q、进出口压降ΔP、努塞尔数Nu和阻力因子f与u和Re的关系,并分析了不同形式换热器换热通道中心面上的温度分布和压力分布情况,得到以下结论:
1) 采用开缝的方法,使翅片表面形成间断,不但可以节省原材料,还可减薄流体传热边界层,增加流体扰动,达到换热增强的目的,大大提高换热器的工作能力。
2) 在相同规格的翅片管和边界条件下,正弦波纹翅片和均匀倾角翅片管换热器的换热量均高于平直翅片,努塞尔数也增加。同时二者的压力损失和阻力因子相对于翅片开缝的增加幅度较小,这说明在较小进口风速下,正弦波纹翅片和均匀倾角波纹翅片可在不产生过多能量损失的情况下,显著提高换热器的换热能力。
3) 通过作者的研究,发现翅片开缝和正弦波纹翅片都对换热器换热效率有明显的提升作用。未来的数值模拟研究可着眼于翅片开缝的形状和排列方式对传热特性的影响,另外还可将正弦波纹与翅片开缝结合起来,在正弦波纹翅片表面做开缝或开孔处理,这种类型的翅片兼具开缝和正弦波的优点,如果其换热能力得到实验验证,即可广泛应用在化工生产中。
| [1] |
周俊杰, 徐国权, 张华俊. FLUENT工程技术与实例分析[M]. 北京: 中国水利水电出版社, 2010. Zhou Junjie, Xu Guoquan, Zhang Huajun. FLUENT engineering and case analysis[M]. Beijing: China Water Power Press, 2010. (in Chinese) |
| [2] |
Lozza G, Merlo U. An experimental investigation of heat transfer and friction losses of interrupted and wavy fins for fin-and-tube heat exchangers[J]. International Journal of Refrigeration, 2001, 24(5): 409-416. DOI:10.1016/S0140-7007(00)00035-9 |
| [3] |
Naphon P. Effect of wavy plate geometry configurations on the temperature and flow distributions[J]. International Communications in Meat and Mass Transfer, 2009, 36(9): 942-946. DOI:10.1016/j.icheatmasstransfer.2009.05.007 |
| [4] |
秦萌, 尤学一. 波纹穿圆孔翅片管换热器换热特性的数值模拟[J]. 天津城建大学学报, 2015(5): 363-368. Qin Meng, You Xueyi. Numerical simulation of corrugated wear round hole fin-and-tube heat exchanger[J]. Journal of Tianjin Urban Construction University, 2015(5): 363-368. DOI:10.3969/j.issn.1006-6853.2015.05.012 (in Chinese) |
| [5] |
韩占忠, 王敬, 兰小平. FLUENT流体工程仿真计算实例与应用[M]. 北京: 北京理工大学出版社, 2004.
|
| [6] |
李慧珍, 屈治国, 程永攀, 等. 开缝翅片流动和传热性能的实验研究及数值模拟[J]. 西安交通大学学报, 2005, 39(3): 229-232. Li Huizhen, Qu Zhiguo, Cheng Yongpan, et al. Experimental and numerical study on heat transfer and fluid flow characteristics of slotted fin-and-tube heat transfer surfaces[J]. Journal of Xi'an Jiaotong University, 2005, 39(3): 229-232. DOI:10.3321/j.issn:0253-987X.2005.03.003 (in Chinese) |
| [7] |
袁益超, 廖飞页, 赵存江, 等. 双向开缝翅片管换热器传热与阻力特性试验研究[J]. 热科学与技术, 2014, 13(3): 235-239. Yuan Yichao, Liao Feiye, Zhao Cunjiang, et al. Experimental study on heat transfer and resistance characteristics of super slit finned tube exchanger[J]. Journal of Thermal Science and Technology, 2014, 13(3): 235-239. (in Chinese) |
| [8] |
Wang C. Empirical correlations for heat transfer and flow friction characteristics of herringbone wavy fin-and-tube heat exchangers[J]. International Journal of Refrigeration, 2003, 25: 673-680. |
| [9] |
孟辉, 晋欣桥, 杜志敏, 等. 开缝翅片管换热器换热和压降特性及其评价方法[J]. 上海交通大学学报, 2009, 43(5): 766-771. Meng Hui, Jin Xinqiao, Du Zhimin, et al. Measurement method and experimental study on heat transfer and pressure drop characteristics of slit fin-tube heat exchangers[J]. Journal of Shanghai Jiaotong Univesity, 2009, 43(5): 766-771. DOI:10.3321/j.issn:1006-2467.2009.05.018 (in Chinese) |
 2019, Vol. 36
2019, Vol. 36





