在可充电电池中,氧化还原液流电池在运行过程中电极不发生物理和化学变化,这使得电池具有更稳定和持久的性能[1],实现了长时间的充放电循环使用寿命。相比其他液流电池,可溶铅酸液流电池的另一个优势是电池体系只使用一种电解液,因此在运行时不需要隔膜,这避免了与通过隔膜产生的电解液的相互污染,并且有利于提升电池的能量效率。
但是实现整个电池存储系统的商业化为这项技术的研究者提出了新的挑战:电池规模的扩大以及性能优化,电解液稳定性的提高,电极材料抗氧化性能的提升等。考虑到成本以及时耗,很多这些问题并不适合单独进行实验室分析。因此,应用模拟和仿真方法来辅助实验室测试,通过模拟的方法研究参数变化对操作条件的影响以及体系的结构,可以缩小实验测试范围,避免大量的实验室研究[2-3]。本研究对可溶铅酸液流电池建立模型,进行模拟和仿真。
1 模型 1.1 模型建立可溶铅酸氧化还原液流电池在21世纪初由Pletcher等[4]提出,电池含有2个惰性电极以及溶有甲基磺酸铅的甲基磺酸单一电解液。电池主要依靠酸中Pb(Ⅱ)的电极反应[5]。充电时,铅沉积在负极,同时二氧化铅沉积在正极;而放电时,铅和二氧化铅层分别通过氧化反应和还原反应溶解为可溶的Pb (Ⅱ)离子,回到电解液中。
正极反应:
| $ {\text{Pb}}_{\left( {{\text{aq}}} \right)}^{2 + } + 2{{\text{H}}_2}{\text{O}} \rightleftharpoons {\text{Pb}}{{\text{O}}_{2\left( {\text{s}} \right)}} + 4{{\text{H}}^ + } + 2{{\text{e}}^ - } $ | (1) |
负极反应:
| $ {\text{Pb}}_{\left( {{\text{aq}}} \right)}^{2 + } + 2{{\text{e}}^ - } \rightleftharpoons {\text{P}}{{\text{b}}_{\left( {\text{s}} \right)}} $ | (2) |
整体电池反应:
| $ 2{\text{Pb}}_{\left( {{\text{aq}}} \right)}^{2 + } + 2{{\text{H}}_2}{\text{O}} \rightleftharpoons {\text{Pb}}{{\text{O}}_{2\left( {\text{s}} \right)}} + {\text{P}}{{\text{b}}_{\left( {\text{s}} \right)}} + 4{{\text{H}}^ + } $ | (3) |
由于对充放电性能的明显影响,复合氧化物沉积(表示为PbOx)的形成与再氧化在模型中不可忽略[6]。作为近似,假设复合氧化物在放电时由PbO2转化而来,在接下来的充电过程再氧化为PbO2。一种可能的电化学机理(当x=1时)表示为:
| $ {\text{Pb}}{{\text{O}}_2} + 2{{\text{e}}^ - } + 2{{\text{H}}^ + } \rightleftharpoons {\text{PbO}} + {{\text{H}}_2}{\text{O}} $ | (4) |
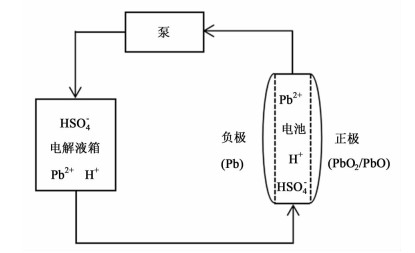
可溶铅酸液流电池系统的运行原理和电池构建如图 1所示[7]。体系装满含有Pb(Ⅱ)离子的甲基磺酸电解液槽,电解液被不断泵入电池堆。Bates等[8]以平板电极建立二维模型进行模拟研究,本研究在其研究基础上,以弧形电极代替平板电极进行仿真模拟。
|
| 图 1 可溶铅酸液流电池和液流体系 Figure 1 The soluble lead-acid battery and the flow system |
| |
研究中应用如下假设:近似采用稀溶液,假设水为主要组分,液流被认为是层流并且不可压缩,Pb和PbO2沉淀厚度与反应器尺寸相比忽略不计。电解液只电离出Pb2+、H+和HSO4-[8-10]。
1.2 模型方程用于液体电解液中各组分(Pb2+、H+和HSO4-)的容积平均法物料衡算可以用式(5)表示:
| $ \frac{{\partial {c_i}}}{{\partial t}} + \nabla {N_i} = - {S_i} $ | (5) |
式(5)中:Si为组分i的源项,定义如表 1所示。
| 源项 | 正极 | 负极 |
| Pb2+ | ||
| H2O | ||
| H+ |
用优化的Nernst-Planck方程表示浓度通量[9],其中带电组分的传输通过扩散,迁移和对流进行,总通量为:
| $ {{\vec N}_l} = - {D_i}\nabla {c_i} - \frac{{{z_i}{c_i}{D_i}}}{{RT}}F\nabla {\varphi _{\rm{e}}} + \vec u{c_i} $ | (6) |
电解液被认为是电中性的,∑izici=0,电解液的体积流速由不可压缩Navier-Stokes[10]方程和连续性方程得到:
| $ \begin{array}{*{20}{c}} {\rho \frac{{\partial \vec u}}{{\partial t}} + \rho \left( {\vec u \cdot \nabla } \right)\vec u = - \nabla p + u{\nabla ^2}\vec u}\\ {\nabla \vec u = 0} \end{array} $ | (7) |
电解液中总的电流密度可以用电中性条件进行计算:
| $ {{\vec i}_{\rm{e}}} = \sum\nolimits_i {{z_i}F{{\vec N}_l}} = - {\sigma _{\rm{e}}}\nabla {\phi _{\rm{e}}} - F\sum\nolimits_i {{z_i}{D_i}\nabla {c_i}} $ | (8) |
其中离子电导率σe表示为:
| $ {\sigma _{\rm{e}}} = \frac{{{F^2}}}{{RT}}\sum\nolimits_i {z_i^2{D_i}{c_i}} $ | (9) |
在所有区域,包括边界,离子和电子流满足电荷守恒:
| $ \nabla \cdot {{\vec i}_{\rm{e}}} + \nabla \cdot {{\vec i}_{\rm{s}}} = 0 $ | (10) |
电极电势由欧姆定律给出:
| $ - {\sigma _{\rm{s}}}{\nabla ^2}{\phi _{\rm{s}}} = - \nabla \cdot \vec i $ | (11) |
用于正反应和逆反应的近似等效电荷转移系数被用在2个电极反应中:
| $ {i_1} = Fk_0^{{\rm{Pb}}{{\rm{O}}_2}}{c_{{\rm{P}}{{\rm{b}}^{2 + }}}}\left( {\frac{{{c_{{{\rm{H}}^ + }}}}}{{c_{{{\rm{H}}^ + }}^0}}} \right)\left[ {\exp \left( {\frac{{F{\eta _ + }}}{{RT}}} \right) - \exp \left( { - \frac{{F{\eta _ + }}}{{RT}}} \right)} \right] $ | (12) |
| $ {i_2} = Fk_0^{{\rm{Pb}}}{c_{{\rm{P}}{{\rm{b}}^{2 + }}}}\left[ {\exp \left( {\frac{{F{\eta _ - }}}{{RT}}} \right) - \exp \left( { - \frac{{F{\eta _ - }}}{{RT}}} \right)} \right] $ | (13) |
过电势表示为:
| $ {\eta _ \pm } = {\phi _{{\rm{s \pm }}}} - {\phi _{\rm{e}}} - {E_ \pm } $ | (14) |
E±分别为反应(1)和(2)的开路电势。由Nernst方程计算得到:
| $ {E_ + } = {E_{0,1}} + \frac{{2.3RT}}{F}\left( {\ln {c_{{\rm{P}}{{\rm{b}}^{2 + }}}} - \ln {c_{{{\rm{H}}^ + }}}} \right) $ | (15) |
| $ {E_ - } = {E_{0,2}} + \frac{{2.3RT}}{F}\ln {c_{{\rm{P}}{{\rm{b}}^{2 + }}}} $ | (16) |
正极PbO形成和再氧化过程的动力学,用Butler-Volmer方程表示:
| $ \begin{array}{*{20}{c}} {{i_{{\rm{PbO}}}} = F\left[ {K_0^{\rm{f}}{{\left( {{c_{{\rm{PbO}}}}} \right)}^{{v_1}}}\exp \left( {\frac{{F{\eta _ + }}}{{RT}}} \right) - } \right.}\\ {\left. {K_0^{\rm{b}}{{\left( {{c_{{\rm{Pb}}{{\rm{O}}_2}}}} \right)}^{{v_2}}}{{\left( {{c_{{{\rm{H}}^ + }}}} \right)}^{{v_3}}}\exp \left( { - \frac{{F{\eta _ + }}}{{RT}}} \right)} \right]} \end{array} $ | (17) |
其中:υ1、υ2和υ3分别是PbO、PbO2和H+的反应级数; K0f和K0b为反应(4)正向和逆向的反应常数。
1.4 能量守恒能量守恒考虑到热传导、对流热交换以及化学反应和欧姆电阻产生的热。作为可靠的第一近似,液相和固相处在同一温度,能量守恒表示为:
| $ \frac{\partial }{{\partial t}}\left( {{\rho _l}{C_l}T} \right) + \nabla \cdot \left( {\bar u{\rho _l}{C_l}T} \right) - \bar \lambda {\nabla ^2}T = \sum\nolimits_k {{Q_k}} $ | (18) |
式(18)中:Qk为热产生项,定义如表 2所示。它们表示活化损失、化学反应和欧姆电阻产生的热。
| 源项 | 正极 | 负极 |
| Qact | η1 |
η2 |
| Qrev | -ΔS1T |
-ΔS2T |
| Qohm | σs| |
σs| |
标准反应熵表示如下:
| $ \Delta {S_{0,j}} = \left( {\sum\nolimits_{{\rm{products}}} {S_{0,j}^{{\rm{products}}}} } \right) - \left( {\sum\nolimits_{{\rm{reactants}}} {S_{0,j}^{{\rm{reactants}}}} } \right) $ | (19) |
其中S0, jproducts,S0, jreactants是反应j(j=1, 2)中产物和反应物的标准生成熵。对于每一个反应j,标准反应熵与反应的标准吉布斯自由能变化ΔG0,j以及标准反应焓变化ΔH0,j有关,热力学关系表示为:
| $ \Delta {G_{0,j}} = \Delta {H_{0,j}} - T\Delta {S_{0,j}} $ | (20) |
用方程(20)和ΔG0,j=-nFE0, j,其中E0, j为反应的标准电势,得到ΔS0,j关于温度的关系式:
| $ - nF\frac{{\partial \Delta {E_{0,j}}}}{{\partial T}} = \frac{{\partial \Delta {G_{0,j}}}}{{\partial T}} = \Delta {S_{0,j}} $ | (21) |
式(21)中:标准电势E0, 1和E0, 2是温度的函数。
| $ E_0^T = E_0^{298} + \left( {T - 298} \right){\left( {\frac{{{\rm{d}}{E_0}}}{{{\rm{d}}T}}} \right)_{298}} $ | (22) |
式(22)中:E0298是T=298 K时标准电极电势,
| $ E_{0,1}^T = E_{0,1}^{298} + \left( {T - 298} \right)\left( { - 253 \times {{10}^{ - 5}}} \right) $ | (23) |
| $ E_{0,2}^T = E_{0,2}^{298} + \left( {T - 298} \right)\left( { - 395 \times {{10}^{ - 5}}} \right) $ | (24) |
反应常数同样是温度的函数,可以写为Arrhenius形式:
| $ {k_j} = {k_{{\rm{ref}},j}}\exp \left( { - \frac{{\Delta {G_{0,j}}}}{R}\left[ {\frac{1}{{{T_{{\rm{ref}},j}}}} - \frac{1}{T}} \right]} \right) $ | (25) |
因此,
| $ {k_j} = {k_{{\rm{ref}},j}}\exp \left( {\frac{{nF{E_{0,j}}}}{R}\left[ {\frac{1}{{{T_{{\rm{ref}},j}}}} - \frac{1}{T}} \right]} \right) $ | (26) |
式(25)~(26)中:kref, j为在给定温度Tref, j(j=1, 2)时的值。
1.5 容器和再循环方程在电极和泵之间电解液的移动导致入口边界处的浓度随时间发生改变。根据体积守恒,出口边界处的体积流ω=υinAout,(截断面积Aout)。由计算得到的在流出边界处的平均浓度为:
| $ c_i^{{\rm{out}}} = \int_{y = h} {{c_i}{\rm{d}}x} $ | (27) |
入口浓度由下式质量守恒近似,式中假设混合瞬时发生且忽略反应在总容器中的电解液体积V,则:
| $ \frac{{{\rm{d}}c_i^{{\rm{in}}}}}{{{\rm{d}}t}} = \frac{w}{v}\left( {c_i^{{\rm{out}}} - c_i^{{\rm{in}}}} \right);c_i^{{\rm{in}}}\left( 0 \right) = c_i^{\rm{0}} $ | (28) |
入口处温度由热平衡决定(假设溶液密度和比热容是常数,且容器中溶液混合即时发生):
| $ \frac{{{\rm{d}}{T^{{\rm{in}}}}}}{{{\rm{d}}t}} = \frac{w}{v}\left( {{T^{{\rm{out}}}} - {T^{{\rm{in}}}}} \right);{T^{{\rm{in}}}}\left( 0 \right) = {T_0} $ | (29) |
式(29)中:Tin和Tout分别为入口和出口边界温度。
1.6 初始边界条件沿边界表面,压力应用Neumann条件:
| $ \nabla p \cdot \vec n = 0\left( {除去入口和出口表面} \right) $ | (30) |
在入口处,电解液中多种组分以预定的体积流速进入,且组分浓度如下:
| $ {c_i} = c_i^{{\rm{in}}}\left( t \right);\vec u = \left( {0,{v_{{\rm{in}}}}} \right)\left( {入口} \right) $ | (31) |
在出口处,液流压力已定,组分扩散流量设置为0:
| $ - {D_i}\nabla {c_i} \cdot \vec n = 0;p = {p_{{\rm{out}}}}\left( {出口} \right) $ | (32) |
在电极表面,应用无滑移条件:
| $ \vec u = 0;x = 0;x = w $ | (33) |
对于电极电势分布的通量条件:
| $ - {\sigma _{\rm{s}}}\nabla {\phi _{\rm{s}}} = 0;x = 0;x = w;y = 0;y = h $ | (34) |
电解液中电势分布定义为(充电时):
| $ - {\sigma _{\rm{e}}}\nabla {\phi _{\rm{e}}} \cdot \vec n = \left\{ \begin{array}{l} {I_{{\rm{app;}}}}x = 0\\ - {I_{{\rm{app;}}}}x = w \end{array} \right. $ | (35) |
放电时,符号变号。
入口处温度:
| $ T = {T^{{\rm{in}}}} $ | (36) |
浓度和电势符合一致性条件:
在正极:
| $ \begin{array}{*{20}{c}} {{c_i} = c_i^0}\\ {{\phi _{{{\rm{s}}^ + }}} = {E_ + }}\\ {\phi = 0} \end{array} $ | (37) |
在负极:
| $ \begin{array}{*{20}{c}} {{c_i} = c_i^0}\\ {{\phi _{{{\rm{s}}^ - }}} = {E_ - }}\\ {\phi = 0} \end{array} $ | (38) |
电池初始温度在电池内均匀分布:
| $ T\left( {t = 0} \right) = {T_0} $ | (39) |
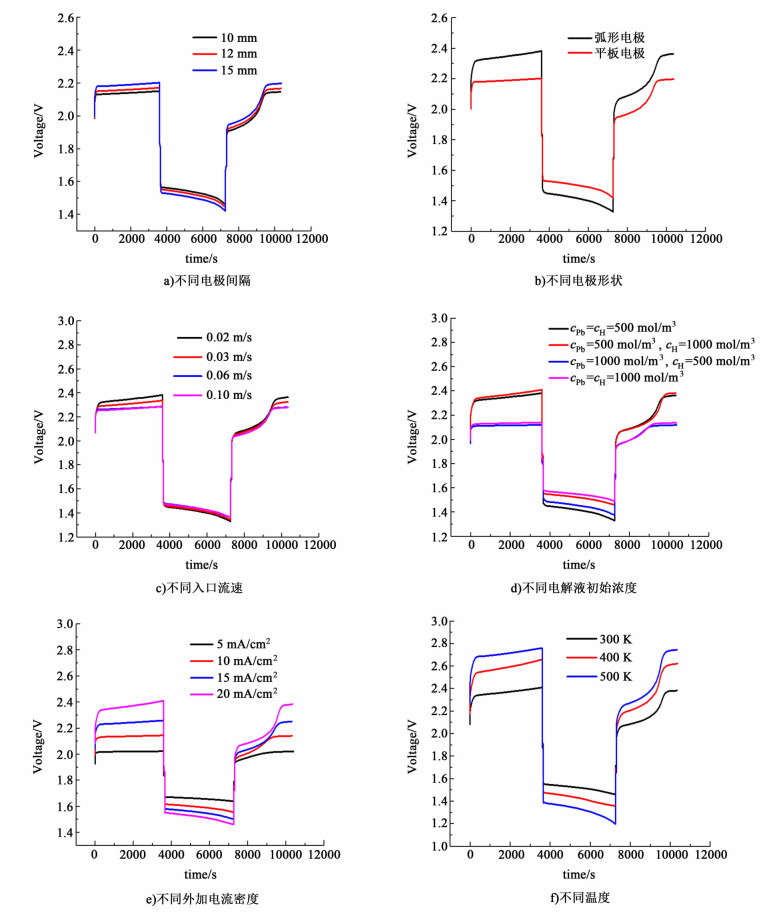
图 2为不同条件下电池的充放电曲线。图 2a)为不同电极间隔条件下电池的充放电曲线。初始温度T0=300 K,Pb(Ⅱ)和H+的初始浓度为500 mol/m3,入口电解液流速为0.02 m/s。充放电阶段各持续3 600 s,充放电之间间隔60 s。随着正负极电极间隔的增大,电池电压在充电时增大,充放电之间的电压降也增大。随电极间隔增大,极板间电解液增多,电阻增大,电流值一定时,IR值增大,从而使充电电压增大。
|
| 图 2 不同条件下电池充放电曲线 Figure 2 Charge/discharge curves in different conditions |
| |
| 名称 | 值 | 描述 |
| DPb(Ⅱ) | 0.7×10-9 m2/s | 电解液中Pb2+扩散系数 |
| DH+ | 9.3×10-9 m2/s | 电解液中H+扩散系数 |
| DHSO4- | 1.33×10-9 m2/s | 电解液中HSO4-扩散系数 |
| T | 300 K | 温度 |
| c0,Pb(Ⅱ) | 500 mol/m3 | Pb2+初始浓度 |
| c0,H+ | 500 mol/m3 | H+初始浓度 |
| pout | 300 kPa | 出口处压力 |
| uin | 0.02 m/s | 入口流速 |
| iapp | 20 mA/cm2 | 外加电流密度 |
| V | 0.0 015 m3 | 电解液槽体积 |
| k0,Pb | 2.1×10-7 m/s | 负极反应速率常数 |
| k0,PbO2 | 2.5×10-7 m/s | 正极主反应速率常数 |
| K0,f | 0.0045 m4/(s·mol) | PbO反应正向速率常数 |
| K0,b | 4.5×10-8 m4/(s·mol) | PbO反应逆向速率常数 |
| tcharge | 3 600 s | 充电时间 |
| tdischarge | 3 600 s | 放电时间 |
| trest | 60 s | 静止时间 |
图 2b)为在正负极电极间隔截面积相同,电极形状不同时电池的充放电曲线。从图 2b)中可以看出,改变电极形状,将电极由平板变为弧形,使得电池电压在充电时显著增加,充放电之间的电压降也明显增大。在截面积相等条件下,改变电极形状,在入口流速相同时,电极间电解液流速因为电极的不同形状会产生流速的差异,从而影响不同电极的充放电性能。
图 2c)为改变入口电解液流速时电池的充放电曲线。从图 2c)中可以看出,降低电解液流速,电池电压在充电阶段增加,在放电阶段,入口电解液流速的改变对电池电压影响很小。在低流速条件下,电解液中Pb2+可以更充分的参与电极表面电化学反应,在正极相比高流速条件下形成更多的铅氧化物,增加了电极电阻,从而使电压增大。
图 2d)为不同初始电解液浓度条件下电池的充放电曲线。从图 2d)中可以看出,增加电解液中H+初始浓度会使充电和放电阶段电池电压升高。增加Pb(Ⅱ)初始浓度使充电阶段电池电压明显降低,而对放电阶段电池电压影响较小。同时增加Pb(Ⅱ)和H+的初始浓度,充电电压和放电电压都发生显著改变,充电电压显著降低,放电电压显著升高。
图 2e)为不同外加电流密度下的充放电曲线,随着外加电流密度的增加,电池电压在充电时增大,在放电时降低,充放电之间的电压降增大。这主要是电流密度增大使得欧姆电阻增大。
不同电流密度条件下充放电时,电池电压峰值列于表 4。
| 外加电流密度/ (mA·cm-2) |
充电时电池电压/V | 放电时电池电压/V |
| 5 | 2.02 | 1.63 |
| 10 | 2.13 | 1.55 |
| 15 | 2.26 | 1.49 |
| 20 | 2.39 | 1.45 |
图 2f)为不同温度条件下的电池充放电曲线。从图 2f)可以看出,温度升高,充电时电池电压升高,但是在放电阶段的电池电压显著降低。不同电池温度条件下电池电压峰值列于表 5。
| 温度/K | 充电时电池电压/V | 放电时电池电压/V |
| 300 | 2.38 | 1.45 |
| 400 | 2.63 | 1.37 |
| 500 | 2.74 | 1.20 |
值得注意的是,第2次充电部分从7 260 s开始,直到充电过程进行过半,电池电压才达到初始电压值,第2次充电时电压的降低是正极表面形成的PbO所引起的[11]。
2.2 不同条件对电极表面Pb(Ⅱ)浓度分布图的影响图 3~图 6为不同条件下电解液中Pb(Ⅱ)靠近电极表面的浓度梯度分布,左边界为负极,右边界为正极。在放电结束时,不同电解液入口流速条件下Pb(Ⅱ)表面浓度分布如图 3a)~图 3d)所示,从中可以看出入口流速对Pb(Ⅱ)表面浓度有较大影响,在研究控制铅酸液流电池中铅沉积的方法时,控制电解液流速可以作为一种解决方案。

|
| 图 3 不同入口流速条件下,放电结束电极表面Pb(Ⅱ)浓度分布图 Figure 3 Pb(Ⅱ) surface concentration on the positive and negative electrode at the ending of discharging |
| |

|
| 图 4 不同初始电解液浓度条件下,放电结束电极表面Pb(Ⅱ)浓度分布图 Figure 4 Pb(Ⅱ) surface concentration on the positive and negative electrode at the ending of discharging |
| |
|
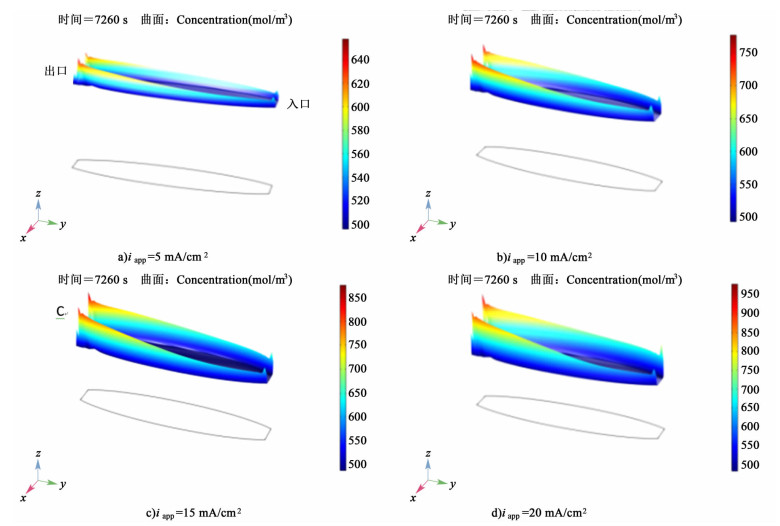
| 图 5 不同外加电流密度条件下,放电结束电极表面Pb(Ⅱ)浓度分布图 Figure 5 Pb(Ⅱ) surface concentration on the positive and negative electrode at the ending of discharging |
| |
|
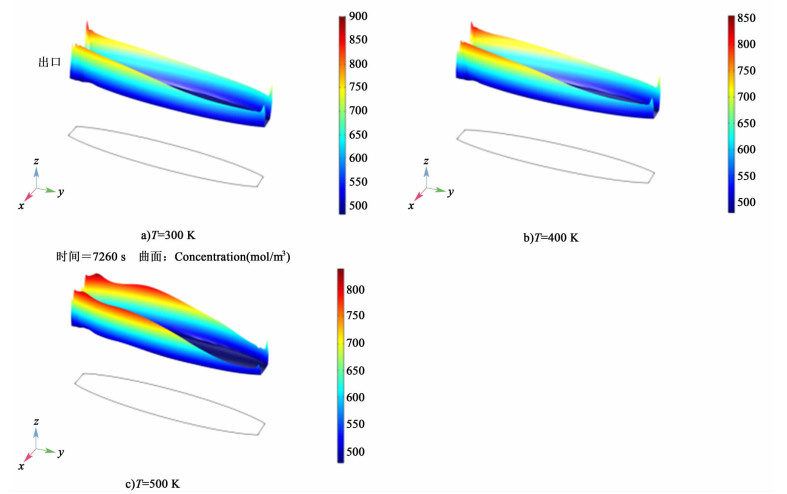
| 图 6 不同温度条件下,放电结束电极表面Pb(Ⅱ)浓度分布图 Figure 6 Pb(Ⅱ) surface concentration on the positive and negative electrode at the ending of discharging |
| |
在放电结束时不同Pb(Ⅱ)和H+初始浓度条件下Pb(Ⅱ)表面浓度分布如图 4a)~图 4d)所示,2种物质的初始浓度均设定为500 mol/m3,增加电解液中的Pb(Ⅱ)初始浓度,Pb(Ⅱ)表面浓度几乎增加相同数量。增加电解液中H+初始浓度使得Pb(Ⅱ)表面浓度稍微增加。同时增加电解液中Pb(Ⅱ)和H+初始浓度对Pb(Ⅱ)表面浓度的影响最大。
不同外加电流密度条件下Pb(Ⅱ)表面浓度分布如图 5a)~图 5d)所示,外加电流密度对Pb(Ⅱ)表面浓度有相当显著的影响。降低电流密度,Pb(Ⅱ)表面浓度随之降低,电流密度越大,对Pb(Ⅱ)表面浓度影响越大。在较低的电流密度条件下,Pb(Ⅱ)表面浓度分布更均匀,主要是因为电流密度越小,电极表面反应速率越慢。
不同温度条件下Pb(Ⅱ)表面浓度分布如图 6a)~图 6c)所示,随温度升高,Pb(Ⅱ)表面浓度发生轻微降低。在模拟的所有温度情况下,出口Pb(Ⅱ)表面浓度变化范围在50 mol/m3之间。升高工作温度对电极Pb(Ⅱ)表面浓度影响不大。
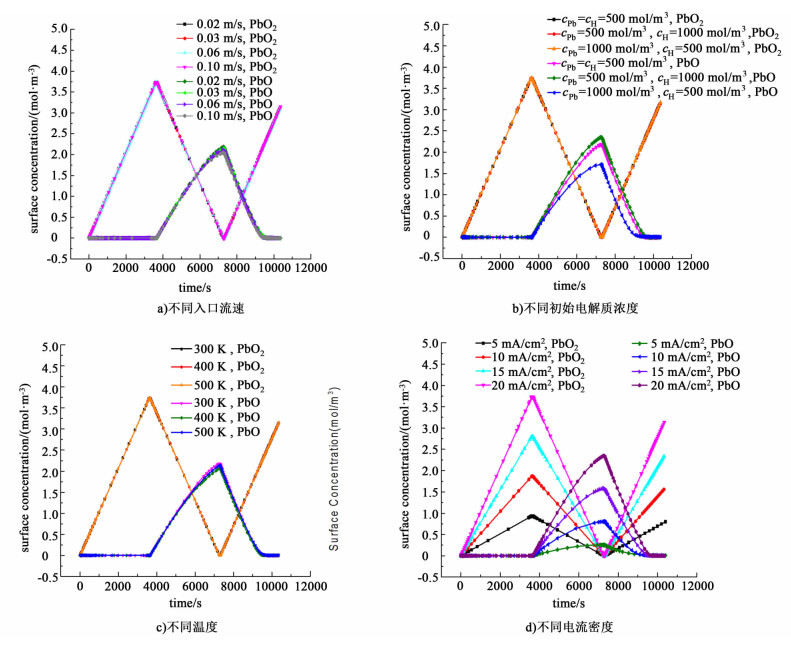
2.3 不同条件对正极表面PbO2和PbO浓度的影响图 7a)~图 7d)为正极上PbO2和PbO表面浓度在不同工作条件下随时间变化的曲线。曲线包括充电,放电和充电3个阶段。充电和放电阶段各持续3 600 s,充放电之间有60 s静止时间。图 7a)为正极PbO2和PbO表面浓度在不同入口流速条件下随时间变化的曲线。正极表面PbO2浓度在充电过程中升高,在放电时降低。PbO表面浓度在充电时升高,在放电时降低。由图 7a)中可以看出改变入口流速对正极表面浓度几乎没有影响。
|
| 图 7 正极表面PbO2和PbO浓度在不同工作条件下随时间变化曲线 Figure 7 Positive electrode surface concentration versus time in different working conditions |
| |
图 7b)为正极PbO2和PbO表面浓度在不同电解质初始浓度条件下随时间变化的曲线,PbO2表面浓度几乎不受电解质初始浓度变化的影响,但是PbO浓度受电解质初始浓度变化的影响较大。增加电解液中H+初始浓度使PbO表面浓度增加,而增加电解液中Pb(Ⅱ)初始浓度使放电过程PbO表面浓度降低。
图 7c)为正极PbO2和PbO表面浓度在不同温度条件下随时间变化的曲线,从图 7c)中看出,正极表面浓度几乎不受温度变化影响。
图 7d)为正极PbO2和PbO表面浓度在不同电流密度条件下随时间变化的曲线。当外加电流密度升高时,PbO和PbO2表面浓度随之增加。类似的,外加电流密度降低,PbO和PbO2表面浓度随之降低。外加电流密度变化时,PbO和PbO2表面浓度峰值列于表 6。
| 外加电流密度/ (mA·cm-2) |
PbO表面浓度/ (mol·m-3) |
PbO2表面浓度/ (mol·m-3) |
| 5 | 0.25 | 0.93 |
| 10 | 0.80 | 1.86 |
| 15 | 1.58 | 2.79 |
| 20 | 2.35 | 3.71 |
在Bates等[8]的研究基础上,通过改变电极形态建立了可溶铅酸液流电池的二维暂态模型,其中包括反应物模型,电荷传递模型,动量守恒模型(Navier-Stokes方程),电荷守恒模型,以及电化学反应的复杂模型,涉及正极表面复杂氧化层的形成以及后续的氧化。模型首先研究了改变电极间隔以及电极形状对电池电压的影响,电池充电电压随电极间隔的增大而增加,将电极由平板改为弧形明显提高了充电时电池电压。
进而研究了改变工作条件,包括外加电流密度、温度、初始电解液流速以及电解液中电解质初始浓度对电池性能的影响。
改变入口电解液流速对电池电压影响不大,但是增加入口电解液流速会使出口Pb(Ⅱ)浓度在放电时降低。增加Pb(Ⅱ)初始浓度,电池电压在充电过程中降低,在放电过程略微升高。增加H+初始浓度,电池电压在充放电过程均增加。
改变电池温度对外部电池电压有很大影响,但是对表面浓度影响很小。这表明电池温度可能是优化铅酸液流电池性能的一个重要因素。改变外加电流密度对Pb(Ⅱ)沉积有明显的影响。当电流密度由10 mA/cm2增加到15 mA/cm2时,电极表面Pb(Ⅱ)浓度增加近100 mol/m3。改变外加电流密度可以用于控制铅酸液流电池中Pb(Ⅱ)的沉积,这将有利于提高电池的循环寿命。
本工作中的模拟仿真对铅酸液流电池的研究提供了一定的参考价值,这些研究使得控制工作电极上的表面沉积变得更加可行。如果电极表面的沉积可以用更便捷的方式进行控制,电池的性能可以得到明显提高。
| 符号 | 定义 | 单位 |
| A | 面积 | m2 |
| C | 比热容 | J/(kg·K) |
| c | 浓度 | mol/m3 |
| D | 扩散系数 | m2/s |
| d | 厚度 | m |
| E | 电势 | V |
| F | 法拉第常数 | C/mol |
| h | 高度 | m |
| I | 电流 | A |
| i | 电流密度 | A/m2 |
| k | 反应速率常数 | m/s |
| N | 通量密度 | mol/(m2·s) |
| n | 电子数 | 无量纲 |
| 法向量 | 无量纲 | |
| p | 压力 | Pa |
| Q | 热源 | W/m3 |
| R | 摩尔气体常数 | J/(mol·K) |
| S | 源/潜项 | mol/(m3·s) |
| T | 温度 | K |
| t | 时间 | s |
| u | X方向速度分量 | m/s |
| 相速度 | m/s | |
| V | 体积 | m3 |
| ν | Y方向速度分量 | m/s |
| 平均速度 | m/s | |
| ω | 宽度 | m |
| z | 电荷数 | 无量纲 |
| ΔG | 吉布斯自由能变化 | J/mol |
| ΔH | 焓变 | J/mol |
| ΔS | 熵变 | J/(mol·K) |
| φe | 离子电势 | V |
| φs | 电子电势 | V |
| η | 过电位 | V |
| λ | 热导率 | W/(mol·K) |
| μ | 动力黏度 | kg/(m·s) |
| ρ | 密度 | kg/m3 |
| σ | 电子电导率 | S/m |
| σe | 离子电导率 | S/m |
| ζυ | 电压效率 | 无量纲 |
| ω | 流量 | m3/s |
| [1] | Wang W, Luo Q, Li B. Recent progress in redoxflow battery research and development[J]. Advanced Functional Materials, 2013, 23(8): 970–986. DOI: 10.1002/adfm.v23.8 |
| [2] |
王佳, 张晶, 黄成德. 直接甲醇液流燃料电池的二维两相模型[J].
化学工业与工程, 2016, 33(3): 76–81.
Wang Jia, Zhang Jing, Huang Chengde. A two-dimensional two-phase model for direct methanol redox fuel cell[J]. Chemcial Industry and Engineering, 2016, 33(3): 76–81. |
| [3] |
余聪聪, 张晶, 黄成德. 锂硫电池模拟与仿真[J].
化学工业与工程, 2017, 34(5): 89–95.
Yu Congcong, Zhang Jing, Huang Chengde. A mathematical model for a lithium-sulfur cell[J]. Chemcial Industry and Engineering, 2017, 34(5): 89–95. DOI: 10.3969/j.issn.1006-7906.2017.05.020 |
| [4] | Hazza A, Pletcher D, Wills R G A. A novel flow battery:A lead acid battery based on an electrolyte with soluble lead(Ⅱ)-PartⅠ.Preliminary studies[J]. Phys Chem Chem Phys, 2004, 6: 1773–1778. DOI: 10.1039/b401115e |
| [5] | Pletcher D, Hantao Z. A novel flow battery:A lead acid battery based on an electrolyte with soluble lead(Ⅱ)-PartⅤ. Studies of the lead negative electrode[J]. Journal of Power Sources, 2008, 180: 621–629. DOI: 10.1016/j.jpowsour.2008.02.024 |
| [6] | Pletcher D, Wills R. A novel flow battery:A lead acid/battery based on an electrolyte with soluble lead(Ⅱ)-PartⅡ.Flow cell studies[J]. Phys Chem Chem Phys, 2004, 6: 1779–1785. DOI: 10.1039/b401116c |
| [7] | Zhang C, Sharkh S M. The performance of a soluble lead-acid flow battery and its comparison to a static lead-acid battery[J]. Energy Conversion and Management, 2011, 52: 3391–3398. DOI: 10.1016/j.enconman.2011.07.006 |
| [8] | Bates A, Mukerjee S, Lee S C. An analytical study of a lead-acid flow battery as an energy storage system[J]. Journal of Power Sources, 2014, 249: 207–218. DOI: 10.1016/j.jpowsour.2013.10.090 |
| [9] | Qury A, Kirchev A. A numerical model for a soluble lead-acid flow battery comprising a three-dimensional honeycomb-shaped positive electrode[J]. Journal of Power Sources, 2014, 246: 703–718. DOI: 10.1016/j.jpowsour.2013.07.101 |
| [10] | Shah A A, Li X, Wills R G A. A mathematical model for the soluble lead-acid flow battery[J]. Journal of the Electrochemical Society, 2010, 157(5): A589–A599. DOI: 10.1149/1.3328520 |
| [11] | Pletcher D, Wills R. A novel flow battery:A lead acid battery based on an electrolyte with soluble lead(Ⅱ)-PartⅢ. The influence of conditions on battery performance[J]. Journal of Power Sources, 2005, 149: 96–102. DOI: 10.1016/j.jpowsour.2005.01.048 |
 2018, Vol. 35
2018, Vol. 35





