2. 天津中昊天久工程技术有限公司, 天津 300072;
3. 天津大学电气自动化与信息工程学院, 天津 300072;
4. 天津大学化工学院, 天津 300072
2. Tianjin Zhonghao Unitech Co., Ltd. Tianjin 300072, China;
3. School of Electrical and Information Tianjin University, Tianjin 300072, China;
4. School of Chemical Engineering and technology, Tianjin University, Tianjin 300072, China
分批精馏具有设备简单、操作灵活、单塔可将多组分混合物分离成不同产品的特点,随着精细化工及制药工业的迅速发展,分批精馏技术的应用越来越多。
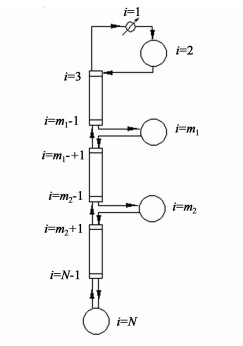
与连续精馏相比,分批精馏过程具有能耗较大的缺点,随着能源的日益紧缺,降低能耗对于分批精馏越来越重要,人们对分批精馏各种操作参数进行优化,但所得到的优化结果往往收效甚微,并且优化策略操作上的困难使其难以应用于实际生产。20世纪90年代以来,学者们相继开发出一些新塔型,期望能从根本上改善分批精馏过程,降低能耗。多罐复合式分批精馏塔是Hasebe等在1995年提出的新塔型(如图 1所示),它由多个分批精馏塔依次连接而成,只在最下面一段塔的塔釜加热,在最上面一段塔的塔顶设冷凝器。该塔型可同时得到多个产品,同时由于相邻塔节之间具有热集成作用,因此具有节能的特点。Hasebe[1-2]、Wittgens[3-4]和Furlonge[5-6]等对多罐塔的各种操作策略的研究结果表明:全回流条件下操作简单且分离效率最高。因此通常多罐复合塔采用全回流操作方式,根据原料组成及原料的量计算出每个贮罐的最终持液量,然后将原料液按上述持液量分布在各个贮罐,采用液面控制系统保持各个贮罐的持液量恒定,最终各产品按沸点由低到高的次序分别在由上到下的各罐中得以浓缩。张雪梅[7]对多罐塔和常规塔进行了比较,结果表明:采用多罐分批精馏塔获得的年利润远高于采用常规分批精馏塔。赵朔[8]提出了带有内部热集成的多储罐间歇精馏全回流操作分离二元混合物的新型操作方式。
|
| 图 1 多罐复合式分批精馏塔的示意图 Figure 1 Scheme of multi-effect batch distillation column |
| |
目前文献中对该塔型的研究主要集中于动态过程的模拟和优化,尚无该塔型设计方法的报道,本研究将以带2个中间罐的复合塔为例对该塔型的设计方法进行研究。
1 平衡程度系数多罐复合式分批精馏塔通常采用全回流操作方式,在实际操作和设计中存在着一个关键问题,即:若全回流操作完全达平衡时产品才达到所要求的浓度,所需操作时间为无限长,因此实际应用中全回流操作不应完全达平衡,为了表示完成一定的分离任务全回流所达到的程度,引入了平衡程度系数概念,用式(1)表示。
| $ {\varphi _{i,j}} = \frac{{{x_{i,j}} - {x_{{\rm{F}}j}}}}{{x_{i,j}^{\rm{t}} - {x_{{\rm{F}}j}}}} $ | (1) |
式(1)中:φi, j表示第i块板上组分j接近平衡程度;xi, j表示塔板第i块板上组分j的摩尔分数;xi, jt表示全回流平衡时第i块板上组分j的摩尔分数的摩尔分数;xFj表示原料中组分j的摩尔分数。
理论上φ值的变化范围在0与1之间,它的值越接近1表示越接近平衡。当塔板数、物料的组成确定时,全回流平衡时塔内各处的平衡浓度xi, jt是唯一确定的。当操作时间无限延长时,这个值可无限接近,但永远不能达到。由于持液的作用使得塔内达平衡需要一个过程,且全回流平衡时塔釜组成已不同于塔釜的初始组成,因此需要求出全回流平衡时的塔釜组成后,利用Fenske方程求塔内各处的平衡浓度,然后利用式(1)即可求出平衡程度系数。
2 全回流过程中多罐复合式分批精馏塔内平衡程度系数变化情况 2.1 基本假设1) 塔顶冷凝器、各罐及各板恒摩尔持液,忽略系统中的汽相持料;2)塔顶冷凝器为全凝器;3)恒摩尔流;4)离开塔板的汽相与塔板上的液相呈相平衡;5)汽相为理想气体,液相为理想溶液,相对挥发度为常数。
2.2 数学模型的建立对图 1所示的多罐复合式分批精馏塔各板及各罐作物料衡算。
1) 塔顶冷凝器,i=1:
| $ {U_1}\frac{{{\rm{d}}{x_{1,j}}}}{{{\rm{d}}V}} = {y_{3,j}} - {x_{1,j}} $ | (2) |
2) 回流罐,i=2:
| $ {U_2}\frac{{{\rm{d}}{x_{2,j}}}}{{{\rm{d}}V}} = {x_{1,j}} - {x_{2,j}} $ | (3) |
3) 上数第1段塔的任意1块板(除最后1块),i=3,4,…,m1-2:
| $ {U_i}\frac{{{\rm{d}}{x_{i,j}}}}{{{\rm{d}}V}} = {x_{i - 1,j}} - {y_{i,j}} - {x_{i,j}} + {y_{i + 1,j}} $ | (4) |
4) 上数第1段塔的最后1块板,i=m1-1:
| $ {U_{{m_1} - 1}}\frac{{{\rm{d}}{x_{{m_1} - 1,j}}}}{{{\rm{d}}V}} = {x_{{m_1} - 2,j}} - {y_{{m_1} - 1,j}} - {x_{{m_1} - 1,j}} + {y_{{m_1} + 1,j}} $ | (5) |
5) 中间罐1,i=m1:
| $ {U_{{m_1}}}\frac{{{\rm{d}}{x_{{m_1},j}}}}{{{\rm{d}}V}} = {x_{{m_1} - 1,j}} - {x_{{m_1},j}} $ | (6) |
6) 上数第2段塔的任意1块板(除最后1块),i=m1+1,m1+2,…,m2-2:
| $ {U_i}\frac{{{\rm{d}}{x_{i,j}}}}{{{\rm{d}}V}} = {x_{i - 1,j}} - {y_{i,j}} - {x_{i,j}} + {y_{i + 1,j}} $ | (7) |
7) 上数第2段塔的最后1块板,i=m2-1:
| $ {U_{{m_2} - 1}}\frac{{{\rm{d}}{x_{{m_2} - 1,j}}}}{{{\rm{d}}V}} = {x_{{m_2} - 2,j}} - {y_{{m_2} - 1,j}} - {x_{{m_2} - 1,j}} + {y_{{m_2} + 1,j}} $ | (8) |
8) 中间罐2,i=m2:
| $ {U_{{m_2}}}\frac{{{\rm{d}}{x_{{m_2},j}}}}{{{\rm{d}}V}} = {x_{{m_2} - 1,j}} - {x_{{m_2},j}} $ | (9) |
9) 上数第3段塔的任意1块板,i=m2+1,m2+2,…,N-1:
| $ {U_i}\frac{{{\rm{d}}{x_{i,j}}}}{{{\rm{d}}V}} = {x_{i - 1,j}} - {y_{i,j}} - {x_{i,j}} + {y_{i + 1,j}} $ | (10) |
10) 塔釜,i=N:
| $ {U_N}\frac{{{\rm{d}}{x_{N,j}}}}{{{\rm{d}}V}} = {x_{N - 1,j}} - {y_{N,j}} $ | (11) |
汽液平衡关系:
| $ {y_{i,j}} = {K_{i,j}}{x_{i,j}} $ | (12) |
式(2)~(12)中:U为塔板上的持液量,kmol;x为液相组成;y为汽相组成;V为塔内累积蒸汽量,kmol;N为精馏塔的理论塔板数;K为汽液平衡常数;i为塔板序号;j为组分序号;m1和m2分别为上数第1和第2个中间罐的塔板序号。
由于塔的截面积只改变过程的快慢,并不影响分离效果,为了消除塔截面积的影响,本文将对以上各式中的塔板持液量、各罐持液量、累积蒸汽量等与广度性质有关的量都除以汽体流率v, 转换成以时间为单位的量[9-10],并仍以原符号表示。
采用2点隐含法解式(2)~(11)构成的刚性方程组,2点隐含法的基本思想为:将微分方程
| $ \begin{array}{*{20}{c}} {z - {z^0} = \int_{{w^0}}^w {{\rm{f}}\left( w \right){\rm{d}}w} }\\ {z - {z^0} = \left[ {\phi {\rm{f}}\left( w \right) + \left( {1 - \phi } \right){\rm{f}}\left( {{w^0}} \right)} \right]\Delta w = }\\ {\phi {\rm{f}}\left( w \right)\Delta w + \left( {1 - \phi } \right){\rm{f}}\left( {{w^0}} \right)\Delta w} \end{array} $ | (13) |
其中:上标0表示差分区间起点,Δw=w-w0为差分区间长度,ϕ为差分格式,本研究采用Galerkin差分格式ϕ=0.6(相当于二次插值,稳定性好)。
2.3 全回流过程中塔内平衡程度系数变化情况在N=45、m1=18和m2=34时,最初投料量F与蒸汽速率v之比为1 h,原料组成xF为(0.25, 0.25, 0.25, 0.25),相对挥发度α为(4.312, 1.960, 1.400, 1.000)(相对挥发度数值为两相邻组分之间的相对挥发度)。单板持液US与蒸汽数速率v之比为0.01 h,冷凝器持液量为单板持液量,塔顶回流罐、中间罐1、中间罐2及塔釜的持液量分别为U2=(F-41US) xF1,Um1=(F-41US) xF2,Um2=(F-41US) xF3,UN=(F-41US)xF4,的条件下,用上述模型考察不同时刻各组分在各板上及各罐中平衡程度系数,结果见图 2。

|
| 图 2 不同时刻各组分在各板上及各罐中平衡程度系数 Figure 2 Column profiles of every component under different degree of approaching equilibrium |
| |
由图 2可以看出:全回流过程中塔内各板及各罐中不同组分在同一时刻平衡程度不同,随着过程的进行,各板及罐中各组分在同一时刻平衡程度差异逐渐减小。全回流过程中某些塔板处出现了φ值小于0或大于1的情况,但在实际应用中与产品分离直接相关的是塔顶回流罐、塔釜及各中间罐,由图 2中可以看出,这些位置处φ值介于0~1之间,因此可以只研究全回流过程中上述位置处相应组分的接近平衡程度变化情况。
3 全回流操作终点平衡程度系数的选取由图 2可知:随着过程的进行,各罐中产品组分的平衡程度系数在0~1的范围内不断增加,全回流操作完全达平衡时各罐中组分k的平衡浓度最大值为1。通常全回流操作的终点为各罐中液相浓度符合相应产品纯度要求,若此时各罐完全达到平衡,操作时间为无限长,因此需选取适宜的全回流操作终点的平衡程度系数。
由平衡程度系数的定义式(1)可知,满足分离要求时各罐中组分k的平衡程度系数的最小值为:
| $ {\left( {{\varphi _{i,k}}} \right)_{\min }} = \frac{{{p_k} - {x_{{\rm{F}}k}}}}{{1 - {x_{{\rm{F}}k}}}} $ | (14) |
式(13)中:pk为产品中组分k的纯度要求。
为了完成分离任务,各罐中组分k的平衡程度系数应在(φk)min~1之间取值。当所选取的平衡程度系数接近最小值时,蒸馏时间较短,但所需塔板数很多,所选取的平衡程度系数增大,蒸馏时间增加,而所需塔板数减少,因此平衡程度系数的选取应综合考虑所需塔板数及操作时间这两方面,一般应稍大于平衡程度系数最小值。
4 多罐复合式分批精馏塔的设计多罐复合式分批精馏塔的设计较为复杂,目前还未见有关其设计方法的报道。对于同一分离任务,若塔板数太少,不能满足产品纯度要求,而塔板数过多,势必造成设备投资增大,本研究提出用平衡程度系数确定全回流塔板数的方法。由于塔身持液量与各罐中持液量比很少,设计中忽略冷凝器和塔身持液量,并假设精馏过程中各组分之间的分离为清晰分割,其它假设见2.1,下面以四元物系为例,求多罐复合式分批精馏塔的塔板数。
已知条件:原料量为F(h);原料组成为(xF 1,xF 2,xF 3,xF 4)(摩尔分数);相对挥发度为(α1,α2,α3,α4);塔顶回流罐、中间罐1、中间罐2、塔釜的相对持液量分别为U2=FxF 1,Um1=FxF 2,Um2=FxF 3,UN=FxF 4;最终产品要求为(p1,p2,p3,p4)(摩尔分数)。计算步骤如下:1)确定各罐达到最终产品要求时的平衡程度系数,一般可使塔顶平衡程度系数稍大,假设塔顶回流罐、中间罐1和中间罐2的相应的产品组分的最终平衡程度系数分别为E1、E2和E3。2)由各罐最终平衡程度系数求出其相应的平衡浓度。
对于塔顶回流罐:塔顶回流罐只有组分1和2,由平衡程度定义式有:
| $ {E_1} = \frac{{{x_{2,1}} - {x_{{\rm{F1}}}}}}{{x_{2,1}^{\rm{t}} - {x_{{\rm{F1}}}}}} = \frac{{{p_1} - {x_{{\rm{F1}}}}}}{{x_{2,1}^{\rm{t}} - {x_{{\rm{F1}}}}}} $ | (15) |
由式(15)可求出平衡时塔顶回流罐中组分1的摩尔分数x2, 1t。
由液相归一化条件x2, 1t+x2, 2t=1,可求塔顶回流罐中组分2的摩尔分数x2, 2t。
对于中间罐1:中间罐1含有组分1、2和3,由平衡程度定义式有:
| $ {E_2} = \frac{{{x_{{m_1},2}} - {x_{{\rm{F2}}}}}}{{x_{{m_1},2}^{\rm{t}} - {x_{{\rm{F2}}}}}} = \frac{{{p_2} - {x_{{\rm{F2}}}}}}{{x_{{m_1},2}^{\rm{t}} - {x_{{\rm{F2}}}}}} $ | (16) |
由式(16)可求出平衡时中间罐1中组分2的摩尔分数xm1, 2t。
由全塔组分1物料守恒有:
| $ F{x_{{\rm{F1}}}} = {U_2}x_{2,1}^{\rm{t}} + {U_{{m_1}}}x_{{m_1},1}^{\rm{t}} $ | (17) |
由式(17)可求出平衡时中间罐1中组分1的摩尔分数xm1, 1t。
由液相归一化条件xm1,1t+xm1,2t+xm1,3t=1,可求出平衡时中间罐1中组分3的摩尔分数xm1, 3t。
对于中间罐2:中间罐2含有组分2、3和4,由平衡程度定义式有:
| $ {E_3} = \frac{{{x_{{m_2},3}} - {x_{{\rm{F3}}}}}}{{x_{{m_2},3}^{\rm{t}} - {x_{{\rm{F3}}}}}} = \frac{{{p_3} - {x_{{\rm{F3}}}}}}{{x_{{m_2},3}^{\rm{t}} - {x_{{\rm{F3}}}}}} $ | (18) |
由式(18)可求出平衡时中间罐2中组分3的摩尔分数xm2, 3t。
由全塔组分2物料守恒有:
| $ F{x_{{\rm{F2}}}} = {U_2}x_{2,2}^{\rm{t}} + {U_{{m_1}}}x_{{m_1},2}^{\rm{t}} + {U_{{m_2}}}x_{{m_2},2}^{\rm{t}} $ | (19) |
由式(19)可求出平衡时中间罐2中组分2的摩尔分数xm2, 2t。
由液相归一化条件xm2,2t+xm2,3t+xm2,4t=1,可求出平衡时中间罐2中组分4的摩尔分数xm2, 4t。
对于塔釜:塔釜含有组分3和4,由全塔组分守恒有:
| $ F{x_{{\rm{F4}}}} = {U_{{m_2}}}x_{{m_2},4}^{\rm{t}} + {U_N}x_{{m_2},4}^{\rm{t}} $ | (20) |
由式(20)可求出平衡时塔釜中组分4的摩尔分数xN, 4t。
由液相归一化条件xN,3t+xN,4t=1,可求出平衡时塔釜中组分3的摩尔分数xN, 3t。
3) 由Fenske方程求最小塔板数。
对于上数第1段塔:塔顶回流罐含组分1和2,中间罐1含组分1、2和3,由于假设清晰分割,组分3不会到塔顶,所以组分1和2分别为该段的轻、重关键组分。
由于无汽相通过中间罐,所以中间罐并不起到分离作用,平衡时中间罐与其相邻的上一塔板液相组成相同,这样由Fenske方程有:
| $ \frac{{x_{2,1}^{\rm{t}}}}{{x_{2,2}^{\rm{t}}}} = \alpha _1^{N_m^1}\frac{{x_{{m_1},1}^{\rm{t}}}}{{x_{{m_1},2}^{\rm{t}}}} $ | (21) |
由式(21)即可求得上数第1段最小塔板数Nm1,将其圆整后作为这一段的塔板数。
对于上数第2段塔:中间罐1含组分1、2和3,中间罐2含组分2、3和4,由于假设清晰分割,组分4不会到中间罐1,组分1不会到中间罐2,所以组分2和3分别为该段的轻、重关键组分。
将中间罐2与其相邻的上1板液相组成相同,由Fenske方程:
| $ \frac{{x_{{m_1},2}^{\rm{t}}}}{{x_{{m_1},3}^{\rm{t}}}} = \alpha _2^{N_m^2}\frac{{x_{{m_2},2}^{\rm{t}}}}{{x_{{m_2},3}^{\rm{t}}}} $ | (22) |
由式(22)即可求得这一段的最小塔板数Nm2,将其圆整后作为这一段的塔板数。
对于最后一段塔:中间罐2含组分2、3和4,塔釜含组分3和4,由清晰分割假设可知组分2不会到塔釜中,所以组分3和4分别为该段的轻、重关键组分。
由于塔釜相当于一块塔板,这样由Fenske方程有:
| $ \frac{{x_{{m_2},3}^{\rm{t}}}}{{x_{{m_2},4}^{\rm{t}}}} = \alpha _3^{\left( {N_m^3 + 1} \right)}\frac{{x_{N,3}^{\rm{t}}}}{{x_{N,4}^{\rm{t}}}} $ | (23) |
由式(23)即可求得这一段的最小塔板数Nm3,将其圆整后作为这一段的塔板数。
用上述方法确定用多罐塔完成下面分离任务所需板数。
分离任务:原料组成xF为(0.25,0.25,0.25,0.25),相对挥发度α为(5,2.4,1.5,1),产品纯度要求为(0.98, 0.95, 0.95, 0.98)。
塔顶回流罐、中间罐1和中间罐2的平衡程度分别取为0.98、0.95、0.95,计算得到3段塔的塔板数分别为15、21和27(由上至下)。
在塔顶回流罐、中间罐1、中间罐2和塔釜持液量均为5 h,塔板持液为0.025 h的条件下,用多罐复合塔的恒摩尔持液模型对该计算结果进行验证,计算出全回流终点各罐相应产品浓度分别为:0.9989、0.9627、0.9500和0.9885,所以用该方法确定的板数能较好地完成分离任务。
5 结论多罐复合式分批精馏塔通常采用全回流操作方式,建立了多罐复合塔的恒摩尔持液模型,引入了平衡程度系数概念来研究全回流过程中塔内各板和各罐内接近平衡程度,考察了各罐内平衡程度系数变化情况,给出了设计中确定全回流操作终点的方法,并提出了多罐复合式分批精馏塔的设计方法,该方法确定的板数能较好地完成分离任务。
| [1] | Hasebe S, Noda M, Hashimoto I. Optimal operation policy for total reflux and multi-effect batch distillation systems[J]. Computers Chem Engng, 1999, 23: 523–532. DOI: 10.1016/S0098-1354(98)00290-7 |
| [2] | Hasebe S, Noda M, Hashimoto I. Optimal operation policy for multi-effect batch distillation system[J]. Computers Chem Engng, 1997, 21(s): 1221–1226. |
| [3] | Wittgens B, Litto R, Sørensen E, et al. Total reflux operation of multivessel batch distillation[J]. Chem Eng Sci, 1996, 20(s): 1041–1047. |
| [4] | Skogestad S, Wittgens B, Litto R, et al. Multivessel batch distillation[J]. AIChE Journal, 1997, 43(4): 971–978. DOI: 10.1002/(ISSN)1547-5905 |
| [5] | Wittgens B, Skogestad S. Closed operation of multivessel batch distillation:Experimental verification[J]. AIChE Journal, 2000, 46(6): 1209–1217. DOI: 10.1002/(ISSN)1547-5905 |
| [6] | Furlong H I, Pantelides C C, Sørensen E. Optimal operation of multivessel batch distillation columns[J]. AIChE Journal, 1999, 45(4): 781–801. DOI: 10.1002/(ISSN)1547-5905 |
| [7] |
张雪梅, 张卫江, 简春贵, 等. 带多个中间贮罐的新型分批精馏塔的研究[J].
化工进展, 2003, 22(3): 254–257.
Zhang Xuemei, Zhang Weijiang, Jian Chungui, et al. Study on the multi-effect batch distillation columns with intermediate vessels[J]. Chemical Industry and Engineering Progress, 2003, 22(3): 254–257. DOI: 10.3321/j.issn:1000-6613.2003.03.008 |
| [8] |
赵朔, 白鹏. 带有内部热集成的多储罐间歇精馏全回流操作[J].
化工学报, 2015, 66(11): 4476–4484.
Zhao Shuo, Bai Peng. Internal heat integrated multivessel batch distillation with constant total reflux operation[J]. CIESC Journal, 2015, 66(11): 4476–4484. |
| [9] |
张雪梅, 张卫江, 简春贵, 等. 分批精馏中的持液作用[J].
化工学报, 2004, 55(11): 1827–1832.
Zhang Xuemei, Zhang Weijiang, Jian Chungui, et al. Role of holdup in batch distillation[J]. CIESC Journal, 2004, 55(11): 1827–1832. DOI: 10.3321/j.issn:0438-1157.2004.11.016 |
| [10] | Zhang X, Jian C, Zhang W. Role of initial still charge on batch distillation[J]. Industrial and Engineering Chemistry Research, 2009, 48(3): 1536–1542. DOI: 10.1021/ie8003607 |
 2018, Vol. 35
2018, Vol. 35





