随着化工行业的发展,精馏塔尺寸逐渐成为制约化工行业向更大规模发展的瓶颈。而填料压降制约着塔径, 且压降越大能耗越大。由于规整填料采用规则的结构固定汽液流动方向,与分散填料相比其压降较小。研究人员不断对规整填料进行改进,以期进一步减小压降。
为减小压降,Li等[1]将Mellapak 125X改进为波浪式波纹板规整填料,将填料盘间接触区域变为平滑结构,使流体流向改变平稳, 压降减小。Shilkin等[2]设计出新型填料PD 10,通过减小2股气体间的相互作用减小压降。Lautenschlegera等[3]对填料PD 10的垫片形状及分布进行了优化,得到效果优于PD10的规整填料。林秀锋等[4]对多种低压降、高通量的规整填料在空分精馏中的开发应用进行了综述。
在对规整填料的研究中,CFD模拟由于成本低、耗时短且易获得流场数据的特点而备受青睐。如Hosseini等[5]、Petre等[6-7]、Tan等[8]、王韬等[9]利用CFD对规整填料内的压降、吸收、传质进行了研究。但此方法需要对数据的可靠性进行实验验证,常用的实验验证方法为流体可视化技术。目前有萘升化可视化技术[10]、显色化学反应可视化方法[11]、激光诱导荧光技术(LIF)[12-14]和断层摄影技术(CT)[15-16]等。
Petre等[6-7]发现波纹片间产生的压降占全塔压降的65%~72%,这是由气体与填料表面、气体与气体间的相互碰撞2部分产生的。前者产生的压降为有效压降。后者虽在一定程度上强化传质,但大量能量的消耗使得压降升高。Monolith型规整填料在波纹填料间添加整块隔板,将上下2股气体隔开,使得压降大幅度减小。然而,有实验表明[17],该结构使液体分布不均,传质性能下降。液体堆积较严重的区域是填料的波谷区域,因此本研究避开波谷区域,将隔板添加至非波谷区,得到改进后的填料Mon-JKB-250Y。采用CFD技术对JKB-250Y和不同隔板边长Mon-JKB-250Y的压降、传质效率和单位压降下的传质系数进行比较,以期得到较适宜的隔板边长,同时采用显色化学反应可视化技术验证CFD数据的可靠性。
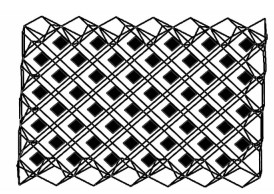
1 CFD模拟 1.1 物理模型以JKB-250Y填料作为研究对象,其填料尺寸为106 mm×147 mm,结构参数如表 1,其中b为填料波长、h为填料高度、d为填料水力直径、α为流道与壁面夹角。2片规整填料间形成若干个传质单元,在每个传质单元的中部加入边长为λ mm的正方形隔板,单个Mon-JKB-250Y传质单元如图 1所示。若干个Mon-JKB-250Y传质单元形成了改进后的填料Mon-JKB-250Y,如图 2所示。实验时,隔板由模具刻出,各隔板之间有少量连接物;CFD模拟时,忽略各隔板间的连接物。取λ=0~21,当λ=0,即为JKB-250Y;当λ=21,即为Monolith型规整填料。
| b/mm | h/mm | d/mm | α/(°) |
| 21 | 12 | 15.95 | 45 |

|
| 图 1 Mon-JKB-250Y传质单元 Figure 1 A unit cell of Mon-JKB-250Y |
| |
|
| 图 2 JKB-250Y物理模型示意图 Figure 2 Physical model of JKB-250Y |
| |
采用ICEM软件对其进行网格划分,对壁面区域进行边界层加密。经网格无关性验证后,采用的网格数约为6 300 000,边界层处网格的最小尺寸为0.1 mm。
1.2 数学模型 1.2.1 控制方程工程上,在流速不高、压力变化小的场合,由于气体运动所引起的密度变化小,可将其视为不可压缩流体。本研究将气体视为不可压缩流体,对于不可压缩流体,其控制方程如下:
质量方程:
| $ \nabla \cdot u = 0 $ | (1) |
动量方程:
| $ \frac{{{\rm{D}}u}}{{{\rm{D}}t}} = g - \frac{1}{\rho }\nabla p + \nu {\nabla ^2}u $ | (2) |
式(1)~(2)中:u为流体速度,m·s-1;t为时间,s;g为重力体积力;ρ为流体密度,kg·m-3;p为流体压力,Pa;ν为流体的运动黏度,m2/s。
1.2.2 湍流模型由于传质主要发生在填料表面,因此需对壁区的流体流动进行模拟。求解壁区流动一般采用壁面函数法或低雷诺数k-ε模型。由于传质现象受壁区湍流及边界层厚度影响,张燕来等[19]发现Lam-Bremhorst低雷诺数模型更准确。因此本研究采用Lam-Bremhorst低雷诺数模型。
1.2.3 表面反应模型将填料中的液体设为壁面物质,故整个流场为气相单相流。气体流经壁面时与壁面物质发生反应,以表面反应模型模拟气相传质过程:
| $ \eqalign{ &\sum\limits_{i = 1}^{{N_{\rm{g}}}} {{{g'}_{i, {\rm{r}}}}} {G_i} + \sum\limits_{i = 1}^{{N_{\rm{b}}}} {{{b'}_{i, {\rm{r}}}}} {B_i} + \sum\limits_{i = 1}^{{N_{\rm{s}}}} {{{s'}_{i, {\rm{r}}}}} {S_i}\buildrel {{K_{\rm{r}}}} \over \longleftrightarrow \sum\limits_{i = 1}^{{N_{\rm{g}}}} {g_{i, {\rm{r}}}^n} {G_i} + \cr &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^{{N_{\rm{b}}}} {{{b''}_{i, {\rm{r}}}}} {B_i} + \sum\limits_{i = 1}^{{N_{\rm{s}}}} {{{s''}_{i, {\rm{r}}}}} {S_i} \cr} $ | (3) |
式(3)中:gi, r'、bi, r'、si, r'、gi, r"、bi, r"、si, r"为气相、吸附项、吸附后生成物的化学计量系数;Gi、Bi、Si为气相、吸附项、吸附后生成物;Ng、Nb、Ns为气相、吸附项、吸附后生成物的物种种数;Kr为反应常数。
1.2.4 传质模型在含有化学反应的过程中,质量传递方程为:
| $ \frac{\partial }{{\partial t}}\left( {\rho {Y_i}} \right) + \nabla \left( {\rho {Y_i}u} \right) = - \nabla {J_i} + {R_i} + {S'_i} $ | (4) |
式(4)中:Yi为组分i的质量分数;Ji为组分i的扩散通量,kg·m-2·s-1;Ri为化学反应的净产生速率,kmol·s-1;Si'为额外产生速率,kmol·s-1。本研究计算的流体为单相流体,故Si'=0。式(4)中的Yi、Ri都可由表面反应模型得到,式(4)得到的Ji即传质速率。
1.2.5 边界条件设置入口采用速度入口,氨气的质量分数为0.01,JKB-250Y的F因子为0.9~2.7 m·s-1·(kg·m-3)0.5,出口采用压力出口,壁面采用恒壁温,无滑脱边界条件。其中:F因子为气相动能因子,
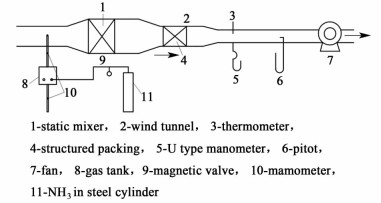
采用显色化学反应可视化技术[11]测量规整填料内氨气的传质系数,实验装置如图 3所示。
|
| 图 3 实验流程示意图 Figure 3 Experimental flow chart |
| |
将贴有滤纸的规整填料固定在基准点上,与8片同型号不贴滤纸的规整填料组成填料盘放入风洞,由定量罐控制的氨气与空气混合后由左侧进入,发生如下反应:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;{\rm{N}}{{\rm{H}}_3} + {{\rm{H}}_{\rm{2}}}{\rm{O}} \Leftrightarrow {\rm{NH}}_4^ + + {\rm{O}}{{\rm{H}}^ - }\\ 2{\rm{N}}{{\rm{H}}_4}{\rm{OH + MnC}}{{\rm{l}}_2} \to 2{\rm{N}}{{\rm{H}}_4}{\rm{Cl + Mn}}{\left( {{\rm{OH}}} \right)_2}\\ \;\;\;\;\;\;{\rm{Mn}}{\left( {{\rm{OH}}} \right)_2} + {{\rm{H}}_{\rm{2}}}{{\rm{O}}_2} \to {\rm{Mn}}{{\rm{O}}_2} \downarrow + 2{{\rm{H}}_{\rm{2}}}{\rm{O}} \end{array} $ |
具体过程为:将浸满双氧水(H2O2)和氯化锰(MnCl2)混合溶液的滤纸贴在填料表面,当NH3接触到滤纸后,迅速与之发生反应,使得滤纸表面颜色发生变化。将变色后的滤纸置于HPScanjet 4850扫描仪(标准分辨率为4 800×9 600 dpi)中进行彩色图像处理,选取红色数值(R)表征颜色强度,用于反映产物MnO2的量。整个过程由气相传质阻力控制,产物的多少反映气相传质系数的大小。
传质过程为:
| $ \int_{t = 0}^{{t_1}} {{N_{\rm{i}}}{\rm{d}}t} = \int_{t = 0}^{{t_1}} {k\left( {{C_{\rm{i}}} - {C_{\rm{w}}}} \right){\rm{d}}t} $ | (5) |
由于氨气易被吸收且反应迅速,可近似认为壁面浓度Cw=0,主体浓度Ci为常数,故:
| $ k = \frac{{NV}}{m} $ | (6) |
式(6)中:Ni为氨气单位时间单位面积的传质量,又称传质速率,kg·m-2·s-1;k为氨气的气相传质系数,m·s-1;Ci为氨气的主体浓度,kg·m-3;Cw为氨气的壁面浓度,kg·m-3;N为氨气的总传质量,kg·m-2;V为混合气体的流量,m3·s-1;m为氨气质量,kg。
2.2 标定原理依据文献[10],在雷诺数为0~600 000范围内,传质系数和气体流速之间的关联式为:
| $ j\sqrt {\frac{{G{D_{\rm{P}}}}}{\mu }} = 1.08 $ | (7) |
| $ j = \frac{{kS{c^{2/3}}}}{u} $ | (8) |
式(7)~(8)中:Sc为Schmidt常数;G为混合气体的质量流率,kg·s-1;Dp为标定所用薄片的水力直径,m;μ为混合气体的黏度,Pa·s。
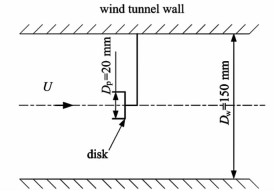
标定方法如图 4所示,在风洞中心放置正方形薄片(20 mm×20 mm),将同等大小润湿后的滤纸贴在薄片上。使流速u保持不变,通过改变进气量m得到不同传质量N,从而建立N与R之间的关系。
|
| 图 4 标定风洞示意图 Figure 4 Schematic diagram of the wind passage and the disk |
| |
如图 5所示为当F=2.1 m·s-1·(kg·m-3)0.5时,JKB-250Y,Mon-JKB-250Y (λ=12.6 mm)的一个传质单元的对称面的湍动能云图,体现的是传质单元内流体的湍流强度。

|
| 图 5 传质单元对称面湍动能云图 Figure 5 Turbulence kinetic energy contour of symmetry plane in a unit cell |
| |
由图 5a)知,JKB-250Y的下部平行区域和上部三角区域湍流强度不大,2区域连接处湍流强度最大,因为上下2股流体在该处相遇,扰动增大、阻力增加。由图 5b)知,在上下部分间加入隔板后,大大减小了交叉区域的湍动能,因为隔板将该处的2股流体隔开,扰动减弱,压降势必减小。湍动能减小是压降减小的一个本质原因。该规律在其余隔板尺寸时相似。
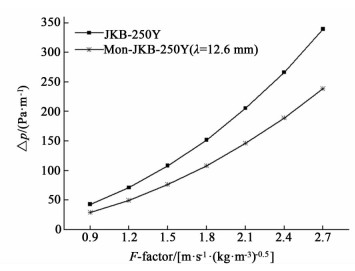
3.2 压降 3.2.1 F因子的影响如图 6所示为JKB-250Y,Mon-JKB-250Y(λ=12.6 mm)的压降与F因子的关系。
|
| 图 6 压降与F因子的关系 Figure 6 Relationship between pressure drop and F factor |
| |
如图 6所示,由于能量损失与气相流速呈指数关系,即与F因子呈指数关系。因此,压降随F因子的增大呈指数地增加。该规律在其余隔板尺寸时相似。
Mon-JKB-250Y(λ=12.6 mm)较JKB-250Y而言,内置隔板减弱了2股交叉流动流体间的碰撞,能量损失降低,压降减小。在F=0.9~2.7 m·s-1·(kg·m-3)0.5时,压降减小了28%~32%。
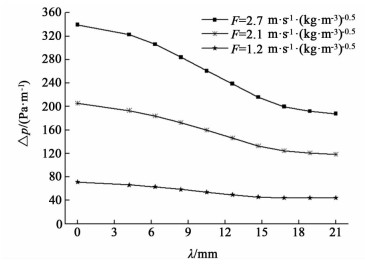
3.2.2 隔板边长的影响如图 7所示为F=1.2、2.1、2.7 m·s-1·(kg·m-3)0.5时,Mon-JKB-250Y的压降与隔板边长的关系。
|
| 图 7 压降与隔板边长的关系 Figure 7 Relationship between pressure drop and length of baffle |
| |
为获得最适宜隔板边长,图 7得到了压降与隔板边长的关系曲线。由图 7可知,压降随隔板边长的增加而减小,即隔板边长越大,越能有效减小交叉通道内的两股流体碰撞,减小能量损失,但两者不呈线性关系。
当F=2.7、2.1、1.2 m·s-1·(kg·m-3)0.5,λ=16 mm时压降的最大减小幅度分别为44.7%、42.3%、38.3%。当λ=16.8 mm时,压降分别减小了39.4%、38.7%、36.9%,其减小压降的平均效果已达到加入整片隔板(λ=21 mm)的88%以上。
3.3 传质效率根据双膜理论,采用Ni=kA(Ci-Cw)考察规整填料的传质效率,往往同时关注传质面积A和平均传质系数k。
加入隔板后,传质面积增加、比表面积a增加。不同隔板边长的Mon-JKB-250Y比表面积和本模型尺寸下的传质面积如表 2所示。
| λ/mm | 0 | 4.2 | 6.3 | 8.4 | 10.5 | 12.6 | 14.7 | 16.8 | 18.9 | 21 |
| a/(m2·m-3) | 250 | 255.08 | 261.43 | 270.32 | 281.75 | 295.72 | 312.23 | 331.28 | 352.87 | 366.9 |
| A/m2 | 0.0468 | 0.0478 | 0.049 | 0.0507 | 0.0528 | 0.0554 | 0.0585 | 0.0621 | 0.0662 | 0.0688 |
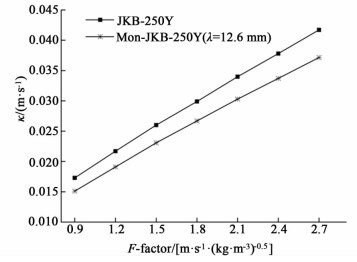
如图 8和图 9所示分别为JKB-250Y,Mon-JKB-250Y(λ=12.6 mm)的k与F因子的关系及kA值与F因子的关系。
|
| 图 8 k与F因子的关系 Figure 8 Relationship between k and F factor |
| |
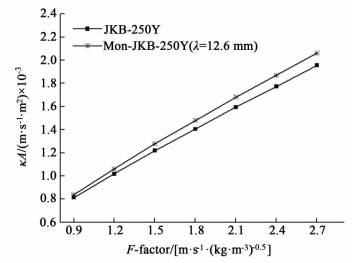
|
| 图 9 kA与F因子的关系 Figure 9 Relationship between kA and F factor |
| |
由图 8可知,由于平均传质系数k与流速呈正比关系,即与F因子呈正关系,故随着F的增加,总传质效率增加。该规律在其余隔板尺寸时相似。
较JKB-250Y而言,Mon-JKB-250Y(λ=12.6 mm)由于加入隔板后,气相碰撞产生的涡流减少,使得强化传质的能力减弱,进而传质系数k减小。在F=0.9~2.7 m·s-1·(kg·m-3)0.5范围内,k减小10.8%~12.6%。
但传质面积A增加18.3%,其增加的程度大于传质系数k减小的程度。由图 9知,在F=0.9~2.7 m·s-1·(kg·m-3)0.5范围内,kA增加3.1%~5.5%,即总传质效率增加3.1%~5.5%。
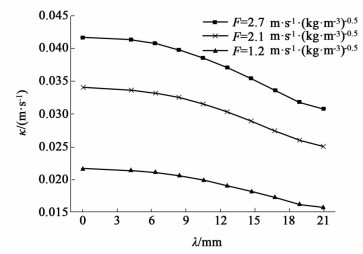
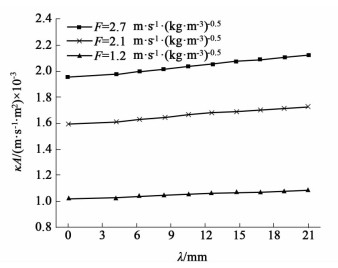
3.3.2 隔板边长的影响如图 10和图 11所示为F=1.2、2.1、2.7 m·s-1·(kg·m-3)0.5时Mon-JKB-250Y的k与隔板边长的关系及kA值与隔板边长的关系。
|
| 图 10 k与隔板边长的关系 Figure 10 Relationship between kand length of baffle |
| |
|
| 图 11 kA与隔板边长的关系 Figure 11 Relationship between kA and length of baffle |
| |
由图 10知,随着隔板边长的增加,气相碰撞产生的涡流减少,使得强化传质的能力减弱,进而传质系数k减小。F=2.7、2.1、1.2 m·s-1·(kg·m-3)0.5时传质系数k最多可分别减少26.1%、26.4%、27.6%。当λ=16.8 mm时,传质系数k分别减少10.9%、10.8%、12.0%。
但是,随着隔板边长的增加,传质面积A增加。λ=21.0 mm时,传质面积A增加46.76%;λ=16.8 mm时,传质面积A增加32.5%。其增加程度大于传质系数k的减小程度。故总传质效率随隔板边长的增加而增大。由图 11知,F=2.7、2.1、1.2 m·s-1·(kg·m-3)0.5时总传质效率最大可分别提高8.2%、8.1%、5.9%。当λ=16.8 mm时,总传质效率已分别提高约7%、6.9%、5.2%,其提高总传质效率的效果已达到加入整片隔板(λ=21 mm)的85%以上。
3.4 单位压降下的传质系数 3.4.1 F因子的影响如图 12所示为JKB-250Y,Mon-JKB-250Y (λ=12.6 mm)的单位压降下的传质系数(k/Δp)与F因子的关系。

|
| 图 12 单位压降下的传质系数与F因子的关系 Figure 12 Relationship between mass transfer coefficient at per pressure drop and F factor |
| |
由图 12知,因为传质系数k与F因子呈正比关系,压降Δp与F因子呈指数关系,所以随着F因子的变大,Δp的增加程度比k的增加程度大,故单位压降下的传质系数减小。
较JKB-250Y而言,Mon-JKB-250Y(λ=12.6 mm)传质系数k虽然有所减小,但压降Δp减小的程度更大,故在F=0.9~2.7 m·s-1·(kg·m-3)0.5范围内,单位压降下的传质系数提高了约29%~38%。
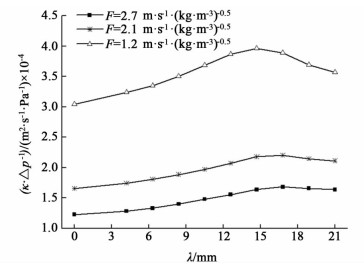
3.4.2 隔板边长的影响图 13所示为JKB-250Y、Mon-JKB-250Y单位压降下传质系数(k/Δp)与隔板边长的关系。图 14为Mon-JKB-250单位压降下的传质系数提高率与隔板边长的关系。
|
| 图 13 单位压降下的传质系数与隔板边长的关系 Figure 13 Relationship between mass transfer coefficient at per pressure drop and length of baffle |
| |

|
| 图 14 单位压降下的传质系数提高率与隔板边长的关系 Figure 14 Relationship between improvement of mass transfer coefficient at per pressure drop and length of baffle |
| |
图 13得到了在F=1.2、2.1和2.7 m·s-1·(kg·m-3)0.5时单位压降下传质系数(k/Δp)随隔板边长的变化曲线。由于传质系数k和压降Δp均随隔板边长的增加而减小,由图 13知两者的比值出现了极值,即存在一个最适宜隔板边长,使得k/Δp的值最大。最适宜隔板边长随着F的增加而增加,即流体流速越大,隔开上下2股流体需要的隔板越大。在F=1.2~2.7 m·s-1·(kg·m-3)0.5范围内,最适宜隔板边长为14.7~16.8 mm。
由图 14知,F=1.2、2.1、2.7 m·s-1·(kg·m-3)0.5时,单位压降下的传质系数最高可分别提高约30%、33%和37%。
3.5 标定曲线当F=1.5 m·s-1·(kg·m-3)0.5、T=300 K、P=101.325 kPa时,标定实验得到的N与R的关系如式(9)所示:
| $ N = B\exp \left( { - R/C} \right) + D $ | (9) |
式(9)中:B=5.48;C=119.20;D=-0.75。
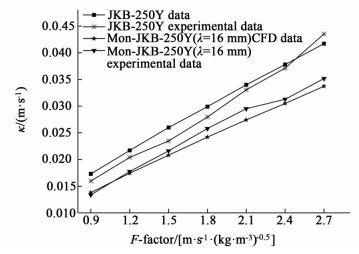
3.6 CFD模拟结果验证如图 15所示为JKB-250Y和Mon-JKB-250Y(λ=16 mm)k值的CFD模拟数据和实验数据比较图。
|
| 图 15 k的CFD模拟数据与实验数据的比较 Figure 15 Comparison of k between CFD data and experimental data |
| |
分别对JKB-250Y和Mon-JKB-250Y(λ=16 mm)采用显色化学反应可视化技术进行分析,比较实验数据与CFD模拟数据。由图 15可知,CFD模拟结果与实验结果平均相对误差小于10%,故模拟结果可靠。
4 结语通过CFD对JKB-250Y规整填料内流体的流动和传质特性的模拟,并佐以显色化学反应可视化实验研究验证,探讨了F因子和规整填料内置隔板边长对压降及传质的影响,得出以下主要结论:
1) 随着F的增加,压降增加、总传质效率增加、单位压降下的传质系数减小。
2) 增大内置隔板边长,压降减小、总传质效率增加、单位压降下的传质系数先增加后减小。在F=1.2~2.7 m·s-1·(kg·m-3)0.5范围内,隔板边长为14.7~16.8 mm的Mon-JKB-250Y是最适宜方案。
3) 优化方法可以减小压降、提高传质性能,该方法对规整填料的优化具有一定的参考价值,且具有一定的实际运用价值,但对于不同型号的规整填料,最适宜内置隔板边长还需要做进一步的研究。
| [1] | Li Q, Wang T, Dai C, et al. Hydrodynamics of novel structured packings:An experimental and multi-scale CFD study[J]. Chemical Engineering Science, 2016, 143: 23–35. DOI: 10.1016/j.ces.2015.12.014 |
| [2] | Shilkin A, Heinen K, Grobmann C, et al. On the development of an energy efficient packing for vacuum distillation[C]. In Proceedings of the International Conference Distillation and Absorption 2010, Eindhoven, 2010: 653-658 |
| [3] | Lautenschleger A, Olenberg A, Kenig E Y. A systematic CFD-based method to investigate and optimize novel structured packings[J]. Chemical Engineering Science, 2015, 122(1): 452–464. |
| [4] |
林秀锋, 陈桂珍. 高通量填料在空分精馏中的开发[J].
深冷技术, 2014, 1: 1–4.
Lin Xiufeng, Chen Guizhen. Development and application of high-flux packings in air separation rectification[J]. Cryogenic Technology, 2014, 1: 1–4. |
| [5] | Hosseini S H, Shojaee S, Ahmadi G, et al. Computational fluid dynamics studies of dry and wet pressure drops in structured packings[J]. Journal of Industrial and Engineering Chemistry, 2012, 18(4): 1465–1473. DOI: 10.1016/j.jiec.2012.02.012 |
| [6] | Larachi F, Petre C F, Iliuta I, et al. Tailoring the pressure drop of structured packings through CFD simulations[J]. Chemical Engineering and Processing, 2003, 42(7): 535–541. DOI: 10.1016/S0255-2701(02)00073-9 |
| [7] | Petre C F, Larachi F, Iliuta I, et al. Pressure drop through structured packings:Breakdown into the contributing mechanisms by CFD modeling[J]. Chemical Engineering Science, 2003, 58(1): 163–177. DOI: 10.1016/S0009-2509(02)00473-6 |
| [8] | Tan L, Shariff A M, Tay W H, et al. Integrated mathematical modeling for prediction of rich CO2 absorption in structured packed column at elevated pressure conditions[J]. Journal of Natural Gas Science and Engineering, 2016, 28: 737–745. DOI: 10.1016/j.jngse.2015.11.004 |
| [9] | 王韬. 新型大通量填料的流体力学和传质性能研究及其CFD模拟[D]. 北京: 北京化工大学, 2015 |
| [10] | Sogin H. Sublimation from disks to air streams flowing normal to their surfaces[J]. Trans ASME, 1958, 80(1): 61–69. |
| [11] | Gaiser G, Kottke V. Flow phenomena and local heat and mass transfer incorrugated passages[J]. Chemical Engineering & Technology, 1989, 12(1): 400–405. |
| [12] | Icardi M, Gavi E, Marchisio D L, et al. Investigation of the flow field in a three-dimensional confined impinging jets reactor by means of microPIV and DNS[J]. Chemical Engineering Journal, 2011, 166(1): 294–305. DOI: 10.1016/j.cej.2010.09.046 |
| [13] |
邵婷, 胡银玉, 王文坦, 等. 气液传质和反应可视化的激光诱导荧光技术[J].
化工学报, 2011, 62(9): 2022–2026.
Shao Ting, Hu Yinyu, Wang Wentan, et al. Visualization of gas-liquid mass transfer and reaction using laser induced fluorescence technique[J]. Journal of Chemical Industry and Engineering, 2011, 62(9): 2022–2026. |
| [14] | Charogiannis A, An J S, Markides C N. A simultaneous planar laser-induced fluorescence, particle image velocimetry and particle tracking velocimetry technique for the investigation of thin liquid-film flows[J]. Experimental Thermal and Fluid Science, 2015, 68: 516–536. DOI: 10.1016/j.expthermflusci.2015.06.008 |
| [15] | Hu B, Langsholt M, Liu L, et al. Flow structure and phase distribution in stratified and slug flows measured by X-ray tomography[J]. International Journal of Multiphase Flow, 2014, 67(Suppl): 162–179. |
| [16] | Escudero D R, Heindel T J. Characterizing jetting in an acoustic fluidized bed using X-ray computed tomography[J]. Journal of Fluids Engineering, 2016, 138(4): 041309. |
| [17] | Behrens M, Saraber P, Jansen H, et al. Performance characteristics of a monolith-like structured packing[J]. Chem Biochem Eng Q, 2001, 15(2): 49–57. |
| [18] | Zhang Y, Zhu H, Yin Q. CFD study on the local mass transfer efficiency in the gas phase of structured packing[J]. Chem Eng Technol, 2013, 36(7): 1138–1146. DOI: 10.1002/ceat.201300097 |
 2018, Vol. 35
2018, Vol. 35





