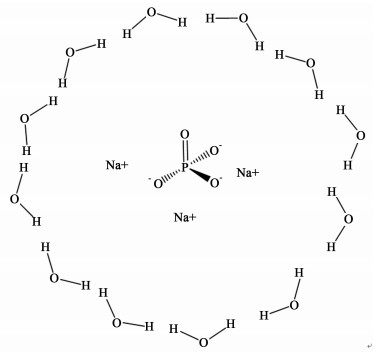
磷酸三钠,为无色至白色结晶或结晶性粉末,主要分为无水物和十二水合物2种,是一种重要的软水剂、洗涤剂和食品改良剂[1]。工业上磷酸三钠十二水合物由磷酸三钠饱和溶液在70~20 ℃冷却结晶得到[2],其分子结构如图 1所示。
|
| 图 1 磷酸三钠十二水合物结构图 Figure 1 The structure of trisodium phosphate dodecahydrate |
| |
水合物,属于假多晶型的一种,是指当化合物从某种溶剂中结晶时,在晶格中化合物分子与溶剂分子结合,同时结晶出来,从而出现的一种新的晶型,或者由原来的无定形转变成某一特定晶型[3]。结晶水能够以不同的方式与晶格内的晶体分子结合,从而导致结晶水合物和其对应的无水物在物理和化学性质上有很大的区别,水合物中由于结晶水分子的存在,影响分子间作用力(内能和焓)和晶体的混乱度(熵),进而影响自由能、溶解度、稳定性和生物利用度等[4-5]。许多文献报道了水合物的脱水过程,例如,Steiner等发现β-环糊精在低湿度下的脱水过程将导致其晶体结构发生不可逆的破坏[6];Morris等发现磷酸铝沸石吸水后结构发生变化,并且在373.15 K时能够脱水再生[7]。在工业储存和热处理过程中,结晶水合物可能发生脱水过程,从而影响产品的质量。因此,研究水合物的脱水过程及脱水机理对于其在工业上的生产和利用具有重要的意义。
标准热分析技术,比如热重TG和差热分析DSC,被广泛用于降解和水合物脱水过程研究,在理论研究和工业生产领域都已逐渐成熟[8]。目前一些新技术,比如X射线衍射XRD、扫描电镜SEM、红外和拉曼也被广泛用于物质晶体结构的转变研究[9-11]。目前,文献中能够对磷酸三钠十二水合物脱水机理的报道较少,Ghule等[12]只是对磷酸三钠十二水合物脱水过程水合物存在形式进行分析,并未推测脱水机理以及水合物在晶格中的存在形式。本研究采用TG多重升温速率法和DSC对其脱水机理进行研究,分别运用Ozawa方程和Friedman方程计算其脱水活化能,推测其脱水机理,并通过PXRD和SEM对其脱水过程结构变化进行分析。
1 实验部分 1.1 实验试剂与仪器实验试剂:磷酸三钠十二水合物,分析纯,质量分数大于98%,天津市三江科技有限公司。
实验仪器:热重分析仪,SDT2960型,美国TA公司;差示扫描量热仪,1/500型,瑞士Mettler Toledo;粉末X射线衍射,D/MAX2500型,日本理学;扫描电镜,TM3000,日本日立公司。
1.2 实验部分 1.2.1 TG测定采用美国TA公司的SDT2960型热重分析仪,进口NEYZSCH铝坩埚,将5~10 mg样品晶体放入铝坩埚中,控制氮气流速为25 mL·min-1,测定温度范围为室温至393.15 K,升温速率分别设定为2.5、5.0、7.5和10.0 K·min-1。
1.2.2 DSC测定采用Mettler Toledo DSC 1/500型差示扫描量热仪,进口NETZSCH铝坩埚,将3~5 mg样品晶体放入铝坩埚中,控制氮气流速为25 mL·min-1,测定温度范围为室温至403.15 K,升温速率设定为10.0 K·min-1。
1.2.3 PXRD测定采用日本理学D/MAX2500型粉末X射线衍射仪分别对298.15、348.15和383.15 K脱水产物进行分析,扫描速率为1 step/s,范围2°~50°。
1.2.4 SEM测定采用Hitachi TM3000型扫描电镜分别对298.15、348.15和383.15 K脱水产物进行分析。
2 结果与讨论 2.1 磷酸三钠十二水合物TG/DSC表征图 2是十二水合磷酸三钠在303.15~413.15 K温度范围内升温速率为10.0 K·min-1时升温过程的TG/DSC曲线。

|
| 图 2 磷酸三钠十二水合物的热重/差热分析图 Figure 2 TG/DSC curves of trisodium phosphate dodecahydrate |
| |
由TG曲线可知,在温度高于303.15 K时,十二水合磷酸三钠开始逐渐失水,当温度升高到393 K时,其质量减少了大约52.14%,该值近似于磷酸三钠十二水合物分子(物质的量浓度为380.14 g·mol-1)脱去11 mol水分子(理论值为52.09%)。
2.2 磷酸三钠十二水合物脱水过程分析根据图 2所示,由DSC曲线可以看出,在303.15~413.15 K温度范围内出现了4个尖锐的吸热峰,第1次脱水吸热量为49.63 J·g-1,脱水的起始温度和峰值温度分别为340.51和347.20 K;第2次脱水吸热量为34.55 J·g-1,脱水的起始温度和峰值温度分别为354.27和358.97 K;第3次脱水吸热量为72.33 J·g-1,脱水的起始温度和峰值温度分别为363.96和369.54 K;第4次脱水吸热量为244.27 J·g-1,脱水的起始温度和峰值温度分别为380.88和385.73 K。
从图 2可以看出在303.15~413.15 K温度范围内,十二水合磷酸三钠逐渐脱去约11个结晶水,且整个脱水过程分为多步反应进行。由Ozawa方程和Friedman方程研究其详细脱水机理。
2.3 磷酸三钠十二水合物脱水机理分析 2.3.1 Ozawa方程结晶水合物的脱水过程可以视为是水合物发生分解反应的化学反应过程,其脱水机理可以用化合物降解分析方法进行研究。脱水反应可以用Arrhenius方程表示。
| $ r = \frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = A\exp \left( {\frac{{ - E}}{{RT}}} \right){\rm{f}}\left( \alpha \right) $ | (1) |
式(1)中:r是脱水速率,α是反应程度,t是反应时间,A是指前因子,E是反应活化能,R是普遍化气体常数,T是温度,f(α)是反应模型。
在脱水过程中,α是百分转化率,也称脱水率。
| $ \alpha = \frac{{{m_i} - {m_\alpha }}}{{{m_i} - {m_{\rm{f}}}}} $ | (2) |
式(2)中:mi和mf分别是样品初始和终止的质量,mα是样品在t时的质量。
假设一个脱水反应是一个简单的n次反应,这个反应模型f(α)可以表示为:
| $ {\rm{f}}\left( \alpha \right) = {\left( {1 - \alpha } \right)^n} $ | (3) |
一般情况下,样品在热重分析设备中以恒定的加热速率β升温。
| $ \beta = \frac{{{\rm{d}}T}}{{{\rm{d}}t}} $ | (4) |
因此,对Arrhenius方程积分可得:
| $ {\rm{g}}\left( \alpha \right) = \int\limits_0^\alpha {\frac{{{\rm{d}}\alpha }}{{{\rm{f}}\left( \alpha \right)}}} = \frac{A}{\beta }\int\limits_0^{T\alpha } {\exp \frac{{ - E}}{{RT}}} {\rm{d}}T $ | (5) |
这个方程没有分析解,通过Doyle's近似,可得到Ozawa方程:
| $ \ln \left( {{\beta _i}} \right) = \ln \left[ {\frac{{A{E_\alpha }}}{{R{\rm{g}}\left( \alpha \right)}}} \right] - 5.3305 - \frac{{1.0516{E_\alpha }}}{{R{T_{\alpha , i}}}} $ | (6) |
其中βi指不同的加热速率。通过方程(6)可以利用不同升温程序下失量情况来计算脱水过程的活化能。如果脱水机理与升温程序无关,g(α)值便与α值无关。因此,式(6)可以简化为:
| $ \ln {\beta _i} = {\rm{Const}} - \frac{{1.0516{E_\alpha }}}{{R{T_{\alpha , i}}}} $ | (7) |
活化能Eα便可通过式(7)由相同脱水反应转化率α下的lnβ和1/RT构成的直线斜率计算而得[13-14]。通过Ozawa方程计算得到物质脱水过程活化能Eα和转化率α的关系后,便可以分析物质脱水过程的脱水反应序列,即脱水机理。
磷酸三钠十二水合物在升温速率分别为2.5、5.0、7.5和10.0 K·min-1时的TG曲线如图 3所示。

|
| 图 3 磷酸三钠十二水合物在不同升温速率下的热重曲线 Figure 3 TG curves of trisodium phosphate dodecahydrate at different heating rates |
| |
从图 3中可以看出,在不同的升温速率下,其脱水速率不同,升温速率越快,热重曲线越平缓。
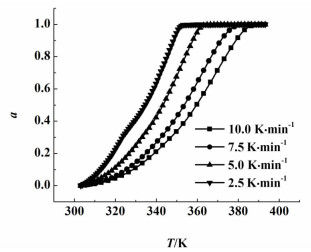
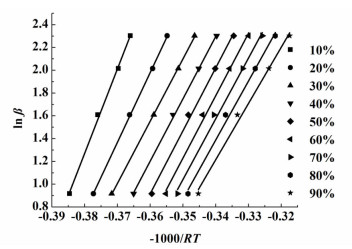
通过TG数据及式(2)可以得到在不同的升温速率下脱水率与温度的关系,脱水率与温度的关系如图 4所示,根据式(7)Ozawa方程便可得到不同脱水率下的活化能。图 5是磷酸三钠十二水合物在脱水率分别为10%、20%、30%、40%、50%、60%、70%、80%和90%下由lnβ对-1000/RT所拟合的直线。从表 1可以看出拟合效果较好,R2均大于0.99。
|
| 图 4 磷酸三钠十二水合物在不同升温速率下脱水率与温度的关系图 Figure 4 The relationship of α-T at different heating rate for trisodium phosphate dodecahydrate |
| |
|
| 图 5 磷酸三钠十二水合物在不同脱水率时的Ozawa直线 Figure 5 Ozawa plot for the dehydration of trisodium phosphate dodecahydrate at different dehydration rate |
| |
| Friedman方程 | Ozawa方程 | |||||
| α | Eα/(kJ·mol-1) | R2 | α | Eα/(kJ·mol-1) | R2 | |
| 0.1 | 70.4974 | 0.9968 | 0.1 | 64.1731 | 0.9916 | |
| 0.2 | 58.2039 | 0.9994 | 0.2 | 47.5453 | 0.9978 | |
| 0.3 | 51.9534 | 0.9997 | 0.3 | 51.6683 | 0.9934 | |
| 0.4 | 51.9982 | 0.9989 | 0.4 | 55.9634 | 0.9884 | |
| 0.5 | 52.5152 | 0.9950 | 0.5 | 57.7400 | 0.9589 | |
| 0.6 | 52.0672 | 0.9942 | 0.6 | 54.6224 | 0.9889 | |
| 0.7 | 50.6637 | 0.9913 | 0.7 | 40.7165 | 0.9397 | |
| 0.8 | 49.1948 | 0.9914 | 0.8 | 34.8863 | 0.9817 | |
| 0.9 | 46.9361 | 0.9908 | 0.9 | 29.3977 | 0.9633 | |
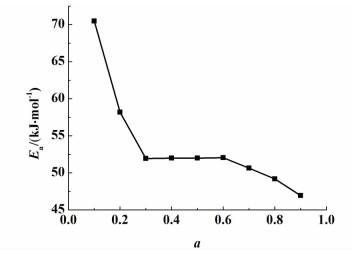
由Ozawa方程计算得到的脱水活化能与脱水率关系曲线如图 6所示。
|
| 图 6 磷酸三钠十二水合物活化能与脱水率关系图 Figure 6 The relationship of Eα-α for trisodium phosphate dodecahydrate |
| |
由图 6可以看出在脱水率0.1 < α < 0.3时,活化能值由70.4974 kJ·mol-1降到51.9534 kJ·mol-1,然后在脱水率0.3 < α < 0.6,活化能值分别为51.9534、51.9982和52.5152 kJ·mol-1,基本保持不变,最后在脱水率0.6 < α < 0.9时,活化能值由52.0672 kJ·mol-1降46.9361 kJ·mol-1,下降速率较慢。
从文献[15]可知,如果脱水过程是一级反应,则活化能值应不随脱水率的变化而变化。如果活化能值随脱水率变化而变化,则脱水反应可能有两种情况:一种是活化能值随脱水率提高而降低,这种脱水机理是1个连续的多步反应,该多步反应可能是由1个不可逆反应与可逆反应构成,或是脱水机理由连续的多步反应转变为物理扩散控制的反应;另一种是活化能值随脱水率的提高而提高,这种脱水机理是1个多步竞争关系的反应。
因此,磷酸三钠十二水合物的脱水机理可以从图 6活化能与脱水率的关系得出。在脱水率0.1 < α < 0.3时,对应于图 2中DSC曲线的第1个吸热峰,活化能随着脱水率的升高而降低且下降速率较快,可以得出是1个连续的两步反应过程,首先是1个不可逆反应过程,随后是可逆反应过程;在脱水率0.3 < α < 0.6时对应于图 2中DSC曲线的第2个吸热峰,活化能值基本上不随脱水率的变化而变化,可以得出该过程是1个一级反应过程;最后在脱水率0.6 < α < 0.9时,对应于图 2中DSC曲线的第3和第4个吸热峰,活化能随着脱水率的升高而降低且下降速率较慢,可以推测该过程是连续的多步反应,且其反应过程由最初的动力学控制转变为随后的扩散控制,即水分子从晶格中的脱离和扩散过程。
2.3.2 Friedman方程Friedman方程[16-18]和Ozawa方程类似,其基本原理都是采用对不同升温速率下所得的多条TG曲线进行动力学分析的方法,在不涉及动力学模式的前提下获得较为可靠的活化能值。式(8)即为Friedman方程。
| $ \ln {\left( {\beta \frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}}} \right)_\alpha } = \ln {\left[ {A{\rm{f}}\left( \alpha \right)} \right]_\alpha } - \frac{{{E_\alpha }}}{{R{T_\alpha }}} $ | (8) |
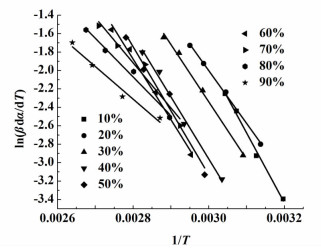
图 4为脱水率α和温度的关系曲线,从曲线的斜率可以得到dα/dT的值,从而以ln(βdα/dT)为纵坐标,1/T为横坐标作图,如图 7所示,由拟合直线斜率即可得活化能值,列于表 1中。
|
| 图 7 不同脱水率时ln(βdα/dT)对1/T的线性回归 Figure 7 The regression line of ln(βdα/dT)- 1/T at different dehydration rate |
| |
从表 1中可以看出R2均大于0.9397,说明线性拟合效果较好,其活化能大小变化规律也基本与Ozawa方程一致,说明前面推测的脱水机理准确,两者计算活化能值均较小,这也解释了磷酸三钠十二水合物工业储存时易风化的原因。但是和Ozawa方程相比数据出现了稍许的偏差,这是因为Friedman方程引进了脱水速率dα/dT,由误差传递导致,同时对仪器稳定性要求较高,微小的波动就将引起误差。因此,Ozawa和Friedman方程均能根据活化能与脱水率关系推测脱水机理。但是,Ozawa方程在实用性和准确性方面要优于Friedman方程。
2.4 磷酸三钠十二水合物脱水产物结构表征 2.4.1 磷酸三钠十二水合物脱水产物PXRD表征磷酸三钠十二水合物在脱水过程中的晶体结构变化可以通过PXRD图来表征。
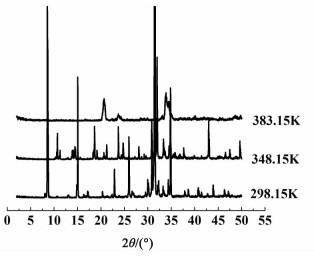
图 8分别为其在293.15、348.15和383.15 K时脱水产物的PXRD图。
|
| 图 8 磷酸三钠十二水合物在不同温度脱水产物的X射线衍射图 Figure 8 The PXRD profiles of trisodium phosphate dodecahydrate and its dehydration product at different temperature |
| |
图 8中可以看出,在脱水过程中,晶体结构发生了变化,即原有的晶格结构被破坏,原子进行重新组合形成了新的晶体结构。
2.4.2 磷酸三钠十二水合物脱水产物SEM表征磷酸三钠十二水合物在脱水过程中的变化可以通过扫描电镜观察,如图 9a)、图 9b)和图 9c)分别为其在298.15、348.15和383.15 K时脱水产物的SEM图。

|
| 图 9 磷酸三钠十二水合物在不同温度脱水产物扫描电镜图 Figure 9 The scanning electron micrographs of trisodium phosphate dodecahydrate and its dehydration product at different temperature |
| |
由图 9可以看出,晶体表面和结构都发生了变化,脱水前表面光滑,结构完整,随着脱水过程的进行,表面逐渐变粗糙,出现了较多的孔洞,这是由脱离晶格中的水分子扩散形成的。随着脱水过程的进一步进行,针状结晶逐渐过渡为结晶性粉末。
结合Ozawa方程和Friedman方程计算的活化能值可以推测,结晶水与钠离子以配位键结合存在于磷酸根离子形成的晶格通道内,属于通道型包容水合物,且位阻较小,容易失去结晶水,随着结晶水的失去,原有的晶格结构被破坏,形成了不同的晶格结构,其宏观形貌发生了变化。
3 结论1) 通过TG、DSC研究了磷酸三钠十二水合物在303.15~413.15 K温度范围内的脱水过程。研究发现其在303.15 K时开始逐渐失去结晶水,在温度达到393.15 K左右时,失去11个结晶水。分别通过Ozawa方程和Friedman方程计算其在脱水过程中的活化能值,在脱水率0.1 < α < 0.3时,活化能随着脱水率的升高而降低且下降速率较快,是一个连续的两步反应过程;在脱水率0.3 < α < 0.6时,活化能值基本上不随脱水率变化而变化,是一个一级反应过程;在脱水率0.6 < α < 0.9时,其反应过程由最初的动力学控制转变为随后的扩散控制,即水分子从晶格中脱离和扩散过程。
2) 由活化能值和不同温度脱水产物的PXRD和SEM图得出结晶水与钠离子以配位键结合存在于磷酸根离子形成的晶格通道内,属于通道型包容水合物,且位阻较小,随着结晶水的失去,原有的晶格结构被破坏,形成了不同的晶格结构,其宏观形貌也发生了变化。
| [1] | 张受谦. 化工手册[M]. 山东科学技术出版社, 1986 |
| [2] |
王颖莉. 高质量磷酸三钠生产工艺控制要点[J].
无机盐工业, 2000, 32(4): 37–38.
Wang Yingli. Controlling points for process technology of high quality trisodium phosphate[J]. Inorganic Chemical Industry, 2000, 32(4): 37–38. |
| [3] | Seddon K R. Pseudopolymorph:A Polemic[J]. Crystal Growth & Design, 2004, 4(6): 1087–1087. |
| [4] | Khankari R K, Grant D J W. Pharmaceutical hydrates[J]. Thermochimica Acta, 1995, 248(1): 61–79. |
| [5] | Han J, Suryanarayanan R. Applications of pressure differential scanning calorimetry in the study of pharmaceutical hydrates. Ⅰ. Carbamazepine dihydrate[J]. Arkivoc Online Journal of Organic Chemistry, 2012, 10(38): 80–99. |
| [6] | Steiner T, Koellner G. Crystalline beta-cyclodextrin hydrate at various humidities:Fast, continuous, and reversible dehydration studied by X-ray diffraction[J]. Journal of the American Chemical Society, 1994, 116(12): 5122–5128. DOI: 10.1021/ja00091a014 |
| [7] | Morris R E, Burton A, Bull L M, et al. SSZ-51-A new aluminophosphate zeotype:Synthesis, crystal structure, NMR, and dehydration properties[J]. Cheminform, 2004, 35(40): 7–9. |
| [8] | Santos A V D, Matos J R. Dehydration studies of rare earth p-toluenesulfonate hydrates by TG/DTG and DSC[J]. Journal of Alloys & Compounds, 2002, 344(s1/2): 195–198. |
| [9] | Duan Y, Li J, Yang X, et al. Kinetic analysis on the non-isothermal dehydration by integral master-plots method and TG-FTIR study of zinc acetate dihydrate[J]. Journal of Analytical & Applied Pyrolysis, 2008, 83(1): 1–6. |
| [10] | Lee S B, Fasina O. TG-FTIR analysis of switchgrass pyrolysis[J]. Journal of Analytical & Applied Pyrolysis, 2009, 86(1): 39–43. |
| [11] | Yonemochi E, Hoshino T, Yoshihashi Y, et al. Evaluation of the physical stability and local crystallization of amorphous terfenadine using XRD-DSC and micro-TA[J]. Thermochimica Acta, 2005, 432(1): 70–75. DOI: 10.1016/j.tca.2005.02.023 |
| [12] | Ghule A, Murugan R, Chang H. Thermo-Raman studies on dehydration of Na3PO4·12H2O[J]. Thermochimica Acta, 2001, 371(1/2): 127–135. |
| [13] | Ekeren P J V. Handbook of thermal analysis and calorimetry[J]. Thermochimica Acta, 2003, 407(1): 121–123. |
| [14] | Ozawa T. A new method of analyzing thermogravimetric data[J]. Bulletin of the Chemical Society of Japan, 1965, 38(11): 1881–1886. DOI: 10.1246/bcsj.38.1881 |
| [15] | Vyazovkin S. A unified approach to kinetic processing of nonisothermal data[J]. International Journal of Chemical Kinetics, 1996, 28(2): 95–101. DOI: 10.1002/(ISSN)1097-4601 |
| [16] | Friedman H L. Kinetics of thermal degradation of cha-forming plastics from thermogravimetry, application to a phenolic plastic[J]. Journal of Polymer Science Part C Polymer Symposia, 2007, 6(1): 183–195. DOI: 10.1002/polc.5070060121 |
| [17] | Ozawa T. Applicability of Friedman plot[J]. Journal of Thermal Analysis, 1986, 31(3): 547–551. DOI: 10.1007/BF01914230 |
| [18] | Friedman H L. Kinetics and gaseous products of thermal decomposition of polymers[J]. Journal of Macromolecular Science:Part A-Chemistry, 1967, 1(1): 57–79. DOI: 10.1080/10601326708053917 |
 2018, Vol. 35
2018, Vol. 35





