2. 武汉科技大学湖北省煤转化与新型炭材料重点实验室, 武汉 430081
2. Key Laboratory of Coal Conversion and New Carbon Materials for Hubei Province, Wuhan 430081, China
赤藓糖醇(meso-Erythritol)是一种新型的多元醇类功能甜味剂和天然糖质,广泛应用于开发低热量保健食品、糖尿病及葡萄糖不适症等人群的功能食品或饮料、儿童专用洁齿用品等,市场前景十分看好[1]。赤藓糖醇工业生产主要采用发酵法,发酵液经净化处理后再结晶制得赤藓糖醇晶体。目前,国产赤藓糖醇生产规模已居世界前列,产能已突破1万t/a,但产品质量较国外产品还存在一定差距,尤其是在晶形、粒度分布、色级等方面[2]。
作为赤藓糖醇工业生产过程的最后一步精制单元操作,结晶是控制其产品质量的关键步骤。赤藓糖醇的溶解度及其固液相平衡模型是研究其工业结晶过程的基础,决定其结晶方式的选择、结晶分离设备的结构设计以及工艺优化等。但文献有关赤藓糖醇在水中的溶解度数据尚不充分。本工作采用合成法测定了赤藓糖醇在水中的溶解度,选用修正的Apelblat方程和λh方程建立了其溶解度模型,并采用修正的van’t Hoff方程求取了赤藓糖醇在水中的溶解焓、熵和吉布斯自由能,为赤藓糖醇工业结晶过程新工艺的优化和结晶设备的设计提供了基础数据。
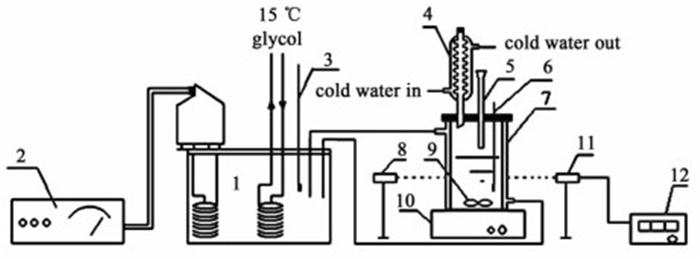
1 实验 1.1 实验装置与试剂合成法测定赤藓糖醇在水中溶解度的实验装置如图 1所示,主要由恒温溶解体系(1~7, 9~10)和激光辅助监测体系(8, 11~12)2部分组成。
|
| 1-超级恒温水浴;2-车需控温仪;3,6-温度计;4-冷凝管;5-加料口;7-结晶器;8-激光发生器;9-磁力搅拌子;10-磁力搅拌器;11-光电转换器;12-光强显示器 图 1 溶解度测定装置示意图 Figure 1 Schematic setup for the solubility determination |
| |
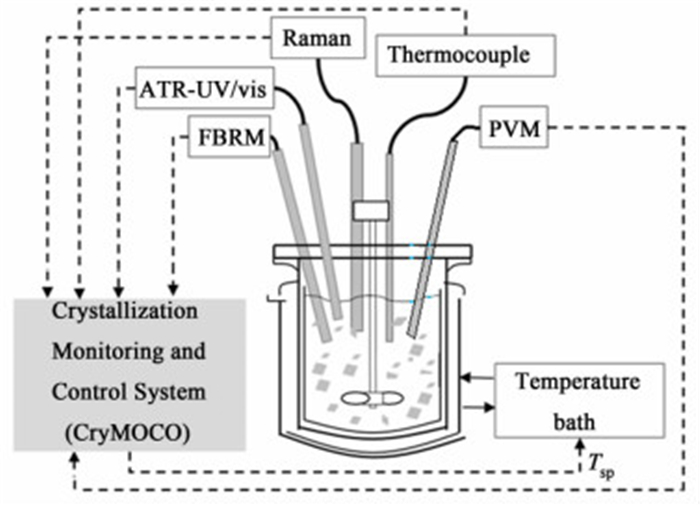
赤藓糖醇在水溶液中的冷却结晶装置如图 2所示。
|
| 图 2 赤藓糖醇结晶过程装置示意图 Figure 2 Schematic setup for meso-Erythiritol crystallization |
| |
实验仪器: AB204-E型电子天平,梅特勒-托利多仪器有限公司;501 A型超级恒温水浴,上海实验仪器有限公司;DW-40型低温浴槽,北京博医康实验仪器公司;CKW-2200型程序控温器,北京朝阳自动化仪表厂;精密温度计(± 0.05 K);NHK250型氦氖激光器,北京大学物理系工厂;JG2型激光能量指示仪,北京大学物理系工厂;SWP-NSR302-1型数字无纸记录仪,福州昌晖自动化系统有限公司;D-MS-I型磁力搅拌器,金坛正基。
实验原料与试剂:赤藓糖醇由山东中舜科技发展有限公司提供,实验室采用重结晶精制得到赤藓糖醇晶体,产品质量分数不低于99.5%;去离子水(实验室自制)。
1.2 实验方法与步骤合成法(Synthetic method)[3]测定固体在液相中溶解度的核心思想是通过缓慢改变体系的温度或液相溶剂的组成,使均相液体溶剂中析出溶质晶体或使液相中悬浮的过量固体溶质粒子消失来判断溶解平衡是否达到。合成法因其方便迅捷、精度高、样品用量少、不用离线取样分析等优点,目前已成为药物、精细化学品等固液相平衡研究中溶解度测定的重要方法[3-6]。
合成法测定赤藓糖醇在水中溶解度的实验具体步骤如下:1)将赤藓糖醇晶体研磨、筛分,收集125~150 μm的粉晶作为溶解度测定的溶质组分;2)按图 1安装好实验装置,开启超级恒温水浴将体系温度稳定在预设值;3)将一定量的溶剂(稍过量)和溶质分别准确称重后加入结晶器中,开启磁力搅拌使溶质充分溶解;4)待体系温度恒定在预设温度30 min后,打开激光辅助监测系统,激光束从结晶器的一侧进入,穿过结晶器内的液体层后,从另一侧透射出来,并由光电转换器接收、转换成电信号后由数显光强显示器输出。由于结晶器内的溶剂略过量,固体溶质完全溶解,光强达到最大值Imax;5)精确称量少量固体溶质加入结晶器内,因搅拌而悬浮在液体中的固体颗粒使穿过液体层的激光大部分甚至全部被反射和遮蔽,导致光强显示仪读数迅速降低,但随着悬浮固体粒子的逐渐溶解,光强又开始缓慢升高,当达到最大值Imax时重复步骤5)的加料过程,直至光强读数稳定30 min不变且未能达到最大值Imax,记录此时物系的准确温度和加入的溶质总量;6)每组实验重复3次,取算数平均值记为该实验温度下的溶解度。
1.3 赤藓糖醇连续震荡结晶过程如图 2所示,将226 g赤藓糖醇加入到250 g水中,搅拌转速350 r/min,先升温至50 ℃,恒温搅拌5 min,再降温至40 ℃,恒温搅拌20 min,最后以-0.1 ℃/min的恒定降温速率降温至25 ℃,恒温搅拌30 min,排出晶浆进行过滤、洗涤、干燥,制得赤藓糖醇晶体产品。
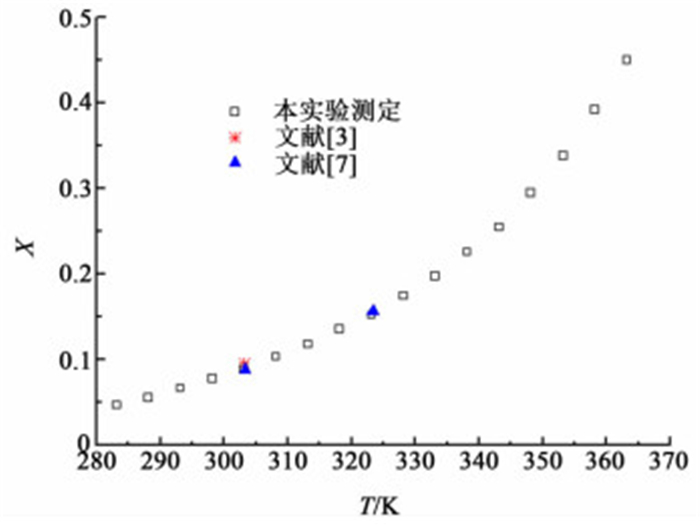
2 结果与讨论 2.1 赤藓糖醇在水中的溶解度实验测定了常压下、283.15~363.15 K温度范围内,赤藓糖醇在水中的溶解度,结果如图 3所示,随着温度地升高,赤藓糖醇在水中的溶解度逐渐增加。本实验测定的赤藓糖醇溶解度与文献值[3, 7]进行了对照,如图 1所示。结果表明本文采用合成法测定的赤藓糖醇溶解度与文献值一致。
|
| 图 3 赤藓糖醇在水中的溶解度 Figure 3 Solubility of meso-Erythritol in water |
| |
关联固体在液体中饱和溶解度的基本方程[8]可表示为:
| $\ln {x_{\rm{1}}}{\gamma _1} = - \left\{ {\frac{{\mathit{\Delta }{H^{{\rm{fus}}}}\left( {{T_{\rm{m}}}} \right)}}{{RT}}\left( {1 - \frac{T}{{{T_{\rm{m}}}}}} \right) + \frac{{\Delta {C_p}}}{R}\left[ {1 - \frac{T}{{{T_{\rm{m}}}}} + \ln \left( {\frac{T}{{{T_{\rm{m}}}}}} \right)} \right]} \right\} $ | (1) |
式(1)中,x1、γ1分别是固体溶质组分1在溶液中的饱和溶解度、活度系数;ΔHfus(Tm)是固体组分1在其熔点融化时的摩尔热焓,Tm是固体组分1的熔点温度;R是气体常数,T是绝对温度;ΔCP=CPL-CPS,CP是组分1的定压热容。
一般而言,固体溶于液体溶剂中形成理想溶液的假定是不合理的。因此,式(1)中的活度系数γ1须从实验数据或溶液模型求解。随着热力学在理论和实践上的不断发展,现已提出了很多半理论半经验的方程来关联非理想溶液中固体溶质组分的活度系数γ和x,其中修正Apelblat方程和λh方程因其关联精度高、适用性广,已成为目前工业结晶过程中最常用的固液相平衡模型[3-6]。
修正Apelblat方程[9]可表示为:
| $\ln \left( {{x_1}} \right) = a + \frac{{\rm{b}}}{T} + c\ln \left( T \right) $ | (2) |
式(2)中,a、b和c是模型参数。
λh方程[10]可表示为:
| $\ln \left[ {1 + \frac{{\mathit{\lambda }\left( {1 - {x_1}} \right)}}{{{x_1}}}} \right] = \mathit{\lambda h}\left( {\frac{1}{T} - \frac{1}{{{T_{\rm{m}}}}}} \right) $ | (3) |
式(3)中,λ和h是模型参数,Tm是熔点。
赤藓糖醇在水中的溶解度实验测定值xexp与模型计算值xcal、模型参数、相对偏差RD和均方根偏差RMSD分别列于表 1~表 3中。表中相对偏差RD定义为:
| T/K | x | RD | T /K | x | RD | ||
| Eq.(2) | Eq.(3) | Eq.(2) | Eq.(3) | ||||
| 283.15 | 0.04707 | -0.02844 | -0.01685 | 323.15 | 0.1521 | -0.00873 | -0.01582 |
| 288.15 | 0.05563 | -0.01197 | -0.00927 | 328.15 | 0.1746 | -0.00694 | -0.01137 |
| 293.15 | 0.06656 | 0.01850 | 0.01494 | 333.15 | 0.1978 | -0.01692 | -0.01852 |
| 298.15 | 0.07769 | 0.02602 | 0.01839 | 338.15 | 0.2259 | -0.01683 | -0.01566 |
| 303.15 | 0.08909 | 0.01807 | 0.00804 | 343.15 | 0.2550 | -0.02718 | -0.02359 |
| 308.15 | 0.1035 | 0.02523 | 0.01444 | 348.15 | 0.2948 | -0.01180 | -0.00657 |
| 313.15 | 0.1182 | 0.01634 | 0.00588 | 353.15 | 0.3387 | -0.00128 | 0.00457 |
| 318.15 | 0.1356 | 0.01381 | 0.00474 | ||||
| a | b | c | RMSD | RAD | |
| 水 | -65.207 | 580.260 | 10.650 | 0.004866 | 0.01766 |
| λ | h/104 | RMSD | RAD | |
| 水 | 0.5530 | 0.4518 | 0.005141 | 0.01462 |
| ${\rm{RD = }}\frac{{{x^{\exp }} - {x^{{\rm{eal}}}}}}{{{x^{{\rm{exp}}}}}} $ | (4) |
均方根偏差RMSD和平均相对偏差RAD分别定义为:
| ${\rm{RMSD = }}{\left[ {\frac{1}{{N - 1}}\sum\limits_{i = 1}^N {{{\left( {x_i^{\exp } - x_i^{{\rm{cal}}}} \right)}^2}} } \right]^{1/2}} $ | (5) |
| ${\rm{RAD = }}\frac{1}{N}\sum\limits_{i = 1}^N {\left| {\frac{{x_i^{\exp } - x_i^{{\rm{eal}}}}}{{x_i^{\exp }}}} \right|} $ | (6) |
式(5)和式(6)中,N为实验点个数。
建立固液相平衡模型的实际目标与工业现实意义在于能对任意温度范围内的溶解度数据进行预测[11]。分别采用修正Apelblat方程和λh方程对赤藓糖醇在水中的溶解度进行计算,模型参数由表 2和表 3得到,其预测计算结果与实验测定溶解度的相对偏差如表 1所示。由表 1可知,采用λh方程预测的赤藓糖醇溶解度相对偏差整体优于修正Apelblat方程,λh方程预测的最大相对偏差为-2.359%,而修正Apelblat方程预测的最大相对偏差为-2.844%。综合比较修正Apelblat方程和λh方程的RD、RMSD和RAD,表明修正Apelblat方程和λh方程对赤藓糖醇在水中溶解度的预测精度足可满足工业应用,λh方程稍优于修正Apelblat方程。
2.3 赤藓糖醇在水中的溶解焓、熵和吉布斯自由能固体溶质在液体溶剂中的溶解焓ΔsolHο(kJ ·mol-1)、熵ΔsolSο (J ·mol-1 ·K-1)和吉布斯自由能ΔsolGο (kJ ·mol-1)是工业结晶过程控制以及结晶设备设计中的重要参数,可通过修正的van’t Hoff方程和Apelblat方程[12]计算如下:
| ${\mathit{\Delta }_{{\rm{sol}}}}{H^{\rm{o}}} = RT\left[ {\frac{{\partial \ln x}}{{\partial \ln T}}} \right] = R\left( { - b + cT} \right) $ | (7) |
| ${\mathit{\Delta }_{{\rm{sol}}}}{S^{\rm{o}}} = RT\left[ {\frac{{\partial \ln x}}{{\partial \ln T}} + \ln x} \right] = R\left[ {a + c\left( {1 + \ln T} \right)} \right] $ | (8) |
| ${\mathit{\Delta }_{{\rm{sol}}}}{G^{\rm{o}}} = {\mathit{\Delta }_{{\rm{sol}}}}{H^{\rm{o}}} - T{\mathit{\Delta }_{{\rm{sol}}}}{\mathit{S}^{\rm{o}}} $ | (9) |
式(7)和式(8)中,R是气体常数,T是绝对温度;a、b和c是式(2)的模型参数,可由实验测定溶解度数据拟合得到。
赤藓糖醇在水中的溶解焓、熵和吉布斯自由能如表 4所示。赤藓糖醇的溶解热为-43 cal/g[7](1 cal=4.18 J),即为21.98 kJ/mol,接近于表 4中20 ℃的溶解焓。
| T/K | ΔsolHο/ (kJ·mol-1) |
ΔsolSο/ (J·mol-1· K-1) |
ΔsolGο/ (kJ· mol-1) |
| 283.15 | 20.247 | 44.673 | 7.598 |
| 288.15 | 20.690 | 46.219 | 7.372 |
| 293.15 | 21.132 | 47.738 | 7.138 |
| 298.15 | 21.575 | 49.231 | 6.897 |
| 303.15 | 22.018 | 50.700 | 6.648 |
| 308.15 | 22.461 | 52.144 | 6.392 |
| 313.15 | 22.903 | 53.565 | 6.129 |
| 318.15 | 23.346 | 54.964 | 5.859 |
| 323.15 | 23.789 | 56.341 | 5.582 |
| 328.15 | 24.231 | 57.696 | 5.298 |
| 333.15 | 24.674 | 59.032 | 5.008 |
| 338.15 | 25.117 | 60.347 | 4.711 |
| 343.15 | 25.560 | 61.643 | 4.407 |
| 348.15 | 26.002 | 62.920 | 4.097 |
| 353.15 | 26.445 | 64.179 | 3.780 |
| 358.15 | 26.888 | 65.420 | 3.457 |
| 363.15 | 27.331 | 66.645 | 3.129 |
赤藓糖醇在水溶液中冷却结晶过程结晶器内的温度、总粒子数以及平均弦长的实时变化趋势如图 4所示:赤藓糖醇加入水溶液后,温度升高至50 ℃并保温搅拌5 min,此时结晶器内的总粒子数与平均弦长迅速降低到接近于0,表明赤藓糖醇几乎完全溶解;当温度由50 ℃降低到40 ℃并保温搅拌20 min,结晶器内的总粒子数与平均弦长几乎不发生变化,仍然趋近于0,表明此阶段降温没有赤藓糖醇结晶析出,该现象也与实验测定的赤藓糖醇结晶热力学数据相符,根据赤藓糖醇溶解度模型(2)可计算出40 ℃时赤藓糖醇在每1 g水中的溶解度为0.9024 g水;当温度从40 ℃以-0.1 ℃/min降低到25 ℃的过程中,当降温至35.86 ℃时结晶器内的总粒子数与平均弦长突然急剧增大,表明赤藓糖醇开始爆发成核,并且温度曲线出现了1个小峰,这是由于赤藓糖醇的溶解热为-179.74 J/g[7],在其爆发成核时会放出大量的热,造成温度曲线出现小峰,而且通过总粒子数突变判定赤藓糖醇的爆发成核温度为35.88 ℃,而温度曲线出现小峰时对应的爆发成核温度是35.86 ℃,二者仅相差0.02 ℃,表明可以通过监控结晶体系温度来测定其结晶诱导期或介稳区宽度;随后的降温过程中,晶体的总粒子数不断增大,而平均弦长趋于稳定,表明赤藓糖醇的冷却结晶过程是成核控制。

|
| 图 4 赤藓糖醇结晶过程粒子数、平均弦长以及温度变化图 Figure 4 Profile of total counts, mean chord length and temperature for meso-erythritol crystallization |
| |
1) 采用合成法测定了赤藓糖醇在水中的溶解度,结果表明赤藓糖醇在水中的溶解度随温度增加而增大。
2) 采用修正Apelblat方程和λh方程对赤藓糖醇在水中的溶解度进行了关联,模型预测精度均可满足工业应用
3) 基于修正的van’t Hoff方程和Apelblat方程计算了赤藓糖醇在水中的溶解焓、熵和吉布斯自由能。
4) 赤藓糖醇在水中的溶解度数据与模型可为其工业结晶过程的工艺优化和结晶设备的设计提供重要的基础数据。
5) 可以通过监控赤藓糖醇冷却结晶体系温度来测定其结晶诱导期或介稳区宽度。
| [1] | Lopes J A J, Nunes S C C, Ramos S M, et al. Erythritol:Crystal growth from the melt[J]. International Journal of Pharmaceutics, 2010(1): 129–135. |
| [2] | 张春桃, 刘帮禹, 姜伟奇, 等. 一种赤藓糖醇的溶析结晶方法: CN, 201210537162. x[P]. 2012-12-10 |
| [3] | Zhang C, Wang J, Wang Y. Solubility of ceftriaxone disodium in acetone, methanol, ethanol, N-N-dimethylformamide, and formamide between 278 and 318 K[J]. J Chem Eng Data, 2005, 50: 1757–1760. DOI: 10.1021/je0501989 |
| [4] | Hao H, Hou B, Wang J, et al. Solubility of erythritol in different solvents[J]. Journal of Chemical & Engineering Data, 2005, 50(4): 1454–1456. |
| [5] | Wang Z, Wang Q, Liu X, et al. Measurement and correlation of solubility of xylitol in binary water+ethanol solvent mixtures between 278.00 K and 323.00 K[J]. Korean Journal of Chemical Engineering, 2013, 30(4931): 936. |
| [6] | Wang N, Fu Q, Yang G. Determination of the solubility, dissolution enthalpy and entropy of icariin in water, ethanol, and methanol[J]. Fluid Phase Equilibria, 2012, 324: 41–43. DOI: 10.1016/j.fluid.2012.03.022 |
| [7] | Mitchell H. Sweeteners and sugar alternatives in food technology[M]. USA: John Wiley & Sons, 2008. |
| [8] | 高光华, 童景山. 化工热力学(第二版)[M]. 北京: 清华大学出版社, 2007 |
| [9] | Manzurola E, Apelblat A. Solubilities of L-glutamic acid, 3-nitrobenzoic acid, p-toluic acid, calcium-L-lactate, calcium gluconate, magnesium-DL-aspartate, and magnesium-L-lactate in water[J]. The Journal of Chemical Thermodynamics, 2002, 34(7): 1127–1136. DOI: 10.1006/jcht.2002.0975 |
| [10] | Buchowski H, Ksiazczak A, Pietrzyk S. Solvent activity along a saturation line and solubility of hydrogen-bonding solids[J]. J Phys Chem, 1980, 84: 975–979. DOI: 10.1021/j100446a008 |
| [11] | Dong Y, Ma P, Xu W. Study on the solubility of maleic anhydride in 1, 2 cyclohexanedicarboxylic acid diisobutyl ester and diethyl ester[J]. J Chem Eng Chin Univ, 2000, 14: 160–163. |
| [12] | Sousa M M V, Almeida J P B, Ferreira A G M, et al. Solubility of HFCs in lower alcohols[J]. Fluid Phase Equilib, 2011, 303: 115–119. DOI: 10.1016/j.fluid.2011.01.003 |
 2018, Vol. 35
2018, Vol. 35





